2. Kristallstrukturen - German Aerospace Center...Kubisch-fl ächenzentriert dichtest gepackt 21...
Transcript of 2. Kristallstrukturen - German Aerospace Center...Kubisch-fl ächenzentriert dichtest gepackt 21...

1
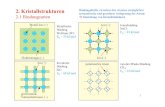
2. Kristallstrukturen2.1 Bindungsarten
polarisiertes AtomIon (+)
gemeinsameValenzelektronen (–)
Ion (+)
Ion (–)
Metall-Ion (+)
Elektronengas (–)
Metallische BindungWolfram (W):EB = 50 kJ/mol
IonenbindungNaCl: EB = 43 kJ/mol
KovalenteBindungSiC:EB = 68 kJ/mol
van-der-Waals-BindungCH4:EB = 0.6 kJ/mol
Bindungskräfte zwischen den Atomen ermöglichen systematische und geordnete Anlagerung der Atome‹ Entstehung von Kristallstrukturen

2
2.2 Metallische Bindung
Überlappung von Energiebändern:· Freie Leitungselektronen· Isotrope Bindungsverhältnisse· Große Vielfalt von Strukturen
Ene
rgie
E
Reziproker Atomabstanda
1s2s
2p3s3p
Mg
Atomabstand
Energie E
N(E
)
Energiezustände im
1. Band
2. Band
Reine metallische Bindung z. B. in Alkali-Metallen durchDelokalisierte Valenz-Elektronen
In 3d Übergangsmetallen zusätzliche Kovalente Bindungsanteile durchÜberlappung gerichteter 3d-Orbitale
· Verstärkung der Bindung Beispiele: W, Fe, Ni, Co....

3
2.3 Kristallstrukturen
Anzahl der Atome in der Basis:
1 in Edelgaskristallen, 2 in Fe, 4 in SiF4, 12 in MoAl12103 in Polymerkristallen, 106 in Viruskristallen
Gittertranslation:T = u a + v b + w cT: Translationsvektora, b, c: primitive Translationsvektoren
Gitter + Basis = Kristallstruktur
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•

4
a
b
TT = -a + 3b
Kristallstruktur: f (r) [ g ( r ) = ∫ f (r - r""‘‘) g (r) dr‘
Basis f (r) (Faltung von Basis und Gitter) Raumgitter g (r)

5
2.4 Translationsinvarianz, Einheitszelle und Ortsvektoren
Kriterium für die Elementarzelle
Sie ist die Zelle mit dem Kleinstmöglichen Volumen
ab
c
Kriterium für den Aufbau von Kristallstrukturen:
Der Raum muß sich lückenlos mit identischen Einheitszellen ausfüllen lassen,Damit eine Translation in den drei Raumrichtungen die Struktur reproduziert.
Koordinationszahl
Die Zahl der nächsten Gitterplätze
Beispiel: pk: 6; krz: 8; kfz: 12

6
a
c
r1
r2
r3
b
r1
r2
r3
a
c
b
x:y:z = 0:1:1x:y:z = 1:1/2:1/2 = 2:1:1x:y:z = 1/2:1:1/2 = 1:2:1
[u,v,w]=[011][u,v,w]=[211][u,v,w]=[121]
krz kfz
Die 6 äquivalenten Richtungen <100>
[001]
[001]
[010][010]
[100]
[100]
a
bc
-
-
-
Ortsvektoren im Kristallgitter
r = x a + y b + z c
r1 = 1 a + 0 b + 1 c
r2 = 1/2 a + 1/2 b + 1/2 c
r2 = 1/2 a + 1/2 b + 1/2 c
Richtungen im Kristallgitter
Richtungsindizes u, v, w
r1 = 0 a + 1 b + 1 c
r2 = 1 a + 1/2 b + 1/2 c
r2 = 1/2 a + 1 b + 1/2 c

7
2.5 Miller-Indizes und Kristallklassen
Bezeichnung von Ebenen im Kristallgitter
a
b
c
1
2
3
12
4
1 2 33 (100) (010) (001)
1/4 : 1/3 : 1/2 = 3 : 4 : 6;
(h,k,l) = (346)
hkl: Miller-Indizes
na = 4; 1/na = 1/4
nb = 3; 1/nb = 1/3
nc = 2; 1/nc = 1/2

8
Gitternetzebenen
(210)
y
z
x[210]
y
z
x
(100) (100)
y
z
x
(111)
x
y
z(011)

9
7 Kristallsysteme
Kubisch
Trigonal
Tetragonal Orthorhombisch
Monoklin Triklin Hexagonal
a = b = ca = b = g = 90°
a ≠ b ≠ ca ≠ b g ≠ 90°
a ≠ b ≠ ca = b = g = 90°
a = b = ca = b = g ≠ 90°
a ≠ b ≠ ca = g = 90°, b ≠ 90°
a ≠ b ≠ ca ≠ b ≠ g ≠ 90°
a ‚= b ≠ ca = b = 90°, g = 120°
a
b
c
b
a g

10
2.6 Die 14 Bravaisgitter
Kubisch I Kubisch P Kubisch F Tetragonal P Tetragonal I
Erweiterung der Kristallklassen durch Hinzufügen weiterer Gitterpunkte 14 Bravais-Gitter
Ortho-Rhombisch P
Ortho-Rhombisch C
Ortho-Rhombisch I
Ortho-Rhombisch F Rhombo-
edrisch RHexa-gonal P
Monoklin P Monoklin C Triklin

11
a
b
c
b
a g
Triklin
Monoklin
Orthorombisch
Tetragonal
Kubisch
Rhomboedrisch
Hexagonal
Gittersystem Anzahl Symbol
Einschränkungenfür Achsen undWinkel
1
2
4
2
3
1
1
P
P,C
P,C,I,F
P,I
R
P
a = b = 90°
(keine)
a = b = g = 90°
a = ba = b = g = 90°
a = b = c
a = ba = b = g ≠ 90°
a = ba = b = 90°g = 120°
P oder scI oder bccF oder fcc
a = b = g = 90°

12
2.7 Änderung der Struktur
kubischraumzentriert(bcc)
kubischflächenzentriert(fcc)
kubischraumzentriert(bcc)
T [°C] schmelz-flüssig
d-Eisen
g-Eisen
a-Eisen
-273
911
1392
1536
≈

13
Kristallstrukturen des Kohlenstoffs (C)
Diamant:Tetraedrische BindungenHärtester FestkörperMetastabile Hochdruckphase
Graphit:Schicht-StrukturWeicher FestkörperStabile Phase
Anisotrope Transporteigenschaften

14
Überstrukturen in geordneten Mischkristallen
T > 793 K:UngeordnetHart und sprödeKubische kfz Struktur
T < 793 K:GeordnetWeich und duktilTetragonale Struktur
CuAu Cu3Au
Geordnete Überstrukturin Cu3AuKubische Struktur
Härte, Zugfestigkeit und Streckgrenze
Elektrische Leitfähigkeit, magn. Suszeptibilität

15
2. 8 Symmetrien
5-zählige Drehachsen sind in der Krisatallographie verboten!keine Translationsinvarianz, keine Raumfüllung!
Erlaubte Drehungen (Drehachsen)
2" (1-zählig)2"/2 (2-zählig)2"/3 (3-zählig)2"/4 (4-zählig)2"/6 (6-zählig)
Symmetrieebenen
Drehung um eine Symmetrieachse, die durch einen Gitterpunkt führt, die den Kristall in sich selbst überführt.
3 vierzählige 4 dreizählige 6 zweizählige
Drehachsen einesWürfels

16
Punktsymmetrien:
†
3 = 3 + 1
†
4 = mm H2O
Spiegelung an einer Ebene: z. B. an der yz-Ebene: y‘ = y, z‘ = z, x‘ = - xDas Vorhandensein einer Spiegelebene wird durch das Symbol m angezeigt.
Inversion (Spiegelung an einem Punkt): y‘ = - y, z‘ = - z, x‘ = - x
Drehachsen, Deckungsgleichheit durch Rotation um einen Winkel, 2-, 3-, 4-, 6-zählig
Drehinversionsachsen: Drehung und gleichzeitige InversionBezeichnung durch
†
2 , 3 , 4 , 6
Drehinversionsachsen
dreizählig vierzählig
2 symmetrischeund 1 antisymmetrischeSchwingungsform

17
Hamilton-Operator H:
zweifache Symmetrie, Invarianz bei entsprechender Koordinatentransformation
Zuordnung von s (Operator) zur Spiegelung, Anwendung auf H , y oder R
· deren Beschreibung in den gespiegelten Koordinaten
Die zwei Spiegelebenen des H2O müssen sich in den physikalischen Eigenschaften des Moleküls ausdrücken
Darstellung in Matrizen: Beispiel: Spiegelung an yz-Ebene:
†
-1 0 00 1 00 0 1
Ê
Ë
Á Á Á
ˆ
¯
˜ ˜ ˜
xyz
Ê
Ë
Á Á Á
ˆ
¯
˜ ˜ ˜
=
-xyz
Ê
Ë
Á Á Á
ˆ
¯
˜ ˜ ˜
Reduzierung der dreidimensionalen Darstellung auf dreieindimensionale Matrizen:[(-1)x; (1)y; (1)z] = (-x; y, z)
Ist H spiegelsymmetrisch, so sind die Operatorenvertauschbar.
Eigenzustände von H verhalten sich symmetrisch oderantisymmetrisch zu diesen Operatoren, oder äquivalent,sie besitzen gerade oder ungerade Parität.
Keine entarteten Energiezustände
(Beispiel: H2-Molekül)
†
s Y+ =1 Y+; C2 Y+ = +1⋅ Y+
s Y- = -1 Y-; C2 Y- = -1⋅ Y-
C2: zweizählige Drehachses2 = 1 und (C2)2 = 1Eigenwerte: ±1

18
2.9 Stereographische ProjektionDarstellung der Flächen eines Kristalls
Flächennormale schneidet Polkugel im PolAbbbildung obere Hälfte, geschlossene SymboleAbbildung untere Hälfte, offene Symbole
Kombination der Symmetrieelemente:·32 Kristallklassen (Punktgruppen)Punktgruppensymbole nach Schönflies:Cj: (j=2,3,4,6) j-zählige DrehachseSj: j-zählige DrehinversionsachseDJ: j zweizählige Drehachsen senkrecht
zu einer j-zähligen HauptdrehachseT: 4 drei und 3 zweizählige DrehachsenO: 4 drei und 3 vierzählige DrehachsenCi: ein InversionszentrumCs: eine Symmetrieebeneh: horizontal = senkrecht zur Drehachsev: vertikal = parallel zur Hauptdrehachsed: diagonal = parallel zur Hauptachse in
der Winkelhalbierenden zwischen denzweizähligen Drehachsen
Symmetrieelemente zweier Punktgruppen;m, s, n: zwei-, drei-, vierzählige DrehachsenAusgezogene Linien: Spiegelebenen
4mm = C4v m = D3d
†
3

19
Texturen
Ausrichtung der Kristallite in polykristallinen Festkörpern in eine Vorzugsrichtung
Punktlinien auf einem Textur-Diagrammmit [111] als Faserachse
Faser-Textur ineinem Draht
Walz-Textur in einem Blech
Entstehung einesTextur-Diagramms
AB: DrehachseOS: einfallender Strahl
0: reflektierende EbeneI, II, II, IV: reflektierteStrahlen, symmetrisch zuEbenen ABVV‘ und0HH‘

20
2.10 Dichteste Packung harter Kugeln
Hexagonal, kubisch-flächenzentriertedichteste Packung harter Kugeln
A
A
B
A A A A
A A A
A A A
A A A A
B B B
B B B
B B B
C C C
C C C
C C C
Metalle: Symmetrische Bindungsverhältnisse· Modell harter Kugeln · Energetisch begünstigt: Dichteste Packung
Schichtfolge: ABABABABHexagonal dichtest gepacktSchichtfolge: ABCABCABCKubisch-flächenzentriertdichtest gepackt

21
2.11 Fünfzählige Symmetrie in Quasikristallen
Ikosaedrisches Raumgitter Elektronenbeugungsbild von Al-14at%-Mn
keine Translationsfernordnung, aber Orientierungsfernordnung
Al6Li3CuIkosaedereinkristall
Pentagons füllen nicht den Raum

22
2.12 Amorphe Strukturen
Systeme mit gerichteter atomarer Bindung: z. B. SiO2
kristallin
amorphSysteme mit symmetrischer atomarer Bindung: z. B. Metalle
kristallin amorph