Einfache Theorie chemischer Elementarreaktionen und die ... · 4.1.2 Quasikontinuierliche...

Kapitel 4

Einfache Theorie chemischer

Elementarreaktionen und die

Temperaturabhangigkeit der

Geschwindigkeitskonstanten

Ziel dieses Kapitels ist ein einfaches Verstandnis der Temperaturabhangigkeit der Geschwin-

digkeitskonstanten chemischer Elementarreaktionen. Ausgangspunkt fur unsere Darstellung ist

eine elementare statistisch-thermodynamische Behandlung der kinetischen Primarprozesse. Die-

se geht im Verstandnis etwas tiefer als eine rein formal quasithermodynamische Diskussion etwa

im Rahmen der thermodynamischen Formulierung der Theorie des Ubergangszustandes. Aller-

dings mussen einige Konzepte, die erst in der Vorlesung PC VI, Statistische Thermodynamik,

vorweggenommen werden.

4.1 Populationsverteilung

In der statistischen Mechanik stellt sich die Frage nach der Verteilung der Molekule auf die Ener-

giezustande im thermischen Gleichgewicht. Im Rahmen der klassischen Mechanik sind beliebige,

kontinuierliche Energiewerte moglich, in der Quantenmechanik fur manche molekularen Bewe-

gungen nur diskrete Energien. Es werden hier zunachst die wichtigsten Ergebnisse fur diskrete

Energien zusammengefasst und danach auf den kontinuierlichen Fall ubertragen.

127

128 KAPITEL 4. THEORIE DER ELEMENTARREAKTIONEN

4.1.1 Boltzmannverteilung auf Energieniveaus im thermischen Gleichgewicht

und chemische Gleichgewichtskonstante

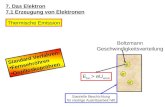
Es seien zwei Energiezustande Ei und Ej gegeben, deren Besetzungswahrscheinlichkeiten (oder

einfach “Besetzungen”) mit pi und pj bezeichnet werden (Bild 4.1). Als Besetzungswahrschein-

lichkeit pj bezeichnet man also die Wahrscheinlichkeit, bei einer Temperatur T ein Atom oder

Molekul – oder allgemein ein Quantensystem – im Energiezustand Ej vorzufinden:

pj =Cj∑k

Ck(4.1)

wobei Cj die Konzentration der Molekule im Quantenzustand Ej ist.

Das Boltzmann-Verteilungsgesetz liefert als Ergebnis das Verhaltnis der beiden Besetzungen fur

jede Temperatur T , und zwar:pjpi

= exp

(−(Ej − Ei)

kBT

)(4.2)

mit

kB =R

NA= 1.38066× 10−23 J K−1, Boltzmannkonstante (4.3)

Das Boltzmann-Verteilungsgesetz lasst sich elementar aus der barometrischen Hohenformel her-

leiten, fundamental folgt es aus der mikrokanonischen Gleichverteilung. Wir wollen das Ergebnis

hier ohne Herleitung als Ausgangspunkt fur die folgenden Uberlegungen akzeptieren. Die Sum-

me der Besetzungen aller einzelnen Energiezustande sei auf eins normiert, d.h. man betrachtet

Besetzungswahrscheinlichkeiten ∑j

pj = 1 (4.4)

Also gilt fur die Besetzung eines Zustandes

pj =1

Qexp

(− EjkBT

)(4.5a)

mit der kanonische Zustandssumme

Q =∑j

exp

(− EjkBT

)(4.5b)

Es ergibt sich oft, dass mehrere Energiezustande fur dieselbe Energie existieren, man spricht

von entarteten Energiezustanden. Diese Zustande derselben Energie konnen in Gruppen oder

”Niveaus” zusammengefasst werden, wobei die Zahl der Zustande gJ zur Energie EJ statistisches

Gewicht heisst (wir verwenden hier grosse Indices fur solche entarteten Niveaus, man spricht auch

von der Entartung oder der Polytropie gJ):

pJ = gJ1

Qexp

(− EJkBT

)(4.6)

PCII - Chemische Reaktionskinetik

4.1. POPULATIONSVERTEILUNG 129

Q =∑J

gJ exp

(− EJkBT

)=∑j

exp

(− EjkBT

)(4.7)

Man beachte die unterschiedlichen Summationsindices in Gl. (4.7), wobei wir hier durch gros-

se Indices entartete Niveaus J von einzelnen Quantenzustanden j unterscheiden. Mittels des

Boltzmann-Verteilungsgesetzes lasst sich nun die chemische Gleichgewichtskonstante eines Sy-

stems aus den molekularen Eigenschaften berechnen. Als Beispiel sei eine Isomerisierungsreak-

tion (A = B) aufgefuhrt (siehe Bild 4.1).

∆E

E

E ′

E ′

A B

(A)

(B)

Abbildung 4.1: Zur Boltzmann-Verteilung fur zwei Isomere A und B.

NB sei die Zahl der Molekule, die sich in einem Quantenzustand befinden, der zum Stoff B gehort

und analog ist auch NA definiert. Dann gilt:

NB

NA= Kc =

cB

cA=pB

pA=

∑i(B)

exp

(−Ei(B)

kBT

)∑i(A)

exp

(−Ei(A)

kBT

) (4.8)

Man summiert jeweils uber die Besetzung von Quantenzustanden, die entweder dem Isomeren A

oder dem Isomeren B zugeordnet werden konnen. Jetzt kann eine neue Energieskala eingefuhrt

werden, in der die Energie E′ jedes Isomers vom tiefsten Energiezustand E0 dieses Isomers

gemessen wird (siehe Bild 4.1):

pB

pA=

∑i(B)

exp

(− E′ikBT

)∑i(A)

exp

(− E′ikBT

) exp

(−∆E

kBT

)=QB

QAexp

(−∆E

kBT

)= Kc (4.9a)

mit

∆E = E0(B)− E0(A) (4.9b)



Die Zustandssummen QA und QB sind gemass Gl. (4.7) definiert, ohne Berucksichtigung der

Existenz des anderen Isomeren. In der statistischen Thermodynamik lassen sich alle Gleichge-

wichtseigenschaften eines Systems aus der Zustandssumme herleiten. Die vorliegende Berech-

nung einer Gleichgewichtskonstanten ist ein einfaches Beispiel aus den allgemeinen statistischen

Berechnungen chemischer Gleichgewichte. Wir haben sie hier vorweggenommen, da wir das Er-

gebnis fur einige der folgenden Uberlegungen benotigen (siehe auch Ubungsanhang).

4.1.2 Quasikontinuierliche Verteilung und Maxwell-

Boltzmann-Geschwindigkeitsverteilung

Werden die Energieunterschiede zwischen benachbarten Zustanden sehr klein, so konnen mehrere

Energiezustande in einem kleinen Intervall dE zusammengefasst werden. Man definiert zu diesem

Zweck die “Zustandsdichte” ρ(E) abstrakt als Zahl der Quantenzustande pro Energieeinheit ganz

analog wie ja auch die Teilchenzahldichte als Zahl der Teilchen pro Volumeneinheit definiert wird

oder eine “Bevolkerungsdichte” als Zahl der Personen pro Flacheneinheit. Die Zustandsdichte

ist offenbar gerade der Kehrwert des Energieabstandes δ(E) bei der Energie E (oder eventuell

geeigneter Mittelwert hierzu, siehe Bild 4.2:

ρ(E) = δ(E)−1 (4.10a)

ρ(E)dE = ′′g(E)′′ (4.10b)

ρ(E)dE = dE/δ(E) ist die Anzahl der Energiezustande im Energieintervall dE, also quasi die

Entartung ′′g(E)′′ fur das Niveau, das dem Intervall dE bei der Energie E entspricht (siehe Bild

4.2).

E

dE

δ E( ) ρ E( )1-

=

dE

Abbildung 4.2: Skizze zur quasikontinuierlichen Energieverteilung mit der Zustandsdichte ρ(E).



Fur die Besetzungsdichte p(E) bei der Energie E gilt dann analog zu Gl. (4.6):

p(E)dE =

ρ(E) exp

(− E

kBT

)dE

∞∫0

ρ(E) exp

(− E

kBT

)dE

(4.11a)

Bei der quasikontinuierlichen Verteilung wird die Zustandssumme aus Gl. (4.7) durch ein ent-

sprechendes Integral ersetzt:

Q =

∫ ∞0

ρ(E) exp(−E/kBT )dE (4.11b)

Hierbei ubernimmt ρ(E)dE die Rolle der Entartung gJ in Gl. (4.7). Die notwendige Voraus-

setzung fur die Gultigkeit dieser Naherung ist die geringe Grosse der Energiedifferenzen δ(E)

zwischen den benachbarten Energiezustanden, wie dies bei den Translationsenergiezustanden

der Fall ist. Als Beispiel diskutieren wir hier die Berechnung der Translationsenergie- und der

Geschwindigkeitsverteilung in einatomigen idealen Gasen. Hier berechnet man zunachst die Zu-

standsdichte ρ (E) fur die Translationszustande unabhangiger Teilchen in einem Kasten mit dem

Volumen V :

ρ(E) = m3/225/2πh−3E1/2V (4.12)

m ist die Masse der Teilchen und h die Plancksche Konstante. Man setzt diese Zustandsdichte

in Gl. (4.11a) ein. Das dann fur Gl. (4.11a) und (4.11b) benotigte Integral lasst sich mit Hilfe

von Tabellen ermitteln (vergl. [Bronstein, Semendjajew 1980]).

∞∫0

E1/2 exp

(− E

kBT

)dE =

√π

2(kBT )3/2 (4.13)

Als Wahrscheinlichkeitsdichte der Besetzung oder kurz Besetzungsdichte bezeichnet man die

Besetzungswahrscheinlichkeit pro Energieintervall, also gemass Gl. (4.6) und (4.11a) p(E) =

p(E)dE/dE. Somit kann die Besetzungsdichte, die auch als Translationsenergieverteilung be-

zeichnet wird, durch folgenden Ausdruck dargestellt werden:

p(E) = E1/2

{√π

2(kBT )3/2

}−1

exp

(− E

kBT

)(4.14)

Obwohl die Energie eine fundamentale Grosse ist, erweist es sich manchmal als nutzlicher, von der

Translationsenergie auf den Betrag v der entsprechenden Geschwindigkeit umzurechnen. So lasst

sich auch die Translationsenergieverteilung auf die Geschwindigkeitsverteilung transformieren:

E =mv2

2(4.15a)



dE = mv dv (4.15b)

p(E)dE = g(v)dv

= v√m/2

(√π

2(kBT )3/2

)−1

exp{−m

2v2 (kBT )−1

}mvdv (4.16)

Es folgt:

g(v) = 4πv2

(m

2πkBT

)3/2

exp

(− mv2

2kBT

)(4.17)

Es resultiert die Maxwell-Boltzmann-Geschwindigkeitsverteilung g(v) idealer Gase bei der Tem-

peratur T .

Man kann diese Verteilung in Atomstrahlexperimenten messen, wie in Bild 4.3 gezeigt ist.

g(v)

v

g(v)

v

O D

Z2Z1

M

Hochvakuum

Verteilung vor Z1

Verteilung nach Z2

dA

=

Zahnrad Z

d

Abbildung 4.3: Messung der Geschwindigkeitsverteilung im Atomstrahl (schematisch). O: Ofen,

aus dem Gasmolekule bei der Temperatur T austreten und nach einer Blende einen Molekulstrahl

bilden; D: Detektor; A: drehbare Achse; ω : Winkelgeschwindigkeit der Zahnrader Z1 und Z2; α

: Winkel, um den sich das Rad wahrend t gedreht hat; d : Abstand der Zahnrader Z1 und Z2.

Ein Teilchen kann genau dann durch die laufenden Rader Z1 und Z2 hindurchfliegen, wenn seine

Geschwindigkeit

v =ω d

α(4.18)



betragt. Dann namlich entspricht der Drehwinkel α zwischen zwei Lucken gerade der Flugzeit t

fur die Strecke d (Analoges gilt fur Vielfache von α).

α = ωt (4.19)

t = d/v = α/ω (4.20)

Vor dem laufenden Zahnrad Z1 findet man die gesamte Geschwindigkeitsverteilung g(v), nach

dem Selektor Z2 sieht man nur noch den Ausschnitt dieser Verteilung, welcher der bekannten

Winkelgeschwindigkeit des Zahnrads entspricht. Bild 4.5 zeigt Beispiele fur thermische Geschwin-

digkeitsverteilungen nach Gl. (4.17).

Xe

O2

H2

0 2000 4000 6000 v / (m s-1)

g(v)

/ (1

0-3 m

s-1)

0

1

2

3

4

Abbildung 4.4: Geschwindigkeitsverteilung fur zwei typische Temperaturen und drei Beispiele

von Atom- oder Molekulmassen: T = 300 K (durchgezogen) und T = 1000 K (gestrichelt) fur

Xenon (m(Xe)= 131.29 u), Sauerstoff (m(O2) = 31.99u) und Wasserstoff (m(H2) = 2.02 u).

Aus den Energie- und Geschwindigkeitsverteilungen kann man Mittelwerte berechnen. Fur die

Mittelwertbildung einer Grosse f(x) gilt allgemein

〈f〉 =

B∫A

p(x)f(x)dx (4.21)

wobei p(x) die Wahrscheinlichkeitsdichtefunktion ist. Anhand der Translationsenergieverteilung

p(E)dE kann man die mittlere Translationsenergie 〈E〉 berechnen (Sonderfall x ≡ E, f(x) = E)

〈E〉 =

∞∫0

p(E)EdE (4.22)

Einsetzen von p(E) ergibt

〈E〉 =

∞∫0

E3/2

(√π

2(kBT )3/2

)−1

exp

(− E

kBT

)dE (4.23)



Man findet das folgende Integral in Tabellen:

∞∫0

xn exp (−ax) dx =Γ(n+ 1)

an+1(4.24)

Γ(n+ 1) ist die Gammafunktion mit dem Argument (n+ 1), eine verallgemeinerte Fakultat mit

der Eigenschaft Γ(n+ 1) = n Γ(n). Hierbei ist n eine beliebige reelle Zahl. Der Zusammenhang

mit der wohlbekannten Fakultat ergibt sich bei Beschrankung auf den Sonderfall der naturlichen

Zahlen. Es gilt hier offenbar Γ(N) = (N − 1)! = (N − 1)× (N − 2)...2× 1. Die Gammafunktion

ist allgemein tabelliert [Bronstein, Semendjajew 1980]. Im vorliegenden Fall findet man den

Tabellenwert fur Γ(3/2) =√π/2 und errechnet hiermit

Γ

(5

2

)=

(3

2

)Γ

(3

2

)=

(3

4

)√π (4.25)

〈E〉 =3

2kBT (4.26)

Die Berechnung der mittleren Geschwindigkeit liefert

〈v〉 =

∞∫0

g (v) vdv =

∞∫0

p (E) v (E) dE (4.27)

mit

v =

√2E

m(4.28)

〈v〉 =

∞∫0

E exp

(− E

kBT

)dE√

2/m((√

π/2)

(kBT )3/2)−1

=

(8kBT

πm

)1/2

≈(

2.55 kBT

m

)1/2

(4.29)

Neben der mittleren Geschwindigkeit werden auch die wahrscheinlichste Geschwindigkeit (Ma-

ximum der Verteilung)

vw =

(2kBT

m

)1/2

(4.30)

und die mittlere quadratische Geschwindigkeit

⟨v2⟩

=2

m〈E〉 =

(3kBT

m

)(4.31)

als charakteristische Grossen angegeben. Bild 4.5 illustriert diese Grossen. Man kann als weitere

charakteristische Grosse der Verteilung auch ihre Halbwertsbreite Γv angeben (das ist die volle

Breite Γv (FWHM), bei halber Hohe 12g (vw) in Bild 4.5, vom Englischen ‘Full Width at Half



Maximum’).

Γv ≈ 1.632 (kBT/m)1/2 ≈(

2.66 kBT

m

)1/2

(4.32)

Abbildung 4.5: Geschwindigkeitsverteilung mit vw, 〈v〉 und√〈v2〉, (schematisch)

Diese Formel ergibt sich aus einer numerischen Nullstellenbestimmung, wobei der Faktor auf drei

Stellen genau berechnet wurde. Tabelle 4.1 stellt einige Zahlenwerte fur Beispiele zusammen.

T/K Teilchen Γv/(m s−1) vw/(m s−1) v(Ew)/(m s−1)

300 H2 1815 1573.1 1112.4

O2 455.6 394.8 279.2

Xe 224.9 194.9 137.9

1000 H2 3314 2872.1 2030.9

O2 831.9 720.9 509.5

Xe 410.7 355.9 251.7

Tabelle 4.1: Halbwertsbreite Γv, wahrscheinlichste Geschwindigkeit vw und Geschwindigkeit

v(Ew) bei der wahrscheinlichsten Energie Ew fur Wasserstoff, Sauerstoff und Xenon bei zwei

Temperaturen.

Es kann zweckmassig sein, eine Darstellung mit reduzierten Energie- und Geschwindigkeitsva-

riablen einzufuhren, die dann fur alle Temperaturen und Molekule gilt. Als reduzierte dimensi-



onslose Energievariable eignet sich

Ered =E

kBT(4.33)

dEred =dE

kBT(4.34)

Damit erhalt man

pred(Ered)dEred = p(E)dE =2√πE

1/2red exp(−Ered)dEred (4.35)

Ebenso erhalt man mit

vred =

(m

kBT

)1/2

v (4.36)

gred(vred)dvred = g(v)dv =

√2

πv2

red exp(−v2red/2) dvred (4.37)

Die beiden Funktionen sind in einer universellen Darstellung in Bild 4.6 zusammengefasst.

2 4 6 8 10

0.1

0.2

0.3

0.4

0.5

0.6

Ú

Ô

´

Ö

µ

Ù

Ò

´

Ú

Ö

µ

Ered, vred

p red(E

red)

, gre

d(v r

ed)

Abbildung 4.6: Geschwindigkeitsverteilung gred(vred) (durchgezogen) und Translationsenergie-

verteilung pred(Ered) (gestrichelt) in reduzierten Geschwindigkeits- und Energievariablen.

Wir haben hier einige sehr einfache Anwendungen der kinetischen Gastheorie besprochen. Wei-

tere Ergebnisse dieser Theorie betreffen die physikalische Kinetik von Diffusions- und Warmelei-

tungsvorgangen, die Viskositat und viele weitere Eigenschaften von Gasen. Wir werden uns der

Berechnung von Geschwindigkeitskonstanten mit dieser Theorie zu wenden.


4.2. ARRHENIUSGLEICHUNG 137

4.2 Arrheniusgleichung

4.2.1 Arrheniusgleichung und Stosstheorie bimolekularer Reaktionen

Stosshaufigkeit

Fur die spezifische bimolekulare Geschwindigkeitskonstante der Reaktion von A mit B bei der

Stossenergie Et hat man

k (Et) = σ (Et)

√2Et

µ(4.38)

wobei Et die relative Translationsenergie der Stosspartner ist, σ (Et) der effektive Reaktions-

querschnitt (energieabhangig) und µ die reduzierte Masse (µ = (m−1A +m−1

B )−1).

Der effektive Stossquerschnitt σ enthalt die quantitative Information uber den reaktiven Stoss.

Eine analoge Gleichung gilt fur nichtreaktive Stosse (mit einem anderen Wert fur σ). Nun wird

der thermische Mittelwert 〈k (Et)〉 gebildet.

〈k (Et)〉 =

∞∫0

p (Et) k (Et) dEt

=

∞∫0

E1/2

(√π

2(kBT )3/2

)−1

exp

(− E

kBT

)σ (E)

√2E/µdE

=

(8kBT

πµ

)1/2∞∫

0

(E

kBT

)σ (E) exp

(− E

kBT

)(dE

kBT

)(4.39)

≡ k (T ) = 〈vrel〉〈σ〉 (4.40)

mit

〈σ〉 =

∞∫0

(E

kBT

)σ (E) exp

(− E

kBT

)(dE

kBT

)(4.41)

Wir haben hier verwendet, dass die Energieverteilung fur die relativen Translationsenergien ei-

ne thermische Gleichgewichtsverteilung (Maxwell-Boltzmann-Verteilung) gemass Gl. (4.14) ist

und haben in der Schreibweise den Ubergang von Et auf eine abstrakte Energievariable E und

die praktische, dimensionslose Energievariable (E/kBT ) als Integrationsvariable vollzogen. Die

Verwendung der reduzierten Masse µ in der thermischen Stossenergieverteilung ist naheliegend

und lasst sich durch eine ausfuhrlichere Rechnung begrunden. Mit Hilfe dieses gewichteten Mit-

telwertes des effektiven Stossquerschnittes lasst sich die Zahl der Stosse fur ein Teilchen A mit

allen Teilchen der Sorte B ausrechnen (Konzentration CB als Teilchenzahldichte genommen):

ZA = k(T )CB = 〈σ〉〈vrel〉CB (4.42)



ZA ist eine Geschwindigkeitskonstante scheinbar erster Ordnung fur Stosse von A mit B. Also

gilt fur die Zahl der Stosse pro Volumeneinheit

ZVAB = 〈σ〉〈vrel〉CA · CB (4.43)

Fur die Anzahl der Stosse gleicher Molekule schreibt man entsprechend

ZVAA =1

2〈σ〉〈vrel〉C2

A (4.44)

Der Faktor 12 muss hier wegen der Doppelzahlung der Stosse A mit A′ und A′ mit A berucksichtigt

werden. In diesem Fall kann auf die absolute Geschwindigkeit umgerechnet werden (mA = mB ≡ m)

〈vrel〉 =

(8kBT

πµ

)1/2

mit µ = m/2, und 〈vrel〉 =(

16kTπm

)1/2=√

2 〈vabs〉.

ZVAA =1√2〈σ〉〈vabs〉C2

A (4.45)

Beispiel: Abschatzung der Zahl der Stosse pro cm3 und pro Sekunde in Ar bei 1 atm

(=101325 Pa) und 300 K. Der geschatzte effektive Stossquerschnitt sei 〈σ〉 ' 0.25 (nm)2. Das

ergibt ZVAA = 4.21 × 1028 cm−3 s−1. Fur die Zahl der Stosse eines Ar-Atoms hat man dement-

sprechend ZA = 3.44× 109 s−1.

Diese Grossenordnung sollte man sich merken, da sie praktisch angibt, bis zu welchen Zeiten man

bei Atmospharendruck unimolekulare Primarprozesse in ”isolierten” Atomen und Molekulen

vorfindet, die nicht wesentlich durch Stosse beeinflusst werden. Das gilt sicher fur Zeiten im fs

Bereich, weitgehend auch im ps Bereich. Dementsprechend kann man sagen, dass eine chemische

Reaktion in Gasen bei Atmospharendruck im Picosekunden- und Subpicosekundenzeitbereich si-

cher nicht bimolekular (oder trimolekular) sein kann. Will man langsamere Prozesse in isolierten

Molekulen untersuchen, so muss man bei geringeren Drucken arbeiten (z.B. mbar Drucke fur

Nanosekunden).

Einfache Modelle fur den Reaktionsquerschnitt

In Kapitel 3.3.7 wurde auf die Natur des Stossquerschnittes σ nicht naher eingegangen, er war

eine beliebige Funktion der Stossenergie Et. Hier sollen nun vier Modelle des funktionalen Zu-

sammenhanges fur σ = f (Et) erlautert werden.



Modell harter Kugeln

Die Stosspartner A und B werden durch harte Kugeln mit den Radien rA und rB approximiert.

Es gilt

rAB = rA + rB (4.46)

Et

σ ( )

σ0

rAB

R(Et)

Abbildung 4.7: Modell harter Kugeln und σ0 als Funktion von Et.

Beruhrung oder Stoss tritt ein, wenn sich die Zentren der beiden Kugeln auf diesen Abstand

nahern. Der effektive Stossquerschnitt entspricht also der Flache des gestrichelten Kreises in

Bild 4.8:

σ0 = π (rA + rB)2 (4.47)

Der Stossquerschnitt σ0 ist konstant fur alle Stossenergien (Bild 4.7). Der thermische Mittelwert

der Reaktionsgeschwindigkeitskonstanten kann durch Integration gemass Gl. (4.39) ermittelt

werden und man erhalt mit σ (E) = σ0

k (T ) =

(8kBT

πµ

)1/2

σ0

∞∫0

x exp (−x) dx (4.48)

Und aus Gl. (4.24)∞∫

0

x exp (−x) dx = 1 (4.49)

k (T ) =

(8kBT

πµ

)1/2

σ0 (4.50)

Modell mit Aktivierungsenergie E0

Im Modell mit einer Schwellenenergie oder Aktivierungsenergie E0 fur die Reaktion muss die

Stossenergie Et einen bestimmten Wert E0 ubersteigen, damit es zur Reaktion kommen kann.



σR(Et) folgt einer Sprungfunktion bei E0. Fur Et > E0 ist σ in diesem Modell eine Konstante

(σ0, Bild 4.8).

σ0

σ

EtE0

R(Et)

Abbildung 4.8: σR als Funktion von Et, Schwellenenergie E0 und Sprungfunktion.

Auch fur dieses Modell lasst sich der thermische Mittelwert der Reaktionsgeschwindigkeits-

konstanten bestimmen.

k (T ) =

(8kBT

πµ

)1/2

σ0

∞∫E0

(E

kBT

)exp

(− E

kBT

)(dE

kBT

)(4.51)

Durch partielle Integration erhalt man fur dieses bestimmte Integral mit der variablen Unter-

grenze E0

k (T ) = σ0

(8kBT

πµ

)1/2(1 +

E0

kBT

)exp

(− E0

kBT

)(4.52)

Modell mit Aktivierungsenergie und langsam wachsendem σR (E)

Hier wird auch eine minimale Energie fur einen erfolgreichen Stoss vorausgesetzt. Wird allerdings

die Energie E0 erreicht, springt σR nicht gleich auf seinen Grenzwert σ0, sondern wachst stetig

bis zu diesem Endwert an (Bild 4.9). Man kann dieses Modell noch naher physikalisch begrunden

und es wird oft auch experimentell ein solches allmahliches Ansteigen gefunden, wobei allerdings

bei hohen Energien kein konstanter Wert erreicht wird, sondern wieder eine Abnahme von σ.

σ (Et) = 0 fur Et < E0

σ (Et) = σ0

(1− E0

Et

)fur Et > E0

(4.53)

Die Integration fur k (T ) ergibt:

k (T ) =

(8kBT

πµ

)1/2

σ0 exp

(− E0

kBT

)(4.54)



σ0

σ

EtE0

R(Et)

Abbildung 4.9: σR als Funktion von Et mit Aktivierungsenergie und langsam wachsendem

σR (E).

Verallgemeinertes Modell mit Aktivierungsenergie

Die Verallgemeinerung der vorhergehenden Modelle erfolgt durch die Einfuhrung einer beliebigen

Funktion f(Et − E0) = f(∆E), welche das Verhalten des Reaktionsquerschnittes oberhalb der

Schwellenenergie E0 beschreibt.

σR(Et) = 0 fur Et < E0

σR(Et) = σ0

(1− E0

Et

)f (∆E) fur Et > E0

(4.55)

Der allgemeine Ausdruck des thermischen Mittelwertes der Geschwindigkeitskonstanten lautet:

k(T ) = σ0

(8kBT

πµ

)1/2

exp

(− E0

kBT

)g(T ) (4.56)

mit

g(T ) =

∞∫0

(∆E

kBT

)f (∆E) exp

(−∆E

kBT

)d∆E

kBT(4.57)

Alle Modelle, ausser demjenigen der harten Kugeln, fuhren zu einem Ausdruck fur die Geschwin-

digkeitskonstanten k(T ), welcher sich in einen stark und einen schwach temperaturabhangigen

Term gliedern lasst. Dies fand auch Arrhenius, dessen Gesetz folgende Form hat:

k(T ) = A(T ) exp

(−EA

RT

)(4.58)

wobei A(T ) schwach temperaturabhangig ist, und exp(−EART

)stark temperaturabhangig ist.

Die Arrhenius-Aktivierungsenergie EA wird unten genauer definiert. Fur grosse Werte von EA ist



sie ungefahr gleich E0. Falls g(T ) genugend ”schwach T-abhangig” ist, bzw. die Schwellenenergie

E0 hoch ist, fuhrt auch das verallgemeinerte Modell zu einem Typus der Arrheniusgleichung,

dann namlich dominiert der exponentielle Term und bestimmt somit die Funktionsform.

Ein spezielles Beispiel fur das verallgemeinerte Modell des Reaktionsquerschnittes mit

f(∆E) = f(Et − E0) = exp

(−Et − E0

a

)(4.59a)

fuhrt zu der Form des Reaktionsquerschnittes

σR(Et ≥ E0) = σ0 (1− E0/Et) exp

(−Et − E0

a

)(4.59b)

Eine solche Form ist in Bild 4.10 fur den Wert a = 3E0 in reduzierter Form dargestellt, mit

σR(Et < E0) = 0:σR

σ0= (1− E0/Et) exp

(1− Et/E0

a/E0

)(4.60)

0.05

0.1

0.15

0.2

0.25

0.3

0.35

¼

Ê

´

µ

¼

2 4 6 8 10

σ0

σR(E

t) /

Et/E0

Abbildung 4.10: Verallgemeinertes Modell des Stossquerschnittes σR(Et)/σ0 nach Gl. (4.60) mit

a = 3E0.

Berechnet man hierfur k(T ) durch partielle Integration, so findet man

k(T ) = σ0

(8kBT

πµ

)1/2

exp

(− E0

kBT

)(1 + kBT/a)−2 (4.61)

Bild 4.11 zeigt diese Geschwindigkeitskonstanten in einem Arrheniusdiagramm fur σ0 = 0.1

nm2, NA E0 = 50 kJ mol−1 und a = 3E0. Die Darstellung erscheint fast linear uber einen

grossen Temperaturbereich, obwohl es quantitative Abweichungen von der Linearitat gibt. Bei

sehr hohen Temperaturen (T > 10000 K) findet man ein Maximum fur ln k(T ) = f(1/T ) mit

negativen Werten von EA(T ) bei noch hoheren Temperaturen. Wertet man dieses Beispiel nu-

merisch aus, so findet man bei 300 K A = 2.81× 10−10 cm3 s−1 und EA = 51.166 kJ mol−1, bei



5000 K entsprechend A = 4.87 × 10−10 cm3 s−1 und EA = 52.743 kJ mol−1, also eine schwache

Temperaturabhangigkeit der Arrheniusparameter.

0 1 2 3 4 5

-50

-45

-40

-35

-30

-25

-20

1000 K / T

ln[k

(T)/

(cm

3 s-1)]

Abbildung 4.11: Arrheniusdiagramm ln[k(T )/(cm3 s−1)] aufgetragen gegen 1/T fur das verall-

gemeinerte Modell, Gl. (4.60) und (4.61), (a = 3E0 und µ = 1.914 u.

4.2.2 Arrheniusgleichung fur unimolekulare Reaktionen

Wir diskutieren hier zunachst ein einfaches Modell fur unimolekulare Reaktionen, das auf die

Arrheniusgleichung fuhrt. Das stabile Molekul Xz besitze die Energie Ez. Die Schwellenenergie,

die X erreichen muss, damit es reagieren kann, betrage E∗ (Bild 4.12). Das kinetische Schema

ist

Xz

k1

�

k2

X∗k3→ Produkte (4.62)

Fur die Geschwindigkeitskonstanten gelte k1 und k2 � k3. Diese Voraussetzung erlaubt die

Annahme eines Gleichgewichtszustandes zwischen Xz und X∗, also

[X∗]

[Xz]=k1

k2= K∗ =

g∗

gzexp

(−∆E

kBT

)(4.63)

g∗ ist die Entartung fur das Niveau bei der Energie E∗ und gz fur das Niveau bei der Energie

Ez. Die Reaktionsgeschwindigkeit fur dieses System ist also

− d [X]

dt= −d ([Xz] + [X∗])

dt= k3 [X∗] = k3 [Xz]

g∗

gzexp

(−∆E

kBT

)(4.64a)



EzXz

k2k1∆E

k3

XEProdukte

* *

Abbildung 4.12: Energieschema des unimolekularen Zerfalls.

Wegen ∆E � kBT folgt [X] ' [Xz]� [X∗] und man kann zusammenfassend schreiben:

−d [X]

dt= keff [X]

mit

keff = k3g∗

gzexp

(−∆E

kBT

)(4.64b)

Der Vergleich mit dem Arrheniusgesetz

k (T ) = A (T ) exp

(−EA

RT

)(4.65a)

zeigt

A (T ) = k3g∗

gz(4.65b)

exp

(−EA

RT

)= exp

(−∆E

kBT

)(4.65c)

Unter diesen Bedingungen sind A und EA konstante Grossen und das logarithmierte Arrheni-

usgesetz kann als Gerade dargestellt werden:

ln k = lnA− EA

RT(4.66)

Im allgemeinen wird das Gleichgewicht durch die Reaktion gestort (Quasistationaritat statt

Gleichgewicht). Es existieren ausserdem viele X∗ mit verschiedenen k3 und E∗. Deshalb findet

man in Wahrheit im Allgemeinen eine schwache Temperaturabhangigkeit fur A und EA.

4.2.3 Temperaturabhangige Arrheniusparameter

Differentielle Form der Arrheniusgleichung

Die logarithmische Darstellung von k(T ) als Funktion von 1/T fuhrt im allgemeinen Fall nicht

zu einer Geraden (s. Bild 4.13). Die Ableitung der Funktion ln k nach 1/T fuhrt zur Tangenti-



algleichung:d ln k (T )

d (1/T )= −EA (T )

R(4.67a)

Diese Gleichung lasst sich auch nach EA aufgelost umschreiben

EA = −R d ln k(T )

d(1/T )= RT 2 d ln k(T )

dT(4.67b)

Man kann diese Form der Gleichung zur Bestimmung von EA verwenden, wenn ln k(T ) als

Funktion von (1/T ) oder von T gemessen wurde. Die Integration von Gl. (4.67a) ergibt die

Arrheniusgleichung mit temperaturabhangigen Parametern

k (T ) = A (T ) exp

(−EA (T )

RT

)(4.68)

Die differentielle Auswertung der Arrheniusgleichung ist die Grundlage der strengen Definition

der Arrheniuskonstanten:

• EA(T ) ist die Aktivierungsenergie nach Arrhenius gemaßDefinition in Gl. (4.67b)

• A(T ) ist der praexponentielle Faktor nach Arrhenius, der durch Auflosen von Gl. (4.68)

nach A(T ) bei aus Gl. (4.67b) bekanntem EA(T ) und bekanntem k(T ) definiert wird

Man muss die Aktivierungsenergie nach Arrhenius von der Schwellenenergie E0 (oder schlicht

der Aktivierungsenergie) unterscheiden.

Bei der einfachsten Auswertung nach Arrhenius nimmt man bei einer Messung der tempe-

raturabhangigen Geschwindigkeitskonstanten uber kleine Bereiche von T an, dass A und EA

temperaturunabhangig sind. Falls die Temperaturabhangigkeit der Arrheniusparameter wichtig

ist, geht man in der Praxis so vor, dass man zunachst eine geeignete, wenn moglich theoretisch

begrundete, nichtlineare Form der logarithmierten Arrheniusgleichung an die experimentellen

Werte anpasst. Sodann bestimmt man fur die gewunschte Temperatur Tx die Ableitung gemass

Gl. (4.67a) und hieraus EA (Tx). A (Tx) errechnet sich dann mit dem so bestimmten Wert von

EA (Tx) und dem Wert fur k (Tx).

A (Tx) = k (Tx) exp [+EA (Tx) /RTx] (4.69)

Neben dieser numerischen Auswertung ist selbstverstandlich auch die direkte graphische Auswer-

tung gemass Bild 4.13 sinnvoll, wenn auch weniger genau. Ein praktisches Anwendungsbeispiel

ist im Ubungsanhang zu finden.



Steigung:E Tx( )

R------------------

kln

1 T⁄

A Tx( )ln

1 Tx⁄

Tangente bei an die Funktion1 Tx⁄ kln

A

Abbildung 4.13: Nichtlineare graphische Darstellung und differentielle Auswertung der Arrheni-

usgleichung mit der Tangente bei 1/Tx und dem Achsenabschnitt der Tangente lnA(Tx).

Analogie zur van’t Hoff-Gleichung

Auch die van’t Hoff-Gleichung (4.70), welche die Temperaturabhangigkeit der Gleichgewichts-

konstanten K beschreibt, kann auf die differentielle Form gebracht werden:

d lnK

d (1/T )= − ∆rH

(T )

R(4.70)

mit

K = exp

(−∆rG

(T )

RT

)= exp

(∆rS

(T )

R

)exp

(−∆rH

(T )

RT

)(4.71)

Hierbei sind ∆rH(T ) die Reaktionsenthalpie und ∆rS

(T ) die Reaktionsentropie unter Stan-

dardbedingungen.

Man erkennt eine vollige Analogie der beiden Auswertungen nach Arrhenius und van’t Hoff.

Diese ist nicht zufallig. Van’t Hoff hatte zunachst die entsprechende Auswertung von ther-

modynamischen Daten eingefuhrt (Bild 4.16). Spater hat er dann die Arrheniusgleichung fur

Geschwindigkeitskonstanten in Analogie zu diesen thermodynamischen Gleichungen vorgeschla-

gen. Streng genommen ist also die Benennung dieser Gleichung nach Arrhenius historisch nicht

gerechtfertigt.


4.3. DIE THEORIE DES UBERGANGSZUSTANDES 147

Steigung:∆H0 Tx( )

R-----------------------

Kpln

1 T⁄1 Tx⁄

Tangente bei an die Funktion1 Tx⁄ Kpln∆S0 Tx( )

R--------------------

Abbildung 4.14: Differentielle Auswertung der van’t Hoff Gleichung (mit Kp = K).

Andere Gleichungen fur die Temperaturabhangigkeit der Geschwindigkeitskonstan-

ten

In der Praxis wird haufig von temperturunabhangigen Arrheniusparametern A und EA ausge-

gangen. Da dies jedoch oft nicht genugt, werden weitere Gleichungen mit mehreren temperatu-

runabhangigen Parametern eingesetzt, um die Temperaturabhangigkeit der Arrheniusparameter

zu modellieren. Eine haufig verwendete Form ist

k(T ) = A′ T b exp

(− Ea

RT

)(4.72)

wobei A′, b und Ea als temperaturunabhangig angenommen werden. Hiermit ergibt sich fur die

temperaturabhangigen Arrheniusparameter

A = A′ (eT )b (4.73a)

EA = Ea + b RT (4.73b)

Tabellen mit entsprechenden Parametern fur zahlreiche Reaktionen finden sich bei

[Warnatz et al. 1999] und [Atkinson 1989].

4.3 Die Theorie des Ubergangszustandes

Die Theorie des Ubergangszustandes gehort zu den fruchtbarsten Theorien der Geschwindigkeits-

konstanten chemischer Elementarreaktionen. Sie wird gelegentlich auch als Theorie des aktivier-

ten Komplexes bezeichnet (englisch ”transition state theory”, TST, oder ”activated complex



theory”, ACT, auch ”absolute rate theory”, ART). Besonders fur unimolekulare Reaktionen ist

auch “Quasigleichgewichtstheorie” (”quasiequilibrium theory”, QET) gebrauchlich. Man kann

sie elementar mit quasithermodynamischen Konzepten einfuhren, wobei ihre Anwendung dann

auf eine Auswertung und Deutung der Temperaturabhangigkeit der Geschwindigkeitskonstanten

beschrankt ist, die nicht wesentlich uber die Auswertung und Deutung im Rahmen der Arrheni-

usgleichung hinausgeht. Ein besserer Zugang erfolgt uber statistisch-thermodynamische Konzep-

te, wobei erkennbar wird, dass die Theorie des Ubergangszustandes prinzipiell zur ”absoluten”

(ab initio) Berechnung von Geschwindigkeitskonstanten geeignet ist. Dies erlaubt ein wesentlich

tieferes Verstandnis der Grundlagen dieser Theorie. Wir werden diesen zweiten Zugang hier im

Rahmen einer sehr einfachen Darstellung wahlen. Wir wollen hier jedoch die wichtigsten Ergeb-

nisse der Theorie zusammenfassen, da sie in allen Bereichen der Chemie, von der anorganischen

uber die organische bis hin zur Biochemie von grundlegender Bedeutung ist.

4.3.1 Die physikalische Grundidee der Theorie des Ubergangszustandes: Eine

Analogie zur Effusion oder Ausstromung aus einem Behalter

Die Grundidee der Theorie des Ubergangszustandes kann man durch die Analogie des Aus-

stromens eines Gases (Teilchenzahl N) durch den engen Flaschenhals einer Flasche in ein Va-

kuum verstehen (Bild 4.15). Der Flaschenhals sei genugend eng, so dass sich der Druck p in der

Flasche nur langsam andert. Zur Berechnung der Ausstromungsgeschwindigkeit −dN/dt muss

man die Geschwindigkeit vs der Molekule am Flaschenhals mit der Querschnittsflache F des

Flaschenhalses und der Konzentration CF der Molekule am Flaschenhals multiplizieren. Die pro

Zeiteinheit ins Vakuum austretende Zahl von Molekulen ist also mit der Idealgasnaherung fur

CF gegeben durch

− dN

dt= vs F CF = vs F

pF

kBT(4.74a)

p C,pkT------=

pF p≤

p 0≈

Strömungsgeschwindigkeit vs

kBT

Abbildung 4.15: Ausstromung eines Gases aus einer Gasflasche mit engem Flaschenhals.



In der Differentialnotation lasst sich dies auch anschaulich schreiben mit dem Volumen V und

dem Differential dV = Fdx, wobei die x-Achse die Stromungsrichtung angibt mit der Konzen-

tration CF = −dN/dV und vs = dx/dt (−dN = CF dV ist positiv)

− dN

dt= −dV

dt

dN

dV=

dx

dtF CF (4.74b)

Wenn die Flasche geschlossen ist, so gilt pF = p (Gleichgewichtsdruck). Bei offener Flasche kann

man bei kleinem Flaschenhals annehmen, dass der Druck am Flaschenhals ungefahr gleich dem

Gleichgewichtsdruck ist, in Wahrheit wird er etwas kleiner sein, also

pF . p (4.75)

− dN

dt= vsF

(pF

kBT

). vsF

(p

kBT

)(4.76)

Die Annahme, dass die Konzentration der Molekule am Flaschenhals gleich der Gleichgewichts-

konzentration ist, erlaubt uns eine einfache Abschatzung der Ausstromungsgeschwindigkeit bei

bekanntem p und vs. Wenn weiterhin der Flaschenhals von molekularer Dimension ist, konnen

wir annehmen, dass die thermische Geschwindigkeitsverteilung nicht wesentlich durch die Aus-

stromung gestort ist. Berucksichtigt man die Tatsache, dass im Mittel nur die Halfte der Mo-

lekule einen Geschwindigkeitsvektor in Richtung einer Ausstromung hat (d.h. CF(Ausfluss)'

p/(2kBT )) und dass fur die hier massgebliche eindimensionale Maxwell-Boltzmann-Verteilung

gilt

vs ≈ 〈|v1D|〉 =1

2〈|v3D|〉 =

√2kBT

πm(4.77)

(〈|v1D|〉 ist der eindimensionale mittlere Geschwindigkeitsbetrag (in einer Richtung), 〈|v3D|〉 der

mittlere Geschwindigkeitsbetrag aus Gl. (4.29)), so findet man

− dN

dt=

1

2

√2kBT

πmF C =

1

2

√2RT

πMF

(p

kBT

)(4.78)

Man bezeichnet den Prozess der molekularen Ausstromung auch als Effusion. Die Effusionsge-

schwindigkeit ist umgekehrt proportional zur Molekulmasse m (Molmasse M) und ist deshalb

prinzipiell zur Molmassenbestimmung oder in einem Gasgemisch von Isotopen verschiedener

Masse zur Isotopentrennung geeignet. Unabhangig davon, ob wir die wahre Stromungsgeschwin-

digkeit vs oder die mittlere thermische Geschwindigkeit 〈|v1D|〉 verwenden, erkennt man, dass

wegen der Ungleichung Gl. (4.75) die Gleichgewichtsannahme zu einer oberen Schranke fur

die wahre Ausstromungsgeschwindigkeit fuhrt. Die Berechnung der Effusionsgeschwindigkeit ist

auch an sich wichtig, und man sollte sie sich neben der allgemeinen Vorgehensweise merken. Das



hier diskutierte Vorgehen zur Berechnung eines Durchsatzes an einem “Flaschenhals” fur ein

kinetisches Phanomen lasst sich in einer Vielzahl von Beispielen anwenden. Wir wollen das Ver-

fahren nun auf die Reaktionskinetik von Molekulen anwenden. Zuvor seien die hauptsachlichen

gedanklichen Schritte bei dieser Vorgehensweise nochmals zusammengefasst:

1. Der kinetische Prozess wird durch einen “Flaschenhals” bestimmt, einen Raumbereich, wo

im Fall der Ausstromung eine enge Begrenzung des Gasflusses, im Falle der Reaktion des

“Reaktionsflusses” zu erwarten ist. Es ist der Ort minimaler Stoffmenge als Funktion der

Stromungsrichtung (im Gleichgewicht).

2. Die Geschwindigkeit des Prozesses wird aus der Konzentration und der Flussgeschwindig-

keit am Flaschenhals berechnet (vF = −dN/dt = vs F CF).

3. Die Konzentration CF am Flaschenhals wird als Gleichgewichtskonzentration C (im Gleich-

gewicht mit dem “Reservoir” in der Flasche oder allgemeiner der Reaktanden) und die

Flussgeschwindigkeit vs als thermische Gleichgewichtsgeschwindigkeit approximiert. Hier-

bei erwartet man, dass diese Approximation einen oberen Grenzwert fur den wahren Wert

liefert.

Bei der Anwendung auf molekulare chemische Prozesse werden wir nun zunachst besprechen,

was dort die Rolle des Flaschenhalses ubernimmt. Sodann werden wir durch Anwendung der

genannten Schritte zur Berechnung der Geschwindigkeitskonstanten mit Hilfe einer geeigneten

Gleichgewichtsannahme am Flaschenhals kommen.

4.3.2 Reaktionskoordinaten, Flaschenhalse, Sattelpunkte und Energiebarrie-

ren auf molekularen Potentialhyperflachen

Die Analogie zwischen dem Ausstromen eines Gases durch eine kleine Offnung und einer chemi-

schen Reaktion lasst sich durch Betrachtung der Landkarte der potentiellen Energien als Funk-

tion der Position der Atome in einer molekularen Umlagerung verstehen. Selbst fur einfachste

Umlagerungen wie etwa die Isomerisierung

HNC� HCN (4.79)

ware eine ”Landkarte” der potentiellen Energie in drei Dimensionen (z. B. zwei Bindungslangen

rCH und rCN sowie ein Winkel) notig. Wir konnen zur Veranschaulichung jedoch vereinfachend

annehmen, dass die CN Bindungslange rCN bei der Isomerisierung konstant bleibt. Dann hat



man wie bei Landkarten mit Hohenlinien auf einer Flache eine Darstellung der potentiellen Ener-

gie durch “Aquipotentiallinien” gleicher Energie auf einer Flache wie in Bild 4.16 dargestellt.

N C

M1M2

=y / 1

00 p

m

x / 100 pm

Abbildung 4.16: Aquipotentiallinien fur die Isomerisierung HNC� HCN bei festgehaltener Bin-

dungslange rCN. Die Graphik zeigt die potentielle Energie als Funktion der Position des H-Atoms

in einer Ebene (x, y) relativ zu C-N wie gezeichnet. x gibt die Position in Richtung der C-N

Achse und y die Position senkrecht hierzu an. Der Ursprung liegt etwa in der Mitte zwischen

C und N. Das tiefere Minimum M1 entspricht der Struktur HCN, das hohere Minimum M2 der

Struktur CNH. Der Energieunterschied zwischen benachbarten Aquipotentiallinien ist 0.5 eV

(ca. 48 kJ mol−1). Die gestrichelte Linie mit Pfeilen gibt die Reaktionskoordinate rq an, 6= mar-

kiert die Struktur des Ubergangszustandes an der Stelle r 6=q die dem “Flaschenhals” entspricht

(Sattelpunkt oder Pass auf dem Energiegebirge) nach [Murrell et al. 1978].

Die chemische Umlagerung lasst sich hier als Wanderung des H-Atoms vom Minimum M2 zum

Minimum M1 verstehen, entsprechend einer “Stromung” der Molekule von der Reaktanden- auf

die Produktseite, ungefahr entlang der eingezeichneten Reaktionskoordinate rq. Hierbei wird wie

bei der Ausstromung eines Gases durch einen Flaschenhals eine besonders ungunstige Stelle mi-

nimaler Wahrscheinlichkeit entlang rq an der Stelle r 6=q entscheidend sein (wegen der Boltzmann-

Verteilung ist die Besetzung hier am geringsten). Es ist gebrauchlich, die Darstellung auf eine

Dimension, also potentielle Energie als Funktion von rq zu beschranken. Wie in Bild 4.17 ge-



zeigt, erscheint der Sattelpunkt aus Bild 4.16 als Maximum der potentiellen Energie entlang der

Reaktionskoordinate rq. Es ist nun naheliegend, die Reaktionsgeschwindigkeit aus dem Gleich-

gewichtsfluss an der Stelle r 6=q zu berechnen, wobei diese Stelle mit einem speziellen Symbol 6=

als Ubergangszustand bezeichnet wird.

Abbildung 4.17: Potentielle Energie als Funktion der Reaktionskoordinate rq fur eine Isomeri-

sierung (schematisch der gestrichelten Linie mit Pfeilen (rq) in Bild 4.16 folgend).

Ganz allgemein ergibt sich die potentielle Energie eines N -atomigen Molekuls als Funktion der

3N − 6 inneren Freiheitsgrade (Koordinaten) aus der Losung der Schrodingergleichung fur die

Elektronenbewegung bei der entsprechenden (festgehaltenen) Position der Atomkerne. Das ent-

spricht der nach Born und Oppenheimer benannten Naherung fur die Molekuldynamik.

4.3.3 Faktorisierung molekularer Zustandssummen

Zur Berechnung der Gleichgewichtsbesetzung am Ubergangszustand mit Hilfe von Gl. (4.5)

bis (4.9) benotigen wir noch einige Ergebnisse aus der statistischen Thermodynamik, die wir

hier kurz zusammenfassen. Es gilt oft in brauchbarer Naherung, dass die Energien Em der

molekularen Energieniveaus als Summe von Beitragen der Translation Et, der Rotation Er, der

Schwingung Ev und der elektronischen Bewegung Ee dargestellt werden kann:

Em = Et + Er + Ev + Ee (4.80)

Wir nehmen hier an, dass nur ein Quantenzustand der elektronischen Bewegung Ee (der elek-

tronische Grundzustand eventuell mit der Entartung ge) eine Rolle spielt (dieser definiert die

Potentialflache, die als Beispiel in Bild 4.16 gezeigt ist). Es folgt aus der Summe in Gl. (4.80)



und der Exponentialform der Zustandssumme, Gl. (4.7), dass die molekulare Zustandssumme

qm entsprechend diesen Beitragen faktorisiert werden kann

qm = qt qr qv ge gKernspin /σ (4.81)

Wir verwenden hier den kleinen Buchstaben q fur die Definition der Zustandssumme von einzel-

nen Molekulen und Atomen, wobei die Energieniveaus sich auf Molekule oder Atome beziehen.

Die allgemeine Zustandssumme Q in Kap. 4.1 konnte sich auch auf eine makroskopische Stoff-

menge, z. B. 1 mol eines Gases beziehen. Die allgemeinen Gleichungen sind aber vollig analog.

Hierbei ist nun in q neben der elektronischen Entartung ge noch die Kernspinentartung

gKernspin =∏i

(2Ii + 1) (4.82)

wobei Ii der Spin des Kerns i im Molekul ist. Die σ sind eine Symmetriekorrektur; Sie sind einfa-

che ganze Zahlen, die sich aus der Symmetriegruppe des Molekuls ermitteln lassen. σ ist gleich 1

fur den Fall asymmetrischer Molekule, sowie auch fur HCN oder HNC. Das Symbol σ ist nicht mit

dem Wirkungsquerschnitt zu verwechseln. Man hat in der Praxis folgende Naherungsgleichungen

fur die Anteile der Zustandssummen:

• fur die Translationszustandssumme:

qt = V

(2πmkBT

h2

)3/2

(4.83)

wobei m die Masse des Molekuls ist und V das Volumen des idealen Gases (Gl. (4.83)

impliziert die Idealgasnaherung unabhangiger Teilchen).

• fur die Vibrationszustandssumme:

qv =

s∏i=1

qvi (4.84)

mit

qvi =

(1− exp

(− hνikBT

))−1

(4.85)

s ist die Zahl der Schwingungsfreiheitsgrade (3N − 6 fur nichtlineare Molekule, 3N − 5 fur

lineare Molekule mit N Atomen). Die νi sind die Schwingungsfrequenzen zur Schwingung

i, wobei Gl. (4.85) auf der Annahme einer harmonischen Schwingung beruht.

• fur die Rotationszustandssumme:

qr =√π

(kBT

hc

)3/2

(ABC)−1/2 (4.86)



fur nichtlineare Molekule mit drei Rotationskonstanten A,B,C und

q`r =kBT

hcB(4.87)

fur lineare Molekule, mit der spektroskopischen Rotationskonstanten B.

Da gemass Gl. (4.81) und (4.83) qm und qt proportional zu V sind, definiert man auch entspre-

chende Zustandssummen pro Volumeneinheit

qm = qm/V (4.88a)

qt = qt/V (4.88b)

Die elektronische Entartung ist in der Regel 1 fur gewohnliche Molekule mit geschlossenen

Schalen (gerade Elektronenzahl), 2 fur freie Radikale mit einem ungepaarten Elektron. Von

dieser Regel gibt es allerdings Ausnahmen (z.B. fur O2 hat man ge = 3).Weiterhin ist noch die

Zustandssumme der Translation eines Teilchens der Masse m in einem eindimensionalen Kasten

der Lange d nutzlich

qt,1D = d

(2πmkBT

h2

)1/2

(4.89a)

Wegen der Additivitat der Energien des Teilchens im Kasten

Enx,ny ,nz = Enx + Eny + Enz (4.89b)

gilt offensichtlich analog zu Gl. (4.81) mit V = d3

qt,3D = (qt,1D)3 = V

(2πmkBT

h2

)3/2

(4.89c)

Es ist auch oft gebrauchlich, die Zustandssummen der inneren Freiheitsgrade zusammenzufassen

und Gl. (4.81) zu schreiben

qm = qt qint (4.90)

qint = qr qv ge gKernspin/σ (4.91)

Fur die meisten thermodynamischen Rechnungen wird gKernspin nicht weiter berucksichtigt, da

es sich bei einer chemischen Reaktion nicht andert. Hiermit haben wir die wichtigsten Formeln

fur statistische Rechnungen nach der Theorie des Ubergangszustandes zusammengestellt.



4.3.4 Statistisch thermodynamische Formulierung der Theorie des Ubergangs-

zustandes

Entsprechend der Grundidee bei der Berechnung der Effusionsgeschwindigkeit aus einem Behalter

in Kap. 4.3.1 wollen wir nun die Reaktionsgeschwindigkeit aus dem Gleichgewichtsfluss der

Molekule am “Flaschenhals” (das entspricht dem Sattelpunkt auf der Energiehyperflache) der

Reaktion berechnen. Hierzu greifen wir auf die statistisch-thermodynamische Berechnung der

Gleichgewichtskonstanten in Kap. 4.1.1 zuruck. Wir betrachten gemass Bild 4.21 Molekule mit

der Konzentration [−→X], die sich im Bereich d = r 6=q + 1

2d−(r 6=q − 1

2d)

der Reaktionskoordinate an

der Stelle des Sattelpunktes r 6=q befinden und sich, wie durch den Pfeil angedeutet, in Richtung

auf die Produktseite des Potentials hin bewegen. Der Bereich des eindimensionalen, virtuellen

“Kastens” der Lange d sei so klein gewahlt, dass das Potential V (rq) in diesem Bereich ungefahr

konstant ist, aber gleichzeitig auch so gross, dass die Zustandssumme durch eine eindimensionale

Translation mit quasikontinuierlichem Spektrum und quasiklassischer Zustandssumme approxi-

miert werden kann (siehe Kap. 4.1.2).

Wir nehmen nun an, dass die Teilchen [−→X], die sich in der Richtung von der Reaktanden- auf

rq

V rq( )

A

B

rq=

E0

d

X[ ]

rq

V rq( )

rq=

d

X[ ]

A B+

C D+

Abbildung 4.18: Potentielle Energie entlang der Reaktionskoordinate rq fur eine unimolekula-

re Isomerisierung (Links) und eine bimolekulare Reaktion (Rechts) mit Molekulen X im Be-

reich d um den Sattelpunkt (siehe auch Diskussion im Text). Streng genommen ist hier die

potentielle Energie entlang rq gezeigt, welche die Nullpunktsenergiebeitrage der Schwingungen

in allen Koordinaten ausser rq einschliesst. E0 ist also die Differenz der Energie des tiefsten

Quantenzustandes des Ubergangszustandes und des tiefsten Quantenzustandes des Reaktanden

A (die Nullpunktsenergie des Ubergangszustandes fur die Bewegung in Richtung rq wird als

vernachlassigbar klein angenommen).



die Produktseite bewegen, im Gleichgewicht mit den Reaktanden sind und dass keine Molekule

[←−X] von der Produktseite kommen. Im Gleichgewicht ware [

−→X] = [

←−X] = 1

2 [X] wobei [X] die

Konzentration der Molekule am Sattelpunkt im tatsachlichen Gleichgewicht ist, die sich zu ge-

nau gleichen Teilen aus [−→X] und [

←−X] zusammensetzt, da diese beiden Flusse “vorwarts” und

“ruckwarts” sich ja genau aufheben mussen. Hiermit konnen wir die Gleichgewichtskonzentrati-

on [−→X]eq berechnen (Beispiel der unimolekularen Reaktion mit Reaktand A, siehe Gl. (4.8) und

(4.9)):−→[X]eq =

q−→X

qA[A] exp

(− E0

kBT

)(4.92)

q−→X

= q 6=1

2d

(2πµkBT

h2

)1/2

(4.93)

q 6= wird als Zustandssumme des Ubergangszustandes bezeichnet, der hiermit bei festgehalte-

nem r 6=q einen inneren Freiheitsgrad (Schwingungsfreiheitsgrad) weniger besitzt als ein normales

nichtlineares Molekul (3N−7 statt 3N−6). Ansonsten erfolgt die Berechnung von q 6= wie bei ei-

nem normalen Molekul. Der ”Ubergangszustand” als terminus technicus bezeichnet den Zustand

bei festgehaltenem Wert r 6=q . Aus dieser Definition ergibt sich, dass der Ubergangszustand im

Gegensatz zu den Molekulen−→X keine meßbare Konzentration besitzt, da die Wahrscheinlichkeit,

ein Molekul mit dem exakten Wert q 6= fur die Reaktionskoordinate zu finden, genau gleich Null

ist. Der zweite Faktor in Gl. (4.93) entspricht der Translationszustandssumme fur die Molekule−→X ( = halber Wert wie fur X). µ ist die reduzierte Masse fur eine Bewegung entlang rq an der

Stelle r 6=q . µ ist in der Regel nicht einfach zu berechnen. Wir werden jedoch sehen, dass es spater

fur die Berechnung der Reaktionsgeschwindigkeit nicht benotigt wird. Man hat namlich fur die

mittlere Geschwindigkeit 〈|v1D|〉 der Bewegung von Reaktand zu Produkt am Sattelpunkt aus

der eindimensionalen Maxwell-Boltzmann-Verteilung:

〈|v1D|〉 =

(2kBT

πµ

)1/2

(4.94)

Man berechnet die Reaktionsgeschwindigkeit als Gleichgewichtsfluss am Sattelpunkt

− d [A]

dt= vc = [

−→X]eq

〈|v1D|〉d

(4.95a)

Analog zu Gl. (4.78) lasst sich auch diese Gleichung anschaulich in der Differentialschreibweise

verstehen, wenn wir −d[A]/drq = [−→X]eq/d setzen und 〈|v1D|〉 = drq/dt (−d[A] ist wiederum

positiv):

− d [A]

dt= −d [A]

drq

drqdt

= [−→X]eq 〈|v1D|〉 /d (4.95b)



Also erhalt man fur die Reaktionsgeschwindigkeit vc mit der Geschwindigkeitskonstanten kuni(T )

der unimolekularen Reaktion mit der Annahme [−→X] = [

−→X]eq aus Gl. (4.92)

− d [A]

dt= vc = kuni(T ) [A]

=q 6=

qAexp

(− E0

kBT

)[A]

d

2h(2πµkBT )1/2

(2kBT

πµ

)1/2 1

d(4.96)

Sowohl die willkurlich gewahlte Lange d des Kastens am Sattelpunkt als auch die schwer zu

berechnende reduzierte Masse µ fur die Bewegung am Sattelpunkt fallen bei der Vereinfachung

dieser Gleichung durch Kurzen weg und man erhalt die 1. Eyringsche Gleichung:

kuni(T ) =kBT

h

q 6=

qAexp

(− E0

kBT

)(4.97)

kBT/h ist ein universeller Frequenzfaktor, der bei 300 K den Wert 6.23×1012 s−1 annimmt, q 6=/qA

wird als ”statistischer Faktor” (oder auch entropischer Faktor, siehe unten) bezeichnet. Das Pro-

dukt dieser beiden Faktoren entspricht ungefahr (aber nicht exakt) dem praexponentiellen Faktor

A (T ) nach Arrhenius. Die Schwellenenergie E0 ist die Differenz zwischen der Energie am Ma-

ximum des effektiven eindimensionalen Potentials in Richtung der Reaktionskoordinate rq und

der Nullpunktsenergie des Reaktanden A (siehe Bild 4.18 links). Wenn E0 gross ist, dominiert

der Beitrag des exponentiellen Faktors exp (−E0/kBT ) und entspricht ungefahr (aber wiederum

nicht genau) dem exponentiellen Faktor mit der Aktivierungsenergie EA nach Arrhenius. q 6=,

qA und exp (−E0/kBT ) sind dimensionslos, dementsprechend hat kuni (T ) in Gl. (4.97) fur die

unimolekulare Reaktion die Dimension Zeit−1.

Sowohl die molekularen Zustandssummen als auch E0 lassen sich prinzipiell alle ab initio, das

heisst aus grundlegenden quantenmechanischen und statistisch mechanischen Gesetzen, berech-

nen. Die Theorie des Ubergangszustandes ist also prinzipiell eine Theorie der Geschwindig-

keit von Elementarreaktionen, wenn auch eine Naherung. In diesem Sinne geht die Theorie des

Ubergangszustandes uber die empirische Arrheniusgleichung hinaus. Gelegentlich findet man

auch noch Formen von Gl. (4.97) und (4.99) mit einem dynamischen Korrekturfaktor, dem

Transmissionskoeffizienten κ, also z.B. statt Gl. (4.97)

k (T ) = κkBT

h

q 6=

qAexp

(− E0

kBT

)(4.98)

wobei in der Regel 0 ≤ κ ≤ 1 angenommen wird, da der berechnete Gleichgewichtsfluss am

Sattelpunkt kleiner oder gleich dem wahren Fluss ist (siehe Kap. 4.3.1). q 6=, qA und qB sowie E0

(wegen diverser Nullpunktsenergiebeitrage) hangen von den Schwingungsfrequenzen und Rotati-

onskonstanten und daher von den Massen der beteiligten Atome ab, was zu einem Isotopeneffekt



fuhrt, dessen Berechnung eine wichtige Anwendung der Theorie des Ubergangszustandes ist. Die

Messung und Berechnung solcher Isotopeneffekte spielt besonders auch in der biochemischen Ki-

netik von Enzymreaktionen eine Rolle (siehe z.B. [Gandour, Schowen 1978]).

Die Nomenklatur im Bereich der Theorie des Ubergangszustandes ist leider nicht sehr einheit-

lich. Es hat sich ziemlich generell durchgesetzt, den Begriff des “Ubergangszustandes” (engl.

“transition state”) als terminus technicus fur das statistische Objekt zu reservieren, das durch

die Zustandssumme q 6= und den festen Wert der Koordinate r 6=q definiert ist. Der Begriff des

”aktivierten Komplexes” wird weniger einheitlich verwendet. Manchmal ist er ein Synonym fur

”Ubergangszustand”, manchmal wird er jedoch auch fur die X oder auch die−→X Molekule ver-

wendet, was nicht dasselbe ist.

4.3.5 Theorie des Ubergangszustandes und Stosstheorie bimolekularer Re-

aktionen

Fur bimolekulare Reaktionen erhalt man aus einer vollig analogen Herleitung

kbi (T ) =kBT

h

q 6=

qA · qBexp (−E0/kBT ) (4.99)

Hier werden die molekularen Zustandssummen pro Volumeneinheit q verwendet. Die Dimension

von kbi (T ) ist Volumen×Zeit−1, wie es auch sein muss.

Gelegentlich wird ein Gegensatz zwischen der Theorie des Ubergangszustandes und der Stosstheo-

rie konstruiert, wobei dann bei Verwendung einfachster Modelle fur den Stossquerschnitt meist

der Theorie des Ubergangszustandes der Vorzug gegeben wird. Wir haben jedoch in Kapitel

4.2 diskutiert, dass das Ergebnis einer Stosstheorie vom verwendeten Modell fur den Reakti-

onsquerschnitt abhangt. Verwendet man einen (berechneten oder gemessenen) ”exakten” Re-

aktionsquerschnitt, so hat man eine exakte Stosstheorie, die unter geeigneten Voraussetzungen

experimentelle Geschwindigkeitskonstanten genau reproduziert. Dementsprechend ist es sinnvoll,

die Theorie des Ubergangszustandes als eine Theorie zur Berechnung des Reaktionsquerschnittes

aufzufassen. Man kann die bimolekulare Geschwindigkeitskonstante Gl. (4.99) nach der Theorie

des Ubergangszustandes in folgender Form schreiben

kbi (T ) =

(8kBT

πµAB

)1/2( h2

8πµABkBT

)(q 6=int

qint,A qint,B

)exp

(− E0

kBT

)(4.100)

Bei dieser Umformung haben wir die Zustandssummen gemass Gl. (4.90) in einen Translations-

anteil qt und einem Anteil qint aufgeteilt, wobei der Translationsanteil gemass Gl. (4.83) und



(4.88b) mit den Massen mA und mB der Reaktionspartner und m6= = mA +mB eingesetzt wird.

Mit der reduzierten Masse

µAB =mAmB

mA +mB(4.101)

fur den Stoss ergibt sich aus Gl. (4.99) schliesslich Gl. (4.100). Aus dem Vergleich mit Gl. (4.40)

folgt der mittlere Reaktionsquerschnitt 〈σR〉 nach der Theorie des Ubergangszustandes

〈σR〉 =h2

8πµABkBT

q 6=int

qint,A qint,Bexp

(− E0

kBT

)(4.102)

Aus verallgemeinerten Theorien des Ubergangszustandes lassen sich auch spezifische, energie-

abhangige Reaktionsquerschnitte berechnen. Man kann die Theorie des Ubergangszustandes

bimolekularer Reaktionen also auch als eine bestimmte Form der Stosstheorie bimolekularer

Reaktionen auffassen [Quack, Troe 1981].

4.3.6 Verallgemeinerte Theorien des Ubergangszustandes

Die beschriebene, statistisch-thermodynamische Herleitung der Theorie des Ubergangszustandes

beruht auf verschiedenen Naherungen. Die wichtigste ist die Annahme des thermischen Gleich-

gewichtes zwischen Reaktandenmolekulen im Grundzustand, energetisch hochangeregten Reak-

tandenmolekulen und den−→X-Molekulen. Diese Annahmen sind nicht immer gerechtfertigt. Zum

Beispiel findet man bei unimolekularen Reaktionen in der Gasphase, dass hochangeregte Re-

aktandenmolekule nicht im Gleichgewicht mit Grundzustandsmolekulen sind, wenn der Druck

gering ist. Man kann die Theorie dann verallgemeinern, indem man fur jede Anregungsenergie E

ein Gleichgewicht zwischen den Reaktandenmolekulen A(E) und den Molekulen−→X (E) annimmt

(mikrokanonisches Gleichgewicht, mikrokanonische Theorie des Ubergangszustandes).

Man kann weiterhin die Gleichgewichtsannahme ganz ersetzen durch andere dynamische Annah-

men, zum Beispiel im statistischen Modell adiabatischer Reaktionskanale, welches auch eine Be-

rechnung zustandsselektierter, energieabhangiger Reaktionsquerschnitte erlaubt [Quack, Troe 1998].

Durch thermische Mittelung erhalt man auch aus solchen verallgemeinerten Theorien Ausdrucke

der Form (4.97) und (4.99) fur die Geschwindigkeitskonstanten, mit etwas geanderter Berech-

nung und Interpretation der q 6=.

Es stellt sich bei Reaktionen ohne Sattelpunkt oder Energiebarriere die Frage nach der Lage des

Ubergangszustandes (Bild 4.19). Man kann zeigen, dass in solchen Fallen aus den verallgemeiner-

ten Theorien folgt, dass die beste Approximation erreicht wird, wenn man den Ubergangszustand



A ′ rq( )

rq rC-C pm⁄≅

V rq( )

A ′ rq 1700K,( )

A ′ rq 300K,( )

V rq( )

100 500

Abbildung 4.19: Statistisch-mechanische Energie A′ (Helmholtzenergie) als Funktion der Reak-

tionskoordinate rq ' rcc beim Zerfall von Ethan, C2H6 → 2 CH3 (schematisch, halbquantitativ

nach [Quack, Troe 1977b]). Das Potential V (rq) (gestrichelte Linie) besitzt hier kein Maximum.

Das Maximum der freien Energie A′ liegt bei 300 K nahe bei 350 pm und bei 1700 K nahe bei

200 pm; es ist also stark T -abhangig. Man kann von einer temperaturabhangigen Position r 6=q

des Ubergangszustandes sprechen.

an der Stelle des Maximums der statistisch-mechanischen freien (Helmholtz-) Energie A′ wahlt,

die mit einer rq-abhangigen inneren Zustandssumme verknupft ist

A6= (T ) = A′ (rq, T )max = −kBT ln[q 6= (T )] (4.103)

wobei

q 6= (T ) = q (rq, T )min bei r 6=q (4.104)

q(rq, T )min entspricht dem Minimum von q(rq, T ) als Funktion von rq bei der Temperatur T .

Der entsprechende Wert r 6=q beim Minimum definiert die Position des Ubergangszustandes bei

der Temperatur T .

Es ist hier explizit vermerkt, dass q 6= (T ) und A 6= (T ) von der Temperatur abhangen. Bild

4.19 erlautert das mit dem Beispiel einer quantitativen Berechnung fur den Zerfall von Ethan,

C2H6 → 2 CH3. Solche Ergebnisse geben den haufig verwendeten Diagrammen ”freier Ener-

gien” und ”freier Aktivierungsenthalpien” als Funktion der Reaktionskoordinate eine gewisse,

wenn auch modifizierte Berechtigung. Die Theorie des Ubergangszustandes mit dem Kriterium

des Maximums der freien (Helmholtz-) Energie als Funktion einer Reaktionskoordinate wird in

der neueren Literatur auch als ”kanonische variationelle Theorie des Ubergangszustandes” be-

zeichnet (man ”variiert” die Position des Ubergangszustandes, bis man ein Maximum der freien



Energie gefunden hat).

4.3.7 Thermodynamische Schreibweise

Analog zu Gl. (4.9) konnen wir eine formale Gleichgewichtskonstante K 6=c definieren

K 6=cdef=

q 6=

qAexp

(− E0

kBT

)(4.105)

Fur eine unimolekulare Reaktion gilt weiterhin die analoge Definition einer Gibbsenergie ∆ 6=G

nach folgender Gleichung

∆ 6=Gdef= −RT lnK 6=p

def= −RT lnK 6=c (4.106)

K 6=c und ∆6=G sind so zwar eindeutig uber die berechenbaren Zustandssummen q 6= (und qA,

E0) definiert, sie haben aber anders als bei den entsprechenden thermodynamischen Beziehungen

keine unabhangige Bedeutung als ”thermodynamische” Grossen, da weder die Konzentrationen

von Ubergangszustanden [6=] noch die entsprechenden Gibbsenergien ∆ 6=G experimentell direkt

messbar sind. In der Tat hat der “Ubergangszustand”, der mit dem Symbol 6= bezeichnet wird

und einen exakt festgelegten Wert der Koordinate r 6=q besitzt, stets exakt die Konzentration Null,

da die Wahrscheinlichkeit, ein Molekul mit einem exakt festgelegten Wert von r 6=q zu finden, Null

ist. Die theoretisch definierten Grossen q 6= und K 6=c sind aber verschieden von Null. Mit diesen

Definitionen erhalt man

kuni (T ) =kBT

hexp

(−∆ 6=G

RT

)(4.107)

Verwendet man weiterhin

∆ 6=G = ∆6=H − T∆ 6=S (4.108)

findet man die 2. Eyringsche Gleichung

kuni (T ) =kBT

hexp

(∆ 6=S

R

)exp

(−∆ 6=H

RT

)(4.109)

Fur bimolekulare Gasreaktionen definiert man

kbi (T ) =kBT

h

(kBT

p

)exp

(−∆ 6=G

RT

)(4.110)

mit dem Standarddruck p und dem molekularen Standardvolumen des idealen Gases

V =kBT

p=

1

C(4.111)



wobei C eine hierdurch definierte Standardkonzentration im idealen Gas ist.

Logarithmiert man den Ausdruck kuni(T )/(kBTh−1), so erhalt man eine der van’t Hoff Darstel-

lung ahnliche Gleichung

ln

(kuni(T )

kBTh−1

)=

∆ 6=S

R− ∆ 6=H

RT(4.112)

Tragt man in einem sogenannten Eyring Diagramm ln[kuni(T )/kBTh−1] als Funktion von 1/T

auf, so erhalt man eine naherungsweise lineare Darstellung mit dem Achsenabschnitt ∆6=S/R

und der Steigung −∆ 6=H/R. Besonders in der physikalisch-organischen Chemie hat diese Form

der Auswertung, deren Analogie zur van’t Hoff Darstellung von Gleichgewichtskonstanten noch

offensichtlicher ist, als das Arrheniusdiagramm, eine weite Verbreitung [Bain 2001].

Die Angabe der nach Gl. (4.112) empirisch aus k (T ) bestimmten Aktivierungsparameter ∆ 6=S

(Aktivierungsentropie) und ∆6=H (Aktivierungsenthalpie) ist eine haufig gewahlte Alternative

zur Angabe der Arrheniusparameter A (T ) und EA (T ). Die ungefahre Beziehung zwischen den

diversen Parametern ergibt sich direkt durch Vergleich der praexponentiellen und Exponenti-

alfaktoren in der 2. Eyringschen Gleichung und der Arrheniusgleichung. Die genaue Beziehung

ergibt sich durch Einsetzen der 2. Eyringschen Gleichung in Gl. (4.65a) bis (4.69).

4.3.8 Interpretation von Arrheniuskonstanten von Elementarreaktionen mit

Hilfe der Theorie des Ubergangszustandes

Die Theorie des Ubergangszustandes erlaubt es im Prinzip, die Zustandssummen q und q 6= und

damit k(T ) zu berechnen. Man kann umgekehrt aber auch die experimentell bestimmten Kon-

stanten des ArrheniusgesetzesA (T ) und EA (T ) im Rahmen der Theorie des Ubergangszustandes

interpretieren. EA (T ) ist ungefahr gleich der Schwellenenergie E0 oder auch der Aktivierungs-

enthalpie ∆ 6=H. Im allgemeinen Fall muss man Korrekturen zu dieser Naherung berechnen,

die aber relativ klein sind, solange E0 � RT . Der praexponentionelle Faktor ist mit der Aktivie-

rungsentropie ∆6=S verknupft. Grosse, positive Werte von ∆ 6=S findet man zum Beispiel bei

einfachen Bindungsbruchreaktionen mit praexponentiellen Faktoren von 1015 s−1 bis 1017 s−1.

Das lasst sich so verstehen, dass ein Teil der positiven thermodynamischen Dissoziationsentro-

pie in der Aktivierungsentropie erscheint. Andererseits haben einfache Isomerisierungsreaktio-

nen wie z.B. cis-trans-Isomerisierungen an der C=C-Doppelbindung Aktivierungsentropien nahe

Null, mit praexponentiellen Faktoren um 1013 s−1, entsprechend A ≈ kBT/h. Negative Aktivie-

rungsentropien findet man, wenn im Ubergangszustand fur die Reaktion eine sehr spezifische,

sterisch eingeschrankte, eventuell besonders starre Struktur eingenommen wird, wie zum Bei-


4.4. ALLGEMEINE THEORIE CHEMISCHER ELEMENTARREAKTIONEN 163

spiel in der folgenden Reaktion:

CH H

H

CH H

Cl

CH2

CH2

HCl+

Abbildung 4.20: Intramolekulare HCl-Eliminierung: A = 1011.5 s−1, EA = 197 kJ mol−1.

Wahrend im Reaktand die CH3 und CH2Cl Gruppen eine nur geringfugig gehinderte Rotations-

bewegung ausfuhren konnen, was einem grossen Beitrag zur Entropie des Reaktanden entspricht,

sind diese Rotationen im Ubergangszustand eingefroren, entsprechend einer reduzierten Entro-

pie fur diese Strukturen. Hier gilt offenbar ∆ 6=S < 0 und A < kBT/h. Oft konnen also die

experimentell gefundenen Werte fur die Aktivierungsentropie eine Aussage enthalten, ob eine for-

mulierte Elementarreaktion ”sinnvoll” ist. Unvernunftige A-Faktoren deuten auf einen anderen

als den vermuteten Verlauf der Reaktion hin. ”Vernunftige” A-Faktoren beweisen andererseits

nichts. Insbesondere hat es gar keinen Sinn, Aktivierungsentropien und Aktivierungsenthalpien

zu interpretieren, bevor man sicher weiss, dass die betrachtete chemische Reaktion eine Elemen-

tarreaktion ist. Die Analyse der Geschwindigkeitskonstanten im Hinblick auf Aktivierungspara-

meter ist das Gebiet der ”thermochemischen Kinetik”. Dieses Spezialgebiet soll hier nicht im

Detail abgehandelt werden, obwohl es zweifellos praktische Bedeutung hat (fur weiterfuhrende

Literatur siehe auch [Benson 1976]).

Wahrend die Angabe der empirischen Arrheniusparameter A(T ) und EA(T ) auch fur Geschwin-

digkeitskonstanten zusammengesetzter Reaktionen sinnvoll ist (siehe Kap. 5), ist die Angabe

von Eyring Parametern aus der 1. oder 2. Eyring Gleichung (∆6=S,∆ 6=H, q 6= etc.) fur solche

Reaktionen vom Konzept her prinzipiell nicht sinnvoll. Die Eyring Gleichungen sind theoretische

Gleichungen fur die Geschwindigkeitskonstanten von Elementarreaktionen.

4.4 Kurzer Uberblick uber die allgemeine Theorie chemischer

Elementarreaktionen

Es soll hier kurz auf die Grundlagen der heutigen Theorie chemischer Elementarreaktionen ein-

gegangen werden, wobei nur die Grundkonzepte erwahnt werden, ohne dass diese hier im Detail

ausgearbeitet und erklart werden konnen.



Ausgangspunkt ist die zeitabhangige Schrodingergleichung (4.113) fur die Zustandsfunktion

(“Wellenfunktion”) Ψ(t) des reaktiven molekularen Systems mit dem Hamiltonoperator H

i~∂Ψ(t)

∂t= HΨ(t) (4.113)

Die Losungen der Schrodingergleichung lassen sich mit Hilfe des Zeitentwicklungsoperators U

schreiben

Ψ(t) = U(t, t0) Ψ(t0) (4.114)

Der Operator U lasst sich formal aus der Losung einer zu Gl. (4.113) analogen Differentialglei-

chung erhalten

i~∂U(t)

∂t= H U (4.115)

Falls der Hamiltonoperator H zeitunabhangig ist, gilt

U(t, t0) = exp[− iH (t− t0)/~

](4.116)

Fur monomolekulare Prozesse lassen sich aus diesen Gleichungen zeitabhangige Wahrscheinlich-

keitsdichten erhalten

P ({rn}, t) = |Ψ({rn}, t)|2 (4.117)

Hierbei geben die {rn} die Gesamtheit der Koordinaten aller Elektronen und Kerne im Molekul

an. Man kann auch Ubergangswahrscheinlichkeiten

Pfi = |Ufi|2 (4.118)

aus einer Matrixdarstellung des Zeitevolutionsoperators mit den Matrixelementen Ufi zwischen

den Anfangs- (i, initial) und den Endquantenzustanden (f, final) angeben.

Fur bimolekulare Reaktionen lasst sich ein Grenzubergang fur die Quantenzustande i beliebig

lange vor dem Stoss und f (nach dem Stoss) ausfuhren, der zur sogenannten Streumatrix des

Streu- oder Stossprozesses fuhrt:

Sfi = Ufi(t→ +∞, t0 → −∞) (4.119)

Die Ubergangswahrscheinlichkeiten fur einen Ubergang vom Quantenzustand i vor dem Stoss

auf einen Quantenzustand f nach dem Stoss sind dann

Pfi = |Sfi|2 (4.120)

Die Grundgleichung, welche die Reaktionsquerschnitte mit der Streumatrix verknupft, ist

σfi =π

ki|δfi − Sfi|2 (4.121)


4.4. ALLGEMEINE THEORIE CHEMISCHER ELEMENTARREAKTIONEN 165

Hierbei ist ki = (1/~)√

2µEt,i die Wellenzahl fur den Stoss, µ die reduzierte Masse und Et,i die

Translationsenergie der Relativbewegung vor dem Stoss. Alle messbaren Reaktionsquerschnitte

und Geschwindigkeitskonstanten lassen sich schliesslich durch geeignete Mittelungsprozesse uber

thermische oder andere Energieverteilungen berechnen:

σFI = 〈σfi〉 (4.122a)

k(T ) = 〈kFI〉 (4.122b)

Bild 4.21 zeigt diesen langen Weg von der zeitabhangigen Schrodingergleichung zu den Ge-

schwindigkeitskonstanten in einem Uberblick. Die am Anfang des Kapitels erwahnten einfachen

Stosstheorien entsprechen der Einfuhrung von Modellfunktionen fur den Reaktionsquerschnitt

(anstelle einer korrekten Berechnung aus der quantenmechanischen Streumatrix). Unter gewis-

sen Voraussetzungen lassen sich einfache Stossmodelle naherungsweise rechtfertigen.

Auch die einfache Theorie des Ubergangszustandes lasst sich heute auf dem Weg in Bild 4.21

uber verallgemeinerte, zustandsselektierte statistische Theorien begrunden [Quack, Troe 1998].

Hierbei werden statistische Naherungen fur die Streumatrix eingesetzt, aus denen dann sowohl

zustandsselektive Streuquerschnitte und spezifische Geschwindigkeitskonstanten, als auch ther-

mische Geschwindigkeitskonstanten berechnet werden konnen. Demgegenuber ist die statistisch

thermodynamische Formulierung der Theorie des Ubergangszustandes in Kapitel 4.3.4 eine di-

rekte Naherungstheorie nur fur die thermischen Geschwindigkeitskonstanten k(T ). Schliesslich

gibt es noch die Moglichkeit, die Freiheitsgrade der elektronischen Bewegung quantenmechanisch

zu behandeln (Berechnung der Born-Oppenheimer Potentialhyperflachen), wahrend fur die Be-

wegung der schweren Atomkerne naherungsweise die Gultigkeit der klassischen Mechanik ange-

nommen wird (Newtonsche oder Hamiltonsche Bewegungsgleichungen). Man spricht in diesem

Fall von der Methode der klassischen Trajektorien oder auch von “Molekuldynamik”. Hier wer-

den oft einfache Modellpotentialfunktionen verwendet (sogenannte Kraftfelder, z.B. GROMOS96

[van Gunsteren et al. 1996]). In der Methode von Car und Parrinello [Car, Parrinello 1985] wer-

den besonders einfache Techniken zur Berechnung der elektronischen (potentiellen) Energiefunk-

tionen durch Dichtefunktionalmethoden eingesetzt, die eine explizite Konstruktion von Potenti-

alhyperflachen vermeiden. Die Genauigkeit der verschiedenen Verfahren, die mit der klassischen

Mechanik die Bewegung von Atomkernen beschreiben, sollte nicht uberschatzt werden. Beson-

ders bei Beteiligung von Wasserstoffatomen an der Reaktion spielen quantenmechanische Effekte

wie der Tunneleffekt oft eine entscheidende Rolle.



Zeitabhängige Schrödingergleichung

ZeitevolutionsoperatorU

Zeitabhängige Wahrschein-lichkeiten, Übergangswahr-scheinlichkeiten

StreumatrixMatrixelemente

SSfi

Streuquerschnitte

Spezifische Geschwindigkeits-

Thermische Mittelung über Trans-

Zustandsselektierte Geschwindigkeits-konstanten

konstanten

Thermische Mittelung über innere

σfi σFI,

kFI E t( )

kFI T( )

k T( ) kFI=

Quantenzustände der R

^

eaktanden

lationsenergieverteilung

Summation überNiveaus derProdukte

Abbildung 4.21: Schritte in der allgemeinen Theorie chemischer Elementarreaktionen.

Ziel dieses Unterkapitels war es, die diversen theoretischen Methoden vorzustellen, um einen

Uberblick uber den aktuellen Stand der Theorie zu geben. Es sollte deutlich gemacht werden,

welche Theorien chemischer Elementarreaktionen heute zum Einsatz kommen und wie man heu-

te einfachere Theorien wie die Theorie des Ubergangszustandes auf einer hoheren theoretischen

Ebene verstehen und begrunden kann. Es ist hier nicht moglich, die weitergehenden Theorien

im Detail zu erklaren, das wurde den Rahmen unserer Darstellung bei weitem sprengen.

4.5 Thermodynamische Randbedingungen in der Kinetik

4.5.1 Detailliertes Gleichgewicht fur Elementarreaktionen in idealen Gasen

Zeitumkehrsymmetrie

Die Zeitumkehrsymmetrie der mechanischen und quantenmechanischen Bewegungsgleichungen

ist ein Naturgesetz, welches nach heutiger Kenntnis fur alle Wechselwirkungen ausser der so-

genannten schwachen Wechselwirkung gilt (diese ist fur die β-Radioaktivitat verantwortlich).

Unter Vernachlassigung sehr kleiner Effekte, welche in Molekulen noch nie, in Elementarteilchen


4.5. THERMODYNAMISCHE RANDBEDINGUNGEN 167

in wenigen Fallen nachgewiesen wurden, gilt die Zeitumkehrsymmetrie fur alle atomaren und

molekularen Prozesse in der Chemie. Hier sollen nur einige wichtige Konsequenzen dieses Geset-

zes fur die Reaktionskinetik zusammengefasst werden. Fur die Ubergangswahrscheinlichkeiten

Pfi = |Ufi|2 zwischen zwei Quantenzustanden f und i findet man diesem Gesetz entsprechend:

Pfi = |Ufi|2 = |Uif |2 = Pif (4.123)

|Ufi| ist das Matrixelement der sogenannten Zeitentwicklungsmatrix. Hieraus folgt weiter das

Prinzip der mikroskopischen Reversibilitat.

Prinzip der mikroskopischen Reversibilitat

Fur Stossquerschnitte σ hat man die folgende Formulierung:

σif gf = σfi gi (4.124)

σfi ist der Querschnitt fur den Ubergang von i nach f. gi und gf sind die statistischen Gewichte

der Niveaus i und f vor und nach dem Stoss. Der physikalische Inhalt von Gl. (4.124), eventuell

kombiniert mit Gl. (4.123), wird als Prinzip der mikroskopischen Reversibilitat bezeichnet, wobei

gelegentlich keine scharfe Unterscheidung zwischen diesem Begriff und der zugrundeliegenden

Zeitumkehrsymmetrie gemacht wird.

Prinzip des detaillierten Gleichgewichts

Man betrachte die Elementarreaktion (siehe Bild 4.22)

A

ka

�

kb

B (4.125)

Durch thermische Mittelung von energieabhangigen Reaktionsquerschnitten und -wahrscheinlich-

keiten folgt mit den Ergebnissen aus den Prinzipen der mikroskopischen Reversibilitat und des

detaillierten Gleichgewichts Prinzip des detaillierten Gleichgewichts das in Gl. (4.126) zusam-

mengefasst ist (fur ideale Gase, Reaktanden und Produkte jeweils fur sich genommen im ther-

mischen Gleichgewicht gemass der Boltzmann-Verteilung):

ka

kb= Kc =

[B]eq

[A]eq

(4.126)



ΔrU

EAa

EAb

r

V r( )

Er⟨ ⟩

EA⟨ ⟩ U

A=

EB⟨ ⟩ U

B=

Abbildung 4.22: 〈Er〉 ist die mittlere Energie der reagierenden Molekule,⟨EA⟩

und⟨EB⟩

sind

die mittleren Energien der Molekule A und B; ∆rU ist die innere Standardreaktionsenergie.

Diese Tatsache hat Konsequenzen fur die Temperaturabhangigkeit der Gleichgewichts- und der

Geschwindigkeitskonstanten (hier fur eine Isomerisierungsreaktion; der Index a steht fur die

Hinreaktion und b fur die Ruckreaktion)

Kp = Kc =ka

kb= exp

(−∆rG

RT

)(4.127)

oder mit Hilfe des Arrheniusgesetzes umformuliert:

Kc =Aa exp (−Ea

A/RT )

Ab exp(−Eb

A/RT) = exp

(∆rS

R

)exp

(−∆rH

RT

)(4.128)

Fur kleine Temperaturintervalle kann der Vorfaktor A und die Aktivierungsenergie EA als tem-

peraturunabhangig betrachtet werden, also gilt (fur eine Isomerisierung):

∆rH = ∆rU

= EaA − Eb

A (4.129)

und

exp

(∆rS

R

)=Aa

Ab(4.130)

oder∆rS

R= ln

(Aa

Ab

)(4.131)

Dieses Ergebnis lasst sich auch aus der Theorie des Ubergangszustandes herleiten, doch ist

dies eine schwachere Begrundung. Fur die einzelnen Reaktionsgeschwindigkeitskonstanten gilt

(wiederum fur eine Isomerisierung, wo Kp = Kc gilt):

ka =kBT

hexp

(−∆ 6=Ga

RT

)=kBT

hexp

(−G6= −GA

RT

)(4.132)



kb =kBT

hexp

(−

∆ 6=GbRT

)=kBT

hexp

(−G6= −GB

RT

)(4.133)

also

ka

kb=

exp(−∆ 6=Ga /RT

)exp

(−∆ 6=Gb /RT

) = exp

(−GB −G

A

RT

)

= exp

(−∆rG

RT

)= Kc (4.134)

∆rG = ∆6=Ga −∆ 6=Gb = GB −G

A (4.135)

Wahrend das Prinzip des detaillierten Gleichgewichts in der Form von Gl. (4.126) und (4.127)

fur Elementarreaktionen unter den angegebenen Voraussetzungen aus sehr grundlegenden phy-

sikalischen Gesetzen folgt, ist seine Gultigkeit im allgemeinen Fall fur andere Reaktionen und

andere Voraussetzungen nicht selbstverstandlich.

4.5.2 Zusammengesetzte Reaktionen

Fur zusammengesetzte Reaktionen gilt das Prinzip des detaillierten Gleichgewichtes nicht mehr

in der einfachen Form, die bereits vorher diskutiert wurde. Um den Gleichgewichtszustand zu

erreichen, mussen allgemein nur die Reaktionsgeschwindigkeiten der Hin- und der Ruckreaktion

gleich gross sein. Dies ist auf verschiedene Weise realisierbar.

Beispiel einer Hin- und Ruckreaktion ohne Reaktionsordnung

Wir wollen hier zunachst eine Verallgemeinerung diskutieren, die bei zusammengesetzten Reak-

tionen mit Ruckreaktionen ofter auftritt und die auch eine interessante Anwendung auf Reak-

tionen in realen Gasen und Losungen hat. Wir betrachten eine Reaktion mit der Stochiometrie:

A + B

ka

=

kb

C + D (4.136)

Im Gleichgewicht gilt:

Kc =[C]eq [D]eq

[A]eq [B]eq (4.137)

Ein mogliches Geschwindigkeitsgesetz ware:

vc =d [C]

dt= −d [A]

dt= ka [A] [B] f {[A] ... [D] , T, x}

−kb [C] [D] f {[A] ... [D] , T, x} (4.138)



x ist ein beliebiger Parameter, so konnen hier zum Beispiel die Konzentrationen von Stoffen

auftreten, die nicht in der stochiometrischen Gleichung vorkommen. f ist eine beliebige Funktion,

fur die Reaktion ”vorwarts” und ”ruckwarts” aber dieselbe. Im Gleichgewicht gilt:

− d [A]eq

dt= ...

d [D]eq

dt= 0 (4.139)

Also schreibt man weiter

ka

kb=

[C]eq [D]eq f {[A] ... [D] , T, x}[A]eq [B]eq f {[A] ... [D] , T, x}

= Kc (4.140)

Die beliebige Funktion f lasst sich durch Kurzen aus der Gleichung schaffen. Dadurch wird

zwar die Form der Beziehung mit derjenigen des detaillierten Gleichgewichts vereinbar, doch

handelt es sich nicht um eine Elementarreaktion, die Reaktionsgeschwindigkeit fur Hin- und

Ruckreaktion kann dann in der Regel nicht auf die Form

vc = k∏i

cmii (4.141)

reduziert werden. ka und kb sind hier auch nicht die gewohnlichen Geschwindigkeitskonstanten

einer Elementarreaktion. Ein konkretes Beispiel dieser Art ist die Bromwasserstoffreaktion. Die

Stochiometrie sei:

H2 + Br2

ka

=

kb

2HBr (4.142)

Das Geschwindigkeitsgesetz lautet:

1

2

d [HBr]

dt= ka [H2] [Br2]

{√[Br2]

(1 +

y [HBr]

[Br2]

)}−1

−kb [HBr]2{√

[Br2]

(1 +

y [HBr]

[Br2]

)}−1

(4.143)

In diesem praktischen Fall hangt die beliebige Funktion f, die hier als Klammerausdruck { }

erscheint, von der Brom- und der Bromwasserstoffkonzentration sowie uber den Koeffizienten y

von der Temperatur ab. y ist eine Konstante, welche sich aus mehreren Geschwindigkeitskon-

stanten der Elementarreaktionen in dem Mechanismus zusammensetzt. Die Reaktion hat keine

Reaktionsordnung, das einfache detaillierte Gleichgewicht gilt nicht, obwohl das Analogon zu

Gl. (4.126) rein rechnerisch durch Kurzen des komplizierten Faktors erfullt wird.



Beispiel einer Hin- und Ruckreaktion mit Reaktionsordnung

Fur die Stochiometrie

aA + bB

ka

=

kb

cC (4.144)

gilt im Gleichgewicht:

Kc =[C]ceq

[A]aeq [B]beq

(4.145)

Das Geschwindigkeitsgesetz fur die Hinreaktion lautet

vhinc = −1

a

(d [A]

dt

)hin

= ka [A]α [B]β [C]γ (4.146)

und fur die Ruckreaktion:

vruckc = −1

c

(d [C]

dt

)ruck

= kb [A]α′[B]β

′[C]γ

′(4.147)

Ferner gilt fur die Reaktionsgeschwindigkeit insgesamt:

− 1

a

(d [A]

dt

)gesamt

=1

c

(d [C]

dt

)gesamt

= vhinc − vruck

c = vc (4.148)

Im Gleichgewicht verschwindet vc, also gilt:

ka

kb=

[A]α′

eq [B]β′

eq [C]γ′

eq

[A]αeq [B]βeq [C]γeq

= f{T} (4.149)

Die Gleichgewichtskonstante ist temperaturabhangig

Kc = g (T ) (4.150)

Man kann T als Umkehrfunktion g−1 von g erhalten (das ist nicht 1/g, wir setzen voraus, dass

eine Umkehrfunktion existiert, wie z.B. fur die Exponentialfunktion der Logarithmus)

T = g−1 (Kc) (4.151)

Man kommt zum sehr allgemeinen Schluss, dass das Verhaltnis der beiden Reaktionsgeschwin-

digkeitskonstanten eine Funktion der Gleichgewichtskonstanten ist.

ka

kb= f

{g−1 (Kc)

}= F (Kc) (4.152)

Als Beispiel sei eine Potenzfunktion angenommen (mit n > 0)

F (Kc) = Knc (4.153)



Also gilt:

[A]α′−α [B]β

′−β [C]γ′−γ =

([C]c

[A]a [B]b

)n(4.154)

Durch Logarithmieren findet man

(α′ − α

)ln[A] +

(β′ − β

)ln[B] +

(γ′ − γ

)ln[C] = −an ln[A]− b n ln[B] + c n ln[C] (4.155)

Der anschliessende Koeffizientenvergleich liefert:

γ′ − γc

= −β′ − βb

= −α′ − αa

= n > 0 (4.156)

Durch Einsetzen von konkreten Zahlenwerten fur den Exponenten und die Reaktionsordnung

der Hinreaktion lassen sich mogliche Reaktionsordnungen der Ruckreaktion bestimmen.

Reaktionsordnung fur die Potenz in Gleichung (4.153)

Ruckreaktion

γ′ = nc+ γ

β′ = − nb+ β

α′ = − na+ α

n = 1 n = 2 n = 2.5

1 2 2.5

0 −1 −1.5

0 −1 −1.5

Tabelle 4.2: Reaktionsordnungen fur die Ruckreaktion.

Als Beispiel treffen wir die folgenden Annahmen fur die stochiometrischen Koeffizienten a =

1, b = 1, c = 1 und die Reaktionsordnung der Hinreaktion α = 1, β = 1, γ = 0. Tabelle 4.2 gibt

fur diesen Fall mogliche Reaktionsordnungen fur die Ruckreaktion. Man liest aus dieser Tabelle

zum Beispiel fur n = 2

vc = ka [A] [B]− kb [A]−1 [B]−1 [C]2 (4.157)

Wiederum bestatigt sich, dass fur zusammengesetzte Reaktionen das Prinzip des detaillierten

Gleichgewichtes in der einfachen Form nicht gilt.


Einfache Theorie chemischer Elementarreaktionen und die ... · 4.1.2 Quasikontinuierliche...

Documents

Transcript of Einfache Theorie chemischer Elementarreaktionen und die ... · 4.1.2 Quasikontinuierliche...