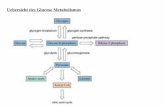
J { L , L ,…, L I KONZEPTE UND DEFINITIONEN -...
Transcript of J { L , L ,…, L I KONZEPTE UND DEFINITIONEN -...

FLUIDDYNAMIK I – ZUSAMMENFASSUNG
© Lukas Mosimann, 09-920-463 [email protected]
KONZEPTE UND DEFINITIONEN
KENNZAHLEN UND SI-EINHEITEN Exa E 1018 Dezi d 10-1 Peta P 1015 Centi c 10-2 Tera T 1012 Milli m 10-3 Giga G 109 Mikro μ 10-6 Mega M 106 Nano n 10-9 Kilo k 103 Pico p 10-12 Hekto H 102 Femto f 10-15 Deka da 101 Atto a 10-18
Grösse 𝐹 𝐿 𝑇 𝜗 𝑀 𝐿 𝑇 𝜗 Einheit Länge 𝑙 0 1 0 0 0 1 0 0 𝑚 Kraft 𝐹 1 0 0 0 1 1 -2 0 𝑁 Masse 𝑚 1 -1 2 0 1 0 0 0 𝑘𝑔 Zeit 𝑡 0 0 1 0 0 0 1 0 𝑠 Temperatur 𝜗 0 0 0 1 0 0 0 1 𝐾 Geschwindigkeit 𝑢 0 1 -1 0 0 1 -1 0 𝑚 𝑠⁄ Beschleunigung 𝑎 0 1 -2 0 0 1 -2 0 𝑚 𝑠⁄ Winkelgeschwindigkeit 𝜔 0 0 -1 0 0 0 -1 0 𝑟𝑒𝑣 𝑠⁄ , 𝑟𝑎𝑑 𝑠⁄ Druck 𝑝 1 -2 0 0 1 -1 -2 0 𝑃𝑎 = 𝑁 𝑚⁄ Energie, Moment, Arbeit 𝐸 1 1 0 0 1 2 -2 0 𝐽 = 𝑊𝑠 =
𝑁𝑚 Leistung, Energiestrom 𝑃 1 1 -1 0 1 2 -3 0 𝑊 = 𝑁𝑚 𝑠⁄ Dichte 𝜌 1 -4 2 0 1 -3 0 0 𝑘𝑔 𝑚⁄ Massenstrom �� 1 -1 1 0 1 0 -1 0 𝑘𝑔 𝑠⁄ Volumenstrom Q 0 3 -1 0 0 3 -1 0 𝑚 𝑠⁄ Dynamische Viskosität 𝜇 1 -2 1 0 1 -1 -1 0 𝑃𝑎 𝑠 =
𝑁𝑠 𝑚⁄ Kinematische Viskosität 𝜐 0 2 -1 0 0 2 -1 0 𝑚 𝑠⁄ Oberflächenspannung 𝜎 1 -1 0 0 1 0 -2 0 𝑁 𝑚⁄ Spez. Wärmekapazität 𝑐 0 2 -2 -1 0 2 -2 1 𝐽 𝑘𝑔 𝐾⁄ Wärmeleitfähigkeit 𝜆 1 0 -1 -1 1 1 -3 -1 𝑊 𝑚 𝐾⁄ Spez. Gaskonstante 𝑅 0 2 -2 -1 0 2 -2 -1 𝐽 𝑘𝑔 𝐾⁄
Reynolds-Zahl 𝑅𝑒 = ∙ = ∙ ∙ Nusselt-Zahl 𝑁𝑢 = ∙
Froude-Zahl 𝐹𝑟 = ∙ Péclet-Zahl 𝑃𝑒 = ∙
Mach-Zahl 𝑀𝑎 = Prandtl-Zahl 𝑃𝑟 =
Euler-Zahl 𝐸𝑢 = ∙ = (𝛾 ∙ 𝑀𝑎 ) Rayleigh-Zahl 𝑅𝑎 =
Knudsen-Zahl 𝐾𝑛 = Stokes-Zahl 𝑆𝑡 = ∙∙
Weber-Zahl 𝑊𝑒 = ∙ ∙ Reibungskoeffizient 𝑐 = ∙
Strouhal-Zahl 𝑆𝑡𝑟 = ∙ Druckkoeffizient 𝑐 = ∙∙
Eckert-Zahl 𝐸𝑐 = ∙ Auftriebsbeiwert 𝑐 = ∙∙ ∙
Fourier-Zahl 𝐹𝑜 = ∙ Widerstandsbeiwert 𝑐 = ∙∙ ∙
Grashof-Zahl 𝐺𝑟 = 𝑔 ∙ 𝑙 ∙ 𝛼 ∙ (𝑇 − 𝑇 ) ∙ 𝜐 Momentenbeiwert 𝜁 = ∙∙ ∙
EIGENSCHAFTEN VON FLUIDEN Ein Fluid ist ein von der Realität abstrahiertes Kontinuum, welches nur Druckkräfte aufnehmen kann. Zug- und Scherkräfte führen zu Fliessbewegungen.
Feststoff: 𝜏 = 𝐺 ∙ 𝛾 Newton’sches Fluid: 𝜏 = 𝜇 ∙ ��
𝜇 dynamische Viskosität 𝜈 = 𝜇 𝜌⁄ kinematische Viskosität �� Deformationsgeschwindigkeit
Elastoviskoses Fluid: (z.B. Maxwell-Fluid)
�� = 𝜏𝜇 + ��
𝐺
für �� = 𝑐𝑜𝑛𝑠𝑡.: 𝜏(𝑡) = �� ∙ 𝜇 ∙ 1 − 𝑒 ∙ ⁄
Thixotropes Fluid: Wird mit der Zeit flüssiger
Rhopexes Fluid: Wird mit der Zeit fester
OBERFLÄCHENSPANNUNG Die Oberflächenspannung ist durch unsymmetrische moleku-lare Kraftwirkung an der Trennfläche zweier Medien bedingt.
Laplace-Gleichung: ∆𝑝 = 𝜎 +
∆𝑝: Drucksprung 𝜎: Oberflächenspannung [𝑁 𝑚⁄ ] 𝑅 / : Krümmungsradien
SCHALLGESCHWINDIGKEIT
𝑎 = |
für Ideales Gas: 𝑎 = 𝛾𝑅𝑇 mit 𝛾 =
DIMENSIONSANALYSE UND ÄHNLICHKEITSTHEORIE Wir versuchen für ein gegebenes Problem eine Funktion Φ in Abhängigkeit dimensionsloser Parameter zu finden:
𝑓(𝑝 , 𝑝 , … , 𝑝 ) = 𝛷(𝛱 , 𝛱 , … , 𝛱 ) 𝑘 = 𝑛 − 𝑟 ≤ 𝑛
Dabei sind die Funktionen 𝑓 und Φ im Allgemeinen unbekannt bzw. müssen gemessen werden.
Modellierung: wenn {𝛱 , … 𝛱 } ≡ {𝛱 , … , 𝛱 }
dann gilt: 𝛷 𝛱 , ≡ 𝛷 𝛱 , sofern die Physik für Modell und Original die gleiche ist.
DIMENSIONSMATRIX Gegeben: � 𝑛 dimensionsbeh., physikalische Grössen {𝑝 , 𝑝 , … , 𝑝 } � eine aus 𝑚 dimensionsbeh. Masseinheiten bestehende
Basis {𝐴 , … , 𝐴 }
[𝑝 ] = 𝐴 ∙ 𝐴 ∙ … ∙ 𝐴 [𝑝 ] = 𝐴 ∙ 𝐴 ∙ … ∙ 𝐴 ⋮ [𝑝 ] = 𝐴 ∙ 𝐴 ∙ … ∙ 𝐴 Dimensionsmatrix
Vorgehen zur Lösung: 1. Aufstellen einer Liste aller dimensionsbehafteten Grössen
des Problems {𝑝 , 𝑝 , … , 𝑝 } in Form der Dimensionsmatrix 2. Notiere: 𝑛 =Anzahl dieser Parameter 3. Bestimmung Anzahl 𝑟 der unabhängigen Basisgrössen
(Masseinheiten) des Problems 4. Errechnen der Anzahl möglichen dimensionsloser
Parameter 𝑘 = 𝑛 − 𝑟 5. Auswahl von r Parametern aus der Liste {𝑝 , 𝑝 , … , 𝑝 } mit
denen die unabhängigen Masseinheiten erfasst werden, d.h. Einführung einer Liste mit Referenzparametern {𝑝 , 𝑝 , … , 𝑝 } ⊂ {𝑝 , 𝑝 , … , 𝑝 }
6. Beschreibung der Dimensionen der 𝑘 restlichen Originalparametern mittels eines Produktansatzes [𝑝 ] = [𝑝 ] ∙ [𝑝 ] ∙ … ∙ [𝑝 ] 𝑖 = 1 … 𝑘
7. Durch Vergleich der Exponenten im zugrundegelegten Masssystem ergibt sich für jeden der 𝑘 Parameter ein lineares 𝑟 × 𝑟 Gleichungssystem
𝑏 ⋯ 𝑏⋮ ⋱ ⋮
𝑏 ⋯ 𝑏∙
𝛼⋮
𝛼=
𝑏⋮
𝑏
8. Die 𝑘 dimensionslosen Parameter berechnen
𝛱 = 𝑝𝑝 𝑝 … 𝑝
⋮ 𝛱 = 𝑝
𝑝 𝑝 … 𝑝

KINEMATIK DES STRÖMUNGSFELDES
BESCHREIBUNG DES STRÖMUNGSFELDES
Lagrange'sche Beschreibung: Das Fluidpartikel wird in seiner Bewegung im Raum verfolgt.
Euler'sche Beschreibung: �Änderung der Strömungsgrössen werden an einer festen Stelle im Raum betrachtet und als Feldgrössen dargestellt.
Beschreibung Lagrange (partikelbezogen)
Euler (raumfest)
Ort 𝜉(𝑡) = 𝜉(𝑡, 𝜉 , 𝑡 ) (Bahnlinie)
��, 𝑡
Geschwindigkeit ��(��, 𝑡)
(Geschw.Feld)
Beschleunigung
(Beschl. im Str.Feld)
SUBSTANTIELLE ABLEITUNG
Die Änderung einer Strömungsgrösse �� für ein einzelnes Fluidpartikel berechnet sich als:
= + �� ∙ 𝛻 �� =
⎣⎢⎢⎢⎡ + 𝑢 + 𝑣 + 𝑤
+ 𝑢 + 𝑣 + 𝑤+ 𝑢 + 𝑣 + ⎦
⎥⎥⎥⎤
Lokale Ableitung: Änderung, die ein (möglicherweise unbe-wegtes) Fluidpartikel dadurch wahrnimmt, dass sich das lokale Strömungsfeld zeitlich ändert.
Konvektive Ableitung: Änderung, die ein mit Geschwindigkeit �� bewegtes Teilchen in einem räumlich variablen (möglicherweise zeitlich konstanten) Strömungsfeld erfährt.
REYNOLDS-TRANSPORTTHEOREM
𝑑𝑑𝑡 𝑓(��, 𝑡)𝑑𝑉
( )= 𝜕
𝜕𝑡( )
𝑓(��, 𝑡)𝑑𝑉 + 𝑓(��, 𝑡)�� ∙ 𝑛( )
𝑑𝑆
Spezialfall: Ortsfestes Volumen
𝑑𝑑𝑡 𝑓(��, 𝑡)𝑑𝑉
( )= 𝜕
𝜕𝑡( )
𝑓(��, 𝑡)𝑑𝑉
KINEMATISCHE EIGENSCHAFTEN VON STRÖMUNGEN
� Inkompressible Strömung: = 0
� Inkompressibles Fluid: 𝜌 = 𝑐𝑜𝑛𝑠𝑡. � Stationäre (instantane) Strömung (. ) = 0
� Gleichförmige Strömung 𝛻 ∙ �� = 0 → Geschw. ortsunabhängig → Stromlinien sind gerade und parallel
� 2dimensionales Problem (. ) = 0
� rotationssymmetrisches Problem (. ) = 0
� in 𝑠-Rtg. Ausgebildete Strömung (��) = 0
� Wirbelstärke 𝜔 = 𝛻 × �� = 𝑟𝑜𝑡 ��
𝜔 =
⎝
⎜⎛
−−− ⎠
⎟⎞
, ,
𝜔 =
⎝
⎜⎛
−−− ⎠
⎟⎞
, ,
� Potentialwirbel rotations-/wirbelfrei 𝜔 = 0 AUSGEZEICHNETE LINIEN
Stromlinien: Parallel zur momentanen Strömung falls 𝑢, 𝑣, 𝑤 = 𝑓(𝑥, 𝑦, 𝑧)
= = → separieren, integrieren falls 𝑢, 𝑣, 𝑤 ≠ 𝑓(𝑥, 𝑦, 𝑧)
= → integrieren
Bahnlinien: Pfad eines einzelnen Partikels falls 𝑢, 𝑣, 𝑤 = 𝑓(𝑥, 𝑦, 𝑧)
= 𝑢, = 𝑣, = 𝑤 → separieren, integrieren falls 𝑢, 𝑣, 𝑤 ≠ 𝑓(𝑥, 𝑦, 𝑧)
= �� → integrieren
Streichlinien: Verbindungslinien aller Partikel, die durch denselben Punkt gegangen sind.
Spezialfall: Stationär Stromlinien=Bahnlinien=Streichlinien
STROMFUNKTION Ψ
�� = 𝛻 × 𝛹 2D: �� =−
,
Inkompressible Kontinuitätsgleichung erfüllt, da 𝑑𝑖𝑣 �� = 𝑑𝑖𝑣 𝑟𝑜𝑡 𝛹 = 0
Auf Stromlinien gilt: 𝛹 = 𝑐𝑜𝑛𝑠𝑡. Volumenstrom zwischen zwei Stromlinien: �� = 𝛹 − 𝛹
Massenfluss: �� = 𝜌 ∙ 𝑏 ∙ (𝛹 − 𝛹 ) wobei 𝑏: Breite der Fluidschicht in 𝑧-Rtg.
ERHALTUNGSSÄTZE
EIGENSCHAFTEN
� Vernachlässigbare Wärmeleitung: −𝛻 ∙ �� = 0 � Kleine Dissipation: 𝜏: 𝛻 ∙ �� = 0
→ punktweise Multiplikation
� Newton’sches Fluid: 𝜏 = 𝜇 +
� Stationär: (… ) = 0 � Adiabate Wand: �� = 0 � Isotherme Wand: 𝑇 = 𝑐𝑜𝑛𝑠𝑡. � mit cost. Wärmestrom geheizte Wand: �� = 𝑐𝑜𝑛𝑠𝑡. � Perfektes Fluid: 𝜏 = 0 � Grosser Querschnitt: �� = 0 � Wandschubspannung: 𝜏 = 𝜏 = 𝜇 + | ( )
MASSENERHALTUNG �� − �� = 0 �� = 𝜌 ∙ �� = 𝜌 ∙ 𝐴 ∙ 𝑢 , �� = ∫ �� ∙ 𝑛 𝑑𝐴
Integreale Formulierung:
𝑑𝑚𝑑𝑡 = 𝜕
𝜕𝑡 𝜌 𝑑𝑉 + 𝜌�� ∙ 𝑛 𝑑𝑆 = 0
Differentielle Form – Kontinuitätsgleichung: 𝜕𝜌𝜕𝑡 + 𝛻 ∙ (𝜌��) = 0
für inkompressible Strömungen: 𝛻 ∙ �� = 0
lokale Ableitung konvektive Ableitung
zeitl. Massenänderung Massenfluss durch S

IMPULSERHALTUNG
𝑃 = ∫ 𝜌�� 𝑑𝑉 = ∑ ��
Integreale Formulierung: 𝐷𝑃𝐷𝑡 = 𝜕
𝜕𝑡 (𝜌𝑢) 𝑑𝑉 + 𝜌𝑢(𝑢 ∙ 𝑛) 𝑑𝑆 = 𝜎 ∙ 𝑛 𝑑𝑆 + 𝜌𝑓 𝑑𝑉 + ��
Oberflächenkräfte:
𝜎 ∙ 𝑛 𝑑𝑆 = − 𝑝𝑛 𝑑𝑆 + 𝜏 ∙ 𝑛 𝑑𝑆
wobei 𝜎 = −𝑝𝕀 + 𝜏 =(−𝑝 + 𝜏 ) 𝜏 𝜏
𝜏 −𝑝 + 𝜏 𝜏𝜏 𝜏 (−𝑝 + 𝜏 )
Differentielle Form: 𝜕(𝜌��)
𝜕𝑡 + 𝛻 ∙ (𝜌����) = −𝛻𝑝 + 𝜌𝑓 + 𝛻𝜏
Impulsgleichung:
𝜌 𝜕��𝜕𝑡 + 𝜌(�� ∙ 𝛻)�� = −𝛻𝑝 + 𝜌𝑓 + 𝛻𝜏
für Hydrostatik: (�� = 0, 𝜏 = 0) 𝜌𝑓 = 𝛻𝑝
REIBUNGSFREIE STRÖMUNG – EULER-GLEICHUNG: Annahme: perfektes Fluid (𝜏 = 0) 𝐷��𝐷𝑡 = 𝜕��
𝜕𝑡 + �� ∙ 𝛻 ∙ �� = − 1𝜌 𝛻𝑝 + 𝑓
Randbedingungen: � An einer festen Wand: 𝑛 ∙ �� = 0, d.h. 𝑢 ≡ 0 � An einer Trennfläche zweier Fluide: : 𝑛 ∙ �� = 𝑛 ∙ ��
d.h. 𝑢 , = 𝑢 , und 𝑝 = 𝑝 REIBUNGSFREIE STRÖMUNG – BERNOULLI-GLEICHUNG:
Annahmen: 𝜌 = 𝑐𝑜𝑛𝑠𝑡., �� = 0, zwei Punkte auf einer Stromlinie oder rotationsfreie Strömung
𝜕��𝜕𝑡 ∙ 𝑑𝑠 + ��
2 + 𝑝𝜌 + 𝑈 = 0
wobei 𝑈 = 𝑔 ∙ 𝑧: Kraftpotential
für stationäre Strömungen: ��2 + 𝑝
𝜌 + 𝑈 = ��2 + 𝑝
𝜌 + 𝑈 = 𝑐𝑜𝑛𝑠𝑡. = 𝐻
gilt nur entlang Stromlinien! falls Strömung rotationsfrei: 𝐻 = 𝑐𝑜𝑛𝑠𝑡. im ganzen Feld
� barotrope Strömung: 𝜌 = 𝜌(𝑝) � barokline Strömung: 𝜌 = 𝜌(𝑝, 𝑇)
Vorgehensweise bei der Anwendung der Bernoulli-Gleichung: 1. Anfangs- und Endpunkte der Stromlinie festlegen 2. Bernoulli-Gleichung aufstellen 3. Bekannte Grössen einsetzen (evtl. Konti / Impulserhaltung) 4. umformen
Hinweise: � An freien Oberflächen herrscht meist Umgebungsdruck � In sehr grossen Querschnitten oder Staupunkten kann die
Geschwindigkeit meist vernachlässigt werden � Die Gleichung darf nicht über Stellen angewendet werden,
an denen eine Phasengrenze vorliegt oder mechanische Energie zugeführt oder entzogen wird (Propeller, Turbulenz durch Strömungsabriss etc.)
¾ Beispiele zur Bernoulli-Gleichung: Toricelli’sche Ausflussgeschwindigkeit 𝑢 = 2𝑔ℎ instationär
𝑢 (𝑡) = 2𝑔ℎ 𝑡𝑎𝑛ℎ ∙√ ∙
für 𝑡 → ∞: 𝑢 = 𝑢 = 2𝑔ℎ Venturi-Rohr
∆𝑝 = 𝜌𝑢 1 −
Prandtl-Rohr
𝑢 = ( ) = ∆
Manometer für �� = 0 ℎ ∶= ℎ =
für �� ≠ 0 𝑢 = 2𝑔𝐻 + 2𝑔ℎ 1 − 2 = 2𝑔 ∆ℎ
mit ∆ℎ = ℎ − ℎ �� = 𝑢 ∙ 𝐴
ENERGIEERHALTUNG 𝐷𝐸𝐷𝑡 = �� ∙ �� + 𝑄
Transport-Theorem:
= ∫ 𝜌 𝑒 + + 𝛻 𝜌�� 𝑒 + 𝑑𝑉
Differentielle Form:
𝜌 𝑒 + + 𝛻 𝜌�� 𝑒 + = 𝜌𝑓 ∙ �� + 𝛻(𝜎 ∙ ��) + 𝜌𝑞 − 𝛻��
REIBUNGSBEHAFTETE STRÖMUNGEN
NAVIER-STOKES-GLEICHUNG Annahmen: 𝜈 = 𝑐𝑜𝑛𝑠𝑡. 𝐷��𝐷𝑡 = 𝜕��
𝜕𝑡 + �� ∙ 𝛻 �� = − 1𝜌 𝛻𝑝 + 𝜈∆�� + 𝑓
wobei ∆= 𝛻 und 𝜈 = 𝜇/𝜌
Randbedingungen: � An einer festen Wand: �� = ��
insb. Wandhaftbedingung: 𝑢 (𝑦 = 0) = 0 � An einer Trennfläche zweier Fluide:
i. �� = �� (Gleichheit der Geschwindigkeiten) ii. 𝑝 = 𝑝 (Gleichheit der Drücke)
iii. 𝜏 ∙ 𝑛 = 𝜏 ∙ 𝑛 (Gleichheit der Scherkraftkomponenten) iv. �� ∙ 𝑛 = �� ∙ 𝑛 (Gleichheit der Wärmeflüsse)
� An einer freien Oberfläche: 𝜇 | = 𝜏 | = 0 (keine Schubspannungen)
Hinweise: � Keine Feldkräfte: 𝑓 = 0 � Reibung vernachlässigbar: 𝜈∆�� = 0 � Stationär: 𝛿 𝛿𝑡⁄ = 0
zeitl. Impulsänderung in 𝑉 = 0 für sationär
Impulsfluss über 𝑆 = 𝛿𝑉 Oberflächenkräfte Volumenkräfte (meist Gravitationskraft 𝑓 = ��)
Druckkräfte = 0 für Freistrahl
Scherkräfte = 0 für reib.frei
Kraft auf das Fluid (im Schwerpunkt)
Druckgradient Kraftfelder Schubspannungstensor
mech. Leistung Wärmezu-/abfuhr
1
2
𝑔 𝑃𝑎
1
2 3
𝑃𝑎 𝑔
1 2
𝐴 𝐴
1
2
Staupunkt 𝑝
𝑢
𝑝
∆𝑝
��
1 2
3 ℎ 𝑧 = 0 𝜌
Sperrflüssigkeit
𝑃𝑎 0 𝑔
𝜌 > 𝜌

Navier-Stokes-Gleichung in 𝒊-Richtung: 𝜕𝑢𝜕𝑡 + 𝑢 ∙ 𝜕𝑢
𝜕𝑥 + 𝑢 ∙ 𝜕𝑢𝜕𝑦 + 𝑢 ∙ 𝜕𝑢
𝜕𝑧 = − 1𝜌
𝜕𝑝𝜕𝑖 + 𝜈 𝜕 𝑢
𝜕𝑥 + 𝜕 𝑢𝜕𝑦 + 𝜕 𝑢
𝜕𝑧 + 𝑓
mit 𝑖 = 𝑥, 𝑦, 𝑧 VEREINFACHUNGEN
Kleine Reynolds-Zahl – Schleichströmung: 𝑅𝑒 = ∙ → 0 (zähflüssig)
𝛻𝑝 = 𝜇𝛻 ��
Lösungswege: 𝛻 𝑝 = 0 𝛻 𝜔 = 0
Dimensionslose Form:
𝑅𝑒 + �� ∙ 𝛻 ∙ �� = − 𝛻𝑝 − 𝛻 ��
Dimensionslose Parameter: �� = 1 𝑢⁄ ∙ �� �� = 1 𝐿⁄ ∙ �� 𝑡 = 𝑢 𝐿⁄ ∙ 𝑡 𝑝 = 𝐿 (𝜇 ∙ 𝑢)⁄ ∙ 𝑝
Grosse Reynolds-Zahl: Skalierung des Druckes 𝑝 = 1 (𝜌 ∙ 𝑢 )⁄ ∙ 𝑝
ohne Wandhaftbedingung: = − 𝛻𝑝 (Euler)
mit Wandhaftbedingung: i. Ausserhalb der Grenzschicht: 𝜈 ≡ 0 (reibungsfrei) → Euler
ii. Innerhalb der Grenzschicht: 𝜈 ≠ 0 → Grenzschichtmodell EXAKTE LÖSUNGEN ZUR NAVIER-STOKES-GLEICHUNG
Ebene Cuette-Strömung = 0
𝑢(𝑦) = 1 +
Poiseuille-Strömung (2D) = 𝑐𝑜𝑛𝑠𝑡.
𝑢(𝑦) = − 1 − = 𝑢 1 −
Hagen-Poiseuille-Strömung (3D) = 𝑐𝑜𝑛𝑠𝑡.
𝑢(𝑦) = − 1 − = 𝑢 1 −
GRENZSCHICHTEN
GRENZSCHICHTGLEICHUNGEN
Grenzschicht: 𝛿~
mit 𝐿: Bezugslänge, 𝛿 ≪ 𝐿
Druck in der Grenzschicht: = 0 → 𝑝(𝑥, 𝑦) = 𝑝 𝑥, 𝑦 = 𝛿(𝑥)
= −𝑢
Impulssatz in 𝒙-Richtung:
𝑢 + 𝑢 = − + 𝜈
Randbedingungen: 𝑢 (𝑥, 𝑦 = 0) = 𝑢 (𝑥, 𝑦 = 0) = 0 (Wandhaftbedingung)
𝑢 (𝑥, 𝑦 = 𝛿) = 𝑢 (Aussenströmung)
GRENZSCHICHTKENNGRÖSSEN Grenzschichtdicke 𝛿: 𝑢 (𝑥, 𝑦 = 𝛿) = 0.99 ∙ 𝑢
Verdrängungsdicke 𝛿 : 𝛿 = ∫ 1 − 𝑑𝑦( )
Impulsverlustdicke 𝛿 : 𝛿 = ∫ 1 − 𝑑𝑦( )
BLASIUS-GRENZSCHICHT – EBENE PLATTE (LAMINARE GRENZSCHICHT)
Ähnlichkeitsvariable: 𝜂(𝑥, 𝑦) = 𝑅𝑒
Reynoldszahl mit Lauflänge: 𝑅𝑒 =
Ansatz für Stromfunktion: 𝛹(𝑥, 𝑦) = 𝑓(𝜂)√𝑢 𝜈 𝑥
Blasius-Gleichung: 2 ∙ 𝑓 + 𝑓 ∙ 𝑓 = 0 mit Randbedingungen: 𝑓(𝜂 = 0) = 0 𝑓′(𝜂 = 0) = 0 𝑓′(𝜂 → ∞) = 0
für 𝑅𝑒 < 𝑅𝑒 = 10 (laminare Grenzschicht) gilt: Grenzschichtdicke: 𝛿 = 5 ~ √𝑥
Verdrängungsdicke: 𝛿 = 1.721 ≈ Impulsverlustdicke: 𝛿 = 0.664 ≈
Örtl.Widerstandskoeff: 𝑐 = = 0.664
FALKNER-SKAN-GRENZSCHICHT – KELI MIT ÖFFNUNGSWINKEL 𝛽
Ähnlichkeitsvariable: 𝜂(𝑥, 𝑦) = 𝑅𝑒
Reynoldszahl mit Lauflänge: 𝑅𝑒 =
Ansatz für Stromfunktion: 𝛹(𝑥, 𝑦) = 𝑓(𝜂) ∙ 𝑢 ∙ 𝑥 𝑅𝑒
= 𝑓(𝜂)𝑐𝑥 ∙
mit 𝑚 = 𝑢 = 𝑐𝑥
Falkner-Skan-Gleichung: 𝑓 + 𝑓 ∙ 𝑓 + 𝑚(1 − 𝑓 ) = 0 mit Randbedingungen: 𝑓(𝜂 = 0) = 0 𝑓′(𝜂 = 0) = 0 𝑓′(𝜂 → ∞) = 1
𝑚 > 0: Beschleunigte Grenzschicht < 0
𝑚 = 0: Blasius-Grenzschicht = 0
𝑚 < 0: Verzögerte Grenzschicht > 0
IMPULSSATZ DER GRENZSCHICHTTHEORIE
+ 2 + ( ) =
Spezialfall: Blasius-Grenzschicht = 0 → = > 0
TURBULENZ Notwendige Bedingungen: x Instationarität, Unstetigkeit x 3D-Geschwindigkeitsfluktuationen (10% - 30% der
mittleren Geschwindigkeit) x Rotationsbehaftete Strömungen (𝜔 = 𝛻 × 𝑢 ≢ 0)
Charakteristische Eigenschaften: x Wirbelstrukturen auf verschiedenen Längenskalen x Turbulenz ist selbsterzeugend x Transition: Umschlag von laminar nach turbulent x Wirbeldiffusion dominiert den Impulsaustausch x Turbulente Energie wird durch Dissipation vernichtet
Transition: Ebene Platte, Kugel, Zylinder: 𝑅𝑒 , = [3 ∙ 10 , 3 ∙ 10 ] Rohrströmung: 𝑅𝑒 , = [2300, 3000]
𝑅𝑒 = 𝑅𝑒 =
Ablösegefahr!

STATISTISCHE MODELLIERUNG
��(��, 𝑡) = ⟨��(��, 𝑡)⟩ + ��′(��, 𝑡)
⟨��(��, 𝑡)⟩: Mittelung von �� ��′: Fluktiation, wobei ⟨��′(��, 𝑡)⟩ ≡ 0
Mittelung: ⟨��(��, 𝑡)⟩ = 𝑙𝑖𝑚
→ ∫ ��(��, 𝑡) 𝑑𝑡 ∶= ��(��, 𝑡) (Rechnung mit Mittelung und Fluktuation siehe Anhang)
RANS – REYNOLDS AVERAGED NAVIER STOKES
𝛻 ∙ (𝜌𝑢𝑢) = −𝛻�� + 𝛻𝜏 − 𝛻 𝜌𝑢′𝑢′ Komponentenweise:
𝜌𝑢 𝑢 = − + 𝜏 − 𝜌𝑢 𝑢
𝜏 = 𝜏 : Molekularer Schubspannungsvektor −𝜌𝑢 𝑢 = 𝜏 : turbulenter Schubspannungsvektor
EMPIRISCHE ANSÄTZE Boussinesq-Annahme: 𝜏 = 𝜌𝜈 mit 𝜈 = 𝑘𝑈∗𝐿∗ [𝑚 𝑠⁄ ]: turb. Viskosität 𝑈∗: charkt. Geschw. 𝐿∗: charakteristische Länge
TURBULENTE GRENZSCHICHT
𝑢 = |𝜏 | 𝜌⁄ : charakteristische Schubspannungsgschw. 𝑦 = 𝜈 𝑢⁄ : viskoses Längenmass
Geschwindigkeitsverteilung: x Wandbereich (viskose Unterschicht)
𝜏 = 𝜏 (𝑥) 𝜏 ≫ 𝜏 x Wandnaher Bereich (logarithmische Schicht)
𝜏 = 𝜏 (𝑥) 𝜏 ≫ 𝜏 = . 𝑙𝑛 + 𝐶 mit 𝐶 abh. von der Wandrauheit
x Aussenbereich 𝜏 = 𝜏(𝑥, 𝑦) 𝜏 ≫ 𝜏
= 𝑙𝑛 + 𝐶 + 𝑠𝑖𝑛
𝑘 ≈ 0.41 𝐶 ≈ 5.0 𝛱 = 𝛱 ≈ 0.6
-Potenz-Gesetz: = 𝑛 ≅ 7
für 𝑅𝑒 > 𝑅𝑒 = 10 (turbulente Grenzschicht) gilt: Grenzschichtdicke: 𝛿 = 0.37 ∙ 𝑥 ∙ 𝑅𝑒 ⁄ Verdrängungsdicke: 𝛿 = 0.046 ∙ 𝑥 ∙ 𝑅𝑒 ⁄ Impulsverlustdicke: 𝛿 = 0.036 ∙ 𝑥 ∙ 𝑅𝑒 ⁄ Örtl.Widerstandskoeff: 𝑐 = = 0.0576 ∙ 𝑅𝑒 ⁄
TURBULENTE ROHRSTRÖMUNG Hydraulisch glattes Rohr:
= 𝑙𝑛 1 + 𝑘 1 −
Nahe der Rohrwand (𝑅 − 𝑟) 𝑅 ≪ 1⁄ : ≈ 𝑙𝑛 1 + 𝑘 ( ) + 𝐶 = < 0
Wandschubgeschwindigkeit: 𝑢 = |𝜏 | 𝜌⁄ 𝑢 = 𝑢 + 3.75𝑢
Druckverlust im Rohr bei laminarer Strömung: ∆ = 𝜆 𝜆: Rohrreibungskoeff./Turb.Verlustkoeff.
𝜆 = =
Druckverlust im Rohr bei turbulenter Strömung Hydraulisch glatt Zwischenbereich Hydraulisch rau
≤ 5 5 ≤ ≤ 70 ≥ 70
𝜆 = 𝜆(𝑅𝑒 ) 𝜆 = 𝜆 𝑅𝑒 , 𝜆 = 𝜆 (siehe Moody-Diagramm – Anhang) wobei 𝑘 : Rauheitshöhe (Tabelle)
Beton 0.9 − 9𝑚𝑚 Verzinktes Met. 0.15𝑚𝑚 Holz 0.2 − 9𝑚𝑚 Baustahl 0.059𝑚𝑚 Gusseisen 0.25𝑚𝑚 gezogene Rohre 0.0015𝑚𝑚
Hydraulisch glatt: 𝑅𝑒 , < 𝑅𝑒 : √ = 2.03 𝑙𝑜𝑔 𝑅𝑒 ∙ √𝜆 − 0.8
𝑅𝑒 , ≤ 𝑅𝑒 ≤ 4 ∙ 10 : 𝜆 = .
Zwischenbereich: Moody-Diagramm – oder Näherungsformel Colebrook-White
√ = 2.03 𝑙𝑜𝑔 .∙√ + 0.27
Hydraulisch rau:
√ = 1.14 − 2 𝑙𝑜𝑔
Hydraulischer Durchmesser: 𝐷 = 4 𝑆: Querschnittsfläche des Fluidstroms
𝑅𝑒 = 𝑈: Benetzer Umfang
VERLUSTBEHAFTETE BERNOULLI-GLEICHUNG Fliessrichtung: 1 → 2 𝑝 + 𝑢 + 𝜌𝑔ℎ = 𝑝 + 𝑢 + 𝜌𝑔ℎ + ∆𝑝 − ∆𝑝
∆𝑝 [𝑃𝑎] =𝑢 𝜆𝑢 𝜁
∆𝑝 > 0 Energiezufuhr (z.B. Pumpe) ∆𝑝 < 0 Energieabfuhr (z.B. Turbine)
Druckverluste bei Maschinen: ∆𝑝 = 𝜂 ∆𝑝 = −
𝑁: Leistung der Maschine 𝜂: Wirkungsgrad ��: Volumenstrom
Turbulenzeinfluss
Rohrverlust
Verlust durch Einbauten (𝜁: Verlustkoeff.)

STRÖMUNGSARTEN 𝑅𝑒 klein/gross wirbelfrei/-
behaftet reibungsfrei/-behaftet
instationär/-stationär
turbulente Strömung gross wirbelbeh reibungsbeh instationär laminare Strömung klein beides reibungsbeh beides Potentialströmung beides wirbelfrei reibungsfrei beides Schleichströmung klein beides reibungsbeh beides Grenzschichtströmung gross wirbelbeh reibungsbeh beides
Ablösung einer turbulenten Grenzschicht um ein Profil mit scharfer Kante
Ablösung einer laminaren Grenzschicht um ein Profil mit scharfer Kante
Ablösung einer turbulenten Grenzschicht von einer Kugel
Ablösung einer laminaren Grenzschicht von einer Kugel
Umströmung eines Zylinders mit 𝑅𝑒 = 1.54
Umströmung eines Zylinders mit 𝑅𝑒 = 10000
Karmansche Wirbelstrasse
Ablösung einer laminaren Grenzschicht von einem Ellipsoid
Übergang laminar – turbulent in einer Rohrströmung
Übergang laminar – turbulent eines runden Strahls
ANHANG
SINUS UND COSINUS α [°] 0° 30° 45° 60° 90° 120° 135° 150° 180° α [π] 0 π/6 π/4 π/3 π/2 2π/3 3π/4 5π5/6 π sinα 0 1 2⁄ √2 2⁄ √3 2⁄ 1 √3 2⁄ √2 2⁄ 1 2⁄ 0 cosα 1 √3 2⁄ √2 2⁄ 1 2⁄ 0 −1 2⁄ −√2 2⁄ −√3 2⁄ -1 tanα 0 √3 3⁄ 1 √3 ∞ −√3 −1 −√3 3⁄ 0
VOLUMINA UND OBERFLÄCHEN DIVERSER KÖRPER KUGEL
Volumen: 𝜋𝑟 Oberfläche: 4𝜋𝑟
ZYLINDER Volumen: 𝜋𝑟 ℎ Oberfläche: 2𝜋𝑟ℎ + 2𝜋𝑟
TORUS 𝑅: Ringradius (gross) 𝑟: Schlauchradius (klein) Volumen: 2𝜋 𝑟 𝑅 Oberfläche: 4𝜋 𝑟𝑅
KEGEL (gerader Kreiskegel)
Volumen: 𝜋𝑟 ℎ Oberfläche: 𝜋𝑟 + 𝜋𝑟√ℎ + 𝑟
ELLIPSOID
Volumen: 𝜋𝑎𝑏𝑐 mit Achsenabschnitten (Radien) 𝑎, 𝑏, 𝑐
KOORDINATENTRANSFORMATIONEN Kartesisch Zylindrisch Sphärisch
𝑥 𝜌 𝑐𝑜𝑠 𝜑 𝑟 𝑠𝑖𝑛 𝜃 𝑐𝑜𝑠 𝜓 𝑦 𝜌 𝑠𝑖𝑛 𝜑 𝑟 𝑠𝑖𝑛 𝜃 𝑠𝑖𝑛 𝜓 𝑧 𝑧 𝑟 𝑐𝑜𝑠 𝜃
𝑥 + 𝑦 𝜌 𝑟 𝑠𝑖𝑛 𝜃 𝑎𝑟𝑐𝑡𝑎𝑛(𝑦 𝑥⁄ ) 𝜑 𝜓
𝑧 𝑧 𝑟 𝑐𝑜𝑠 𝜃 𝑥 + 𝑦 + 𝑧 𝜌 + 𝑧 𝑟
𝑎𝑟𝑐𝑡𝑎𝑛(𝑦 𝑥⁄ ) 𝜑 𝜓 𝑎𝑟𝑐𝑡𝑎𝑛 𝑥 + 𝑦 𝑧⁄ 𝑎𝑟𝑐𝑡𝑎𝑛(𝜌 𝑧⁄ ) 𝜃
JACOBI-DETERMINANTEN Polarkoordinaten:
𝑥 = 𝑟 𝑐𝑜𝑠 𝜑 𝑦 = 𝑟 𝑠𝑖𝑛 𝜑 𝑑𝐹 = 𝑟𝑑𝑟𝑑𝜑 Zylinderkoordinaten:
𝑥 = 𝑟 𝑐𝑜𝑠 𝜑 𝑦 = 𝑟 𝑠𝑖𝑛 𝜑 𝑧 = 𝑧 𝑑𝑉 = 𝑑𝑥𝑑𝑦𝑑𝑧 = 𝑟𝑑𝑟𝑑𝜑𝑑𝑧
Kugelkoordinaten: 𝑥 = 𝑟 𝑐𝑜𝑠 𝜑 𝑠𝑖𝑛 𝜃 𝑦 = 𝑟 𝑠𝑖𝑛 𝜑 𝑠𝑖𝑛 𝜃 𝑧 = 𝑟 𝑐𝑜𝑠 𝜃 europäisch (θ von oben) 𝑑𝑉 = 𝑑𝑥𝑑𝑣𝑑𝑦 = 𝑟 𝑠𝑖𝑛 𝜃𝑑𝑟𝑑𝜑𝑑𝜃
RECHENREGELN DIFFERENTIAL (𝑓 ± 𝑔) = 𝑓 ± 𝑔 (𝑥 ) = 𝑛 ∙ 𝑥 (𝑐 ∙ 𝑓) = 𝑐 ∙ 𝑓′ (𝑓 ∙ 𝑔) = 𝑓 𝑔 + 𝑓𝑔′
=
𝑓(𝑔) ′ = 𝑓(𝑔)𝑔′ (𝑓 ) = ( )
RECHENREGELN INTEGRAL
∫(𝑓 ± 𝑔) 𝑑𝑥 = ∫ 𝑓𝑑𝑥 ± ∫ 𝑔𝑑𝑥 ∫(𝑐 ⋅ 𝑓)𝑑𝑥 = 𝑐 ⋅ ∫ 𝑓𝑑𝑥
∫ 𝑓𝑑𝑥 + ∫ 𝑓𝑑𝑥 = ∫ 𝑓𝑑𝑥
∫ 𝑓𝑑𝑥 = − ∫ 𝑓𝑑𝑥 𝑖𝑛𝑠𝑏. ∫ 𝑓𝑑𝑥 = 0
falls 𝑓(𝑥) ≤ 𝑔(𝑥) ⇒ ∫ 𝑓𝑑𝑥 ≤ ∫ 𝑔𝑑𝑥
PARTIELLE INTEGRATION
∫ (𝑓′ ⋅ 𝑔) 𝑑𝑥 = [𝑓 ⋅ 𝑔] − ∫ (𝑓 ⋅ 𝑔′) 𝑑𝑥
GRADIENT, DIVERGENZ UND ROTATION
𝑔𝑟𝑎𝑑(𝑓) = 𝛻 ∙ 𝑓 = 𝑓 , 𝑓 , 𝑓
𝑑𝑖𝑣(��) = 𝛻 ∙ �� = + +
𝑟𝑜𝑡(��) = 𝛻 × �� = − , − , −
MECHANIK
Impulssatz: �� = 𝑚 ∙ �� = ∑ �� , Spinsatz: 𝜃 �� = ∑ 𝑟 , ◊ �� , + ∑ 𝑀 Drallsatz: �� = 𝜃 �� + 𝑚 ∙ 𝑟 ◊ �� = ∑ 𝑟 , ◊ �� , + ∑ 𝑀
IDEALE GASGLEICHUNG
𝒑 ∙ 𝑽 = 𝒎 ∙ 𝑹 ∙ 𝑻 = 𝒎 ∙ 𝑹𝑴 ∙ 𝑻
𝑝 ∙ 𝑣 = 𝑅 ∙ 𝑇 𝑝 = 𝜌 ∙ 𝑅 ∙ 𝑇 𝑅 = 𝑐 − 𝑐 = 𝜌 = 𝑣


















![schrauben B.ppt [Schreibgeschützt] - n.ethz.chn.ethz.ch/~webemarc/download/4. semester/Dimensionieren II... · Vorlesung 6: Wiederholung Schrauben Schrauben - Funktion - Geometrische](https://static.fdokument.com/doc/165x107/5ba0a44309d3f2df578d3e1c/schrauben-bppt-schreibgeschuetzt-nethzchnethzchwebemarcdownload4-semesterdimensionieren.jpg)