Quantum Zeno Dynamics from General QuantumOperationsDaniel Burgarth1, Paolo Facchi2,3, Hiromichi Nakazato4, Saverio Pascazio2,3, and KazuyaYuasa4

1Center for Engineered Quantum Systems, Dept. of Physics & Astronomy, Macquarie University, 2109 NSW,Australia

2Dipartimento di Fisica and MECENAS, Università di Bari, I-70126 Bari, Italy3INFN, Sezione di Bari, I-70126 Bari, Italy4Department of Physics, Waseda University, Tokyo 169-8555, JapanJune 30, 2020

We consider the evolution of an arbitrary quantum dynamical semigroupof a finite-dimensional quantum system under frequent kicks, where each kickis a generic quantum operation. We develop a generalization of the Baker-Campbell-Hausdorff formula allowing to reformulate such pulsed dynamics asa continuous one. This reveals an adiabatic evolution. We obtain a generaltype of quantum Zeno dynamics, which unifies all known manifestations in theliterature as well as describing new types.

1 IntroductionPhysics is a science that is often based on approximations. From high-energy physics tothe quantum world, from relativity to thermodynamics, approximations not only help usto solve equations of motion, but also to reduce the model complexity and focus on im-portant effects. Among the largest success stories of such approximations are the effectivegenerators of dynamics (Hamiltonians, Lindbladians), which can be derived in quantummechanics and condensed-matter physics. The key element in the techniques employed fortheir derivation is the separation of different time scales or energy scales.

Recently, in quantum technology, a more active approach to condensed-matter physicsand quantum mechanics has been taken. Generators of dynamics are reversely engineeredby tuning system parameters and device design. This allows the creation of effective genera-tors useful for many information-theoretic tasks, such as adiabatic quantum computing [1],reservoir engineering [2], quantum gates [3], to name a few.

A key player for such approximations has been the adiabatic theorem [4,5]. It exploitsa clear separation of slow and fast time scales and has fascinated generations of physicistsdue to its simplicity, its beauty, and its intriguing geometric interpretations. In its origi-nal formulation, the adiabatic theorem deals with generators of dynamics. On the otherhand, in quantum technology, we often deal with discrete dynamics such as fixed gatesand quantum maps. It is not always straightforward, and sometimes seemingly impossi-ble, to translate between continuous and discrete descriptions. This difficulty can be seenmore clearly in the case of non-Markovian quantum channels: these are physical operations[completely positive and trace-preserving (CPTP) maps [6]] for which there are no physi-cal (e.g. Lindbladian) generators [a non-Markovian quantum channel cannot be realized by

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 1

arX

iv:1

809.

0957

0v3

[qu

ant-

ph]

1 J

ul 2

020

the time-ordered integral of an infinitesimal CPTP generator of the Gorini-Kossakowski-Lindblad-Sudarshan (GKLS) form [7,8]]. Such maps typically arise from unitary dynamicson larger (but finite-dimensional) spaces, such as two-level fluctuators forming the envi-ronment of solid-state qubits. This makes them rather common in experiments [9].

The key question we pose in this article is if discrete dynamics can give rise to a limitevolution? We provide a positive answer to this question by providing a general mappingfrom pulsed to continuous dynamics. Such connections had been noted before only fora specific unitary case. For the generic situation, we need to develop a more powerfulframework. This is because in the nonunitary case one has to take into account bothnondiagonalizability and noninvertibility of the maps.

We focus on finite-dimensional systems and provide a route to connecting strong-coupling limits and frequent pulsed dynamics using three key ingredients. The first isa slight generalization of the Baker-Campbell-Hausdorff (BCH) theorem [10] (Lemma 1 inSec. 5). We employ operator logarithms to describe discrete maps by (potentially unphys-ical) generators and unify the product of exponentials as a new exponential up to the firstorder in a sense explained later. This only works for invertible maps (there is no logarithmof a noninvertible map since the logarithm of the vanishing eigenvalue does not exist), sothe second ingredient is a delicate error estimate allowing us to take logarithms of only theinvertible part of a generic map: the remaining part decays anyway (Lemma 3 in Sec. 5).We believe that these key lemmas might find applications in other areas of quantum tech-nology. The third and ultimate ingredient is a strong-coupling theorem developed by thepresent authors recently in Ref. [11] (see also Ref. [12]), which can be applied to unphysicalgenerators (Theorem 1 of Ref. [11]). Even though the logarithm of a physical operation isnot of the GKLS form in general, one can deal with it by the adiabatic theorem provedin Ref. [11]. Through the adiabatic theorem, low-energy components are eliminated andthe physicality of the generator is restored. Our approach therefore works for arbitraryquantum maps without unnecessary structural assumptions.

Our generalization goes in two main directions: 1) the unitary dynamics e−itH is gen-eralized to an arbitrary quantum semigroup etL; 2) the projective measurement P is gen-eralized to an arbitrary quantum operation E . Moreover, we also generalize to 3) kickeddynamics of cycles of quantum operations E1, . . . , Em. This unifies many applications,such as the quantum Zeno effect (QZE) and dynamical decoupling, and provides a deeperrelationship through adiabaticity. The main result of the present work is Theorem 1 inSec. 4. It reveals that in quantum technology one has more freedom than previously thoughtto achieve effective generators (see the next section for a brief summary of the previousresults). In addition, we derive explicit bounds on matrix functions and the BCH formulafor nondiagonalizable matrices (Lemma 9 and Proposition 2 in Appendix B), which maybe of interest independently.

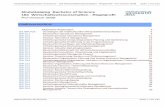
2 Relation to Previous WorkThe type of dynamics encountered in our main theorem can be considered as a general typeof quantum Zeno dynamics (QZD). Different manifestations of QZD are known [13,14], via(i) frequent projective measurements [15,16], via (ii) frequent unitary kicks [17,18], via (iii)strong continuous coupling/fast oscillations [19, 20], and via (iv) strong damping [21–25](see Refs. [26, 27] for experimental comparisons). Dynamical decoupling [28–34] (see alsoRef. [35]) is also regarded as a manifestation of the QZD. See Fig. 1 for a summary ofthese different manifestations of the QZD.

Since pulsed strategies will be the main subject of this article, it is convenient to

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 2

(iii) strong continuous coupling / fast oscillations

eit(K+H) eitKeitHZ<latexit sha1_base64="uF4VVxyoHfqwIZj8QhMOXodm4SA=">AAAKI3icjZbdbts2FMfldh+xV6/perkbYUaBbnMNyXGb9i5ABqzDMCArkraY6RkURTuESUkgqaQGw7fYK+xpdjfsZhd9l5GybEuUbUxBEvLwd/46h4c6UpRRImQQ/Nu6d/+TTz/7/Kjd+eJB98uHx4++eivSnCN8hVKa8vcRFJiSBF9JIil+n3EMWUTxu2hxbtff3WAuSJpcymWGJwzOEzIjCEpjmh7fgjiiOe4A/Lt6BogvnyoQcxyDOWQMAgblNYJU/az195vJa/2t7gBB2NariZcyG2DrPP1N6870uBcMguLym4OwHPS88rqYPjr6A8QpyhlOJKJQiHEYZHKiIJcEUay7IBc4g2gB53hshglkWExUsUPaf2IssT9LuflNpF9Yqx4KMiGWLDKkDVS4a9a4c43jm5rfk+piusgZRDzd6RmxXeZxLmcvJ4okWS5xglaRz3Lqy9S39fNjwjGSdGkGRpqY5H10DTlE0lS52wUcJ/gWpaYaSWxqoFVstqZqwqY0En+QCmvt4mS9RrTjxUkizaL5C2IiMgqXlDAiRUPijdW3aaVZqWUsGiTpHv4n5vLGUuOrtOQubSx76csGfXmAXmCpx+FE3aleqAGHybw4VlUk4rBAAC1WLXjXRIQeDydK6anqDTW4Fqa0+Dv1LBgMGdMHXE0AK++TSTGxjNE4aWoYzGo3b42KJIabCHvhXW+4O5cfsHR3x5r2bs8bLJqVFdoNIrtxqYv9mpjPXNqaDvFohwM66EF2eJD9HoIkjXsUtr0e5407nB/Qh7FLG0uF7nRBjGemnRdNStkuqhWfR1oFgxejvumRJ/1AO5Dt4Wuqb34GL1xizjFOtshg1BRJ7TkxMogtFyvodNgPzb+woWbeIqYPw01gL0enlhu9ssqvAvN6qHWhIgdQScjZkzJ+UM3GRcoEQC0fF1qnAOopudgmfODk4wRejXtH2P8npFpmuxJzY9mEUsfQEm5vVUwcYIkpTW83SDl1Crfen7JsRbme9916Obu43sROTSqBN8uN0MnqRJljV1daQaDi4QAMXqdzmGygsX1vxxP1y9rutpecZxS79MXK2igPbOj+aG2NEpm+WamRnbkHHlMst4/G4Hm/eMx013zHhO5XS3PwdjgIzePx66h3dlZ+0Rx5X3vfeE+90Dv1zrzX3oV35SHvY+t+60Gr2/6z/Vf77/Y/K/Req/R57NWu9sf/AHqG0Vo=</latexit><latexit sha1_base64="uF4VVxyoHfqwIZj8QhMOXodm4SA=">AAAKI3icjZbdbts2FMfldh+xV6/perkbYUaBbnMNyXGb9i5ABqzDMCArkraY6RkURTuESUkgqaQGw7fYK+xpdjfsZhd9l5GybEuUbUxBEvLwd/46h4c6UpRRImQQ/Nu6d/+TTz/7/Kjd+eJB98uHx4++eivSnCN8hVKa8vcRFJiSBF9JIil+n3EMWUTxu2hxbtff3WAuSJpcymWGJwzOEzIjCEpjmh7fgjiiOe4A/Lt6BogvnyoQcxyDOWQMAgblNYJU/az195vJa/2t7gBB2NariZcyG2DrPP1N6870uBcMguLym4OwHPS88rqYPjr6A8QpyhlOJKJQiHEYZHKiIJcEUay7IBc4g2gB53hshglkWExUsUPaf2IssT9LuflNpF9Yqx4KMiGWLDKkDVS4a9a4c43jm5rfk+piusgZRDzd6RmxXeZxLmcvJ4okWS5xglaRz3Lqy9S39fNjwjGSdGkGRpqY5H10DTlE0lS52wUcJ/gWpaYaSWxqoFVstqZqwqY0En+QCmvt4mS9RrTjxUkizaL5C2IiMgqXlDAiRUPijdW3aaVZqWUsGiTpHv4n5vLGUuOrtOQubSx76csGfXmAXmCpx+FE3aleqAGHybw4VlUk4rBAAC1WLXjXRIQeDydK6anqDTW4Fqa0+Dv1LBgMGdMHXE0AK++TSTGxjNE4aWoYzGo3b42KJIabCHvhXW+4O5cfsHR3x5r2bs8bLJqVFdoNIrtxqYv9mpjPXNqaDvFohwM66EF2eJD9HoIkjXsUtr0e5407nB/Qh7FLG0uF7nRBjGemnRdNStkuqhWfR1oFgxejvumRJ/1AO5Dt4Wuqb34GL1xizjFOtshg1BRJ7TkxMogtFyvodNgPzb+woWbeIqYPw01gL0enlhu9ssqvAvN6qHWhIgdQScjZkzJ+UM3GRcoEQC0fF1qnAOopudgmfODk4wRejXtH2P8npFpmuxJzY9mEUsfQEm5vVUwcYIkpTW83SDl1Crfen7JsRbme9916Obu43sROTSqBN8uN0MnqRJljV1daQaDi4QAMXqdzmGygsX1vxxP1y9rutpecZxS79MXK2igPbOj+aG2NEpm+WamRnbkHHlMst4/G4Hm/eMx013zHhO5XS3PwdjgIzePx66h3dlZ+0Rx5X3vfeE+90Dv1zrzX3oV35SHvY+t+60Gr2/6z/Vf77/Y/K/Req/R57NWu9sf/AHqG0Vo=</latexit><latexit sha1_base64="uF4VVxyoHfqwIZj8QhMOXodm4SA=">AAAKI3icjZbdbts2FMfldh+xV6/perkbYUaBbnMNyXGb9i5ABqzDMCArkraY6RkURTuESUkgqaQGw7fYK+xpdjfsZhd9l5GybEuUbUxBEvLwd/46h4c6UpRRImQQ/Nu6d/+TTz/7/Kjd+eJB98uHx4++eivSnCN8hVKa8vcRFJiSBF9JIil+n3EMWUTxu2hxbtff3WAuSJpcymWGJwzOEzIjCEpjmh7fgjiiOe4A/Lt6BogvnyoQcxyDOWQMAgblNYJU/az195vJa/2t7gBB2NariZcyG2DrPP1N6870uBcMguLym4OwHPS88rqYPjr6A8QpyhlOJKJQiHEYZHKiIJcEUay7IBc4g2gB53hshglkWExUsUPaf2IssT9LuflNpF9Yqx4KMiGWLDKkDVS4a9a4c43jm5rfk+piusgZRDzd6RmxXeZxLmcvJ4okWS5xglaRz3Lqy9S39fNjwjGSdGkGRpqY5H10DTlE0lS52wUcJ/gWpaYaSWxqoFVstqZqwqY0En+QCmvt4mS9RrTjxUkizaL5C2IiMgqXlDAiRUPijdW3aaVZqWUsGiTpHv4n5vLGUuOrtOQubSx76csGfXmAXmCpx+FE3aleqAGHybw4VlUk4rBAAC1WLXjXRIQeDydK6anqDTW4Fqa0+Dv1LBgMGdMHXE0AK++TSTGxjNE4aWoYzGo3b42KJIabCHvhXW+4O5cfsHR3x5r2bs8bLJqVFdoNIrtxqYv9mpjPXNqaDvFohwM66EF2eJD9HoIkjXsUtr0e5407nB/Qh7FLG0uF7nRBjGemnRdNStkuqhWfR1oFgxejvumRJ/1AO5Dt4Wuqb34GL1xizjFOtshg1BRJ7TkxMogtFyvodNgPzb+woWbeIqYPw01gL0enlhu9ssqvAvN6qHWhIgdQScjZkzJ+UM3GRcoEQC0fF1qnAOopudgmfODk4wRejXtH2P8npFpmuxJzY9mEUsfQEm5vVUwcYIkpTW83SDl1Crfen7JsRbme9916Obu43sROTSqBN8uN0MnqRJljV1daQaDi4QAMXqdzmGygsX1vxxP1y9rutpecZxS79MXK2igPbOj+aG2NEpm+WamRnbkHHlMst4/G4Hm/eMx013zHhO5XS3PwdjgIzePx66h3dlZ+0Rx5X3vfeE+90Dv1zrzX3oV35SHvY+t+60Gr2/6z/Vf77/Y/K/Req/R57NWu9sf/AHqG0Vo=</latexit><latexit sha1_base64="uF4VVxyoHfqwIZj8QhMOXodm4SA=">AAAKI3icjZbdbts2FMfldh+xV6/perkbYUaBbnMNyXGb9i5ABqzDMCArkraY6RkURTuESUkgqaQGw7fYK+xpdjfsZhd9l5GybEuUbUxBEvLwd/46h4c6UpRRImQQ/Nu6d/+TTz/7/Kjd+eJB98uHx4++eivSnCN8hVKa8vcRFJiSBF9JIil+n3EMWUTxu2hxbtff3WAuSJpcymWGJwzOEzIjCEpjmh7fgjiiOe4A/Lt6BogvnyoQcxyDOWQMAgblNYJU/az195vJa/2t7gBB2NariZcyG2DrPP1N6870uBcMguLym4OwHPS88rqYPjr6A8QpyhlOJKJQiHEYZHKiIJcEUay7IBc4g2gB53hshglkWExUsUPaf2IssT9LuflNpF9Yqx4KMiGWLDKkDVS4a9a4c43jm5rfk+piusgZRDzd6RmxXeZxLmcvJ4okWS5xglaRz3Lqy9S39fNjwjGSdGkGRpqY5H10DTlE0lS52wUcJ/gWpaYaSWxqoFVstqZqwqY0En+QCmvt4mS9RrTjxUkizaL5C2IiMgqXlDAiRUPijdW3aaVZqWUsGiTpHv4n5vLGUuOrtOQubSx76csGfXmAXmCpx+FE3aleqAGHybw4VlUk4rBAAC1WLXjXRIQeDydK6anqDTW4Fqa0+Dv1LBgMGdMHXE0AK++TSTGxjNE4aWoYzGo3b42KJIabCHvhXW+4O5cfsHR3x5r2bs8bLJqVFdoNIrtxqYv9mpjPXNqaDvFohwM66EF2eJD9HoIkjXsUtr0e5407nB/Qh7FLG0uF7nRBjGemnRdNStkuqhWfR1oFgxejvumRJ/1AO5Dt4Wuqb34GL1xizjFOtshg1BRJ7TkxMogtFyvodNgPzb+woWbeIqYPw01gL0enlhu9ssqvAvN6qHWhIgdQScjZkzJ+UM3GRcoEQC0fF1qnAOopudgmfODk4wRejXtH2P8npFpmuxJzY9mEUsfQEm5vVUwcYIkpTW83SDl1Crfen7JsRbme9916Obu43sROTSqBN8uN0MnqRJljV1daQaDi4QAMXqdzmGygsX1vxxP1y9rutpecZxS79MXK2igPbOj+aG2NEpm+WamRnbkHHlMst4/G4Hm/eMx013zHhO5XS3PwdjgIzePx66h3dlZ+0Rx5X3vfeE+90Dv1zrzX3oV35SHvY+t+60Gr2/6z/Vf77/Y/K/Req/R57NWu9sf/AHqG0Vo=</latexit>

et(DiH) eitHZ P'<latexit sha1_base64="yrmlVl7ZZBskG0QNVusVhY4oRU4=">AAAKGXicjZbPb9s2FMeVdD9ib97S7biLMKNAN7iG5LhNewuQAusOA7wiaYuZnkFRtE2YlASScmcw/C9221+z27BrT/tTdhspy45E2cYUJCEfP++r9/ioJ0UZJUIGwT8npw8++viTT89a7c8+73zx5fnDr96INOcI36KUpvxdBAWmJMG3kkiK32UcQxZR/DZaXtv1tyvMBUmTG7nO8ITBeUJmBEFpTNNzBuKI5rgN8K9KPlYg5jgGc8gYBAzKBYJUvdT6CSC76Sv9nW4DQVi7pI2nWfdlhZj+ovVuOtJTsII8W5D29Lwb9IPi8puDsBx0vfIaTR+e/Q7iFOUMJxJRKMQ4DDI5UZBLgijWHZALnEG0hHM8NsMEMiwmqtgX7T8yltifpdz8JtIvrFUPBZkQaxYZ0gYr3DVr3LvG8arm96i6mC5zBhFP93pGbJ95nMvZ84kiSZZLnKBN5LOc+jL1bdX8mHCMJF2bgZEmJnkfLSCHSJradjqA4wS/R6kpWxKbsmgVm62pmrBWQOLfpMJauzjZrhHteHGSSLNo/oKYiIzCNSWMSNGQeG31bVppVmoZiwZJeoD/kbm8sdT4Ki25SxvLQfqmQd8coZdY6nE4UXeqG2rAYTIvjlUViTgsEECLVQveNRGhx4OJUnqqugMNFsKUFn+vngT9AWP6iKsJYON9MSkmljEaF00Ng1nt5q1RkcRgF2E3vOsO9ufyEkt3d6zp4Pa8xqJZWaHdILKVS40Oa2I+c2lrOsajPQ7oqAfZ40EOewiSNO5R2A56XDfucH1EH8YubSwVut0BMZ6ZJl40KWUbq1Z8HmkV9J8Ne6ZHXvQC7UC2c2+pnvnpP3OJOcc4uUf6w6ZIas+JkUFsvdxAl4NeaP6FDTXz7jB9GO4Cez68tNzwhVV+EZjXQq0LFTmASkLOnpTxg2o2LlImAGr5uNA2BVBPycV24QMnHyfwatx7wv4/IdUy25eYG8sulDqG1vD+VsXEAdaY0vT9DimnTuG2+1OWrSjX055bL2cXt5vYrkklcLXeCV1sTpQ5dnWlDQQqHg7A4CKdw2QHje17O56on7Z2t73kPKPYpUcba6M8sKH7g7U1SmT6ZqVGduYeeEyxvH80+k97xWOmO+Y7JnS/WpqDN4N+aB6Pn4fdq6vyi+bM+8b71nvshd6ld+W98kberYe8D96/J6cnD1p/tP5s/dX6e4OenpQ+X3u1q/XhP21SzvE=</latexit><latexit sha1_base64="yrmlVl7ZZBskG0QNVusVhY4oRU4=">AAAKGXicjZbPb9s2FMeVdD9ib97S7biLMKNAN7iG5LhNewuQAusOA7wiaYuZnkFRtE2YlASScmcw/C9221+z27BrT/tTdhspy45E2cYUJCEfP++r9/ioJ0UZJUIGwT8npw8++viTT89a7c8+73zx5fnDr96INOcI36KUpvxdBAWmJMG3kkiK32UcQxZR/DZaXtv1tyvMBUmTG7nO8ITBeUJmBEFpTNNzBuKI5rgN8K9KPlYg5jgGc8gYBAzKBYJUvdT6CSC76Sv9nW4DQVi7pI2nWfdlhZj+ovVuOtJTsII8W5D29Lwb9IPi8puDsBx0vfIaTR+e/Q7iFOUMJxJRKMQ4DDI5UZBLgijWHZALnEG0hHM8NsMEMiwmqtgX7T8yltifpdz8JtIvrFUPBZkQaxYZ0gYr3DVr3LvG8arm96i6mC5zBhFP93pGbJ95nMvZ84kiSZZLnKBN5LOc+jL1bdX8mHCMJF2bgZEmJnkfLSCHSJradjqA4wS/R6kpWxKbsmgVm62pmrBWQOLfpMJauzjZrhHteHGSSLNo/oKYiIzCNSWMSNGQeG31bVppVmoZiwZJeoD/kbm8sdT4Ki25SxvLQfqmQd8coZdY6nE4UXeqG2rAYTIvjlUViTgsEECLVQveNRGhx4OJUnqqugMNFsKUFn+vngT9AWP6iKsJYON9MSkmljEaF00Ng1nt5q1RkcRgF2E3vOsO9ufyEkt3d6zp4Pa8xqJZWaHdILKVS40Oa2I+c2lrOsajPQ7oqAfZ40EOewiSNO5R2A56XDfucH1EH8YubSwVut0BMZ6ZJl40KWUbq1Z8HmkV9J8Ne6ZHXvQC7UC2c2+pnvnpP3OJOcc4uUf6w6ZIas+JkUFsvdxAl4NeaP6FDTXz7jB9GO4Cez68tNzwhVV+EZjXQq0LFTmASkLOnpTxg2o2LlImAGr5uNA2BVBPycV24QMnHyfwatx7wv4/IdUy25eYG8sulDqG1vD+VsXEAdaY0vT9DimnTuG2+1OWrSjX055bL2cXt5vYrkklcLXeCV1sTpQ5dnWlDQQqHg7A4CKdw2QHje17O56on7Z2t73kPKPYpUcba6M8sKH7g7U1SmT6ZqVGduYeeEyxvH80+k97xWOmO+Y7JnS/WpqDN4N+aB6Pn4fdq6vyi+bM+8b71nvshd6ld+W98kberYe8D96/J6cnD1p/tP5s/dX6e4OenpQ+X3u1q/XhP21SzvE=</latexit><latexit sha1_base64="yrmlVl7ZZBskG0QNVusVhY4oRU4=">AAAKGXicjZbPb9s2FMeVdD9ib97S7biLMKNAN7iG5LhNewuQAusOA7wiaYuZnkFRtE2YlASScmcw/C9221+z27BrT/tTdhspy45E2cYUJCEfP++r9/ioJ0UZJUIGwT8npw8++viTT89a7c8+73zx5fnDr96INOcI36KUpvxdBAWmJMG3kkiK32UcQxZR/DZaXtv1tyvMBUmTG7nO8ITBeUJmBEFpTNNzBuKI5rgN8K9KPlYg5jgGc8gYBAzKBYJUvdT6CSC76Sv9nW4DQVi7pI2nWfdlhZj+ovVuOtJTsII8W5D29Lwb9IPi8puDsBx0vfIaTR+e/Q7iFOUMJxJRKMQ4DDI5UZBLgijWHZALnEG0hHM8NsMEMiwmqtgX7T8yltifpdz8JtIvrFUPBZkQaxYZ0gYr3DVr3LvG8arm96i6mC5zBhFP93pGbJ95nMvZ84kiSZZLnKBN5LOc+jL1bdX8mHCMJF2bgZEmJnkfLSCHSJradjqA4wS/R6kpWxKbsmgVm62pmrBWQOLfpMJauzjZrhHteHGSSLNo/oKYiIzCNSWMSNGQeG31bVppVmoZiwZJeoD/kbm8sdT4Ki25SxvLQfqmQd8coZdY6nE4UXeqG2rAYTIvjlUViTgsEECLVQveNRGhx4OJUnqqugMNFsKUFn+vngT9AWP6iKsJYON9MSkmljEaF00Ng1nt5q1RkcRgF2E3vOsO9ufyEkt3d6zp4Pa8xqJZWaHdILKVS40Oa2I+c2lrOsajPQ7oqAfZ40EOewiSNO5R2A56XDfucH1EH8YubSwVut0BMZ6ZJl40KWUbq1Z8HmkV9J8Ne6ZHXvQC7UC2c2+pnvnpP3OJOcc4uUf6w6ZIas+JkUFsvdxAl4NeaP6FDTXz7jB9GO4Cez68tNzwhVV+EZjXQq0LFTmASkLOnpTxg2o2LlImAGr5uNA2BVBPycV24QMnHyfwatx7wv4/IdUy25eYG8sulDqG1vD+VsXEAdaY0vT9DimnTuG2+1OWrSjX055bL2cXt5vYrkklcLXeCV1sTpQ5dnWlDQQqHg7A4CKdw2QHje17O56on7Z2t73kPKPYpUcba6M8sKH7g7U1SmT6ZqVGduYeeEyxvH80+k97xWOmO+Y7JnS/WpqDN4N+aB6Pn4fdq6vyi+bM+8b71nvshd6ld+W98kberYe8D96/J6cnD1p/tP5s/dX6e4OenpQ+X3u1q/XhP21SzvE=</latexit><latexit sha1_base64="yrmlVl7ZZBskG0QNVusVhY4oRU4=">AAAKGXicjZbPb9s2FMeVdD9ib97S7biLMKNAN7iG5LhNewuQAusOA7wiaYuZnkFRtE2YlASScmcw/C9221+z27BrT/tTdhspy45E2cYUJCEfP++r9/ioJ0UZJUIGwT8npw8++viTT89a7c8+73zx5fnDr96INOcI36KUpvxdBAWmJMG3kkiK32UcQxZR/DZaXtv1tyvMBUmTG7nO8ITBeUJmBEFpTNNzBuKI5rgN8K9KPlYg5jgGc8gYBAzKBYJUvdT6CSC76Sv9nW4DQVi7pI2nWfdlhZj+ovVuOtJTsII8W5D29Lwb9IPi8puDsBx0vfIaTR+e/Q7iFOUMJxJRKMQ4DDI5UZBLgijWHZALnEG0hHM8NsMEMiwmqtgX7T8yltifpdz8JtIvrFUPBZkQaxYZ0gYr3DVr3LvG8arm96i6mC5zBhFP93pGbJ95nMvZ84kiSZZLnKBN5LOc+jL1bdX8mHCMJF2bgZEmJnkfLSCHSJradjqA4wS/R6kpWxKbsmgVm62pmrBWQOLfpMJauzjZrhHteHGSSLNo/oKYiIzCNSWMSNGQeG31bVppVmoZiwZJeoD/kbm8sdT4Ki25SxvLQfqmQd8coZdY6nE4UXeqG2rAYTIvjlUViTgsEECLVQveNRGhx4OJUnqqugMNFsKUFn+vngT9AWP6iKsJYON9MSkmljEaF00Ng1nt5q1RkcRgF2E3vOsO9ufyEkt3d6zp4Pa8xqJZWaHdILKVS40Oa2I+c2lrOsajPQ7oqAfZ40EOewiSNO5R2A56XDfucH1EH8YubSwVut0BMZ6ZJl40KWUbq1Z8HmkV9J8Ne6ZHXvQC7UC2c2+pnvnpP3OJOcc4uUf6w6ZIas+JkUFsvdxAl4NeaP6FDTXz7jB9GO4Cez68tNzwhVV+EZjXQq0LFTmASkLOnpTxg2o2LlImAGr5uNA2BVBPycV24QMnHyfwatx7wv4/IdUy25eYG8sulDqG1vD+VsXEAdaY0vT9DimnTuG2+1OWrSjX055bL2cXt5vYrkklcLXeCV1sTpQ5dnWlDQQqHg7A4CKdw2QHje17O56on7Z2t73kPKPYpUcba6M8sKH7g7U1SmT6ZqVGduYeeEyxvH80+k97xWOmO+Y7JnS/WpqDN4N+aB6Pn4fdq6vyi+bM+8b71nvshd6ld+W98kberYe8D96/J6cnD1p/tP5s/dX6e4OenpQ+X3u1q/XhP21SzvE=</latexit>

(iv) strong damping (with no persistent oscillations)

Pulsed QZDs (n ! +1)<latexit sha1_base64="ckoiePMUmKvKIdd+TLuVFK84yws=">AAAJwXicjZbdbts2FMfVrt1ir97SDb3ajTGjQD88Q3Lcpr0LkAHdLgZkRdIWMI2Aoo4dwhQlkFRageFb9AV6uz3R3maULDsSZRuVYYc6/J0/zwfFKEwZlcr3/7tz95t797/97qDT/f5B74cfDx/+9E4mmSBwQRKWiA8hlsAohwtFFYMPqQAchwzeh8vTYv79NQhJE36u8hRmMV5wOqcEK2u6PHyEooUA4N0nHKnkOaJ8rvKnl4cDf+SXV789CKrBwKuus8uHB59RlJAsBq4Iw1JOAz9VM42FooSB6aFMQorJEi9gaoccxyBnuozf9B9bS9SfJ8J+ueqX1rqHxrGUeRxaMsbqSrpzhXHrnIDrht/j+mSyzGJMRLLVM4y3maeZmr+aacrTTAEnq8jnGeurpF9Utx9RAUSx3A6sNLXJ98kVFpgo24NeDwng8JEkcYx5pFFkdGRLUzeB0UjBJ6XBGBen6zlqHC9BubKT9hdFVKYM54zGVMmWxNtCv0grSSstazGIJzv4P2OXt5YGX6eVcGlr2Umft+jzPfQSlJkGM32jB4FBAvNFua3qSChwiSBWzhbgTRuRZjqeaW0u9WBs0JW0rYVn+jd/NI5js8fVBrDyPpqVNwVjNY7aGhYrtNtLkzKJ8SbCQXAzGG/P5XdQbnUK087yvAXZ7qw0bhDptUud7dYEMXfpwrSPJ1scyF4PusWD7vaQlLfWKG07PU5bK5zu0ceRS1tLje72UARze9iWh5SOBFgHsQiN9kcvJ0N7Rh4NfeNAIctgTQ3tZ/TSJcoz+BYZTdoiSbFPrAyJ8+UKOh4PA/snaKnZM96ew3gT2KvJccFNXhfKr33TbaS8ygHVEnJqUsWP6tm4SJUAauTjQusUUDMlF9uEj5x8nMDrcW8J+2tCamS2LTE3lk0oTYzk+Hap8sYBcmAs+bhBqluncev6VG0r2/Vi6PbLqeK6iN2GFMfX+UboaLWj7LZrKq0gVPNwgBhfJQvMN9C0+L8dzfRfa7t7vGQiZeDSZytrqz24pfumsLVaZM/NWo+KO3fDAwN1+2iMXgzLx8z07HtM4L61tAfvxqPAPh5/TwYnJ9UbzYH3i/er98QLvGPvxPvDO/MuPOJp74v3j/dv57RDO2lHrNC7dyqfn73G1dH/A0wwq0o=</latexit><latexit sha1_base64="ckoiePMUmKvKIdd+TLuVFK84yws=">AAAJwXicjZbdbts2FMfVrt1ir97SDb3ajTGjQD88Q3Lcpr0LkAHdLgZkRdIWMI2Aoo4dwhQlkFRageFb9AV6uz3R3maULDsSZRuVYYc6/J0/zwfFKEwZlcr3/7tz95t797/97qDT/f5B74cfDx/+9E4mmSBwQRKWiA8hlsAohwtFFYMPqQAchwzeh8vTYv79NQhJE36u8hRmMV5wOqcEK2u6PHyEooUA4N0nHKnkOaJ8rvKnl4cDf+SXV789CKrBwKuus8uHB59RlJAsBq4Iw1JOAz9VM42FooSB6aFMQorJEi9gaoccxyBnuozf9B9bS9SfJ8J+ueqX1rqHxrGUeRxaMsbqSrpzhXHrnIDrht/j+mSyzGJMRLLVM4y3maeZmr+aacrTTAEnq8jnGeurpF9Utx9RAUSx3A6sNLXJ98kVFpgo24NeDwng8JEkcYx5pFFkdGRLUzeB0UjBJ6XBGBen6zlqHC9BubKT9hdFVKYM54zGVMmWxNtCv0grSSstazGIJzv4P2OXt5YGX6eVcGlr2Umft+jzPfQSlJkGM32jB4FBAvNFua3qSChwiSBWzhbgTRuRZjqeaW0u9WBs0JW0rYVn+jd/NI5js8fVBrDyPpqVNwVjNY7aGhYrtNtLkzKJ8SbCQXAzGG/P5XdQbnUK087yvAXZ7qw0bhDptUud7dYEMXfpwrSPJ1scyF4PusWD7vaQlLfWKG07PU5bK5zu0ceRS1tLje72UARze9iWh5SOBFgHsQiN9kcvJ0N7Rh4NfeNAIctgTQ3tZ/TSJcoz+BYZTdoiSbFPrAyJ8+UKOh4PA/snaKnZM96ew3gT2KvJccFNXhfKr33TbaS8ygHVEnJqUsWP6tm4SJUAauTjQusUUDMlF9uEj5x8nMDrcW8J+2tCamS2LTE3lk0oTYzk+Hap8sYBcmAs+bhBqluncev6VG0r2/Vi6PbLqeK6iN2GFMfX+UboaLWj7LZrKq0gVPNwgBhfJQvMN9C0+L8dzfRfa7t7vGQiZeDSZytrqz24pfumsLVaZM/NWo+KO3fDAwN1+2iMXgzLx8z07HtM4L61tAfvxqPAPh5/TwYnJ9UbzYH3i/er98QLvGPvxPvDO/MuPOJp74v3j/dv57RDO2lHrNC7dyqfn73G1dH/A0wwq0o=</latexit><latexit sha1_base64="ckoiePMUmKvKIdd+TLuVFK84yws=">AAAJwXicjZbdbts2FMfVrt1ir97SDb3ajTGjQD88Q3Lcpr0LkAHdLgZkRdIWMI2Aoo4dwhQlkFRageFb9AV6uz3R3maULDsSZRuVYYc6/J0/zwfFKEwZlcr3/7tz95t797/97qDT/f5B74cfDx/+9E4mmSBwQRKWiA8hlsAohwtFFYMPqQAchwzeh8vTYv79NQhJE36u8hRmMV5wOqcEK2u6PHyEooUA4N0nHKnkOaJ8rvKnl4cDf+SXV789CKrBwKuus8uHB59RlJAsBq4Iw1JOAz9VM42FooSB6aFMQorJEi9gaoccxyBnuozf9B9bS9SfJ8J+ueqX1rqHxrGUeRxaMsbqSrpzhXHrnIDrht/j+mSyzGJMRLLVM4y3maeZmr+aacrTTAEnq8jnGeurpF9Utx9RAUSx3A6sNLXJ98kVFpgo24NeDwng8JEkcYx5pFFkdGRLUzeB0UjBJ6XBGBen6zlqHC9BubKT9hdFVKYM54zGVMmWxNtCv0grSSstazGIJzv4P2OXt5YGX6eVcGlr2Umft+jzPfQSlJkGM32jB4FBAvNFua3qSChwiSBWzhbgTRuRZjqeaW0u9WBs0JW0rYVn+jd/NI5js8fVBrDyPpqVNwVjNY7aGhYrtNtLkzKJ8SbCQXAzGG/P5XdQbnUK087yvAXZ7qw0bhDptUud7dYEMXfpwrSPJ1scyF4PusWD7vaQlLfWKG07PU5bK5zu0ceRS1tLje72UARze9iWh5SOBFgHsQiN9kcvJ0N7Rh4NfeNAIctgTQ3tZ/TSJcoz+BYZTdoiSbFPrAyJ8+UKOh4PA/snaKnZM96ew3gT2KvJccFNXhfKr33TbaS8ygHVEnJqUsWP6tm4SJUAauTjQusUUDMlF9uEj5x8nMDrcW8J+2tCamS2LTE3lk0oTYzk+Hap8sYBcmAs+bhBqluncev6VG0r2/Vi6PbLqeK6iN2GFMfX+UboaLWj7LZrKq0gVPNwgBhfJQvMN9C0+L8dzfRfa7t7vGQiZeDSZytrqz24pfumsLVaZM/NWo+KO3fDAwN1+2iMXgzLx8z07HtM4L61tAfvxqPAPh5/TwYnJ9UbzYH3i/er98QLvGPvxPvDO/MuPOJp74v3j/dv57RDO2lHrNC7dyqfn73G1dH/A0wwq0o=</latexit><latexit sha1_base64="ckoiePMUmKvKIdd+TLuVFK84yws=">AAAJwXicjZbdbts2FMfVrt1ir97SDb3ajTGjQD88Q3Lcpr0LkAHdLgZkRdIWMI2Aoo4dwhQlkFRageFb9AV6uz3R3maULDsSZRuVYYc6/J0/zwfFKEwZlcr3/7tz95t797/97qDT/f5B74cfDx/+9E4mmSBwQRKWiA8hlsAohwtFFYMPqQAchwzeh8vTYv79NQhJE36u8hRmMV5wOqcEK2u6PHyEooUA4N0nHKnkOaJ8rvKnl4cDf+SXV789CKrBwKuus8uHB59RlJAsBq4Iw1JOAz9VM42FooSB6aFMQorJEi9gaoccxyBnuozf9B9bS9SfJ8J+ueqX1rqHxrGUeRxaMsbqSrpzhXHrnIDrht/j+mSyzGJMRLLVM4y3maeZmr+aacrTTAEnq8jnGeurpF9Utx9RAUSx3A6sNLXJ98kVFpgo24NeDwng8JEkcYx5pFFkdGRLUzeB0UjBJ6XBGBen6zlqHC9BubKT9hdFVKYM54zGVMmWxNtCv0grSSstazGIJzv4P2OXt5YGX6eVcGlr2Umft+jzPfQSlJkGM32jB4FBAvNFua3qSChwiSBWzhbgTRuRZjqeaW0u9WBs0JW0rYVn+jd/NI5js8fVBrDyPpqVNwVjNY7aGhYrtNtLkzKJ8SbCQXAzGG/P5XdQbnUK087yvAXZ7qw0bhDptUud7dYEMXfpwrSPJ1scyF4PusWD7vaQlLfWKG07PU5bK5zu0ceRS1tLje72UARze9iWh5SOBFgHsQiN9kcvJ0N7Rh4NfeNAIctgTQ3tZ/TSJcoz+BYZTdoiSbFPrAyJ8+UKOh4PA/snaKnZM96ew3gT2KvJccFNXhfKr33TbaS8ygHVEnJqUsWP6tm4SJUAauTjQusUUDMlF9uEj5x8nMDrcW8J+2tCamS2LTE3lk0oTYzk+Hap8sYBcmAs+bhBqluncev6VG0r2/Vi6PbLqeK6iN2GFMfX+UboaLWj7LZrKq0gVPNwgBhfJQvMN9C0+L8dzfRfa7t7vGQiZeDSZytrqz24pfumsLVaZM/NWo+KO3fDAwN1+2iMXgzLx8z07HtM4L61tAfvxqPAPh5/TwYnJ9UbzYH3i/er98QLvGPvxPvDO/MuPOJp74v3j/dv57RDO2lHrNC7dyqfn73G1dH/A0wwq0o=</latexit>

Continuous QZDs ( ! +1)<latexit sha1_base64="MUZGFWH1+5qT1DtipDGq4UKaCdQ=">AAAJxXicjZbdbts2FMfV7iv25i3drobeGDMKdJtrSI7btHcBMqDtxYCsSNoCphFQ1LFDWKQEknInKERfYq/Q2+159jYjZdmRKNuYDDvU4e/8eT4oRmEaU6l8/9979z/7/IsvvzrqdL/+pvftd8cPvn8rk0wQuCJJnIj3IZYQUw5XiqoY3qcCMAtjeBcuz+38uxUISRN+qfIUZgwvOJ1TgpUxXR//iKIwzqD7GC0wYxip5FdE+VzlP18fD/yRX1799iCoBgOvui6uHxz9haKEZAy4IjGWchr4qZoVWChKYtA9lElIMVniBUzNkGMGclaUOej+I2OJ+vNEmC9X/dJa9ygwkzJnoSEZVjfSnbPGnXMCVg2/R/XJZJkxTESy0zNku8zTTM2fzwrK00wBJ+vI51ncV0nfVrgfUQFExbkZGGlqku+TGywwUaYPvR4SwOEDSUy1eVSgSBeRKU3dBLpACv5UBWjt4nQzR7XjJShXZtL8oojKNMZ5TBlVsiXxxurbtJK00jIWjXiyh3/NXN5YGnydVsKljWUvfdmiLw/QS1B6GsyK22IQaCQwX5Tbqo6EApcIistZC962Eamn41lR6OtiMNboRprWwi/FE380ZkwfcDUBrL1PZuWNZYzGSVvDYFa7vTQpkxhvIxwEt4Px7lx+A+VWx5r2lucNyHZnpXaDSFcudbFfE8Tcpa3pEE92OJCDHnSHB93vISlvrVHa9nqct1Y4P6CPI5c2lhrd7aEI5ubALQ+pIhJgHMQi1IU/ejYZmjPyZOhrB7Kn7IYams/omUssBAC/Q0aTtkhi94mRISxfrqHT8TAwf4KWmjnnzTmMt4E9n5xabvLCKr/wdbeR8joHVEvIqUkVP6pn4yJVAqiRjwttUkDNlFxsGz5y8nECr8e9I+z/E1Ijs12JubFsQ2liJMd3S5U3DpBDHCcftkh16zRuU5+qbWW7ng7dfjlV3BSx25DieJVvhU7WO8psu6bSGkI1Dwdg+CZZYL6Fpvb/djQrft/Y3eMlE2kMLn2xtrbag1u6L62t1SJzbtZ6ZO/cDQ8xqLtHY/R0WD5mumfeYwL3raU9eDseBebx+GMyODur3miOvIfeT95jL/BOvTPvlXfhXXnE++h98v72/um87LCO6qzW6P17lc8PXuPqfPwPVZCs+g==</latexit><latexit sha1_base64="MUZGFWH1+5qT1DtipDGq4UKaCdQ=">AAAJxXicjZbdbts2FMfV7iv25i3drobeGDMKdJtrSI7btHcBMqDtxYCsSNoCphFQ1LFDWKQEknInKERfYq/Q2+159jYjZdmRKNuYDDvU4e/8eT4oRmEaU6l8/9979z/7/IsvvzrqdL/+pvftd8cPvn8rk0wQuCJJnIj3IZYQUw5XiqoY3qcCMAtjeBcuz+38uxUISRN+qfIUZgwvOJ1TgpUxXR//iKIwzqD7GC0wYxip5FdE+VzlP18fD/yRX1799iCoBgOvui6uHxz9haKEZAy4IjGWchr4qZoVWChKYtA9lElIMVniBUzNkGMGclaUOej+I2OJ+vNEmC9X/dJa9ygwkzJnoSEZVjfSnbPGnXMCVg2/R/XJZJkxTESy0zNku8zTTM2fzwrK00wBJ+vI51ncV0nfVrgfUQFExbkZGGlqku+TGywwUaYPvR4SwOEDSUy1eVSgSBeRKU3dBLpACv5UBWjt4nQzR7XjJShXZtL8oojKNMZ5TBlVsiXxxurbtJK00jIWjXiyh3/NXN5YGnydVsKljWUvfdmiLw/QS1B6GsyK22IQaCQwX5Tbqo6EApcIistZC962Eamn41lR6OtiMNboRprWwi/FE380ZkwfcDUBrL1PZuWNZYzGSVvDYFa7vTQpkxhvIxwEt4Px7lx+A+VWx5r2lucNyHZnpXaDSFcudbFfE8Tcpa3pEE92OJCDHnSHB93vISlvrVHa9nqct1Y4P6CPI5c2lhrd7aEI5ubALQ+pIhJgHMQi1IU/ejYZmjPyZOhrB7Kn7IYams/omUssBAC/Q0aTtkhi94mRISxfrqHT8TAwf4KWmjnnzTmMt4E9n5xabvLCKr/wdbeR8joHVEvIqUkVP6pn4yJVAqiRjwttUkDNlFxsGz5y8nECr8e9I+z/E1Ijs12JubFsQ2liJMd3S5U3DpBDHCcftkh16zRuU5+qbWW7ng7dfjlV3BSx25DieJVvhU7WO8psu6bSGkI1Dwdg+CZZYL6Fpvb/djQrft/Y3eMlE2kMLn2xtrbag1u6L62t1SJzbtZ6ZO/cDQ8xqLtHY/R0WD5mumfeYwL3raU9eDseBebx+GMyODur3miOvIfeT95jL/BOvTPvlXfhXXnE++h98v72/um87LCO6qzW6P17lc8PXuPqfPwPVZCs+g==</latexit><latexit sha1_base64="MUZGFWH1+5qT1DtipDGq4UKaCdQ=">AAAJxXicjZbdbts2FMfV7iv25i3drobeGDMKdJtrSI7btHcBMqDtxYCsSNoCphFQ1LFDWKQEknInKERfYq/Q2+159jYjZdmRKNuYDDvU4e/8eT4oRmEaU6l8/9979z/7/IsvvzrqdL/+pvftd8cPvn8rk0wQuCJJnIj3IZYQUw5XiqoY3qcCMAtjeBcuz+38uxUISRN+qfIUZgwvOJ1TgpUxXR//iKIwzqD7GC0wYxip5FdE+VzlP18fD/yRX1799iCoBgOvui6uHxz9haKEZAy4IjGWchr4qZoVWChKYtA9lElIMVniBUzNkGMGclaUOej+I2OJ+vNEmC9X/dJa9ygwkzJnoSEZVjfSnbPGnXMCVg2/R/XJZJkxTESy0zNku8zTTM2fzwrK00wBJ+vI51ncV0nfVrgfUQFExbkZGGlqku+TGywwUaYPvR4SwOEDSUy1eVSgSBeRKU3dBLpACv5UBWjt4nQzR7XjJShXZtL8oojKNMZ5TBlVsiXxxurbtJK00jIWjXiyh3/NXN5YGnydVsKljWUvfdmiLw/QS1B6GsyK22IQaCQwX5Tbqo6EApcIistZC962Eamn41lR6OtiMNboRprWwi/FE380ZkwfcDUBrL1PZuWNZYzGSVvDYFa7vTQpkxhvIxwEt4Px7lx+A+VWx5r2lucNyHZnpXaDSFcudbFfE8Tcpa3pEE92OJCDHnSHB93vISlvrVHa9nqct1Y4P6CPI5c2lhrd7aEI5ubALQ+pIhJgHMQi1IU/ejYZmjPyZOhrB7Kn7IYams/omUssBAC/Q0aTtkhi94mRISxfrqHT8TAwf4KWmjnnzTmMt4E9n5xabvLCKr/wdbeR8joHVEvIqUkVP6pn4yJVAqiRjwttUkDNlFxsGz5y8nECr8e9I+z/E1Ijs12JubFsQ2liJMd3S5U3DpBDHCcftkh16zRuU5+qbWW7ng7dfjlV3BSx25DieJVvhU7WO8psu6bSGkI1Dwdg+CZZYL6Fpvb/djQrft/Y3eMlE2kMLn2xtrbag1u6L62t1SJzbtZ6ZO/cDQ8xqLtHY/R0WD5mumfeYwL3raU9eDseBebx+GMyODur3miOvIfeT95jL/BOvTPvlXfhXXnE++h98v72/um87LCO6qzW6P17lc8PXuPqfPwPVZCs+g==</latexit><latexit sha1_base64="MUZGFWH1+5qT1DtipDGq4UKaCdQ=">AAAJxXicjZbdbts2FMfV7iv25i3drobeGDMKdJtrSI7btHcBMqDtxYCsSNoCphFQ1LFDWKQEknInKERfYq/Q2+159jYjZdmRKNuYDDvU4e/8eT4oRmEaU6l8/9979z/7/IsvvzrqdL/+pvftd8cPvn8rk0wQuCJJnIj3IZYQUw5XiqoY3qcCMAtjeBcuz+38uxUISRN+qfIUZgwvOJ1TgpUxXR//iKIwzqD7GC0wYxip5FdE+VzlP18fD/yRX1799iCoBgOvui6uHxz9haKEZAy4IjGWchr4qZoVWChKYtA9lElIMVniBUzNkGMGclaUOej+I2OJ+vNEmC9X/dJa9ygwkzJnoSEZVjfSnbPGnXMCVg2/R/XJZJkxTESy0zNku8zTTM2fzwrK00wBJ+vI51ncV0nfVrgfUQFExbkZGGlqku+TGywwUaYPvR4SwOEDSUy1eVSgSBeRKU3dBLpACv5UBWjt4nQzR7XjJShXZtL8oojKNMZ5TBlVsiXxxurbtJK00jIWjXiyh3/NXN5YGnydVsKljWUvfdmiLw/QS1B6GsyK22IQaCQwX5Tbqo6EApcIistZC962Eamn41lR6OtiMNboRprWwi/FE380ZkwfcDUBrL1PZuWNZYzGSVvDYFa7vTQpkxhvIxwEt4Px7lx+A+VWx5r2lucNyHZnpXaDSFcudbFfE8Tcpa3pEE92OJCDHnSHB93vISlvrVHa9nqct1Y4P6CPI5c2lhrd7aEI5ubALQ+pIhJgHMQi1IU/ejYZmjPyZOhrB7Kn7IYams/omUssBAC/Q0aTtkhi94mRISxfrqHT8TAwf4KWmjnnzTmMt4E9n5xabvLCKr/wdbeR8joHVEvIqUkVP6pn4yJVAqiRjwttUkDNlFxsGz5y8nECr8e9I+z/E1Ijs12JubFsQ2liJMd3S5U3DpBDHCcftkh16zRuU5+qbWW7ng7dfjlV3BSx25DieJVvhU7WO8psu6bSGkI1Dwdg+CZZYL6Fpvb/djQrft/Y3eMlE2kMLn2xtrbag1u6L62t1SJzbtZ6ZO/cDQ8xqLtHY/R0WD5mumfeYwL3raU9eDseBebx+GMyODur3miOvIfeT95jL/BOvTPvlXfhXXnE++h98v72/um87LCO6qzW6P17lc8PXuPqfPwPVZCs+g==</latexit>

et(D+L) etDetLZ P'<latexit sha1_base64="LeFxBiBzMKea8EcSQZnkN2sFV1k=">AAAKK3icjZbdjuI2FMfD9mtgSzvbj6veoKKVti1FCbA7u3cjzUptpVaiq5ndVTFFjmPAwk4i22GLPFZfoq/Rp+lVq97ue9QOgUkcQA1ixj7+nX/O8TEnCVNKhPT9vxv33nn3vfc/OGu27n/Y/ujj8wefvBRJxhG+QQlN+OsQCkxJjG8kkRS/TjmGLKT4Vbi6suuv1pgLksTXcpPiKYOLmMwJgtKYZue/gyikGW4B/KuSjxSIOI7AAjIGAYNyiSBVz7X+Zj/5UX+lW0AQtvWoo61CI1+985r9ovV+OtYzsIY8XZLW7Lzr9/386tQHQTHoesU1nj04+wNECcoYjiWiUIhJ4KdyqiCXBFGs2yATOIVoBRd4YoYxZFhMVb5TuvPQWKLOPOHmG8tObi17KMiE2LDQkDZY4a5Z48E1jtcVv4flxWSVMYh4ctAzZIfMk0zOn04VidNM4hhtI59ntCOTjq1jJyIcI0k3ZmCkiUm+g5aQQyRNtdttwHGM36DEVCeOTEm0iszWlE1YKyDxb1JhrV2c7NaIdrw4iaVZNH9BRERK4YYSRqSoSbyw+jatJC20jEWDODnC/8Bc3lgqfJmW3KWN5Sh9XaOvT9ArLPUkmKpb1Q004DBe5MeqjIQc5gig+aoFb+uI0JPBVCk9U92BBkthSou/Vt/6/QFj+oSrCWDrPZzmE8sYjWFdw2BWu35rlCcx2EfYDW67g8O5PMfS3R1rOro9L7CoV1ZoN4h07VLj45qYz13amk7x6IADOulBDniQ4x6CxLV75LajHle1O1yd0IeRSxtLiW61QYTnpq3nTUrZpqoVX4Ra+f0no57pkcOerx3I9vId1TOf/hOXWHCM4zukP6qLJPacGBnENqstdDHoBeZfUFMzTxPTh+E+sKejC8uNnlnlZ755VFS6UJ4DKCXk7EkRPyhn4yJFAqCSjwvtUgDVlFxsHz5w8nECL8d9IOz/E1Ils0OJubHsQ6liaAPvbpVPHGCDKU3e7JFi6hRutz9F2fJyPe659XJ2cbeJrYpUDNebvdBwe6LMsasqbSFQ8nAABpfJAsZ7aGKf29FU/bSzu+0l4ynFLj3eWmvlgTXd76ytViLTN0s1sjP3wGOK5d1Po/+4l//MdNu8xwTuW0t98HLQD4b9wc+j7uVl8UZz5n3hfek98gLvwrv0vvfG3o2HvLeN+43PGp83/2z+1fyn+e8WvdcofD71Klfz7X8VndY/</latexit>

Ref. [11]Thm. 1

(Emet

mn L · · · E1et

mn L)n En'etLZ

<latexit sha1_base64="CkgdwbtmQRdM3j7AFQ0fw9R81ow=">AAAKrXicjZbxb+M0FMfT44ARKLeDH/kluuqkA5Ve05Xb3W9DAwESiHHadifqruc4bms1TiLb7VF5/gfhL+C/wU6zNrGTiUzbnO/7vOf3Xhw7UZ4QLobDfzsPPnj44UcfH33if/pZ9/NHx4+/uObZmiF8hbIkY28jyHFCUnwliEjw25xhSKMEv4lW58b+ZoMZJ1l6KbY5nlK4SMmcICi0NDv+G8QLhnHqP5MgZjgGFIolgon8Uc2oAoziGwnmDCIplKQ7JkiV2nO/6jGKM8F9N0D4PwN8fSMPBh9wQqtRwAayfEluZKrKKYqgIqiEmP2p1Oy4NxwMiytwB2E56HnldTF7fPQPiDO0pjgVKIGcS8gEQQlWXbDmOIdoBRd4oocppJhPZdFuFTzVShzMM6Z/UxEUatVDQsr5lkaaNBly22bERhvDm5rf06oxW60pRCxr9IxokzxZi/nLqSRpvhY4RbvM5+skEFlgFkMQE4aRSLZ6oEMTXXyAllA/LKGXTLcLUvweZZTCNJa66bHuv5mDURkrZVvxwYpdKzlYiWMlqV4bQP8FMeF5ArcJoURwjTFcBV/fzZHlEgj8l5BaUSDNWvhfqM1rpcZXacFsWiut9KVDX95Dr7BQk3Aqb2XPvBQwXRSrrIpEDBYISAqrAW9dhKvJaCqlmsneSIEl108afyO/HQ5GVL+u7a46gZ33ybS4MYyOceLG0JiJ7U6NiiJG+wx74W1v1FzLD1jY3TFSa3teY+4+Wa7sJPKNTV20x8RsbtNGuo9HDQ7oXg/S4EHaPThJnTkKrdXj3Jnh/J74MLZprVRov0Zfw+oaLt9OI7Z6nGcb18OIrR7fb7DlEUV6U6/yXRDjuT6+in1Umg1eSbaIlBwOXoz7egM/6Q+VBUXJGt9Rff0zeGETxal2QAZjN0hm1q4Og+h2tYNOR/1Q/wudaPrU1IcE3Cf2cnxquPErE/nV0Cp6VwOoFGQ9pzJ/UK3GRsoCQK0eG7orAdRLsrF9+sCqx0q8mndD2vWUGjOqFdZUl53KPpM6hrbwMFNxYwFbnCTZ+z1S3lpQvT0Tc4zHU/l7Y5MoXGYLmG5t+rc73d6M1ixPnNgXO9VpHHTi/mQ0p3t6l620z9zZSxEnWBwW7eC7fvECqK7+/Antjx13cD0ahCeD0R/j3tlZ+SF05H3lPfGeeaF36p15P3sX3pWHOsPOdWfWeec/96984N/s0Aed0udLr3b5i/8A1psPsQ==</latexit>

cycles of general operations for general Lindbladians

bang-bang decoupling / dynamical decoupling

(i) frequent measurements

(ii) frequent unitary kicks(Pei t

n H)n eitHZ P<latexit sha1_base64="lzrT+9kJHYkd+A/CNFMrSgtDhFc=">AAAKKnicjZbBjts2EIblNG3Xbt1smt56EWoESAvHkLxONrktsAGaHgq4wW4S1HQMiqK9hElJIKlNDS77FHmMPk1vQa55kJKy7JUo26gM29Twm18zHGqkKKNEyCD42Lrzxd0vv/r6qN355tvud/eO73//WqQ5R/gSpTTlbyMoMCUJvpREUvw24xiyiOI30fLczr+5xlyQNLmQqwxPGVwkZE4QlMY0O/4bxAuOcdJ5pEDMcQwYlFcIUjXWGuB36jEgPphziJTUao34iZnaYC+1/vldZaIDBGGdUqv0lxV69mfFeaxnx71gEBSH3xyE5aDnlcd4dv/oA4hTlDOcSEShEJMwyORUQS4Jolh3QS5wBtESLvDEDBPIsJiqYqG0/9BYYn+ecvNNpF9Yqx4KMiFWLDKkjVG4c9a4c47j65rfw+pkuswZRDzd6RmxXeZJLufPpookWS5xgtaRz3Pqy9S3ZfRjwjGSdGUGRpqY5H10BU2dpCl2tws4TvB7lDIGk9hUQ6vYLE3VhLUCEv8lFdbaxclmjmjHi5PE7ANgfkFMREbhihJGpGhIvLL6Nq00K7WMRYMk3cP/xlzeWGp8lZbcpY1lL33RoC8O0Ess9SScqhvVCzXgMFkU26qKRBwWCKDFrAVvmojQk+FUKT1TvaEGV8KUFv+iHgeDIWP6gKsJYO19Mi1OLGM0TpoaBrPazUujIonhNsJeeNMb7s7lBZbu6ljT3uV5hUWzskK7QWTXLjXer4n53KWt6RCPdjiggx5khwfZ7yFI0rhGYdvrcd64wvkBfRi7tLFU6E4XxHhuunrRpJTtp1rxRaRVMHg66pseedIPtANFNMcbqm8+g6cuUTT7W2Qwaoqkdp8YGcRWyzV0OuyH5i9sqJmHienDcBvYs9Gp5UbPrfLzwDwNal2oyAFUEnLWpIwfVLNxkTIBUMvHhTYpgHpKLrYNHzj5OIFX494R9v8JqZbZrsTcWLah1DG0greXKk4cYIUpTd9vkfLUKdxmfcqyFeV60nfr5aziZhE7NakEXq+2QifrHWW2XV1pDYGKhwMweJUuYLKFJva5HU/V7xu7215ynlHs0uO1tVEe2ND91doaJTJ9s1Ije+ZueEyxvL01Bk/6xW2mu+Y9JnTfWpqD18NBaG6PP0a9s7PyjebI+9H7yXvkhd6pd+a99MbepYe8z61O60Hrh/Y/7X/bH9uf1uidVunzwKsd7c//AcHL1cM=</latexit><latexit sha1_base64="lzrT+9kJHYkd+A/CNFMrSgtDhFc=">AAAKKnicjZbBjts2EIblNG3Xbt1smt56EWoESAvHkLxONrktsAGaHgq4wW4S1HQMiqK9hElJIKlNDS77FHmMPk1vQa55kJKy7JUo26gM29Twm18zHGqkKKNEyCD42Lrzxd0vv/r6qN355tvud/eO73//WqQ5R/gSpTTlbyMoMCUJvpREUvw24xiyiOI30fLczr+5xlyQNLmQqwxPGVwkZE4QlMY0O/4bxAuOcdJ5pEDMcQwYlFcIUjXWGuB36jEgPphziJTUao34iZnaYC+1/vldZaIDBGGdUqv0lxV69mfFeaxnx71gEBSH3xyE5aDnlcd4dv/oA4hTlDOcSEShEJMwyORUQS4Jolh3QS5wBtESLvDEDBPIsJiqYqG0/9BYYn+ecvNNpF9Yqx4KMiFWLDKkjVG4c9a4c47j65rfw+pkuswZRDzd6RmxXeZJLufPpookWS5xgtaRz3Pqy9S3ZfRjwjGSdGUGRpqY5H10BU2dpCl2tws4TvB7lDIGk9hUQ6vYLE3VhLUCEv8lFdbaxclmjmjHi5PE7ANgfkFMREbhihJGpGhIvLL6Nq00K7WMRYMk3cP/xlzeWGp8lZbcpY1lL33RoC8O0Ess9SScqhvVCzXgMFkU26qKRBwWCKDFrAVvmojQk+FUKT1TvaEGV8KUFv+iHgeDIWP6gKsJYO19Mi1OLGM0TpoaBrPazUujIonhNsJeeNMb7s7lBZbu6ljT3uV5hUWzskK7QWTXLjXer4n53KWt6RCPdjiggx5khwfZ7yFI0rhGYdvrcd64wvkBfRi7tLFU6E4XxHhuunrRpJTtp1rxRaRVMHg66pseedIPtANFNMcbqm8+g6cuUTT7W2Qwaoqkdp8YGcRWyzV0OuyH5i9sqJmHienDcBvYs9Gp5UbPrfLzwDwNal2oyAFUEnLWpIwfVLNxkTIBUMvHhTYpgHpKLrYNHzj5OIFX494R9v8JqZbZrsTcWLah1DG0greXKk4cYIUpTd9vkfLUKdxmfcqyFeV60nfr5aziZhE7NakEXq+2QifrHWW2XV1pDYGKhwMweJUuYLKFJva5HU/V7xu7215ynlHs0uO1tVEe2ND91doaJTJ9s1Ije+ZueEyxvL01Bk/6xW2mu+Y9JnTfWpqD18NBaG6PP0a9s7PyjebI+9H7yXvkhd6pd+a99MbepYe8z61O60Hrh/Y/7X/bH9uf1uidVunzwKsd7c//AcHL1cM=</latexit><latexit sha1_base64="lzrT+9kJHYkd+A/CNFMrSgtDhFc=">AAAKKnicjZbBjts2EIblNG3Xbt1smt56EWoESAvHkLxONrktsAGaHgq4wW4S1HQMiqK9hElJIKlNDS77FHmMPk1vQa55kJKy7JUo26gM29Twm18zHGqkKKNEyCD42Lrzxd0vv/r6qN355tvud/eO73//WqQ5R/gSpTTlbyMoMCUJvpREUvw24xiyiOI30fLczr+5xlyQNLmQqwxPGVwkZE4QlMY0O/4bxAuOcdJ5pEDMcQwYlFcIUjXWGuB36jEgPphziJTUao34iZnaYC+1/vldZaIDBGGdUqv0lxV69mfFeaxnx71gEBSH3xyE5aDnlcd4dv/oA4hTlDOcSEShEJMwyORUQS4Jolh3QS5wBtESLvDEDBPIsJiqYqG0/9BYYn+ecvNNpF9Yqx4KMiFWLDKkjVG4c9a4c47j65rfw+pkuswZRDzd6RmxXeZJLufPpookWS5xgtaRz3Pqy9S3ZfRjwjGSdGUGRpqY5H10BU2dpCl2tws4TvB7lDIGk9hUQ6vYLE3VhLUCEv8lFdbaxclmjmjHi5PE7ANgfkFMREbhihJGpGhIvLL6Nq00K7WMRYMk3cP/xlzeWGp8lZbcpY1lL33RoC8O0Ess9SScqhvVCzXgMFkU26qKRBwWCKDFrAVvmojQk+FUKT1TvaEGV8KUFv+iHgeDIWP6gKsJYO19Mi1OLGM0TpoaBrPazUujIonhNsJeeNMb7s7lBZbu6ljT3uV5hUWzskK7QWTXLjXer4n53KWt6RCPdjiggx5khwfZ7yFI0rhGYdvrcd64wvkBfRi7tLFU6E4XxHhuunrRpJTtp1rxRaRVMHg66pseedIPtANFNMcbqm8+g6cuUTT7W2Qwaoqkdp8YGcRWyzV0OuyH5i9sqJmHienDcBvYs9Gp5UbPrfLzwDwNal2oyAFUEnLWpIwfVLNxkTIBUMvHhTYpgHpKLrYNHzj5OIFX494R9v8JqZbZrsTcWLah1DG0greXKk4cYIUpTd9vkfLUKdxmfcqyFeV60nfr5aziZhE7NakEXq+2QifrHWW2XV1pDYGKhwMweJUuYLKFJva5HU/V7xu7215ynlHs0uO1tVEe2ND91doaJTJ9s1Ije+ZueEyxvL01Bk/6xW2mu+Y9JnTfWpqD18NBaG6PP0a9s7PyjebI+9H7yXvkhd6pd+a99MbepYe8z61O60Hrh/Y/7X/bH9uf1uidVunzwKsd7c//AcHL1cM=</latexit><latexit sha1_base64="lzrT+9kJHYkd+A/CNFMrSgtDhFc=">AAAKKnicjZbBjts2EIblNG3Xbt1smt56EWoESAvHkLxONrktsAGaHgq4wW4S1HQMiqK9hElJIKlNDS77FHmMPk1vQa55kJKy7JUo26gM29Twm18zHGqkKKNEyCD42Lrzxd0vv/r6qN355tvud/eO73//WqQ5R/gSpTTlbyMoMCUJvpREUvw24xiyiOI30fLczr+5xlyQNLmQqwxPGVwkZE4QlMY0O/4bxAuOcdJ5pEDMcQwYlFcIUjXWGuB36jEgPphziJTUao34iZnaYC+1/vldZaIDBGGdUqv0lxV69mfFeaxnx71gEBSH3xyE5aDnlcd4dv/oA4hTlDOcSEShEJMwyORUQS4Jolh3QS5wBtESLvDEDBPIsJiqYqG0/9BYYn+ecvNNpF9Yqx4KMiFWLDKkjVG4c9a4c47j65rfw+pkuswZRDzd6RmxXeZJLufPpookWS5xgtaRz3Pqy9S3ZfRjwjGSdGUGRpqY5H10BU2dpCl2tws4TvB7lDIGk9hUQ6vYLE3VhLUCEv8lFdbaxclmjmjHi5PE7ANgfkFMREbhihJGpGhIvLL6Nq00K7WMRYMk3cP/xlzeWGp8lZbcpY1lL33RoC8O0Ess9SScqhvVCzXgMFkU26qKRBwWCKDFrAVvmojQk+FUKT1TvaEGV8KUFv+iHgeDIWP6gKsJYO19Mi1OLGM0TpoaBrPazUujIonhNsJeeNMb7s7lBZbu6ljT3uV5hUWzskK7QWTXLjXer4n53KWt6RCPdjiggx5khwfZ7yFI0rhGYdvrcd64wvkBfRi7tLFU6E4XxHhuunrRpJTtp1rxRaRVMHg66pseedIPtANFNMcbqm8+g6cuUTT7W2Qwaoqkdp8YGcRWyzV0OuyH5i9sqJmHienDcBvYs9Gp5UbPrfLzwDwNal2oyAFUEnLWpIwfVLNxkTIBUMvHhTYpgHpKLrYNHzj5OIFX494R9v8JqZbZrsTcWLah1DG0greXKk4cYIUpTd9vkfLUKdxmfcqyFeV60nfr5aziZhE7NakEXq+2QifrHWW2XV1pDYGKhwMweJUuYLKFJva5HU/V7xu7215ynlHs0uO1tVEe2ND91doaJTJ9s1Ije+ZueEyxvL01Bk/6xW2mu+Y9JnTfWpqD18NBaG6PP0a9s7PyjebI+9H7yXvkhd6pd+a99MbepYe8z61O60Hrh/Y/7X/bH9uf1uidVunzwKsd7c//AcHL1cM=</latexit>

(Uei tn H)n UneitHZ

<latexit sha1_base64="fqD5UwTD2T0O8X79npZn12uM5T0=">AAAKLHicjZbdbts2FMfl7iv26i1d0d3sRphRoBtcQ3Lcpr0LkAHrLgZkRdIWMx2DomiHMEUJJJXWYAj0IfYce5reFMNu+xwjZdmRKNuYDNvU4e/8dQ4PdaQoo0TIIPjYuvPZ5198+dVBu/P13e433x7e++6VSHOO8AVKacrfRFBgShi+kERS/CbjGCYRxa+jxamdf32NuSApO5fLDE8SOGdkRhCUxjQ9fA/iOceYdR4pEHMcgwTKKwSputAa4Ev1GBAfzDhESmq1QnxmptbYC61/uqxMdIAgSaeicslK4VJMVlynf2o9PewFg6A4/OYgLAc9rzzOpvcO/gJxivIEM4koFGIcBpmcKMglQRTrLsgFziBawDkemyGDCRYTVSyV9h8aS+zPUm6+TPqFteqhYCLEMokMaeMU7pw1bp3j+Lrm97A6mS7yBCKebvWMkm3mcS5nzyaKsCyXmKFV5LOc+jL1bSH9mHCMJF2agZEmJnkfXUFTKWnK3e0Cjhl+i9IkgSw2JdAqNktTNWGtgMTvpMJauzhZzxHteHHCzE4A5hfERGQULilJiBQNiZdW36aVZqWWsWjA0h38b4nLG0uNr9KSu7Sx7KTPG/T5HnqBpR6HE3WjeqEGHLJ5sa2qSMRhgQBazFrwpokIPR5OlNJT1RtqcCVMafHP6nEwGCaJ3uNqAlh5H02KE8sYjaOmhsGsdvPSqEhiuImwF970httz+QVLd3WsaefyvMSiWVmh3SCya5c6262J+cylrWkfj7Y4oL0eZIsH2e0hCGtco7Dt9DhtXOF0jz6MXdpYKnSnC2I8M329aFLKNlGt+DzSKhg8HfVNjzzqB9qBIprjNdU3n8FTlyja/S0yGDVFUrtPjAxKlosVdDzsh+YvbKiZx4npw3AT2LPRseVGz63y88A8D2pdqMgBVBJy1qSMH1SzcZEyAVDLx4XWKYB6Si62CR84+TiBV+PeEvb/CamW2bbE3Fg2odQxtIS3lypOHGCJKU3fbpDy1Cncen3KshXletJ36+Ws4noROzUpBq+XG6Gj1Y4y266utIJAxcMBEniVziHbQGP73I4n6ve13W0vOc8odumzlbVRHtjQ/dXaGiUyfbNSI3vmbnhMsby9NQZP+sVtprvmPSZ031qag1fDQWhujz9GvZOT8o3mwPvB+9F75IXesXfivfDOvAsPeZ9ad1sPWt+3/25/aP/T/neF3mmVPve92tH+9B9J+dat</latexit><latexit sha1_base64="fqD5UwTD2T0O8X79npZn12uM5T0=">AAAKLHicjZbdbts2FMfl7iv26i1d0d3sRphRoBtcQ3Lcpr0LkAHrLgZkRdIWMx2DomiHMEUJJJXWYAj0IfYce5reFMNu+xwjZdmRKNuYDNvU4e/8dQ4PdaQoo0TIIPjYuvPZ5198+dVBu/P13e433x7e++6VSHOO8AVKacrfRFBgShi+kERS/CbjGCYRxa+jxamdf32NuSApO5fLDE8SOGdkRhCUxjQ9fA/iOceYdR4pEHMcgwTKKwSputAa4Ev1GBAfzDhESmq1QnxmptbYC61/uqxMdIAgSaeicslK4VJMVlynf2o9PewFg6A4/OYgLAc9rzzOpvcO/gJxivIEM4koFGIcBpmcKMglQRTrLsgFziBawDkemyGDCRYTVSyV9h8aS+zPUm6+TPqFteqhYCLEMokMaeMU7pw1bp3j+Lrm97A6mS7yBCKebvWMkm3mcS5nzyaKsCyXmKFV5LOc+jL1bSH9mHCMJF2agZEmJnkfXUFTKWnK3e0Cjhl+i9IkgSw2JdAqNktTNWGtgMTvpMJauzhZzxHteHHCzE4A5hfERGQULilJiBQNiZdW36aVZqWWsWjA0h38b4nLG0uNr9KSu7Sx7KTPG/T5HnqBpR6HE3WjeqEGHLJ5sa2qSMRhgQBazFrwpokIPR5OlNJT1RtqcCVMafHP6nEwGCaJ3uNqAlh5H02KE8sYjaOmhsGsdvPSqEhiuImwF970httz+QVLd3WsaefyvMSiWVmh3SCya5c6262J+cylrWkfj7Y4oL0eZIsH2e0hCGtco7Dt9DhtXOF0jz6MXdpYKnSnC2I8M329aFLKNlGt+DzSKhg8HfVNjzzqB9qBIprjNdU3n8FTlyja/S0yGDVFUrtPjAxKlosVdDzsh+YvbKiZx4npw3AT2LPRseVGz63y88A8D2pdqMgBVBJy1qSMH1SzcZEyAVDLx4XWKYB6Si62CR84+TiBV+PeEvb/CamW2bbE3Fg2odQxtIS3lypOHGCJKU3fbpDy1Cncen3KshXletJ36+Ws4noROzUpBq+XG6Gj1Y4y266utIJAxcMBEniVziHbQGP73I4n6ve13W0vOc8odumzlbVRHtjQ/dXaGiUyfbNSI3vmbnhMsby9NQZP+sVtprvmPSZ031qag1fDQWhujz9GvZOT8o3mwPvB+9F75IXesXfivfDOvAsPeZ9ad1sPWt+3/25/aP/T/neF3mmVPve92tH+9B9J+dat</latexit><latexit sha1_base64="fqD5UwTD2T0O8X79npZn12uM5T0=">AAAKLHicjZbdbts2FMfl7iv26i1d0d3sRphRoBtcQ3Lcpr0LkAHrLgZkRdIWMx2DomiHMEUJJJXWYAj0IfYce5reFMNu+xwjZdmRKNuYDNvU4e/8dQ4PdaQoo0TIIPjYuvPZ5198+dVBu/P13e433x7e++6VSHOO8AVKacrfRFBgShi+kERS/CbjGCYRxa+jxamdf32NuSApO5fLDE8SOGdkRhCUxjQ9fA/iOceYdR4pEHMcgwTKKwSputAa4Ev1GBAfzDhESmq1QnxmptbYC61/uqxMdIAgSaeicslK4VJMVlynf2o9PewFg6A4/OYgLAc9rzzOpvcO/gJxivIEM4koFGIcBpmcKMglQRTrLsgFziBawDkemyGDCRYTVSyV9h8aS+zPUm6+TPqFteqhYCLEMokMaeMU7pw1bp3j+Lrm97A6mS7yBCKebvWMkm3mcS5nzyaKsCyXmKFV5LOc+jL1bSH9mHCMJF2agZEmJnkfXUFTKWnK3e0Cjhl+i9IkgSw2JdAqNktTNWGtgMTvpMJauzhZzxHteHHCzE4A5hfERGQULilJiBQNiZdW36aVZqWWsWjA0h38b4nLG0uNr9KSu7Sx7KTPG/T5HnqBpR6HE3WjeqEGHLJ5sa2qSMRhgQBazFrwpokIPR5OlNJT1RtqcCVMafHP6nEwGCaJ3uNqAlh5H02KE8sYjaOmhsGsdvPSqEhiuImwF970httz+QVLd3WsaefyvMSiWVmh3SCya5c6262J+cylrWkfj7Y4oL0eZIsH2e0hCGtco7Dt9DhtXOF0jz6MXdpYKnSnC2I8M329aFLKNlGt+DzSKhg8HfVNjzzqB9qBIprjNdU3n8FTlyja/S0yGDVFUrtPjAxKlosVdDzsh+YvbKiZx4npw3AT2LPRseVGz63y88A8D2pdqMgBVBJy1qSMH1SzcZEyAVDLx4XWKYB6Si62CR84+TiBV+PeEvb/CamW2bbE3Fg2odQxtIS3lypOHGCJKU3fbpDy1Cncen3KshXletJ36+Ws4noROzUpBq+XG6Gj1Y4y266utIJAxcMBEniVziHbQGP73I4n6ve13W0vOc8odumzlbVRHtjQ/dXaGiUyfbNSI3vmbnhMsby9NQZP+sVtprvmPSZ031qag1fDQWhujz9GvZOT8o3mwPvB+9F75IXesXfivfDOvAsPeZ9ad1sPWt+3/25/aP/T/neF3mmVPve92tH+9B9J+dat</latexit><latexit sha1_base64="fqD5UwTD2T0O8X79npZn12uM5T0=">AAAKLHicjZbdbts2FMfl7iv26i1d0d3sRphRoBtcQ3Lcpr0LkAHrLgZkRdIWMx2DomiHMEUJJJXWYAj0IfYce5reFMNu+xwjZdmRKNuYDNvU4e/8dQ4PdaQoo0TIIPjYuvPZ5198+dVBu/P13e433x7e++6VSHOO8AVKacrfRFBgShi+kERS/CbjGCYRxa+jxamdf32NuSApO5fLDE8SOGdkRhCUxjQ9fA/iOceYdR4pEHMcgwTKKwSputAa4Ev1GBAfzDhESmq1QnxmptbYC61/uqxMdIAgSaeicslK4VJMVlynf2o9PewFg6A4/OYgLAc9rzzOpvcO/gJxivIEM4koFGIcBpmcKMglQRTrLsgFziBawDkemyGDCRYTVSyV9h8aS+zPUm6+TPqFteqhYCLEMokMaeMU7pw1bp3j+Lrm97A6mS7yBCKebvWMkm3mcS5nzyaKsCyXmKFV5LOc+jL1bSH9mHCMJF2agZEmJnkfXUFTKWnK3e0Cjhl+i9IkgSw2JdAqNktTNWGtgMTvpMJauzhZzxHteHHCzE4A5hfERGQULilJiBQNiZdW36aVZqWWsWjA0h38b4nLG0uNr9KSu7Sx7KTPG/T5HnqBpR6HE3WjeqEGHLJ5sa2qSMRhgQBazFrwpokIPR5OlNJT1RtqcCVMafHP6nEwGCaJ3uNqAlh5H02KE8sYjaOmhsGsdvPSqEhiuImwF970httz+QVLd3WsaefyvMSiWVmh3SCya5c6262J+cylrWkfj7Y4oL0eZIsH2e0hCGtco7Dt9DhtXOF0jz6MXdpYKnSnC2I8M329aFLKNlGt+DzSKhg8HfVNjzzqB9qBIprjNdU3n8FTlyja/S0yGDVFUrtPjAxKlosVdDzsh+YvbKiZx4npw3AT2LPRseVGz63y88A8D2pdqMgBVBJy1qSMH1SzcZEyAVDLx4XWKYB6Si62CR84+TiBV+PeEvb/CamW2bbE3Fg2odQxtIS3lypOHGCJKU3fbpDy1Cncen3KshXletJ36+Ws4noROzUpBq+XG6Gj1Y4y266utIJAxcMBEniVziHbQGP73I4n6ve13W0vOc8odumzlbVRHtjQ/dXaGiUyfbNSI3vmbnhMsby9NQZP+sVtprvmPSZ031qag1fDQWhujz9GvZOT8o3mwPvB+9F75IXesXfivfDOvAsPeZ9ad1sPWt+3/25/aP/T/neF3mmVPve92tH+9B9J+dat</latexit>

(Um · · · U1)neitHZ

<latexit sha1_base64="H2BVrfIcg8MgEZd/zgipqrrL2Us=">AAAJ+3icjZbNjts2EMeV9Gvt1u2mPfYi1AiQFo4heZ1sAvQQYAs0PRTdBrtJUNMxKIr2EiYpgaQ2Nbh8i75Bb0WveZii1/Y9SsqyV6JsozJsk3/+ZjjDoSglOSVSRdFfd+6+9/4HH3501Ol+/Env08+O733+UmaFQPgSZTQTrxMoMSUcXyqiKH6dCwxZQvGrZHnmxl9dYyFJxi/UKsdTBheczAmCykqz459AuhAY8y6QhHUfAAbVFYJUX5oZAyjNlKxL8ddvuAapwCnAb/RDQEK1HX5uZr8YMzvuR8OovMJ2I64a/aC6zmf3jn4DaYYKhrlCFEo5iaNcTTUUiiCKTQ8UEucQLeECT2yTQ4blVJeZm/C+VdJwngn75Sos1bqFhkzKFUss6eKU/pgTd44JfN2wu18fzJYFg0hkOy0TtkueFGr+ZKoJzwuFOVpHPi9oqLLQ1SVMicBI0ZVtWNfEJh+iKyggUrZ6vR4QmOO3KGMM8tSWwOjULk1dwkYDhX9VGhvj42QzRoxnJQhXdtD+gpTInMIVJYwo2XLxwvl3aWV55csqBvBsD/8D83mrNPg6rYRPW2UvfdGiLw7QS6zMJJ7qG92PDRCQL8ptVUcSAUsE0HLUgTdtRJrJaKq1men+yIAraUuLv9EPo+GIMXPA1Aawtj6Zlh3HWB8nbR8Wc77bU6MyidE2wn580x/tzuU7rPzVcdLe5XmBZbuy0vhB5Nc+db7fJxZzn3bSIR7tMEAHLcgOC7LfQhLemqPU9lqctWY4O+Afpj5tlRrd7YEUz+0xXR5S2h2iRotFYnQ0fDwe2DPyZBAZD0pogTfUwH6Gj32iPL1vkeG47SRz+8S6QWy1XEOno0Fs/+KWN/t0sOcw3Ab2ZHzquPFT5/lpZLqNlNc5gFpC3ppU8YN6Nj5SJQAa+fjQJgXQTMnHtuEDLx8v8HrcO8L+PyE1MtuVmB/LNpQmhlbwdqqy4wErTGn2dotUXa9wm/WpylaW69HAr5e3iptF7DZccXi92jo6We8ou+2antYQqFl4AINX2QLyLTRxz+10qn/c6P7xUoicYp8+X6ut8sCW3++d1iqRPTdrNXI9f8NjitXtrTF8NChvM9Oz7zGx/9bSbrwcDWN7e/w87j/7tnqjOQq+DL4KHgRxcBo8C54H58FlgIJ3wd/BP8G/HdP5vfNH5881evdOZfNF0Lg67/4DjQzEQQ==</latexit><latexit sha1_base64="H2BVrfIcg8MgEZd/zgipqrrL2Us=">AAAJ+3icjZbNjts2EMeV9Gvt1u2mPfYi1AiQFo4heZ1sAvQQYAs0PRTdBrtJUNMxKIr2EiYpgaQ2Nbh8i75Bb0WveZii1/Y9SsqyV6JsozJsk3/+ZjjDoSglOSVSRdFfd+6+9/4HH3501Ol+/Env08+O733+UmaFQPgSZTQTrxMoMSUcXyqiKH6dCwxZQvGrZHnmxl9dYyFJxi/UKsdTBheczAmCykqz459AuhAY8y6QhHUfAAbVFYJUX5oZAyjNlKxL8ddvuAapwCnAb/RDQEK1HX5uZr8YMzvuR8OovMJ2I64a/aC6zmf3jn4DaYYKhrlCFEo5iaNcTTUUiiCKTQ8UEucQLeECT2yTQ4blVJeZm/C+VdJwngn75Sos1bqFhkzKFUss6eKU/pgTd44JfN2wu18fzJYFg0hkOy0TtkueFGr+ZKoJzwuFOVpHPi9oqLLQ1SVMicBI0ZVtWNfEJh+iKyggUrZ6vR4QmOO3KGMM8tSWwOjULk1dwkYDhX9VGhvj42QzRoxnJQhXdtD+gpTInMIVJYwo2XLxwvl3aWV55csqBvBsD/8D83mrNPg6rYRPW2UvfdGiLw7QS6zMJJ7qG92PDRCQL8ptVUcSAUsE0HLUgTdtRJrJaKq1men+yIAraUuLv9EPo+GIMXPA1Aawtj6Zlh3HWB8nbR8Wc77bU6MyidE2wn580x/tzuU7rPzVcdLe5XmBZbuy0vhB5Nc+db7fJxZzn3bSIR7tMEAHLcgOC7LfQhLemqPU9lqctWY4O+Afpj5tlRrd7YEUz+0xXR5S2h2iRotFYnQ0fDwe2DPyZBAZD0pogTfUwH6Gj32iPL1vkeG47SRz+8S6QWy1XEOno0Fs/+KWN/t0sOcw3Ab2ZHzquPFT5/lpZLqNlNc5gFpC3ppU8YN6Nj5SJQAa+fjQJgXQTMnHtuEDLx8v8HrcO8L+PyE1MtuVmB/LNpQmhlbwdqqy4wErTGn2dotUXa9wm/WpylaW69HAr5e3iptF7DZccXi92jo6We8ou+2antYQqFl4AINX2QLyLTRxz+10qn/c6P7xUoicYp8+X6ut8sCW3++d1iqRPTdrNXI9f8NjitXtrTF8NChvM9Oz7zGx/9bSbrwcDWN7e/w87j/7tnqjOQq+DL4KHgRxcBo8C54H58FlgIJ3wd/BP8G/HdP5vfNH5881evdOZfNF0Lg67/4DjQzEQQ==</latexit><latexit sha1_base64="H2BVrfIcg8MgEZd/zgipqrrL2Us=">AAAJ+3icjZbNjts2EMeV9Gvt1u2mPfYi1AiQFo4heZ1sAvQQYAs0PRTdBrtJUNMxKIr2EiYpgaQ2Nbh8i75Bb0WveZii1/Y9SsqyV6JsozJsk3/+ZjjDoSglOSVSRdFfd+6+9/4HH3501Ol+/Env08+O733+UmaFQPgSZTQTrxMoMSUcXyqiKH6dCwxZQvGrZHnmxl9dYyFJxi/UKsdTBheczAmCykqz459AuhAY8y6QhHUfAAbVFYJUX5oZAyjNlKxL8ddvuAapwCnAb/RDQEK1HX5uZr8YMzvuR8OovMJ2I64a/aC6zmf3jn4DaYYKhrlCFEo5iaNcTTUUiiCKTQ8UEucQLeECT2yTQ4blVJeZm/C+VdJwngn75Sos1bqFhkzKFUss6eKU/pgTd44JfN2wu18fzJYFg0hkOy0TtkueFGr+ZKoJzwuFOVpHPi9oqLLQ1SVMicBI0ZVtWNfEJh+iKyggUrZ6vR4QmOO3KGMM8tSWwOjULk1dwkYDhX9VGhvj42QzRoxnJQhXdtD+gpTInMIVJYwo2XLxwvl3aWV55csqBvBsD/8D83mrNPg6rYRPW2UvfdGiLw7QS6zMJJ7qG92PDRCQL8ptVUcSAUsE0HLUgTdtRJrJaKq1men+yIAraUuLv9EPo+GIMXPA1Aawtj6Zlh3HWB8nbR8Wc77bU6MyidE2wn580x/tzuU7rPzVcdLe5XmBZbuy0vhB5Nc+db7fJxZzn3bSIR7tMEAHLcgOC7LfQhLemqPU9lqctWY4O+Afpj5tlRrd7YEUz+0xXR5S2h2iRotFYnQ0fDwe2DPyZBAZD0pogTfUwH6Gj32iPL1vkeG47SRz+8S6QWy1XEOno0Fs/+KWN/t0sOcw3Ab2ZHzquPFT5/lpZLqNlNc5gFpC3ppU8YN6Nj5SJQAa+fjQJgXQTMnHtuEDLx8v8HrcO8L+PyE1MtuVmB/LNpQmhlbwdqqy4wErTGn2dotUXa9wm/WpylaW69HAr5e3iptF7DZccXi92jo6We8ou+2antYQqFl4AINX2QLyLTRxz+10qn/c6P7xUoicYp8+X6ut8sCW3++d1iqRPTdrNXI9f8NjitXtrTF8NChvM9Oz7zGx/9bSbrwcDWN7e/w87j/7tnqjOQq+DL4KHgRxcBo8C54H58FlgIJ3wd/BP8G/HdP5vfNH5881evdOZfNF0Lg67/4DjQzEQQ==</latexit><latexit sha1_base64="H2BVrfIcg8MgEZd/zgipqrrL2Us=">AAAJ+3icjZbNjts2EMeV9Gvt1u2mPfYi1AiQFo4heZ1sAvQQYAs0PRTdBrtJUNMxKIr2EiYpgaQ2Nbh8i75Bb0WveZii1/Y9SsqyV6JsozJsk3/+ZjjDoSglOSVSRdFfd+6+9/4HH3501Ol+/Env08+O733+UmaFQPgSZTQTrxMoMSUcXyqiKH6dCwxZQvGrZHnmxl9dYyFJxi/UKsdTBheczAmCykqz459AuhAY8y6QhHUfAAbVFYJUX5oZAyjNlKxL8ddvuAapwCnAb/RDQEK1HX5uZr8YMzvuR8OovMJ2I64a/aC6zmf3jn4DaYYKhrlCFEo5iaNcTTUUiiCKTQ8UEucQLeECT2yTQ4blVJeZm/C+VdJwngn75Sos1bqFhkzKFUss6eKU/pgTd44JfN2wu18fzJYFg0hkOy0TtkueFGr+ZKoJzwuFOVpHPi9oqLLQ1SVMicBI0ZVtWNfEJh+iKyggUrZ6vR4QmOO3KGMM8tSWwOjULk1dwkYDhX9VGhvj42QzRoxnJQhXdtD+gpTInMIVJYwo2XLxwvl3aWV55csqBvBsD/8D83mrNPg6rYRPW2UvfdGiLw7QS6zMJJ7qG92PDRCQL8ptVUcSAUsE0HLUgTdtRJrJaKq1men+yIAraUuLv9EPo+GIMXPA1Aawtj6Zlh3HWB8nbR8Wc77bU6MyidE2wn580x/tzuU7rPzVcdLe5XmBZbuy0vhB5Nc+db7fJxZzn3bSIR7tMEAHLcgOC7LfQhLemqPU9lqctWY4O+Afpj5tlRrd7YEUz+0xXR5S2h2iRotFYnQ0fDwe2DPyZBAZD0pogTfUwH6Gj32iPL1vkeG47SRz+8S6QWy1XEOno0Fs/+KWN/t0sOcw3Ab2ZHzquPFT5/lpZLqNlNc5gFpC3ppU8YN6Nj5SJQAa+fjQJgXQTMnHtuEDLx8v8HrcO8L+PyE1MtuVmB/LNpQmhlbwdqqy4wErTGn2dotUXa9wm/WpylaW69HAr5e3iptF7DZccXi92jo6We8ou+2antYQqFl4AINX2QLyLTRxz+10qn/c6P7xUoicYp8+X6ut8sCW3++d1iqRPTdrNXI9f8NjitXtrTF8NChvM9Oz7zGx/9bSbrwcDWN7e/w87j/7tnqjOQq+DL4KHgRxcBo8C54H58FlgIJ3wd/BP8G/HdP5vfNH5881evdOZfNF0Lg67/4DjQzEQQ==</latexit>

(Umei tmn H · · · U1e

i tmn H)n

<latexit sha1_base64="tUsOzSGUO7Urto6f/IJDN0ijHaQ=">AAAKP3icjZbdbts2FMfl7iv25i3dLndRYUaBdHANyXGbFthFgQxYdzEgK5K2gOkaFEU7hClKIKl0BsOnaF+oj7En2N2w296NlGRHouygMmxTh7/z1/mgKEUZJUIGwd+dO599/sWXXx10e19/0//2u8O7378Uac4RvkApTfnrCApMCcMXkkiKX2ccwySi+FW0OrXzr64wFyRl53Kd4VkCl4wsCILSmOaH70C85Biz3pECMccxSKC8RJCqCz1PNMBv1ENAwIJDpKRWSQn5TOst+NyMUZxK0RYIP1XgwRt1M9GbHw6CUVAcfnsQVoOBVx1n87sH70GcojzBTCIKhZiGQSZnCnJJEMW6D3KBM4hWcImnZshggsVMFdXT/n1jif1Fys2XSb+w1j0UTIRYJ5EhbcjCnbPGnXMcXzX87tcn01WeQMTTnZ5Rsss8zeXiyUwRluUSM1RGvsipL1Pf9taPCcdI0rUZGGlikvfRJTSll2YF9PuAY4bfojRJIItNvbWKTWnqJqwVkPgvqbDWLk42c0Q7Xpww01pgfkFMREbhmpKESNGSeGH1bVppVmkZiwYs3cP/nri8sTT4Oi25SxvLXvq8RZ/fQq+w1NNwpq7VwCxqDtmyWFZ1JOKwQAAtZi143UaEno5nSum5Gow1uBSmtfhn9TAYjRNzu+13NQGU3sez4sQyRuO4rWEwq92+NCqSGG8jHITXg/HuXH7F0q2ONe0tzwss2p0V2g0iu3Kps/2amC9c2ppu49EOB3SrB9nhQfZ7CMJa1yhsez1OW1c4vUUfxi5tLDW61wcxXpitvtiklN0xteLLSKtg9HgyNHvk8TDQDhTRHG+oofmMHrtE8QS4QUaTtkhq14mRQcl6VUIn42Fo/sKWmnnCmH0YbgN7Mjmx3OSpVX4a6F4j5TIHUEvIqUkVP6hn4yJVAqCRjwttUgDNlFxsGz5w8nECr8e9I+xPCamR2a7E3Fi2oTQxtIY3lypOHGCNKU3fbpHq1Gncpj5V24p2PRq6/XKquCliryHF4NV6K3Rcriiz7JpKJQRqHg6QwMt0CdkWmtrndjxTf2zs7vaS84xilz4rra32wJbub9bWapHZN2s9smfugscUy5tbY/RoWNxmum/eY0L3raU9eDkeheb2+HMyePZL9UZz4P3o/eQdeaF34j3znntn3oWHvI+de52jzoPuh+4/3X+7/5XonU7l84PXOLof/wc72OAL</latexit><latexit sha1_base64="tUsOzSGUO7Urto6f/IJDN0ijHaQ=">AAAKP3icjZbdbts2FMfl7iv25i3dLndRYUaBdHANyXGbFthFgQxYdzEgK5K2gOkaFEU7hClKIKl0BsOnaF+oj7En2N2w296NlGRHouygMmxTh7/z1/mgKEUZJUIGwd+dO599/sWXXx10e19/0//2u8O7378Uac4RvkApTfnrCApMCcMXkkiKX2ccwySi+FW0OrXzr64wFyRl53Kd4VkCl4wsCILSmOaH70C85Biz3pECMccxSKC8RJCqCz1PNMBv1ENAwIJDpKRWSQn5TOst+NyMUZxK0RYIP1XgwRt1M9GbHw6CUVAcfnsQVoOBVx1n87sH70GcojzBTCIKhZiGQSZnCnJJEMW6D3KBM4hWcImnZshggsVMFdXT/n1jif1Fys2XSb+w1j0UTIRYJ5EhbcjCnbPGnXMcXzX87tcn01WeQMTTnZ5Rsss8zeXiyUwRluUSM1RGvsipL1Pf9taPCcdI0rUZGGlikvfRJTSll2YF9PuAY4bfojRJIItNvbWKTWnqJqwVkPgvqbDWLk42c0Q7Xpww01pgfkFMREbhmpKESNGSeGH1bVppVmkZiwYs3cP/nri8sTT4Oi25SxvLXvq8RZ/fQq+w1NNwpq7VwCxqDtmyWFZ1JOKwQAAtZi143UaEno5nSum5Gow1uBSmtfhn9TAYjRNzu+13NQGU3sez4sQyRuO4rWEwq92+NCqSGG8jHITXg/HuXH7F0q2ONe0tzwss2p0V2g0iu3Kps/2amC9c2ppu49EOB3SrB9nhQfZ7CMJa1yhsez1OW1c4vUUfxi5tLDW61wcxXpitvtiklN0xteLLSKtg9HgyNHvk8TDQDhTRHG+oofmMHrtE8QS4QUaTtkhq14mRQcl6VUIn42Fo/sKWmnnCmH0YbgN7Mjmx3OSpVX4a6F4j5TIHUEvIqUkVP6hn4yJVAqCRjwttUgDNlFxsGz5w8nECr8e9I+xPCamR2a7E3Fi2oTQxtIY3lypOHGCNKU3fbpHq1Gncpj5V24p2PRq6/XKquCliryHF4NV6K3Rcriiz7JpKJQRqHg6QwMt0CdkWmtrndjxTf2zs7vaS84xilz4rra32wJbub9bWapHZN2s9smfugscUy5tbY/RoWNxmum/eY0L3raU9eDkeheb2+HMyePZL9UZz4P3o/eQdeaF34j3znntn3oWHvI+de52jzoPuh+4/3X+7/5XonU7l84PXOLof/wc72OAL</latexit><latexit sha1_base64="tUsOzSGUO7Urto6f/IJDN0ijHaQ=">AAAKP3icjZbdbts2FMfl7iv25i3dLndRYUaBdHANyXGbFthFgQxYdzEgK5K2gOkaFEU7hClKIKl0BsOnaF+oj7En2N2w296NlGRHouygMmxTh7/z1/mgKEUZJUIGwd+dO599/sWXXx10e19/0//2u8O7378Uac4RvkApTfnrCApMCcMXkkiKX2ccwySi+FW0OrXzr64wFyRl53Kd4VkCl4wsCILSmOaH70C85Biz3pECMccxSKC8RJCqCz1PNMBv1ENAwIJDpKRWSQn5TOst+NyMUZxK0RYIP1XgwRt1M9GbHw6CUVAcfnsQVoOBVx1n87sH70GcojzBTCIKhZiGQSZnCnJJEMW6D3KBM4hWcImnZshggsVMFdXT/n1jif1Fys2XSb+w1j0UTIRYJ5EhbcjCnbPGnXMcXzX87tcn01WeQMTTnZ5Rsss8zeXiyUwRluUSM1RGvsipL1Pf9taPCcdI0rUZGGlikvfRJTSll2YF9PuAY4bfojRJIItNvbWKTWnqJqwVkPgvqbDWLk42c0Q7Xpww01pgfkFMREbhmpKESNGSeGH1bVppVmkZiwYs3cP/nri8sTT4Oi25SxvLXvq8RZ/fQq+w1NNwpq7VwCxqDtmyWFZ1JOKwQAAtZi143UaEno5nSum5Gow1uBSmtfhn9TAYjRNzu+13NQGU3sez4sQyRuO4rWEwq92+NCqSGG8jHITXg/HuXH7F0q2ONe0tzwss2p0V2g0iu3Kps/2amC9c2ppu49EOB3SrB9nhQfZ7CMJa1yhsez1OW1c4vUUfxi5tLDW61wcxXpitvtiklN0xteLLSKtg9HgyNHvk8TDQDhTRHG+oofmMHrtE8QS4QUaTtkhq14mRQcl6VUIn42Fo/sKWmnnCmH0YbgN7Mjmx3OSpVX4a6F4j5TIHUEvIqUkVP6hn4yJVAqCRjwttUgDNlFxsGz5w8nECr8e9I+xPCamR2a7E3Fi2oTQxtIY3lypOHGCNKU3fbpHq1Gncpj5V24p2PRq6/XKquCliryHF4NV6K3Rcriiz7JpKJQRqHg6QwMt0CdkWmtrndjxTf2zs7vaS84xilz4rra32wJbub9bWapHZN2s9smfugscUy5tbY/RoWNxmum/eY0L3raU9eDkeheb2+HMyePZL9UZz4P3o/eQdeaF34j3znntn3oWHvI+de52jzoPuh+4/3X+7/5XonU7l84PXOLof/wc72OAL</latexit><latexit sha1_base64="tUsOzSGUO7Urto6f/IJDN0ijHaQ=">AAAKP3icjZbdbts2FMfl7iv25i3dLndRYUaBdHANyXGbFthFgQxYdzEgK5K2gOkaFEU7hClKIKl0BsOnaF+oj7En2N2w296NlGRHouygMmxTh7/z1/mgKEUZJUIGwd+dO599/sWXXx10e19/0//2u8O7378Uac4RvkApTfnrCApMCcMXkkiKX2ccwySi+FW0OrXzr64wFyRl53Kd4VkCl4wsCILSmOaH70C85Biz3pECMccxSKC8RJCqCz1PNMBv1ENAwIJDpKRWSQn5TOst+NyMUZxK0RYIP1XgwRt1M9GbHw6CUVAcfnsQVoOBVx1n87sH70GcojzBTCIKhZiGQSZnCnJJEMW6D3KBM4hWcImnZshggsVMFdXT/n1jif1Fys2XSb+w1j0UTIRYJ5EhbcjCnbPGnXMcXzX87tcn01WeQMTTnZ5Rsss8zeXiyUwRluUSM1RGvsipL1Pf9taPCcdI0rUZGGlikvfRJTSll2YF9PuAY4bfojRJIItNvbWKTWnqJqwVkPgvqbDWLk42c0Q7Xpww01pgfkFMREbhmpKESNGSeGH1bVppVmkZiwYs3cP/nri8sTT4Oi25SxvLXvq8RZ/fQq+w1NNwpq7VwCxqDtmyWFZ1JOKwQAAtZi143UaEno5nSum5Gow1uBSmtfhn9TAYjRNzu+13NQGU3sez4sQyRuO4rWEwq92+NCqSGG8jHITXg/HuXH7F0q2ONe0tzwss2p0V2g0iu3Kps/2amC9c2ppu49EOB3SrB9nhQfZ7CMJa1yhsez1OW1c4vUUfxi5tLDW61wcxXpitvtiklN0xteLLSKtg9HgyNHvk8TDQDhTRHG+oofmMHrtE8QS4QUaTtkhq14mRQcl6VUIn42Fo/sKWmnnCmH0YbgN7Mjmx3OSpVX4a6F4j5TIHUEvIqUkVP6hn4yJVAqCRjwttUgDNlFxsGz5w8nECr8e9I+xPCamR2a7E3Fi2oTQxtIY3lypOHGCNKU3fbpHq1Gncpj5V24p2PRq6/XKquCliryHF4NV6K3Rcriiz7JpKJQRqHg6QwMt0CdkWmtrndjxTf2zs7vaS84xilz4rra32wJbub9bWapHZN2s9smfugscUy5tbY/RoWNxmum/eY0L3raU9eDkeheb2+HMyePZL9UZz4P3o/eQdeaF34j3znntn3oWHvI+de52jzoPuh+4/3X+7/5XonU7l84PXOLof/wc72OAL</latexit>

general strong coupling for general Lindbladians

Figure 1: Different manifestations of QZD [13,14] (experimental comparisons are found in Refs. [26,27]).The standard way to induce the QZD is to (i) frequently perform projective measurements, eachrepresented by a projection P [15, 16]. It can also be induced via (ii) frequent unitary kicks withan instantaneous unitary U [17, 18], or via cycles of a bang-bang sequence of multiple unitaries Uj(j = 1, . . . ,m) [28–34]. In contrast to these pulsed strategies, the QZD can be induced by (iii)continuously applying a strong external field represented by a unitary generator K [19, 20], or by (iv)putting the system under strong damping D relaxing the system to a steady subspace as etD → Pϕas t → +∞ [21–25, 36, 37]. In any case, a unitary generator H is projected to a Zeno generator HZ .See the text concerning how it is actually projected. In Ref. [11], we unified the continuous strategiesand generalized them for general Lindbladians D and L on the basis of an adiabatic theorem. In thispaper, we focus on the pulsed strategies, which we unify and generalize for general quantum operationsEj (j = 1, . . . ,m) and general Lindbladian L in Theorem 1.

recapitulate their main features.

(i) Frequent projective measurements: The standard way to induce the QZD isto perform projective measurements frequently [20, 38]. Consider a quantum system on afinite-dimensional Hilbert space with a Hamiltonian H = H†. During the unitary evolutione−itH for time t with H = [H, q ], we perform projective measurement n times at regulartime intervals. The measurement is represented by a set of orthogonal projection operatorsPk acting on the Hilbert space, satisfying PkP` = Pkδk` and

∑k Pk = I. We retain no

outcome of the measurement, i.e., our measurement is a nonselective one, described by theprojection P acting on a density operator ρ as

P(ρ) =∑k

PkρPk. (2.1)

In the limit of infinitely frequent measurements (Zeno limit), the evolution of the systemis described by [14] (

Pe−i tnH)n

= e−itHZP +O(1/n) as n→ +∞, (2.2)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 3

where HZ = [HZ , q ] withHZ =

∑k

PkHPk. (2.3)

In the Zeno limit, the transitions among the subspaces specified by the projection operatorsPk are suppressed. This is the QZE. The system meanwhile evolves unitarily within thesubspaces (Zeno subspaces [20]) with the projected Hamiltonian (Zeno Hamiltonian) HZ .This is the QZD.

(ii) Frequent unitary kicks: Instead of measurement, we can apply a series of unitarykicks to induce the QZD [17, 18]. During the unitary evolution e−itH for time t, we applyan instantaneous unitary transformation U = U q U †, with U † = U−1, repeatedly n timesat regular time intervals t/n. In the limit of infinitely frequent unitary kicks, the evolutionof the system is described by [17](

Ue−i tnH)n

= Une−itHZ +O(1/n) as n→ +∞, (2.4)

where HZ = [HZ , q ] with HZ defined by Eq. (2.3) with the eigenprojections Pk of thespectral representation of the unitary U =

∑k e−iηkPk.1 In this way, the frequent unitary

kicks project the Hamiltonian H in essentially the same way as the frequent projectivemeasurements do, and the QZD is induced.

Instead of repeating the same unitary U , one can think of applying cycles of differentunitaries Uj (j = 1, . . . ,m) as [17](

Ume−i tmnH · · · U1e−i t

mnH)n

= (Um · · · U1)ne−itHZ +O(1/n) as n→ +∞. (2.5)

In this case, the Hamiltonian H is projected to HZ as

HZ =∑k

PkHPk, H = 1m

(H +

m∑j=2

U †1 · · ·U†j−1HUj−1 · · ·U1

), (2.6)

where Pk are the spectral projections of the product of the unitaries Um · · ·U1 =∑k e−iηkPk. Such schemes have been eagerly studied as methods of decoupling the dy-

namics of a system from an environment, and are called bang-bang control or dynamicaldecoupling [28–34]. Roughly speaking, the idea is to rotate the Hamiltonian describing theinteraction with an environment around all possible directions to average it out. This canbe regarded as a manifestation of the QZD.

In a previous article [11], we have unified and generalized the continuous strategies (iii)and (iv), by proving (Theorem 2 of Ref. [11]), for arbitrary Markovian generators L andD of the GKLS form [7,8],

et(γD+L) = etγDetLZPϕ +O(1/γ) as γ → +∞ (2.7)

withLZ =

∑αk∈iR

PkLPk, (2.8)

where Pk is the spectral projection onto the eigenspace of D belonging to the eigenvalueαk and Pϕ =

∑αk∈iR Pk is the projection onto the peripheral spectrum of D (i.e. its purely

imaginary eigenvalues).

1In this unitary case, one can think of this Zeno limit also in the Hilbert space, namely, we can studythe limit of (Ue−i t

nH)n instead of (Ue−i t

nH)n. The structure of the Zeno generator HZ =

∑kPkHPk,

where Pk are the spectral projections of U , is inherited by the structure of the Zeno HamiltonianHZ =

∑kPkHPk. A proof of the equivalence of the two formulations can be found in Ref. [11, Eq. (3.21)].

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 4

(iii) Strong continuous coupling/fast oscillations: If D and L are both unitarygenerators D = −iK = −i[K, q ] and L = −iH = −i[H, q ] with some Hamiltonians K andH, the theorem (2.7) is reduced to

e−it(γK+H) = e−itγKe−itHZ +O(1/γ) as γ → +∞, (2.9)

where HZ = [HZ , q ] with HZ again given by Eq. (2.3) with the spectral projections Pkof K [19, 20,39].

(iv) Strong damping (with no persistent oscillations): If D is a generator describ-ing an amplitude-damping to a stationary subspace specified by a projection Pϕ with nopersistent oscillations there, i.e. if etD → Pϕ as t→ +∞, then the theorem (2.7) reproduces

et(γD−iH) = e−itHZPϕ +O(1/γ) as γ → +∞, (2.10)

where HZ = PϕHPϕ [21–25,36,37].

In this way, theorem (2.7) includes both previously known QZDs (iii) and (iv), andboth mechanisms can be effective simultaneously. It also generalizes the QZDs (iii) and(iv) to nonunitary (Markovian) evolutions, projecting generic GKLS generators insteadof Hamiltonians. This theorem has been proved by the generalized adiabatic theorem(Theorem 1 of Ref. [11]), which is an extension of the adiabatic theorem proved by Kato [5]for unitary evolution.

With our main Theorem 1 below, we further unify the pulsed strategies (i) and (ii)with the continuous ones (iii) and (iv). This also enables us to unify and generalize bang-bang decoupling/dynamical decoupling to those by cycles of multiple quantum operations(Theorem 1), including non-Markovian (indivisible) ones [40]: structural assumptions forthe pulses (kicks) are relaxed in our main Theorem 1. As an interesting variant of it, wepresent the QZD via cycles of different selective projective measurements (Corollary 2),generalizing the standard QZD via (i) frequent selective projective measurements. We shalllook at some simple examples and show that realistic unsharp (nonprojective) measure-ments can be practically more efficient to induce the QZD than the strong (projective)measurements (Sec. 8). This generalizes Refs. [41,42] for the QZD by a particular type ofweak measurement. The generalization to the QZD via general quantum operations wasalso explored in Ref. [43], where it is required that the generator be a Hamiltonian, and asingle kick is repeated; most importantly, the initial state must be an invariant state of thekick. Our Theorem 1 does not require such structural assumptions: it deals with cycles ofmultiple general quantum operations, and works for generic Markovian dynamics with aGKLS generator for arbitrary initial conditions.

3 Some Preliminaries on Quantum OperationsLet us recall that every linear operator A on a finite-dimensional space can be expressed(essentially) uniquely in terms of its Jordan normal form (canonical form or spectral rep-resentation) [44]:

A =∑k

(λkPk +Nk), (3.1)

where λk, the spectrum of A, is the set of distinct eigenvalues of A (λk 6= λ` for k 6= `),Pk, the spectral projections of A, are the corresponding eigenprojections, satisfying

PkP` = δk`Pk,∑k

Pk = I, (3.2)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 5

for all k and `, and Nk are the corresponding nilpotents of A, satisfying for all k and `

PkN` = N`Pk = δk`Nk, Nnkk = 0, (3.3)

for some integer 1 ≤ nk ≤ rankPk.Notice that the spectral projections, which determine a partition of the space through

the resolution of identity (3.2), are not Hermitian in general, Pk 6= P †k . An eigenvalueλk of A is called semisimple or diagonalizable if the corresponding nilpotent Nk is zero(equivalently, nk = 1). The operator A is diagonalizable if and only if all its eigenvaluesare semisimple.

The main actors in our investigation are the quantum operations [6], that is, mapsE that are completely positive (CP) and trace-nonincreasing, tr[E(ρ)] ≤ tr ρ. We recallthat a map E on a d-dimensional quantum system is a quantum operation iff it has anoperator-sum (Kraus) representation of the form

E(X) =m∑j=1

KjXK†j with

m∑j=1

K†jKj ≤ I, (3.4)

where m ≤ d2. When∑jK†jKj = I, the map is trace-preserving (TP) and one gets a

completely positive trace-preserving (CPTP) map, also known as a quantum channel.In the following, it will be convenient to endow the space of operators on a d-dimensional

Hilbert space with the Hilbert-Schmidt inner product 〈A|B〉2 = tr(A†B), which makes thespace of operators a d2-dimensional Hilbert space T2. We get that the adjoint E† [withrespect to the Hilbert-Schmidt inner product, defined through 〈A|E(B)〉2 = 〈E†(A)|B〉2for all A,B ∈ T2] of the quantum operation E in Eq. (3.4) has the operator sum

E†(X) =∑j

K†jXKj , (3.5)

and thus is subunital E†(I) ≤ I. It is unital iff E is CPTP. Moreover, given a Hermitian op-erator H = H†, then the corresponding superoperator H = [H, q ] is also Hermitian (withrespect to the Hilbert-Schmidt inner product), H = H†, namely 〈A|H(B)〉2 = 〈H(A)|B〉2for all A,B ∈ T2. As a consequence, the unitary group t 7→ e−itH is lifted to a unitarygroup t 7→ e−itH = e−itH q eitH . Finally, a (Hermitian) projection P = P 2 (= P †) is liftedto a (Hermitian) projection P = P q P , satisfying P = P2 (= P†).

We mainly use the operator norm (2–2 norm), when we need to specify the norm of amap A : T2 → T2,

‖A‖ = sup‖X‖2=1

‖A(X)‖2, (3.6)

where ‖X‖2 = (〈X|X〉2)1/2 for X ∈ T2. It coincides with the largest singular value of A,

‖A‖ = sup‖X‖2=1

(〈A(X)|A(X)〉2)1/2 = sup‖X‖2=1

(〈X|(A†A)(X)〉2)1/2 = r(A†A)1/2, (3.7)

with r(A†A) being the spectral radius of A†A.We now state without proofs some useful spectral properties of the quantum operations.

For further details and proofs see e.g. Refs. [45,46], and in particular Propositions 6.1–6.3and Theorem 6.1 of Ref. [45].

Proposition 1 (Spectral properties of quantum operations). Let E be a quantum operationon a finite-dimensional space. Then, the following properties hold:

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 6

(i) The spectrum λk of E is confined in the closed unit disc D = λ ∈ C, |λ| ≤ 1.Moreover, all the “peripheral” eigenvalues, belonging to the boundary of D, i.e. onthe unit circle ∂D = λ ∈ C, |λ| = 1, are semisimple. If E is TP, then λ = 1 is aneigenvalue of E.

(ii) The canonical form of E reads

E = Eϕ +∑|λk|<1

(λkPk +Nk), (3.8)

where Pk and Nk are the spectral projections and the nilpotents of E, respectively,and

Eϕ =∑|λk|=1

λkPk (3.9)

is the “peripheral” part of E, i.e. its component belonging to the peripheral spectrumon the unit circle ∂D.

(iii) The peripheral part Eϕ and the projection onto the peripheral spectrum of E,

Pϕ =∑|λk|=1

Pk, (3.10)

are both quantum operations, and Eϕ = EPϕ = PϕE. The maps Eϕ and Pϕ are TPiff E is TP.

(iv) The inverse of Eϕ on the range of Pϕ,

E−1ϕ =

∑|λk|=1

λ−1k Pk, (3.11)

satisfying E−1ϕ Eϕ = EϕE−1

ϕ = Pϕ, is also a quantum operation, and it is TP if E isTP.

Similar properties hold for GKLS generators L, whose exponential etL is CPTP for allt ≥ 0. See Proposition 2 of Ref. [11].

Remark 1. Note that if the peripheral spectrum is empty then all peripheral maps arenull, Pϕ = Eϕ = E−1

ϕ = 0. By property (i), this cannot happen if E is TP.

4 Main TheoremThe main result of this paper is the unification of the pulsed QZDs, via (i) frequent pro-jective measurements and via (ii) frequent unitary kicks, which at the same time allows usto generalize the pulses to arbitrary quantum operations. We further generalize the bang-bang decoupling/dynamical decoupling to cycles of generic kicks. These are all summarizedin the following theorem, which will be proved in Sec. 7:

Theorem 1 (QZD by cycles of generic kicks). Let E1, . . . , Em be a finite set of quantumoperations and L be a GKLS generator acting on a finite-dimensional quantum system.Then, we have (

EmetmnL · · · E1e

tmnL)n

= EnϕetLZ +O(1/n) as n→ +∞, (4.1)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 7

uniformly in t on compact intervals of [0,+∞), with

LZ =∑|λk|=1

PkLPk, L = 1m

(L+ E−1

ϕ

m∑j=2Em · · · EjLEj−1 · · · E1

), (4.2)

where Pk is the spectral projection of E = Em · · · E1 belonging to the eigenvalue λk, and Eϕand E−1

ϕ are the peripheral part of E and its peripheral inverse, respectively.

In particular, for m = 1, we have the following corollary, which covers both QZDs via(i) projective measurements and via (ii) unitary kicks, and generalizes them to generickicks:

Corollary 1 (QZD by generic kicks). Let E be a quantum operation and L be a GKLSgenerator of a finite-dimensional quantum system. Then, we have(

EetnL)n

= EnϕetLZ +O(1/n) as n→ +∞, (4.3)

uniformly in t on compact intervals of [0,+∞), with

LZ =∑|λk|=1

PkLPk, (4.4)

where Pk is the spectral projection of E belonging to the eigenvalue λk, and Eϕ is theperipheral part of E.

If in the above statements the maps E and E1, . . . , Em are assumed to be CPTP and de-scribe measurement processes, they are nonselective measurements. An interesting corol-lary of Theorem 1 is available for selective measurements. In particular, we provide acorollary for the QZD via cycles of multiple selective projective measurements. This is ageneralization of the standard QZD via (i) frequent selective projective measurements.

Corollary 2 (QZD by cycles of projective measurements). Let P1, . . . ,Pm be a finiteset of CP Hermitian projections on the Hilbert-Schmidt space T2 of operators on a finite-dimensional Hilbert space, and L be a GKLS generator. The projections are not assumedto be pairwise orthogonal, i.e. PiPj 6= 0 for i 6= j, in general. Then, we have(

PmetmnL · · · P1e

tmnL)n

= PϕetPϕLPϕ +O(1/n) as n→ +∞, (4.5)

uniformly in t on compact intervals of R, where Pϕ = P1 ∧ P2 ∧ · · · ∧ Pm is the Hermi-tian projection onto the intersection of the ranges of the projections P1, . . . ,Pm. If suchintersection is trivial, then Pϕ = 0, and the sequence in Eq. (4.5) just decays to zero.

Proof. The proof makes use of the crucial fact that the peripheral part of the product ofthe Hermitian projections E = Pm · · · P1 reads

Eϕ = E−1ϕ = Pϕ (4.6)

(λ = 1 is the only peripheral eigenvalue of E), and PϕPj = PjPϕ = Pϕ for all j = 1, . . . ,m.This will be proved in Lemma 8 in Appendix A. Then, Eq. (4.6) implies that Enϕ = Pnϕ =Pϕ, and L in Eq. (4.2) of Theorem 1 is simplified to

L = 1m

(L+ PϕL

m∑j=2Pj−1 · · · P1

). (4.7)

Therefore, LZ in Eq. (4.2) of Theorem 1 reads

LZ = PϕLPϕ = PϕLPϕ, (4.8)

and Eq. (4.1) of Theorem 1 becomes Eq. (4.5).

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 8

repeated meas. unitary kicks generic kicks

BB, DD, multi generic kicks, multi meas.

strong damping & strong field

BCH

Generalized Adiabatic Thm.

Corollary 1

Theorem 1, Corollary 2

Theorem 2 of [11]

Theorem 1 of [11]

Lemmas 1 and 2

Lemma 3

enA+tP'LP'P'<latexit sha1_base64="heK9j1G117IQwFUZ4EFC4/zQi80=">AAAJ53icjZbdjuM0FMfT5Ws6UJhdLrkJVCuh3VI1nWEWxM0uAwIkEGU1M7tSXSrHOW29dZzIdrpUHr8DNyBueSyehRuc9Ct10opUbexzfuf4b+fUTpgyKlWv90/j3htvvvX2OyfN03ffa73/wdn9B7cyyQSBG5KwRLwMsQRGOdwoqhi8TAXgOGTwIpxf5f4XCxCSJvxaLVMYxXjK6YQSrKxpfPYHikKWwSmCX7VGkYDI50YjSwFX2N7VjGCmnxnzWFn/VADwrXVgxmiBRTqjuwhFWQR6i/xojKnhjTk9ks2Mz9q9bq+4/GojWDfa3voajO+ffIWihGSx1UAYlnIY9FI10lgoShiYFsokpJjMrcqhbXIcgxzpYv2M/9BaIn+SCPvlyi+s5QiNYymXcWjJXKx0fbmx1idgsRf3sOxM5lmMiUhqI8O4zjzM1OSLkaY8zRRwslI+yZivEj9/un5EBRDFlrZhU1M7eZ/MsMBE2RpotZAADq9JEseYR/YBmNWDErGOjF2jsg92Psh9+5HUaOoECMqVjbG/KKIyZXjJaEyVrMQ+36ROUo0U/Ka0tRjEkwP8D7HLW8seX6aVcGlrOUhfV+jrI/SzRVl6fg9D/e1h/haLKn97mJ+DMsNgpO90OzBIYD4tSreMhAIXCGKFNwfvqog0w/5IazPW7b5BM2nLBx7pz3rdfhybI6FWwCr6fFR0csbmOK/msFieuzo0KSbR3ypsB3ftfv1cvgHlrn5uOrg8z0FWK0caV0S6cKnB4ZwgJi6dm47xpCaAHI2gNRH0cISkvDJGYTsYcVUZ4epIfhy5tLWU6NMWimBiD5RiI9T5oWC0mIZG97qXFx27D593esaB8lNkQ3Xsp3vpEsVuv0O6F9UkSV4nNg2Jl/MV9KTfCewtuHTmsBKFSgpdYCUIleW5yFoR2hPoQhtNaF+ju/uV5NSo+T8j7Qmu07s+YrfMpu9gZIl3QxUdB1gCY8nrLbLuOtD+tIf5gRmN9M+1k4/xLJlivnTpnzZ29x+aiZRVcg9W1srK4Ure73JbZfXs1lNavrznlhcwULvq6n7eKSrVtOzrRuC+XFQbN/3ul93gl4v206/X7x0n3kfeJ96nXuA98Z5633sD78Yj3r+NjxuPGo+br5q/N/9s/rVC7zXWMR96e1fz7/8AryvCxw==</latexit><latexit sha1_base64="heK9j1G117IQwFUZ4EFC4/zQi80=">AAAJ53icjZbdjuM0FMfT5Ws6UJhdLrkJVCuh3VI1nWEWxM0uAwIkEGU1M7tSXSrHOW29dZzIdrpUHr8DNyBueSyehRuc9Ct10opUbexzfuf4b+fUTpgyKlWv90/j3htvvvX2OyfN03ffa73/wdn9B7cyyQSBG5KwRLwMsQRGOdwoqhi8TAXgOGTwIpxf5f4XCxCSJvxaLVMYxXjK6YQSrKxpfPYHikKWwSmCX7VGkYDI50YjSwFX2N7VjGCmnxnzWFn/VADwrXVgxmiBRTqjuwhFWQR6i/xojKnhjTk9ks2Mz9q9bq+4/GojWDfa3voajO+ffIWihGSx1UAYlnIY9FI10lgoShiYFsokpJjMrcqhbXIcgxzpYv2M/9BaIn+SCPvlyi+s5QiNYymXcWjJXKx0fbmx1idgsRf3sOxM5lmMiUhqI8O4zjzM1OSLkaY8zRRwslI+yZivEj9/un5EBRDFlrZhU1M7eZ/MsMBE2RpotZAADq9JEseYR/YBmNWDErGOjF2jsg92Psh9+5HUaOoECMqVjbG/KKIyZXjJaEyVrMQ+36ROUo0U/Ka0tRjEkwP8D7HLW8seX6aVcGlrOUhfV+jrI/SzRVl6fg9D/e1h/haLKn97mJ+DMsNgpO90OzBIYD4tSreMhAIXCGKFNwfvqog0w/5IazPW7b5BM2nLBx7pz3rdfhybI6FWwCr6fFR0csbmOK/msFieuzo0KSbR3ypsB3ftfv1cvgHlrn5uOrg8z0FWK0caV0S6cKnB4ZwgJi6dm47xpCaAHI2gNRH0cISkvDJGYTsYcVUZ4epIfhy5tLWU6NMWimBiD5RiI9T5oWC0mIZG97qXFx27D593esaB8lNkQ3Xsp3vpEsVuv0O6F9UkSV4nNg2Jl/MV9KTfCewtuHTmsBKFSgpdYCUIleW5yFoR2hPoQhtNaF+ju/uV5NSo+T8j7Qmu07s+YrfMpu9gZIl3QxUdB1gCY8nrLbLuOtD+tIf5gRmN9M+1k4/xLJlivnTpnzZ29x+aiZRVcg9W1srK4Ure73JbZfXs1lNavrznlhcwULvq6n7eKSrVtOzrRuC+XFQbN/3ul93gl4v206/X7x0n3kfeJ96nXuA98Z5633sD78Yj3r+NjxuPGo+br5q/N/9s/rVC7zXWMR96e1fz7/8AryvCxw==</latexit><latexit sha1_base64="heK9j1G117IQwFUZ4EFC4/zQi80=">AAAJ53icjZbdjuM0FMfT5Ws6UJhdLrkJVCuh3VI1nWEWxM0uAwIkEGU1M7tSXSrHOW29dZzIdrpUHr8DNyBueSyehRuc9Ct10opUbexzfuf4b+fUTpgyKlWv90/j3htvvvX2OyfN03ffa73/wdn9B7cyyQSBG5KwRLwMsQRGOdwoqhi8TAXgOGTwIpxf5f4XCxCSJvxaLVMYxXjK6YQSrKxpfPYHikKWwSmCX7VGkYDI50YjSwFX2N7VjGCmnxnzWFn/VADwrXVgxmiBRTqjuwhFWQR6i/xojKnhjTk9ks2Mz9q9bq+4/GojWDfa3voajO+ffIWihGSx1UAYlnIY9FI10lgoShiYFsokpJjMrcqhbXIcgxzpYv2M/9BaIn+SCPvlyi+s5QiNYymXcWjJXKx0fbmx1idgsRf3sOxM5lmMiUhqI8O4zjzM1OSLkaY8zRRwslI+yZivEj9/un5EBRDFlrZhU1M7eZ/MsMBE2RpotZAADq9JEseYR/YBmNWDErGOjF2jsg92Psh9+5HUaOoECMqVjbG/KKIyZXjJaEyVrMQ+36ROUo0U/Ka0tRjEkwP8D7HLW8seX6aVcGlrOUhfV+jrI/SzRVl6fg9D/e1h/haLKn97mJ+DMsNgpO90OzBIYD4tSreMhAIXCGKFNwfvqog0w/5IazPW7b5BM2nLBx7pz3rdfhybI6FWwCr6fFR0csbmOK/msFieuzo0KSbR3ypsB3ftfv1cvgHlrn5uOrg8z0FWK0caV0S6cKnB4ZwgJi6dm47xpCaAHI2gNRH0cISkvDJGYTsYcVUZ4epIfhy5tLWU6NMWimBiD5RiI9T5oWC0mIZG97qXFx27D593esaB8lNkQ3Xsp3vpEsVuv0O6F9UkSV4nNg2Jl/MV9KTfCewtuHTmsBKFSgpdYCUIleW5yFoR2hPoQhtNaF+ju/uV5NSo+T8j7Qmu07s+YrfMpu9gZIl3QxUdB1gCY8nrLbLuOtD+tIf5gRmN9M+1k4/xLJlivnTpnzZ29x+aiZRVcg9W1srK4Ure73JbZfXs1lNavrznlhcwULvq6n7eKSrVtOzrRuC+XFQbN/3ul93gl4v206/X7x0n3kfeJ96nXuA98Z5633sD78Yj3r+NjxuPGo+br5q/N/9s/rVC7zXWMR96e1fz7/8AryvCxw==</latexit><latexit sha1_base64="heK9j1G117IQwFUZ4EFC4/zQi80=">AAAJ53icjZbdjuM0FMfT5Ws6UJhdLrkJVCuh3VI1nWEWxM0uAwIkEGU1M7tSXSrHOW29dZzIdrpUHr8DNyBueSyehRuc9Ct10opUbexzfuf4b+fUTpgyKlWv90/j3htvvvX2OyfN03ffa73/wdn9B7cyyQSBG5KwRLwMsQRGOdwoqhi8TAXgOGTwIpxf5f4XCxCSJvxaLVMYxXjK6YQSrKxpfPYHikKWwSmCX7VGkYDI50YjSwFX2N7VjGCmnxnzWFn/VADwrXVgxmiBRTqjuwhFWQR6i/xojKnhjTk9ks2Mz9q9bq+4/GojWDfa3voajO+ffIWihGSx1UAYlnIY9FI10lgoShiYFsokpJjMrcqhbXIcgxzpYv2M/9BaIn+SCPvlyi+s5QiNYymXcWjJXKx0fbmx1idgsRf3sOxM5lmMiUhqI8O4zjzM1OSLkaY8zRRwslI+yZivEj9/un5EBRDFlrZhU1M7eZ/MsMBE2RpotZAADq9JEseYR/YBmNWDErGOjF2jsg92Psh9+5HUaOoECMqVjbG/KKIyZXjJaEyVrMQ+36ROUo0U/Ka0tRjEkwP8D7HLW8seX6aVcGlrOUhfV+jrI/SzRVl6fg9D/e1h/haLKn97mJ+DMsNgpO90OzBIYD4tSreMhAIXCGKFNwfvqog0w/5IazPW7b5BM2nLBx7pz3rdfhybI6FWwCr6fFR0csbmOK/msFieuzo0KSbR3ypsB3ftfv1cvgHlrn5uOrg8z0FWK0caV0S6cKnB4ZwgJi6dm47xpCaAHI2gNRH0cISkvDJGYTsYcVUZ4epIfhy5tLWU6NMWimBiD5RiI9T5oWC0mIZG97qXFx27D593esaB8lNkQ3Xsp3vpEsVuv0O6F9UkSV4nNg2Jl/MV9KTfCewtuHTmsBKFSgpdYCUIleW5yFoR2hPoQhtNaF+ju/uV5NSo+T8j7Qmu07s+YrfMpu9gZIl3QxUdB1gCY8nrLbLuOtD+tIf5gRmN9M+1k4/xLJlivnTpnzZ29x+aiZRVcg9W1srK4Ure73JbZfXs1lNavrznlhcwULvq6n7eKSrVtOzrRuC+XFQbN/3ul93gl4v206/X7x0n3kfeJ96nXuA98Z5633sD78Yj3r+NjxuPGo+br5q/N/9s/rVC7zXWMR96e1fz7/8AryvCxw==</latexit>

et(D+L)<latexit sha1_base64="36fQDtdnROrgs5Y5SetQmoEaPJY=">AAAJhXicjZbRbts2FIbVbuvidG7T7nI3xowCXesKlpOmG3axbumwFujQtEjSAKYXUNSxQ5iUBJJKZzB8kD3NbttH2NuMlO1EpmSjMmyR53zn8OcRTSrOGZWq3//vxs0vvvzq1tdbre3b37Tv3N25d/9EZoUgcEwylonTGEtgNIVjRRWD01wA5jGD9/H0wPnfX4CQNEuP1CyHEceTlI4pwcqaznZ2URKzArYR/KXVQ40SAQmaYM6xQRyrc4KZfmEeX7Vfmx/M2U63H/bLq1NvRItGN1hch2f3tn5GSUYKDqkiDEs5jPq5GmksFCUMTBsVEnJMpngCQ9tMMQc50uXsTOeBtSSdcSbsN1Wd0lqN0JhLOeOxJZ1K6fucsdEn4GIl7kHVmU0LjonIGiNj3mQeFmr840jTNC8UpGSufFywjso6rvadhAogis1sw6amdvIdco4FJso+oXYbCUjhA8ls8dPEPgqjy7ILrhNja1T1wbUPnG81khpNvQBBU2Vj7C9KqMwZnjHKqZK12HfL1FmukYK/lbYWg9JsDf+K+7y1rPBVWgmftpa19FGNPtpA/3pRle7ucax/X8+fYFHnT9bzU1BmGI30pe5GBgmcTsqlW0VigUsEsdLrwMs6Is1wMNLanOnuwKBzaZcPPNJP+uGAc7Mh1AqYR++Oyo5jbI7deg6Ludz1oUk5icGVwm502R00z+UFKL/6zrS2PO9A1leONL6I/MKnDtfnBDH2aWfaxJOGALIxgjZE0PURkqa1MUrb2oiD2ggHG/LjxKetpUJvt1ECY7vdlxuhdhu20WISG90P9/d6dh/e7fWNB7k9fkn17Cfc94mJAEivkXCvniRz68SmIXw2nUPPBr3I3qJ9bw5zUaii0AfmglBVno8sFKEVgT601IRWNfq7X0VOg5rPGWlFcJNee7Da4w1fMcu+h5EZvh6q7HjADBjLPlwhi64HrU576A7MZKTfNE6e4/NsgtOZT/+5tPv/0ELkrJb7cG6tVQ7X8v7hbLXq2a2nUj7X85cXMFDXqyt82itXqmnb143If7moN44H4U9h9Hav+/y3xXvHVvBd8H3wMIiCZ8Hz4GVwGBwHJPgn+Df4GHxqbbXC1l5rf47evLGI+TZYuVq//A+0OJlo</latexit><latexit sha1_base64="36fQDtdnROrgs5Y5SetQmoEaPJY=">AAAJhXicjZbRbts2FIbVbuvidG7T7nI3xowCXesKlpOmG3axbumwFujQtEjSAKYXUNSxQ5iUBJJKZzB8kD3NbttH2NuMlO1EpmSjMmyR53zn8OcRTSrOGZWq3//vxs0vvvzq1tdbre3b37Tv3N25d/9EZoUgcEwylonTGEtgNIVjRRWD01wA5jGD9/H0wPnfX4CQNEuP1CyHEceTlI4pwcqaznZ2URKzArYR/KXVQ40SAQmaYM6xQRyrc4KZfmEeX7Vfmx/M2U63H/bLq1NvRItGN1hch2f3tn5GSUYKDqkiDEs5jPq5GmksFCUMTBsVEnJMpngCQ9tMMQc50uXsTOeBtSSdcSbsN1Wd0lqN0JhLOeOxJZ1K6fucsdEn4GIl7kHVmU0LjonIGiNj3mQeFmr840jTNC8UpGSufFywjso6rvadhAogis1sw6amdvIdco4FJso+oXYbCUjhA8ls8dPEPgqjy7ILrhNja1T1wbUPnG81khpNvQBBU2Vj7C9KqMwZnjHKqZK12HfL1FmukYK/lbYWg9JsDf+K+7y1rPBVWgmftpa19FGNPtpA/3pRle7ucax/X8+fYFHnT9bzU1BmGI30pe5GBgmcTsqlW0VigUsEsdLrwMs6Is1wMNLanOnuwKBzaZcPPNJP+uGAc7Mh1AqYR++Oyo5jbI7deg6Ludz1oUk5icGVwm502R00z+UFKL/6zrS2PO9A1leONL6I/MKnDtfnBDH2aWfaxJOGALIxgjZE0PURkqa1MUrb2oiD2ggHG/LjxKetpUJvt1ECY7vdlxuhdhu20WISG90P9/d6dh/e7fWNB7k9fkn17Cfc94mJAEivkXCvniRz68SmIXw2nUPPBr3I3qJ9bw5zUaii0AfmglBVno8sFKEVgT601IRWNfq7X0VOg5rPGWlFcJNee7Da4w1fMcu+h5EZvh6q7HjADBjLPlwhi64HrU576A7MZKTfNE6e4/NsgtOZT/+5tPv/0ELkrJb7cG6tVQ7X8v7hbLXq2a2nUj7X85cXMFDXqyt82itXqmnb143If7moN44H4U9h9Hav+/y3xXvHVvBd8H3wMIiCZ8Hz4GVwGBwHJPgn+Df4GHxqbbXC1l5rf47evLGI+TZYuVq//A+0OJlo</latexit><latexit sha1_base64="36fQDtdnROrgs5Y5SetQmoEaPJY=">AAAJhXicjZbRbts2FIbVbuvidG7T7nI3xowCXesKlpOmG3axbumwFujQtEjSAKYXUNSxQ5iUBJJKZzB8kD3NbttH2NuMlO1EpmSjMmyR53zn8OcRTSrOGZWq3//vxs0vvvzq1tdbre3b37Tv3N25d/9EZoUgcEwylonTGEtgNIVjRRWD01wA5jGD9/H0wPnfX4CQNEuP1CyHEceTlI4pwcqaznZ2URKzArYR/KXVQ40SAQmaYM6xQRyrc4KZfmEeX7Vfmx/M2U63H/bLq1NvRItGN1hch2f3tn5GSUYKDqkiDEs5jPq5GmksFCUMTBsVEnJMpngCQ9tMMQc50uXsTOeBtSSdcSbsN1Wd0lqN0JhLOeOxJZ1K6fucsdEn4GIl7kHVmU0LjonIGiNj3mQeFmr840jTNC8UpGSufFywjso6rvadhAogis1sw6amdvIdco4FJso+oXYbCUjhA8ls8dPEPgqjy7ILrhNja1T1wbUPnG81khpNvQBBU2Vj7C9KqMwZnjHKqZK12HfL1FmukYK/lbYWg9JsDf+K+7y1rPBVWgmftpa19FGNPtpA/3pRle7ucax/X8+fYFHnT9bzU1BmGI30pe5GBgmcTsqlW0VigUsEsdLrwMs6Is1wMNLanOnuwKBzaZcPPNJP+uGAc7Mh1AqYR++Oyo5jbI7deg6Ludz1oUk5icGVwm502R00z+UFKL/6zrS2PO9A1leONL6I/MKnDtfnBDH2aWfaxJOGALIxgjZE0PURkqa1MUrb2oiD2ggHG/LjxKetpUJvt1ECY7vdlxuhdhu20WISG90P9/d6dh/e7fWNB7k9fkn17Cfc94mJAEivkXCvniRz68SmIXw2nUPPBr3I3qJ9bw5zUaii0AfmglBVno8sFKEVgT601IRWNfq7X0VOg5rPGWlFcJNee7Da4w1fMcu+h5EZvh6q7HjADBjLPlwhi64HrU576A7MZKTfNE6e4/NsgtOZT/+5tPv/0ELkrJb7cG6tVQ7X8v7hbLXq2a2nUj7X85cXMFDXqyt82itXqmnb143If7moN44H4U9h9Hav+/y3xXvHVvBd8H3wMIiCZ8Hz4GVwGBwHJPgn+Df4GHxqbbXC1l5rf47evLGI+TZYuVq//A+0OJlo</latexit><latexit sha1_base64="36fQDtdnROrgs5Y5SetQmoEaPJY=">AAAJhXicjZbRbts2FIbVbuvidG7T7nI3xowCXesKlpOmG3axbumwFujQtEjSAKYXUNSxQ5iUBJJKZzB8kD3NbttH2NuMlO1EpmSjMmyR53zn8OcRTSrOGZWq3//vxs0vvvzq1tdbre3b37Tv3N25d/9EZoUgcEwylonTGEtgNIVjRRWD01wA5jGD9/H0wPnfX4CQNEuP1CyHEceTlI4pwcqaznZ2URKzArYR/KXVQ40SAQmaYM6xQRyrc4KZfmEeX7Vfmx/M2U63H/bLq1NvRItGN1hch2f3tn5GSUYKDqkiDEs5jPq5GmksFCUMTBsVEnJMpngCQ9tMMQc50uXsTOeBtSSdcSbsN1Wd0lqN0JhLOeOxJZ1K6fucsdEn4GIl7kHVmU0LjonIGiNj3mQeFmr840jTNC8UpGSufFywjso6rvadhAogis1sw6amdvIdco4FJso+oXYbCUjhA8ls8dPEPgqjy7ILrhNja1T1wbUPnG81khpNvQBBU2Vj7C9KqMwZnjHKqZK12HfL1FmukYK/lbYWg9JsDf+K+7y1rPBVWgmftpa19FGNPtpA/3pRle7ucax/X8+fYFHnT9bzU1BmGI30pe5GBgmcTsqlW0VigUsEsdLrwMs6Is1wMNLanOnuwKBzaZcPPNJP+uGAc7Mh1AqYR++Oyo5jbI7deg6Ludz1oUk5icGVwm502R00z+UFKL/6zrS2PO9A1leONL6I/MKnDtfnBDH2aWfaxJOGALIxgjZE0PURkqa1MUrb2oiD2ggHG/LjxKetpUJvt1ECY7vdlxuhdhu20WISG90P9/d6dh/e7fWNB7k9fkn17Cfc94mJAEivkXCvniRz68SmIXw2nUPPBr3I3qJ9bw5zUaii0AfmglBVno8sFKEVgT601IRWNfq7X0VOg5rPGWlFcJNee7Da4w1fMcu+h5EZvh6q7HjADBjLPlwhi64HrU576A7MZKTfNE6e4/NsgtOZT/+5tPv/0ELkrJb7cG6tVQ7X8v7hbLXq2a2nUj7X85cXMFDXqyt82itXqmnb143If7moN44H4U9h9Hav+/y3xXvHVvBd8H3wMIiCZ8Hz4GVwGBwHJPgn+Df4GHxqbbXC1l5rf47evLGI+TZYuVq//A+0OJlo</latexit>

et(B+C) etBetP

k PkCPkP'<latexit sha1_base64="dlH3R/oVtztPgAdSLH3TGlguqQA=">AAAJt3icjZZRk9s0EMfdQuFybeAKj7x4yHSmLSET544r0JdrA1N4YEg7d9fORGmQ5U2iiWUbSU6b0ekT8gn4GLzCC7Kd3Nmyk6kziaX//na1WiuS/SSkQvb7f9+6/dHHdz759KB1ePde+7PPj+5/cSnilBO4IHEY8zc+FhDSCC4klSG8SThg5ofw2l8OM/vrFXBB4+hcrhOYMDyP6IwSLI00PQIU+GEKhwjeKvlQoYBDgOaYMayffzN8pA+RoKywVo26EAtNpGy6HE2XQ/PVhptzgMgdTdEK82RB9fSo0+/188utN7xNo+NsrtH0/sFTFMQkZRBJEmIhxl4/kROFuaQkBN1GqYAEkyWew9g0I8xATFReD+0+MErgzmJuvpF0c7XsoTATYs18QzIsF8K2ZWKjjcOq4vegbIyXKcOEx42ePmuSx6mcfT9RNEpSCREpMp+loStjN3tabkA5EBmuTcOEpmbyLllgjok0z7TdRhwieEdi80SiwNTd1D4bgzMVaFOjsg1ubJDZqp5UK2o5cBpJ42N+UUBFEuJ1SBmVoub7ahs6ThSS8F4qo2gUxTv4X5nNG6XCl2nJbdooO+nzGn2+h362Kqee3X1f/bybv8S8zl/u5pcg9dibqCvV8TTiOJrnS7eM+BznCApzawZe1RGhx4OJUnqqOgONFsIsH3isvu33BozpPa4mgcL7eJJ3MsbEOK7HMFgWuz40yScxuM6w4111Bs1z+QmkXf1M2lmeVyDqK0doO4lkZVOj3TGBz2w6k/bxpMGB7PWgDR50t4egUW2MXNvpMayNMNwTHwc2bZQSfdhGAczMAZFvhCrbsbXic1+rfu/0pGv24eNuX1tQdipsqa759E5tIt/kb5DeST1InK0TE4aw9bKAngy6nrl5p9YciqRQKUMbKBJC5fRsZJMRqiRoQ9ucUDVHe/crpdOQzYeMVEm4KV9zFJvjDV8z276FkTW+GSrvWMAawjB+d41suhZUnfY4OzCDifq9cfIML+I5jtY2/dtWt/+hKU/CWuxRodYqh2txX2RarXpm6ymVL+vZywtCkDerq/ddN1+pum1eNzz75aLeuBj0fuh5L086Z2eb944D5yvna+eh4zlPnDPnF2fkXDjE+cv5x/nX+a/1Y+uP1qy1KNDbtzY+XzqVq/Xn/4sgrcs=</latexit><latexit sha1_base64="dlH3R/oVtztPgAdSLH3TGlguqQA=">AAAJt3icjZZRk9s0EMfdQuFybeAKj7x4yHSmLSET544r0JdrA1N4YEg7d9fORGmQ5U2iiWUbSU6b0ekT8gn4GLzCC7Kd3Nmyk6kziaX//na1WiuS/SSkQvb7f9+6/dHHdz759KB1ePde+7PPj+5/cSnilBO4IHEY8zc+FhDSCC4klSG8SThg5ofw2l8OM/vrFXBB4+hcrhOYMDyP6IwSLI00PQIU+GEKhwjeKvlQoYBDgOaYMayffzN8pA+RoKywVo26EAtNpGy6HE2XQ/PVhptzgMgdTdEK82RB9fSo0+/188utN7xNo+NsrtH0/sFTFMQkZRBJEmIhxl4/kROFuaQkBN1GqYAEkyWew9g0I8xATFReD+0+MErgzmJuvpF0c7XsoTATYs18QzIsF8K2ZWKjjcOq4vegbIyXKcOEx42ePmuSx6mcfT9RNEpSCREpMp+loStjN3tabkA5EBmuTcOEpmbyLllgjok0z7TdRhwieEdi80SiwNTd1D4bgzMVaFOjsg1ubJDZqp5UK2o5cBpJ42N+UUBFEuJ1SBmVoub7ahs6ThSS8F4qo2gUxTv4X5nNG6XCl2nJbdooO+nzGn2+h362Kqee3X1f/bybv8S8zl/u5pcg9dibqCvV8TTiOJrnS7eM+BznCApzawZe1RGhx4OJUnqqOgONFsIsH3isvu33BozpPa4mgcL7eJJ3MsbEOK7HMFgWuz40yScxuM6w4111Bs1z+QmkXf1M2lmeVyDqK0doO4lkZVOj3TGBz2w6k/bxpMGB7PWgDR50t4egUW2MXNvpMayNMNwTHwc2bZQSfdhGAczMAZFvhCrbsbXic1+rfu/0pGv24eNuX1tQdipsqa759E5tIt/kb5DeST1InK0TE4aw9bKAngy6nrl5p9YciqRQKUMbKBJC5fRsZJMRqiRoQ9ucUDVHe/crpdOQzYeMVEm4KV9zFJvjDV8z276FkTW+GSrvWMAawjB+d41suhZUnfY4OzCDifq9cfIML+I5jtY2/dtWt/+hKU/CWuxRodYqh2txX2RarXpm6ymVL+vZywtCkDerq/ddN1+pum1eNzz75aLeuBj0fuh5L086Z2eb944D5yvna+eh4zlPnDPnF2fkXDjE+cv5x/nX+a/1Y+uP1qy1KNDbtzY+XzqVq/Xn/4sgrcs=</latexit><latexit sha1_base64="dlH3R/oVtztPgAdSLH3TGlguqQA=">AAAJt3icjZZRk9s0EMfdQuFybeAKj7x4yHSmLSET544r0JdrA1N4YEg7d9fORGmQ5U2iiWUbSU6b0ekT8gn4GLzCC7Kd3Nmyk6kziaX//na1WiuS/SSkQvb7f9+6/dHHdz759KB1ePde+7PPj+5/cSnilBO4IHEY8zc+FhDSCC4klSG8SThg5ofw2l8OM/vrFXBB4+hcrhOYMDyP6IwSLI00PQIU+GEKhwjeKvlQoYBDgOaYMayffzN8pA+RoKywVo26EAtNpGy6HE2XQ/PVhptzgMgdTdEK82RB9fSo0+/188utN7xNo+NsrtH0/sFTFMQkZRBJEmIhxl4/kROFuaQkBN1GqYAEkyWew9g0I8xATFReD+0+MErgzmJuvpF0c7XsoTATYs18QzIsF8K2ZWKjjcOq4vegbIyXKcOEx42ePmuSx6mcfT9RNEpSCREpMp+loStjN3tabkA5EBmuTcOEpmbyLllgjok0z7TdRhwieEdi80SiwNTd1D4bgzMVaFOjsg1ubJDZqp5UK2o5cBpJ42N+UUBFEuJ1SBmVoub7ahs6ThSS8F4qo2gUxTv4X5nNG6XCl2nJbdooO+nzGn2+h362Kqee3X1f/bybv8S8zl/u5pcg9dibqCvV8TTiOJrnS7eM+BznCApzawZe1RGhx4OJUnqqOgONFsIsH3isvu33BozpPa4mgcL7eJJ3MsbEOK7HMFgWuz40yScxuM6w4111Bs1z+QmkXf1M2lmeVyDqK0doO4lkZVOj3TGBz2w6k/bxpMGB7PWgDR50t4egUW2MXNvpMayNMNwTHwc2bZQSfdhGAczMAZFvhCrbsbXic1+rfu/0pGv24eNuX1tQdipsqa759E5tIt/kb5DeST1InK0TE4aw9bKAngy6nrl5p9YciqRQKUMbKBJC5fRsZJMRqiRoQ9ucUDVHe/crpdOQzYeMVEm4KV9zFJvjDV8z276FkTW+GSrvWMAawjB+d41suhZUnfY4OzCDifq9cfIML+I5jtY2/dtWt/+hKU/CWuxRodYqh2txX2RarXpm6ymVL+vZywtCkDerq/ddN1+pum1eNzz75aLeuBj0fuh5L086Z2eb944D5yvna+eh4zlPnDPnF2fkXDjE+cv5x/nX+a/1Y+uP1qy1KNDbtzY+XzqVq/Xn/4sgrcs=</latexit><latexit sha1_base64="dlH3R/oVtztPgAdSLH3TGlguqQA=">AAAJt3icjZZRk9s0EMfdQuFybeAKj7x4yHSmLSET544r0JdrA1N4YEg7d9fORGmQ5U2iiWUbSU6b0ekT8gn4GLzCC7Kd3Nmyk6kziaX//na1WiuS/SSkQvb7f9+6/dHHdz759KB1ePde+7PPj+5/cSnilBO4IHEY8zc+FhDSCC4klSG8SThg5ofw2l8OM/vrFXBB4+hcrhOYMDyP6IwSLI00PQIU+GEKhwjeKvlQoYBDgOaYMayffzN8pA+RoKywVo26EAtNpGy6HE2XQ/PVhptzgMgdTdEK82RB9fSo0+/188utN7xNo+NsrtH0/sFTFMQkZRBJEmIhxl4/kROFuaQkBN1GqYAEkyWew9g0I8xATFReD+0+MErgzmJuvpF0c7XsoTATYs18QzIsF8K2ZWKjjcOq4vegbIyXKcOEx42ePmuSx6mcfT9RNEpSCREpMp+loStjN3tabkA5EBmuTcOEpmbyLllgjok0z7TdRhwieEdi80SiwNTd1D4bgzMVaFOjsg1ubJDZqp5UK2o5cBpJ42N+UUBFEuJ1SBmVoub7ahs6ThSS8F4qo2gUxTv4X5nNG6XCl2nJbdooO+nzGn2+h362Kqee3X1f/bybv8S8zl/u5pcg9dibqCvV8TTiOJrnS7eM+BznCApzawZe1RGhx4OJUnqqOgONFsIsH3isvu33BozpPa4mgcL7eJJ3MsbEOK7HMFgWuz40yScxuM6w4111Bs1z+QmkXf1M2lmeVyDqK0doO4lkZVOj3TGBz2w6k/bxpMGB7PWgDR50t4egUW2MXNvpMayNMNwTHwc2bZQSfdhGAczMAZFvhCrbsbXic1+rfu/0pGv24eNuX1tQdipsqa759E5tIt/kb5DeST1InK0TE4aw9bKAngy6nrl5p9YciqRQKUMbKBJC5fRsZJMRqiRoQ9ucUDVHe/crpdOQzYeMVEm4KV9zFJvjDV8z276FkTW+GSrvWMAawjB+d41suhZUnfY4OzCDifq9cfIML+I5jtY2/dtWt/+hKU/CWuxRodYqh2txX2RarXpm6ymVL+vZywtCkDerq/ddN1+pum1eNzz75aLeuBj0fuh5L086Z2eb944D5yvna+eh4zlPnDPnF2fkXDjE+cv5x/nX+a/1Y+uP1qy1KNDbtzY+XzqVq/Xn/4sgrcs=</latexit>

enAetP

k PkLPkP'<latexit sha1_base64="NY9FZEJmXR+7MC53+iaHgvGYPuU=">AAAJ5nicjZbvj9s0GMfTMdi1UHaDl7yJVk2CqVRN77iBeLNxQwMJRJnubpPqrnIct7VqJ5HtdFQ+/w28YeIt/xb/yl5hp78SJ63I6S7283y+j792fE7ClBIh+/1/G3c+uPvhR/dOmq2PP2l/ev/0wWc3Isk4wtcooQl/HUKBKYnxtSSS4tcpx5CFFL8KF5c2/2qJuSBJfCVXKR4zOIvJlCAoTWhy+heIQprhFsBvlAIRx5EfawUMhWMJzV3OEaTqmdY6Z2TOAJGxyWKXHerJYq9JzHjWjtrlfzHqEqxbZqwZxzguhsES8nROdGty2un3+vnlVxvBptHxNtdw8uDkexAlKGPGAKJQiFHQT+VYQS4Joli3QSZwCtHCWByZZgwZFmOVL5/2H5lI5E8Tbn5j6efRokJBJsSKhYa0boWbs8HaHMfLku5RMZksMgYRT2qVIasLjzI5/XasSJxmEsdo7XyaUV8mvn24fkQ4RpKuTMOUJmbyPppDDpE0W6DdBhzH+C1KGINxZJ6AXj8izlSkzRoVc3ifwzZXVhKtiCPgJJZGY/6CiIiUwhUljEhR0b7clk5SBST+QyoT0SBODvA/M5c3kRJfpCV3aRM5SF9V6Ksj9LNl0bq9h6H68TB/A3mVvznML7DUo2CsblUn0IDDeJZv3SIScpgjgOZZC95WEaFHg7FSeqI6Aw3mwmwf/Fh93e8NGNNHpMbAWn02zjuWMTXOqjUMZmtXh0b5JAY7h53gtjOon8tzLN3Vt6GDy/MSi+rOEdo1kS5dani4JuZTl7ahYzyqEaCjClKjIIcVgsSVMfLYQcVlZYTLI/Vh5NImUqBbbRDhqTnA84NQ2fNeKz4Lter3Ls675hw+6/a1A9mXyJbqmp/ehUvkx/0e6Z1XiyR2n5gyiK0Wa+jJoBuYW3DhzGFtChQcusDaECjac5GNI1Ay6EJbT6Ds0T39CnZq3PyfkUqG6/xu3q87Ztt3MLSC+6HyjgOsMKXJ2x2y6TpQedoj+8KMxuq32skzOE9mMF659K/buPsfmvGUVmoP19HKysFK3Rc2Vlk9c/QUls/23O2FKZb73dX7ppvvVN02nxuB+3FRbVwPet/1gt/PO09/2Hx3nHhfeA+9L73Ae+I99X7yht61h7z3Db/xVeNxkzT/bL5r/r1G7zQ2ms+90tX85z+ZBsHG</latexit><latexit sha1_base64="NY9FZEJmXR+7MC53+iaHgvGYPuU=">AAAJ5nicjZbvj9s0GMfTMdi1UHaDl7yJVk2CqVRN77iBeLNxQwMJRJnubpPqrnIct7VqJ5HtdFQ+/w28YeIt/xb/yl5hp78SJ63I6S7283y+j792fE7ClBIh+/1/G3c+uPvhR/dOmq2PP2l/ev/0wWc3Isk4wtcooQl/HUKBKYnxtSSS4tcpx5CFFL8KF5c2/2qJuSBJfCVXKR4zOIvJlCAoTWhy+heIQprhFsBvlAIRx5EfawUMhWMJzV3OEaTqmdY6Z2TOAJGxyWKXHerJYq9JzHjWjtrlfzHqEqxbZqwZxzguhsES8nROdGty2un3+vnlVxvBptHxNtdw8uDkexAlKGPGAKJQiFHQT+VYQS4Joli3QSZwCtHCWByZZgwZFmOVL5/2H5lI5E8Tbn5j6efRokJBJsSKhYa0boWbs8HaHMfLku5RMZksMgYRT2qVIasLjzI5/XasSJxmEsdo7XyaUV8mvn24fkQ4RpKuTMOUJmbyPppDDpE0W6DdBhzH+C1KGINxZJ6AXj8izlSkzRoVc3ifwzZXVhKtiCPgJJZGY/6CiIiUwhUljEhR0b7clk5SBST+QyoT0SBODvA/M5c3kRJfpCV3aRM5SF9V6Ksj9LNl0bq9h6H68TB/A3mVvznML7DUo2CsblUn0IDDeJZv3SIScpgjgOZZC95WEaFHg7FSeqI6Aw3mwmwf/Fh93e8NGNNHpMbAWn02zjuWMTXOqjUMZmtXh0b5JAY7h53gtjOon8tzLN3Vt6GDy/MSi+rOEdo1kS5dani4JuZTl7ahYzyqEaCjClKjIIcVgsSVMfLYQcVlZYTLI/Vh5NImUqBbbRDhqTnA84NQ2fNeKz4Lter3Ls675hw+6/a1A9mXyJbqmp/ehUvkx/0e6Z1XiyR2n5gyiK0Wa+jJoBuYW3DhzGFtChQcusDaECjac5GNI1Ay6EJbT6Ds0T39CnZq3PyfkUqG6/xu3q87Ztt3MLSC+6HyjgOsMKXJ2x2y6TpQedoj+8KMxuq32skzOE9mMF659K/buPsfmvGUVmoP19HKysFK3Rc2Vlk9c/QUls/23O2FKZb73dX7ppvvVN02nxuB+3FRbVwPet/1gt/PO09/2Hx3nHhfeA+9L73Ae+I99X7yht61h7z3Db/xVeNxkzT/bL5r/r1G7zQ2ms+90tX85z+ZBsHG</latexit><latexit sha1_base64="NY9FZEJmXR+7MC53+iaHgvGYPuU=">AAAJ5nicjZbvj9s0GMfTMdi1UHaDl7yJVk2CqVRN77iBeLNxQwMJRJnubpPqrnIct7VqJ5HtdFQ+/w28YeIt/xb/yl5hp78SJ63I6S7283y+j792fE7ClBIh+/1/G3c+uPvhR/dOmq2PP2l/ev/0wWc3Isk4wtcooQl/HUKBKYnxtSSS4tcpx5CFFL8KF5c2/2qJuSBJfCVXKR4zOIvJlCAoTWhy+heIQprhFsBvlAIRx5EfawUMhWMJzV3OEaTqmdY6Z2TOAJGxyWKXHerJYq9JzHjWjtrlfzHqEqxbZqwZxzguhsES8nROdGty2un3+vnlVxvBptHxNtdw8uDkexAlKGPGAKJQiFHQT+VYQS4Joli3QSZwCtHCWByZZgwZFmOVL5/2H5lI5E8Tbn5j6efRokJBJsSKhYa0boWbs8HaHMfLku5RMZksMgYRT2qVIasLjzI5/XasSJxmEsdo7XyaUV8mvn24fkQ4RpKuTMOUJmbyPppDDpE0W6DdBhzH+C1KGINxZJ6AXj8izlSkzRoVc3ifwzZXVhKtiCPgJJZGY/6CiIiUwhUljEhR0b7clk5SBST+QyoT0SBODvA/M5c3kRJfpCV3aRM5SF9V6Ksj9LNl0bq9h6H68TB/A3mVvznML7DUo2CsblUn0IDDeJZv3SIScpgjgOZZC95WEaFHg7FSeqI6Aw3mwmwf/Fh93e8NGNNHpMbAWn02zjuWMTXOqjUMZmtXh0b5JAY7h53gtjOon8tzLN3Vt6GDy/MSi+rOEdo1kS5dani4JuZTl7ahYzyqEaCjClKjIIcVgsSVMfLYQcVlZYTLI/Vh5NImUqBbbRDhqTnA84NQ2fNeKz4Lter3Ls675hw+6/a1A9mXyJbqmp/ehUvkx/0e6Z1XiyR2n5gyiK0Wa+jJoBuYW3DhzGFtChQcusDaECjac5GNI1Ay6EJbT6Ds0T39CnZq3PyfkUqG6/xu3q87Ztt3MLSC+6HyjgOsMKXJ2x2y6TpQedoj+8KMxuq32skzOE9mMF659K/buPsfmvGUVmoP19HKysFK3Rc2Vlk9c/QUls/23O2FKZb73dX7ppvvVN02nxuB+3FRbVwPet/1gt/PO09/2Hx3nHhfeA+9L73Ae+I99X7yht61h7z3Db/xVeNxkzT/bL5r/r1G7zQ2ms+90tX85z+ZBsHG</latexit><latexit sha1_base64="NY9FZEJmXR+7MC53+iaHgvGYPuU=">AAAJ5nicjZbvj9s0GMfTMdi1UHaDl7yJVk2CqVRN77iBeLNxQwMJRJnubpPqrnIct7VqJ5HtdFQ+/w28YeIt/xb/yl5hp78SJ63I6S7283y+j792fE7ClBIh+/1/G3c+uPvhR/dOmq2PP2l/ev/0wWc3Isk4wtcooQl/HUKBKYnxtSSS4tcpx5CFFL8KF5c2/2qJuSBJfCVXKR4zOIvJlCAoTWhy+heIQprhFsBvlAIRx5EfawUMhWMJzV3OEaTqmdY6Z2TOAJGxyWKXHerJYq9JzHjWjtrlfzHqEqxbZqwZxzguhsES8nROdGty2un3+vnlVxvBptHxNtdw8uDkexAlKGPGAKJQiFHQT+VYQS4Joli3QSZwCtHCWByZZgwZFmOVL5/2H5lI5E8Tbn5j6efRokJBJsSKhYa0boWbs8HaHMfLku5RMZksMgYRT2qVIasLjzI5/XasSJxmEsdo7XyaUV8mvn24fkQ4RpKuTMOUJmbyPppDDpE0W6DdBhzH+C1KGINxZJ6AXj8izlSkzRoVc3ifwzZXVhKtiCPgJJZGY/6CiIiUwhUljEhR0b7clk5SBST+QyoT0SBODvA/M5c3kRJfpCV3aRM5SF9V6Ksj9LNl0bq9h6H68TB/A3mVvznML7DUo2CsblUn0IDDeJZv3SIScpgjgOZZC95WEaFHg7FSeqI6Aw3mwmwf/Fh93e8NGNNHpMbAWn02zjuWMTXOqjUMZmtXh0b5JAY7h53gtjOon8tzLN3Vt6GDy/MSi+rOEdo1kS5dani4JuZTl7ahYzyqEaCjClKjIIcVgsSVMfLYQcVlZYTLI/Vh5NImUqBbbRDhqTnA84NQ2fNeKz4Lter3Ls675hw+6/a1A9mXyJbqmp/ehUvkx/0e6Z1XiyR2n5gyiK0Wa+jJoBuYW3DhzGFtChQcusDaECjac5GNI1Ay6EJbT6Ds0T39CnZq3PyfkUqG6/xu3q87Ztt3MLSC+6HyjgOsMKXJ2x2y6TpQedoj+8KMxuq32skzOE9mMF659K/buPsfmvGUVmoP19HKysFK3Rc2Vlk9c/QUls/23O2FKZb73dX7ppvvVN02nxuB+3FRbVwPet/1gt/PO09/2Hx3nHhfeA+9L73Ae+I99X7yht61h7z3Db/xVeNxkzT/bL5r/r1G7zQ2ms+90tX85z+ZBsHG</latexit>

En'et

Pk PkLPkP'

<latexit sha1_base64="yI5ZNNGD+YCoQJDbK9VPazf/esQ=">AAAJ6nicjZbdjuM0FMfT5Ws6UHYWLrmJKCsh1I2azjAL4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8VNwA+KWl+JlEHb6MamdVmQ0rX3O75zzt3PqJCkoEbLf/6f14I0333r7nZP26bvvdd5/ePbog1uRlxzhG5TTnL9MoMCUZPhGEknxy4JjyBKKXySLK+t/scRckDy7lqsCjxmcZWRKEJTGNDn7A6QJLfGpAumMY5wBBuUcQaq+0xOwhLyYk1fKODlOw0xrDfArJaspECWbLHb8UE8WysxmOJMQ5KamlaR2/p9scB3Wfs3hrqY+nZx1+1G/ukJ/EG8G3WBzDSePTr4CaY5KZgQgCoUYxf1CjhXkkiCKdQeUAhcQLYzEkRlmkGExVtUW6vCxsaThNOfmP5NhZa1HKMiEWLHEkFatcH3W2OjjeLkX97juzBclg4jnjZEJazKPSjn9YqxIVpQSZ2itfFrSUOahvcFhSjhGkq7MwKQmZvEhmkMOkTRt0OkAjjP8GuWMwSw1d0CvbxFnKtVmj+o+fO/D1rcfSbQiTgAnmTQx5hOkRBQUrihhRAov9vk2dV4oIPFvUhmLBll+gP+Rubyx7PF1WnKXNpaD9LVHXx+hv17WpdvvJDG/lYP8LeQ+f3uYX2CpR/FY3alurAGH2axq3TqScFghgFZeC975iNCjwVgpPVHdgQZzYdoHf6ae9KMBY/pIqBGwjj4fVxPLmBznfg6D2dx+aVQtYrBT2I3vuoPmtXyLpbv71nRwe55j4XeO0K6IYulSw8M5MZ+6tDUd41FDADoaQRoiyOEIQTKvRmU7GHHlVbg6kh+mLm0sNfq0A1I8NQd4dRAqe95rxWeJVv3o8qJnzuHzXl87kH2QbKme+YsuXaI67u+R6MJPkts+MWkQWy3W0NNBLzZf8aWzhrUoUFPoAmtBoC7PRTaKwJ5AF9pqAvsa3dOvJqdBzf+ptCe4Se/m+bpjtnMHQyt4X6qaOMAKU5q/3iGbqQPtL3tkH5jpWP3SuHgG5/kMZiuX/nlrd3+hJS+ol3u4tno7B72831ubt3vm6Kltn5257YUplvfdFX3eqzpVd8zrRuy+XPiDm0H0ZRT/etF99s3mveMk+Cj4OPg0iIOnwbPgh2AY3AQo+Lf1SetJK2qz9u/tP9t/rdEHrU3Mh8He1f77PxWXxAQ=</latexit><latexit sha1_base64="yI5ZNNGD+YCoQJDbK9VPazf/esQ=">AAAJ6nicjZbdjuM0FMfT5Ws6UHYWLrmJKCsh1I2azjAL4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8VNwA+KWl+JlEHb6MamdVmQ0rX3O75zzt3PqJCkoEbLf/6f14I0333r7nZP26bvvdd5/ePbog1uRlxzhG5TTnL9MoMCUZPhGEknxy4JjyBKKXySLK+t/scRckDy7lqsCjxmcZWRKEJTGNDn7A6QJLfGpAumMY5wBBuUcQaq+0xOwhLyYk1fKODlOw0xrDfArJaspECWbLHb8UE8WysxmOJMQ5KamlaR2/p9scB3Wfs3hrqY+nZx1+1G/ukJ/EG8G3WBzDSePTr4CaY5KZgQgCoUYxf1CjhXkkiCKdQeUAhcQLYzEkRlmkGExVtUW6vCxsaThNOfmP5NhZa1HKMiEWLHEkFatcH3W2OjjeLkX97juzBclg4jnjZEJazKPSjn9YqxIVpQSZ2itfFrSUOahvcFhSjhGkq7MwKQmZvEhmkMOkTRt0OkAjjP8GuWMwSw1d0CvbxFnKtVmj+o+fO/D1rcfSbQiTgAnmTQx5hOkRBQUrihhRAov9vk2dV4oIPFvUhmLBll+gP+Rubyx7PF1WnKXNpaD9LVHXx+hv17WpdvvJDG/lYP8LeQ+f3uYX2CpR/FY3alurAGH2axq3TqScFghgFZeC975iNCjwVgpPVHdgQZzYdoHf6ae9KMBY/pIqBGwjj4fVxPLmBznfg6D2dx+aVQtYrBT2I3vuoPmtXyLpbv71nRwe55j4XeO0K6IYulSw8M5MZ+6tDUd41FDADoaQRoiyOEIQTKvRmU7GHHlVbg6kh+mLm0sNfq0A1I8NQd4dRAqe95rxWeJVv3o8qJnzuHzXl87kH2QbKme+YsuXaI67u+R6MJPkts+MWkQWy3W0NNBLzZf8aWzhrUoUFPoAmtBoC7PRTaKwJ5AF9pqAvsa3dOvJqdBzf+ptCe4Se/m+bpjtnMHQyt4X6qaOMAKU5q/3iGbqQPtL3tkH5jpWP3SuHgG5/kMZiuX/nlrd3+hJS+ol3u4tno7B72831ubt3vm6Kltn5257YUplvfdFX3eqzpVd8zrRuy+XPiDm0H0ZRT/etF99s3mveMk+Cj4OPg0iIOnwbPgh2AY3AQo+Lf1SetJK2qz9u/tP9t/rdEHrU3Mh8He1f77PxWXxAQ=</latexit><latexit sha1_base64="yI5ZNNGD+YCoQJDbK9VPazf/esQ=">AAAJ6nicjZbdjuM0FMfT5Ws6UHYWLrmJKCsh1I2azjAL4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8VNwA+KWl+JlEHb6MamdVmQ0rX3O75zzt3PqJCkoEbLf/6f14I0333r7nZP26bvvdd5/ePbog1uRlxzhG5TTnL9MoMCUZPhGEknxy4JjyBKKXySLK+t/scRckDy7lqsCjxmcZWRKEJTGNDn7A6QJLfGpAumMY5wBBuUcQaq+0xOwhLyYk1fKODlOw0xrDfArJaspECWbLHb8UE8WysxmOJMQ5KamlaR2/p9scB3Wfs3hrqY+nZx1+1G/ukJ/EG8G3WBzDSePTr4CaY5KZgQgCoUYxf1CjhXkkiCKdQeUAhcQLYzEkRlmkGExVtUW6vCxsaThNOfmP5NhZa1HKMiEWLHEkFatcH3W2OjjeLkX97juzBclg4jnjZEJazKPSjn9YqxIVpQSZ2itfFrSUOahvcFhSjhGkq7MwKQmZvEhmkMOkTRt0OkAjjP8GuWMwSw1d0CvbxFnKtVmj+o+fO/D1rcfSbQiTgAnmTQx5hOkRBQUrihhRAov9vk2dV4oIPFvUhmLBll+gP+Rubyx7PF1WnKXNpaD9LVHXx+hv17WpdvvJDG/lYP8LeQ+f3uYX2CpR/FY3alurAGH2axq3TqScFghgFZeC975iNCjwVgpPVHdgQZzYdoHf6ae9KMBY/pIqBGwjj4fVxPLmBznfg6D2dx+aVQtYrBT2I3vuoPmtXyLpbv71nRwe55j4XeO0K6IYulSw8M5MZ+6tDUd41FDADoaQRoiyOEIQTKvRmU7GHHlVbg6kh+mLm0sNfq0A1I8NQd4dRAqe95rxWeJVv3o8qJnzuHzXl87kH2QbKme+YsuXaI67u+R6MJPkts+MWkQWy3W0NNBLzZf8aWzhrUoUFPoAmtBoC7PRTaKwJ5AF9pqAvsa3dOvJqdBzf+ptCe4Se/m+bpjtnMHQyt4X6qaOMAKU5q/3iGbqQPtL3tkH5jpWP3SuHgG5/kMZiuX/nlrd3+hJS+ol3u4tno7B72831ubt3vm6Kltn5257YUplvfdFX3eqzpVd8zrRuy+XPiDm0H0ZRT/etF99s3mveMk+Cj4OPg0iIOnwbPgh2AY3AQo+Lf1SetJK2qz9u/tP9t/rdEHrU3Mh8He1f77PxWXxAQ=</latexit><latexit sha1_base64="yI5ZNNGD+YCoQJDbK9VPazf/esQ=">AAAJ6nicjZbdjuM0FMfT5Ws6UHYWLrmJKCsh1I2azjAL4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8VNwA+KWl+JlEHb6MamdVmQ0rX3O75zzt3PqJCkoEbLf/6f14I0333r7nZP26bvvdd5/ePbog1uRlxzhG5TTnL9MoMCUZPhGEknxy4JjyBKKXySLK+t/scRckDy7lqsCjxmcZWRKEJTGNDn7A6QJLfGpAumMY5wBBuUcQaq+0xOwhLyYk1fKODlOw0xrDfArJaspECWbLHb8UE8WysxmOJMQ5KamlaR2/p9scB3Wfs3hrqY+nZx1+1G/ukJ/EG8G3WBzDSePTr4CaY5KZgQgCoUYxf1CjhXkkiCKdQeUAhcQLYzEkRlmkGExVtUW6vCxsaThNOfmP5NhZa1HKMiEWLHEkFatcH3W2OjjeLkX97juzBclg4jnjZEJazKPSjn9YqxIVpQSZ2itfFrSUOahvcFhSjhGkq7MwKQmZvEhmkMOkTRt0OkAjjP8GuWMwSw1d0CvbxFnKtVmj+o+fO/D1rcfSbQiTgAnmTQx5hOkRBQUrihhRAov9vk2dV4oIPFvUhmLBll+gP+Rubyx7PF1WnKXNpaD9LVHXx+hv17WpdvvJDG/lYP8LeQ+f3uYX2CpR/FY3alurAGH2axq3TqScFghgFZeC975iNCjwVgpPVHdgQZzYdoHf6ae9KMBY/pIqBGwjj4fVxPLmBznfg6D2dx+aVQtYrBT2I3vuoPmtXyLpbv71nRwe55j4XeO0K6IYulSw8M5MZ+6tDUd41FDADoaQRoiyOEIQTKvRmU7GHHlVbg6kh+mLm0sNfq0A1I8NQd4dRAqe95rxWeJVv3o8qJnzuHzXl87kH2QbKme+YsuXaI67u+R6MJPkts+MWkQWy3W0NNBLzZf8aWzhrUoUFPoAmtBoC7PRTaKwJ5AF9pqAvsa3dOvJqdBzf+ptCe4Se/m+bpjtnMHQyt4X6qaOMAKU5q/3iGbqQPtL3tkH5jpWP3SuHgG5/kMZiuX/nlrd3+hJS+ol3u4tno7B72831ubt3vm6Kltn5257YUplvfdFX3eqzpVd8zrRuy+XPiDm0H0ZRT/etF99s3mveMk+Cj4OPg0iIOnwbPgh2AY3AQo+Lf1SetJK2qz9u/tP9t/rdEHrU3Mh8He1f77PxWXxAQ=</latexit>

etDetP

k PkLPkP'<latexit sha1_base64="i2oDrWuUVRee0671mz8LXmnI81I=">AAAJynicjZbvj9M2GMdTYON6W+FgL3lTrUKapq5qescB4g3jQNukoXXo7kCqS+U4bmvVTiLbKUQ+v+Of5A1/y+ykvUuctFqqNvbzfJ7HX/+o7SChRMjh8Gvr1u07331/96B9+MOPnXv3jx48vBRxyhG+QDGN+YcACkxJhC8kkRR/SDiGLKD4fbA6s/73a8wFiaNzmSV4yuAiInOCoDSm2dFnEAY0xYcAf1RSgZDjECwgY1ADBuUSQapea124C69I2Wx17RzrUuVvXbFrk2/BMY7KVrCGPFkSPTvqDQfD/OnWC/6m0PM2z3j24OAFCGOUMhxJRKEQE3+YyKmCXBJEse6AVOAEohVc4IkpRpBhMVX5EOnuY2MJu/OYm28ku7m1HKEgEyJjgSGtWOH6rLHRx/G6Eve47IxXKYOIx42RAWsyT1I5fzZVJEpSiSNUKJ+ntCvjrp3Abkg4RpJmpmBSE9P5LlpCDpE009zpAI4j/AnFZgqj0EyAmQTbBmcq1GaMyj5848PWV40kWhEngJNImhjzC0IiEgozShiRohb7bps6ThSQ+LNUxqJBFO/g/2IubywVvkxL7tLGspM+r9Hne+jf12Xp9h0E6s1u/hLyOn+5m19hqSf+VF2pnq8Bh9EiX7plJOAwRwDNvRa8qiNCT0ZTpfRM9UYaLIVZPvhX9dtwMGJM7wk1Aoro42lesYzJcVzPYTCbu940yjsxulbY8696o+a+vMbSHX1r2jk877CorxyhXRHJ2qXGu3NiPndpa9rHo4YAtDeCNESQ3RGCRLU2ctvOiLNaC2d78sPQpY2lRB92QIjn5szIN0JlN3at+CLQajg4Pembffi4P9QOZA+KLdU3n8GpS+S7/Q0yOKknie06MWkQy1YF9HTU983LP3X6UIgCJYUuUAgCZXkuslEEKgJdaKsJVDW6u19JToOa/9NSRXCTXnM6m+MNXjPbuoOhDN40lVccIMOUxp+ukU3VgardntgDM5yqfxo7z+AyXsAoc+m3W7v7D015Qmu5x4W1NnKwlvcPa6uNntl6SsNna+7ywhTLm9U1eNLPV6rumOuG714u6oWL0eD5wP/3pPfy1ebeceA98n72fvF876n30vvTG3sXHvK+te60Oq177bdt0c7aqkBvtTYxP3mVp/3lP3u+tcg=</latexit><latexit sha1_base64="i2oDrWuUVRee0671mz8LXmnI81I=">AAAJynicjZbvj9M2GMdTYON6W+FgL3lTrUKapq5qescB4g3jQNukoXXo7kCqS+U4bmvVTiLbKUQ+v+Of5A1/y+ykvUuctFqqNvbzfJ7HX/+o7SChRMjh8Gvr1u07331/96B9+MOPnXv3jx48vBRxyhG+QDGN+YcACkxJhC8kkRR/SDiGLKD4fbA6s/73a8wFiaNzmSV4yuAiInOCoDSm2dFnEAY0xYcAf1RSgZDjECwgY1ADBuUSQapea124C69I2Wx17RzrUuVvXbFrk2/BMY7KVrCGPFkSPTvqDQfD/OnWC/6m0PM2z3j24OAFCGOUMhxJRKEQE3+YyKmCXBJEse6AVOAEohVc4IkpRpBhMVX5EOnuY2MJu/OYm28ku7m1HKEgEyJjgSGtWOH6rLHRx/G6Eve47IxXKYOIx42RAWsyT1I5fzZVJEpSiSNUKJ+ntCvjrp3Abkg4RpJmpmBSE9P5LlpCDpE009zpAI4j/AnFZgqj0EyAmQTbBmcq1GaMyj5848PWV40kWhEngJNImhjzC0IiEgozShiRohb7bps6ThSQ+LNUxqJBFO/g/2IubywVvkxL7tLGspM+r9Hne+jf12Xp9h0E6s1u/hLyOn+5m19hqSf+VF2pnq8Bh9EiX7plJOAwRwDNvRa8qiNCT0ZTpfRM9UYaLIVZPvhX9dtwMGJM7wk1Aoro42lesYzJcVzPYTCbu940yjsxulbY8696o+a+vMbSHX1r2jk877CorxyhXRHJ2qXGu3NiPndpa9rHo4YAtDeCNESQ3RGCRLU2ctvOiLNaC2d78sPQpY2lRB92QIjn5szIN0JlN3at+CLQajg4Pembffi4P9QOZA+KLdU3n8GpS+S7/Q0yOKknie06MWkQy1YF9HTU983LP3X6UIgCJYUuUAgCZXkuslEEKgJdaKsJVDW6u19JToOa/9NSRXCTXnM6m+MNXjPbuoOhDN40lVccIMOUxp+ukU3VgardntgDM5yqfxo7z+AyXsAoc+m3W7v7D015Qmu5x4W1NnKwlvcPa6uNntl6SsNna+7ywhTLm9U1eNLPV6rumOuG714u6oWL0eD5wP/3pPfy1ebeceA98n72fvF876n30vvTG3sXHvK+te60Oq177bdt0c7aqkBvtTYxP3mVp/3lP3u+tcg=</latexit><latexit sha1_base64="i2oDrWuUVRee0671mz8LXmnI81I=">AAAJynicjZbvj9M2GMdTYON6W+FgL3lTrUKapq5qescB4g3jQNukoXXo7kCqS+U4bmvVTiLbKUQ+v+Of5A1/y+ykvUuctFqqNvbzfJ7HX/+o7SChRMjh8Gvr1u07331/96B9+MOPnXv3jx48vBRxyhG+QDGN+YcACkxJhC8kkRR/SDiGLKD4fbA6s/73a8wFiaNzmSV4yuAiInOCoDSm2dFnEAY0xYcAf1RSgZDjECwgY1ADBuUSQapea124C69I2Wx17RzrUuVvXbFrk2/BMY7KVrCGPFkSPTvqDQfD/OnWC/6m0PM2z3j24OAFCGOUMhxJRKEQE3+YyKmCXBJEse6AVOAEohVc4IkpRpBhMVX5EOnuY2MJu/OYm28ku7m1HKEgEyJjgSGtWOH6rLHRx/G6Eve47IxXKYOIx42RAWsyT1I5fzZVJEpSiSNUKJ+ntCvjrp3Abkg4RpJmpmBSE9P5LlpCDpE009zpAI4j/AnFZgqj0EyAmQTbBmcq1GaMyj5848PWV40kWhEngJNImhjzC0IiEgozShiRohb7bps6ThSQ+LNUxqJBFO/g/2IubywVvkxL7tLGspM+r9Hne+jf12Xp9h0E6s1u/hLyOn+5m19hqSf+VF2pnq8Bh9EiX7plJOAwRwDNvRa8qiNCT0ZTpfRM9UYaLIVZPvhX9dtwMGJM7wk1Aoro42lesYzJcVzPYTCbu940yjsxulbY8696o+a+vMbSHX1r2jk877CorxyhXRHJ2qXGu3NiPndpa9rHo4YAtDeCNESQ3RGCRLU2ctvOiLNaC2d78sPQpY2lRB92QIjn5szIN0JlN3at+CLQajg4Pembffi4P9QOZA+KLdU3n8GpS+S7/Q0yOKknie06MWkQy1YF9HTU983LP3X6UIgCJYUuUAgCZXkuslEEKgJdaKsJVDW6u19JToOa/9NSRXCTXnM6m+MNXjPbuoOhDN40lVccIMOUxp+ukU3VgardntgDM5yqfxo7z+AyXsAoc+m3W7v7D015Qmu5x4W1NnKwlvcPa6uNntl6SsNna+7ywhTLm9U1eNLPV6rumOuG714u6oWL0eD5wP/3pPfy1ebeceA98n72fvF876n30vvTG3sXHvK+te60Oq177bdt0c7aqkBvtTYxP3mVp/3lP3u+tcg=</latexit><latexit sha1_base64="i2oDrWuUVRee0671mz8LXmnI81I=">AAAJynicjZbvj9M2GMdTYON6W+FgL3lTrUKapq5qescB4g3jQNukoXXo7kCqS+U4bmvVTiLbKUQ+v+Of5A1/y+ykvUuctFqqNvbzfJ7HX/+o7SChRMjh8Gvr1u07331/96B9+MOPnXv3jx48vBRxyhG+QDGN+YcACkxJhC8kkRR/SDiGLKD4fbA6s/73a8wFiaNzmSV4yuAiInOCoDSm2dFnEAY0xYcAf1RSgZDjECwgY1ADBuUSQapea124C69I2Wx17RzrUuVvXbFrk2/BMY7KVrCGPFkSPTvqDQfD/OnWC/6m0PM2z3j24OAFCGOUMhxJRKEQE3+YyKmCXBJEse6AVOAEohVc4IkpRpBhMVX5EOnuY2MJu/OYm28ku7m1HKEgEyJjgSGtWOH6rLHRx/G6Eve47IxXKYOIx42RAWsyT1I5fzZVJEpSiSNUKJ+ntCvjrp3Abkg4RpJmpmBSE9P5LlpCDpE009zpAI4j/AnFZgqj0EyAmQTbBmcq1GaMyj5848PWV40kWhEngJNImhjzC0IiEgozShiRohb7bps6ThSQ+LNUxqJBFO/g/2IubywVvkxL7tLGspM+r9Hne+jf12Xp9h0E6s1u/hLyOn+5m19hqSf+VF2pnq8Bh9EiX7plJOAwRwDNvRa8qiNCT0ZTpfRM9UYaLIVZPvhX9dtwMGJM7wk1Aoro42lesYzJcVzPYTCbu940yjsxulbY8696o+a+vMbSHX1r2jk877CorxyhXRHJ2qXGu3NiPndpa9rHo4YAtDeCNESQ3RGCRLU2ctvOiLNaC2d78sPQpY2lRB92QIjn5szIN0JlN3at+CLQajg4Pembffi4P9QOZA+KLdU3n8GpS+S7/Q0yOKknie06MWkQy1YF9HTU983LP3X6UIgCJYUuUAgCZXkuslEEKgJdaKsJVDW6u19JToOa/9NSRXCTXnM6m+MNXjPbuoOhDN40lVccIMOUxp+ukU3VgardntgDM5yqfxo7z+AyXsAoc+m3W7v7D015Qmu5x4W1NnKwlvcPa6uNntl6SsNna+7ywhTLm9U1eNLPV6rumOuG714u6oWL0eD5wP/3pPfy1ebeceA98n72fvF876n30vvTG3sXHvK+te60Oq177bdt0c7aqkBvtTYxP3mVp/3lP3u+tcg=</latexit>

(Eetn L)n

<latexit sha1_base64="iGcjR9Kg7OX0CnmFIndukjKrIec=">AAAJnnicjZbdbts2FMfV7ivO5i3dLncjzCjQDZ5hOVk6YDfdsk9sRbMiSQOYbkBRxw5hkhJIKp3B8KH2NMPutjcZKduJTMnGZNgiz/mdwz/JY0ppwajSw+HfDx6+9fY7776319l//4Puhx8dPPr4QuWlJHBOcpbLyxQrYFTAuaaawWUhAfOUwat0fuL9r25AKpqLM70oYMLxTNApJVg709XBryhLWQn7T8yygTjW1wQz84O1CF4bNJWYGG2N80vIYuHMa+Q3az9/XXNcHfSGg2F1xc1Gsmr0otV1evVo7xuU5aTkIDRhWKlxMiz0xGCpKWFgu6hUUGAyxzMYu6bAHNTEVLO28WNnyeJpLt1X6Liy1iMM5koteOpIr1iFPm9s9Um42Yh7XHfm85JjIvPWyJS3mcelnn49MVQUpQZBlsqnJYt1Hvs9iTMqgWi2cA2XmrrJx+Qau4XXbue6XSRBwBuSc45F5pbbmmoLJDeZdWtU98G9D7xvM5JaQ4MASYXbXOR+UUZVwfCCUU61asS+XKfOC4M0/KGNs1gk8i38LzzknWWDr9NahrSzbKXPGvTZDvrbm7p0f0/Tqry38BdYNvmL7fwctB0nE3NreolFEotZVbp1JJW4QhCrvB68bSLKjkcTY+yV6Y0sulaufOAL8+VwMOLc7gh1ApbRh5Oq4xmX47CZw2E+d3NoUk1idKewl9z2Ru1z+R50uPretHV5XoJqVo6yoYjiJqROt+cEOQ1pb9rFk5YAsjOCtkTQ7RGKisYYlW1rxEljhJMd+XEW0s5So/e7KIOpewxUB6Hxh7I1cpZaMxwcH/XdOXzYH9oA8kf+muq7z+A4JGYSQNwjg6NmktzXiUtD+GK+hJ6O+om7JcfBHJaiUE1hCCwFobq8EFkpQhsCQ2itCW1qDE+/mpwWNf9npA3BbXrdA9c93vAds+4HGFng+6GqTgAsgLH8zR2y6gbQ5rTH/oGZTcyL1slzfJ3PsFiE9PO1PfyHlrJgjdynS2tj5XAj70/e1lg9d/TUls/3wvICBvq+ugZf9atKtV33upGELxfNxsVokLhK/P2o9+y71YvHXvRp9Fn0JEqip9Gz6OfoNDqPSPRn9Ff0T/RvJ+782HneebFEHz5YxXwSbVydy/8AdsmkqA==</latexit><latexit sha1_base64="iGcjR9Kg7OX0CnmFIndukjKrIec=">AAAJnnicjZbdbts2FMfV7ivO5i3dLncjzCjQDZ5hOVk6YDfdsk9sRbMiSQOYbkBRxw5hkhJIKp3B8KH2NMPutjcZKduJTMnGZNgiz/mdwz/JY0ppwajSw+HfDx6+9fY7776319l//4Puhx8dPPr4QuWlJHBOcpbLyxQrYFTAuaaawWUhAfOUwat0fuL9r25AKpqLM70oYMLxTNApJVg709XBryhLWQn7T8yygTjW1wQz84O1CF4bNJWYGG2N80vIYuHMa+Q3az9/XXNcHfSGg2F1xc1Gsmr0otV1evVo7xuU5aTkIDRhWKlxMiz0xGCpKWFgu6hUUGAyxzMYu6bAHNTEVLO28WNnyeJpLt1X6Liy1iMM5koteOpIr1iFPm9s9Um42Yh7XHfm85JjIvPWyJS3mcelnn49MVQUpQZBlsqnJYt1Hvs9iTMqgWi2cA2XmrrJx+Qau4XXbue6XSRBwBuSc45F5pbbmmoLJDeZdWtU98G9D7xvM5JaQ4MASYXbXOR+UUZVwfCCUU61asS+XKfOC4M0/KGNs1gk8i38LzzknWWDr9NahrSzbKXPGvTZDvrbm7p0f0/Tqry38BdYNvmL7fwctB0nE3NreolFEotZVbp1JJW4QhCrvB68bSLKjkcTY+yV6Y0sulaufOAL8+VwMOLc7gh1ApbRh5Oq4xmX47CZw2E+d3NoUk1idKewl9z2Ru1z+R50uPretHV5XoJqVo6yoYjiJqROt+cEOQ1pb9rFk5YAsjOCtkTQ7RGKisYYlW1rxEljhJMd+XEW0s5So/e7KIOpewxUB6Hxh7I1cpZaMxwcH/XdOXzYH9oA8kf+muq7z+A4JGYSQNwjg6NmktzXiUtD+GK+hJ6O+om7JcfBHJaiUE1hCCwFobq8EFkpQhsCQ2itCW1qDE+/mpwWNf9npA3BbXrdA9c93vAds+4HGFng+6GqTgAsgLH8zR2y6gbQ5rTH/oGZTcyL1slzfJ3PsFiE9PO1PfyHlrJgjdynS2tj5XAj70/e1lg9d/TUls/3wvICBvq+ugZf9atKtV33upGELxfNxsVokLhK/P2o9+y71YvHXvRp9Fn0JEqip9Gz6OfoNDqPSPRn9Ff0T/RvJ+782HneebFEHz5YxXwSbVydy/8AdsmkqA==</latexit><latexit sha1_base64="iGcjR9Kg7OX0CnmFIndukjKrIec=">AAAJnnicjZbdbts2FMfV7ivO5i3dLncjzCjQDZ5hOVk6YDfdsk9sRbMiSQOYbkBRxw5hkhJIKp3B8KH2NMPutjcZKduJTMnGZNgiz/mdwz/JY0ppwajSw+HfDx6+9fY7776319l//4Puhx8dPPr4QuWlJHBOcpbLyxQrYFTAuaaawWUhAfOUwat0fuL9r25AKpqLM70oYMLxTNApJVg709XBryhLWQn7T8yygTjW1wQz84O1CF4bNJWYGG2N80vIYuHMa+Q3az9/XXNcHfSGg2F1xc1Gsmr0otV1evVo7xuU5aTkIDRhWKlxMiz0xGCpKWFgu6hUUGAyxzMYu6bAHNTEVLO28WNnyeJpLt1X6Liy1iMM5koteOpIr1iFPm9s9Um42Yh7XHfm85JjIvPWyJS3mcelnn49MVQUpQZBlsqnJYt1Hvs9iTMqgWi2cA2XmrrJx+Qau4XXbue6XSRBwBuSc45F5pbbmmoLJDeZdWtU98G9D7xvM5JaQ4MASYXbXOR+UUZVwfCCUU61asS+XKfOC4M0/KGNs1gk8i38LzzknWWDr9NahrSzbKXPGvTZDvrbm7p0f0/Tqry38BdYNvmL7fwctB0nE3NreolFEotZVbp1JJW4QhCrvB68bSLKjkcTY+yV6Y0sulaufOAL8+VwMOLc7gh1ApbRh5Oq4xmX47CZw2E+d3NoUk1idKewl9z2Ru1z+R50uPretHV5XoJqVo6yoYjiJqROt+cEOQ1pb9rFk5YAsjOCtkTQ7RGKisYYlW1rxEljhJMd+XEW0s5So/e7KIOpewxUB6Hxh7I1cpZaMxwcH/XdOXzYH9oA8kf+muq7z+A4JGYSQNwjg6NmktzXiUtD+GK+hJ6O+om7JcfBHJaiUE1hCCwFobq8EFkpQhsCQ2itCW1qDE+/mpwWNf9npA3BbXrdA9c93vAds+4HGFng+6GqTgAsgLH8zR2y6gbQ5rTH/oGZTcyL1slzfJ3PsFiE9PO1PfyHlrJgjdynS2tj5XAj70/e1lg9d/TUls/3wvICBvq+ugZf9atKtV33upGELxfNxsVokLhK/P2o9+y71YvHXvRp9Fn0JEqip9Gz6OfoNDqPSPRn9Ff0T/RvJ+782HneebFEHz5YxXwSbVydy/8AdsmkqA==</latexit><latexit sha1_base64="iGcjR9Kg7OX0CnmFIndukjKrIec=">AAAJnnicjZbdbts2FMfV7ivO5i3dLncjzCjQDZ5hOVk6YDfdsk9sRbMiSQOYbkBRxw5hkhJIKp3B8KH2NMPutjcZKduJTMnGZNgiz/mdwz/JY0ppwajSw+HfDx6+9fY7776319l//4Puhx8dPPr4QuWlJHBOcpbLyxQrYFTAuaaawWUhAfOUwat0fuL9r25AKpqLM70oYMLxTNApJVg709XBryhLWQn7T8yygTjW1wQz84O1CF4bNJWYGG2N80vIYuHMa+Q3az9/XXNcHfSGg2F1xc1Gsmr0otV1evVo7xuU5aTkIDRhWKlxMiz0xGCpKWFgu6hUUGAyxzMYu6bAHNTEVLO28WNnyeJpLt1X6Liy1iMM5koteOpIr1iFPm9s9Um42Yh7XHfm85JjIvPWyJS3mcelnn49MVQUpQZBlsqnJYt1Hvs9iTMqgWi2cA2XmrrJx+Qau4XXbue6XSRBwBuSc45F5pbbmmoLJDeZdWtU98G9D7xvM5JaQ4MASYXbXOR+UUZVwfCCUU61asS+XKfOC4M0/KGNs1gk8i38LzzknWWDr9NahrSzbKXPGvTZDvrbm7p0f0/Tqry38BdYNvmL7fwctB0nE3NreolFEotZVbp1JJW4QhCrvB68bSLKjkcTY+yV6Y0sulaufOAL8+VwMOLc7gh1ApbRh5Oq4xmX47CZw2E+d3NoUk1idKewl9z2Ru1z+R50uPretHV5XoJqVo6yoYjiJqROt+cEOQ1pb9rFk5YAsjOCtkTQ7RGKisYYlW1rxEljhJMd+XEW0s5So/e7KIOpewxUB6Hxh7I1cpZaMxwcH/XdOXzYH9oA8kf+muq7z+A4JGYSQNwjg6NmktzXiUtD+GK+hJ6O+om7JcfBHJaiUE1hCCwFobq8EFkpQhsCQ2itCW1qDE+/mpwWNf9npA3BbXrdA9c93vAds+4HGFng+6GqTgAsgLH8zR2y6gbQ5rTH/oGZTcyL1slzfJ3PsFiE9PO1PfyHlrJgjdynS2tj5XAj70/e1lg9d/TUls/3wvICBvq+ugZf9atKtV33upGELxfNxsVokLhK/P2o9+y71YvHXvRp9Fn0JEqip9Gz6OfoNDqPSPRn9Ff0T/RvJ+782HneebFEHz5YxXwSbVydy/8AdsmkqA==</latexit>

(Emet

mn L · · · E1et

mn L)n<latexit sha1_base64="Elg1HWgHtfhfeeVxJ1P1LiotMhE=">AAAJ4HicjZZRb9s2EMfldl3jtF7T7mnoi1CjQDt4huWk6YC9dM2KbUCHpUWSFjBdg6JohzApCSSVzmD4vpdh2Gu/2T7HvsBOsh3LlBRUhm3y7nfHP8kTpTDlTOnB4N/WjZtf3Pry9k57987dzlf39u4/OFNJJgk9JQlP5PsQK8pZTE8105y+TyXFIuT0XTg/yv3vLqhULIlP9CKlY4FnMZsygjWYJnt/oSjkGd19YpYNJLA+J5ibV3YiLKIfDJpKTIy2RgAiaeTH1l5Rr6FNokSrmvDgs8KffjAbx2SvO+gPisuvNoJVo+utruPJ/Z0fUJSQTNBYE46VGgWDVI8NlpoRTm0HZYqmmMzxjI6gGWNB1dgU62b9x2CJ/Gki4Rtrv7CWIwwWSi1ECGSuWLm+3Fjrk/RiK+5x2ZnMM4GJTGojQ1FnHmV6+v3YsDjNNI3JUvk0475O/HxX/YhJSjRfQANSM5i8T84xrLyGve90kKQx/UgSIXAcwXJbU2yBFCaysEZlH934aO7bjmTWMCdAshh2F8EviphKOV5wJphWldi369RJapCmf2gDFovipIH/Vbg8WLb4Mq2lS4OlkT6p0CfX0D9elKXn/2EIFd7In2FZ5c+a+TnVdhSMzaXpwk0jcTwrSreMhBIXCOKFNwcvq4iyo+HYGDsx3aFF5wrKh35rvhv0hwJu5uZQELCM3h8XnZyBHPvVHIDluatDk2ISwyuF3eCyO6yfy09Uu6ufmxqX5y1V1cpR1hWRXrjUcXNOKqcunZuu40lNALk2gtVEsOYIxeLKGIWtMeKoMsLRNflx5NJgKdG7HRTRKTxIioPQ5IeyNXIWWjPoHx704Bze7w2sA+Wn/prqwad/6BIzSWm8QfoH1SRJXieQhojFfAk9H/YC+AsOnTksRaGSQhdYCkJleS6yUoS2BLrQWhPa1uiefiU5NWo+Z6QtwXV64ZENjzd8xaz7DkYWeDNU0XGABeU8+XiFrLoOtD3tUf7AjMbm99rJC3yezHC8cOnf1nb3Ds1kyiu5j5fWysrhSt6fc1tl9eDoKS1f3nPLi3KqN9XVf9YrKtV24HUjcF8uqo2zYT+ASnxz0H3xcvXiseM99B55T7zAe+698H7xjr1Tj3j/tb5pPWp122H7z/bf7X+W6I3WKuZrb+tqf/ofaNe/Lw==</latexit><latexit sha1_base64="Elg1HWgHtfhfeeVxJ1P1LiotMhE=">AAAJ4HicjZZRb9s2EMfldl3jtF7T7mnoi1CjQDt4huWk6YC9dM2KbUCHpUWSFjBdg6JohzApCSSVzmD4vpdh2Gu/2T7HvsBOsh3LlBRUhm3y7nfHP8kTpTDlTOnB4N/WjZtf3Pry9k57987dzlf39u4/OFNJJgk9JQlP5PsQK8pZTE8105y+TyXFIuT0XTg/yv3vLqhULIlP9CKlY4FnMZsygjWYJnt/oSjkGd19YpYNJLA+J5ibV3YiLKIfDJpKTIy2RgAiaeTH1l5Rr6FNokSrmvDgs8KffjAbx2SvO+gPisuvNoJVo+utruPJ/Z0fUJSQTNBYE46VGgWDVI8NlpoRTm0HZYqmmMzxjI6gGWNB1dgU62b9x2CJ/Gki4Rtrv7CWIwwWSi1ECGSuWLm+3Fjrk/RiK+5x2ZnMM4GJTGojQ1FnHmV6+v3YsDjNNI3JUvk0475O/HxX/YhJSjRfQANSM5i8T84xrLyGve90kKQx/UgSIXAcwXJbU2yBFCaysEZlH934aO7bjmTWMCdAshh2F8EviphKOV5wJphWldi369RJapCmf2gDFovipIH/Vbg8WLb4Mq2lS4OlkT6p0CfX0D9elKXn/2EIFd7In2FZ5c+a+TnVdhSMzaXpwk0jcTwrSreMhBIXCOKFNwcvq4iyo+HYGDsx3aFF5wrKh35rvhv0hwJu5uZQELCM3h8XnZyBHPvVHIDluatDk2ISwyuF3eCyO6yfy09Uu6ufmxqX5y1V1cpR1hWRXrjUcXNOKqcunZuu40lNALk2gtVEsOYIxeLKGIWtMeKoMsLRNflx5NJgKdG7HRTRKTxIioPQ5IeyNXIWWjPoHx704Bze7w2sA+Wn/prqwad/6BIzSWm8QfoH1SRJXieQhojFfAk9H/YC+AsOnTksRaGSQhdYCkJleS6yUoS2BLrQWhPa1uiefiU5NWo+Z6QtwXV64ZENjzd8xaz7DkYWeDNU0XGABeU8+XiFrLoOtD3tUf7AjMbm99rJC3yezHC8cOnf1nb3Ds1kyiu5j5fWysrhSt6fc1tl9eDoKS1f3nPLi3KqN9XVf9YrKtV24HUjcF8uqo2zYT+ASnxz0H3xcvXiseM99B55T7zAe+698H7xjr1Tj3j/tb5pPWp122H7z/bf7X+W6I3WKuZrb+tqf/ofaNe/Lw==</latexit><latexit sha1_base64="Elg1HWgHtfhfeeVxJ1P1LiotMhE=">AAAJ4HicjZZRb9s2EMfldl3jtF7T7mnoi1CjQDt4huWk6YC9dM2KbUCHpUWSFjBdg6JohzApCSSVzmD4vpdh2Gu/2T7HvsBOsh3LlBRUhm3y7nfHP8kTpTDlTOnB4N/WjZtf3Pry9k57987dzlf39u4/OFNJJgk9JQlP5PsQK8pZTE8105y+TyXFIuT0XTg/yv3vLqhULIlP9CKlY4FnMZsygjWYJnt/oSjkGd19YpYNJLA+J5ibV3YiLKIfDJpKTIy2RgAiaeTH1l5Rr6FNokSrmvDgs8KffjAbx2SvO+gPisuvNoJVo+utruPJ/Z0fUJSQTNBYE46VGgWDVI8NlpoRTm0HZYqmmMzxjI6gGWNB1dgU62b9x2CJ/Gki4Rtrv7CWIwwWSi1ECGSuWLm+3Fjrk/RiK+5x2ZnMM4GJTGojQ1FnHmV6+v3YsDjNNI3JUvk0475O/HxX/YhJSjRfQANSM5i8T84xrLyGve90kKQx/UgSIXAcwXJbU2yBFCaysEZlH934aO7bjmTWMCdAshh2F8EviphKOV5wJphWldi369RJapCmf2gDFovipIH/Vbg8WLb4Mq2lS4OlkT6p0CfX0D9elKXn/2EIFd7In2FZ5c+a+TnVdhSMzaXpwk0jcTwrSreMhBIXCOKFNwcvq4iyo+HYGDsx3aFF5wrKh35rvhv0hwJu5uZQELCM3h8XnZyBHPvVHIDluatDk2ISwyuF3eCyO6yfy09Uu6ufmxqX5y1V1cpR1hWRXrjUcXNOKqcunZuu40lNALk2gtVEsOYIxeLKGIWtMeKoMsLRNflx5NJgKdG7HRTRKTxIioPQ5IeyNXIWWjPoHx704Bze7w2sA+Wn/prqwad/6BIzSWm8QfoH1SRJXieQhojFfAk9H/YC+AsOnTksRaGSQhdYCkJleS6yUoS2BLrQWhPa1uiefiU5NWo+Z6QtwXV64ZENjzd8xaz7DkYWeDNU0XGABeU8+XiFrLoOtD3tUf7AjMbm99rJC3yezHC8cOnf1nb3Ds1kyiu5j5fWysrhSt6fc1tl9eDoKS1f3nPLi3KqN9XVf9YrKtV24HUjcF8uqo2zYT+ASnxz0H3xcvXiseM99B55T7zAe+698H7xjr1Tj3j/tb5pPWp122H7z/bf7X+W6I3WKuZrb+tqf/ofaNe/Lw==</latexit><latexit sha1_base64="Elg1HWgHtfhfeeVxJ1P1LiotMhE=">AAAJ4HicjZZRb9s2EMfldl3jtF7T7mnoi1CjQDt4huWk6YC9dM2KbUCHpUWSFjBdg6JohzApCSSVzmD4vpdh2Gu/2T7HvsBOsh3LlBRUhm3y7nfHP8kTpTDlTOnB4N/WjZtf3Pry9k57987dzlf39u4/OFNJJgk9JQlP5PsQK8pZTE8105y+TyXFIuT0XTg/yv3vLqhULIlP9CKlY4FnMZsygjWYJnt/oSjkGd19YpYNJLA+J5ibV3YiLKIfDJpKTIy2RgAiaeTH1l5Rr6FNokSrmvDgs8KffjAbx2SvO+gPisuvNoJVo+utruPJ/Z0fUJSQTNBYE46VGgWDVI8NlpoRTm0HZYqmmMzxjI6gGWNB1dgU62b9x2CJ/Gki4Rtrv7CWIwwWSi1ECGSuWLm+3Fjrk/RiK+5x2ZnMM4GJTGojQ1FnHmV6+v3YsDjNNI3JUvk0475O/HxX/YhJSjRfQANSM5i8T84xrLyGve90kKQx/UgSIXAcwXJbU2yBFCaysEZlH934aO7bjmTWMCdAshh2F8EviphKOV5wJphWldi369RJapCmf2gDFovipIH/Vbg8WLb4Mq2lS4OlkT6p0CfX0D9elKXn/2EIFd7In2FZ5c+a+TnVdhSMzaXpwk0jcTwrSreMhBIXCOKFNwcvq4iyo+HYGDsx3aFF5wrKh35rvhv0hwJu5uZQELCM3h8XnZyBHPvVHIDluatDk2ISwyuF3eCyO6yfy09Uu6ufmxqX5y1V1cpR1hWRXrjUcXNOKqcunZuu40lNALk2gtVEsOYIxeLKGIWtMeKoMsLRNflx5NJgKdG7HRTRKTxIioPQ5IeyNXIWWjPoHx704Bze7w2sA+Wn/prqwad/6BIzSWm8QfoH1SRJXieQhojFfAk9H/YC+AsOnTksRaGSQhdYCkJleS6yUoS2BLrQWhPa1uiefiU5NWo+Z6QtwXV64ZENjzd8xaz7DkYWeDNU0XGABeU8+XiFrLoOtD3tUf7AjMbm99rJC3yezHC8cOnf1nb3Ds1kyiu5j5fWysrhSt6fc1tl9eDoKS1f3nPLi3KqN9XVf9YrKtV24HUjcF8uqo2zYT+ASnxz0H3xcvXiseM99B55T7zAe+698H7xjr1Tj3j/tb5pPWp122H7z/bf7X+W6I3WKuZrb+tqf/ofaNe/Lw==</latexit>

(E'etn P'LP')n

<latexit sha1_base64="yJ/1cLpVcb22n0W3P+Nop/FLns0=">AAAJ63icjZZdj+M0FIbT5Ws6UJiFS24qykoL6lZNZ5hF4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8a/gBiFu+VH8GcRx+jGpk1ZkNK19/LzHr51TJ1HGmdL9/j+NB2+8+dbb75w0T999r/X+B2cPP7xVaS4JvSEpT+XLCCvKWUJvNNOcvswkxSLi9EW0uHLjL5ZUKpYm13qV0bHAs4RNGcEaQpOzP1Ac8ZyePjYonklKEySwnhPMzXd2gpZYZnNmEX1l0FRiYrQ1AEoatxNrK5LhTmIgNqOJxiiF2Z05s6N+stbWSKz97FUp+eSs0+/1i6tdbYSbRifYXMPJw5OvUJySXMC0hGOlRmE/02ODpWaEU9tCuaIZJgswNoJmggVVY1NsoW0/gkjcnqYS/hPdLqJlhcFCqZWIgHTWlT/mgrVjki73dI/Kg+kiF5jItFYZibrwKNfTL8eGJVmuaULWzqc5b+u07W5wO2aSEs1X0IDUDBbfJnMMN09DGbRaSNKEviapEDiJYbvt+sZIYWILe1Qeo/dj1I3tK5k1zBNIlkCBIPhEMVMZxyvOBNOqon2+TZ1mBmn6mzYQsShJD/A/Cp+HyB5fprX0aYgcpK8r9PUR+utl2br7jiL4qRzkb7Gs8reH+QXVdhSOzZ3phBZJnMyK0i0jkcQFgngx6sC7KqLsaDA2xk5MZ2DRXEH50M/Nk35vIIQ9IgUDa/X5uOg4BnKcV3MA5nJXpybFIgY7h53wrjOoX8u3VPu770IHt+c5VdXKUdY3kS19ang4J5VTn3ahYzypEZCjClajYIcViiWVOYrYQcVVZYarI/lx7NMQKdGnLRTTKRzbxUFo3KFsjZxF1vR7lxddOIfPu33rQe5BsqW68Ne79InicXGP9C6qSVJXJ5CGiNViDT0ddEP4Ci+9NaxNoZJDH1gbQmV7PrJxhPYM+tDWE9r36J9+JTs1bv7PTHuG6/xunqo7Ztv3MLLC91MVHQ9YUc7T1ztk0/Wg/WWP3AMzHptfahcv8Dyd4WTl0z9v4/4vNJcZr+QerqOVncOVvN+7WGX34OgpbZ/r+eVFOdX31dX7oltUqm3B60bov1xUG7eDXgiV+OtF59k3mxePk+Dj4JPgcRAGT4NnwQ/BMLgJSPBv49PGk0avKZq/N/9s/rVGHzQ2mo+Cvav5939JFsST</latexit><latexit sha1_base64="yJ/1cLpVcb22n0W3P+Nop/FLns0=">AAAJ63icjZZdj+M0FIbT5Ws6UJiFS24qykoL6lZNZ5hF4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8a/gBiFu+VH8GcRx+jGpk1ZkNK19/LzHr51TJ1HGmdL9/j+NB2+8+dbb75w0T999r/X+B2cPP7xVaS4JvSEpT+XLCCvKWUJvNNOcvswkxSLi9EW0uHLjL5ZUKpYm13qV0bHAs4RNGcEaQpOzP1Ac8ZyePjYonklKEySwnhPMzXd2gpZYZnNmEX1l0FRiYrQ1AEoatxNrK5LhTmIgNqOJxiiF2Z05s6N+stbWSKz97FUp+eSs0+/1i6tdbYSbRifYXMPJw5OvUJySXMC0hGOlRmE/02ODpWaEU9tCuaIZJgswNoJmggVVY1NsoW0/gkjcnqYS/hPdLqJlhcFCqZWIgHTWlT/mgrVjki73dI/Kg+kiF5jItFYZibrwKNfTL8eGJVmuaULWzqc5b+u07W5wO2aSEs1X0IDUDBbfJnMMN09DGbRaSNKEviapEDiJYbvt+sZIYWILe1Qeo/dj1I3tK5k1zBNIlkCBIPhEMVMZxyvOBNOqon2+TZ1mBmn6mzYQsShJD/A/Cp+HyB5fprX0aYgcpK8r9PUR+utl2br7jiL4qRzkb7Gs8reH+QXVdhSOzZ3phBZJnMyK0i0jkcQFgngx6sC7KqLsaDA2xk5MZ2DRXEH50M/Nk35vIIQ9IgUDa/X5uOg4BnKcV3MA5nJXpybFIgY7h53wrjOoX8u3VPu770IHt+c5VdXKUdY3kS19ang4J5VTn3ahYzypEZCjClajYIcViiWVOYrYQcVVZYarI/lx7NMQKdGnLRTTKRzbxUFo3KFsjZxF1vR7lxddOIfPu33rQe5BsqW68Ne79InicXGP9C6qSVJXJ5CGiNViDT0ddEP4Ci+9NaxNoZJDH1gbQmV7PrJxhPYM+tDWE9r36J9+JTs1bv7PTHuG6/xunqo7Ztv3MLLC91MVHQ9YUc7T1ztk0/Wg/WWP3AMzHptfahcv8Dyd4WTl0z9v4/4vNJcZr+QerqOVncOVvN+7WGX34OgpbZ/r+eVFOdX31dX7oltUqm3B60bov1xUG7eDXgiV+OtF59k3mxePk+Dj4JPgcRAGT4NnwQ/BMLgJSPBv49PGk0avKZq/N/9s/rVGHzQ2mo+Cvav5939JFsST</latexit><latexit sha1_base64="yJ/1cLpVcb22n0W3P+Nop/FLns0=">AAAJ63icjZZdj+M0FIbT5Ws6UJiFS24qykoL6lZNZ5hF4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8a/gBiFu+VH8GcRx+jGpk1ZkNK19/LzHr51TJ1HGmdL9/j+NB2+8+dbb75w0T999r/X+B2cPP7xVaS4JvSEpT+XLCCvKWUJvNNOcvswkxSLi9EW0uHLjL5ZUKpYm13qV0bHAs4RNGcEaQpOzP1Ac8ZyePjYonklKEySwnhPMzXd2gpZYZnNmEX1l0FRiYrQ1AEoatxNrK5LhTmIgNqOJxiiF2Z05s6N+stbWSKz97FUp+eSs0+/1i6tdbYSbRifYXMPJw5OvUJySXMC0hGOlRmE/02ODpWaEU9tCuaIZJgswNoJmggVVY1NsoW0/gkjcnqYS/hPdLqJlhcFCqZWIgHTWlT/mgrVjki73dI/Kg+kiF5jItFYZibrwKNfTL8eGJVmuaULWzqc5b+u07W5wO2aSEs1X0IDUDBbfJnMMN09DGbRaSNKEviapEDiJYbvt+sZIYWILe1Qeo/dj1I3tK5k1zBNIlkCBIPhEMVMZxyvOBNOqon2+TZ1mBmn6mzYQsShJD/A/Cp+HyB5fprX0aYgcpK8r9PUR+utl2br7jiL4qRzkb7Gs8reH+QXVdhSOzZ3phBZJnMyK0i0jkcQFgngx6sC7KqLsaDA2xk5MZ2DRXEH50M/Nk35vIIQ9IgUDa/X5uOg4BnKcV3MA5nJXpybFIgY7h53wrjOoX8u3VPu770IHt+c5VdXKUdY3kS19ang4J5VTn3ahYzypEZCjClajYIcViiWVOYrYQcVVZYarI/lx7NMQKdGnLRTTKRzbxUFo3KFsjZxF1vR7lxddOIfPu33rQe5BsqW68Ne79InicXGP9C6qSVJXJ5CGiNViDT0ddEP4Ci+9NaxNoZJDH1gbQmV7PrJxhPYM+tDWE9r36J9+JTs1bv7PTHuG6/xunqo7Ztv3MLLC91MVHQ9YUc7T1ztk0/Wg/WWP3AMzHptfahcv8Dyd4WTl0z9v4/4vNJcZr+QerqOVncOVvN+7WGX34OgpbZ/r+eVFOdX31dX7oltUqm3B60bov1xUG7eDXgiV+OtF59k3mxePk+Dj4JPgcRAGT4NnwQ/BMLgJSPBv49PGk0avKZq/N/9s/rVGHzQ2mo+Cvav5939JFsST</latexit><latexit sha1_base64="yJ/1cLpVcb22n0W3P+Nop/FLns0=">AAAJ63icjZZdj+M0FIbT5Ws6UJiFS24qykoL6lZNZ5hF4mZhQIAEoqxmZlequ5XjuK1VO4lsp0vl8a/gBiFu+VH8GcRx+jGpk1ZkNK19/LzHr51TJ1HGmdL9/j+NB2+8+dbb75w0T999r/X+B2cPP7xVaS4JvSEpT+XLCCvKWUJvNNOcvswkxSLi9EW0uHLjL5ZUKpYm13qV0bHAs4RNGcEaQpOzP1Ac8ZyePjYonklKEySwnhPMzXd2gpZYZnNmEX1l0FRiYrQ1AEoatxNrK5LhTmIgNqOJxiiF2Z05s6N+stbWSKz97FUp+eSs0+/1i6tdbYSbRifYXMPJw5OvUJySXMC0hGOlRmE/02ODpWaEU9tCuaIZJgswNoJmggVVY1NsoW0/gkjcnqYS/hPdLqJlhcFCqZWIgHTWlT/mgrVjki73dI/Kg+kiF5jItFYZibrwKNfTL8eGJVmuaULWzqc5b+u07W5wO2aSEs1X0IDUDBbfJnMMN09DGbRaSNKEviapEDiJYbvt+sZIYWILe1Qeo/dj1I3tK5k1zBNIlkCBIPhEMVMZxyvOBNOqon2+TZ1mBmn6mzYQsShJD/A/Cp+HyB5fprX0aYgcpK8r9PUR+utl2br7jiL4qRzkb7Gs8reH+QXVdhSOzZ3phBZJnMyK0i0jkcQFgngx6sC7KqLsaDA2xk5MZ2DRXEH50M/Nk35vIIQ9IgUDa/X5uOg4BnKcV3MA5nJXpybFIgY7h53wrjOoX8u3VPu770IHt+c5VdXKUdY3kS19ang4J5VTn3ahYzypEZCjClajYIcViiWVOYrYQcVVZYarI/lx7NMQKdGnLRTTKRzbxUFo3KFsjZxF1vR7lxddOIfPu33rQe5BsqW68Ne79InicXGP9C6qSVJXJ5CGiNViDT0ddEP4Ci+9NaxNoZJDH1gbQmV7PrJxhPYM+tDWE9r36J9+JTs1bv7PTHuG6/xunqo7Ztv3MLLC91MVHQ9YUc7T1ztk0/Wg/WWP3AMzHptfahcv8Dyd4WTl0z9v4/4vNJcZr+QerqOVncOVvN+7WGX34OgpbZ/r+eVFOdX31dX7oltUqm3B60bov1xUG7eDXgiV+OtF59k3mxePk+Dj4JPgcRAGT4NnwQ/BMLgJSPBv49PGk0avKZq/N/9s/rVGHzQ2mo+Cvav5939JFsST</latexit>

eAetn L eA+ t

n L<latexit sha1_base64="m5oD/ViI7UwgPqn4qJaC3TE5WfQ=">AAAJxXicjZZRb9s2EMeVdlvjbN7S7XEvwowCw+YZlpOlBfaSIi26AR2WFUlawPQCiqJtwiQlkJQ7gyH6NbsvM+wk27FMycZk2CLvfnf880hTijPOtOn3/zl48PCTTz97dNg6+vyL9pdfHT/++kanuSL0mqQ8Ve9irClnkl4bZjh9lymKRczp23h2UfjfzqnSLJVXZpHRkcATycaMYAOm22OFkpjn9AjRv6xF4KTS4PC5c6UFjRUm1jhwJYomoXTuNXg0E7WAHxvYjR8ZxhNqXztIfHvc6ff65RXWG9Gq0QlW1+Xt48NfUJKSXEAqwrHWw6ifmZHFyjDCqWujXNMMkxkMNoSmxILqkS2L48InYEnCcargK01YWqsRFgutFyIGUmAz1b6vMDb6FJ1vxT2pOtNZLjBRaWNkLJrMw9yMn40sk1luqCRL5eOchyYNi6ULE6YoMXwBDUjNYPIhmWKouoEFbreRopK+J6kQWCawCGX5zVQJmzioUdVHNz5a+LYjmbPMC1BMwsoi+EUJ0xnHC84EM7oW+2adOs0sMvRvY8HikEx38L8JnwfLFl+ljfJpsOykr2r01R76+bwqvbjHsX25m7/Bqs7f7OZn1LhhNLJ3thM5pLCclFu3isQKlwjipbcA7+qIdsPByFp3azsDh6Yatg/9wf7U7w2EcHtCQcAy+mRUdgoGcpzUcwBW5K4PTcpJDO4VdqK7zqB5Li+o8atfmHaW5w3V9Z2jnS8im/vU5e6cVI19ujDt40lDANkbwRoi2O4IzWRtjNK2M+KiNsLFnvw48WmwVOijNkroGJ4W5UFoi6PaWTWJne33zk67cA6fdPvOg4pHxJrqwqd35hMTRancIL3TepK02CeQhojFbAk9HXQjuEVn3hyWolBFoQ8sBaGqPB9ZKUJbAn1orQlta/RPv4qcBjX/Z6QtwU16V0/Ke2bd9zCywJuhyo4HLCjn6ft7ZNX1oO1pD4sHZjKyfzROXuBpOsFy4dO/r+3+PzRXGa/lvlxaa5XDtbyvClutenD0VMpX9PztRTk1m93V+7lb7lTXhteNyH+5qDduBr3opDf487Rzfr568TgMvg2+C74PouBpcB78GlwG1wEJPgb/Hjw6OGy9aomWac2X6IODVcw3wdbV+vAfc1yyMw==</latexit>

Enn (PEnP )n

<latexit sha1_base64="olZfcHzZDUlX+nNKsDm8SR5XQhA=">AAAJaHicjZZBb9s2FMeVtlvjdl7T9VAUvQgxAnSDa1hOlu6YIg22Hop6RZIWMF2DomiHMEkJJJXOYPjJ+kl67LX9CLuMlJ1EouRgMmyRj7/3+Ocj/aQ4o0Sqfv/Lxq3bd3748e5m6979n9o/P9h6+MupTHOB8AlKaSo+xFBiSjg+UURR/CETGLKY4vfx/NCNvz/HQpKUH6tFhscMzjiZEgSVNU22TkAS0xzfO5poDRKBk5Ab87HUBpKwZ7Y7ExjzcGgqYMn+a9lpstXp9/rFFdYb0arRCVbXcPLw7r8gSVHOMFeIQilHUT9TYw2FIohi0wa5xBlEczjDI9vkkGE51sX6TbhjLUk4TYX9chUW1rKHhkzKBYstyaA6k/6YMzaOCXxe8dspD6bznEEk0kbPmDWZR7ma/jHWhGe5whwtlU9zGqo0dLsTJkRgpOjCNmxoYhcfojMoIFJ2D9ttIDDHn1DKGOSJTbfRiU1N2YSNdtmqcsRo4nGCcGW3z/6ChMiMwgUljChZ831nIwK3kDTTQOF/lLYWA3i6hn/NfN5aKnyZVsKnrWUtfVyjj2+gX56Xpbt7HOuj9fwpFHX+dD0/x8qMorG+0J3IAAH5rDioZSQWsEAALUYdeFFHpBkNxlqbie4MDDiT9rDg3/Tzfm/AmLnB1QpYeu+Oi45jbIzdegyLudj1qVGxiMGVwk500Rk0r+UVVn72nWltet5hWT850vgisnOfGq6PicXUp53pJh41OKAbPUiDB1nvIQmvzVHY1noc1mY4rMZvgwRPbUEvCpl2RdVoMYuN7vf297q2ju52+8aDXBW/pLr209v3iaJSXyO9vXqQ1O28DYPYYr6EXgy6kb1F+94alqJASaEPLAWBsjwfWSkCFYE+dKkJVDX69awkp0HN/5mpIrhJr3102scTvGIu+x6GFvB6qqLjAQtMafrpCll1Pai67JF74CVj/bZx8QyepTPIFz795tLu/+dykdFa7OHSWsscrMX909lq2bPFpJQ+1/OPF6ZYXZ+u3u/d4qSatn1diPyXg3rjdNCLdnuDv/c6BwerF4fN4GmwHTwLouBFcBD8FQyDkwAFn4Ovwbfg++a31lbrcevJEr21sfJ5FFSu1vZ/DXyNkw==</latexit>

Figure 2: Sketch of the proof steps.

Remark 2. Let us consider a unitary evolution, L = −i[H, q ] with H = H†. For Pj =Pj q Pj , with P1, . . . , Pm being Hermitian projections, Eq. (4.5) particularizes to(

Pme−i tmn

H · · ·P1e−i tmn

H)n

= Pϕe−itPϕHPϕ +O(1/n) as n→ +∞, (4.9)

where Pϕ = P1∧P2∧· · ·∧Pm is the Hermitian projection onto the intersection of the rangesof P1, . . . , Pm, and one gets a QZD by cycles of (nonorthogonal) selective measurements.More generally, if

Pj =nj∑k=1

P(j)k

q P (j)k , (4.10)

where P (j)1 , . . . , P

(j)nj j=1,...,m are sets of Hermitian projections with P

(j)k P

(j)` = δk`P

(j)k ,

then one gets a QZD by cycles of (nonorthogonal) partially selective measurements. Aparticular case is when

∑njk=1 P

(j)k = I for all j = 1, . . . ,m, and one has a cycle of nons-

elective (i.e. CPTP) measurements. There exist more general CP Hermitian projections,that cannot be cast in the form (4.10). For instance, P = I

d tr( q ) is a CPTP Hermi-tian projection for a d-dimensional system. Corollary 2 works for general CP Hermitianprojections including such a projection.

The proof of Theorem 1 consists of several steps as outlined in Fig. 2. Before we provethe theorem, we provide the key lemmas in the next section.

5 Key LemmasThe key idea is to bridge from the pulsed strategies to the continuous strategies via theBCH formula [10], and then prove the Zeno limit by the generalized adiabatic theorem,which was proved and used to unify the continuous strategies in Ref. [11] (Theorems 1 and 2therein). In this way, the pulsed strategies are unified with the continuous strategies. Thekey lemma for the bridge is the following generalized BCH formula:

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 9

Lemma 1 (Pulsed vs continuous for invertible kicks). Let E and L be linear operatorson a finite-dimensional Banach space, with E invertible. Let A = logE be a primarylogarithm of E so that eA = E. Then, we have(

EetnL)n

= enA+tL+O(1/n) as n→ +∞, (5.1)

uniformly in t on compact intervals of R, with

L = g(adA)(L), (5.2)

where g is the meromorphic function on C defined by

g(z) =

z

1− e−z (z /∈ 2πiZ),

1 (z = 0),(5.3)

and adA = [A, q ].

Proof. We will prove it in Sec. 6.

Remark 3. The assumption that A be a primary logarithm of E [47, 48] is necessary toget Eq. (5.1), as the following example shows. Take E = I and L = X, the identity andthe first Pauli matrix on C2, respectively. Then, we have(

EetnL)n

=(Ie

tnX)n

= etX . (5.4)

On the other hand, consider A = 2πiZ, where Z is the third Pauli matrix. Then, eA =e2πiZ = I = E, but A is not a primary logarithm of E. It is apparent that there exists nomatrix L such that

etX = e2nπiZ+tL +O(1/n), (5.5)

since e2nπiZ+tL = etLZ +O(1/n) as a strong-coupling limit [11], with LZ a diagonal matrix.Thus, Eq. (5.1) does not hold for A = 2πiZ.

We can apply this lemma to physical situations where E are invertible quantum opera-tions and L are GKLS generators. This lemma is however useful only for invertible E, andcannot accommodate e.g. the standard QZD via projective measurements. To circumventthis problem, we consider instead the primary logarithm of E + Q, with Q a projectiononto the kernel of E, and by projecting L on a complementary space:

Lemma 2 (Pulsed vs continuous for noninvertible kicks). Let E and L be linear operatorson a finite-dimensional Banach space. Let Q be a projection onto kerE and set P = 1−Q.Let A = log(E + Q) be a primary logarithm of the invertible operator E + Q, so thateA = E +Q. Then, we have(

EetnPLP

)n= enA+tL+O(1/n)P as n→ +∞, (5.6)

uniformly in t on compact intervals of R, with

L = Pg(adA)(L)P, (5.7)

where g is the meromorphic function on C defined in Eq. (5.3).

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 10

Proof. Notice first that, even when E is not invertible, F = E + Q is invertible, and wecan consider one of its primary logarithms, say A = logF . Then, we can apply Lemma 1as (

EetnPLP

)n=(F e

tnPLP

)nP =

(eAe

tnPLP

)nP = enA+tg(adA)(PLP )+O(1/n)P (5.8)

for large n. Since [P, F ] = 0 and A = logF is primary, it implies [P,A] = 0, and we have

g(adA)(PLP ) = Pg(adA)(L)P = L. (5.9)

The statement of the lemma thus holds.

Remark 4. If E is invertible, i.e. kerE = 0, then Q = 0 and P = 1, and Lemma 2 isreduced to Lemma 1.Remark 5. If L in the exponent on the left-hand side of Eq. (5.6) is not projected by Pas PLP , we are not allowed to promote E to E +Q to define A = log(E +Q), since e

tnL

is in general not commutative with P .The second ingredient to bridge a pulsed dynamics to a continuous one is the following

approximation lemma:

Lemma 3 (Asymptotic projection of a sequence of operators). Let (En) be a sequenceof linear operators on a finite-dimensional Banach space and P (= P 2) be a projection.Assume that the following conditions hold:

1. The operators En asymptotically commute with P as

PEn = EnP +O(1/n) as n→ +∞. (5.10)

2. There exist M ≥ 0 and n0 > 0 such that, for all n ≥ n0,

‖(PEnP )k‖ ≤M, ∀k ∈ N. (5.11)

3. There exist K ≥ 0, µ ∈ [0, 1), and n0 > 0 such that, for all n ≥ n0,

‖(En − PEnP )k‖ ≤ Kµk, ∀k ∈ N. (5.12)

Then, we haveEnn = (PEnP )n +O(1/n) as n→ +∞. (5.13)

Proof. The proof is given in Appendix C.

Remark 6. For a sequence of quantum operations (En) converging to a quantum operationE as En = E +O(1/n) as n → +∞, all the conditions 1–3 of Lemma 3 are automaticallyfulfilled with the peripheral projection Pϕ of E taken as P . See Lemmas 4 and 5 inAppendix A, which guarantee conditions 2 and 3 for the sequence of quantum operations(En). Then, according to Lemma 3, we have

Enn = (PϕEnPϕ)n +O(1/n) as n→ +∞. (5.14)

We will use these lemmas to prove Theorem 1.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 11

<latexit sha1_base64="W9ZCNYIwsNMnTEapDoJ41xA0IvM=">AAAJ7XicjZZPj9M4FMADC+x0lvJnOXKptkJarUqVdAoDN8QgsXtAmkUzA1JdjRznteOt7US2M1B58h24cGC12ut+nj3ybXDStE2ctiJVW+e933t+f2wnYcKo0r7/9dr1H27cvPXjXmv/p9vtO3fv3f/5TMWpJHBKYhbL9yFWwKiAU001g/eJBMxDBu/C2VGuf3cJUtFYnOh5AmOOp4JOKMHais7Qa8w5Pr/X9ft+cXWag6AcdL3yOj6/v/c/imKSchCaMKzUKPATPTZYakoYZG2UKkgwmeEpjOxQYA5qbIpws84jK4k6k1jar9CdQlq1MJgrNeehJTnWF8rV5cKNOgmXNbtHVWU8SzkmMt5oGfJN4lGqJ8/Ghook1SDIIvJJyjo67uTF7ERUAtFsbgfWNbXJd8gFlphoW/J2G0kQ8IHEtsQiMijKDMrnkNxEma1RVSc5rLXQ1NK1lja0VGirtr8ooipheM4op1plbgBvl3PEiUEaPmpjJRkS8Rb+D+7yVlLjq7SWLm0lW+mTBn2yg56BzkbB2FyZbpAhicW0WGVVJJS4QBArtDl41URUNhqMjcnOTXeQoQtlOw2/mcd+f8B5tsPUBrCwPhgXNzljfRw0fVgs992cmhRJDFYRdoOr7mBzLq9Au9XJRVvL8xZUs7Mqc4NILl3qeLtPkBOXzkW7eLLBgOy0oBss6HYLRUVjjkK21eKoMcPRDv84cmkrqdD79SVcgcu9eVKj2yiCiT2YixPORBKsezkNM+P3nw579oA96PmZA4UshSXVs5/+U5eYSgCxRvrDppM4X1XWDeHz2QI6HPQC+xc0vNnngT3E8SqwZ8PDnBs+zz0/952UFzmgSkJOBcv4UTUbFykTQLV8XGiZAqqn5GKr8JGTjxN4Ne4NYX9PSLXMNiXmxrIKpY6ROV5PVdw4wBwYiz+skPLWadyyPmXbinY96bn9cqq4LOJ+zZXAl/OVo4PFirLLru5pAaGKhQNwfBFPsVhBo/yhH43Nm6XcPYxSmTBw6eOFtNEe3PD7Opc1WmRP2UqP8jt3wQMDvd4a/Se9YptlbfsSFLivPM3B2aAf2O3x57D74mX5OrTnPfR+8X71Au/Qe+H97h17px7x/vI+eV+8v1tx63Prn9a/C/T6tdLmgVe7Wv99A1suv/w=</latexit><latexit sha1_base64="W9ZCNYIwsNMnTEapDoJ41xA0IvM=">AAAJ7XicjZZPj9M4FMADC+x0lvJnOXKptkJarUqVdAoDN8QgsXtAmkUzA1JdjRznteOt7US2M1B58h24cGC12ut+nj3ybXDStE2ctiJVW+e933t+f2wnYcKo0r7/9dr1H27cvPXjXmv/p9vtO3fv3f/5TMWpJHBKYhbL9yFWwKiAU001g/eJBMxDBu/C2VGuf3cJUtFYnOh5AmOOp4JOKMHais7Qa8w5Pr/X9ft+cXWag6AcdL3yOj6/v/c/imKSchCaMKzUKPATPTZYakoYZG2UKkgwmeEpjOxQYA5qbIpws84jK4k6k1jar9CdQlq1MJgrNeehJTnWF8rV5cKNOgmXNbtHVWU8SzkmMt5oGfJN4lGqJ8/Ghook1SDIIvJJyjo67uTF7ERUAtFsbgfWNbXJd8gFlphoW/J2G0kQ8IHEtsQiMijKDMrnkNxEma1RVSc5rLXQ1NK1lja0VGirtr8ooipheM4op1plbgBvl3PEiUEaPmpjJRkS8Rb+D+7yVlLjq7SWLm0lW+mTBn2yg56BzkbB2FyZbpAhicW0WGVVJJS4QBArtDl41URUNhqMjcnOTXeQoQtlOw2/mcd+f8B5tsPUBrCwPhgXNzljfRw0fVgs992cmhRJDFYRdoOr7mBzLq9Au9XJRVvL8xZUs7Mqc4NILl3qeLtPkBOXzkW7eLLBgOy0oBss6HYLRUVjjkK21eKoMcPRDv84cmkrqdD79SVcgcu9eVKj2yiCiT2YixPORBKsezkNM+P3nw579oA96PmZA4UshSXVs5/+U5eYSgCxRvrDppM4X1XWDeHz2QI6HPQC+xc0vNnngT3E8SqwZ8PDnBs+zz0/952UFzmgSkJOBcv4UTUbFykTQLV8XGiZAqqn5GKr8JGTjxN4Ne4NYX9PSLXMNiXmxrIKpY6ROV5PVdw4wBwYiz+skPLWadyyPmXbinY96bn9cqq4LOJ+zZXAl/OVo4PFirLLru5pAaGKhQNwfBFPsVhBo/yhH43Nm6XcPYxSmTBw6eOFtNEe3PD7Opc1WmRP2UqP8jt3wQMDvd4a/Se9YptlbfsSFLivPM3B2aAf2O3x57D74mX5OrTnPfR+8X71Au/Qe+H97h17px7x/vI+eV+8v1tx63Prn9a/C/T6tdLmgVe7Wv99A1suv/w=</latexit><latexit sha1_base64="W9ZCNYIwsNMnTEapDoJ41xA0IvM=">AAAJ7XicjZZPj9M4FMADC+x0lvJnOXKptkJarUqVdAoDN8QgsXtAmkUzA1JdjRznteOt7US2M1B58h24cGC12ut+nj3ybXDStE2ctiJVW+e933t+f2wnYcKo0r7/9dr1H27cvPXjXmv/p9vtO3fv3f/5TMWpJHBKYhbL9yFWwKiAU001g/eJBMxDBu/C2VGuf3cJUtFYnOh5AmOOp4JOKMHais7Qa8w5Pr/X9ft+cXWag6AcdL3yOj6/v/c/imKSchCaMKzUKPATPTZYakoYZG2UKkgwmeEpjOxQYA5qbIpws84jK4k6k1jar9CdQlq1MJgrNeehJTnWF8rV5cKNOgmXNbtHVWU8SzkmMt5oGfJN4lGqJ8/Ghook1SDIIvJJyjo67uTF7ERUAtFsbgfWNbXJd8gFlphoW/J2G0kQ8IHEtsQiMijKDMrnkNxEma1RVSc5rLXQ1NK1lja0VGirtr8ooipheM4op1plbgBvl3PEiUEaPmpjJRkS8Rb+D+7yVlLjq7SWLm0lW+mTBn2yg56BzkbB2FyZbpAhicW0WGVVJJS4QBArtDl41URUNhqMjcnOTXeQoQtlOw2/mcd+f8B5tsPUBrCwPhgXNzljfRw0fVgs992cmhRJDFYRdoOr7mBzLq9Au9XJRVvL8xZUs7Mqc4NILl3qeLtPkBOXzkW7eLLBgOy0oBss6HYLRUVjjkK21eKoMcPRDv84cmkrqdD79SVcgcu9eVKj2yiCiT2YixPORBKsezkNM+P3nw579oA96PmZA4UshSXVs5/+U5eYSgCxRvrDppM4X1XWDeHz2QI6HPQC+xc0vNnngT3E8SqwZ8PDnBs+zz0/952UFzmgSkJOBcv4UTUbFykTQLV8XGiZAqqn5GKr8JGTjxN4Ne4NYX9PSLXMNiXmxrIKpY6ROV5PVdw4wBwYiz+skPLWadyyPmXbinY96bn9cqq4LOJ+zZXAl/OVo4PFirLLru5pAaGKhQNwfBFPsVhBo/yhH43Nm6XcPYxSmTBw6eOFtNEe3PD7Opc1WmRP2UqP8jt3wQMDvd4a/Se9YptlbfsSFLivPM3B2aAf2O3x57D74mX5OrTnPfR+8X71Au/Qe+H97h17px7x/vI+eV+8v1tx63Prn9a/C/T6tdLmgVe7Wv99A1suv/w=</latexit><latexit sha1_base64="W9ZCNYIwsNMnTEapDoJ41xA0IvM=">AAAJ7XicjZZPj9M4FMADC+x0lvJnOXKptkJarUqVdAoDN8QgsXtAmkUzA1JdjRznteOt7US2M1B58h24cGC12ut+nj3ybXDStE2ctiJVW+e933t+f2wnYcKo0r7/9dr1H27cvPXjXmv/p9vtO3fv3f/5TMWpJHBKYhbL9yFWwKiAU001g/eJBMxDBu/C2VGuf3cJUtFYnOh5AmOOp4JOKMHais7Qa8w5Pr/X9ft+cXWag6AcdL3yOj6/v/c/imKSchCaMKzUKPATPTZYakoYZG2UKkgwmeEpjOxQYA5qbIpws84jK4k6k1jar9CdQlq1MJgrNeehJTnWF8rV5cKNOgmXNbtHVWU8SzkmMt5oGfJN4lGqJ8/Ghook1SDIIvJJyjo67uTF7ERUAtFsbgfWNbXJd8gFlphoW/J2G0kQ8IHEtsQiMijKDMrnkNxEma1RVSc5rLXQ1NK1lja0VGirtr8ooipheM4op1plbgBvl3PEiUEaPmpjJRkS8Rb+D+7yVlLjq7SWLm0lW+mTBn2yg56BzkbB2FyZbpAhicW0WGVVJJS4QBArtDl41URUNhqMjcnOTXeQoQtlOw2/mcd+f8B5tsPUBrCwPhgXNzljfRw0fVgs992cmhRJDFYRdoOr7mBzLq9Au9XJRVvL8xZUs7Mqc4NILl3qeLtPkBOXzkW7eLLBgOy0oBss6HYLRUVjjkK21eKoMcPRDv84cmkrqdD79SVcgcu9eVKj2yiCiT2YixPORBKsezkNM+P3nw579oA96PmZA4UshSXVs5/+U5eYSgCxRvrDppM4X1XWDeHz2QI6HPQC+xc0vNnngT3E8SqwZ8PDnBs+zz0/952UFzmgSkJOBcv4UTUbFykTQLV8XGiZAqqn5GKr8JGTjxN4Ne4NYX9PSLXMNiXmxrIKpY6ROV5PVdw4wBwYiz+skPLWadyyPmXbinY96bn9cqq4LOJ+zZXAl/OVo4PFirLLru5pAaGKhQNwfBFPsVhBo/yhH43Nm6XcPYxSmTBw6eOFtNEe3PD7Opc1WmRP2UqP8jt3wQMDvd4a/Se9YptlbfsSFLivPM3B2aAf2O3x57D74mX5OrTnPfR+8X71Au/Qe+H97h17px7x/vI+eV+8v1tx63Prn9a/C/T6tdLmgVe7Wv99A1suv/w=</latexit>

c

Figure 3: An example of contour Γ to define a primary logarithm function of an operator E. Thecrosses represent the eigenvalues of E, the cut c does not intersect any eigenvalue, and the contour Γruns in the domain of analiticity ∆ = C \ c of a branch h(z) = log z of the logarithm function, andencloses all the eigenvalues.

6 Proof of Lemma 1Let us prove Lemma 1, which is the key to the proof of Theorem 1.

Proof of Lemma 1. First, let us recall some properties of functions of operators on a finite-dimensional Banach space (see e.g. Refs. [44], [47, Chap. 1], and [48, Sec. 6.2]). Given afunction h(z) on the complex plane, we wish to define a function h(X) of operators X.Notice that, in general, an operator function h(X) does not have a series expansion, unlessthe spectrum of X lies within the convergence radius of a power series of the function h(z).Neverthless, by making use of the resolvent (zI −X)−1 of the operator X, we can definefunctions h(X) of X for a large class of functions h.

Suppose that h(z) is holomorphic in a domain ∆ of the complex plane containing thespectrum of X, and let Γ ⊂ ∆ be a smooth curve with positive direction enclosing all theeigenvalues in its interior. Then, a primary function h(X) is defined by the Dunford-Taylorintegral

h(X) = 12πi

∮Γ

dz h(z) 1zI −X

. (6.1)

More generally, Γ may consist of several simple closed curves, such that the union of theirinteriors contains all the eigenvalues of X. Note that Eq. (6.1) does not depend on Γ aslong as the latter satisfies these conditions, that is h(z) is holomorphic in ∆ and Γ ⊂ ∆.

Now, let us start the proof of Lemma 1.

Step 1. We wish to define a logarithm of E. Since E is invertible, its spectrum σ(E)does not contain 0. Choose a half-line c = reiϕ ∈ C | r ≥ 0 such that c ∩ σ(E) = ∅, andlet h(z) = log z denote a branch of the logarithm function. Take a contour Γ enclosing allthe eigenvalues of E and contained in ∆ = C\ c. See Fig. 3. Since h(z) is analytic in ∆, itcan be taken as a stem function to define a primary logarithm function A = logE by Eq.(6.1), and eA = E is inherited from the functional properties of the function h(z). Notethat there is a neighborhood of E on which this logarithm function is well-defined [44,49].

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 12

Step 2. Given the operator A = logE, we follow the proof of the BCH formula givenin Sec. 5.5 of Ref. [10]. For n large enough, eAe

snL = Ee

snL is invertible and lies in the

neighborhood of E for all 0 ≤ s ≤ t, whence its logarithm is defined by the integral (6.1)along the same contour Γ. Let

Z(s) = log(eAesnL) (6.2)

for 0 ≤ s ≤ t. Z(s) is an analytic operator-valued function and

e−Z(s) ddseZ(s) = (eAe

snL)−1eAe

snL 1nL = 1

nL. (6.3)

On the other hand, by Theorem 5.4 of Ref. [10], we have

e−Z(s) ddseZ(s) = f(adZ(s))

(dZ(s)ds

), (6.4)

where

f(z) =∞∑n=0

(−1)n

(n+ 1)!zn =

1− e−z

z(z 6= 0),

1 (z = 0)(6.5)

is an entire analytic function, and the superoperator f(adZ(s)) is defined by Eq. (6.1)for a given curve Γ enclosing the spectrum of adZ(s) for all 0 ≤ s ≤ t. Notice thatf(adZ(0)) = f(adA), and that f(z) = 0 only at the imaginary points zk = 2πik withk ∈ Z \ 0.

Step 3. Now, we wish to invert Eq. (6.4) in order to obtain an explicit expression for thederivative dZ(s)/ds. We claim that f(adA) is invertible. That is to say that all eigenvaluesof adA are not zeros of f(z), namely that ker(adA−zk) = 0 for all k ∈ Z \ 0. Indeed,let the operator X∗ belong to ker(adA−zk) for some k ∈ Z \ 0. Then,

adA(X∗) = [A,X∗] = zkX∗. (6.6)

By exponentiating it, we get et adA(X∗) = etAX∗e−tA = etzkX∗ for all t ∈ R. In particular,at t = 1,

eAX∗e−A = ezkX∗, (6.7)

that is EX∗E−1 = X∗, whence [E,X∗] = 0. But this implies that also A = logE, as afunction of E, commutes with X∗, namely

adA(X∗) = [A,X∗] = 0, (6.8)

which, together with Eq. (6.6), implies that X∗ = 0, since zk 6= 0.Hence the superoperator f(adA) is invertible. Furthermore, this implies that the in-

verse of f(adZ(s)) does exist for all 0 ≤ s ≤ t, if n is large enough. It is given by g(adZ(s)),defined by the stem function g(z) = 1/f(z), that is the meromorphic function given inEq. (5.3).

We can then combine Eqs. (6.3) and (6.4) to obtain

dZ(s)ds = 1

ng(adZ(s))(L). (6.9)

Noting that Z(0) = A, we integrate Eq. (6.9) to get

Z(t) = log(eAetnL) = A+ 1

n

∫ t

0ds g(adZ(s))(L). (6.10)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 13

Step 4. We are only interested in terms up to O(1/n) as n → +∞. In general, bythe integral representation (6.1) for h(z) analytic on a domain ∆ and for the spectrumof X + 1

nY enclosed by Γ ⊂ ∆, where X and Y are operators of order O(1) on a finite-dimensional Banach space, we have

h

(X + 1

nY

)= 1

2πi

∮Γ

dz h(z) 1zI −X − 1

nY

= 12πi

∮Γ

dz h(z)(

1zI −X

+ 1n

1zI −X

Y1

zI −X − 1nY

)

= h(X) +O(1/n), (6.11)

for all n > n0 for some n0 > 0. Therefore, for h(z) = log z we get Z(s) = log(eAesnL) =

A +O(1/n) by choosing X = eA and Y = neA(esnL − I) = O(1), which implies adZ(s) =

adA +O(1/n). Then, expanding g(adZ(s)) in Eq. (6.10), we get

log(eAetnL) = A+ 1

n

∫ t

0ds g(adA)(L) +O(1/n2)

= A+ t

ng(adA)(L) +O(1/n2)

= A+ t

nL+O(1/n2), (6.12)

with L as in Eq. (5.2). Exponentiating it, we obtain

eAetnL = eA+ t

nL+O(1/n2), (6.13)

whence(eAe

tnL)n = enA+tL+O(1/n), (6.14)

which gives the result (5.1) for E invertible. Uniformity in t on compact intervals of Ris straightforward. We provide, in Proposition 2 in Appendix B, a concise and explicitexpression for the bound on the correction O(1/n2) in Eq. (6.12), which ensures that thecorrection in Eq. (6.14) is O(1/n) for any finite t.

Remark 7. We remark that, compared to the BCH formula, this lemma does not have toimpose the condition on E−I or L being small. The difference is that we have the freedomto choose n large, and that we have the freedom to choose an appropriate logarithm A.Remark 8. Furthermore, we note that implementing g(adA) for the stem function g(z)given in Eq. (5.3) numerically (for a matrix A) is a difficult business because 1 − e−adA

of its denominator is not invertible itself. We can define such matrix functions in generalthrough Jordan form and the derivatives of the stem function g(z). However, this bringsin the usual stability issues of the Jordan form. Instead, we can implement it via

f(adA)(X) =(

1− e−adA

adA

)(X) = e−A d

dteA+tX

∣∣∣∣t=0

, (6.15)

which is obtained by applying the formula (6.4) to Z(s) = A + sX. Notice that thederivative d

dteA+tX

∣∣∣t=0

on the right-hand side is easy to implement. For instance [47,Theorem 3.6], it is given by the top-right block of

exp(A X0 A

). (6.16)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 14

We vectorize the matrixX and eventually get the matrix elements of the supermap f(adA),which we then invert.

7 Proof of Theorem 1Now, we prove Theorem 1.

Proof of Theorem 1. The proof consists of three steps. We first use Lemma 3 to cut thenonperipheral part of the kick. Then, we apply Lemma 2 to bridge from the pulsedstrategy to the continuous strategy, which opens a way to carry out the Zeno limit by thegeneralized adiabatic theorem (Theorem 1 of Ref. [11]).

Step 1. First, we claim that as n→ +∞ one gets(Eme

tmnL · · · E1e

tmnL)n

=(Eϕe

tnPϕLPϕ+O(1/n2)

)n+O(1/n) as n→ +∞, (7.1)

where L is given in Eq. (4.2), Pϕ is the projection onto the peripheral spectrum ofE = Em · · · E1, and Eϕ and E−1

ϕ are the peripheral part of E and its peripheral inverse,respectively. Indeed, En = Eme

tmnL · · · E1e

tmnL is a quantum operation, and it approaches

E as

En = EmetmnL · · · E1e

tmnL

= E + t

mn

(EL+

m∑j=2Em · · · EjLEj−1 · · · E1

)+O(1/n2) (7.2)

as n increases. An explicit bound on ‖En − E‖, which is O(1/n), is given in Lemma 6 inAppendix A. Thus, the conditions for Lemma 3 are all satisfied (see Remark 6), and byLemma 3 we have

Enn = (PϕEnPϕ)n +O(1/n). (7.3)

An explicit bound on ‖Enn − (PϕEnPϕ)n‖, which is O(1/n), is given in Eq. (C.17), in theproof of Lemma 3 in Appendix C. Since

PϕEnPϕ = PϕEmetmnL · · · E1e

tmnLPϕ

= Pϕ[E + t

mn

(EL+

m∑j=2Em · · · EjLEj−1 · · · E1

)+O(1/n2)

]Pϕ

= Eϕ[1 + t

mnPϕ(L+ E−1

ϕ

m∑j=2Em · · · EjLEj−1 · · · E1

)Pϕ +O(1/n2)

]

= Eϕ(

1 + t

nPϕLPϕ +O(1/n2)

)= Eϕe

tnPϕLPϕ+O(1/n2), (7.4)

Eq. (7.3) implies Eq. (7.1). The correction O(1/n2) in the exponent of the last expressionin Eq. (7.4) can be bounded by using Lemma 9 in Appendix B.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 15

Step 2. By applying Lemma 2 with E = Eϕ, L = L, and P = Pϕ to the right-hand sideof Eq. (7.1), one gets for large n(

EmetmnL · · · E1e

tmnL)n

= enA+tL+O(1/n)Pϕ +O(1/n), (7.5)

where A is a primary logarithm of Eϕ + (1− Pϕ), and

L = Pϕg(adA)(L)Pϕ. (7.6)

Step 3. Now, we set n = γt and consider eγtA+tL+O(1/n)Pϕ for arbitrary γ, noting thatfor γt noninteger this in general is not a physical (quantum operation) map. Since Eϕ and1− Pϕ are both diagonalizable, A is also diagonalizable,

A =∑

|λk|=1,λk 6=1akPk + a0[P0 + (1− Pϕ)], (7.7)

with purely imaginary spectrum ak, such that eak = λk, where Pk is the spectral projectionof E belonging to the eigenvalue λk with P0 belonging to the unit eigenvalue λ0 = 1 [notethat P0 + (1−Pϕ) is the spectral projection of Eϕ + (1−Pϕ) belonging to the eigenvalueλ0 = 1 and hence the spectral projection of the primary logarithm A of Eϕ + (1 − Pϕ)belonging to the eigenvalue a0, which is an integer multiple of 2πi], so that Theorem 1 ofRef. [11] (generalized adiabatic theorem) can be applied. In the adiabatic limit, Eq. (7.5)becomes (

EmetmnL · · · E1e

tmnL)n

= enAetP(L)+O(1/n)Pϕ +O(1/n), (7.8)

where the evolution is projected by

P( q ) =∑

|λk|=1,λk 6=1Pk q Pk + [P0 + (1− Pϕ)] q [P0 + (1− Pϕ)]. (7.9)

We notice thatP(Pϕ q Pϕ) = PϕP( q )Pϕ =

∑|λk|=1

Pk q Pk. (7.10)

In addition, we have P adA = 0 and hence P g(adA) = P. Therefore,

P(L) = P(Pϕg(adA)(L)Pϕ) = PϕP(g(adA)(L))Pϕ = PϕP(L)Pϕ =∑|λk|=1

PkLPk = LZ .

(7.11)Equation (7.8) is thus nothing but Eq. (4.1) of the theorem.

Remark 9. Let us see how the correction to the QZD in Eq. (4.1) of Theorem 1 dependson t and n. As proved in Lemma 6 in Appendix A, the correction O(1/n) in Eq. (7.2) isbounded by a function of t

n‖L‖. This is inherited by the correction O(1/n) in Eq. (7.3),through Cn in the explicit bound (C.17) in the proof of Lemma 3 in Appendix C: thebound is a function of t

n‖L‖ andt2

n ‖L‖2, say, G( tn‖L‖,

t2

n ‖L‖2) (apart from a correction

which is exponentially small in n). The correction O(1/n2) in the exponent of the lastexpression in Eq. (7.4) can be bounded by using Lemma 9 in Appendix B, which gives abound as a function of t

n‖L‖ again. Collecting all these elements, the corrections O(1/n2)in the exponent and O(1/n) in the last term in Eq. (7.1) are bounded by a function oftn‖L‖ and G( tn‖L‖,

t2

n ‖L‖2), respectively.

To get Eq. (7.5) from Eq. (7.1) at Step 2, we apply the generalized BCH formula inLemma 2. It yields the correction O(1/n) in the exponent of Eq. (7.5), which can be

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 16

bounded by using Proposition 2 in Appendix B, and the bound is a function of tn‖L‖

multiplied by n. Finally, at Step 3, Theorem 1 of Ref. [11] (generalized adiabatic theorem)is applied and it induces an additional correction, which can be bounded by (M1

tn∆‖L‖+

M2t2

n ‖L‖2)F1( tn‖L‖)e

M3t‖L‖F2( tn‖L‖), with the spectral gap ∆ = mink 6=` |ak − a`|, some

positive constants Mi (i = 1, 2, 3), and monotonically increasing functions Fi(x) (i = 1, 2)which shrink to 1 as x→ 0. This plus a bound G( tn‖L‖,

t2

n ‖L‖2) from the last contribution

in Eq. (7.1), which is O(1/n) for large n, gives the bound on the overall correction to theQZD in Eq. (4.1) of Theorem 1. Certainly, this is not a sharp bound, but it suffices toestablish that the error is O(1/n) as n→ +∞, for any finite t.

8 Examples8.1 QZD by Pulsed Weak MeasurementsLet us look at an example of the Zeno limit presented in Corollary 1 for the QZD viafrequent applications of quantum operations, which is a particular case of Theorem 1.This corollary unifies and generalizes the QZDs via (i) frequent projective measurementsand via (ii) frequent unitary kicks. Here, we provide a simple but analytically tractablemodel for the QZD via frequent weak measurements.

We consider a two-level system with a Hamiltonian

H = 12ΩZ, (8.1)

where Z = |0〉〈0|−|1〉〈1|. We will also use X = |0〉〈1|+ |1〉〈0| and Y = −i(|0〉〈1|−|1〉〈0|) inthe following. During the unitary evolution e−itH with H = [H, q ], we repeatedly performweak nonselective measurement on X, whose action on the system state is described bythe CPTP map

E = (1− p)1 + pP, (8.2)

whereP = P q P +Q q Q = 1

2(1 +X q X) (8.3)

is a projection (P2 = P) with projection operators

P = I +X

2 , Q = I −X2 . (8.4)

The parameter p ranges from 0 to 1, and controls the strength of the measurement: forp = 1 the map E describes the perfect projective measurement P, while for p = 0 it doesnothing, gaining no information on X. We focus on the case p > 0 in the following. Theevolution of the system under the repeated measurements is described by (Ee−i t

nH)n, and

we are interested in how the dynamics is projected in the Zeno limit n → +∞ (QZD bythis type of weak measurement is studied in Refs. [41, 42]).

It is possible to analyze this dynamics analytically. Indeed, we can explicitly writedown the spectral representation of the map,(

Ee−i tnH)n

=∑

s,s′=±λnss′Pss′ , (8.5)

whereλ++ = 1, λ+− = 1− p, λ−± =

(1− p

2

)cos(Ωt/n)± p

2η (8.6)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 17

10 102 103 104

n

0.0

0.2

0.4

0.6

0.8

1.0

p

‖(Ee−i tnH)n − P‖

100

10−1

10−2

10−3

Figure 4: Contour plot of ‖(Ee−i tnH)n−P‖ versus the number of measurements n and the strength of

the measurement p, for the model analyzed in Sec. 8.1 [the first term in Eq. (8.11) is actually plotted].The parameter is set at Ωt = 1. The convergence to the QZD is faster with a stronger (larger p)measurement.

are the eigenvalues and

P+± = 14(1 + Z q Z ± [X(t/n) q X(t/n) + Y (t/n) q Y (t/n)]

),

P−± = 14

1− Z q Z ± 1

η

[X(t/n) q X(t/n)− Y (t/n) q Y (t/n)

− i(2p− 1

)sin(Ωt/n)[Z, q ]

] (8.7)

are the spectral projections, with

η =

√1−

(2p− 1

)2sin2(Ωt/n) (8.8)

and X(t) = X cos Ωt

2 − Y sin Ωt2 ,

Y (t) = Y cos Ωt2 +X sin Ωt

2 .

(8.9)

In the Zeno limit n→ +∞, two of the eigenvalues of the map (8.5) survive as λn++ = 1 andλn−+ = 1+O(1/n), while the others decay under the condition p > 0. Since P++ +P−+ →12(1 +X q X) = P, we get (

Ee−i tnH)n→ P as n→ +∞. (8.10)

It is in accordance with Corollary 1. Indeed, the spectrum of E in Eq. (8.2) is given by1, 1 − p, with its peripheral projection being P in Eq. (8.3). The peripheral part of Eis the projection Eϕ = P, and the unitary generator −iH with the Hamiltonian (8.1) isprojected to LZ = −iPHP = 0.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 18

In more detail, it is possible to estimate how it converges to the limit:

‖(Ee−i tnH)n − P‖ = 1

2nΩt(2p− 1

)√14(Ωt)2 + 1 +

√14(Ωt)2 +

(2p− 1

)−2+O(1/n2),

(8.11)where we have chosen the operator norm defined in Eq. (3.6) to estimate the distance. Fora large but finite n, the correction is O(1/n), as stated in Corollary 1, and the correctiondepends on the chosen evolution time t and the strength of the measurement p.

In Fig. 4, the distance ‖(Ee−i tnH)n − P‖ in Eq. (8.11) is plotted as a function of the

number of measurements n and the strength of the measurement p. The convergence tothe QZD is faster with a stronger (larger p) measurement.

8.2 QZD by CPTP Kicks with Persistent OscillationsLet us look at another example of the Zeno limit presented in Corollary 1 for the QZDvia frequent CPTP kicks. Here, we provide a model in which two mechanisms work toinduce the QZD: relaxation and persistent oscillations. This situation was intractable bypreviously developed theories.

We consider a three-level system evolving with the GKLS generator

L = −i[K, q ]− 12(L†L q + q L†L− 2L q L†) (8.12)

with

K = Ω0|0〉〈0|+ Ω1|1〉〈1|+ Ω2|2〉〈2| =

Ω0Ω1

Ω2

, (8.13)

L =√

Γ(|1〉〈1|+ |2〉〈2|

)=√

Γ

01

1

. (8.14)

During the evolution, we repeatedly kick the system by the CPTP map

E = K0 q K†0 +K1 q K†1 (8.15)

with

K0 = |0〉〈1|+ |1〉〈0|+√q |2〉〈2| =

0 11 0 √

q

, (8.16)

K1 =√

1− q |0〉〈2| =

0 0√

1− q0 0 00 0 0

. (8.17)

Namely, we look at the evolution (EetnL)n with large n. The generator L describes pure

dephasing between |0〉 and the rest. On the other hand, the CPTP map induces transitionfrom |2〉 to |0〉 with a rate 1− q (0 ≤ q < 1) and at the same time flips the system between|0〉 ↔ |1〉. We here restrict ourselves to the case q < 1. By repeatedly applying E , thesystem relaxes to the subspace spanned by |0〉, |1〉, where the system keeps on oscillatingbetween |0〉 and |1〉. In the Zeno limit n → +∞, the generator L is projected by the two

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 19

1 10 102 10310−3

10−2

10−1

1

‖(Ee

t nL)n

−En ϕ

etLZ‖

1 10 102 10310−3

10−2

10−1

1

1 10 102 10310−3

10−2

10−1

1

1 10 102 10310−3

10−2

10−1

1q = 0.0, Γt = 0.0 q = 0.3, Γt = 0.0 q = 0.6, Γt = 0.0 q = 0.9, Γt = 0.0

1 10 102 103

n

10−3

10−2

10−1

1

‖(Ee

t nL)n

−En ϕ

etLZ‖

1 10 102 103

n

10−3

10−2

10−1

1

1 10 102 103

n

10−3

10−2

10−1

1

1 10 102 103

n

10−3

10−2

10−1

1q = 0.0, Γt = 2.0 q = 0.3, Γt = 2.0 q = 0.6, Γt = 2.0 q = 0.9, Γt = 2.0

Figure 5: The convergence to the QZD via the repeated CPTP kicks in the model analyzed in Sec. 8.2.The parameters other than q and Γt are set at Ω0t = 0.0, Ω1t = 1.0, and Ω2t = 2.0. The dashedlines indicate 1/n. We have chosen the operator norm defined in Eq. (3.6) to estimate the distance.There appear to be two sequences in each panel: one is for odd n and the other for even n. The formerasymptotically decays as O(1/n), while the latter decays faster.

mechanisms: by the relaxation from |2〉 to |0〉 and by the persistent oscillations between|0〉 and |1〉. Notice that the two Kraus operators K0 and K1 do not commute and the twomechanisms act nontrivially.

Let us first see how the system evolves by the repeated applications of E . Applying Erepeatedly n times results in

En =

Kn

0q Kn

0 + 1− qn

1 + q

(q|0〉〈0|+ |1〉〈1|

)〈2| q |2〉 (n even),

Kn0

q Kn0 + 1

1 + q

((1− qn+1)|0〉〈0|+ q(1− qn−1)|1〉〈1|

)〈2| q |2〉 (n odd).

(8.18)

As n increases, it asymptotically behaves as

En ∼ Un∞Pϕ, (8.19)

with the asymptotic unitary U∞ = (X + |2〉〈2|) q (X + |2〉〈2|) and the projection

Pϕ = P q P + 12

(P − 1− q

1 + qZ

)〈2| q |2〉 (8.20)

onto the peripheral spectrum of E , where P = |0〉〈0| + |1〉〈1|, X = |0〉〈1| + |1〉〈0|, Y =−i(|0〉〈1| − |1〉〈0|), and Z = |0〉〈0| − |1〉〈1|. The peripheral spectrum of E consists of twoperipheral eigenvalues, λ0 = 1 and λ1 = −1, with the corresponding spectral projectionsgiven by

P0 = 12(P tr( q ) +X tr(X q )

),

P1 = 12

(Y tr(Y q ) + Z tr(Z q )− 1− q

1 + qZ〈2| q |2〉) . (8.21)

Then, according to Corollary 1, the generator L is projected to

LZ =∑k=0,1

PkLPk = −12Γ(|0〉〈0| q |1〉〈1|+ |1〉〈1| q |0〉〈0|) (8.22)

in the Zeno limit n→ +∞, with

Eϕ = U∞Pϕ = X q X + 12

(P + 1− q

1 + qZ

)〈2| q |2〉. (8.23)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 20

See Fig. 5, where the convergence to the QZD is numerically demonstrated for several setsof parameters.

8.3 QZD by Cycles of Multiple CPTP KicksIn the previous subsections, we have provided two examples to illustrate Corollary 1, i.e.the QZD by repeating the same quantum operation. Here, we provide an example thatallows us to display Theorem 1, i.e. the QZD by cycles of two different kicks E1 and E2.

We consider a three-level system evolving with a GKLS generator L, and being kickedalternately by E1 and E2 defined by

Ej = K(j)0

q K(j)†0 +K

(j)1

q K(j)†1 (j = 1, 2), (8.24)

with

K(1)0 = Z +√q |2〉〈2| =

1 00 −1 √

q

, (8.25)

K(2)0 = Y +√q |2〉〈2| =

0 −ii 0 √

q

, (8.26)

K(1)1 = K

(2)1 =

√1− q |0〉〈2| =

0 0√

1− q0 0 00 0 0

. (8.27)

We again use P = |0〉〈0| + |1〉〈1|, X = |0〉〈1| + |1〉〈0|, Y = −i(|0〉〈1| − |1〉〈0|), and Z =|0〉〈0| − |1〉〈1|. The kicks E1 and E2 rotate the system within the subspace spanned by|0〉, |1〉 around different axes, and at the same time induce decay from |2〉 to |0〉 with arate 1− q (0 ≤ q < 1). We here restrict ourselves to the case q < 1. The kicked evolutionis described by (E2e

t2nLE1e

t2nL)n, and we are interested in its Zeno limit n→ +∞.

For the Zeno limit stated in Theorem 1, the peripheral spectrum of E = E2E1 matters.The nth power of E reads

En =

Kn0

q Kn0 + 1− q2n

1 + q2

((1− q + q2)|0〉〈0|+ q|1〉〈1|

)〈2| q |2〉 (n even),

Kn0

q Kn0 + 1

1 + q2

([q − (1− q + q2)q2n]|0〉〈0|

+ (1− q + q2 − q2n+1)|1〉〈1|)〈2| q |2〉 (n odd),

(8.28)

whereK0 = K

(2)0 K

(1)0 = iX + q|2〉〈2|. (8.29)

As n increases, the system relaxes to the subspace |0〉, |1〉, where the system keeps onoscillating between |0〉 and |1〉, and it asymptotically behaves as

En ∼ Un∞Pϕ, (8.30)

with the asymptotic unitary U∞ = (X + |2〉〈2|) q (X + |2〉〈2|) and the projection

Pϕ = P q P + 12

(P + (1− q)2

1 + q2 Z

)〈2| q |2〉 (8.31)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 21

1 10 102 10310−3

10−2

10−1

1

‖(E 2e

t 2nLE 1e

t 2nL)n

−En ϕ

etLZ‖

1 10 102 10310−3

10−2

10−1

1

1 10 102 10310−3

10−2

10−1

1

1 10 102 10310−3

10−2

10−1

1q = 0.0, Γt = 0.0 q = 0.3, Γt = 0.0 q = 0.6, Γt = 0.0 q = 0.9, Γt = 0.0

1 10 102 103

n

10−3

10−2

10−1

1

‖(E 2e

t 2nLE 1e

t 2nL)n

−En ϕ

etLZ‖

1 10 102 103

n

10−3

10−2

10−1

1

1 10 102 103

n

10−3

10−2

10−1

1

1 10 102 103

n

10−3

10−2

10−1

1q = 0.0, Γt = 2.0 q = 0.3, Γt = 2.0 q = 0.6, Γt = 2.0 q = 0.9, Γt = 2.0

Figure 6: The convergence to the QZD by alternating the kicks E1 and E2 in the model analyzed inSec. 8.3. The evolution L to be projected is the same as the one considered in Fig. 5. The parametersother than q and Γt are set at Ω0t = 0.0, Ω1t = 1.0, and Ω2t = 2.0. The dashed lines are the plots of1/n. We have chosen the operator norm defined in Eq. (3.6) to estimate the distance. There appear tobe two sequences in each panel: one is for odd n and the other for even n. The former asymptoticallydecays as O(1/n), while the latter decays faster.

onto the peripheral spectrum of E . The peripheral spectrum of E consists of two peripheraleigenvalues, λ0 = 1 and λ1 = −1, with the corresponding spectral projections given by

P0 = 12(P tr( q ) +X tr(X q )

),

P1 = 12

(Y tr(Y q ) + Z tr(Z q ) + (1− q)2

1 + q2 Z〈2| q |2〉) . (8.32)

In this way, in this example, we have two different kicks and nontrivial peripheral eigen-values. Then, according to Theorem 1, the generator L is projected to LZ as Eq. (4.2) inthe Zeno limit n → +∞. For the GKLS generator L in Eqs. (8.12)–(8.14) considered inthe previous subsection, it reads

LZ = 12∑k=0,1

Pk(L+ E−1ϕ E2LE1)Pk = −1

2Γ(|0〉〈0| q |1〉〈1|+ |1〉〈1| q |0〉〈0|), (8.33)

where

E−1ϕ = Eϕ = EPϕ = U∞Pϕ = X q X + 1

2

(P − (1− q)2

1 + q2 Z

)〈2| q |2〉. (8.34)

See Fig. 6, where the convergence to the QZD is numerically demonstrated for several setsof parameters.

8.4 QZD by Multiple Projective MeasurementsIn Corollary 2, we presented the QZD via cycles of multiple selective projective measure-ments. It is a generalization of the standard QZD via frequent repetitions of a projectivemeasurement, and is a variant of the QZD via cycles of multiple CPTP kicks proved inTheorem 1. Here we provide simple examples for Corollary 2 and Theorem 1.

Let us consider a three-level system with a Hamiltonian H, and two different projectivemeasurements: one is characterized by a pair of Hermitian projection operators

P1 = |1〉〈1|+ |2〉〈2| =

01

1

, Q1 =

10

0

, (8.35)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 22

and the other by another pair of Hermitian projection operators

P2 = |0〉+ |1〉√2〈0|+ 〈1|√

2+ |2〉〈2| =

1/2 1/21/2 1/2

1

, Q2 =

1/2 −1/2−1/2 1/2

0

. (8.36)

If we concatenate the two selective projective measurements P1 and P2, we get

P2P1 = 12(|0〉+ |1〉

)〈1|+ |2〉〈2| =

0 1/20 1/2

1

. (8.37)

This admits three eigenvalues 1, 1/2, and 0, and its peripheral part is given by

Pϕ = |2〉〈2| =

00

1

, (8.38)

which is Hermitian (although P2P1 is not) and is the simultaneous eigenprojection of P1and P2 belonging to the unit eigenvalue 1. This demonstrates Lemma 8 used in Corollary 2.According to Corollary 2, the bang-bang sequence of the selective measurements P1 andP2 during the unitary evolution e−itH projects the dynamics to

(P2e−i t2nHP1e−i t2nH)n → Pϕe−itPϕHPϕ as n→ +∞. (8.39)

The system is confined in the one-dimensional space |2〉, and the Zeno Hamiltonian HZ =PϕHPϕ ∝ |2〉〈2| yields just a phase as time goes on. See Fig. 7(a), where this convergenceis numerically demonstrated for the Hamiltonian

H = g(|0〉〈1|+ |1〉〈0|+ |1〉〈2|+ |2〉〈1|

)=

0 g 0g 0 g0 g 0

. (8.40)

If we do not collect any outcomes of the measurements, the bang-bang sequence in Eq.(8.39) is modified to (P2e−i t2nHP1e−i t2nH)n with CPTP projections

Pj = Pj q Pj +Qj q Qj (j = 1, 2) (8.41)

representing the nonselective measurements, and H = [H, q ]. In this case, we get

P2P1 = 12P tr(P q )+|2〉〈2| q |2〉〈2|+1

2(|0〉+|1〉

)〈1| q |2〉〈2|+1

2 |2〉〈2|q |1〉 (〈0|+〈1|), (8.42)

where P = |0〉〈0|+ |1〉〈1|. The spectrum of P2P1 consists of the eigenvalues 1, 1/2, and 0,with the projection onto the peripheral spectrum given by

Pϕ = 12P tr(P q ) + |2〉〈2| q |2〉〈2|. (8.43)

According to Corollary 2 or Theorem 1, the bang-bang sequence of the nonselective mea-surements P1 and P2 during the unitary evolution e−itH projects the dynamics to

(P2e−i t2nHP1e−i t2nH)n → Pϕe−itHZ as n→ +∞, (8.44)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 23

(a) (b) (c)

1 10 102 103

n

10−3

10−2

10−1

1

‖(P2e−

it 2nHP1e

t 2nH)n

−Pϕ‖

1 10 102 10310−3

10−2

10−1

1

‖(P

2e

t 2nLP

1e

t 2nL)n

−P

ϕet

LZ‖

1 10 102 10310−3

10−2

10−1

1

‖(P

2e

t 2nLP

1e

t 2nL)n

−P

ϕet

LZ‖Γt = 0.0 Γt = 0.0

1 10 102 103

n

10−3

10−2

10−1

1

‖(P

2e

t 2nLP

1e

t 2nL)n

−P

ϕet

LZ‖

1 10 102 103

n

10−3

10−2

10−1

1

‖(P

2e

t 2nLP

1e

t 2nL)n

−P

ϕet

LZ‖Γt = 2.0 Γt = 2.0

Figure 7: The convergence to the QZD in the model analyzed in Sec. 8.4: (a) via alternating theselective measurements P1 and P2 during the unitary evolution by the Hamiltonian H in Eq. (8.40);(b) via alternating the selective measurements P1 and P2 and (c) via alternating the nonselectivemeasurements P1 and P2, during the evolution by the GKLS generator L in Eq. (8.46)–(8.47) withthe same Hamiltonian H as in (a). The parameter other than Γt is set at gt = 1.0. The dashed linesindicate 1/n. We have chosen the operator norm to estimate the distance.

whereHZ = PϕHPϕ = 0 (8.45)

for any Hamiltonian H. The Hilbert space is split into three subspaces |0〉, |1〉, and|2〉. It is essentially the same as the QZD in Eq. (8.39) by the selective measurements,concerning the subspace |2〉.

For the nonunitary evolution

L = −i[H, q ]− 12(L†L q + q L†L− 2L q L†) (8.46)

with

L =√

Γ |1〉〈2| =√

Γ

0 0 00 0 10 0 0

, (8.47)

alternating selective measurements

Pj = Pj q Pj (j = 1, 2) (8.48)

projects the dynamics as

(P2et

2nLP1et

2nL)n → PϕetLZ as n→ +∞, (8.49)

whereLZ = PϕLPϕ = −Γ|2〉〈2| q |2〉〈2|, Pϕ = Pϕ q Pϕ, (8.50)

while alternating the nonselective measurements P1 and P2 projects the dynamics as

(P2et

2nLP1et

2nL)n → PϕetLZ as n→ +∞, (8.51)

whereLZ = PϕLPϕ = −Γ

(|2〉〈2| − 1

2P)〈2| q |2〉. (8.52)

See Figs. 7(b) and (c), where the convergences to the QZD in Eqs. (8.49) and (8.51)via alternating the selective measurements P1,P2 and via alternating the nonselectivemeasurements P1, P2, respectively, are numerically verified.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 24

Figure 8: A sequence of n measurements with finite measurement times τ performed at regular timeintervals t/n+ τ .

(a) p(τ) = 1− e−τ/T (b) p(τ) = sin(πτ/2T ) (c) p(τ) = sin2(πτ/2T )

10 102 103 104

nτ/T

0

1

2

3

4

5

τ/T

‖(Ee−i tnH)n − P‖

10−1

10−2

10−3

τopt = 0

10 102 103 104

nτ/T

0.0

0.2

0.4

0.6

0.8

1.0

τ/T

‖(Ee−i tnH)n − P‖10

−2

10−3

10−4

τopt = 0.45T

10 102 103 104

nτ/T

0.0

0.2

0.4

0.6

0.8

1.0

τ/T

‖(Ee−i tnH)n − P‖

100

10−1

10−2

10−3

τopt = 0.80T

Figure 9: Contour plots of ‖(Ee−i tnH)n − P‖ versus the total measurement time nτ and the time τ

spent for each measurement, for the model given in Sec. 8.1 [the first term in Eq. (8.11) is actuallyplotted]. We choose three different functions p(τ) for the strength p of the measurement E : (a)p(τ) = 1 − e−τ/T , (b) p(τ) = sin(πτ/2T ), and (c) p(τ) = sin2(πτ/2T ), where T is a characteristictime of each measurement process. The parameter is set at Ωt = 1. The optimal measurement timeτopt which minimises the total measurement time given a certain degree of convergence is indicated bya red line for each measurement model.

8.5 Efficiency in Time by Pulsed Weak MeasurementsIn real experiments, it takes time to perform strong (projective) measurements (it takestime to project a system). While the convergence to QZD would be faster with a strongermeasurement (requiring less number of measurements; see Fig. 4), it would consume moreexperimental time. Since Theorem 1 tells us that QZD can be induced even via weakmeasurements, it could be better to proceed to the next measurement without waiting fora system being projected by a measurement, to save experimental time. It is actually thecase. Let us see the efficiency in inducing QZD in terms of experimental time.

Consider, for instance, the model analyzed in Sec. 8.1. Suppose that we spend time τfor each measurement E . The strength of the measurement p is a monotonically increasingfunction of the measurement time τ in general. We perform n measurements E at timeintervals t/n, i.e., the system evolves as (Ee−i t

nH)n. Here, we assume that the unitary

evolution of the system is turned off during the measurement process, or that the couplingto the measurement apparatus is strong enough so that the unitary evolution during themeasurement process is negligible. The total time spent for the n measurements is givenby nτ and the total experimental time is nτ + t. See Fig. 8.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 25

We consider three models for the strength of the measurement p(τ) as a function ofmeasurement time τ : (a) p(τ) = 1 − e−τ/T , (b) p(τ) = sin(πτ/2T ), and (c) p(τ) =sin2(πτ/2T ), where T is a characteristic time of each measurement process. In the firstmodel (a) projective measurement p → 1 is realized in the limit τ → +∞, while in theother models (b) and (c) the measurement becomes perfectly projective p = 1 at τ = T . InFig. 9, the distance ‖(Ee−i t

nH)n − P‖ to the QZD is shown versus the total measurement

time nτ and the time τ spent for each measurement, for the measurement models (a)–(c).We see that it is better to proceed with nonprojective measurements to save time in theseexamples.

9 ConclusionsOur unification and generalization of QZDs has revealed an adiabatic evolution as the keyingredient. It is remarkable that such a variety of limits can be reduced to adiabaticity. Weleft for future studies a discussion of the tightness of our error bounds, and how they scalewith the dimensionality of the Hilbert space. We also did not consider infinite-dimensionalsystems. Since the adiabatic theorem has itself many generalizations to infinite-dimensionalsystems and unbounded operators, this connection might pave the way to QZDs withunbounded operators, where there remain many open problems [12,14,38,50–52]. However,our proof via a generalized Baker-Campbell-Hausdorff formula does not easily generalizeto infinite dimensions, and finding a more direct bridge between kicked dynamics and theadiabatic theorem would be desirable.

AcknowledgmentsDB acknowledges support by Waseda University and partial support by the EPSRC GrantNo. EP/M01634X/1. This work was supported by the Top Global University Project fromthe Ministry of Education, Culture, Sports, Science and Technology (MEXT), Japan. KYwas supported by the Grants-in-Aid for Scientific Research (C) (No. 18K03470) and forFostering Joint International Research (B) (No. 18KK0073) both from the Japan Societyfor the Promotion of Science (JSPS), and by the Waseda University Grant for SpecialResearch Projects (No. 2018K-262). PF and SP are supported by INFN through the project‘QUANTUM’ and by MIUR via PRIN 2017 (Progetto di Ricerca di Interesse Nazionale),project QUSHIP (2017SRNBRK). PF is supported by the Italian National Group ofMathematical Physics (GNFM-INdAM). PF and SP are supported by Regione Puglia andby QuantERA ERA-NET Cofund in Quantum Technologies (GA No. 731473), projectPACE-IN.

Appendix

A Some Basic LemmasHere we prove five basic lemmas. The first one (Lemma 4) concerns a bound on themaps representing quantum operations. It gives a universal bound valid for any quan-tum operation. The second one (Lemma 5) is related to the relaxation to the peripheraleigenspace of quantum operation by its repeated applications. Such bounds are known (e.g.Refs. [45, Lemma 8.5 and Theorem 8.24], [53], and [54]), but we need a generalized versionof them for our purpose. The point is that, to apply Lemma 3, we need to bound families

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 26

of maps like (PϕEnPϕ)k and (En − PϕEnPϕ)k as in Eqs. (5.11) and (5.12) universally forany n large enough. To make the bounds in Lemma 5 more explicit for the particularsequence of quantum maps relevant to Theorem 1, we prove Lemmas 6 and 7. Finally, inLemma 8, we prove some facts on the product of Hermitian projection operators, whichare used to get Corollary 2 from Theorem 1.

Lemma 4 (Norm of quantum operation [55]). Consider the d2-dimensional Hilbert spaceT2 of operators on a d-dimensional Hilbert space H, with the Hilbert-Schmidt inner product〈X|Y 〉2 = tr(X†Y ) for X,Y ∈ T2. The operator norm of any quantum operation E : T2 →T2 is bounded by

‖E‖ ≤√d. (A.1)

Proof. Recall the definition of the operator norm of A : T2 → T2 in Eq. (3.6):

‖A‖ = sup‖X‖2=1

‖A(X)‖2, (A.2)

where ‖X‖2 = [tr(X†X)]1/2. We have ‖A†‖ = ‖A‖. Moreover, for any operator X on theHilbert space H, we have that

‖X‖∞ ≤ ‖X‖2 ≤√d ‖X‖∞, (A.3)

where ‖X‖∞ = sup‖v‖=1 ‖Xv‖ with v ∈ H.Now, we have that ‖E†(X)‖∞ ≤ ‖E†(I)‖∞‖X‖∞ by a theorem of Russo and Dye

[56, Corollary 2.9]. But the adjoint of a quantum operation E is subunital, E†(I) ≤ I.Therefore,

‖E†(X)‖2 ≤√d ‖E†(X)‖∞ ≤

√d ‖E†(I)‖∞‖X‖∞

≤√d ‖I‖∞‖X‖∞ =

√d ‖X‖∞ ≤

√d ‖X‖2, (A.4)

whence‖E‖ = ‖E†‖ ≤

√d. (A.5)

We note that a more natural choice of norm for CP maps would be the trace norm,in which they are contractive. However, to prove the next Lemma 5, the operator normis more useful since we need to deal with spectral radius. A universal bound on quantumoperation in the operator norm is required in Lemma 5, and therefore, we have derived itin Lemma 4. Using the trace norm does not simplify matters and we stick to the operatornorm.

The next lemma is a variant of Refs. [45, Lemma 8.5 and Theorem 8.24] and [53].

Lemma 5. Let (En) be a convergent sequence of quantum operations on a d-dimensionalquantum system with

En → E as n→ +∞. (A.6)

Let Pϕ be the peripheral spectral projection of the quantum operation E, and µ0 = r(E −Eϕ) < 1 the spectral radius of its nonperipheral part. Then, for any µ ∈ (µ0, 1) there existsan integer n0 > 0 and a positive number K > 0 such that

‖(En − PϕEnPϕ)k‖ ≤ Kµk, (A.7)

for all k ∈ N and for all n > n0.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 27

Proof. Given µ ∈ (µ0, 1), fix a µ1 ∈ (µ0, µ) and define E ′n = En − PϕEnPϕ. Since

r(E ′n)→ r(E − PϕEPϕ) = µ0 < 1, (A.8)

as n→ +∞, there exists an integer n0 > 0 such that

r(E ′n) < µ1 < µ < 1, ∀n > n0. (A.9)

Recall now that E ′n can be transformed into an upper-triangular matrix by a unitarytransformation Un (Schur triangulation),

E ′n = U†n(Λn +Nn)Un, (A.10)

where Λn is diagonal whileNn is a strictly upper-triangular matrix with vanishing diagonalelements, which is nilpotent,

N d2n = 0. (A.11)

Since Pϕ is a quantum operation by Proposition 1 (iii), PϕEnPϕ is also a quantumoperation. Then, the operator norm of the nilpotent part Nn is bounded as

‖Nn‖ = ‖UnE ′nU†n − Λn‖≤ ‖E ′n‖+ ‖Λn‖≤ ‖En‖+ ‖PϕEnPϕ‖+ ‖Λn‖≤ 2√d+ µ1, (A.12)

where we have used the fact that ‖En‖, ‖PϕEnPϕ‖ ≤√d by Lemma 4, and the fact that

‖Λn‖ = r(E ′n) ≤ µ1.Now, we estimate the norm ‖E ′kn ‖ = ‖(Λn + Nn)k‖. To this end, notice that, in the

binomial expansion of (Λn +Nn)k, the terms in which Nn appears more than d2− 1 timesvanish, irrespective of the fact that Λn and Nn do not commute in general. Then, we canbound the norm as

‖E ′kn ‖ = ‖(Λn +Nn)k‖

≤min(k,d2−1)∑

j=0

(kj

)‖Λn‖k−j‖Nn‖j

≤min(k,d2−1)∑

j=0

(kj

)µk−j1 (2

√d+ µ1)j

≤d2−1∑j=0

kj

j! µk−j1 (2

√d+ µ1)j

≤ kd2−1µk1

+∞∑j=0

1j!

(2√d

µ1+ 1

)j= e2

√d/µ1+1kd

2−1µk1, ∀k ∈ N, ∀n > n0, (A.13)

that is‖(En − PϕEnPϕ)k‖ ≤ K1k

d2−1µk1, ∀k ∈ N, ∀n > n0, (A.14)

with K1 = e2√d/µ1+1.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 28

Finally, since µ > µ1, we can always find a K ≥ K1 such that

K1kDµk1 ≤ Kµk, ∀k ∈ N, (A.15)

where D = d2 − 1. Indeed, we have

log Kµk

K1kDµk1= log K

K1+ k log µ

µ1−D log k

≥ log K

K1+D −D log D

log(µ/µ1) . (A.16)

We can make it nonnegative by choosing

K ≥ K1

(D

e log(µ/µ1)

)D= e2

√d/µ1+1

(d2 − 1

e log(µ/µ1)

)d2−1

. (A.17)

Together with Eq. (A.14) this gives the bound (A.7) of the lemma.

Remark 10. The constant in Eq. (A.7) can be chosen as

K = e2√d/µµ0+1

(2(d2 − 1)

e log(µ/µ0)

)d2−1

, (A.18)

by putting µ1 = √µµ0 in the lower bound in Eq. (A.17). Note that it was assumedthat µ1 ∈ (µ0, µ) in the proof of Lemma 5. Moreover, notice that in fact in the proof ofLemma 5 we have obtained the tighter bound (A.14):

‖(En − PϕEnPϕ)k‖ ≤ Kkd2−1µk, ∀k ∈ N, ∀n > n0, (A.19)

with K = e2√d/µ+1.

In the proof of Theorem 1, we use Lemma 5 for the sequence of quantum opera-tions En = Eme

tmnL · · · E1e

tmnL in Eq. (7.2), which converges to a quantum operation

E = Em · · · E1 in the limit n→ +∞. The following lemma explicitly clarifies the bound onthe speed of the convergence En → E .

Lemma 6. Let E1, . . . , Em be a finite set of quantum operations and L be a GKLSgenerator of a d-dimensional quantum system. Then, we have

‖EmetmnL · · · E1e

tmnL − E‖ ≤ dm/2 t

n‖L‖e

tn‖L‖, ∀n ∈ N, (A.20)

uniformly in t on compact intervals of [0,+∞), where E = Em · · · E1, and we have chosenthe operator norm.Proof. We split each piece of the evolution as e

tmnL = 1 + (e

tmnL− 1). The deviation from

the identity map is bounded by

‖etmnL − 1‖ ≤ e

tmn‖L‖ − 1. (A.21)

Then, the distance is bounded by

‖EmetmnL · · · E1e

tmnL − E‖ ≤ dm/2

m∑j=1

(mj

)‖e

tmnL − 1‖j

= dm/2[(

1 + ‖etmnL − 1‖

)m− 1

]≤ dm/2

(etn‖L‖ − 1

)= dm/2

t

n‖L‖e

t∗n‖L‖

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 29

≤ dm/2 tn‖L‖e

tn‖L‖, (A.22)

where we have used ‖Ej‖ ≤√d (j = 1, . . . ,m) for the operator norm (Lemma 4) and the

mean-value theorem, [F (t) − F (0)]/t = F ′(t∗) for some t∗ ∈ [0, t], for F (t) = etn‖L‖, with

F ′(t) denoting the derivative of F (t) with respect to t.

Lemma 5 states that for any µ ∈ (µ0, 1) there exists an integer n0 > 0 such thatEq. (A.7) holds for all n > n0. The smaller µ is, the faster the bound shrinks as kincreases. However, if we demand that µ is (larger than but) close to µ0 = r(E −PϕEPϕ),the spectral radius of the nonperipheral part of the limit map E , namely the largest amongthe magnitudes of its nonperipheral eigenvalues, we would need a large n0. The followinglemma clarifies such a trade-off between n0 and µ, for the bang-bang sequence En =Eme

tmnL · · · E1e

tmnL in Eq. (7.2) relevant to Theorem 1.

Lemma 7. Let E1, . . . , Em be a finite set of quantum operations and L be a GKLSgenerator of a d-dimensional quantum system. We consider the sequence of quantumoperations En = Eme

tmnL · · · E1e

tmnL, which converges to E = Em · · · E1 in the limit n →

+∞, and let Pϕ the peripheral spectral projection of E. Then, to bound ‖(En−PϕEnPϕ)k‖by Lemma 5, we can choose n0 satisfying

µ0 +(

(1 + d)dm/2+2 t

n0‖L‖e

tn0‖L‖)1/d2 (

1 + ‖Nn0‖)≤ µ < 1, (A.23)

where Nn is the nilpotent part of Θn = (En − E)− Pϕ(En − E)Pϕ.

Proof. The constant µ > µ0 = r(E − PϕEPϕ) is to bound the spectral radius r(E ′n) ofE ′n = En−PϕEnPϕ for all n > n0. We wish to know how much µ should be larger than µ0to bound r(E ′n) from above.

To this end, we use Theorem 7.2.3 of Ref. [57] concerning how much the eigenvalues canbe altered by a perturbation for generic matrices (including nondiagonalizable ones). Letλ denote the largest (in magnitude) eigenvalue of E ′ = E −PϕEPϕ and λ` the eigenvaluesof E ′n. According to Theorem 7.2.3 of Ref. [57], we have

min`|λ` − λ| ≤ maxθn, θ1/pn

n , (A.24)

where

θn = ‖Θn‖pn−1∑j=0‖Nn‖j , (A.25)

with Θn = E ′n − E ′, Nn being its nilpotent part, and pn being the smallest integer suchthat N pn

n = 0. Caring about the worst case, we have a bound

r(E ′n) ≤ r(E ′) + maxθn, θ1/pnn . (A.26)

Using Lemma 6, ‖Θn‖ is bounded by

‖Θn‖ ≤ (1 + d)‖En − E‖ ≤ (1 + d)dm/2 tn‖L‖e

tn‖L‖, (A.27)

and θn by

θn ≤ (1 + d)dm/2+2 t

n‖L‖e

tn‖L‖

(1 + ‖Nn‖

)d2

. (A.28)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 30

Note that ‖Pϕ‖ ≤√d (Lemma 4),

∑pn−1j=0 ‖Nn‖j ≤ pn max1, ‖Nn‖pn−1 ≤ d2(1+‖Nn‖)d

2 ,and pn ≤ d2. Once this upper bound on θn becomes smaller than 1 by increasing n, thebound (A.26) is reduced to

r(E ′n) ≤ r(E ′) + θ1/d2n

≤ r(E ′) +(

(1 + d)dm/2+2 t

n‖L‖e

tn‖L‖)1/d2 (

1 + ‖Nn‖), (A.29)

and we get the condition (A.23) on n0. Note that µ should be strictly smaller than 1;otherwise it does not make sense.

Lemma 8 (Peripheral part of the product of Hermitian projections). Let P1, . . . , Pm bea set of Hermitian projection operators, P 2

j = Pj = P †j for j = 1, . . . ,m, on a Hilbert space.Then, the peripheral part of the product Pm · · ·P1 is given by the Hermitian projection

Pϕ = P1 ∧ · · · ∧ Pm (A.30)

onto the intersection of the ranges ranP1 ∩ · · · ∩ ranPm. We get PϕPj = PjPϕ = Pϕ forall j = 1, . . . ,m.

Proof. Suppose that P2P1 admits a peripheral eigenvalue λ, and let u 6= 0 be the corre-sponding eigenvector,

P2P1u = λu with |λ| = 1. (A.31)

By the Cauchy-Schwarz inequality, we have

‖u‖2 = ‖P2P1u‖2 = 〈P1u|P2P1u〉 ≤ ‖P1u‖‖P2P1u‖ ≤ ‖u‖2, (A.32)

where we have used ‖Pj‖ ≤ 1 and Eq. (A.31). The two inequalities are actually saturated,implying

P1u = u. (A.33)

This simplifies Eq. (A.31) toP2u = λu, (A.34)

and hence one gets that λ = 1. In this way, the peripheral eigenvalue of P2P1, if any, is 1,and the corresponding eigenvector u is a simultaneous eigenvector of P1 and P2 belongingto their nonvanishing eigenvalue 1. Moreover, since we have

(P2P1)†u = P1P2u = u, (A.35)

the conjugate of u is a left-eigenvector of P2P1 belonging to the same eigenvalue 1. There-fore, the peripheral part of P2P1 is diagonalizable and is the Hermitian projection

Pϕ = P1 ∧ P2 (A.36)

onto ranP1 ∩ ranP2, the intersection of the ranges of P1 and P2.By induction we get that the peripheral part of Pm · · ·P1 is given by the Hermitian

projectionPϕ = P1 ∧ · · · ∧ Pm (A.37)

onto the intersection of the ranges ranP1 ∩ · · · ∩ ranPm.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 31

B Bounding the BCH Formula for Lemma 1It is known that in general the BCH series converges only for small operators [58]. Thisis related to the issue of the convergence of the Magnus expansion [59]. For our purpose,however, this is not a problem. We just need contributions up to the first order in 1/n inthe BCH formula Z(t) = log(eAe

tnL), and the higher-order corrections are under control,

as proved in Lemma 1. Here we provide a concise and explicit bound on the corrections.We first need to know how to bound ‖h(X+Y )−h(X)‖ for a primary operator function

h(X). If a series expansion exists for the stem function h(z), e.g.

h(z) =∞∑n=0

cnzn, (B.1)

it can be easily bounded as [48, Theorem 6.2.30]

‖h(X + Y )− h(X)‖ ≤ h′abs(‖X‖+ ‖Y ‖)‖Y ‖, (B.2)

where

habs(z) =∞∑n=0|cn|zn, (B.3)

and h′abs(z) is its derivative. It is, however, not always the case that a good series expansionexists for h(z). For instance, suppose that the spectrum of X is distributed on the complexplane as in Fig. 3 and h(X) = logX. Due to the singularity at the origin, there is no seriesexpansion of log z defined for all the eigenvalues. In addition, even if every eigenvalue ofX lies within the convergence radius of the series expansion of h(z), the norm ‖X‖ canexceed the convergence radius, and in such a case the bound (B.2) is not applicable. Thiswould happen in particular when X is not diagonalizable and possesses nilpotents in itsspectral representation. We want a bound valid for any X, not necessarily diagonalizable.

Lemma 9. Let X be an operator on a D-dimensional Banach space, whose spectral rep-resentation is

X =∑k

(xkPk +Nk), (B.4)

with Pk and Nk being the spectral projection and the nilpotent belonging to the kth eigen-value xk of X. Let h(z) be analytic on and inside a closed contour Γ in the complexplane that encloses the R-neighborhood of the spectrum of X, spec(X) = xk, that is,dist(Γ, spec(X)) ≥ R > 0, and let

h(X) = 12πi

∮Γ

dz h(z) 1z −X

. (B.5)

Setβ = DP

R

1− (N/R)D

1−N/R , where P = maxk‖Pk‖, N = max

k‖Nk‖, (B.6)

andM = 1

2π

∮Γ|dz||h(z)|. (B.7)

Then, for any operator Y satisfying β‖Y ‖ < 1, we have

‖h(X + Y )− h(X)‖ ≤M β2‖Y ‖1− β‖Y ‖ . (B.8)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 32

Proof. We wish to bound

h(X + Y )− h(X) = 12πi

∮Γ

dz h(z)( 1zI −X − Y

− 1zI −X

)=∞∑n=1

12πi

∮Γ

dz h(z) 1zI −X

(Y

1zI −X

)n. (B.9)

Let us estimate the resolvent,

1zI −X

=∑k

1(z − xk)I −Nk

Pk =∑k

nk−1∑q=0

1(z − xk)q+1N

qkPk. (B.10)

On the contour Γ, it is bounded by∥∥∥∥ 1zI −X

∥∥∥∥ ≤∑k

nk−1∑q=0

1Rq+1 ‖Nk‖q‖Pk‖ ≤ D

D−1∑q=0

1Rq+1N

qP = DP

R

1− (N/R)D

1−N/R = β.

(B.11)Using this bound, we get

‖h(X + Y )− h(X)‖ ≤ 12π

∮Γ|dz||h(z)|

∞∑n=1‖Y ‖nβn+1 ≤M β2‖Y ‖

1− β‖Y ‖ , (B.12)

provided that β‖Y ‖ < 1.

We apply Lemma 9 to log z and to g(z) defined in Eq. (5.3) to bound the BCH formula(6.10). Let us try to get more informative expressions for M for these specific functions,where we see how the spectrum of the input operator and the singularities of the stemfunction matter.

In the case of log z, we find it convenient to take care of its branch cut before applyingLemma 9. We take the contour Γ depicted in Fig. 10(a), which consists of a circle ΓR ofradius r(X) + R, with r(X) the spectral radius of X, and a contour Γc going around abranch cut c. Note that R is bounded by the gap δ between the spectrum of X and thebranch cut c, i.e. R < δ = dist(c, spec(X)). The integral along Γc simplifies, yielding

log(X + Y )− logX = −∞∑n=1

eiφc∫ r(X)+R

0dy 1

yeiφcI −X

(Y

1yeiφcI −X

)n+∞∑n=1

12πi

∫ΓR

dz log z 1zI −X

(Y

1zI −X

)n, (B.13)

where φc = arg z along the branch cut c. Each of the two contributions can be boundedas done in Lemma 9, and ‖log(X + Y )− logX‖ is bounded by Eq. (B.8) with

Mlog(X,R) = [r(X) +R](

1 +√

log2[r(X) +R] + max[φ2c , (φc + 2π)2]

)(B.14)

in place of M .On the other hand, for g(z) defined in Eq. (5.3), let us take the rectangular contour

Γ shown in Fig. 10(b). Note that the function g(z) has poles at z = 2nπi (n ∈ Z \ 0),while in bounding the BCH formula the spectrum of X will be confined to the stripIm z ∈ (−2π, 2π). We take R < δ, where δ = 2π − maxk |Im xk| is the gap between thespectral band and the poles at ±2πi, and let the horizontal lines of the rectangular contour

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 33

(a) (b)

c

R<latexit sha1_base64="IORxkiu3K2o98fx92enFizQ9EWg=">AAAKDXicjZbdbts2FIDV7qdxNq8/u9yNMaNAUXiGZLtNe1csBdpdDMgCpw1gGgFFHTuESUogqXQGo2cYsNv1NXY39HbPsKfYK4ySZVuibGMy7FDnfOfw/JAMw4RRpX3/nzt3P/v8iy/vHbWOv/q6/c39Bw8fvVNxKglckJjF8jLEChgVcKGpZnCZSMA8ZPA+XJzm+vc3IBWNxVgvE5hyPBd0RgnWVnSJ3mDO8dX51YOu3/eLp9McBOWg65XP2dXDo39RFJOUg9CEYaUmgZ/oqcFSU8Iga6NUQYLJAs9hYocCc1BTUwScdR5bSdSZxdJ+he4U0qqFwVypJQ8tybG+Vq4uF+7USbip2T2uKuNFyjGR8U7LkO8ST1I9ezE1VCSpBkFWkc9S1tFxJy9nJ6ISiGZLO7CuqU2+Q66xxETborfbSIKADyS2RRaRQVFmUD6H5CbKbI2qOsnr2mNHC1stNG3pVksbWiq0VdtfFFGVMLxklFOtMje88/UccWKQhl+1sZIMiXgP/xN3eSup8VVaS5e2kr30uEGPD9AL0NkkmJpb0w0yJLGYF2uwioQSFwhihTYHb5uIyiaDqTHZlekOMnSt7DqAp+YHvz/gPDtgagNYWQ+nxUvOWB/Dpg+L5b6bU5MiicEmwm5w2x3szuU1aLc6uWhvec5BNTurMjeI5Malzvb7BDlz6Vx0iCc7DMhBC7rDgu63UFQ05ihkey1OGzOcHvCPI5e2kgpd37PjClzuzXGNbqMIZvbgLs4/E0mw7uU8zIzffz7q2eN32PMzBwpZCmuqZz/95y4xlwBii/RHTSdxvqqsG8KXixV0MugF9k/Q8Gb/X9gjHm8CezE6ybnRy9zzS99JeZUDqiTkVLCMH1WzcZEyAVTLx4XWKaB6Si62CR85+bjnayXuHWH/n5Bqme1KzI1lE0odI0u8nap4cYAlMBZ/2CDlq9O4dX3KthXtetZz++VUcV3E45orgW+WG0fD1Yqyy67uaQWhioUDcHwdz7HYQJP8ShBNzc9ruXsYpTJh4NJnK2mjPbjh900ua7TInrKVHuVv7oIHBnq7NfrPesU2y9r2ihS4F6Lm4N2gHwz7g19G3Vc/lpelI+8773vviRd4J94r76135l14xGPe794f3sfWb60/W3+1Pq3Qu3dKm2+92tP6+z/ItM3Y</latexit>

c<latexit sha1_base64="nMbJ6WfsQAz8JPqr+6DwLDaD3wg=">AAAKGHicjZZPb9s2FMDVdn/ibF6T7biLMaPAMHiGZLtNeyuWAd0OA7LCaQuYhkFRzw5hkRJIKqnB8IsM2HX7GrsNu+62T7GvMEqWbYmyjcmwQ733e4/vD8kwTGMqle//8+Dhow8+/Ojjk9bpJ5+2P3t8dv75G5lkgsA1SeJEvAuxhJhyuFZUxfAuFYBZGMPbcHmZ69/egpA04WO1SmHK8ILTOSVYWdHs7By9wozhGWJY3QimiZmddf2+Xzyd5iAoB12vfK5m5yf/oighGQOuSIylnAR+qqYaC0VJDKaNMgkpJku8gIkdcsxATnURu+k8sZKoM0+E/XLVKaRVC42ZlCsWWjIPUbq6XLhXJ+C2ZvekqkyWGcNEJHstQ7ZPPMnU/PlUU55mCjhZRz7P4o5KOnllOxEVQFS8sgPrmtrkO+QGC0yUrX+7jQRwuCOJrTaPNIqM3tQ8MrZGVZ1gde2po4WdFpq2dKelDS3lyqrtL4qoTGO8iimjSho3vNebOZJUIwXvlbYSg3hygP+RubyV1PgqrYRLW8lBetygx0foJSgzCab6XncDgwTmi2INVpFQ4AJBcaHNwfsmIs1kMNXazHR3YNCNtOsAvtHf+v0BY+aIqQ1gbT2cFi85Y30Mmz4slvtuTk2KJAbbCLvBfXewP5fvQbnVyUUHy/MaZLOz0rhBpLcudXXYJ4i5S+eiYzzZY0COWtA9FvSwhaS8MUchO2hx2Zjh8oh/HLm0lVTo+p4dV+Byb45rdBtFMLdneHH+6UiAdS8WodF+/9moZ4/fYc83DhTGGWyonv30n7nEQgDwHdIfNZ0k+aqybghbLdfQxaAX2D9Bw5v912GPeLwN7PnoIudGL3LPL3wn5XUOqJKQU8EyflTNxkXKBFAtHxfapIDqKbnYNnzk5OOer5W494T9f0KqZbYvMTeWbSh1jKzwbqrixQFWEMfJ3RYpX53GbepTtq1o19Oe2y+nipsintZccXy72joarleUXXZ1T2sIVSwcgOGbZIH5FprkV4Joqn/ayN3DKBNpDC59tZY22oMbfl/lskaL7Clb6VH+5i54iEHttkb/aa/YZqZtr0iBeyFqDt4M+sGwP/h51H35XXlZOvG+9L7yvvYC78J76f3gXXnXHvHuvF+937zfW7+0/mj92fprjT58UNp84dWe1t//Adkl0lE=</latexit>

<latexit sha1_base64="+3qU0/QKO2InXAP9zr+8Hb78eK8=">AAAKC3icjZbNjts2EICVpG3W27r56bEXo0aAonANyXayCZBDgC3Q9FBgG3g3AUxjQVFjL2OSEkhqE4OrRyjQa/sauQW59iH6FH2FUrJsS5RtVIa91Mw3w/khuQwTRpX2/X9u3b7z2edf3D1qHX/5Vfvre/cfPLxQcSoJnJOYxfJNiBUwKuBcU83gTSIB85DB63BxmutfX4NUNBZjvUxgyvFc0BklWFvRBYqAaXx5v+v3/eLpNAdBOeh65XN2+eDoXxTFJOUgNGFYqUngJ3pqsNSUMMjaKFWQYLLAc5jYocAc1NQU4WadR1YSdWaxtF+hO4W0amEwV2rJQ0tyrK+Uq8uFO3USrmt2j6rKeJFyTGS80zLku8STVM+eTg0VSapBkFXks5R1dNzJi9mJqASi2dIOrGtqk++QKywx0bbk7TaSIOAdiTnHIjIoygzK55DcRJmtUVUneV177Ghhq4WmLd1qaUNLhbZq+4siqhKGl4xyqlXmhvdqPUecGKThvTZWkiER7+F/4S5vJTW+Smvp0laylx436PEBegE6mwRTc2O6QYYkFvNiDVaRUOICQazQ5uBNE1HZZDA1Jrs03UGGrpRdB/CD+dHvDzjPDpjaAFbWw2nxkjPWx7Dpw2K57+bUpEhisImwG9x0B7tz+Qm0W51ctLc8r0A1O6syN4jk2qXO9vsEOXPpXHSIJzsMyEELusOC7rdQVDTmKGR7LU4bM5we8I8jl7aSCl3fs+MKXO7NcY1u28N3Zo/t4vwzkQTrXs7DzPj9J6OePX6HPT9zoJClsKZ69tN/4hJzCSC2SH/UdBLnq8q6IXy5WEEng15g/wQNb/a/hT3i8Sawp6OTnBs9yz0/852UVzmgSkJOBcv4UTUbFykTQLV8XGidAqqn5GKb8JGTj3u+VuLeEfb/CamW2a7E3Fg2odQxssTbqYoXB1gCY/G7DVK+Oo1b16dsW9Guxz23X04V10U8rrkS+Hq5cTRcrSi77OqeVhCqWDgAx1fxHIsNNMmvBNHU/LqWu4dRKhMGLn22kjbagxt+f85ljRbZU7bSo/zNXfDAQG+3Rv9xr9hmWdtekQL3QtQcXAz6wbA/+G3UffG8vCwded9633nfe4F34r3wXnpn3rlHvLfeH96f3l+t31sfWh9bn1bo7VulzTde7Wn9/R821c00</latexit>

R<latexit sha1_base64="OzI8W1kBZla3KMBNLSBR4fxYsLc=">AAAKBnicjZbNjts2EICVpG3W27r5O+Zi1AhQFK4h2U42AXIIsAXaHgpsFt4kgGksKGrsJUxSAkltYnB1D9Br+xq9Bbn2NfoUfYVSsmxLlG1Uhr3UzDfD+SG5DBNGlfb9f27dvvPFl1/dPWodf/1N+9t79x88fKPiVBK4IDGL5bsQK2BUwIWmmsG7RALmIYO34eI017+9BqloLMZ6mcCU47mgM0qwtqLX55f3u37fL55OcxCUg65XPmeXD47+RVFMUg5CE4aVmgR+oqcGS00Jg6yNUgUJJgs8h4kdCsxBTU0RadZ5YiVRZxZL+xW6U0irFgZzpZY8tCTH+kq5uly4Uyfhumb3pKqMFynHRMY7LUO+SzxJ9ez51FCRpBoEWUU+S1lHx528jp2ISiCaLe3AuqY2+Q65whITbavdbiMJAt6TmHMsIoOizKB8DslNlNkaVXWS17XHjha2Wmja0q2WNrRUaKu2vyiiKmF4ySinWmVueOfrOeLEIA0ftLGSDIl4D/8rd3krqfFVWkuXtpK99LhBjw/QC9DZJJiaG9MNMiSxmBdrsIqEEhcIYoU2B2+aiMomg6kx2aXpDjJ0pew6gB/Mj35/wHl2wNQGsLIeTouXnLE+hk0fFst9N6cmRRKDTYTd4KY72J3LT6Dd6uSiveU5B9XsrMrcIJJrlzrb7xPkzKVz0SGe7DAgBy3oDgu630JR0ZijkO21OG3McHrAP45c2koqdH3PjitwuTfHNbqNIpjZE7s4/0wkwbqX8zAzfv/ZqGeP32HPzxwoZCmsqZ799J+5xFwCiC3SHzWdxPmqsm4IXy5W0MmgF9g/QcOb/Udhj3i8Cez56CTnRi9yzy98J+VVDqiSkFPBMn5UzcZFygRQLR8XWqeA6im52CZ85OTjnq+VuHeE/X9CqmW2KzE3lk0odYws8Xaq4sUBlsBY/H6DlK9O49b1KdtWtOtpz+2XU8V1EY9rrgS+Xm4cDVcryi67uqcVhCoWDsDxVTzHYgNN8itBNDW/reXuYZTKhIFLn62kjfbght+fc1mjRfaUrfQof3MXPDDQ263Rf9ortlnWtlekwL0QNQdvBv1g2B+8HnVfvSwvS0feY+8773sv8E68V94v3pl34REPvN+9P7w/Wx9bf7U+tT6v0Nu3SptHXu1p/f0fSf3K7g==</latexit>

r(X)

<latexit sha1_base64="pkABXtcX2NbjHTVGg5zUGE1DZMk=">AAAKCXicjZbNjts2EICV9Cfrbd389NiLUSNAWriGZDvZzS3ABmh7KLANvMkCprGgqLFNmKQEktrU4OoJCvSavkZvRa99ij5FX6GULNsSZRuVYS81881wfkguw4RRpX3/n3v3P/r4k08fnLROP/u8/cXDR4+fvFVxKglckZjF8jrEChgVcKWpZnCdSMA8ZPAuXF7k+ne3IBWNxVivEphyPBd0RgnWuUg+u/7m5lHX7/vF02kOgnLQ9crn8ubxyb8oiknKQWjCsFKTwE/01GCpKWGQtVGqIMFkiecwsUOBOaipKYLNOk+tJOrMYmm/QncKadXCYK7UioeW5FgvlKvLhXt1Em5rdk+ryniZckxkvNcy5PvEk1TPzqeGiiTVIMg68lnKOjru5KXsRFQC0WxlB9Y1tcl3yAJLTLQteLuNJAh4T2LOsYgMijKD8jkkN1Fma1TVSV7Xnjpa2GmhaUt3WtrQUqGt2v6iiKqE4RWjnGqVueG92cwRJwZp+EUbK8mQiA/wP3KXt5IaX6W1dGkrOUiPG/T4CL0EnU2Cqbkz3SBDEot5sQarSChxgSBWaHPwromobDKYGpPdmO4gQwtl1wF8a77z+wPOsyOmNoC19XBavOSM9TFs+rBY7rs5NSmSGGwj7AZ33cH+XF6DdquTiw6W5w2oZmdV5gaR3LrU5WGfIGcunYuO8WSPATlqQfdY0MMWiorGHIXsoMVFY4aLI/5x5NJWUqHre3Zcgcu9Oa7RbRTBzB7axflnIgnWvZyHmfH7L0Y9e/wOe37mQCFLYUP17Kf/wiXmEkDskP6o6STOV5V1Q/hquYbOBr3A/gka3uz/CnvE421g56OznBu9zD2/9J2U1zmgSkJOBcv4UTUbFykTQLV8XGiTAqqn5GLb8JGTj3u+VuLeE/b/CamW2b7E3Fi2odQxssK7qYoXB1gBY/H7LVK+Oo3b1KdsW9Gu5z23X04VN0U8rbkS+Ha1dTRcryi77Oqe1hCqWDgAx4t4jsUWmuRXgmhqftrI3cMolQkDl75cSxvtwQ2/3+eyRovsKVvpUf7mLnhgoHdbo/+8V2yzrG2vSIF7IWoO3g76wbA/+HnUfXVeXpZOvK+8r71nXuCdea+8H7xL78oj3sL7zfvg/d76tfVH68/WX2v0/r3S5kuv9rT+/g9ifcvR</latexit>

c<latexit sha1_base64="nMbJ6WfsQAz8JPqr+6DwLDaD3wg=">AAAKGHicjZZPb9s2FMDVdn/ibF6T7biLMaPAMHiGZLtNeyuWAd0OA7LCaQuYhkFRzw5hkRJIKqnB8IsM2HX7GrsNu+62T7GvMEqWbYmyjcmwQ733e4/vD8kwTGMqle//8+Dhow8+/Ojjk9bpJ5+2P3t8dv75G5lkgsA1SeJEvAuxhJhyuFZUxfAuFYBZGMPbcHmZ69/egpA04WO1SmHK8ILTOSVYWdHs7By9wozhGWJY3QimiZmddf2+Xzyd5iAoB12vfK5m5yf/oighGQOuSIylnAR+qqYaC0VJDKaNMgkpJku8gIkdcsxATnURu+k8sZKoM0+E/XLVKaRVC42ZlCsWWjIPUbq6XLhXJ+C2ZvekqkyWGcNEJHstQ7ZPPMnU/PlUU55mCjhZRz7P4o5KOnllOxEVQFS8sgPrmtrkO+QGC0yUrX+7jQRwuCOJrTaPNIqM3tQ8MrZGVZ1gde2po4WdFpq2dKelDS3lyqrtL4qoTGO8iimjSho3vNebOZJUIwXvlbYSg3hygP+RubyV1PgqrYRLW8lBetygx0foJSgzCab6XncDgwTmi2INVpFQ4AJBcaHNwfsmIs1kMNXazHR3YNCNtOsAvtHf+v0BY+aIqQ1gbT2cFi85Y30Mmz4slvtuTk2KJAbbCLvBfXewP5fvQbnVyUUHy/MaZLOz0rhBpLcudXXYJ4i5S+eiYzzZY0COWtA9FvSwhaS8MUchO2hx2Zjh8oh/HLm0lVTo+p4dV+Byb45rdBtFMLdneHH+6UiAdS8WodF+/9moZ4/fYc83DhTGGWyonv30n7nEQgDwHdIfNZ0k+aqybghbLdfQxaAX2D9Bw5v912GPeLwN7PnoIudGL3LPL3wn5XUOqJKQU8EyflTNxkXKBFAtHxfapIDqKbnYNnzk5OOer5W494T9f0KqZbYvMTeWbSh1jKzwbqrixQFWEMfJ3RYpX53GbepTtq1o19Oe2y+nipsintZccXy72joarleUXXZ1T2sIVSwcgOGbZIH5FprkV4Joqn/ayN3DKBNpDC59tZY22oMbfl/lskaL7Clb6VH+5i54iEHttkb/aa/YZqZtr0iBeyFqDt4M+sGwP/h51H35XXlZOvG+9L7yvvYC78J76f3gXXnXHvHuvF+937zfW7+0/mj92fprjT58UNp84dWe1t//Adkl0lE=</latexit>

r(X)

<latexit sha1_base64="pkABXtcX2NbjHTVGg5zUGE1DZMk=">AAAKCXicjZbNjts2EICV9Cfrbd389NiLUSNAWriGZDvZzS3ABmh7KLANvMkCprGgqLFNmKQEktrU4OoJCvSavkZvRa99ij5FX6GULNsSZRuVYS81881wfkguw4RRpX3/n3v3P/r4k08fnLROP/u8/cXDR4+fvFVxKglckZjF8jrEChgVcKWpZnCdSMA8ZPAuXF7k+ne3IBWNxVivEphyPBd0RgnWuUg+u/7m5lHX7/vF02kOgnLQ9crn8ubxyb8oiknKQWjCsFKTwE/01GCpKWGQtVGqIMFkiecwsUOBOaipKYLNOk+tJOrMYmm/QncKadXCYK7UioeW5FgvlKvLhXt1Em5rdk+ryniZckxkvNcy5PvEk1TPzqeGiiTVIMg68lnKOjru5KXsRFQC0WxlB9Y1tcl3yAJLTLQteLuNJAh4T2LOsYgMijKD8jkkN1Fma1TVSV7Xnjpa2GmhaUt3WtrQUqGt2v6iiKqE4RWjnGqVueG92cwRJwZp+EUbK8mQiA/wP3KXt5IaX6W1dGkrOUiPG/T4CL0EnU2Cqbkz3SBDEot5sQarSChxgSBWaHPwromobDKYGpPdmO4gQwtl1wF8a77z+wPOsyOmNoC19XBavOSM9TFs+rBY7rs5NSmSGGwj7AZ33cH+XF6DdquTiw6W5w2oZmdV5gaR3LrU5WGfIGcunYuO8WSPATlqQfdY0MMWiorGHIXsoMVFY4aLI/5x5NJWUqHre3Zcgcu9Oa7RbRTBzB7axflnIgnWvZyHmfH7L0Y9e/wOe37mQCFLYUP17Kf/wiXmEkDskP6o6STOV5V1Q/hquYbOBr3A/gka3uz/CnvE421g56OznBu9zD2/9J2U1zmgSkJOBcv4UTUbFykTQLV8XGiTAqqn5GLb8JGTj3u+VuLeE/b/CamW2b7E3Fi2odQxssK7qYoXB1gBY/H7LVK+Oo3b1KdsW9Gu5z23X04VN0U8rbkS+Ha1dTRcryi77Oqe1hCqWDgAx4t4jsUWmuRXgmhqftrI3cMolQkDl75cSxvtwQ2/3+eyRovsKVvpUf7mLnhgoHdbo/+8V2yzrG2vSIF7IWoO3g76wbA/+HnUfXVeXpZOvK+8r71nXuCdea+8H7xL78oj3sL7zfvg/d76tfVH68/WX2v0/r3S5kuv9rT+/g9ifcvR</latexit>

2i<latexit sha1_base64="3ksboLivsIXPj4T+clnZFoG0yDc=">AAAKE3icjZbNjts2EICV9G+9rdukPeYixAhQFK4hyU52cwuwAdIcAmwDbxLAdBcUNfYSFimBpDY1uHqMALkmr5FbkWsfoE/RVygly7ZE2UZl2EvNfDOcH5LLMI2pVJ73z63bX3z51dffHHWOv/2u+/0Pd+7++EommSBwQZI4EW9CLCGmHC4UVTG8SQVgFsbwOlycFfrX1yAkTfhYLVOYMjzndEYJVkb0B4oERG6AUooEo5d3et7AKx+3PfCrQc+pnvPLu0f/oighGQOuSIylnPheqqYaC0VJDHkXZRJSTBZ4DhMz5JiBnOoy7Nx9YCSRO0uE+XLlltK6hcZMyiULDcmwupK2rhDu1Am4btg9qCuTRcYwEclOy5DtEk8yNTudasrTTAEnq8hnWeyqxC2K6kZUAFHx0gyMa2qSd8kVFpgoU/puFwng8JYkjGEeaRTlGhVzCKaj3NSorhOsqT22tLDVQtuWbrW0paVcGbX5RRGVaYyXMWVUydwO7+V6jiTVSMGfShtJjniyh3/ObN5IGnydVsKmjWQvPW7R4wP0AlQ+8af6Rvf8HAnM5+UarCOhwCWC4lJbgDdtROaTYKp1fql7QY6upFkH8Iv+1RsEjOUHTE0AK+vhtHwpGONj2PZhsMJ3e2pSJhFsIuz5N71gdy5PQdnVKUR7y/MSZLuzMreDSK9t6ny/TxAzmy5Eh3iyw4ActKA7LOh+C0l5a45SttfirDXD2QH/OLJpI6nRzT07rsHV3hw36C6KYGaO7/L808WBnGsxD3PtDR6N+ub4Hfa93ILCOIM11TefwSObmAsAvkUGo7aTpFhVxg1hy8UKOgn6vvnjt7yZ/xrmiMebwE5HJwU3elx4fuxZKa9yQLWErApW8aN6NjZSJYAa+djQOgXUTMnGNuEjKx/7fK3FvSPs/xNSI7NdidmxbEJpYmSJt1OVLxawhDhO3m6Q6tVq3Lo+VdvKdj3s2/2yqrgu4nHDFcfXy42j4WpFmWXX9LSCUM3CAhi+SuaYb6BJcSWIpvrFWm4fRplIY7Dp85W01R7c8vuskLVaZE7ZWo+KN3vBQwxquzUGD/vlNsu75ork2xei9uBVMPCHg+D3Ue/JaXVZOnLuOfednx3fOXGeOL85586FQxzhvHc+OB877zqfOn91Pq/Q27cqm5+cxtP5+z83/dBA</latexit>

2i<latexit sha1_base64="ed6sW9ZyfH/hdcDsYjFf7/EZmYM=">AAAKE3icjZbNjts2EICVpD/rbd0k7bEXo0aAonAMSXaym1uALdD2UGAbeJMAprugqLGXsEgJJLWJweVjFOi1fY3eil77AH2KvkIpWbYlyjYqw15q5pvh/JBcRllCpfL9f+7df/DBhx99fNI5/eTT7mcPHz3+/LVMc0HgiqRJKt5GWEJCOVwpqhJ4mwnALErgTbS8KPRvbkFImvKJWmUwY3jB6ZwSrKzoZxQLiJ+GKKNIMHr9qO8P/fLptQdBNeh71XN5/fjkXxSnJGfAFUmwlNPAz9RMY6EoScB0US4hw2SJFzC1Q44ZyJkuwza9J1YS9+apsF+ueqW0bqExk3LFIksyrG6kqyuEe3UCbht2T+rKdJkzTES61zJi+8TTXM3PZ5ryLFfAyTryeZ70VNoritqLqQCikpUdWNfUJt8jN1hgomzpu10kgMM7kjKGeaxRbDQq5hBMx8bWqK4TrKk9dbSw00Lblu60tKWlXFm1/UUxlVmCVwllVEnjhvdqM0eaaaTgvdJWYhBPD/A/MJe3kgZfp5VwaSs5SE9a9OQIvQRlpsFM3+l+YJDAfFGuwToSCVwiKCm1BXjXRqSZhjOtzbXuhwbdSLsO4Bv91B+GjJkjpjaAtfVoVr4UjPUxavuwWOG7PTUpkwi3EfaDu364P5dvQbnVKUQHy/MKZLuz0rhBZLcudXnYJ4i5SxeiYzzZY0COWtA9FvSwhaS8NUcpO2hx0Zrh4oh/HLu0ldTo5p6d1OBqb04adBfFMLfHd3n+6eJANlosIqP94fPxwB6/o4FvHChKcthQA/sZPneJhQDgO2Q4bjtJi1Vl3RC2Wq6hs3AQ2D9By5v9r2GPeLwN7Hx8VnDjF4XnF76T8joHVEvIqWAVP6pn4yJVAqiRjwttUkDNlFxsGz5y8nHP11rce8L+PyE1MtuXmBvLNpQmRlZ4N1X54gArSJL03RapXp3GbepTta1s17OB2y+nipsinjZccXy72joarVeUXXZNT2sI1SwcgOGbdIH5FpoWV4J4pn/cyN3DKBdZAi59uZa22oNbfr8rZK0W2VO21qPizV3wkIDabY3hs0G5zUzXXpEC90LUHrwOh8FoGP407r88ry5LJ96X3lfe117gnXkvve+9S+/KI57wfvV+837v/NL5o/Nn5681ev9eZfOF13g6f/8HtZ/QTQ==</latexit>

R<latexit sha1_base64="OzI8W1kBZla3KMBNLSBR4fxYsLc=">AAAKBnicjZbNjts2EICVpG3W27r5O+Zi1AhQFK4h2U42AXIIsAXaHgpsFt4kgGksKGrsJUxSAkltYnB1D9Br+xq9Bbn2NfoUfYVSsmxLlG1Uhr3UzDfD+SG5DBNGlfb9f27dvvPFl1/dPWodf/1N+9t79x88fKPiVBK4IDGL5bsQK2BUwIWmmsG7RALmIYO34eI017+9BqloLMZ6mcCU47mgM0qwtqLX55f3u37fL55OcxCUg65XPmeXD47+RVFMUg5CE4aVmgR+oqcGS00Jg6yNUgUJJgs8h4kdCsxBTU0RadZ5YiVRZxZL+xW6U0irFgZzpZY8tCTH+kq5uly4Uyfhumb3pKqMFynHRMY7LUO+SzxJ9ez51FCRpBoEWUU+S1lHx528jp2ISiCaLe3AuqY2+Q65whITbavdbiMJAt6TmHMsIoOizKB8DslNlNkaVXWS17XHjha2Wmja0q2WNrRUaKu2vyiiKmF4ySinWmVueOfrOeLEIA0ftLGSDIl4D/8rd3krqfFVWkuXtpK99LhBjw/QC9DZJJiaG9MNMiSxmBdrsIqEEhcIYoU2B2+aiMomg6kx2aXpDjJ0pew6gB/Mj35/wHl2wNQGsLIeTouXnLE+hk0fFst9N6cmRRKDTYTd4KY72J3LT6Dd6uSiveU5B9XsrMrcIJJrlzrb7xPkzKVz0SGe7DAgBy3oDgu630JR0ZijkO21OG3McHrAP45c2koqdH3PjitwuTfHNbqNIpjZE7s4/0wkwbqX8zAzfv/ZqGeP32HPzxwoZCmsqZ799J+5xFwCiC3SHzWdxPmqsm4IXy5W0MmgF9g/QcOb/Udhj3i8Cez56CTnRi9yzy98J+VVDqiSkFPBMn5UzcZFygRQLR8XWqeA6im52CZ85OTjnq+VuHeE/X9CqmW2KzE3lk0odYws8Xaq4sUBlsBY/H6DlK9O49b1KdtWtOtpz+2XU8V1EY9rrgS+Xm4cDVcryi67uqcVhCoWDsDxVTzHYgNN8itBNDW/reXuYZTKhIFLn62kjfbght+fc1mjRfaUrfQof3MXPDDQ263Rf9ortlnWtlekwL0QNQdvBv1g2B+8HnVfvSwvS0feY+8773sv8E68V94v3pl34REPvN+9P7w/Wx9bf7U+tT6v0Nu3SptHXu1p/f0fSf3K7g==</latexit>

R<latexit sha1_base64="OzI8W1kBZla3KMBNLSBR4fxYsLc=">AAAKBnicjZbNjts2EICVpG3W27r5O+Zi1AhQFK4h2U42AXIIsAXaHgpsFt4kgGksKGrsJUxSAkltYnB1D9Br+xq9Bbn2NfoUfYVSsmxLlG1Uhr3UzDfD+SG5DBNGlfb9f27dvvPFl1/dPWodf/1N+9t79x88fKPiVBK4IDGL5bsQK2BUwIWmmsG7RALmIYO34eI017+9BqloLMZ6mcCU47mgM0qwtqLX55f3u37fL55OcxCUg65XPmeXD47+RVFMUg5CE4aVmgR+oqcGS00Jg6yNUgUJJgs8h4kdCsxBTU0RadZ5YiVRZxZL+xW6U0irFgZzpZY8tCTH+kq5uly4Uyfhumb3pKqMFynHRMY7LUO+SzxJ9ez51FCRpBoEWUU+S1lHx528jp2ISiCaLe3AuqY2+Q65whITbavdbiMJAt6TmHMsIoOizKB8DslNlNkaVXWS17XHjha2Wmja0q2WNrRUaKu2vyiiKmF4ySinWmVueOfrOeLEIA0ftLGSDIl4D/8rd3krqfFVWkuXtpK99LhBjw/QC9DZJJiaG9MNMiSxmBdrsIqEEhcIYoU2B2+aiMomg6kx2aXpDjJ0pew6gB/Mj35/wHl2wNQGsLIeTouXnLE+hk0fFst9N6cmRRKDTYTd4KY72J3LT6Dd6uSiveU5B9XsrMrcIJJrlzrb7xPkzKVz0SGe7DAgBy3oDgu630JR0ZijkO21OG3McHrAP45c2koqdH3PjitwuTfHNbqNIpjZE7s4/0wkwbqX8zAzfv/ZqGeP32HPzxwoZCmsqZ799J+5xFwCiC3SHzWdxPmqsm4IXy5W0MmgF9g/QcOb/Udhj3i8Cez56CTnRi9yzy98J+VVDqiSkFPBMn5UzcZFygRQLR8XWqeA6im52CZ85OTjnq+VuHeE/X9CqmW2KzE3lk0odYws8Xaq4sUBlsBY/H6DlK9O49b1KdtWtOtpz+2XU8V1EY9rrgS+Xm4cDVcryi67uqcVhCoWDsDxVTzHYgNN8itBNDW/reXuYZTKhIFLn62kjfbght+fc1mjRfaUrfQof3MXPDDQ263Rf9ortlnWtlekwL0QNQdvBv1g2B+8HnVfvSwvS0feY+8773sv8E68V94v3pl34REPvN+9P7w/Wx9bf7U+tT6v0Nu3SptHXu1p/f0fSf3K7g==</latexit>

R<latexit sha1_base64="OzI8W1kBZla3KMBNLSBR4fxYsLc=">AAAKBnicjZbNjts2EICVpG3W27r5O+Zi1AhQFK4h2U42AXIIsAXaHgpsFt4kgGksKGrsJUxSAkltYnB1D9Br+xq9Bbn2NfoUfYVSsmxLlG1Uhr3UzDfD+SG5DBNGlfb9f27dvvPFl1/dPWodf/1N+9t79x88fKPiVBK4IDGL5bsQK2BUwIWmmsG7RALmIYO34eI017+9BqloLMZ6mcCU47mgM0qwtqLX55f3u37fL55OcxCUg65XPmeXD47+RVFMUg5CE4aVmgR+oqcGS00Jg6yNUgUJJgs8h4kdCsxBTU0RadZ5YiVRZxZL+xW6U0irFgZzpZY8tCTH+kq5uly4Uyfhumb3pKqMFynHRMY7LUO+SzxJ9ez51FCRpBoEWUU+S1lHx528jp2ISiCaLe3AuqY2+Q65whITbavdbiMJAt6TmHMsIoOizKB8DslNlNkaVXWS17XHjha2Wmja0q2WNrRUaKu2vyiiKmF4ySinWmVueOfrOeLEIA0ftLGSDIl4D/8rd3krqfFVWkuXtpK99LhBjw/QC9DZJJiaG9MNMiSxmBdrsIqEEhcIYoU2B2+aiMomg6kx2aXpDjJ0pew6gB/Mj35/wHl2wNQGsLIeTouXnLE+hk0fFst9N6cmRRKDTYTd4KY72J3LT6Dd6uSiveU5B9XsrMrcIJJrlzrb7xPkzKVz0SGe7DAgBy3oDgu630JR0ZijkO21OG3McHrAP45c2koqdH3PjitwuTfHNbqNIpjZE7s4/0wkwbqX8zAzfv/ZqGeP32HPzxwoZCmsqZ799J+5xFwCiC3SHzWdxPmqsm4IXy5W0MmgF9g/QcOb/Udhj3i8Cez56CTnRi9yzy98J+VVDqiSkFPBMn5UzcZFygRQLR8XWqeA6im52CZ85OTjnq+VuHeE/X9CqmW2KzE3lk0odYws8Xaq4sUBlsBY/H6DlK9O49b1KdtWtOtpz+2XU8V1EY9rrgS+Xm4cDVcryi67uqcVhCoWDsDxVTzHYgNN8itBNDW/reXuYZTKhIFLn62kjfbght+fc1mjRfaUrfQof3MXPDDQ263Rf9ortlnWtlekwL0QNQdvBv1g2B+8HnVfvSwvS0feY+8773sv8E68V94v3pl34REPvN+9P7w/Wx9bf7U+tT6v0Nu3SptHXu1p/f0fSf3K7g==</latexit>

R<latexit sha1_base64="OzI8W1kBZla3KMBNLSBR4fxYsLc=">AAAKBnicjZbNjts2EICVpG3W27r5O+Zi1AhQFK4h2U42AXIIsAXaHgpsFt4kgGksKGrsJUxSAkltYnB1D9Br+xq9Bbn2NfoUfYVSsmxLlG1Uhr3UzDfD+SG5DBNGlfb9f27dvvPFl1/dPWodf/1N+9t79x88fKPiVBK4IDGL5bsQK2BUwIWmmsG7RALmIYO34eI017+9BqloLMZ6mcCU47mgM0qwtqLX55f3u37fL55OcxCUg65XPmeXD47+RVFMUg5CE4aVmgR+oqcGS00Jg6yNUgUJJgs8h4kdCsxBTU0RadZ5YiVRZxZL+xW6U0irFgZzpZY8tCTH+kq5uly4Uyfhumb3pKqMFynHRMY7LUO+SzxJ9ez51FCRpBoEWUU+S1lHx528jp2ISiCaLe3AuqY2+Q65whITbavdbiMJAt6TmHMsIoOizKB8DslNlNkaVXWS17XHjha2Wmja0q2WNrRUaKu2vyiiKmF4ySinWmVueOfrOeLEIA0ftLGSDIl4D/8rd3krqfFVWkuXtpK99LhBjw/QC9DZJJiaG9MNMiSxmBdrsIqEEhcIYoU2B2+aiMomg6kx2aXpDjJ0pew6gB/Mj35/wHl2wNQGsLIeTouXnLE+hk0fFst9N6cmRRKDTYTd4KY72J3LT6Dd6uSiveU5B9XsrMrcIJJrlzrb7xPkzKVz0SGe7DAgBy3oDgu630JR0ZijkO21OG3McHrAP45c2koqdH3PjitwuTfHNbqNIpjZE7s4/0wkwbqX8zAzfv/ZqGeP32HPzxwoZCmsqZ799J+5xFwCiC3SHzWdxPmqsm4IXy5W0MmgF9g/QcOb/Udhj3i8Cez56CTnRi9yzy98J+VVDqiSkFPBMn5UzcZFygRQLR8XWqeA6im52CZ85OTjnq+VuHeE/X9CqmW2KzE3lk0odYws8Xaq4sUBlsBY/H6DlK9O49b1KdtWtOtpz+2XU8V1EY9rrgS+Xm4cDVcryi67uqcVhCoWDsDxVTzHYgNN8itBNDW/reXuYZTKhIFLn62kjfbght+fc1mjRfaUrfQof3MXPDDQ263Rf9ortlnWtlekwL0QNQdvBv1g2B+8HnVfvSwvS0feY+8773sv8E68V94v3pl34REPvN+9P7w/Wx9bf7U+tT6v0Nu3SptHXu1p/f0fSf3K7g==</latexit>

<latexit sha1_base64="1h3c/kWsZ7CDv9RHNQa1MCU3J88=">AAAKC3icjZbNjts2EICVpG3W27rNz7EXo0aAonANyXayyS3IFkh6KLANvJsAprGgqLGXNUkJJLWJwdUjFOi1fY3cglz7EH2KvkIpWbYlyjYqw15q5pvh/JBchgmjSvv+P7du3/ns8y/uHrWOv/yq/fU39+4/uFBxKgmck5jF8m2IFTAq4FxTzeBtIgHzkMGbcHGa699cg1Q0FmO9TGDK8VzQGSVYW9EFeok5x5f3un7fL55OcxCUg65XPmeX94/+RVFMUg5CE4aVmgR+oqcGS00Jg6yNUgUJJgs8h4kdCsxBTU0RbtZ5ZCVRZxZL+xW6U0irFgZzpZY8tCTH+kq5uly4Uyfhumb3qKqMFynHRMY7LUO+SzxJ9ezp1FCRpBoEWUU+S1lHx528mJ2ISiCaLe3AuqY2+Q65whITbUvebiMJAt6R2JZYRAZFmUH5HJKbKLM1quokr2uPHS1stdC0pVstbWip0FZtf1FEVcLwklFOtcrc8F6v54gTgzS818ZKMiTiPfzP3OWtpMZXaS1d2kr20uMGPT5AL0Bnk2Bqbkw3yJDEYl6swSoSSlwgiBXaHLxpIiqbDKbGZJemO8jQlbLrAH4wP/r9AefZAVMbwMp6OC1ecsb6GDZ9WCz33ZyaFEkMNhF2g5vuYHcuP4F2q5OL9pbnNahmZ1XmBpFcu9TZfp8gZy6diw7xZIcBOWhBd1jQ/RaKisYchWyvxWljhtMD/nHk0lZSoet7dlyBy705rtFtFMHMHtvF+WciCda9nIeZ8ftPRj17/A57fuZAIUthTfXsp//EJeYSQGyR/qjpJM5XlXVD+HKxgk4GvcD+CRre7H8Le8TjTWBPRyc5N3qWe37mOymvckCVhJwKlvGjajYuUiaAavm40DoFVE/JxTbhIycf93ytxL0j7P8TUi2zXYm5sWxCqWNkibdTFS8OsATG4ncbpHx1GreuT9m2ol2Pe26/nCqui3hccyXw9XLjaLhaUXbZ1T2tIFSxcACOr+I5Fhtokl8Joqn5ZS13D6NUJgxc+mwlbbQHN/y+zGWNFtlTttKj/M1d8MBAb7dG/3Gv2GZZ216RAvdC1BxcDPrBsD/4ddR9/qK8LB1533rfed97gXfiPfdeeWfeuUe837w/vD+9v1q/tz60PrY+rdDbt0qbh17taf39H8BSzRM=</latexit>

<latexit sha1_base64="QrEA3xp60oLrBc5iaCD8JiZlx1w=">AAAJ53icfZbNjts2EMeV9CPrtG6S9piLUSNAUbiG5XWzCdBDgm2R9hB0G+xuApjGgqLGXsakJJCUU4OrZ2hOQZNbnqdP0LcJKXttiZQtwzb1n98MZ0YUpShjVKrB4P8bNz/7/Isvbx20bn/1dfubO3fvfXsu01wQOCMpS8WrCEtgNIEzRRWDV5kAzCMGL6P5sbW/XICQNE1O1TKDCcezhE4pwcpI5ygGpvDF3e6gPyiPjj8I14NusD5OLu4d/IfilOQcEkUYllJjoShhULRRLiHDZI5nMDbDBHOQE10mWnQeGCXuTFNhvonqlGrVQ2Mu5ZJHhuRYXUrXZsVGm4BFze9B1ZjOc46JSBs9I94kj3M1fTTRNMlyBQlZZT7NWUelHdvGTkwFEMWWZmBCU1N8h1xigYkyzW63UQJvSMo5TmKNBI8Ljewcguu4KFwrbK3gW+nWSj0rTZQxm18UU5kxvGSUUyUNJqAKvrieI800UvC30kYpUJLu4P/gLm+UGl+llXBpo+ykTz36dA89B1WMw4m+0t2wQAIns3KVVZFI4BJBrLRa8MpHZDEeTrQuLnR3WKBLaa40/Kh/GvSHnBd7XE0CK+/DSXliGRPj0I9hMBvbn5qURQw3GXbDq+6wuZZfQbndsdLO9rwA6V9ZWbhJZAuXOtkdE8TUpa20jycNDmSvB23woLs9JE28OUptp8exN8Pxnvg4dmmjVOjbNfocV9fw+u604k6P43The1hxp8fTBTgeUaR/q/Fts31PzcZf7qM6FmCKELOo0IP+w1HPbOCHvUHhQBHL4ZrqmU//oUvMBECyRfojP0hq164JQ/hyvoKOhr3Q/IVeNPO8MQ8JvEns0ejIcqPHNvLjgVP0qgZUKci5Tuv8UbUaF1kXgGr1uNB1Cahekott0kdOPU7i1bwb0q6n1JhRrbCmutxUNpnUMbLE25nKEwdYAmPpmw2yPnWgenvG9jEeT/SfjU3i+DKd4WTp0s+vdXczykXGvNgnK9VrHPbiPrOa1z2zy1baZ8/cpQgM1HbR9n/ulTdA0TavP6H7suMPzof98LA//GvUffLL+kXoILgffB/8EITBUfAk+D04Cc4CErwO3gbvgw8t2vqn9a717wq9eWPt811QO1ofPwHIgsIl</latexit>

<latexit sha1_base64="QrEA3xp60oLrBc5iaCD8JiZlx1w=">AAAJ53icfZbNjts2EMeV9CPrtG6S9piLUSNAUbiG5XWzCdBDgm2R9hB0G+xuApjGgqLGXsakJJCUU4OrZ2hOQZNbnqdP0LcJKXttiZQtwzb1n98MZ0YUpShjVKrB4P8bNz/7/Isvbx20bn/1dfubO3fvfXsu01wQOCMpS8WrCEtgNIEzRRWDV5kAzCMGL6P5sbW/XICQNE1O1TKDCcezhE4pwcpI5ygGpvDF3e6gPyiPjj8I14NusD5OLu4d/IfilOQcEkUYllJjoShhULRRLiHDZI5nMDbDBHOQE10mWnQeGCXuTFNhvonqlGrVQ2Mu5ZJHhuRYXUrXZsVGm4BFze9B1ZjOc46JSBs9I94kj3M1fTTRNMlyBQlZZT7NWUelHdvGTkwFEMWWZmBCU1N8h1xigYkyzW63UQJvSMo5TmKNBI8Ljewcguu4KFwrbK3gW+nWSj0rTZQxm18UU5kxvGSUUyUNJqAKvrieI800UvC30kYpUJLu4P/gLm+UGl+llXBpo+ykTz36dA89B1WMw4m+0t2wQAIns3KVVZFI4BJBrLRa8MpHZDEeTrQuLnR3WKBLaa40/Kh/GvSHnBd7XE0CK+/DSXliGRPj0I9hMBvbn5qURQw3GXbDq+6wuZZfQbndsdLO9rwA6V9ZWbhJZAuXOtkdE8TUpa20jycNDmSvB23woLs9JE28OUptp8exN8Pxnvg4dmmjVOjbNfocV9fw+u604k6P43The1hxp8fTBTgeUaR/q/Fts31PzcZf7qM6FmCKELOo0IP+w1HPbOCHvUHhQBHL4ZrqmU//oUvMBECyRfojP0hq164JQ/hyvoKOhr3Q/IVeNPO8MQ8JvEns0ejIcqPHNvLjgVP0qgZUKci5Tuv8UbUaF1kXgGr1uNB1Cahekott0kdOPU7i1bwb0q6n1JhRrbCmutxUNpnUMbLE25nKEwdYAmPpmw2yPnWgenvG9jEeT/SfjU3i+DKd4WTp0s+vdXczykXGvNgnK9VrHPbiPrOa1z2zy1baZ8/cpQgM1HbR9n/ulTdA0TavP6H7suMPzof98LA//GvUffLL+kXoILgffB/8EITBUfAk+D04Cc4CErwO3gbvgw8t2vqn9a717wq9eWPt811QO1ofPwHIgsIl</latexit>

Figure 10: (a) Contour Γ to estimate a bound on ‖log(X + Y )− logX‖. The crosses represent theeigenvalues xk of X, and c is the chosen branch cut of log z (red thin straight line). We take R < δsmaller than the gap δ between the spectrum of X and the branch cut c (dashed curve running aroundthe branch cut), and draw a contour Γ (solid closed directed curve) which consists of a circle ΓR ofradius r(X) + R, with r(X) the spectral radius of X (dashed circle), and a contour Γc going aroundthe branch cut c. (b) Contour Γ to estimate a bound on ‖g(X + Y )− g(X)‖ for g(z) defined in Eq.(5.3). The black crosses represent the eigenvalues xk of X, while the red crosses are the two poles ofg(z) at ±2πi. For our purpose of bounding the BCH formula, the spectrum of X is confined to a stripbetween the two poles, Im z ∈ (−2π + δ, 2π − δ), with a nonvanishing gap δ from the poles (dashedhorizontal lines). We take R < δ and draw a rectangular contour Γ with its horizontal lines runningalong Im z = ±(2π − δ +R) and its vertical lines along Re z = ±[r(X) +R].

Γ run along Im z = ±(2π − δ + R) and the vertical lines along Re z = ±[r(X) + R]. Byusing the following two bounds,

|g(x+ iy)| =√

x2 + y2

1− 2e−x cos y + e−2x ≤

√x2 + y2

|1− e−x| ,√x2 + y2

θ(cos y)|sin y|+ θ(−cos y) ,(B.15)

valid for any real x and y, where θ(x) is the step function [θ(x) = 1 for x > 0 and 0 forx < 0], we can easily bound the integral in Eq. (B.7) for g(z) along the rectangular contourΓ (the maximum of |g(z)| multiplied by the path length along each of the four straightlines of the rectangular contour), and we get a bound (B.8) on ‖g(X + Y )− g(X)‖ with

Mg(X,R) = 2π

√[r(X) +R]2 + (2π − δ +R)2

(2π − δ +R

2 coth r(X) +R

2

+ r(X) +R

θ(cos(δ −R))|sin(δ −R)|+ θ(−cos(δ −R))

)(B.16)

in place of M .We can now proceed to bound the BCH formula. To get a concise expression for the

bound, we make use of a similarity transformation which brings X into a Jordan normalform. In the standard Jordan form, we put “1”s next to the eigenvalues whose eigenspacesare not diagonalizable. We point out that we can freely tune the similarity transformationso that the “1”s are scaled to some positive constant ν. Let us transform X into such a

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 34

Jordan form by a similarity transformation Tν ,

X = T−1ν XTν =

∑k

(xkPk + Nk), (B.17)

where Pk are diagonal projections and Nk are the nilpotents with entries ν or 0on the next diagonal. Notice that the infinity norms (the largest singular values) of Pkand Nk are ‖Pk‖∞ = 1 and ‖Nk‖∞ = ν or 0, respectively.2 This helps us simplify thebound. The infinity norms before the similarity transformation are estimated as ‖Pk‖∞ ≤‖T−1

ν ‖∞‖Pk‖∞‖Tν‖∞ = χν and ‖Nk‖∞ ≤ χνν or 0, with χν = ‖T−1ν ‖∞‖Tν‖∞ ≥ 1 called

“condition number” of the similarity transformation Tν [60].We now present a bound on the BCH formula (6.10).

Proposition 2 (Bounding the BCH formula). Let X and Y be operators on a D-dimen-sional Banach space, with the spectrum of X, spec(X) = xk, confined within a stripIm z ∈ (φc, φc + 2π) for some φc. We choose a primary logarithm such that log eX = X.Then, for small enough t ≥ 0, the correction W (t) in the BCH formula

Z(t) = log(eXetY ) = X + tg(adX)(Y ) +W (t) (B.18)

is bounded by

‖W (t)‖∞ ≤(32M2D9eα+ν/R4)t2χ3

ν‖Y ‖2∞etχν‖Y ‖∞1− (1 + 8MD4/R2)(2D2eα+ν/R)tχν‖Y ‖∞etχν‖Y ‖∞

, (B.19)

where g(z) is the function defined in Eq. (5.3), R is a positive constant fulfilling

R < δ1, δ2 (B.20)

for the gaps

δ1 = mink

miny≥0|exk − yeiφc |, δ2 = 2π −max

k,`Im(xk − x`), (B.21)

andM = max[Mlog(eX , R),Mg(adX , R)], (B.22)

with Mlog and Mg defined in Eqs. (B.14) and (B.16), respectively. χν is the conditionnumber of the similarity transformation turning X into a Jordan form with ν in the nextdiagonal in the nilpotents, and ν is tuned so that

νeα+ν , 2Dν ≤ R/2, α = maxk

Rexk (B.23)

are satisfied. t should be small enough to satisfy

(1 + 8MD4/R2)(2D2eα+ν/R)tχν‖Y ‖∞etχν‖Y ‖∞ < 1. (B.24)

Proof. We start by preparing the spectral representations of eX and adX on the basis ofthe spectral representation of X in Eq. (B.17).

2The infinity norm of operator X can be defined by ‖X‖∞ = sup‖v‖=1 ‖Xv‖, through the Euclideannorm ‖v‖ of vector v.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 35

Spectral representation of eX : The spectral representation of eX can be constructedfrom the spectral representation of X in Eq. (B.17) as

eX =∑k

exknk−1∑q=0

1q!N

qk Pk =

∑k

(exk Pk + N(e)k ), (B.25)

where the spectral projections of eX are identical with those of X while the nilpotentsN

(e)k of eX are given in terms of the nilpotents Nk of X by

N(e)k = exk

nk−1∑q=1

1q!N

qk . (B.26)

Note that exk 6= ex` for k 6= ` thanks to the restriction Im xk ∈ (φc, φc+2π). The nilpotentsN

(e)k are bounded by

‖N (e)k ‖∞ ≤ |e

xk |nk−1∑q=1

1q!ν

q ≤ |exk |(eν − 1) ≤ |exk |νeν ≤ νeα+ν , (B.27)

while the exponential eX itself is bounded by

‖eX‖∞ ≤∑k

|exk |nk−1∑q=0

1q!ν

q ≤ Deα+ν . (B.28)

Spectral representation of adX : We can also construct the spectral representationof adX = [X, q ] from the spectral representation of X in Eq. (B.17) as

adX =∑k,`

(xkPk + Nk) q P` −∑k,`

Pk q (x`P` − N`)

=∑k,`

(xk − x`)Pk q P` +∑k,`

(Nkq P` − Pk q N`)

=∑m

(λmPm + Nm), (B.29)

where the spectrum λm of adX is given by the differences xk−x` among the eigenvaluesxk of X, and the spectral projections Pm and the nilpotents Nm are given by

Pm =∑k,`

δλm,xk−x`Pkq P`, Nm =

∑k,`

δλm,xk−x`(Nkq P` − Pk q N`). (B.30)

Note that Imλm ∈ (−2π, 2π) due to the restriction Im xk ∈ (φc, φc +2π). In this proof, weuse the norm induced by the infinity norm (∞–∞ norm) ‖A‖∞−∞ = sup‖X‖∞=1 ‖A(X)‖∞for superoperators. In this norm, the spectral projections Pm and the nilpotents Nm arebounded by

‖Pm‖∞−∞ ≤∑k,`

δλm,xk−x` ≤ D, ‖Nm‖∞−∞ ≤ 2ν∑k,`

δλm,xk−x` ≤ 2Dν. (B.31)

Since ν is tuned to satisfy the condition (B.23), we have

‖N (e)k ‖∞/R ≤ 1/2, ‖Nm‖∞−∞/R ≤ 1/2. (B.32)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 36

Bounding ‖Z(t) − X‖: We are now ready to bound the correction W (t). For Y =T−1ν Y Tν , we have

‖etY − I‖ ≤ et‖Y ‖ − 1 ≤ t‖Y ‖et‖Y ‖, ‖Y ‖∞ ≤ χν‖Y ‖∞. (B.33)

Then, for Z(t) = log(eXetY ), we use Lemma 9 to bound

‖Z(t)− X‖∞ = ‖log(eXetY )− X‖∞= ‖log[eX + eX(etY − I)]− log eX‖∞

≤M (2D/R)2‖eX(etY − I)‖∞1− (2D/R)‖eX(etY − I)‖∞

≤ (2MD/R) (2D2eα+ν/R)t‖Y ‖∞et‖Y ‖∞

1− (2D2eα+ν/R)t‖Y ‖∞et‖Y ‖∞, (B.34)

where we have bounded as [1 − (N/R)D]/(1 − N/R) ≤ 2 for N = maxk ‖N(e)k ‖∞, under

the condition in Eq. (B.32).

Bounding ‖g(adZ(t))− g(adX)‖: Next, by noting

‖adZ(t)− adX‖∞−∞ ≤ 2‖Z(t)− X‖∞, (B.35)

we use Lemma 9 to bound

‖g(adZ(t))− g(adX)‖∞−∞ ≤M(2D3/R)2‖adZ(t)− adX‖∞−∞

1− (2D3/R)‖adZ(t)− adX‖∞−∞

≤ (2MD3/R)(8MD4/R2) (2D2eα+ν/R)t‖Y ‖∞et‖Y ‖∞

1−(2D2eα+ν/R)t‖Y ‖∞et‖Y ‖∞

1− (8MD4/R2) (2D2eα+ν/R)t‖Y ‖∞et‖Y ‖∞1−(2D2eα+ν/R)t‖Y ‖∞et‖Y ‖∞

.

(B.36)

Therefore,

W (t) =∫ t

0ds [g(adZ(s))− g(adX)](Y )

= T−1ν

(∫ t

0ds [g(adZ(s))− g(adX)](Y )

)Tν (B.37)

is bounded by Eq. (B.19).

Remark 11. The conditions (B.23) can be relaxed to νeα+ν , 2Dν < R, but to get a simplerexpression for the bound we have strengthened the conditions to Eq. (B.23).Remark 12. If X is diagonalizable, we can set ν = 0 and replace R/2 with R in the bound(B.19). If X can be diagonalized by a unitary transformation, we can further set χν = 1.

C Proof of Lemma 3Here we prove one of our key lemmas, Lemma 3.

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 37

Proof of Lemma 3. We split En into two parts by the projection P as

En = PEnP + E′n, (C.1)

and consider the expansion

Enn = (PEnP + E′n)n

= (PEnP )n +bn2 c∑`=1

Rn,2` +bn2 c∑`=1

R′n,2` +bn−1

2 c∑`=1

Rn,2`+1 +bn−1

2 c∑`=1

R′n,2`+1 + E′nn (C.2)

with

Rn,2` =∑

k,k′∈N`|k|+|k′|=n

(PEnP )k1E′k′1n (PEnP )k2E

′k′2n · · · (PEnP )k`E′k

′`

n , (C.3)

R′n,2` =∑

k,k′∈N`|k|+|k′|=n

E′k′1n (PEnP )k1E

′k′2n (PEnP )k2 · · ·E′k

′`

n (PEnP )k` , (C.4)

Rn,2`+1 =∑

k∈N`+1, k′∈N`|k|+|k′|=n

(PEnP )k1E′k′1n (PEnP )k2E

′k′2n · · ·E

′k′`n (PEnP )k`+1 , (C.5)

R′n,2`+1 =∑

k∈N`, k′∈N`+1

|k|+|k′|=n

E′k′1n (PEnP )k1E

′k′2n (PEnP )k2 · · · (PEnP )k`E

′k′`+1n , (C.6)

where k = (k1, . . . , kj) and k′ = (k′1, . . . , k′j) are multi-indices of integers with j = ` or`+ 1, |k| = k1 + · · ·+ kj denotes the order of k, and bxc denotes the greatest integer lessthan or equal to x. We are going to show that the corrections to the first contribution(PEnP )n in Eq. (C.2) accumulate only up to O(1/n).

We first note that, since PE′nP = 0 by construction, the contributions with k′i = 1for some i between two (PEnP )’s vanish and do not contribute to Rm or R′m. Therefore,k′i ≥ 2 for any i sandwiched by (PEnP )’s. Second, PEn = EnP + O(1/n) [Eq. (5.10) incondition 1] implies

PEnP = PEn +O(1/n) = EnP +O(1/n), (C.7)

and hence, since E′n = En − PEnP ,

PE′n = O(1/n), E′nP = O(1/n). (C.8)

Therefore, each contact between PEnP and E′n yields O(1/n), and we are advised tocount the number of the contacts in the corrections to see the orders of the contributions:R2` and R′2` have (2`− 1) contacts, while R2`+1 and R′2`+1 have 2` contacts. Third, since‖PEnP‖ and ‖E′n‖ can be greater than 1, it is not helpful to bound the corrections like‖(PEnP )k1E

′k′1n · · · ‖ ≤ ‖PEnP‖k1‖E′n‖k

′1 · · · . On the other hand, we have the bounds

(5.11) and (5.12) (conditions 2 and 3), which facilitate bounding the corrections.Let us start estimating the corrections. Thanks to Eq. (5.12) (condition 3), the last

correction in Eq. (C.2) is bounded by

‖E′nn ‖ ≤ Kµn, (C.9)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 38

which is o(1/n) as n→ +∞.Let us set

Cn = max‖E′nP‖, ‖PE′n‖ = O(1/n), (C.10)

where we have used Eq. (C.8). By the bounds (5.11) and (5.12) (conditions 3 and 4), thecorrection Rn,2` is bounded as

‖Rn,2`‖ ≤∑

k∈N`, k′≥(2,...,2,1)|k|+|k′|=n

‖(PEnP )k1‖‖PE′n‖‖E′k′1−2n ‖‖E′nP‖‖(PEnP )k2‖ · · ·

· · · ‖E′k′`−1−2n ‖‖E′nP‖‖(PEnP )k`‖‖PE′n‖‖E

′k′`−1n ‖

≤M `K`C2`−1n

∑k∈N`, k′≥(2,2,...,1)|k|+|k′|=n

µ|k′|−2`+1

= M `K`C2`−1n

∑k′∈N`

|k′|≤n−2`+1

µ|k′|−` ∑

k∈N`|k|=n−|k′|−`+1

1

= M `K`C2`−1n

∑k′∈N`

|k′|≤n−2`+1

(n− |k′| − `

`− 1

)µ|k′|−`

≤M `K`C2`−1n

n`−1

(`− 1)!∑k′∈N`

|k′|≤n−2`+1

µ|k′|−`

≤M `K`C2`−1n

n`−1

(`− 1)!1

(1− µ)`

≡ an,`, (C.11)

where we have used the identities

∑k∈N`|k|=m

1 =(m− 1`− 1

),

∑k∈N`

µ|k|−` =(∑j≥0

µj)`

= 1(1− µ)` , (C.12)

and the inequality (n−mj

)≤ nj

j! . (C.13)

The correction R′n,2` is bounded as

‖R′n,2`‖ ≤∑

k∈N`, k′≥(1,2,...,2)|k|+|k′|=n

‖E′k′1−1

n ‖‖E′nP‖‖(PEnP )k1‖‖PE′n‖‖E′k′2−2n ‖ · · ·

· · · ‖(PEnP )k`−1‖‖PE′n‖‖E′k′`−2n ‖‖E′nP‖‖(PEnP )k`‖

≤M `K`C2`−1n

∑k∈N`, k′≥(1,2,...,2)|k|+|k′|=n

µ|k′|−2`+1

= M `K`C2`−1n

∑k′∈N`

|k′|≤n−2`+1

µ|k′|−` ∑

k∈N`|k|=n−|k′|−`+1

1

≤ an,`, (C.14)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 39

as for ‖Rn,2`‖.The correction Rn,2`+1 is bounded as

‖Rn,2`+1‖ ≤∑

k∈N`+1, k′≥(2,...,2)|k|+|k′|=n

‖(PEnP )k1‖‖PE′n‖‖E′k′1−2n ‖‖E′nP‖‖(PEnP )k2‖ · · ·

· · · ‖(PEnP )k`‖‖PE′n‖‖E′k′`−2n ‖‖E′nP‖‖(PEnP )k`+1‖

≤M `+1K`C2`n

∑k∈N`+1, k′≥(2,...,2)|k|+|k′|=n

µ|k′|−2`

= M `+1K`C2`n

∑k′∈N`

|k′|≤n−2`−1

µ|k′|−` ∑

k∈N`+1

|k|=n−|k′|−`

1

= M `+1K`C2`n

∑k′∈N`

|k′|≤n−2`−1

(n− |k′| − `− 1

`

)µ|k′|−`

≤M `+1K`C2`n

n`

`!1

(1− µ)`

≡ bn,`. (C.15)Finally, the correction R′n,2`+1 is bounded as

‖R′n,2`+1‖ ≤∑

k∈N`, k′≥(1,2,...,2,1)|k|+|k′|=n

‖E′k′1−1

n ‖‖E′nP‖‖(PEnP )k1‖‖PE′n‖‖E′k′2−2n ‖ · · ·

· · · ‖E′k′`−2

n ‖‖E′nP‖‖(PEnP )k`‖‖PE′n‖‖E′k′`+1−1n ‖

≤M `K`+1C2`n

∑k∈N`, k′≥(1,2,...,2,1)

|k|+|k′|=n

µ|k′|−2`

= M `K`+1C2`n

∑k′∈N`+1

µ|k′|−`−1 ∑

k∈N`|k|=n−|k′|−`+1

1

= M `K`+1C2`n

∑k′∈N`+1

(n− |k′| − `

`− 1

)µ|k′|−`−1

≤M `K`+1C2`n

n`−1

(`− 1)!1

(1− µ)`+1

≡ cn,`. (C.16)Collecting all these bounds, the correction to the leading contribution (PEnP )n in Eq.

(C.2) is bounded by∥∥∥∥∥bn2 c∑`=1

Rn,2` +bn2 c∑`=1

R′n,2` +bn−1

2 c∑`=1

Rn,2`+1 +bn−1

2 c∑`=1

R′n,2`+1 + E′nn

∥∥∥∥∥≤ 2

∞∑`=1

an,` +∞∑`=1

bn,` +∞∑`=1

cn,` +Kµn

= M

[(1 + K

1− µCn)2

eMK1−µnC

2n − 1

]+Kµn

= O(1/n), (C.17)

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 40

since Cn = O(1/n) by Eq. (C.10). This proves the lemma.

References[1] T. Albash and D. A. Lidar, Adiabatic Quantum Computation, Rev. Mod. Phys. 90,

015002 (2018).

[2] M. Müller, S. Diehl, G. Pupillo, and P. Zoller, Engineered Open Systems and QuantumSimulations with Atoms and Ions, in Advances in Atomic, Molecular, and OpticalPhysics, edited by P. Berman, E. Arimondo, and C. Lin (Elsevier, Amsterdam, 2012),Vol. 61, pp. 1–80.

[3] F. Arute et al., Quantum Supremacy Using a Programmable Superconducting Proces-sor, Nature 574, 505 (2019).

[4] A. Messiah, Quantum Mechanics (Dover, New York, 2017).

[5] T. Kato, On the Adiabatic Theorem of Quantum Mechanics, J. Phys. Soc. Jpn. 5, 435(1950).

[6] M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information,10th anniversary ed. (Cambridge University Press, Cambridge, 2010).

[7] R. Alicki and K. Lendi, Quantum Dynamical Semigroups and Applications, 2nd ed.(Springer, Berlin, 2007).

[8] D. Chruściński and S. Pascazio, A Brief History of the GKLS Equation, Open Sys.Inf. Dyn. 24, 1740001 (2017).

[9] P. Krantz, M. Kjaergaard, F. Yan, T. P. Orlando, S. Gustavsson, and W. D. Oliver,A Quantum Engineer’s Guide to Superconducting Qubits, Appl. Phys. Rev. 6, 021318(2019).

[10] B. C. Hall, Lie Groups, Lie Algebras, and Representations: An Elementary Introduc-tion, 2nd ed. (Springer, Cham, 2015).

[11] D. Burgarth, P. Facchi, H. Nakazato, S. Pascazio, and K. Yuasa, Generalized AdiabaticTheorem and Strong-Coupling Limits, Quantum 3, 152 (2019).

[12] M. Fraas, Quantum Adiabatic Theory Ventures into Zeno Dynamics, Quantum Views3, 18 (2019).

[13] P. Facchi, S. Tasaki, S. Pascazio, H. Nakazato, A. Tokuse, and D. A. Lidar, Controlof Decoherence: Analysis and Comparison of Three Different Strategies, Phys. Rev. A71, 022302 (2005).

[14] P. Facchi and S. Pascazio, Quantum Zeno Dynamics: Mathematical and PhysicalAspects, J. Phys. A: Math. Theor. 41, 493001 (2008).

[15] B. Misra and E. C. G. Sudarshan, The Zeno’s Paradox in Quantum Theory, J. Math.Phys. 18, 756 (1977).

[16] P. Facchi, H. Nakazato, and S. Pascazio, From the Quantum Zeno to the InverseQuantum Zeno Effect, Phys. Rev. Lett. 86, 2699 (2001).

[17] P. Facchi, D. A. Lidar, and S. Pascazio, Unification of Dynamical Decoupling and theQuantum Zeno Effect, Phys. Rev. A 69, 032314 (2004).

[18] J. Z. Bernád, Dynamical Control of Quantum Systems in the Context of Mean ErgodicTheorems, J. Phys. A: Math. Theor. 50, 065303 (2017).

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 41

[19] L. S. Schulman, Continuous and Pulsed Observations in the Quantum Zeno Effect,Phys. Rev. A 57, 1509 (1998).

[20] P. Facchi and S. Pascazio, Quantum Zeno Subspaces, Phys. Rev. Lett. 89, 080401(2002).

[21] S. Pascazio, On Noise-Induced Superselection Rules, J. Mod. Opt. 51, 925 (2004).

[22] O. Oreshkov and J. Calsamiglia, Adiabatic Markovian Dynamics, Phys. Rev. Lett.105, 050503 (2010).

[23] P. Zanardi and L. Campos Venuti, Coherent Quantum Dynamics in Steady-State Man-ifolds of Strongly Dissipative Systems, Phys. Rev. Lett. 113, 240406 (2014).

[24] P. Zanardi and L. Campos Venuti, Geometry, Robustness, and Emerging Unitarity inDissipation-Projected Dynamics, Phys. Rev. A 91, 052324 (2015).

[25] J. Marshall, L. Campos Venuti, and P. Zanardi, Noise Suppression via Generalized-Markovian Processes, Phys. Rev. A 96, 052113 (2017).

[26] E. W. Streed, J. Mun, M. Boyd, G. K. Campbell, P. Medley, W. Ketterle, and D. E.Pritchard, Continuous and Pulsed Quantum Zeno Effect, Phys. Rev. Lett. 97, 260402(2006).

[27] F. Schäfer, I. Herrera, S. Cherukattil, C. Lovecchio, F. S. Cataliotti, F. Caruso, andA. Smerzi, Experimental Realization of Quantum Zeno Dynamics, Nat. Commun. 5,3194 (2014).

[28] L. Viola and S. Lloyd, Dynamical Suppression of Decoherence in Two-State QuantumSystems, Phys. Rev. A 58, 2733 (1998).

[29] L. Viola, E. Knill, and S. Lloyd, Dynamical Decoupling of Open Quantum Systems,Phys. Rev. Lett. 82, 2417 (1999).

[30] D. Vitali and P. Tombesi, Using Parity Kicks for Decoherence Control, Phys. Rev. A59, 4178 (1999).

[31] P. Zanardi, Symmetrizing Evolutions, Phys. Lett. A 258, 77 (1999).

[32] L.-M. Duan and G.-C. Guo, Suppressing Environmental Noise in Quantum Computa-tion through Pulse Control, Phys. Lett. A 261, 139 (1999).

[33] L. Viola, Quantum Control via Encoded Dynamical Decoupling, Phys. Rev. A 66,012307 (2002).

[34] C. Uchiyama and M. Aihara, Multipulse Control of Decoherence, Phys. Rev. A 66,032313 (2002).

[35] F. Ticozzi, L. Zuccato, P. D. Johnson, and L. Viola, Alternating Projections Methodsfor Discrete-Time Stabilization of Quantum States, IEEE Trans. Autom. Control 63,819 (2018).

[36] K. Macieszczak, M. Guţă, I. Lesanovsky, and J. P. Garrahan, Towards a Theory ofMetastability in Open Quantum Dynamics, Phys. Rev. Lett. 116, 240404 (2016).

[37] V. V. Albert, B. Bradlyn, M. Fraas, and L. Jiang, Geometry and Response of Lind-bladians, Phys. Rev. X 6, 041031 (2016).

[38] P. Facchi and M. Ligabò, Quantum Zeno Effect and Dynamics, J. Math. Phys. 51,022103 (2010).

[39] D. Burgarth, P. Facchi, G. Gramegna, and S. Pascazio, Generalized Product Formulasand Quantum Control, J. Phys. A: Math. Theor. 52, 435301 (2019).

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 42

[40] M. M. Wolf and J. I. Cirac, Dividing Quantum Channels, Commun. Math. Phys. 279,147 (2008).

[41] G. A. Paz-Silva, A. T. Rezakhani, J. M. Dominy, and D. A. Lidar, Zeno Effect forQuantum Computation and Control, Phys. Rev. Lett. 108, 080501 (2012).

[42] J. M. Dominy, G. A. Paz-Silva, A. T. Rezakhani, and D. A. Lidar, Analysis of theQuantum Zeno Effect for Quantum Control and Computation, J. Phys. A: Math.Theor. 46, 075306 (2013).

[43] Y. Li, D. A. Herrera-Martí, and L. C. Kwek, Quantum Zeno Effect of General Quan-tum Operations, Phys. Rev. A 88, 042321 (2013).

[44] T. Kato, Perturbation Theory for Linear Operators, 2nd ed. (Springer, Berlin, 1980).

[45] M. M. Wolf, “Quantum Channels & Operations: Guided Tour,” URL: https://www-m5.ma.tum.de/foswiki/pub/M5/Allgemeines/MichaelWolf/QChannelLecture.pdf.

[46] J. Watrous, The Theory of Quantum Information (Cambridge University Press, Cam-bridge, 2018).

[47] N. J. Higham, Functions of Matrices: Theory and Computation (SIAM, Philadelphia,2008).

[48] R. A. Horn and C. R. Johnson, Topics in Matrix Analysis (Cambridge UniversityPress, Cambridge, 1991).

[49] P. D. Lax, Linear Algebra and Its Applications, 2nd ed. (Wiley, Hoboken, NJ, 2007).

[50] P. Exner and Y. Ichinose, A Product Formula Related to Quantum Zeno Dynamics,Ann. Henri Poincaré 6, 195 (2005).

[51] C. Arenz, D. Burgarth, P. Facchi, and R. Hillier, Dynamical Decoupling of UnboundedHamiltonians, J. Math. Phys. 59, 032203 (2018).

[52] D. Burgarth, P. Facchi, M. Fraas, and R. Hillier, A Quantum Environment Leading toNon-Exponential Decay with Zeno Region Which Cannot be Dynamically Decoupled,arXiv:1904.03627 [quant-ph].

[53] O. Szehr, D. Reeb, and M. M. Wolf, Spectral Convergence Bounds for Classical andQuantum Markov Processes, Commun. Math. Phys. 333, 565 (2015).

[54] B. M. Terhal and D. P. DiVincenzo, Problem of Equilibration and the Computation ofCorrelation Functions on a Quantum Computer, Phys. Rev. A 61, 022301 (2000).

[55] D. Pérez-García, M. M. Wolf, D. Petz, and M. B. Ruskai, Contractivity of Positiveand Trace-Preserving Maps under Lp Norms, J. Math. Phys. 47, 083506 (2006).

[56] V. Paulsen, Completely Bounded Maps and Operator Algebras (Cambridge UniversityPress, Cambridge, 2002).

[57] G. H. Golub and C. F. Van Loan, Matrix Computations, 4th ed. (Johns HopkinsUniversity Press, Baltimore, 2013).

[58] S. Blanes and F. Casas, On the Convergence and Optimization of the Baker-Campbell-Hausdorff Formula, Linear Algebra Appl. 378, 135 (2004).

[59] S. Blanes, F. Casas, J. A. Oteo, and J. Ros, The Magnus Expansion and Some of ItsApplications, Phys. Rep. 470, 151 (2009).

[60] R. A. Horn and C. R. Johnson, Matrix Analysis, 2nd ed. (Cambridge University Press,Cambridge, 2012).

Accepted in Quantum 2020-06-30, click title to verify. Published under CC-BY 4.0. 43