Skript zur Vorlesung - Institut für Theoretische Informatik · 2 Klassische Kryptosysteme 2.1...
Transcript of Skript zur Vorlesung - Institut für Theoretische Informatik · 2 Klassische Kryptosysteme 2.1...

Skript zur Vorlesung:
Kryptologie
Sommersemester 2007
Dr. Andreas Jakoby
Institut fur Theoretische InformatikUniversitat zu Lubeck


Inhaltsverzeichnis
1 Einfuhrung 1
2 Klassische Kryptosysteme 3
2.1 Zwei-Wege Kryptosysteme: Das Kryptosystem von Julius Caesar . . . . . . . . . . . . 3
2.2 Affine Kryptosysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 6
2.3 Das PLAYFAIR-System . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
2.4 Polyalphabetische Kryptosysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.4.1 Vigenere System . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.4.2 Die Kryptoanalyse des Vigenere Verfahrens . . . . . . . . . . . . . . . . . . . . 11
2.4.3 Die Kryptoanalyse bei unbekannter Schlussellange: Der Kasiski-Test . . . . . . 12
2.4.4 Der Friedman-Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.4.5 Eine Verallgemeinerung des Vigenere Verfahrens . . . . . . . . . . . . . . . . . 17
2.5 Rotor-Chiffriermaschinen: Die Enigma . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3 Der Begriff der Sicherheit 22
3.1 Kryptosysteme mit perfekter Sicherheit . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3.2 A priori Annahmen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
3.2.1 Variante 1: 1-Gramm-Quellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.2.2 Variante 2: 2-Gramm-Quellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3.2.3 Variante 3: Markov-Ketten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 30
3.3 Bayes’scher Ansatz in der Kryptoanalyse . . . . . . . . . . . . . . . . . . . . . . . . . . 31
4 Symmetrische Verschlusselungsalgorithmen 35
4.1 Der Data Encryption Standard (DES) . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.1.1 Aufbau des DES-Kryptosystems . . . . . . . . . . . . . . . . . . . . . . . . . . 35
4.1.2 Berechnung der Funktion f . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 37
4.1.3 Die Teilschlussel Ki . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
4.1.4 Die Entschlusseloung eines DES-Cyphertextes . . . . . . . . . . . . . . . . . . . 41
I

4.2 Das Triple DES-Kryptosystem (TDES) . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4.3 Iterierte Blockkryptosysteme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4.4 Differentielle Kryptoanalyse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
4.5 Lineare Kryptoanalyse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
4.5.1 Ein erster Algorithmus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51
4.5.2 Zusammensetzung von affin-linearen Approximationen . . . . . . . . . . . . . . 52
4.5.3 Angriff auf den letzten Rundenschlussel fur ein SPN-Kryptosystem . . . . . . . 55
4.6 Advanced Encryption Standard (AES) . . . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.6.1 Mathematische Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 57
4.6.2 Zustand des AES . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
4.6.3 Die Unterfunktionen des AES . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
4.6.4 Die Rundenschlussel beim AES . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
4.6.5 Der AES-Algorithmus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
5 Public Key Kryptographie 69
5.1 Das generelle Schema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 69
5.2 Das Merkle-Hellman Kryptosystem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
5.2.1 Konstruktion des offentlichen Schlussels . . . . . . . . . . . . . . . . . . . . . . 71
5.2.2 Entschlusselungsverfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
5.2.3 Attacke von Shamir . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
5.3 Probleme aus der Zahlentheorie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74
5.3.1 Grundlegende Probleme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
5.4 Das RSA-Kryptosystem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
II

1 Einfuhrung
Die Geschichte der Kryptologie geht zuruck bis in die Antike. Die Anwendungsbereiche der Kryptologiesind historisch mehr im militarischen Bereich angesiedelt, jedoch gelangte die Kryptologie im Verlaufedes letzten Jahrhunderts immer mehr ins Zentrum des allgemeinen Interesses. So benutzen wir heutefast alltaglich kryptographische Protokolle beim elektronischen Zahlungsverkehr oder beim Umgangmit einem Geldautomaten.
Die Kryptologie besteht aus zwei wesentlichen Disziplinen:
1. der Kryptographie, d.h. die Kunst eine Nachricht zu verschlusseln, so dass es fur einen Unbe-fugten nicht moglich ist diese zu lesen oder zu manipulieren, und
2. der Kryptoanalyse, d.h. der Kunst dieses doch zu tun.
Das allgemeine Szenario in der Kryptologie besteht aus drei Personen, die wir Alice, Bob und Evenennen. Alice mochte eine Nachricht uber einen unsicheren Kanal an Bob senden, so dass es furEve, die Zugriff auf den Kanal hat, nicht moglich ist den Inhalt der Nachricht zu erkennen oder zumanipulieren. Wir konnen also folgendes Bild fur das Basismodell der Kryptologie zeichnen:
Verschlusselt die
Nachricht und
sendet sie an Bob.
unsicherer Kanal
unsicherer Kanal
Eve:Greift auf den Kanal zu, versucht
die verschlusselte Nachricht zu
entschlusseln oder zu andern.
Bob:Empfangt die verschlusselte
Nachricht und entschlusselt
sie.
Alice:
Abbildung 1: Basismodell der Kryptologie.
Die Nachricht, die von Alice an Bob gesendet werden soll, nennen wir Plaintext und die verschlusselteNachricht Ciphertext. Um ein praktikables Kryptosystem zu erhalten, muss sichergestellt sein, dass
1. die Verschlusselung des Plaintextes fur Alice einfach zu berechnen ist,
2. die Entschlusselung des Ciphertextes fur Bob einfach zu berechnen ist und
3. die Entschlusselung bzw. die Manipulation des Ciphertextes fur Eve nur mit enormen Aufwandmoglich ist.
Die klassische Losung dieser Problemstellung fuhrt uns zu den sogenannten Secret-Key-Krypto-systemen, wo sowohl Alice als auch Bob einen geheimen Schlussel besitzen, der es ihnen erlaubt einenPlaintext effizient zu verschlusseln bzw. den Ciphertext effizient zu entschlusseln.
Bevor wir auf verschiedene Kryptoverfahren im Detail eingehen, wollen wir den Begriff der Sicherheitnaher formalisieren. Zunachst mussen wie hierbei die Rolle von Eve etwas naher betrachten. Wir oben
1

gesagt, versucht Eve den Ciphertext zu entschlusseln oder zu manipulieren. Prinzipiell konnen wirzwei verschiedene Formen einer solchen Attacke unterscheiden:
1. Die aktive Attacke: Hierbei erlauben wir es Eve die Nachricht von Alice an Bob zu verandern.
2. Die passive Attacke: Hierbei ist es Eve nur erlaubt die Nachricht von Alice an Bob abzuhoren.Bestehend auf diesem Wissen kann Eve versuchen den Plaintext zu bestimmen.
Erlauben wir aktive Attacken, so mussen wir zunachst die Frage beantworten, welches Ziel Eve verfolgt.So ist es moglich, dass sie nur den Ciphertext entschlusseln mochte oder aber diesen so manipulierenwill, dass Bob eine falsche Nachricht erhalt. Da sich diese Frage bei passiven Attacke nicht stellt,konnen wir fur diesen Fall eine einfache Definition angeben, die auf der Ununterscheidbarkeit derKommunikation zwischen Alice und Bob basiert. Wir definieren hierfur zunachst:
Definition 1 Seien X = {Xi}i∈N und Y = {Yi}i∈N zwei Familien von Zufallsvariablen, wobei wirfur ein festes Polynom p die Variablen Xi, Yi nur Werte aus {0, 1}≤p(i) annehmen. Dann nennenwir X und Y ununterscheidbar, wenn fur alle i und alle w ∈ {0, 1}≤p(i) gilt
Pr[Xi = w] = Pr[Yi = w] .
Wir nennen X, Y statistisch ununterscheidbar, wenn fur alle Polynome q und fur alle hinrei-chend große i gilt ∑
w∈{0,1}≤p(i)
|Pr[Xi = w] − Pr[Yi = w]| ≤ 1q(i)
.
Wir nennen X, Y berechenbar ununterscheidbar, wenn fur alle probabilistischen polynomial-zeitbeschrankten Algorithmen E , fur alle Polynome q und fur alle hinreichend große i gilt
|Pr[E(i,Xi) = 1] − Pr[E(i, Yi) = 1]| ≤ 1q(i)
.
Als Xi und Yi konnen wir die moglichen Kommunikationssequnezen zwischen Alice und Bob bzw.den ubertragenen Ciphertext bei einem Plaintext x bzw. y sehen. Wunschenswert ware es, wenn einKryptosystem so sicher ware, dass Eve keinen Unterschied zwischen dem moglichen Ciphertexten fur xund y erkennen konnte. Dieses wurde bedeuten, dass Xi und Yi ununterscheidbar sind. Die wenigenKryptosysteme, welche diese Sicherheit gewahrleisten sind sogenannte One-Time Pad Verfahren.
Betrachten wir nun die Definition von berechenbarer Ununterscheidbarkeit. Den Algorithmus E ,den wir hier herangezogen haben, konnen wir als die Attacke von Eve betrachten, die das Ver-schlusselungsverfahren von Alice polynomiell oft befragen bzw. belauschen kann. Ware die Differenz|Pr[E(i,Xi) = 1] − Pr[E(i, Yi) = 1]| großer als 1
q(i) fur ein Polynom q , dann konnte Eve nach q(i)Versuchen mit großer Wahrscheinlichkeit zwischen x und y unterscheiden. Das Verfahren ware alsonicht besonders sicher. Es ware somit erstrebenswert, wenn ein Kryptosystem zumindest berechenbareUnunterscheidbarkeit der Ciphertexte gewahrleisten konnte. Leider konnte diese Gute fur die meistenheute benutzten Kryptosystem (noch) nicht nachgewiesen werden – jedoch auch nicht das Gegenteil.Nichtsdestotrotz stellen diese Verfahren einen wesentlichen Pfeiler der Informatik dar.
Mit diesem etwas dusteren Bild, dass nur zur Vorsicht mahnen soll, wollen wir die Vorlesung beginnen.
2

2 Klassische Kryptosysteme
2.1 Zwei-Wege Kryptosysteme: Das Kryptosystem von Julius Caesar
Sei Σ = {A, . . . , Z, β} das lateinische Alphabet, wobei β das Leerzeichen darstellt. Die Verschlusse-lung erfolgt mit Hilfe einer einfachen Permutation der Buchstaben. Hierzu schreiben wir zunachst dieSymbole aus Σ in eine Reihe und dann diese Symbole noch einmal geshiftet darunter. Ein Beispielist in der folgenden Tabelle illustriert.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z βY Z β A B C D E F G H I J K L M N O P Q R S T U V W X
Um einen Plaintext zu verschlusseln oder den Ciphertext zu entschlusseln, genugt es die Zeichendes entsprechenden Textes gemaß der Tabelle zu ersetzen, d.h. im Plaintext ersetzen wir A durchY, B durch Z usw. Analog ersetzen wir im Ciphertext Y durch A, Z durch B usw. Das angegebeneVerfahren erfullt somit die ersten beiden Bedingungen, die wir an ein Kryptoverfahren gestellt haben.Es verbleibt somit noch zu untersuchen, ob ein Ciphertext auch schwierig fur Eve zu entschlusseln ist,d.h. wie schwierig die Kryptoanalyse fur dieses Verfahren ist.
Wir unterscheiden bei der Kryptoanalyse zwei Szenarien:
1. Das Kryptosystem, welches fur die Verschlusselung herangezogen wurde, ist unbekannt.
2. Das Kryptosystem, welches fur die Verschlusselung herangezogen wurde, ist bekannt, aber deraktuelle Schlussel ist unbekannt.
Im Folgenden gehen wir davon aus, dass das Kryptosystem bekannt ist. Fur diese Annahme sprechendrei Grunde:
• Ist das Verfahren sicher in diesem Fall, dann ist es auch sicher fur den Fall, dass das Systemnicht bekannt ist.
• Die Erfahrung zeigt, dass sich die Struktur eines Kryptosystems im Allgemeinen nicht langegeheim halten lasst.
• Die Anzahl der bekannten Kryptosysteme ist recht klein, daher ist es im Prinzip moglich allesinnvollen Verfahren parallel zu attackieren.
Als nachstes mussen wir uns fragen, welche Informationen Eve zur Verfugung stehen. Hierbei zeigensich mehrere Moglichkeiten:
1. nur den Ciphertext,
2. Ciphertexte und einige dazugehorige Plaintexte oder
3. Ciphertexte und einige dazugehorige Plaintexte, die von Eve bestimmt werden konnen, d.h. Evekann Alice dazu zwingen einige bestimmt Texte zu verschlusseln.
3

In der Praxis tauchen je nach Form der Attacke alle drei Falle auf. Es ist daher interessant allediese Falle zu untersuchen. Da es sich bei dem Verfahren von Caesar um einen einfache zyklischeShiftoperation handelt, kann ein entsprechend verschlusselter Ciphertext sehr einfach entschlusseltwerden.
Wir wollen nun versuchen das Caesar-Kryptoverfahren zu verallgemeinern. Hierzu fuhren wir folgendeAbstraktion durch:
Transformiere jede Einheit des Plaintexts und jede Einheit des Ciphertexts in ein mathe-matisches Objekt, welches wir einfach manipulieren konnen. Diese Transformation soll ef-fizient zu berechnen sein. Fur das Caesar-Kryptosystem ist dieses der Z26 = {0, . . . , 26} .Diese Transformation hat den Vorteil, dass wir jetzt auf die Operationen Addition undMultiplikation (modulo 27) zuruckgreifen konnen. Im Folgenden identifizieren wir oft dieTexteinheiten und deren mathematische Reprasentation.
Das Caesar-Kryptosystem hat nun die Form f(x) = (x + r) mod 27 , wobei wir A durch 0, B durch1, usw. reprasentieren. In unserem Beispiel oben ist r = 24 .
Allgemein konnen wir das Caesar-Kryptosystem fur ein Alphabet der Große m fur ein r ∈ {0, . . . ,m−1} durch die Formel
f(x) = (x + r) mod m
darstellen. Der Schlussel bei diesem Verfahren ist somit r . Da es nur m Moglichkeiten gibt denSchlussel zu wahlen, folgt die Unsicherheit dieses Verfahrens aus folgender Beobachtung:
Beobachtung 1 Damit ein Kryptosystem sicher ist, muss es eine große Auswahl von moglichenSchlusseln geben.
Um die Anzahl der Schlussel zu vergroßern, konnen wir zwei mogliche Verallgemeinerungen vornehmen:
1. Wir fassen eine Folge von k Buchstaben zu einem Symbol zusammen, d.h. wir betrachtensogenannte k -Gramme. Sei x1 . . . xk ein solches k -Gramm, dann erhalten wir folgende Ver-schlusselungsformel:
f(x1 . . . xk) =
(r +
k∑i=1
xi ·mi−1
)mod mk mit r ∈ {0, . . . ,mk − 1} .
Wir erhalten mk verschiedene Schlussel r .
2. Wir fuhren einen zweiten Schlussel ein und betrachten
f(x) = (a · x + r) mod m mit r, a ∈ {0, . . . ,m− 1} .
Es gibt somit m2 viele Schlussel (a, r) . Diese Verallgemeinerung hat jedoch den Nachteil, dassf nicht mehr injektiv sein muss: Sei (a, r) = (3, 3) und m = 27 , dann gilt f(8) = f(17) = 0 .
Sei a−1 das multiplikative Inverse zu a modulo m , d.h. a · a−1 mod m = 1 , dann gilt fur dieEntschlusselung
f−1(y) = (a−1 · y − a−1 · r) mod m .
Existiert das multiplikative Inverse von a , so konnen wir den Ciphertext effizient entschlusseln. Esgilt:
4

Lemma 1 Die Gleichung a ·x ≡ 1 mod m hat genau dann eine Losung, wenn a und m teilerfremdsind. Hat a · x ≡ 1 mod m eine Losung, so ist diese eindeutig.
Um die Wahl von a nicht unnotig einzuschranken, wahlen wir daher meistens eine Primzahl fur m .
Wenden wir uns nun wieder der Analyse der Sicherheit von Caesars Kryptoverfahren zu. Es gilt:
Theorem 1 Seien p eine Primzahl, a, r ∈ {0, . . . , p− 1} zwei Schlussel und x1, x2 ∈ {0, . . . , p− 1}zwei Nachrichten mit x1 6= x2 . Kennt Eve x1, x2, f(x1), f(x2) , so kann sie den Schlussel (a, r) desKryptosystems f(x) = (a · x + r) mod p einfach berechnen.
Beweis: Seien n1 = f(x1) und n2 = f(x1) . Es gilt
n1 − n2 ≡ a · (x1 − x2) mod p .
Da p eine Primzahl ist, existiert auch das multiplikative Inverse (x1 − x2)−1 von (x1 − x2) . MitHilfe dieses Wertes konnen wir a und schließlich r effizient bestimmen.
Eine weitere Verallgemeinerung von Caesars Kryptoverfahren erhalten wir, indem wir beliebige Per-mutationen der Buchstaben zulassen. In diesem Fall ist die Permutation selber der Schlussel. Manbeachte, dass es 27! viele Permutationen und somit 27! verschiedene Schlussel gibt. Es ist hierbeijedoch nicht notig alle diese Schlussel zu testen, da uns im Allgemeinen eine einfache Haufigkeitsana-lyse der Buchstaben in den moglichen Plaintexten und eine entsprechende Ersetzung der Buchstabenim Ciphertext weiter hilft. Eine Haufigkeitsanalyse der deutschen Sprache ergibt die folgende Tabelle
E N I R S A T U D18,46 % 11,42 % 8,02 % 7,14 % 7,04 % 5,38 % 5,22 % 5,01 % 4,94 %
Solche Tabelle muss man jedoch mit einer gewissen Vorsicht genießen, da die Haufigkeiten der Buch-staben oft vom Kontext der analysierten Texte abhangen. Um einen Text zu entschlusseln, machenwir jetzt eine Haufigkeitsanalyse der Buchstaben im Ciphertext und ersetzten das am haufigsten vorkommende Symbol im Ciphertext durch das Symbol, welches in unserer Tabelle das hochste Gewichthat, usw.
Aufgabe 1 Beweisen Sie Lemma 1.
Aufgabe 2 Bestimmen Sie die Komplexitat des Verfahrens aus dem Beweis von Theorem 1.
Aufgabe 3 Der nachfolgende Text ist mit Hilfe der Formel f(x) = (a · x + r) mod m entstanden.Bekannt ist, dass die Symbol Q und X am seltensten im Plaintext benutzt wurde. Bestimmen Sie denSchlussel (a, r) .
UELYMJLNQLHQXXLP β FNEQPLHTQETQCLTFYMZLUZSQZFUEJLOMZO β ZDECFOELMZLQZUSYML β RLETUDLWUZPLHTUOTLTFYMZL
UZSQZFUEJLYMJLZ β ELNJLAC β AQCLYAAXUOMEU β ZLCQD β XGQLQLMLA β Q
5

2.2 Affine Kryptosysteme
Wir betrachten wie zuvor ein endliches Alphabet Σ der Machtigkeit N . Wie schon im letzten Ab-schnitt konnen wir die Symbole aus Σ durch Zahlen aus ZN darstellen. Wir betrachten hierfureine bijektive Kodierungsfunktion C : Σ → ZN . Der Einfachheit halber erweitern wir die Funktion Cauch auf Zeichenfolgen. Ein Plaintext w = wm−1 . . . w0 kann somit auch als Zahl im ZNm dargestelltwerden:
C(w) =m−1∑i=0
C(wi) ·N i .
Wir konnen folglich w als eine m -stellige N -nare Zahl auffassen. Bei einem affinem Kryptosystemerhalten wir den verschlusselten Text durch die Transformation t
t(C(w)) =m−1∑i=0
yi ·N i = (a · C(w) + r) mod Nm mit a, r ∈ ZNm
wobei y0, . . . , ym−1 ∈ ZN . Die Zeichenfolge C−1(ym−1) . . . C−1(y0) gibt dann den Ciphertext wieder.
Als Schlussel dienen die beiden Zahlen (a, r) . Um eine Entschlusselung des Ciphertexts zu garantieren,verlangen wir, dass a und Nm teilerfremd sind, d.h. ggT(a,NM ) = 1 . Um den Text zu entschlusseln,benotigen wir die Zahlen (a, r) wobei a = a−1 mod Nm und r = Nm − a−1 · r mod Nm ist. DieSchlussel (a, r) und (a, r) mussen vom Sender, d.h. Alice, und dem Empfanger, d.h. Bob, sicheraufbewahrt werden.
Betrachten wir zunachst die Frage, wieviele Werte es fur a gibt, die wie als Schlussel wahlen konnen.Es gilt:
Die Menge aller Zahlen in Zn , die teilerfremd zu n sind bezeichnen wir mit
Z∗n = { k ∈ Zn | ggT(k, n) = 1 } .
Die Machtigkeit dieser Menge wird auch als Eulersche ϕ -Funktion bezeichnet. Es gilt
ϕ(n) = |Z∗n| = n ·∏
Primzahlen p mit ggT(p,n) 6=1
(1− 1
p
).
Wichtige Spezialfalle der ϕ -Funktion fur Primzahlen p, q und α ∈ N+ sind
ϕ(p) = p− 1ϕ(pq) = (p− 1)(q − 1)ϕ(pα) = pα−1(p− 1) .
Betrachten wir nun die Sicherheit dieses Kryptoverfahrens, so erkennen wir, das wir auch fur diesesVerfahren die in Theorem 1 beschriebene Attacke heranziehen konnen. Sind also einige Plaintexteund die dazugehorigen Ciphertexte bekannt, dann konnen wir den Schlussel effizient bestimmen. Wirwollen nun der Frage nachgehen, ob der Schlussel auch in dem Fall gefunden werden kann, wenn nurCiphertexte zur Verfugung stehen. Um eine mogliche Attacke besser zu verstehen, beginnen wir miteinem Beispiel:
Beispiel 1 Betrachten wir das lateinische Alphabet Σ = {β, A,B, . . . , Z} und die Kodierungsfunk-tion C , die den Elementen von Σ in der oben gegebenen Reihenfolge die Werte von 0 bis 26
6

zuordnet. Ferner betrachten wir den Schlussel (7, 26) . Dann gilt C(KL) = 309 , t(C(KL)) = 2 undC−1(T (C(KL))) = βB sowie C(ZL) = 714 , t(C(ZL)) = 650 und C−1(T (C(ZL))) = XB . Indiesem Beispiel haben sowohl die Plaintexte als auch die Ciphertexte den gleichen Suffix. Es stellt sichalso die Frage, ob dieses immer der Fall ist, d.h. haben Ciphertexte immer den gleichen Suffix, wenndie dazugehorigen Plaintexte den gleichen Suffix haben?
Theorem 2 Sei Σ ein festes endliches nicht leeres Alphabet mit |Σ| = N und m eine feste Plain-textlange. Ferner sein (a, r) ein Schlussel mit ggT(a,Nm) = 1 und w,w′ ∈ Σm zwei Nachrichten,die einen gemeinsamen Suffix der Lange i ≤ m haben, dann haben fur alle KodierungsfunktionenC : Σ → ZN auch die Ciphertexte C−1(t(C(w))) und C−1(t(C(w′))) einen gemeinsamen Suffix derLange i .
Beweis: Sei C(w) =∑m−1
j=0 C(wj)·N j =∑m−1
j=0 xj ·N j und C(w′) =∑m−1
j=0 C(w′j)·N j =∑m−1
j=0 x′j ·N j
wobei fur alle j < i gilt xj = x′j . Ferner sei
y = t(C(w)) = a · w + r mod Nm =m−1∑j=0
yj ·N j
y′ = t(C(w′)) = a · w′ + r mod Nm =m−1∑j=0
y′j ·N j .
Wir haben zu zeigen, dass fur alle j < i gilt yj = y′j . Nach Konstruktion gilt:
a ·m−1∑j=0
xj ·N j +r ≡m−1∑j=0
yj ·N j mod Nm und a ·m−1∑j=0
x′j ·N j +r ≡m−1∑j=0
y′j ·N j mod Nm .
Betrachten wir die N -nare Darstellung von a und r , so folgt aus diesen Aquivalenzen fur alle ` ≤ m :
a ·m−1∑j=0
xj ·N j + r ≡ a ·`−1∑j=0
xj ·N j + r =`−1∑j=0
yj ·N j mod N `
a ·m−1∑j=0
x′j ·N j + r ≡ a ·`−1∑j=0
x′j ·N j + r =`−1∑j=0
y′j ·N j mod N `
Aus der Annahme, dass xj = x′j fur alle j < i , folgt unmittelbar, dass
`−1∑j=0
xj ·N j + r =`−1∑j=0
x′j ·N j + r mod N i .
Da die N -nare Reprasentation einer Zahl eindeutig ist, folgt die Gleichheit der Werte yj und y′j furalle j < i .
Kombinieren wir Theorem 2 mit einer Haufigkeitsanalyse, so konnen wir sukzessive die Suffixe derNachricht dekodieren. Wir fassen hierbei den geratenen Suffix der Lange ` als tatsachlichen Suffixder Nachricht auf und konnen den Schlussel – oder besser einen moglichen Schlussel – modulo N `
bestimmen. Wir beginnen somit mit dem Schlussel modulo N , mit Hilfe dieses Schlussels bestimmenwir den Schlussel modulo N2 , u.s.w.
Aufgabe 4 Beweisen Sie, dass ein affines Kryptosystem mit Schlusseln (a, r) ∈ N2 und a, r <Nm bei einmaliger Anwendung und einem Plaintext w ∈ Σm perfekte Sicherheit bietet, d.h. dieZufallsvariablen der Ciphertexte fur alle Plaintexte aus Σm sind ununterscheidbar.
7

Aufgabe 5 Geben Sie ein Verfahren an, mit dessen Hilfe ein affines Kryptosystem mit Schlusseln(a, r) ∈ N2 und a, r < Nm geknackt werden kann. Gehen Sie hierbei davon aus, dass fur ein hinrei-chend großes k der Plaintext die Lange m · k hat und daher in k Blocke Bi der Lange m zerlegtwurde. Jeder dieser Blocke wurde anschließend mit Hilfe der gleichen Schlussel verschlusselt.
2.3 Das PLAYFAIR-System
Um die oben beschriebene Schwache der affinen Kryptosysteme zu uberwinden, wurde von Sir CharlesWheatstone folgendes Verfahren vorgeschlagen:
Man nehme die Symbole A,B, . . . , Z ohne J und verteile diese zufallig in einer 5 × 5 -Matrix, z.B.:
S Y D W ZR I P U LH C A X FT N O G EB K M Q V
Die Verschlusselung erfolgt nach den folgenden Regeln:
1. Erweitere den Plaintext, so dass er von gerader Lange ist.
2. Partitioniere den Plaintext in Blocke der Lange 2, wobei wir garantieren mussen, dassin keinem Block zwei gleiche Symbole stehen.
3. Sind die beiden Symbole in der gleichen Spalte, dann ersetzen wir diese durch diezyklisch nach unten versetzen Symbole in der Matrix, z.B. SH → RT , IK → CY .
4. Sind die beiden Symbole in der gleichen Zeile, dann ersetzen wir diese durch diezyklisch nach rechts versetzen Symbole in der Matrix, z.B. AX → XF .
5. In den verbleibenden Fallen spannen die Symbole im Block ein Rechteck auf, z.B.PF . Wir ersetzen dann diese Symbole durch die Symbole in der gleichen Zeile, diedie jeweiligen freien Ecken des Rechtecks darstellen, z.B. PF → LA .
Bei diesem Verfahren wird das Problem, dass ein gleicher Suffix im Plaintext auch einen gleichen Suffixim Ciphertext zur Folge hat, gelost. Jedoch gilt diese Beobachtung nicht fur Suffixe gerader Lange.
Das Verfahren kann einfach auf Matrizen anderer Dimension erweitert werden, z.B. auf 3×9 -Matrizen.Ferner konnen diese Matrizen durch einen einfachen Schlussel generiert werden. Man nehme eineneinfachen Begriff, z.B. MAGIC, fulle die ersten Positionen der Matrix mit diesen Symbolen und fulledie verbleibenden Positionen mit den verbleibenden Symbolen des Alphabets auf. So erhalten wir z.B.:
M A G I CB D E F HK L N O PQ R S T UV W X Y Z
Die wesentlichen Schwachstellen diese Verfahrens sind:
1. Es vernachlassigt die Haufigkeiten von 2-Grammen. So machen die 18 haufigsten 2-Gramme ca.90% eines Textes in deutsch aus.
8

2. Beim PLAYFAIR-Verfahren fuhren verschiedene Schlussel zur gleichen Verschlusselung, z.B.:
P A L M E E P A L M U H I K QR S T O N N R S T O Z V W X YB C D F G G B C D F E P A L MH I K Q U U H I K Q N R S T OV W X Y Z Z V W X Y G B C D F
Eine Matrix, die sich durch einen zyklischen Shift aller Spalten b.z.w. Zeilen einer anderen Matrixum den gleichen Wert ergibt, fuhrt zu einem aquivalenten Schlussel. Dieses reduziert die Anzahlder moglichen Schlussel und somit die Komplexitat, den Schlussel zu knacken.
PLAYFAIR wurde vom britischen Außenministerium vom Krim- bis zum Ersten Weltkrieg eingesetzt.
2.4 Polyalphabetische Kryptosysteme
Die bisher untersuchten Kryptosysteme benutzen nur eine Regel zur Verschlusselung, daher nennenwir diese monoalphabetische Kryptosysteme. Ein polyalphabetisches Kryptosystem stelltmehrere Regeln zur Auswahl. Wir zerlegen den Text in verschiedene Einheiten und verschlusseln dieerste Einheit mit Hilfe der ersten Regel, die zweite mit Hilfe der zweiten Regel, u.s.w. Wenn k Regelnzur Verfugung stehen, wird die ` te Einheit nach der (` mod k) + 1 ten Regel verschlusselt.
2.4.1 Vigenere System
Eines der bekanntesten und altesten polyalphabetische Kryptosysteme ist das Vigenere System,welches auf der nachfolgenden Tabelle beruht, die auch Vigenere Tabelle genannt wird:
A B C D E F G H I J K L M N O P Q R S T U V W X Y ZB C D E F G H I J K L M N O P Q R S T U V W X Y Z AC D E F G H I J K L M N O P Q R S T U V W X Y Z A BD E F G H I J K L M N O P Q R S T U V W X Y Z A B CE F G H I J K L M N O P Q R S T U V W X Y Z A B C DF G H I J K L M N O P Q R S T U V W X Y Z A B C D EG H I J K L M N O P Q R S T U V W X Y Z A B C D E FH I J K L M N O P Q R S T U V W X Y Z A B C D E F GI J K L M N O P Q R S T U V W X Y Z A B C D E F G HJ K L M N O P Q R S T U V W X Y Z A B C D E F G H IK L M N O P Q R S T U V W X Y Z A B C D E F G H I JL M N O P Q R S T U V W X Y Z A B C D E F G H I J KM N O P Q R S T U V W X Y Z A B C D E F G H I J K LN O P Q R S T U V W X Y Z A B C D E F G H I J K L MO P Q R S T U V W X Y Z A B C D E F G H I J K L M NP Q R S T U V W X Y Z A B C D E F G H I J K L M N OQ R S T U V W X Y Z A B C D E F G H I J K L M N O PR S T U V W X Y Z A B C D E F G H I J K L M N O P QS T U V W X Y Z A B C D E F G H I J K L M N O P Q RT U V W X Y Z A B C D E F G H I J K L M N O P Q R SU V W X Y Z A B C D E F G H I J K L M N O P Q R S TV W X Y Z A B C D E F G H I J K L M N O P Q R S T UW X Y Z A B C D E F G H I J K L M N O P Q R S T U VX Y Z A B C D E F G H I J K L M N O P Q R S T U V WY Z A B C D E F G H I J K L M N O P Q R S T U V W XZ A B C D E F G H I J K L M N O P Q R S T U V W X Y
9

Dieses System wurde im 16. Jahrhundert von Blaise de Vigenere (1523-1596) entwickelt. Es basiert aufArbeiten von Alberti, Trithemius und Porta, welche sich schon vor ihm mit der polyalphabetischenVerschlusselung befasst hatten.
Dieses System kann als eine Verallgemeinerung des Caesar-Verfahrens angesehen werden. Neben derTabelle benotigt man fur dieses System noch ein Schlusselwort w = w0 . . . wk−1 , in dem alle Symboledes Alphabets maximal einmal vorkommen. Die Verschlusselung eines Plaintextes x = x0 . . . xm−1
erfolgt nach folgender Regel:
Ersetze das Symbol xi im Plaintext durch das C(xi) te Symbol in der C(wi mod k) mod26 ten Zeile der Vigenere Tabelle, wobei C : Σ → Z|Σ| eine adaquate Kodierungsfunktionist.1
Wollen wir mit einem Schlussel MAGIC den Text CRYPTOLOGY verschlusseln, so erhalten wirOREXVALUOA.
Zur Entschlusselung eines Ciphertextes y = y0 . . . ym−1 verfahren wir wie folgt:
Sei yi das j te Symbol in der C(wi mod k) mod 26 ten Zeile der Vigenere Tabelle, dann istdas dazugehorige Plaintextsymbol C−1(j) .
Es ist einfach zu erkennen, dass dieser Algorithmus nicht auf die Vigenere Tabelle beschrankt werdenmuss. Benutzen wir anstelle der Berechnung der Zeile und Spalte ein Suchverfahren nach der Zeile,deren ersten Eintrag wi mod k und fur die Verschlusselung die Spalte, deren erster Eintrag xi ist,so konnen wir diesen Verschlusselungsalgorithmus auch auf andere Tabellen wie z.B. die BeaufortTabelle anwenden.
Z Y X W V U T S R Q P O N M L K J I H G F E D C B AA Z Y X W V U T S R Q P O N M L K J I H G F E D C BB A Z Y X W V U T S R Q P O N M L K J I H G F E D CC B A Z Y X W V U T S R Q P O N M L K J I H G F E DD C B A Z Y X W V U T S R Q P O N M L K J I H G F EE D C B A Z Y X W V U T S R Q P O N M L K J I H G FF E D C B A Z Y X W V U T S R Q P O N M L K J I H GG F E D C B A Z Y X W V U T S R Q P O N M L K J I HH G F E D C B A Z Y X W V U T S R Q P O N M L K J II H G F E D C B A Z Y X W V U T S R Q P O N M L K JJ I H G F E D C B A Z Y X W V U T S R Q P O N M L KK J I H G F E D C B A Z Y X W V U T S R Q P O N M LL K J I H G F E D C B A Z Y X W V U T S R Q P O N MM L K J I H G F E D C B A Z Y X W V U T S R Q P O NN M L K J I H G F E D C B A Z Y X W V U T S R Q P OO N M L K J I H G F E D C B A Z Y X W V U T S R Q PP O N M L K J I H G F E D C B A Z Y X W V U T S R QQ P O N M L K J I H G F E D C B A Z Y X W V U T S RR Q P O N M L K J I H G F E D C B A Z Y X W V U T SS R Q P O N M L K J I H G F E D C B A Z Y X W V U TT S R Q P O N M L K J I H G F E D C B A Z Y X W V UU T S R Q P O N M L K J I H G F E D C B A Z Y X W VV U T S R Q P O N M L K J I H G F E D C B A Z Y X WW V U T S R Q P O N M L K J I H G F E D C B A Z Y XX W V U T S R Q P O N M L K J I H G F E D C B A Z YY X W V U T S R Q P O N M L K J I H G F E D C B A Z
1Beim Aufzahlen der Zeilen und Symbole der Zeilen starten wir mit 0.
10

Die Entschlusselung erfolgt in solchen Tabellen nach folgender Regel:
Sei yi das j te Symbol in der Zeile, die mit C(wi mod k) beginnt. Ersetze yi durch dasj te Symbol in der ersten Zeile.
Damit eine Tabelle zur Verschlusselung herangezogen werden kann, muss sie den folgenden Bedingun-gen genugen:
1. In jeder Zeile mussen alle Symbole aus Σ genau einmal vorkommen.
2. In jeder Spalte mussen alle Symbole aus Σ genau einmal vorkommen. Diese Regel konnen wirauch darauf beschranken, dass in der ersten Spalte alle Symbole aus Σ genau einmal vorkommen.
Aufgabe 6 Beweisen Sie, dass das affinen Kryptosysteme bei einmaliger Benutzung fur den Fall,dass die Lange von r im Schlussel genau der Lange der Nachricht entspricht, perfekte Sicherheitbietet.
Aufgabe 7 Geben Sie ein Verfahren zum Knacken des PLAYFAIR-Verfahren an. Bestimmen siedessen Zeitkomplexitat.
Aufgabe 8 Verallgemeinern Sie das PLAYFAIR-Verfahren auf k -dimensionale Matrizen. Betrach-ten Sie hierbei, dass zunachst nur ein festes Alphabet Σ zur Verfugung steht.
2.4.2 Die Kryptoanalyse des Vigenere Verfahrens
Bei der Kryptoanalyse des Vigenere Verfahren unterscheiden wir zwei Szenarien:
1. Die Schlussellange k des Schlussels w = w0 . . . wk−1 ist bekannt.
2. Die Schlussellange k ist unbekannt.
Die Kryptoanalyse bei bekannter Schlussellange
Sei x = x0 . . . xm−1 der Plaintext, der verschusselt werden soll. Platzieren wir nun in einer Tabelle dieSymbole des Plaintextes so, dass die Symbole, deren Verschusselungsregel durch das gleiche Schlussel-symbol bestimmt wird, eine Spalte bilden, so erkennen wir, dass die Verschlusselungsregeln periodischwechseln. Sei ` = bm/kc , so erhalten wir:
w0 w1 . . . wk−2 wk−1
x0 x1 . . . xk−2 xk−1
xk xk+1 . . . x2k−2 x2k−1
......
......
x(`−1)k x(`−1)k+1 . . . x(`−1)k−2 x(`−1)k−1
x`k x`k+1 . . . xm
Lemma 2 Sei k die Lange des Schlusselworts, dann kann das Vigenere Verfahren in k monoalpha-betische Verschlusselungverfahren untergliedert werden.
11

Wir erkennen, dass alle Symbole xi des Plaintexts mit Hilfe der i mod k ten monoalphabetischenVerschlusselungsregel verschlusselt wurden. D.h. fur alle i ∈ Zk konnen wir xixk+ix2k+i . . . alsmonoalphabetisch verschlusselten Text betrachten, und diesen versuchen mit Hilfe der bereits disku-tierten Hilfsmittel zu entschlusseln. In vielen Abhandlungen uber das Vigenere Verfahren wird vomSchlusselwort verlangt, dass jedes Element des Alphabets maximal einmal vorkommt. Somit ist dieSchlusselwortlange durch |Σ| beschrankt. Eine andere Methode, die Schlussellange (zumindest mithoher Wahrscheinlichkeit korreck) zu bestimmen, wurde von dem englischen Mathematiker CharlesBabbage (1854) gefunden und von dem preussischen Major Friedrich W. Kasiski (1863) zum erstenMal eingesetzt. Dieses Verfahren ist als Kasiski-Test bekannt.
2.4.3 Die Kryptoanalyse bei unbekannter Schlussellange: Der Kasiski-Test
Der Kasiski-Test versucht, wie bereits oben beschrieben, die Schlussellange zu bestimmen. DiesesVerfahren basiert auf folgender Beobachtung:
Beobachtung 2 Wenden wir auf zwei gleiche Textfragmente im Plaintext jeweils die gleichen Ver-schlusselungssequenzen an, so erhalten wir zweimal die gleichen Fragmente im Ciphertext.
Dieses Verhalten wird in folgenden Beispiel aus [S90] sichtbar. Die Leerzeichen in diesem Text sindnur der bessern Ubersicht halber eingefugt:
AVXZH HCSBZ HALVX HFMVT LHIGHKALBR VIMOF HDKTA SKVBM OSLACGLGMO STPFU LQHTS LTCKL VNTWWHBWMS XSGAV HMLFR VITYS MOILHPELHH LLILF BLBVL PHAVW YMTURABABK VXHHB UGTBB TAVXH FMVTLHIGHP NPZWP BZPGG VHWPG VBGLLRALFX AVXTC LAQHT AHUAB ZHTRSBUPNP ZWPBZ HGTBB TPGMV VTCSMVCLTO ESOLA COLKB AVMVC YLKLACGLGB MHALG MVJXP GHUZR HABZSKHPEL HBUMF LHTSP HEKBA VTJCNWZXVT LACGL GHUHH WHALB MOSKVCFJOG UCMIS ALOML RIYCI LFEFIGSSLZ WMPGO LFRZA TSZGL JXYPXZHBUU RDWMO HALVX HFMVT LHIGH
Wie wir sehen, kommt das Fragment VXHFMVTLHIGH dreimal im Ciphertext vor. Die Wahrschein-lichkeit, dass zwei gleiche Textfragmente im Ciphertext durch zwei gleiche Textfragmente im Plaintextentstanden sind, ist großer als die Wahrscheinlichkeit, dass diese durch zwei unterschiedliche Fragmenteentstanden sind. Der Kasiski-Test nutzt diese Eigenschaft wie folgt aus:
1. Bestimme alle Fragmente v0, v1, . . . , v` , die im Ciphertext zumindest zweimal vorkommen. In
12

unserem Beispiel sind dieses:
v0 = HALVXHFMVTLHIGH (zweimal)v1 = VXHFMVTLHIGH (dreimal)v2 = VXH (viermal)v3 = AVX (dreimal)v4 = HAL (viermal)v5 = VX (sechsmal)
2. Bestimme fur alle Paare von Vorkommen eines Fragments vi die Partition des Ciphertextes inwviqvir und die dazgehorigen Langen von viq . Wir bezeichnen die Lange viq fur das j te Paarvon vi mit `i,j . Fur unser Beispiel erhalten wir
`0,1 = 375`1,1 = 129 `1,2 = 246 `1,3 = 375`2,1 = 12 . . .`3,1 = 141 `3,2 = 39 . . .`4,1 = 246 `4,2 = 60 `4,3 = 69 . . .`5,1 = 180 . . .
3. Bestimme alle Teiler der Werte `i,j und sortiere diese nach ihrer Haufigkeit. Wir erhalten
fur 375 1, 3, 5, 25, 125, 15, 75, 375,fur 129 1, 3, 43, 129,fur 246 1, 2, 3, 41, 6, 82, 123, 246,fur 180 1, 2, 3, 4, 6, 5, 10, 15, 20, 45, 12, 36, 60, 180,fur 141 1, 3, 47, 141,fur 60 1, 2, 3, 4, 6, 5, 10, 15, 20, 12, 60,fur 69 1, 3, 23, 69,fur 12 1, 2, 3, 4, 6, 12 .
Der am haufigsten vorkommende Teiler ist die 3. Wir werden sehen, dass dieser Teiler schonzum Erfolg fuhrt. Daher werden wir auf die Analyse des Ciphertextes fur die weiteren Teilerverzichten. Im Allgemeinen fuhrt jedoch die erste Wahl nicht immer zum Erfolg.
4. Betrachte den im letzten Schritt gefundenen Teiler als Lange k des Schlussels. Nach Lemma 2konnen wir den Ciphertext in k Teile aufteilen, welche alle mit Hilfe einen monoalphabetischenVerfahrens verschlusselt wurden. Fur unser Beispiel erhalten wir bei k = 3 :
y0y1y2 y0y1y2 y0y1y2 y0y1y2 y0y1y2 y0y1y2 y0y1y2 y0y1y2 y0y1y2
AVX ZHH CSB ZHA LVX HFM VTL HIG HKALBR VIM OFH DKT ASK VBM OSL ACG LGMOST PFU LQH TSL TCK LVN TWW HBW MSXSGA VHM LFR VIT YSM OIL HPE LHH LLILFB LBV LPH AVW YMT URA BAB KVX HHBUGT BBT AVX HFM VTL HIG HPN PZW PBZPGG VHW PGV BGL LRA LFX AVX TCL AQHTAH UAB ZHT RSB UPN PZW PBZ HGT BBTPGM VVT CSM VCL TOE SOL ACO LKB AVMVCY LKL ACG LGB MHA LGM VJX PGH UZRHAB ZSK HPE LHB UMF LHT SPH EKB AVTJCN WZX VTL ACG LGH UHH WHA LBM OSKVCF JOG UCM ISA LOM LRI YCI LFE FIGSSL ZWM PGO LFR ZAT SZG LJX YPX ZHBUUR DWM OHA LVX HFM VTL HIG H
13

Zahlen wir die Vorkommen der einzelnen Buchstaben so erhalten wir:
s0 s1 s2 s0 s1 s2 s0 s1 s2
A 12 5 9 J 2 2 0 S 5 13 0B 4 9 12 K 1 5 4 T 6 4 13C 2 11 0 L 27 1 13 U 9 1 1D 2 0 0 M 2 2 17 V 14 11 2E 1 0 4 N 0 0 4 W 2 3 6F 1 10 2 O 6 4 2 X 0 1 12G 0 13 10 P 10 7 0 Y 4 0 1H 15 14 11 Q 0 2 0 Z 7 5 2I 1 7 3 R 1 3 5
Wissen wir zudem, dass der Text in Englisch geschrieben wurde, so konnen wir bekannte stati-stische Daten uber die Buchstabenhaufigkeiten im Englischen heranziehen:
E 12,31% O 7,94% S 6,59%
T 10,45% N 7,19% R 6,03%
A 8,05% I 7,18% H 5,14%
In einem ersten Ansatz konnen wir versuchen den Buchstaben E auf den Buchstaben im Cipher-text zu setzen, welcher am haufigsten vorkommt. Ein alternativer Ansatz versucht die DreierfolgeRST auf die Folge von 3 Buchstaben im Alphabet zu ubertragen, welche am haufigsten im Ci-phertext vorkommt. Wir erhalten zwei mogliche Verschlusselungsfunktionen
(a) R−→T, S−→U, T−→VDiese Funktion hatte zur Folge, dass W−→Y, X−→ Z, Y−→A. Somit kamen im Plaintextder Buchstabe W viermal, der Buchstabe X siebenmal und der Buchstabe Y zwolfmal vor.Dieses ist jedoch nach unserer Buchstabenhaufigkeitstabelle im Englischen sehr unwahr-scheinlich.
(b) R−→Y, S−→ Z, T−→ADieses resultiert in einer Verschlusselungsfunktion von f0(x) = x + 7 mod 26 .
Analog erhalten wir fur f1(x) = x + 14 mod 26 und f2(x) = x + 19 mod 26 .
Der Schlussel konnte somit HOT sein. Entschlusseln wir den Ciphertext mit Hilfe dieses Schlussels,so erhalten wir:
THESTOVEISTHEHEARTOFSAUNA. . .
2.4.4 Der Friedman-Test
Eine weitere Moglichkeit einen Kandidaten fur die Lange eines Schlusselworts zu bekommen, stelltder Friedman-Test (William Friedman, 1925) dar. Die wesentliche Idee bei diesem Text basiert aufder Analyse, mit welcher Wahrscheinlichkeit zwei zufallig und unabhangig ausgewahlte Buchstabenim Plaintext gleich sind.
Sei x = x0 . . . xn−1 ∈ Σn ein Plaintext der Lange n und fur alle b ∈ Σ sei nb die Anzahl der b inx , dann gilt n =
∑b∈Σ nb . Die Anzahl der Paare in x ist gegeben durch
m = n2
und die Anzahl der Paare die Form xi = xj = b ist
mb = n2b .
14

Die Anzahl der Paare die aus zwei identischen Buchstaben bestehen ist
mΣ =∑b∈Σ
mb .
Wir betrachten hierbei Paare bei denen die Reihenfolge berucksichtigt wird und eine Position zweimalgezogen werden darf.
Die Wahrscheinlichkeit bei einem zufallig unabhangig gewahlten Paar auf zwei identischen Buchstabenzu treffen ist
p(x) =mΣ
m. (1)
Diese Wahrscheinlichkeit wird oft auch als Koinzidenzindex bezeichnet. Es ist einfach zu erkennen,dass unser oben angestellten Uberlegungen fur jede beliebige Zeichenkette x ∈ Σn gultig ist.
Die Wahrscheinlichkeit, dass ein zufallige Position in einem hinreichend langen englischen Text denBuchstabe b ∈ {A, . . . , Z} binhaltet ist in folgender Tabell beschrieben:
pb pb pb pb
A 0,0856 H 0,0528 O 0,0797 V 0,0092B 0,0139 I 0,0627 P 0,0199 W 0,0149C 0,0279 J 0,0013 Q 0,0012 X 0,0017D 0,0378 K 0,0042 R 0,0677 Y 0,0199E 0,1304 L 0,0339 S 0,0607 Z 0,0008F 0,0289 M 0,0249 T 0,1045G 0,0199 N 0,0707 U 0,0249
Die Wahrscheinlichkeit, dass zwei zufallige Positionen in einem englischen Text zwei identische Buch-staben beinhalten ist
p =∑b∈Σ
p2b
wohingegen in einer zufalligen Zeichenkette diese Wahrscheinlichkeit durch
p =∑b∈Σ
|Σ|−2 =1|Σ|
gegeben ist. Fur die englische Sprache gilt
p = 0, 06873314 . . . und p = 0, 03846 . . . .
Fur einen monoalphabetisches Verschlusselungsverfahren gilt:
Beobachtung 3 Sei x ein Plaintext und y ein zu x gehoriger Ciphertext, welcher durch ein mono-alphabetisches Verschlusselungsverfahren erzeugt wurde, dann gilt p(x) = p(y) , d.h. x und y habenden gleichen Koinzidenzindex.
Im Folgenden werden wir sehen, dass der Koinzidenzindex fur einen Ciphertext der uber das VigenereVerfahrens erzeugt wurde mit der Lange des Schlusselwortes fallt. Um zu entscheiden, ob ein Cipher-text uber ein mono- oder ein polyalphabetisches Verfahren erzeut wurde konnen wir folgende Regelbenutzen:
15

Ist p ≈ p , so wurde der Ciphertext uber ein monoalphabetische Verfahren erzeugt. Giltp ≈ p , so wurde der Ciphertext uber ein polyalphabetische Verfahren erzeugt.
Sei k die Lange des Schlusselworts. Wie wir aus Lemma 2 wissen zerfallt ein uber das VigenereVerfahren erzeugtes Ciphertext in k Teile, die uber ein monoalphabetische Verschlusselungverfahrengeneriert werden. Ist der Text lang genug, so konnen wir aus Beobachtung 3 folgern, dass in jedemdieser Teile der Koinzidenzindex des Plaintextes unverandert beibehalten wird. Betrachten wir jedochein Positionspaar mit zwei Positionen, die zu unterschiedlichen monoalphabetische Verschlusselung-verfahren gehoren, so reduziert sich die Wahrscheinlichkeit auf ein identisches Paar zu stossen. Imgunstigsten Fall ist diese Wahrscheinlichkeit gleich 1/26 .
Im Folgenden werden wir als Arbeitshypothese annehmen, dass bei einem Paar von Posi-tionen innerhalb eines Teil, der mit einem monoalpabetischen Verschlusselungsverfahrensgeneriert wurde die Wahrscheinlichkeit fur gleiche Symbole durch p gegeben ist. Bei einemPaar aus zwei verschiedenen Teilen, ist diese Wahrscheinlichkeit p .
Jeder Teil, der uber eine bestimmtes monoalpabetisches Verschlusselungsverfahren generiert wird hateine Große von n/k . Es gibt somit n Moglichkeiten die erste Position zu wahlen und n
k Moglichkeitdie zweite Position im gleichen Teil des Ciphertextes zu wahlen. Es gibt somit
q =n2
k
Paare von Positionen, die sich in einem Teil des Ciphertextes befinden. Die Anzahl der Paare vonPositionen aus unterschiedlichen Teilen des Ciphertextes ist gegeben durch
q =n2(k − 1)
k.
Die Anzahl der Positionspaare mit identischen Buchstaben ist somit
mΣ = p · n2
k+ p · n2(k − 1)
k.
Folglich gilt
p(y) =mΣ
n2=
p + p · (k − 1)k
.
Mit Hilfe dieser Formel und den angegebenen Abschatzungen fur p und p erhalten wir
k ≈ 0, 06873− 1/26p(y)− 1/26
≈ 0, 0303p(y)− 0, 03846
. (2)
Betrachten wir das in Kapitel 2.4.2 diskutierte Beispiel, so erhalten wir:
ni ni ni ni
A 26 H 40 O 12 V 27B 25 I 11 P 17 W 11C 13 J 4 Q 2 X 13D 2 K 10 R 9 Y 5E 5 L 41 S 18 Z 14F 13 M 21 T 23 n 400G 23 N 4 U 11
16

Aus dieser Tabelle und mit Hilfe der Gleichung 1 erhalten wir p(y) = 0, 05565 . und aus der Appro-ximation 2 den Wert k = 1, 8 . . . . Dieser Wert kann als ein Indiez dafur gesehen werden dass zurVerschlusselung des Ciphertextes ein sehr kurzer Schlussel benutzt wurden.
Betrachten wir nun die Approximation 2 in ihren Extremen: Fur ein monoalphabetisches Verfahrenerhalten wir p(y) ≈ 0, 06873 und somit k ≈ 1 . Fur einen zufallig gewahlten Text z erhalten wirp(z) ≈ 1
26 und somit k →∞ .
2.4.5 Eine Verallgemeinerung des Vigenere Verfahrens
Auf Vigenere geht auch eine Verallgemeinerung des Vigenere Verfahrens zuruck, wohingegen sich dieLiteratur nicht einig ist, wer der Entwickler des Vigenere Verfahrens ist [K67].
Die Verallgemeinerung, die wir nun kurz vorstellen wollen, bezieht den Nachrichtentext bei der Schlussel-generierung mit ein. Sei w = w1 . . . wk ein Schlussel und x = x1 . . . xn eine Nachricht – beide ohneLeerzeichen – dann erhalten wir den neuen Schlussel durch
w′ = w1 . . . wkx1 . . . xn−k .
Verschlusseln wir eine Nachricht mit Hilfe dieses Verfahrens, so mussen wir zunachst einen Prafix desCiphertextes entschlusselt haben, um den Schlussel fur den nachsten Teil des Ciphertextes zu erhalten.Die Eigenschaft einer Periodizitat konnen wir zum Knacken dieses Verfahrens nicht mehr ausnutzen.
Aufgabe 9 Benutzen Sie den Test von Kasiski um folgenden Text zu entschlusseln
KSMEHZBBLKSMEMPOGAJXSEJCSFLZSY .
Aufgabe 10 Versuchen Sie den folgenden Text zu entschlusseln
TPOGDJRJFSUBSFCSQLGPCOFUQNFDSFCLVIFOTGNWGT .
2.5 Rotor-Chiffriermaschinen: Die Enigma
Das Prinzip der Rotor-Chiffriermaschine wurde zu Beginn des letzten Jahrhunderts unabhangig vonmehreren Personen erfunden. Zu nennen sind hier vor allem: Der Amerikaner E. H. Hebern (1917, Pa-tent 1924), der Deutsche A. Scherbius (Patent 1918), der Niederlander H. A. Koch (Patent 7.10.1919)und der Schwede A. G. Damm (Patent 10.10.1919).
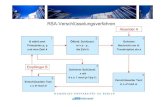
Das Prinzip der Rotor-Chiffriermaschine basiert wie die schon fruher diskutierten Verfahren von Cae-sar und Vigenere auf der Permutation der Buchstaben eines Alphabets Σ = {A, . . . , Z} . Bei derEnigma kamen hierbei je nach Typ die sukzessive Ausfuhrung von 3 bis 4 Permutationen zum Ein-satz. Im Folgenden bezeichnen wir diese Permutationen mit Π1,Π2,Π3,Π4 . In Abbildung 2 wird dieHintereinanderausfuhrung von zwei Permutationen illustriert.
17

A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A B C E F J M O SD GH I K X N P R QT WYZ U VL
L D HI A BCK E FX NP JG R MT OZ Y WU QV S
Abbildung 2: Hintereinanderausfuhrung von zwei Permutationen.
Die sukzessive Ausfuhrung von 3 bis 4 Permutationen bringt jedoch keinen zusatzlichen Sicherheits-gewinn. Auf die Grunde fur dieses Verfahren werden wir spater eingehen.
G H I J K L M N O P Q R S T U V W X Y Z
R LQ GF KM EB V X T J S O N W YUCIZDAH
R
R
Q
Q
F
F
M
M
B
B
V
V
X
X
H
H
T
T
A
A
P
J
J
P
P
L
L
K
K
S
S
O
O
D
D
N
N
Z
Z
I
I
G
G
C
C
U
U
W
W
E
E
Y
Y
A B C E F J M O SD GH I K X N P R QT WYZ U VL
L D HI A BCK E FX NP JG R MT OZ Y WU QV S
A B C D E F G H I J K L M N O P Q R S T U V W X Y
A
Z
B C D E F
Abbildung 3: Die Funktion f = Π−11 ◦Π−1
2 ◦Π5 ◦Π2 ◦Π1 .
Auf die so permutierte Folge wenden wir eine weitere Permutation Π5 an, welche eine paarweiseSymbolvertauschung realisiert. Diese Permutation wird auch Reflektor oder Umkehrwalze genannt.Abschließend durchlaufen wir die Permutationen Π1,Π2,Π3,Π4 noch einmal ruckwarts in umgekehr-ter Reihenfolge. Die resultierende Verschlusselungsfunktion ist somit
f = Π−11 ◦Π−1
2 ◦Π−13 ◦Π−1
4 ◦Π5 ◦Π4 ◦Π3 ◦Π2 ◦Π1 .
18

Die Funktion von f ist in Abbildung 3 illustriert.
Den Vorteil dieser Verschlusselungsfunktion konnen wir schnell erkennen, wenn wir das Verfahrenzweimal hintereinander anwenden. Sei
y = Π−11 (Π−1
2 (Π−13 (Π−1
4 (Π5(Π4(Π3(Π2(Π1(x))))))))) ,
dann gilt
Π−11 (Π−1
2 (Π−13 (Π−1
4 (Π5(Π4(Π3(Π2(Π1(y)))))))))= Π−1
1 (Π−12 (Π−1
3 (Π−14 (Π5(Π4(Π3(Π2(Π1(Π−1
1 (Π−12 (Π−1
3 (Π−14 (Π5(Π4(Π3(Π2(Π1(x))))))))))))))))))
= Π−11 (Π−1
2 (Π−13 (Π−1
4 (Π5(Π5(Π4(Π3(Π2(Π1(x)))))))))) .
Beachten wir, dass eine paarweise Symbolvertauschung ihre eigene Umkehrfunktion darstellt, so er-halten wir
x = Π−11 (Π−1
2 (Π−13 (Π−1
4 (Π5(Π4(Π3(Π2(Π1(y))))))))) .
Die von der Enigma realisierte Funktion stellt somit ihre eigene Umkehrfunktion dar. Geben wir zumBeispiel das Symbol H in unserem Beispiel (Abbildung 3) ein, so erhalten wir in der Verschlusselungdas Symbol X. Geben wir jetzt wiederum das Symbol X ein, so erhalten wir H. Die Enigma konntealso ohne Umbau sowohl zur Verschlusselung als auch zur Entschlusselung benutzt werden. Da dieRealisierung jedoch auf einem Stromkreis basierte, war es bei der Realisierung verboten, dass einSymbol auf sich selbst abgebildet wurde.
Die einzelnen Permutationen wurden auf einer Walze realisiert, so dass durch das Drehen einer WalzeΠi eine neue Permutation Π′
i ensteht. Der wesentliche Trick besteht nun darin, dass sich die ersteWalze mit jedem Symbol um eine Position in der Permutation dreht, die zweite Walze mit jedem26 ten Symbol dreht, die dritte Walze mit jedem 262 ten Symbol dreht, und die letzte Walze mitjedem 263 ten Symbol dreht.
Um die Sicherheit zu erhohen, wurden zudem noch vor der eigentlichen Enigma-Verschlusselung vierBuchstabenpaare aus den 26 Buchstaben vertauscht. Dieses wurde mit Hilfe eines Steckerbrett rea-lisiert. Ferner konnten die Walzen gegen andere Walzen ausgetauscht und untereinander permutiertwerden. Zur Verfugung standen 5 Walzen. Der Tagesschlussel bestand aus folgenden Punkten:
1. Walzenauswahl
2. Walzenreihenfolge
3. Walzengrundstellung
4. Steckerbrettverkabelung.
Insgesamt gab es somit
5 · 4 · 3 · 2 · 264 ·(262
)·(242
)·(222
)·(202
)4 !
= 8995419473040000
mogliche Schlussel. Mit der Nachricht wurde auch der Nachrichtenschlussel ubermittelt. Dieser bestandaus den ersten sechs Zeichen der Nachricht – die Einstellung der Walzen wurde einmal wiederholt. Mitdiesem wurden die Walzen in eine neue Ausgangsposition gebracht. Mit dem so erhaltenen Systemkonnte mit der Entschlusselung des eigentlichen Textes begonnen werden.
19

XF NJ K CDE M GH ZP RL I TO VQ B AYU WSA
C DF E IKJ LMN OP QR ST UV WYZG H
A B
AB XX
R S I B U Z N J K H P O A L W Y M Q C X F G D T E V R
S IB UZ NJ KH PO A LWY MQ CX FGDT EV R Z
ZF GM D R EER C TP VL I AO XKW UBYQ HN JS
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
Abbildung 4: Die Funktion f = Π−11 ◦Π−1
2 ◦Π5 ◦Π2 ◦Π1 fur das 28te Symbol.
Die Kryptoanalyse der Enigma gestalltete sich im zweiten Weltkrieg als eine sehr aufwendiges Problem.So beschaftigten bei den Alliierten bis zu 10000 Mathematiker, Ingenieure und Hilfskrafte zwischen1939 und 1945 mit dieser Aufgabe. Es muss hier noch erwahnt werden, dass es einer polnischen Gruppevon 15 Mathematikern um M. Rejewski bereits vor Beginn des zweiten Weltkries gelungen war dasVerfahren der ersten Varianten der Enigma zu knacken.
Besonders Hilfreich bei der Kryptoanalyse zeigen sich hierbei einige Fehler der Deutschen bei derVerschlusselung. So wurde in vielen Fallen als Testsignal eine langere Folge von A’s verschlusselt. Auchdie Eigenschaft, dass jede Nachricht mit einer zweifachen Wiederholung des Nachrichtenschlusselsbegann konnten sich die Alliierten zu Nutze machen, um den Suchraum fur den Tagesschlussel von9 · 1018 stark einzugrenzen. Zudem kamen den Alliierten noch einige Zufalle zu Hilfe, so konnten siein einigen versenkten U-Booten und durch Spionage die Walzen der Enigma erbeuten. Ferner fiehlenihnen hin und wieder Schlusselbucher in die Hande. Leider gibt es nur eine sehr beschrankte Literaturuber die Kryptoanalyse der Enigma. Daher werden wir uns nun von den klassischen Verfahren langsamverabschieden und uns der modernen Kryptologie zuwenden.
Eine gute Darstellung der Enigmaverschlusselung ist im Internet unter
http://de.wikipedia.org/wiki/Enigma %28Maschine%29
und unter
20

http://www.mywiseowl.com/articles/Enigma machine
zu finden. Auf diesen Seiten wird auch auf einige Details in der Konstruktion der Enigma eingegangen.
21

3 Der Begriff der Sicherheit
Wir wollen uns nun wieder dem Problem zuwenden, mit dem wir uns schon in der ersten Stunde kurzbeschaftigt haben: Was verstehen wir unter dem Begriff Sicherheit? Wie wir schon gesehen habenkonnen wir kryptographische Verfahren in verschiedene Stufen der Sicherheit einsortieren:
• perfekte oder uneingeschrankte Sicherheit,
• probabilistische Sicherheit,
• Sicherheit gegen algorithmische Attacken und
• unsicher.
Fur viele bekannte Verfahren ist jedoch die Zuordnung zu einer dieser Sicherheitsklassen noch nichtbekannt. Um trotz dem eine Klassifikation dieser Verfahren zu erhalten, fuhren wir eine weitere Si-cherheitsklasse ein, die
• beweisbare Sicherheit.
Diese Form der Sicherheit basiert auf dem Begriff der Reduktion. Um zu zeigen, dass ein Verfahrenbeweisbar sicher ist, zeigen wir, dass das knacken einer signifikanten Anzahl von Schlusseln auch daseffiziente Losen bestimmter (vermutlich) schwieriger Probleme zur Folge hatte. Ein oft benutztes Bei-spiel fur ein solches vermutlich schwieriges Problem, ist das Problem der große Zahlen zu faktorisieren.
Wir wollen uns nun mit einigen dieser Sicherheitsbegriffen etwas naher auseinander setzen. Sei
Zm = {0, 1, . . . ,m− 1} und Zm,n = Znm .
Dann definieren wir die Menge aller moglichen Plaintexte als
Pt :=⋃n∈N
Zm,n
und die Menge aller moglichen Ciphertexte als
Ct :=⋃n∈N
Zm,n .
Definition 2 Eine kryptographische Transformation ist eine Familie von bijektiven Transfor-mationen T = (T (n))n∈N mit
T (n) : Zm,n → Zm,n
fur ein beliebiges aber festes Alphabet Zm . Hangt die kryptographische Transformation von der Wahleines Schlussels w ab, so schreiben wir auch Tw = (T (n)
w )n∈N .
Ein Kryptosystem ist eine Familie von kryptographischen Transformationen
T = { Tw | w ∈ K }
wobei K die Menge aller moglichen Schussel ist.
22

Fur die Kryptoanalyse gehen wir davon aus, dass das Kryptosystem bekannt jedoch der Schlusselunbekannt ist. Zusammenfassend besitzt ein Angreifer auf das Kryptosystem folgende Kenntnisseuber das System:
• a priori Annahmen uber die Wahrscheinlichkeitsverteilung PrPt der moglichen Plaintexte Pt,
• a priori Annahmen uber die Wahrscheinlichkeitsverteilung Pr K der moglichen Schlussel K ,
• das benutzte Kryptosystem T ,
• einige Beispiele y = Tw(x) fur verschiedene w ∈ K und x ∈Pt und
• der zu entschlusselnde Ciphertext Y .
Aus dem a priori Wissen uber PrPt und Pr K konnen wir folgende Wahrscheinlichkeiten bestimmen:
1. PrPt, K (x,w) , d.h. die Wahrscheinlichkeit, dass zur Verschlusselung von x der Schlussel wbenutzt wird:
PrPt, K (x,w) = PrPt(x) · Pr K (w) .
Wir gehen davon aus, dass Plaintext und Schlussel unabhangig von einander gewahlt werden.
2. PrCt(y) , d.h. die Wahrscheinlichkeit, dass der Ciphertext y vorkommt:
PrCt(y) =∑
(x,w)∈Pt×K mit y=Tw(x)
PrPt, K (x,w) .
3. PrPt,Ct(x, y) , d.h. die Wahrscheinlichkeit, dass y die Verschlusselung von x ist:
PrPt,Ct(x, y) =∑
w∈K mit Tw(x)=y
PrPt, K (x,w) .
4. PrCt,Pt(y, x) , d.h. die Wahrscheinlichkeit, dass y die Verschlusselung von x ist:
PrCt,Pt(y, x) =∑
w∈K mit T−1w (y)=x
PrPt, K (x,w) .
5. PrCt, K (y, w) , d.h. die Wahrscheinlichkeit, dass bei y der Schlussel w benutzt wurde:
PrCt, K (y, w) =∑
x∈Pt mit Tw(x)=y
PrPt, K (x,w) .
6. PrPt|Ct(x|y) , d.h. die bedingte Wahrscheinlichkeit vom Plaintext x unter der Voraussetzung,das der Ciphertext y vorliegt:
PrPt|Ct(x|y) =PrCt,Pt(y, x)
PrCt(y).
7. Pr K |Ct(w|y) , d.h. die bedingte Wahrscheinlichkeit vom Schlussel w unter der Voraussetzung,das der Ciphertext y vorliegt:
PrK|Ct(w|y) =PrCt, K (y, w)
PrCt(y).
23

8. PrCt|Pt(y|x) , d.h. die bedingte Wahrscheinlichkeit vom Ciphertext y unter der Voraussetzung,das der Plaintext x vorliegt:
PrCt|Pt(y|x) =PrPt,Ct(x, y)
PrCt(y).
Bei den Definitionen der bedingten Wahrscheinlichkeiten mussen wir davon ausgehen, dass
PrCt(y) > 0 bzw. PrPt(x) > 0
ist. Im Fall, dass diese Wahrscheinlichkeiten gleich Null sind, so definieren wir auch die entsprechendenbedingten Wahrscheinlichkeiten als Null.
3.1 Kryptosysteme mit perfekter Sicherheit
Mit Hilfe dieser Wahrscheinlichkeiten konnen wir nun den Begriff der perfekten Sicherheit definieren:
Definition 3 Ein Kryptosystem T nennen wir genau dann uneingeschrankt bzw. perfekt sicher,wenn fur alle Plaintexte x und alle Ciphertexte y mit PrCt(y) > 0 gilt
PrPt|Ct(x|y) = PrPt(x) .
In anderen Worten, wann immer ein Kryptoanalytiker einen Ciphertext sieht, erhalt er uber denPlaintext keine zusatzliche Information.
Aufgabe 11 Beweisen Sie: Ein Kryptosystem T ist genau dann uneingeschrankt sicher, wenn furalle Plaintexte x und alle Ciphertexte y mit PrPt(x) > 0 gilt
PrCt|Pt(y|x) = PrCt(y) .
Aufgabe 12 Betrachten Sie das in Abbildung 3 eingeschrankte Enigma-Verfahren. Verschlusseln Siedie Nachricht x = ABCABC. Sei y die verschlusselte Nachricht. Welchen Text erhalten Sie, wennSie zur Entschlusselung die beiden Permutationen vertauschen.
Wir wollen nun eine Beziehung zwischen der Anzahl der Schlussel und der Anzahl der moglichenPlaintexte herleiten.
Theorem 3 Sei T Kryptosystem, welches fur alle n -Gramme x, y mit PrPt(x) > 0 und PrCt(y) >0 uneingeschrankte Sicherheit bietet. Dann gilt
|K| ≥ |{ x ∈ Zm,n | PrPt(x) > 0 }| .
Beweis: Definiere
Zm,n,Pt := { x ∈ Zm,n | PrPt(x) > 0 }Zm,n,Ct := { x ∈ Zm,n | PrCt(x) > 0 } .
Im Folgenden nehmen wir an, dass alle Schlussel in w ∈ K mit strikt positiver Wahrscheinlichkeitvorkommen, d.h. Pr K (w) > 0 . Es gilt:
24

Lemma 3 Fur alle Schlussel w ∈ K ist die (eingeschrankte) Transformation Tw : Zm,n,Pt → Zm,n,Ct
injektiv.
Beweis: Aus der Definition folgt, dass vollstandige Tw : Zm,n → Zm,n bijektiv ist. Ferner gilt
PrCt(y) =∑
(x,w)∈Pt×K mit y=Tw(x)
PrPt(x) · Pr K (w) .
Somit gilt genau dann PrCt(y) > 0 , wenn fur ein Paar (x,w) mit y = Tw(x) die WahrscheinlichkeitenPrPt(x) und Pr K (w) strikt positiv sind, d.h. PrPt(x) > 0 und Pr K (w) > 0 . Da alle Schlusselaus K mit einer strikt positiven Wahrscheinlichkeit gewahlt werden, gilt fur alle Schlussel w ∈ KTw(Zm,n,Pt) ⊆ Zm,n,Ct . Folglich ist die (eingeschrankte) Transformation Tw : Zm,n,Pt → Zm,n,Ct
injektiv.
Lemma 4 Fur alle Ciphertexte y ∈ Zm,n,Ct gilt:
∀x ∈ Zm,n,Pt ∃w ∈ K : Tw(x) = y .
Beweis: Der Beweis erfolgt uber eine Widerspruchsannahme. Fur y ∈ Zm,n,Ct sei x ∈ Zm,n,Pt einPlaintext, fur den kein Schlussel w mit Tw(x) = y existiert. Da T ein Kryptosystem mit perfekterSicherheit ist, wissen wir
PrPt(x) = PrPt|Ct(x|y) =PrPt,Ct(x, y)
PrCt(y)
=
∑w mit Tw(x)=y PrPt(x) · PrK(w)
PrCt(y)= 0 .
Dieses widerspricht der Voraussetzung von x ∈ Zm,n,Pt und somit PrPt(x) > 0 .
Lemma 5 Fur alle x1, x2 ∈ Zm,n,Pt mit x1 6= x2 und fur alle w1, w2 ∈ K mit Tw1(x1) = Tw2(x2)gilt w1 6= w2 .
Beweis: Der Beweis erfolgt wieder uber eine Widerspruchsannahme. Seien x1, x2 ∈ Zm,n,Pt mitx1 6= x2 zwei Plaintexte mit Tw(x1) = Tw(x2) fur einen Schlussel w ∈ K . Wie wir oben gesehenhaben, ist Tw eingeschrankt auf Zm,n,Pt injektiv. Somit folgt aus Tw(x1) = Tw(x2) unmittelbar,dass x1 = x2 ist.
Fassen wir die letzten beiden Lemmata zusammen, so sehen wir, dass es fur jeden Ciphertext in Zm,n,Ct
und fur jeden Plaintext x ∈ Zm,n mit PrPt(x) > 0 genau einen fur x individuellen Schlussel w ∈ Kgeben muss, so dass Tw(x) = y ist. Folglich muss es mindestens so viele Schlussel wie Plaintexte ineinem uneingeschrankt sicheren Kryptosystem geben.
Zunachst scheint die Generierung von uneingeschrankt sicheren Kryptosystemen wegen der enormenSchlusselmenge eine schwierige Aufgabe darzustellen. Betrachten wir jedoch so genannte One-Time-Pads, so sehen wir, dass diese Verfahren eine sehr einfache Struktur haben konnen. One-Time-Pad-Verfahren wurden 1918 von dem Amerikaner G. S. Vernam eingefuhrt und von C. Shannon [S49]naher untersucht. Das wesentliche Problem bei diesen Verfahren ist die Schlusselubergabe, da, wiewir gesehen haben, die Anzahl der Schlussel nach unten durch die Anzahl aller moglichen Plaintextebeschrankt ist.
25

Sei w = (w0, . . . , wn−1) eine Folge von n unabhangigen uniform verteilten Zufallsvariablen uber Zm .Das bedeutet: Fur alle i ∈ {0, . . . , n− 1} und fur alle z ∈ Zm gilt Pr(wi = z) = 1
m . One-Time-Padsdefinieren wir als die bijektive Funktion
T (n) : X = (x0, . . . , xn−1) −→ Y = (y0, . . . , yn−1)
mit einem randomisiert generierten Schlussel w = (w0, . . . , wn−1) , wobei fur alle i ∈ {0, . . . , n − 1}gilt
yi = T (n)wi
(xi) := (xi + wi) mod m .
Somit gilt Pr K (w) = 1mn . Zudem gilt K = Zm,n und folglich |K| = mn . Da wir den Plaintext
ebenfalls aus Zm,n wahlen, gibt es mindestens so viele Schlussel wie Plaintexte. Fur den One-Time-Pad gilt:
Theorem 4 Fur jede Plaintextquelle S , sind die Zufallsvariablen y0, . . . , yn−1 , die wir uber denoben definierten One-Time-Pad erhalten, unabhangig und uniform verteilt uber Zm . Es gilt
PrCt((y0, . . . , yn−1)) =1
mnfur alle y = (y0, . . . , yn−1) ∈ Zm,n .
Beweis: Die Werte xi, yi bestimmen eindeutig den Wert wi uber die Formel (yi−xi) ≡ wi mod m .Ferner sind die Werte wi unabhangig und uniform aus Zm gewahlt. Somit gilt
PrPt,Ct(x, y) =∑
k∈K mit T(n)w (x)=y
PrPt(x) · PrK(w)
= PrPt(x) · 1mn
·∑
w∈K mit T(n)w (x)=y
1
= PrPt(x) · 1mn
und somit
PrCt(y) =∑
x∈Zm,n
PrPt,Ct(x, y)
=1
mn·∑
x∈Zm,n
PrPt(x)
=1
mn.
Analog konnen wir fur jede einzelne Position yi im Ciphertext zeigen, dass
PrCt(yi) =1m
.
Fassen wir diese beiden Beobachtungen zusammen, so folgt, dass die Zufallsvariablen y0, . . . , yn−1
unabhangig und uniform verteilt sind.
Aus diesem Theorem folgt:
PrPt|Ct(x|y) =PrPt,Ct(x, y)
PrCt(y)
=
∑w∈K mit T
(n)w (x)=y
PrPt(x) · PrK(w)
PrCt(y)
=1
mn · PrPt(x)1
mn
= PrPt(x) .
26

Dieses impliziert:
Theorem 5 Der oben definierte One-Time-Pad ist ein perfekt sicheres Kryptosystem fur alle Plain-texte der Lange n .
3.2 A priori Annahmen
Zu Beginn dieses Kapitels sind wir kurz auf die a priori Annahmen uber Pr K (w) und PrPt(x)eingegangen. Eine naheliegende Annahme ist, dass die Schlussel w uber Pr K uniform verteilt sind,d.h. jeder Schlussel kommt mit der gleichen Wahrscheinlichkeit vor. Abhangig von der Umgebung istdiese Annahme jedoch mit Vorsicht zu genießen, da ein Mensch, der sich einen Schlussel frei wahlenkann, zumeist einen Schlussel wahlt, den er sich einfach merken kann. In vielen Bereichen sind wirjedoch nicht auf das Erinnerungsvermogen von Menschen angewiesen, in diesen Fallen konnen wir voneiner uniformen Schlusselverteilung ausgehen.
Fur den Plaintext ist die Situation komplizierter. Zur Vereinfachung werden wir davon ausgehen, dassdie Sprache des Plaintextes dem Kryptoanalytiker bekannt ist (Analysen zur Spracherkennung sindin [B94] zu finden). Um ein Modell fur die Verteilung des Plaintextes zu bekommen konnen wir alleZeichenketten der Lange n dieser Sprache auflisten und die entsprechenden Wahrscheinlichkeitenbestimmen. Dieses Modell zeigt jedoch zwei wesentliche Schwachstellen auf:
1. Eine entsprechende Datenbank muss eine enorme Menge an Daten verwalten.
2. Die zu berucksichtigenden Wahrscheinlichkeiten sind nummerisch schwer zu behandeln.
Daher wollen wir verschiedene eingeschrankte Modell betrachten. Diese Modelle sollen folgende Ei-genschaften aufweisen:
1. Das Modell soll charakteristische Eigenschaften der Sprache hinreichend genau reflektieren. Einedieser Eigenschaften kann zu Beispiel die Haufigkeit bestimmter Buchstabenkombinationen sein.So kommt in vielen Sprachen (z.B. Deutsch, Franzosisch, Englisch) nach dem Buchstaben qimmer der Buchstabe u. Somit existieren die Kombinationen qa und qz in diesen Sprachennicht.
2. Berechnungen innerhalb der Sprachreprasentation sollen ohne große Probleme moglich sein.
Prinzipiell kann jede Sprache mit einer beliebig hohen Genauigkeit reprasentiert werden, jedoch steigtder Aufwand der Reprasentation sehr schnell.
Die grundlegende Idee zur Modellierung einer Sprache beruht auf einen probabilistischen Prozess. EinePlaintextquelle modellieren wir mit Hilfe einer (endlichen oder unendlichen) Sequenz von Zufallsva-riablen X0, X1, . . . . Einen Plaintext x = x0, x1, . . . erhalten wir dann uber ein Zufallsexperiment ausdiesen Variablen, wobei
PrPt(x) = Pr(X0 = x0, X1 = x1, . . .)
ist. Eine Plaintextquelle fur n -Gramme definieren wir uber die Wahrscheinlichkeiten
Pr(Xj = x0, Xj+1 = x1, . . . , Xj+n−1 = xn−1)
fur alle (x0, . . . , xn−1) ∈ Zm,n und alle j, n ∈ N .
Um ein solides mathematisches Modell zu erhalten, mussen wir garantieren, dass die folgenden Be-dingungen erfullt sind:
27

1. PrPt(x0, . . . , xn−1) ≥ 0 fur alle n ∈ N und (x0, . . . , xn−1) ∈ Zm,n .
2.∑
(x0,...,xn−1)∈Zm,nPrPt(x0, . . . , xn−1) = 1 fur alle n ∈ N .
3. PrPt(x0, . . . , xn−1) =∑
(xn,...,xs−1)∈Zm,n−sPrPt(x0, . . . , xs−1) fur alle n, s ∈ N mit s > n .
Die ersten beiden Bedingungen sind zwei klassische Axiome fur Wahrscheinlichkeitsverteilungen, nichtNegativitat und Normalisierung. Die dritte Bedingung ist ein Spezialfall von Kolmogoroffs Konsistenz-forderung. Diese stellt eine Verbindung zwischen Prafixen und deren Verlangerungen dar. Die Bedeu-tung dieser Eigenschaft zeigt sich zum Beispiel im Deutschen bei der Verknupfung von einzelnenWorten, wie zum Beispiel: Bugeleisen, Bugelbrett, usw.
Wir wollen jetzt auf verschiedene Quellenmodelle eingehen.
3.2.1 Variante 1: 1-Gramm-Quellen
Die einfachste Form eines Quellenmodells ist die 1-Gramm-Quelle:
Definition 4 Eine Plaintextquelle generiert 1-Gramme uber Zm , indem sie eine Folge von n Sym-bolen x0, . . . , xn−1 aus Zm unabhangig voneinander jeweils mit einer Wahrscheinlichkeit von p(xi)wahlt. Wir erhalten somit
PrPt(x0, . . . , xn−1) =n−1∏i=0
p(xi) .
Die Wahrscheinlichkeiten p(xi) fur xi ∈ Zm mussen wir empirisch uber eine Haufigkeitsanalyse be-stimmen. Eine entsprechende Tabelle fur Englisch haben wir bereits im Abschnitt uber den Friedman-Test angegeben. Es ist einfach zu erkennen, das 1-Gramm-Quellen die drei mathematischen Bedingun-gen erfullen, die wir an eine Plaintextquelle gerichtet haben. Jedoch werden von einer 1-Gramm-Quelleviele charakteristische Eigenschaften von Sprachen nicht reflektiert, so ist PrPt(QE) ≈ 0, 000156 > 0 .
3.2.2 Variante 2: 2-Gramm-Quellen
Definition 5 Eine Plaintextquelle generiert 2-Gramme uber Zm , indem sie eine Folge von n/2 Paa-ren von Symbolen x0, . . . , xn−1 aus Zm unabhangig voneinander jeweils mit einer Wahrscheinlichkeitvon p(x2ix2i+1) wahlt. Wir erhalten somit
PrPt(x0, . . . , xn−1) =(n−1)/2∏
i=0
p(x2ix2i+1) .
Wie schon fur 1-Gramme mussen wir auch fur 2-Gramme die Wahrscheinlichkeiten p(x2ix2i+1) empi-risch bestimmen. Um eine hinreichend gute Aussage uber die Wahrscheinlichkeiten p(x2ix2i+1) her-leiten zu konnen, mussen wir entsprechend große Texte analysieren. Die nachfolgenden Tabellen zeigendie Haufigkeiten aller 262 2-Gramme eines englischen Textes der aus 67320 2-Grammen besteht. DieWerte N(i, j) , dass heißt der Eintrag in der i ten Spalte und j ten Zeile steht fur das 2-Gramm(i, j) . Um die entsprechenden Wahrscheinlichkeiten zu erhalten, mussen wir p(i, j) = N(i, j)/67320berechnen.
28

A B C D E F G H I J K L M
A 7 125 251 304 13 65 151 13 311 13 67 681 182
B 114 7 2 1 394 – – – 74 7 – 152 6
C 319 – 52 1 453 – – 339 202 – 86 98 4
D 158 3 4 33 572 1 20 1 273 5 – 19 27
E 492 27 323 890 326 106 93 16 118 4 27 340 253
F 98 – – – 150 108 – – 188 – – 35 1
G 122 – – 2 271 – 20 145 95 – – 23 3
H 646 2 5 3 2053 – – 2 426 – – 6 6
I 236 51 476 285 271 80 174 1 10 – 31 352 184
J 18 – – – 26 – – – 5 – – – –
K 14 1 – 1 187 1 – 7 56 – 4 7 1
L 359 5 6 197 513 28 29 – 407 – 21 378 22
M 351 65 5 – 573 2 – – 259 – – 2 126
N 249 2 281 761 549 46 630 6 301 4 30 33 47
O 48 57 91 130 21 731 46 14 52 8 44 234 397
P 241 – 1 – 310 – – 42 75 – – 144 13
Q – – – – – – – – – – – – –
R 470 15 79 129 1280 14 80 8 541 – 94 75 139
S 200 4 94 9 595 8 – 186 390 – 30 48 37
T 381 2 22 1 872 4 1 2161 865 – – 62 27
U 72 87 103 51 91 11 80 2 54 – 3 230 69
V 65 – – 2 522 – – – 223 – – – 1
W 282 1 – 4 239 – – 175 259 – – 5 –
X 9 – 15 – 17 – – 1 15 – – – 1
Y 17 1 3 2 84 – – – 20 – 1 5 11
Z 18 – – – 36 – – – 17 – – 1 –
N O P Q R S T U V W X Y Z
A 1216 5 144 – 764 648 1019 89 137 37 17 202 15
B – 118 – – 81 28 6 89 2 – – 143 –
C 3 606 – 1 113 23 237 92 – – – 25 –
D 8 111 – 1 49 75 2 91 15 6 – 40 –
E 1029 30 143 25 1436 917 301 36 160 153 113 90 3
F 1 326 – – 142 3 58 54 – – – 5 –
G 51 129 – – 150 29 28 58 – – – 6 –
H 14 287 – – 56 10 85 31 – 4 – 15 –
I 1550 554 62 5 212 741 705 7 155 – 14 1 49
J – 45 – – 1 – – 48 – – – – –
K 20 7 – – 3 39 1 1 – – – 4 –
L 1 208 11 – 9 104 68 72 15 3 – 219 –
M 8 240 139 – 5 47 1 65 1 – – 37 –
N 88 239 2 3 5 340 743 56 31 8 1 71 2
O 1232 125 164 – 861 201 223 533 188 194 7 23 2
P 1 268 103 – 409 32 51 81 – – – 3 –
Q – – – – – – – 73 – – – – –
R 149 510 25 – 97 300 273 88 65 8 1 140 –
S 7 234 128 3 9 277 823 192 – 13 – 27 –
T 9 756 2 – 295 257 131 120 3 54 – 125 3
U 318 4 81 – 306 256 263 6 3 – 2 3 1
V – 46 – – – 2 – 1 1 – – 5 –
W 44 159 – – 13 45 2 – – – – 3 –
X – 1 47 – – – 23 – – – 5 – –
Y 5 64 9 – 9 44 5 4 – 3 – 2 1
Z – 4 – – – – – 1 – – – – 2
29

Es ist einfach zu erkennen, dass eine 2-Gramm-Quelle die englische Sprache viel besser reflektiert alseine 1-Gramm-Quelle. So gilt PrPt(QE) = 0 und PrPt(HELP ) = 0, 0000061 > 0 = PrPt(LHEP ) .Auf der anderen Seite gilt
PrPt(HELP ) = 0, 0000061 < 0, 0000064 = PrPt(HEPL) ,
obwohl HEPL kein englischer Begriff ist. Um solche Fehlerwahrscheinlichkeiten noch weiter zu redu-zieren, mussen wir t -Gramme fur t > 2 analysieren. Hier entsteht jedoch das Problem, dass diedazugehorigen Tabellen exponentiell in t wachsen und die benotigte Datenmenge enorm ist.
3.2.3 Variante 3: Markov-Ketten
Eine dritte Variante zur Modellierung von Plaintextquellen erhalten wir uber das Markov-Kettenmodell.
Definition 6 Eine Plaintextquelle generiert 1-Gramme aus Zm uber eine Markov-Kette mit Uber-gangswahrscheinlichkeiten P = (p(s|t))s,t∈Zm und mit Initialwahrscheinlichkeiten π = (π(s))s∈Zm ,wenn fur alle n ∈ N und alle x = (x0, . . . , xn−1) ∈ Zm,n gilt
PrPt(x0, . . . , xn−1) = π(x0) ·n−2∏i=0
p(xi+1|xi) .
Ferner mussen die folgenden Bedingungen erfullt sein:
1. p(s|t) ≥ 0 fur alle s, t ∈ Zm .
2.∑
s∈Zmp(s|t) = 1 fur alle t ∈ Zm .
3. π(s) ≥ 0 fur alle s ∈ Zm und∑
s∈Zmπ(s) = 1 .
4. π(s) =∑
t∈Zmπ(t) · p(s|t) fur alle s ∈ Zm .
Das Ziel des Markov-Ketten Modells ist es, die Sprache mit Hilfe eines probabilistischen endlichen Au-tomaten zu beschreiben, der m Zustande besitzt. Mit der Wahrscheinlichkeitsverteilung π bestimmenwir das Symbol, mit dem der Text beginnen soll. Die Wahrscheinlichkeiten p(s|t) beschreiben unsdann eine Fortsetzung des Textes. Die Wahrscheinlichkeiten p(s|t) konnen wir mit Hilfe der Tabelleder 2-Gramme im letzten Abschnitt berechnen. Es gilt
p(s|t) =N(t, s)∑
h∈ZmN(h, t)
.
Die Wahrscheinlichkeiten π fur die englische Sprache sind in der nachfolgenden Tabelle wiedergegeben.
π π π π
A 0,0723 H 0,0402 O 0,0716 V 0,0117B 0,0060 I 0,0787 P 0,0161 W 0,0078C 0,0282 J 0,0006 Q 0,0007 X 0,0030D 0,0483 K 0,0064 R 0,0751 Y 0,0168E 0,1566 L 0,0396 S 0,0715 Z 0,0010F 0,0167 M 0,0236 T 0,0773G 0,0216 N 0,0814 U 0,0272
30

Die Werte von π konnen aus den bedingten Wahrscheinlichkeiten P wie folgt bestimmt werden:Stellen wir π als (Zeilen-)Vektor und P als Matrix dar, so folgt aus der vierten Eigenschaft, die wirvon dem Markov-Ketten Modell gefordert haben:
π = π · P .
Sei π(`)(j) die Wahrscheinlichkeit, dass die Markov-Kette im ` ten Schritt im Zustand j ist, dassheißt π(`)(j) = Pr(X`−1 = j) . Aus der Definition folgt unmittelbar π(0)(j) = π(j) und aus der viertenEigenschaft der Markov-Ketten π(`)(j) = π(j) fur alle ` ∈ N . Die Wahrscheinlichkeiten π(`)(j) sindsomit stationar. Um die Wahrscheinlichkeiten π zu erhalten, genugt es somit die Gleichung π = π ·Pzu losen. Die Losung dieses Systems wird in vielen Standardwerken beschrieben, siehe hierzu [F68].
Es ist jedoch auch fur das Markov-Ketten Modell einfach zu erkennen, dass es eine Sprache nichtperfekt beschreibt. So gilt weiterhin
PrPt(HELP ) < PrPt(HEPL) .
Aufgabe 13 Betrachten Sie folgendes Szenario: Alice mochte, dass Bob einen Multiple-Choice Testausfullt. Hierzu wurfelt sie fur jedes Kastchen ki des Tests ein Zufallsbit ri und sendet den Testmit der Zufallssequenz r = (r0, . . . , rn−1) an Bob mit Hilfe eines Kuriers Eve. Bob fullt jetzt denTest aus, indem er die Sequenz x = (r0 ⊕ x0, . . . , rn−1 ⊕ xn−1) berechnet. Hierbei stehen die Wertexi fur die binare Kodierung der Ja/Nein-Antwort fur Kastchen ki . Im Anschluss nimmt Bob miteinem neuen Kurierdienst Eva Kontakt auf. Nachdem er sich davon uberzeigt hat, dass Eva nicht Eveist, sendet er seine Antworten uber Eva an Alice. Zeigen Sie, dass das so benutzte Verfahren perfekteSicherheit fur die Antworten von Bob garantiert.
Aufgabe 14 Weisen Sie fur die drei oben beschriebenen Varianten von Plaintextquellen nach, dassdiese die drei geforderten mathematischen Bedingungen an eine Plaintextquelle erfullen.
Aufgabe 15 Erweitern Sie das Markov-Ketten Modell darauf, dass es bei den bedingten Wahrschein-lichkeiten die letzten ` Symbole des Plaintextes berucksichtigt.
3.3 Bayes’scher Ansatz in der Kryptoanalyse
Im Folgenden wollen wir uns mit der Aufgabe des Kryptoanalytikers naher beschaftigen. Diese bestehtin erster Linie aus der Suche nach einer Funktion δ , welche einen gegebenen Ciphertext korrektentschlusselt.
Definition 7 Eine deterministische Entscheidungsfunktion δ = (δ(n))n∈N ist eine Sequenz vonTransformationen δ(n) : Zm,n → Zm,n . Die Menge aller deterministischen Entscheidungsfunktionenbezeichnen wir mit ∆D .
Wie oben schon angedeutet, soll eine Entscheidungsfunktion einen verschlusselten Text entschlusseln,dass heißt, sie soll auf Eingabe einen Ciphertextes y einen Plaintext x ausgeben, so dass bei der Wahleines entsprechenden Schlussels w y = Tw(x) ist. Da diese Funktion deterministisch ist, generiertsie auch fur andere Plaintext-Schlussel-Paare (x′, w′) mit y = Tw′(x′) als Ausgabe den Plaintext x .Ergebnisse der Form Tw′(x′) 6= x′ sind fehlerhaft. Um die Qualitat einer deterministischen Entschei-dungsfunktion bei der Entschlusselung von Ciphertexten zu messen, definieren wir den Verlust einerEntscheidungsfunktion:
31

Definition 8 Sei δ ∈ ∆D , dann definieren wir die Verlustfunktion Lδ von δ fur alle x ∈Pt undy ∈Ct durch
Lδ(x, y) ={
1 fur δ(y) 6= x0 fur δ(y) = x .
Da es sich beim Plaintext und dem Ciphertext um Zufallsvariablen handelt, interessiert uns unteranderem der erwartete Verlust einer Entscheidungsfunktion. Wir definieren daher
Ln,δ := E[Lδ(n) ] =∑
x,y∈Zm,n
PrPt,Ct(x, y) · Lδ(x, y)
undLδ := { Ln,δ | n ∈ N } .
Unser Ziel ist es einen Entscheidungsfunktion zu finden, welche den erwarteten Verlust minimiert.
Definition 9 Eine deterministische Entscheidungsfunktion δ∗ nennen wir optimal, wenn
1. δ∗ ∈ ∆D ist und
2. fur alle δ ∈ ∆D und alle n ∈ N gilt Ln,δ∗ ≤ Ln,δ .
Eine spezielle Form der Entscheidungsfunktionen erhalten wir mit folgender Definition:
Definition 10 Eine deterministische Entscheidungsfunktion δB nennen wir Bayes’sche Entschei-dungsfunktion, wenn
PrPt|Ct(δB(y)|y) = maxx∈Zm,n
PrPt|Ct(x|y) .
Man beachte, dass δB(y) genau dann definiert ist, wenn PrCt(y) > 0 ist.
Abhangig von der Verteilung PrPt ist es moglich, dass fur verschiedene Ciphertexte y Plaintexte xexistieren, so dass bei geeignetem Schlussel w Tw(x) = y ist und zudem PrPt(x) maximal ist. Eskann daher mehrere verschiedene Bayes’sche Entscheidungsfunktion geben. Die wesentliche Bedeutungdieser Entscheidungsfunktionen folgt aus dem nachfolgenden Theorem:
Theorem 6 Eine deterministische Entscheidungsfunktion δ ist genau dann optimal, wenn sie eineBayes’sche Entscheidungsfunktion ist.
Beweis: Es gilt:
Ln,δ = E[Lδ(n) ]
=∑
x,y∈Zm,n
PrPt,Ct(x, y) · Lδ(x, y)
=∑
x,y∈Zm,n
PrCt(y) · PrPt|Ct(x|y) · Lδ(x, y)
=∑
y∈Zm,n
∑x∈Zm,n
PrCt(y) · PrPt|Ct(x|y) · Lδ(x, y)
=∑
y∈Zm,n
PrCt(y) ·∑
x∈Zm,n
PrPt|Ct(x|y) · Lδ(x, y)
32

Zur Vereinfachung der zweiten Summe setzen wir nun unser Wissen uber die Definition von Lδ(x, y)ein: Lδ(x, y) ist genau dann 0, wenn δ(y) = x ist.
Ln,δ =∑
y∈Zm,n
PrCt(y) ·∑
x∈Zm,n mit δ(y) 6=x
PrPt|Ct(x|y) · Lδ(x, y)
=∑
y∈Zm,n
PrCt(y) ·∑
x∈Zm,n mit δ(y) 6=x
PrPt|Ct(x|y)
Da fur jedes y maximal ein x existiert, so dass δ(y) = x ist, konnen wir im nachsten Schritt dieseFormel insoweit vereinfachen, dass wir in der zweiten Summe die Komplementarmenge betrachten:
Ln,δ =∑
y∈Zm,n
PrCt(y) ·
1−∑
x∈Zm,n mit δ(y)=x
PrPt|Ct(x|y)
=
∑y∈Zm,n
PrCt(y) ·(1− PrPt|Ct(δ(n)(y)|y)
).
Wir wollen nun die beiden Richtungen des Theorems beweisen:
1. Die Entscheidungsfunktion δ ist genau dann optimal, wenn Ln,δ minimal ist.
2. Da die Entscheidungsfunktion δ(n) fur jedes y unabhangig von anderen Ciphertexten y′ gewahltwerden kann, und PrCt(y) unabhangig von δ(n)(y) ist, gilt: Ln,δ ist genau dann minimal, wennfur alle y PrPt|Ct(δ(n)(y)|y) maximal ist, d.h.
PrPt|Ct(δ(n)(y)|y) = maxx∈Zn,m
PrPt|Ct(x|y) .
Fassen wir zusammen: Die Entscheidungsfunktion δ ist genau dann optimal, wenn δ eine Bayes’scheEntscheidungsregel ist.
Wir wollen nun ein Beispiel fur Entscheidungsfunktionen diskutieren. Als Verschlusselungsfunktionbetrachten wir
T7(i) ≡ i + 7 mod 26
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25A B C D E F G H I J K L M N O P Q R S T U V W X Y ZH I J K L M N O P Q R S T U V W X Y Z A B C D E F G
Wir verschlusseln den Plaintext SENDHELP und erhalten den Ciphertext ZLUKOLSW. Um eine op-timale Entscheidungsfunktion zu finden, benotigen wir die Werte der bedingten Wahrscheinlichkeiten
PrPt|Ct(x|ZLUKOLSW ) .
Fur alle 268 8-Gramme x . Da wir jedoch annehmen, dass der Kryptoanalytiker das benutzte Ver-schlusselungsverfahren kennt, konnen wir die Anzahl der betrachteten 8-Gramme auf 26 reduzieren.Ersetzen wir in y die Zeichen durch die entsprechenden Werte, so erhalten wir
y = (y0, y1, y2, y3, y4, y5, y6, y7) = (25, 11, 20, 10, 14, 11, 18, 22)
und fur die interessanten 8-Gramme
y − w = (y0 − w, y1 − w, y2 − w, y3 − w, y4 − w, y5 − w, y6 − w, y7 − w)= (25− w, 11− w, 20− w, 10− w, 14− w, 11− w, 18− w, 22− w) mod 26 .
33

Fur die zu betrachtenden Wahrscheinlichkeiten gilt
PrPt,Ct(x, y) =
126 · PrPt(y − w mod 26) fur x = y − w mod 26
mit k ∈ {0, . . . , 25}0 sonst.
und
PrCt(y) =∑
x∈Z26,8
PrPt,Ct(x, y) =25∑
w=0
126· PrPt(y − w mod 26) .
Fassen wir zusammen:
PrPt|Ct(y − w mod 26|y) =PrPt(y − w mod 26)∑25k=0 PrPt(y − k mod 26)
.
Die nachfolgende Tabelle fasst die Wahrscheinlichkeiten PrPt|Ct(y − w mod 26|y) fur die Plaintext-quellen aus Definition 4 bis 6 zusammen:
k Y − k PrPt PrPt PrPt
nach Def. 4 nach Def. 5 nach Def. 60 ZLUKOLSW 0,00002353 0,00000089 0,000003091 YKTJNKRV 0,00000736 0,00000000 0,000000002 XJSIMJQU 0,00000003 0,00000000 0,000000003 WIRHLIPT 0,05269719 0,00418837 0,000338154 VHQGKHOS 0,00004373 0,00000000 0,000000005 UGPFJGNR 0,00012522 0,00000000 0,000000006 TFOEIFMQ 0,00601645 0,00000000 0,000000007 SENDHELP 0,35013155 0,99580491 0,999657668 RDMCGDKO 0,00158882 0,00000088 0,000000009 QCLBFCJN 0,00000412 0,00000000 0,0000000010 PBKAEBIM 0,00100489 0,00000000 0,0000000011 OAJZDAHL 0,00013951 0,00000000 0,0000000012 NZIYCZGK 0,00000043 0,00000000 0,0000000013 MYHXBYFJ 0,00000164 0,00000000 0,0000000014 LXGWAXEI 0,00007197 0,00000000 0,0000000015 KWFVZWDH 0,00000134 0,00000000 0,0000000016 JVEUYVCG 0,00001388 0,00000000 0,0000000017 IUDTXUBF 0,00037299 0,00000000 0,0000000018 HTCSWTAE 0,58014350 0,00000495 0,0000011119 GSBRVSZD 0,00006560 0,00000000 0,0000000020 FRAQURTC 0,00066643 0,00000000 0,0000000021 EQZPTQXB 0,00000002 0,00000000 0,0000000022 DPYOSPWA 0,00658287 0,00000000 0,0000000023 COXNROVZ 0,00003584 0,00000000 0,0000000024 BNWMQNUY 0,00005462 0,00000000 0,0000000025 AMVLPMTX 0,00020646 0,00000000 0,00000000
Demnach wurde eine optimale Entscheidungsfunktion unter der Annahme, dass eine 1-Gramm Plain-textquelle vorliegt den Text HTCSWTAE liefern und fur die beiden anderen oben vorgestellten Plain-textquellen den Plaintext SENDHELP.
34

4 Symmetrische Verschlusselungsalgorithmen
Definition 11 Ein symmetrisches Kryptosystem ist ein Verschlusselungssystem, welches dengleichen Schlussel zur Ver- und Entschlusselung verwendet. Bei manchen symmetrischen Verfahren(z. B. IDEA) ist es notwendig, den aus dem Verschlusselungs-Schlussel einen Entschlusselungs-Schlussel zu berechnen. Im Gegensatz hierzu benutzt ein asymmetrischen Kryptosystem zur Ver-und Entschlusselung ein Schlusselpaar.
Wir unterteilt die symmetrischen Verfahren in Blockchiffren und Stromchiffren.
• Bei einem Stromchiffre wird der Plaintext Zeichen fur Zeichen ver- bzw. entschlusselt.
• Bei einem Blockchiffre wird der Plaintext Block fur Block ver- bzw. entschlusselt, wobei die Blockeeine feste Große haben. In einem Schritt werden somit mehrere Zeichen ver- bzw. entschlusselt.
Die bisher vorgestellten Verfahren zahlen (mehr oder weniger) zu den Stromchiffresysteme. Im Folgen-den werden wir nun die beiden bekanntesten symmetrischen Verschlusselungsalgorithmen vorstellen:den DES und den AES.
4.1 Der Data Encryption Standard (DES)
Bis 1970 wurde die Kryptographie vom Militar dominiert. 1973 wurde daher vom National Bureau ofStandards (NBS) der USA eine erste Ausschreibung fur ein standardisiertes Verschlusselungsverfahrengestartet. 1975 wurde das DES im Federal Register veroffentlicht und galt viele Jahre als Standard-kryptosystem fur kommerzielle Anwendungen. Seit 1994 gelang es das DES durch immer weiter ver-besserte Verfahren immer schneller zu knacken. Daraufhin wurde 1999 der Triple-DES (TDES, 3DES)als neuer Standard veroffentlicht und 2005 der DES als Standard außer Kraft gesetzt. 2006 wurde einFPGA-basierte Parallelrechner COPACOBANA vorgestellt mit dessen Hilfe das DES in weniger als9 Tagen geknackt werden konnte. Die Materialkosten dieses Rechners liegen unter 10.000 Dollar. Diefolgende Beschreibung des DES und des TDES folgt der Beschreibung aus [FIPS99].
4.1.1 Aufbau des DES-Kryptosystems
Das DES-System verschlusselt einen 64-Bit Block mit Hilfe eines 64-Bit Schlussels K . 56 Bit desSchlussels sind frei wahlbar. Jedes 8-te Bit des Schlussels ist so gewahlt, dass in jedem 8-Bit Blockdes Schlussels eine ungerade Anzahl von 1-en stehen. Die Verschlusselung geschieht in 18 Stufen:
• Die erste und die letzte Stufe bestehen aus einer festen Permutation der Eingabe bzw. derAusgabe.
• Die eigentliche Verschlusselung geschieht in den 16 verbleibenden Stufen.
Aus dem Plaintext x wird mit Hilfe einer Permutation IP (initial permutation) die permutierteEingabe generiert, die wir in zwei Halften L0 und R0 aufteilen.
35

Fur die nachsten 16 Stufen (den Verschlusselungsstufen) generieren wir aus dem Schlussel K jeweilsein 48-Bit Teilschlussel Ki . In den Verschlusselungsstufen berechnen wir fur i ∈ [1..16]
Li := Ri−1
Ri := Li−1 ⊕ f(Ri−1,Ki)
wobei ⊕ das Bitweise xor der beiden binaren Zeichenketten bezeichnet. Auf die Berechnung von fwerden wir noch eingehen. Nach den 16 Verschlusselungsstufen erhalten wir den Preoutput R16L16
aus dem wir uber die inverse Permutation IP −1 die Ausgabe generieren.
L0R0 = IP (x)
K1
L1 = R0 L16 = R15
R16 = L15 ⊕ f(R15, K16)
R1 = L0 ⊕ f(R0, K1)
⊕
T
L0
U
OR1
L1
IP −1f
R16
IP
L16
I
N
P
U
T
P
U
T
R0
Die einzelnen Permutationen (in der Konstruktion von f und bei der Erzeugung der Teilschlussel wer-den noch weitere Permutationen vorgestellt) sollen unter anderem eine moglichst gut Durchmischungder Bits des Plaintextes garantieren. Neben der gut Durchmischung soll durch die Permutationenauch garantiert werden, dass einzelne Bits des Plaintexts moglichst viele Stellen des Ciphertextesbeeinflussen. So unterscheidet sich die Ciphertexte von
x1 = 064 und x2 = 0631
bereits nach der 3-ten Verschlusselungsstufen in 21 Bits und nach Abschluß der DES Verschlusselungin 34 Bits. Einen derartigen Effekt nennen wir auch Lawineneffekt.
Im Folgenden zahlen wir die Bitpositionen in einem Binarstring mit den Werten i = 1, 2, . . . , 64 auf.Fur IP bzw. fur IP −1 wahlen wir:
IP58 50 42 34 26 18 10 260 52 44 36 28 20 12 462 54 46 38 30 22 14 664 56 48 40 32 24 16 857 49 41 33 25 17 9 159 51 43 35 27 19 11 361 53 45 37 29 21 13 563 55 47 39 31 23 15 7
36

IP−1
40 8 48 16 56 24 64 3239 7 47 15 55 23 63 3138 6 46 14 54 22 62 3037 5 45 13 53 21 61 2936 4 44 12 52 20 60 2835 3 43 11 51 19 59 2734 2 42 10 50 18 58 2633 1 41 9 49 17 57 25
Die Lesweise dieser Tabellen ist wie folgt:
• Fur eine n×m -Tabelle T sei T [i, j] der Wert in der i -ten Spalte und j -ten Zeile von T .
• Fur einen n ·m -Bit String w ist u = T (w) der String, der an der Position i + (j − 1) · n miti ∈ [1..n] und j ∈ [1..m] das T [i, j] -te Zeichen von w stehen hat.
Somit steht in der permutierten Eingabe IP (x) an der ersten Stelle das 58-ste Bit der Eingabe, ander zweiten Stelle das 50-ste Bit der Eingabe, u.s.w.
4.1.2 Berechnung der Funktion f
Die Funktion f verknupft wie folgt Ri mit dem Teilschlussel Ki+1 :
1. Mit Hilfe der Tabelle E expandieren wir Ri auf 48 Bits, indem wir 16 der 32 Bits verdoppeln.
2. Das expandierte Ri wird bitweise mit Ki+1 ge-xor-ed.
3. Den resultierenden String teilen wir in 8 Blocke Bi a 6 Bit auf, d.h.
B1 . . . B8 = Ki+1 ⊕ E(Ri) .
4. Auf den i -ten 6-Bit Block Bi wenden wir die uber Si gegebene S -Box-Operation Si(Bi) an.Diese S -Box-Operation reduziert die 6-Bit eines Blocks Bi auf 4-Bits.
5. Die konkatenierte Folge der 4-Bit Blocke Si(Bi) permutieren wir abschließende mit Hilfe derPermutation P . Das 32-Bit Resultat dieser Permutation gibt uns das Resultat Funktion f an.
Ri+1 (32 Bits)
48 Bits
S8
Ri (32 Bits)
S1
⊕
Ki+1 (48 Bits)
E
P
37

Wir wollen nun zunachst die beiden Tabellen E und P vorstellen, und im Anschluß auf die S -Box-Operation eingehen. Die Expandierungstabelle E hat die folgende Gestallt:
32 1 2 3 4 54 5 6 7 8 98 9 10 11 12 13
12 13 14 15 16 1716 17 18 19 20 2120 21 22 23 24 2524 25 26 27 28 2928 29 30 31 32 1
Die erste Zeile von E(Ri) wird (nach dem xor-en mit einem Teil des Teilschlussel) in der erstenS -Box-Operation weiterverarbeitet, die zweite Zeile in der zweiten S -Box-Operation und so weiter.Man beachte, dass die letzten beiden Eintrage jeder Zeile den ersten beiden Eintragen der Folgezeileentsprechen.
Die Tabelle P hat die folgende Gestallt:
16 7 20 2129 12 28 171 15 23 265 18 31 102 8 24 14
32 27 3 919 13 30 622 11 4 25
Wie die Permutation IP realisiert die Permutation P wieder eine gute Durchmischung des resultie-renden Binarstrings. Beachte, dass dieses bei E nicht der Fall ist.
Die Si -Box-Operation ist wie folgt aufgebaut:
• Wir betrachten den 6-Bit Block Bi und unterteilen den Binarstring in zwei Teile: in die erstenbeiden Bits B1
i und in die verbleibenden 4 Bits B2i .
• Das Ergebnis der Si -Box-Operation ist der Binarstring des Werts der Tabelle Si in der B1i -ten
Zeile und der B2i -ten Spalte. Hierbei werden B1
i und B2i als Zahlen interpretiert.
Designkriterien fur gut S -Boxen wurden in [C94] veroffentlicht. Im Folgenden werden wir die S -Boxen des DES-Systems vorstellen:
S1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 14 4 13 1 2 15 11 8 3 10 6 12 5 9 0 71 0 15 7 4 14 2 13 1 10 6 12 11 9 5 3 82 4 1 14 8 13 6 2 11 15 12 9 7 3 10 5 03 15 12 8 2 4 9 1 7 5 11 3 14 10 0 6 13
38

S2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 15 1 8 14 6 11 3 4 9 7 2 13 12 0 5 101 3 13 4 7 15 2 8 14 12 0 1 10 6 9 11 52 0 14 7 11 10 4 13 1 5 8 12 6 9 3 2 153 13 8 10 1 3 15 4 2 11 6 7 12 0 5 14 9
S3 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 10 0 9 14 6 3 15 5 1 13 12 7 11 4 2 81 13 7 0 9 3 4 6 10 2 8 5 14 12 11 15 12 13 6 4 9 8 15 3 0 11 1 2 12 5 10 14 73 1 10 13 0 6 9 8 7 4 15 14 3 11 5 2 12
S4 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 7 13 14 3 0 6 9 10 1 2 8 5 11 12 4 151 13 8 11 5 6 15 0 3 4 7 2 12 1 10 14 92 10 6 9 0 12 11 7 13 15 1 3 14 5 2 8 43 3 15 0 6 10 1 13 8 9 4 5 11 12 7 2 14
S5 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 2 12 4 1 7 10 11 6 8 5 3 15 13 0 14 91 14 11 2 12 4 7 13 1 5 0 15 10 3 9 8 62 4 2 1 11 10 13 7 8 15 9 12 5 6 3 0 143 11 8 12 7 1 14 2 13 6 15 0 9 10 4 5 3
S6 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 12 1 10 15 9 2 6 8 0 13 3 4 14 7 5 111 10 15 4 2 7 12 9 5 6 1 13 14 0 11 3 82 9 14 15 5 2 8 12 3 7 0 4 10 1 13 11 63 4 3 2 12 9 5 15 10 11 14 1 7 6 0 8 13
S7 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 4 11 2 14 15 0 8 13 3 12 9 7 5 10 6 11 13 0 11 7 4 9 1 10 14 3 5 12 2 15 8 62 1 4 11 13 12 3 7 14 10 15 6 8 0 5 9 23 6 11 13 8 1 4 10 7 9 5 0 15 14 2 3 12
S8 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 150 13 2 8 4 6 15 11 1 10 9 3 14 5 0 12 71 1 15 13 8 10 3 7 4 12 5 6 11 0 14 9 22 7 11 4 1 9 12 14 2 0 6 10 13 15 3 5 83 2 1 14 7 4 10 8 13 15 12 9 0 3 5 6 11
4.1.3 Die Teilschlussel Ki
Die Konstruktion der Teilschlussel Ki erfolgt wieder in mehreren Stufen:
39

1. Im ersten Schritt werden mit Hilfe der Tabelle PC-1 der Schlussel K permutiert und die red-undanten Kontroll-Bits heraus gefiltert. Dieses sind die Bits 8, 16, 24, 32, 40, 48, 56, 64.
2. Die verbleibenden 56 Bits werden in zwei 28-Bit Blocke aufgeteilt: C0 und D0 .
3. Sukzessive generieren wir aus C0 die Folge C1, . . . , C16 und aus D0 die Folge D1, . . . , D16 .Hierbei erhalten wir aus Ci−1 und Di−1 uber zyklische Shifts die Blocke Ci und Di . DieAnzahl der Shifts ist von i abhangig.
4. Aus der Konkatenation der Blocken Ci und Di selektieren wir uber die Tabelle PC-2 denTeilschlussel Ki .
Die folgende Graphik illustriert das zusammenwirken der einzelnen Schritte:
C0D0 = PC-1 (K)
Links-
Links-shift
shiftLinks-shifts
Links-shifts
K16K1
e
y
K
C0
D0
C1
D1
PC-2 PC-2
C2
D2
C16
D16
K
PC-1
Die Tabelle PC-1 hat die folgende Gestalt:
57 49 41 33 25 17 91 58 50 42 34 26 18
10 2 59 51 43 35 2719 11 3 60 52 44 3663 55 47 39 31 23 157 62 54 46 38 30 22
14 6 61 53 45 37 2921 13 5 28 20 12 4
und die Tabelle PC-2 die folgende Gestalt:
14 17 11 24 1 53 28 15 6 21 10
23 19 12 4 26 816 7 27 20 13 241 52 31 37 47 5530 40 51 45 33 4844 49 39 56 34 5346 42 50 36 29 32
40

Die Anzahl der Shifts um aus Ci−1 den Block Ci bzw. aus Di−1 den Block Di zu generieren hangtvon i ab:
i: 1 2 3 4 5 6 7 8Anzahl der Shifts: 1 1 2 2 2 2 2 2
i: 9 10 11 12 13 14 15 16Anzahl der Shifts: 1 2 2 2 2 2 2 1
Mit Hilfe der Tabelle PC-2 wahlen wir wahlen wir die 48 Bits des Teilschlussels Ki des 56-BitSchlussels CiDi aus. Der Schlussel setzt sich bei jedem Auswahlschritt aus der Konkatenation derbeiden aktuellen Blocke CiDi zusammen. Da wir die beiden Blocke des 56-Bit Schlussels vor jedemAuswahlschritt zyklisch Shiften, wird bei jedem Auswahlschritt eine veranderte Kollektion an Bitsausgewahlt.
4.1.4 Die Entschlusseloung eines DES-Cyphertextes
Die Entschlusselung eines DES-Cyphertextes geschieht mehr oder weniger uber das gleiche Verfahren,mit dem wir die Verschlusselung vorgenommen haben. Wir starten mit der folgenden Beobachtung:
Da sich Li ohne Veranderung aus Ri−1 ergibt, konnen wir die Formel
Ri = Li−1 ⊕ f(Ri−1,Ki)
umstellen zuRi = Li−1 ⊕ f(Li,Ki) .
Die Teilschlussel Ki sind unabhangig von Eingabe und von Li und Ri und konnen daher un-abhangig vom aktuellen Zustand des Systems generiert werden. Daher ist es moglich die obige Formelso umzustellen, dass wir den Wert Li−1 aus Ri und Li bestimmen konnen. Wir erhalten
Li−1 = Ri ⊕ f(Li,Ki) .
und nach KonstruktionRi−1 = Li .
Die folgenden Graphik illustriert die Entschlusseloung eines DES-Cyphertextes:
L15 = R16 ⊕ f(L16, K16)
L0 = R1 ⊕ f(L1, K1)
R15 = L16 R0 = L1R16L16 = IP (y)
⊕
K16
L15L16I
N
P
U
T
P
U
T
T
U
O
R16 R0
L0
IP −1
R15
fIP
41

4.2 Das Triple DES-Kryptosystem (TDES)
Aufgrund der immer schnelleren Attacken gegen das DES-System wurde 1999 ein modifiziertes DES-System, das TDES, vorgestellt. Ziel des TDES-Kryptosystems war es, dass DES-Kryptosystem sicherergegen Angriffe zu machen. Hierbei sollte sowohl die Verschlusselung als auch die Entschlusselung mitHilfe des einfachen DES moglich sein. Ferner sollte es mit dem neuen System auch moglich seinCiphertexte, die mit DES verschlusselt wurden, zu entschlusseln.
Ein erster Ansatz besteht darin einen Text mehrmals mit DES unter verschiedenen Schlusseln zuverschlusseln. Dieses wurde zwar das System sicherer machen, jedoch wurden die Schwachen des DESerhalten bleiben. Der TDES wahlt einen anderen Ansatz.
Sei EK(x) die Verschlusselung von x mit Hilfe des DES-Kryptosystems unter dem Schlussel K undsei DK(y) die Entschlusselung von y mit Hilfe des DES-Kryptosystems unter dem Schlussel K .Seien K1,K2,K3 drei Schlussel, dann erhalten wir die Verschlusselung von x mit Hilfe des TDES-Kryptosystems unter dem Schlussel K1,K2,K3 uber
EK3(DK2(EK1(x)))
und die dazugehorige Entschlusselung uber
DK1(EK2(DK3(x)))
Beim TDES unterscheiden wir drei verschiedene Betriebsformen:
1. Alle Schlussel sind paarweise unterschiedlich,
2. K1 = K3 6= K2 und
3. K1 = K2 = K3 . Dieses entspricht dem DES-Kryptosystems, der TDES ist somit abwartskom-patibel.
4.3 Iterierte Blockkryptosysteme
Bevor wir auf die Kryptoanalyse des DES-Kryptosystems eingehen, werden wir noch einige Verallge-meinerungen des DES-Kryptosystems vorstellen.
Definition 12 Ein iteriertes r -Runden Blockkryptosystem besteht aus einer Rundenfunk-tion g : Zm,n × Zk,l → Zm,n , welche in r Runden den Plaintext x ∈ Zm,n mit Hilfe der Runden-schlussel K1, . . . , Kr ∈ Zk,l verschlusselt. Setzen wir y0 := x , so erhalten wir
yi = g(yi−1,Ki)
und erhalten den Ciphertext y := yr . Um den Ciphertext entschlusseln zu konnen, muss es moglichsein fur jeden festen Rundenschlussel die Umkehrfunktion von g zu berechnen.
Viele Kryptosysteme basieren auf den Operationen auf endlichen Korpern, daher werden wir nachfol-gend einige Begriffe wiederholen.
Definition 13 Sei K eine Menge (mit mindestens zwei Elementen) und + , · zwei Verknupfungenauf K . (K, +, ·) heißt Korper, wenn fur alle a, b, c ∈ K die folgenden Gesetzmaßigkeiten gelten:
42

Assoziativgesetz bezuglich +
• : a + (b + c) = (a + b) + c
Kommutativgesetz bezuglich +
• : a + b = b + a
Assoziativgesetz bezuglich ·• : a · (b · c) = (a · b) · c
Kommutativgesetz bezuglich ·• : a · b = b · a
Distributivegesetz
• : a · (b + c) = a · b + a · cneutrales Element bezuglich +
• : ∃0 ∈ K∀a ∈ K : a + 0 = a
inverses Element bezuglich +
• : ∀a ∈ K∃ − a ∈ K : −a + a = 0
neutrales Element bezuglich ·• : ∃1 ∈ K∀a ∈ K : a · 1 = a
inverses Element bezuglich ·• : ∀a ∈ K∃a−1 ∈ K : a−1 · a = 1
Fur den endlichen Korper mit zwei Elementen {0, 1} mit
0 + 0 = 1 + 1 = 0, 0 + 1 = 1 + 0 = 1, 0 · 0 = 0 · 1 = 1 · 0 = 0, 1 · 1 = 1
bezeichnen wir mit F2 oder GF (2) .
Besonders interessieren uns endlichen Korper.
Definition 14 Einen endlichen Korper, d.h. den Menge K des Korpers (K, +, ·) umfasst endlichviele Elemente, nennen wir auch Galoiskorper oder Galoisfeld GF (|K|) . Von besonderem In-teresse sind Galoisfelder deren Große eine Primzahlpotenz ist, d.h. Galoisfelder mit |K| = pn fureine Primzahl p . Wir bezeichnen ein solches Feld auch mit GF (pn) . Da alle endlichen Korper dergleichen Kardinalitat zueinander isomorph sind, konnen wir uns auf die Polynomreprasentation desKorpers einschranken:
• Es sei K ein Korper. Dann heißt ein Polynom f ∈ K[x] in der Variable x irreduzibel, wennf nicht konstant ist und es keine nicht konstanten Polynome g, h ∈ K[x] gibt, so dass f = g ·hist.
• Eine Polynomreprasentation von GF (pn) generieren wir wie folgt:
– Wahle ein irreduzibels Polynom g ∈ GF(p)[x] vom Grad n und Koeffizienten in GF (p) –ein solchen Polynom existiert immer wenn GF (pn) existiert.
– Wir erhalten die gewunschte Reprasentation uber GF (p)[x]/(g(x)) :
∗ Die Elemente von GF (p)[x]/(g(x)) erhalten wir uber die Menge aller Polynome mitGrad kleiner n und Koeffizienten aus GF (p) .
43

∗ + entspricht der Polynomaddition, wobei wir die jeweiligen Koeffizienten modulo paddieren.
∗ · entspricht der Polynommultiplikation, wobei wir zunachst den Grad mit Hilfe der Po-lynomdivision durch g(x) reduzieren. Der Rest bei der Division, d.h. das Polynom miteinem Grad kleiner n , stellt das gesuchte Ergebnis von · dar, wobei wir abschließendnoch die Koeffizienten modulo p berechnen.
Aus der Definition der Addition innerhalb der Polynomreprasentation von GF (2n) erhalten wir:
Stellen wir die Koeffizienten der Elemente von GF (2n) in der Polynomreprasentation alseinen Binarstring der Lange n dar, dann entspricht die Addition zweier Elemente desGF (2n) dem bitweise xor dieser Strings.
Mit Hilfe von GF (2n) konnen wir nun eine spezielle Form von iterierten Blockkryptosystemen vor-stellen:
Definition 15 Ein iteriertes r -Runden Blockkryptosystem nennen wir ein r -Runden Feistel-Kryptosystem, wenn der Plaintext x gerade Lange hat, d.h. x = x1x2 mit |x1| = |x2| , und furdie Rundenfunktion g gilt:
g : GF(2n)×GF(2n)×GF(2m) → GF(2n)×GF(2n)
wobeig(x1, x2, z) = (x2 ⊕ h(x1, z), x1)
ist. Die Funktion h : GF(2n)×GF(2m) → GF(2n) ist hierbei beliebig und ⊕ das xor der Binarstringsx2 und h(x1, z) .
Sei x = xLxR ein gegebener Plaintext mit xL, xR ∈ Z2,n , K1, . . . ,Kr ∈ Z2,m die Rundenschlussel,die mit Hilfe eines Schlusselgenerierungsalgorithmus aus einem Schlussel K generiert werden. Wirsetzen y0
L := xL und y1R := xR und erhalten y = yr
LyrR mit
(yiL, yi
R) := (yi−1R , yi−1
L ⊕ h(yi−1R ,Ki)) fur alle i ∈ [1..r] .
Schranken wir die Abbildung h weiter ein, so kommen wir zu Kryptosystemen, die weitgehend mitdem DES-System ubereinstimmen.
Definition 16 Eine Abbildung f : Zm,n → Zm,k uber einen Korper (Zm,+, ·) nennen wir affin,wenn wir wir sie mit Hilfe einer k× n -Matrix A ∈ Zk×n
m und einem Translationsvektor t ∈ Zkm
uberf(x) = A · x + t
fur x ∈ Znm beschreiben laßt. Die Operationen innerhalb dieses Matrix-Vektor-Produkts und die in-
nerhalb nachfolgende Vektor-Vektor-Addition entsprechen den Korperoperationen.
Ist t der 0-Vektor, wobei 0 das neutrale Element bez. + ist, dann nennen wir die Abbildung auchlinear.
44

Definition 17 Ein r -Runden Feistel-Blockkryptosystem nennen wir ein iteriertes r -RundenDES-Kryptosystem, wenn fur die Funktion h : GF(2n)×GF(2m) → GF(2n) in
g(x1, x2, z) = (x2 ⊕ h(x1, z), x1)
gilth(x1, z) = f(E(x)⊕ z)
wobei f : GF(2m) → GF(2n) mit m ≥ n ist und E : GF(2n) → GF(2m) affine Expansionsfunktionist.
Den nichtlinearen Anteil in f bezeichnen wir in Anlehnung an DES als S -Box-Operation.
In der Literatur wird noch auf eine weitere Form von iterierte r -Runden Blockkryptosystem unter-sucht:
Definition 18 Ein iteriertes r -Runden Blockkryptosystem nennen wir ein r -Runden Substitutions-Permutations-Kryptosystem (kurz. SPN-Kryptosystem), wenn wir g wir folgt beschreibenkonnen: sei
• S0, . . . , Sk−1 : Z2,m → Z2,m eine Folge von k Abbildungen,
• π : [0..k ·m− 1] → [0..k ·m− 1] eine Permutation der Positionen eines k ·m Bit-Binarstringsund
• K1, . . . ,Kr ∈ Z2,k·m eine Folge von r Rundenschlussel,
dann erhalten wir yi = g(yi−1,Ki) uber
wi = yi−1 ⊕Ki
und fur die Aufteilung wi0, . . . , w
ik−1 des Binarstrings wi in k Blocke der Lange m
yi = π(S0(wi0) . . . Sk−1(wi
k−1)) .
Den nichtlinearen Anteil in den Abbildungen Sj bezeichnen wir wieder als S -Box-Operation.
Die nachfolgende Abbildung zeigt uns ein 2-Runden SPN-Kryptosystems mit einer Aufteilung in 2Blocke.
⊕
π
⊕
K1
π
K2
w21w1
1
S0
S1
y20y1
0
y11 y2
1
y00
y01
w20 S0
S1
w10
Wir wollen nun noch einen letzten Typ von iterierten Blockkryptosystemen vorstellen.
45

Definition 19 Ein iteriertes r -Runden Blockkryptosystem nennen wir ein lineares r -RundenKryptosystem uber F2 wenn
• fur jede Runde i ∈ [0..r]
yi := Ci(x) ={
x fur i = 0πi(yi−1 ⊕Ki) fur i ∈ [1..r]
ist, wobei πi eine feste Permutation der n Bits, Ki der Rundenschlussel und yi der Runden-text angibt.
Im nachfolgenden Abschnitt werden wir die differentielle Kryptoanalyse vorstellen. Im Wesentlichenbasiert diese auf den folgenden Beobachtungen uber lineare Abbildungen bzw. uber lineare Kryptosy-stem.
Beobachtung 4 Es gilt
• Fur eine lineare Abbildung f und alle Eingabe x1, x2 gilt f(x1 + x2) = f(x1) + f(x2) .
• Somit gilt fur alle Plaintexte x1, x2 und alle i ∈ [1..r]
Ci(x1 ⊕ x2) = Ci(x1)⊕ Ci(x2) ,
d.h. die Differenz der Ciphertexte hangt nur von der Differenz der Plaintexte ab.
• Es gilt
yi1 ⊕ yi
2 = πi(yi−11 ⊕Ki)⊕ πi(yi−1
2 ⊕Ki)= πi(yi−1
1 ⊕Ki ⊕ yi−12 ⊕Ki)
= πi(yi−11 ⊕ yi−1
2 )= πi(· · · (π1(x1 ⊕ x2)) · · · )= πi(· · · (π1(x1)) · · · )⊕ πi(· · · (π1(x2)) · · · ),
d.h. der Schlussel beeinflusst die Differenz in der i -ten Runde nicht.
Beobachtung 5 Seien x1, x2, x3, x4 ∈ Z2,n mit x1 ⊕ x2 = x3 ⊕ x4 , dann gilt fur unser linearesKryptosystem und fur alle i ∈ [1..r]
Ci(x1)⊕ Ci(x2) = Ci(x3)⊕ Ci(x4) .
Fur die nichtlineare S -Box-Operation gilt diese Beobachtung im Allgemeinen nicht, d.h. fur vieleBinarstrings x1, x2, x3, x4 ∈ Z2,n mit x1 ⊕ x2 = x3 ⊕ x4 gilt
S(x1)⊕ S(x2) 6= S(x3)⊕ S(x4) .
46

4.4 Differentielle Kryptoanalyse
Zur Kryptoanalyse des DES-Kryptosystems wurden 1990 die differentielle und 1993 die lineare Kryp-toanalyse vorgestellt. Die wesentliche Ideen dieser Attacken werden wir im Folgenden vorstellen.
Es zeigte sich jedoch, dass das DES-System weitgehend immun gegen differentielle Attacken ist. Diesesliegt vorallem in dem nichtlinearen Anteil des DES, der im Wesentlichen auf den S -Boxen-Operationenbasiert. Aus den von Coppersmith veroffentlichten Entwurfsprinzipien der S -Boxen konnen wir schlie-ßen, dass diese Form der Analyse schon lange vor deren Veroffentlichung bekannt war. Eine Betrach-tung der differentielle Kryptoanalyse zeigt uns somit ein wesentliches Entwurfskriterium des S -Boxendes DES-Systems.
Die differentielle Kryptoanalyse basiert auf der Betrachtung zweier simultan verschlusselter Plaintextex1, x2 . Hierbei analysieren wir nicht die jeweiligen resultierenden Ciphertexte y1, y2 von x1, x2 ,sondern richten unser Augenmerk auf die Differenz x1 − x2 . Rechnen wir in F2 , dann ist x1 − x2 =x1 + x2 und x1 + x2 = x1 ⊕ x2 .
Sei S eine feste S -Box. Fur x,∆E ,∆A ∈ Z2,n definieren wir:
• die Ausgabedifferenz ∆S(∆E, x) := S(x)⊕ S(x⊕∆E) ,
• die Anzahl der Ubergange ∆E → ∆A AS(∆E, ∆A) := |{x | ∆S(∆E , x) = ∆A}|
• die Ubergangswahrscheinlichkeit
p(S;∆E ,∆A) :=AS(∆E ,∆A)
2n
fur den Ubergang ∆E → ∆A und die bedingten Wahrscheinlichkeiten
p(S;∆A|∆E) :=AS(∆E ,∆A)∑∆′
AAS(∆E ,∆′
A).
Betrachten wir eine gegebene Menge von S -Boxen, dann konnen wir diese Wahrscheinlichkeitenp(S;∆E ,∆A) fur alle S -Boxen bestimmen. Ein Kryptosystem bietet einen Angriffspunk fur diedifferentielle Kryptoanalyse, wenn sich die Ubergangswahrscheinlichkeiten fur eine S -Box deutlichunterscheiden. Unter dieser Voraussetzung konnen wir einige Bits des Rundenschlussels bestimmen.
Wir definieren weiter:
• Seien x1, x2 zwei Plaintexte und yi1, yi
2 die dazugehorigen Ciphertexte nach der i -ten Runde.Arbeitet unser Kryptosystem in r Runden, dann gilt
y01 = x1 und y0
2 = x2
und fur die zu x1 und x2 gehorigen Ciphertexte y1 und y2
y1 = yr1 und y2 = yr
2 .
• Wir definieren die Rundendifferenz von x1, x2 uber
∆i(x1, x2) = yi1 ⊕ yi
2 .
Insbesondere gilt
∆0(x1, x2) = x1 ⊕ x2 und ∆r(x1, x2) = y1 ⊕ y2 .
47

Betrachten wir anstelle einer Differenz die Entwicklung der Differenz uber die einzelnen Runden, soerhalten wir die sogenannte Charakteristik eines Blockkryptosystems:
Definition 20 [Charakteristik eines Blockkryptosystems]
• Eine Folge von `+1 aufeinander folgenden Differenzen z0, . . . , z` nennen wir ` -Runden-Cha-rakteristik.
• Ein Plaintextpaar x0, x1 besitzt die ` -Runden Charakteristik z0, . . . , z` , wenn fur allej ∈ [0..`]
∆j(x1, x2) = zj
ist.
Die differentielle Kryptoanalyse untersucht die Wahrscheinlichkeiten verschiedener Charakteristikenund versucht mit Hilfe einer r − 1 -Runden-Charakteristik Bits des letzten Rundenschlussels Kr zubestimmen. Die verbleibenden Bits des Rundenschlussels mussen wir dann uber die Betrachtung allerverbleibenden Kombinationen (exhaustive search) bestimmen. Es besteht jedoch die Hoffnung, dasssich die Anzahl der verbleibenden moglichen Schlussel mit Hilfe der differentiellen Kryptoanalyse starkstark reduzieren lasst.
Fur die differentielle Kryptoanalyse bestimmen wir nun fur jede Charakteristik die Wahrscheinlichkeit,dass diese Charakteristik auch tatsachlich auftritt. Sei z0, . . . , z` eine ` -Runden Charakteristik undsei ∆i die Zufallsvariable der Rundendifferenz fur die i -te Runde. Dann gilt:
• Sind die Rundenschlussel der einzelnen Runden voneinander unabhangig, so gilt
Pr[∆` = z`|∆0 = z0] =∏
i∈[1..`]
Pr[∆i = zi|∆i−1 = zi−1] .
• Sind die Rundenschlussel der einzelnen Runden nicht voneinander unabhangig, d.h. sie wurdendurch einen Algorithmus aus einem Schlussel K generiert, dann kann die WahrscheinlichkeitPr[∆` = z`|∆0 = z0] nicht mehr durch unsere obige Formel bestimmt werden.
• In vielen Fallen (so beim DES, LOKI, FEAL) habe experimentelle Untersuchungen gezeigt,dass die obige Formel eine gute Approximation fur Pr[∆` = z`|∆0 = z0] darstellt, so dasswir in vielen Fallen davon ausgehen konnen, dass die Rundenschlussel tatsachlich unabhangigvoneinander sind.
Wie bestimmen wir nun die Wahrscheinlichkeiten Pr[∆i = zi|∆i−1 = zi−1] ? Beschreiben wir dieVerschlusselung in einer Runde nur mit einer S -Box, dann gilt
Pr[∆i = zi|∆i−1 = zi−1] = p(S; zi|zi−1) .
Arbeiten mehrere S -Boxen in jeder Runde parallel, so mussen wir die einzelnen Wahrscheinlichkeitenmiteinander in Beziehung setzten, z.B. indem wir das Produkt der entsprechenden Wahrscheinlich-keiten betrachten. Oder die Verschlusselung der einzelnen Runden mit Hilfe einer großeren S -Boxmodellieren.
Wird nach der S -Box noch eine lineare Transformation T auf das Ergebnis der S -Box ausgefuhrt,so muss dieses ebenfalls berucksichtigt werden:
Pr[∆i = zi|∆i−1 = zi−1] = p(S;T−1(zi)|zi−1) .
48

Der Einfachheit halber konnen wir diese linearen Transformationen als Teil der S -Box-Operationbetrachten. Mit diesen Wahrscheinlichkeiten erhalten wir den folgenden Basisalgorithmus fur diedifferentielle Kryptoanalyse:
1. Sei fur jeden Rundenschlussel Kr initiiere dessen Erfolgszahler e(Kr) mit 0.
2. Wahle eine wahrscheinliche r − 1 -Runden Charakteristik z0, . . . , zr−1 ,.
3. Wahle einen Plaintext x0 und bestimme x1 = x0 ⊕ z0 , sowie die dazugehorigen Ciphertextey0, y1 .
4. Bestimme alle Kandidaten fur den Rundenschlussel Kr , so dass
S−1(y0,Kr)⊕ S−1(y1,Kr) = zr−1.
gilt. Fur jeden gefundenen Kandidaten Kr setze e(Kr) := e(KR) + 1 .
5. Wiederhole die Schritte 3 bis 5 bis der Erfolgszahler eines Rundenschlussels im Vergleich zuden anderen Rundenschlusseln signifikant großer ist. Wir wahlen diesen Schlussel als aktuellenRundenschlussel.
Als Faustregel gilt: Wir benotigen O(1/Pr[∆` = z`|∆0 = z0]) Plaintextpaare fur diesen Angriff. Dawir die Verschlusselung dem Besitzer des Schlussels uberlassen mussen (in Schritt 3), gehort dieserAngriff zu den sogenannten chosen-plaintext-Angriffen.
Betrachten wir unseren Basisalgorithmus etwas naher, so sehen wir, dass wir von der Charakteristiknur z0 und zr−1 benotigen. Dieses fuhrt uns zu der Betrachtung des sogenannten Differentials.
Definition 21 Ein ` -Runden Differential ist ein Paar von Differenzen z0, z` wobei z0 die Plain-textdifferenz und z` die Differenz von zwei Rundentexten der ` -ten Runde darstellt.
Analog zur bedingen Wahrscheinlichkeit einer ` -Runden Charakteristik konnen wir auch die bedingeWahrscheinlichkeit eines ` -Runden Differentials z0, z` bestimmen
Pr[∆` = z`|∆0 = z0] =∑
z1,...,z`−1
∏i∈[1..`]
Pr[∆i = zi|∆i−1 = zi−1] .
Die Wahrscheinlichkeit fur ein Differential kann sich um einige Großenordnungen von der Wahrschein-lichkeit einer Charakteristik unterscheiden.
Wollen wir die differentielle Kryptoanalyse mit Hilfe der Differentiale betreiben, dann konnen wirwieder den oben vorgestellten Basisalgorithmus heranziehen.
Abhangig von dem vorhandenen Kryptosystem werden in der Literatur noch verschiedene Variantender differentielle Kryptoanalyse untersucht. Wir werden auf diese jedoch nicht naher eingehen.
Wie bereits zuvor angedeutet, wurden die S -Boxen des DES so konstruiert, dass mit Hilfe der dif-ferentiellen Kryptoanalyse kein erfolgversprechender Angriff zu erwarten ist. Die differentielle Kryp-toanalyse ist jedoch so allgemein gefasst, dass wir sie gegen jede Form von Kryptosystem einsetzenkonnen. Inwiefern wir jedoch mit einem Erfolg rechnen konnen, wollen wir hier nicht untersuchen.
49

4.5 Lineare Kryptoanalyse
Im Folgenden nehmen wir an, dass eine Verschlusselung eine Boolesche Transformation der EingabebitsX0, . . . , Xn−1 in die Ausgabebits Y0, . . . , Yn−1 darstellt.
• Einen linearen Ausdruck A(X0, . . . , Xn−1) in X0, . . . , Xn−1 mit den Koeffizienten a0, . . . ,an−1 ∈ {0, 1} definieren wir uber
n−1∑i=0
ai ·Xi .
• Einen affin-linearen Ausdruck A(X0, . . . , Xn−1) in X0, . . . , Xn−1 mit den Koeffizientena0, . . . , an−1 ∈ {0, 1} definieren wir uber
n−1∑i=0
ai ·Xi + 1 .
Die Terme sind hierbei uber GF (2) definiert.
Ein Paar (AE, AA) nennen wir eine affin-lineare Approximation einer Transformation T , wennAE = AE(X0, . . . , Xn−1) ein affin-linearen Ausdruck in den Eingabebits und AA = AA(Y0, . . . , Yn−1)ein affin-linearen Ausdruck in den Ausgabebits von T ist.
Zwischen den Bits X0, . . . , Xn−1 und den Bits Y0, . . . , Yn−1 besteht
• eine lineare Beziehung, wenn fur a0, . . . , an−1, b0, . . . , bn−1 ∈ {0, 1}
n−1∑i=0
ai ·Xi =n−1∑i=0
bi · Yi
ist und
• eine (nichtlineare) affin-lineare Beziehung, wenn
n−1∑i=0
ai ·Xi =n−1∑i=0
bi · Yi + 1
ist.
Eine affin-lineare Approximation (AE , AA) wir von einer Eingabe x0, . . . , xn−1 und der dazugehori-gen Ausgabe y0, . . . , yn−1 erfullt, wenn eine affin-lineare Beziehung zwischen den Ausdrucken be-steht, d.h. wenn AE(x0, . . . , xn−1) = AA(y0, . . . , yn−1) ist. Eine affin-lineare Approximation(AE , AA) ist im deterministischen Sinne gultig, wenn (AE , AA) fur alle Eingaben und den da-zugehorigen Ausgaben erfullt ist.
Ist eine affin-lineare Approximation nicht im deterministischen Sinne gultig, dann untersuchen wir dieWahrscheinlichkeit, mit der diese Approximation fur eine zufallige Eingabe-Ausgabekombinationengultig ist. Die Wahrscheinlichkeit p(AE, AA) fur eine affin-lineare Approximation (AE , AA) ist derAnteil aller Eingabe-Ausgabekombinationen, die die affin-lineare Approximation (AE , AA) erfullen,d.h.
p(AE , AA) := |{x ∈ {0, 1}n|AE(x) = AA(T (x))}| · 2−n .
50

Beobachtung 6
• Die lineare und die affine-lineare Beziehung sind komplementar zueinander:
n−1∑i=0
ai ·Xi =n−1∑i=0
bi · Yi ⇐⇒n−1∑i=0
ai ·Xi 6=n−1∑i=0
bi · Yi + 1 .
• Fur jede affine-lineare Approximation (AE , AA) gilt
p(AE , AA) = 1− p(AE + 1, AA) .
Die lineare Kyptoanalyse basiert auf der Annahme, dass bei optimaler Nichtlinearitat einer Transfor-mation T , fur jede affine-lineare Approximation (AE , AA) die Wahrscheinlichkeit p(AE , AA) etwa12 ist.
Mit Hilfe einer affin-linearen Approximation (AE , AA) , fur die die Wahrscheinlichkeit p(AE , AA)deutlich von 1
2 abweicht, konnen wir dann hoffen, einzelne Schlusselbits bestimmen zu konnen.
4.5.1 Ein erster Algorithmus
Wir betrachten zunachst den Fall, dass einem Angreifer eine affine-lineare Approximation (AE , AA)fur ein Kryptosystem bekannt ist, so dass
AE =n−1∑i=0
ai · x[i] = AA =n−1∑i=0
bi · y[i] +n−1∑i=0
ci ·K[i]
fur alle Schlussel K = K[0] . . .K[n−1] mit einer Wahrscheinlichkeit pL 6= 12 gilt. x = x[0] . . . x[n−1]
gibt hierbei den Plaintext und y = y[0] . . . y[n − 1] den Ciphertext an. Den Wert |pL − 12| nennen
wir auch die Verzerrung oder den Bias der Approximation.
Um eine solche Approximation zu finden, kann ein Angreifer ein Kryptosystem uber eine langere Zeitanalysieren. Hierbei sucht der Angreifer nach einer affine-lineare Approximation (AE , AA) , fur dieder Wert des Bias maximal ist. Wir gehen im Folgenden davon aus, dass bei einer konkreten Attackedem Angreifer die Koeffizienten ai, bi, ci fur i ∈ [0..n− 1] bekannt sind.
Lineare Kryptoanalyse — Basisalgorithmus:
Gegeben eine affine-lineare Approximation (AE , AA) mit maximalem Bias pL . Sei N die Anzahlder Plaintext-Ciphertext-Paare (xj , yj) , die wir benutzen.
1. Bestimme die Anzahl N ′ der Plaintext-Ciphertext-Paare (xi, yi) fur die∑n−1
i=0 ai · xj [i] =∑n−1i=0 bi · yj [i] gilt.
2. Ist N ′ > N/2 , so setzen (oder besser raten) wir∑n−1
i=0 ci ·K[i] = 0 und fur N ′ ≤ N/2 ratenwir
∑n−1i=0 ci ·K[i] = 1 .
Dieses Verfahren gibt uns 1 Bit Information uber den Schlussel und somit nicht notwendigerweise 1Bit des Schlussels.
Als Faustregel konnen wir angeben, dass ca. |pL− 12 |−2 Plaintext- Ciphertext-Paare benotigt werden,
um dieses Bit an Information mit hinreichend großer Wahrscheinlichkeit bestimmen zu konnen.
51

4.5.2 Zusammensetzung von affin-linearen Approximationen
Wir wollen nun auf die Frage eingehen, wie wir eine affine-lineare Approximation (AE , AA) einesKryptosystems bestimmen konnen?
1. Wir analysieren alle moglichen affin-lineare Approximationen (AE , AA) fur unser Kryptosystemund bestimmen die jeweiligen Wahrscheinlichkeiten p(AE , AA) . Der Aufwand fur diese Analysewachst exponentiell in der Anzahl der Eingabe-, Ausgabe- und Schlusselbits.
2. Oft ist es einfacher anstelle der affin-lineare Approximationen des ganzen Systems die affin-lineare Approximationen der einzelnen S -Boxen zu bestimmen und diese dann zu kombinieren.Im Folgenden wollen wir darauf eingehen, wie affine-lineare Approximationen (bei Unabhangig-keit der einzelnen Rundenschlussel) kombiniert werden konnen.
Wir betrachten ein SPN-Kryptosystem und untersuchen, wie wir aus den affine-lineare Approximationder einzelnen S -Boxen eine affine-lineare Approximation des ganzen Systems erhalten. Hierbei sei
(Ai,jE , Ai,j
A )
die affin-lineare Approximation der S -Box Sj in der i -ten Runde. Das xor-en eines Rundentextesmit einem Rundenschlussel geschieht zwischen zwei Runden, bzw. zwischen den dazugehorigen S -Box-Operation.
Zunachst wollen wir zeigen, wie affin-lineare Approximationen einer Runde kombiniert werden konnen.Im Anschluß werden wir zeigen, wie wir die resultierenden affin-linearen Approximationen aller Rundenkombinieren konnen.
Zusammensetzung von parallel arbeitenden S -Boxen einer Runde:
Wir betrachten die affin-lineare Approximation der S -Boxen einer Runde. Der Einfachheit halberbezeichnen wir diese mit (Aj
E , AjA) und
pj = p(AjE , Aj
A) =12
+ εj .
Die zusammengesetzte affin-lineare Approximation ist dann
(∑
j∈[0..k−1]
AjE ,
∑j∈[0..k−1]
AjA) .
Man beachte, dass eine Wahl der Belegung der Eingabe- und Ausgabebits die zusammengesetzte affin-lineare Approximation genau dann erfullt, wenn die Anzahl der durch diese Belegung nicht erfulltenaffin-lineare Approximation (Aj
E , AjA) gerade ist.2
Lemma 6 Sei p(AjE , Aj
A) = 12 + εj fur alle j ∈ [0..k − 1] , dann gilt
p(∑
j∈[0..k−1]
AjE ,
∑j∈[0..k−1]
AjA) =
12
+ 2k−1 ·∏
j∈[0..k−1]
εj .
2Zur Erinnerung, die Wahrscheinlichkeit, dass eine Belegung eine affin-lineare Approximation (AjE , Aj
A) nicht erfullt,
ist p(AjE + 1, Aj
A) = 1− pj = 12− εj .
52

Beweis: Der Beweis folgt uber eine vollstandige Induktion uber k , indem wir die Wahrscheinlichkeitenpk und qk untersuchen.
• p` ist die Wahrscheinlichkeit, dass in den ersten ` affin-lineare Approximationen eine geradeAnzahl von Approximationen nicht erfullt sind.
• q` = 1− p` ist die Wahrscheinlichkeit, dass in den ersten ` affin-lineare Approximationen eineungerade Anzahl von Approximationen nicht erfullt sind.
Fur ` > 1 gilt
p` =(
12
+ ε`
)· p`−1 +
(12− ε`
)· q`−1 .
Setzen wir die Induktionsannahme
p`−1 =12
+ 2`−1 ·∏
j∈[0..`−1]
εj
in diese Gleichung ein, so folgt, dass fur alle `
p` =12
+ 2` ·∏
j∈[0..`]
εj
gilt und somit
p(∑
j∈[0..k−1]
AjE ,
∑j∈[0..k−1]
AjA) = pk =
12
+ 2k−1 ·∏
j∈[0..k−1]
εj
ist.
Zusammensetzung mehrerer Runde:
Aufgrund der obigen Zusammenfassung aller S -Boxen einer Runde konnen folgendes vereinfachtesSPN-Kryptosystem betrachten:
• Zu Beginn der i -ten Runde xor-en wir den Rundenschlussel Ki mit dem Rundentexte yi−1
der i− 1 -ten Runde.
• Anschließend fuhren wir die S -Box-Operation aus, die durch eine S -Box gegeben ist.
• Zum Abschluß einer Runde permutieren wir das Ergebnis mit Hilfe einer Permutation π .
Sei (AiE , Ai
A) die affin-lineare Approximation der S -Box der i -ten Runde und sei
p(AiE , Ai
A) =12± εi .
Wie wir bereits gesagt haben, interessieren wir uns fur eine Approximation mit maximalem Bias, daherbetrachten wir im Folgenden sowohl positive als auch negative Abweichungen der Wahrscheinlichkeitp(Ai
E , AiA) von 1
2 .
Wir zeigen zunachst, wie wir die beiden ersten Runden zusammenfassen konnen, sowie welche Appro-ximation (AE , AA) und Wahrscheinlichkeit p(AE , AA) daraus resultiert:
53

• Sei (A0E , A0
A) die Approximation der S -Box der ersten und (A1E , A1
A) die Approximation derS -Box der zweiten Runde.
• Unser Ziel ist die Approximation (A0E, A1
A) fur die ersten beiden Runden.
Die beiden Approximationen (A0E , A0
A) und (A1E , A1
A) konnen wir jedoch nur dann zur Approxima-tionen (A0
E , A1A) zusammensetzen, wenn die rechte Seite der ersten Approximation zur linken Seite
der zweiten Approximation passt. Hierbei mussen wir berucksichtigen, dass zwischen den beiden S -Boxen die Ausgabe der ersten S -Box permutiert und der Rundenschlussel R1 der zweien Rundeaddiert wird. Es gilt somit Y 0
i = X1π(i) ⊕K1[i] .
Wir betrachten daher nur Approximationspaare (A0E , A0
A) und (A1E , A1
A) mit
A0A(y0
0 , . . . , y0n−1) = A1
E(π(y00 , . . . , y0
n−1)⊕K1).
Wir wollen nun versuchen, die Anforderungen an die beiden Approximation (A0E , A0
A) und (A1E , A1
A)etwas einfacher darzustellen. Sei
A1E(x1
0, . . . , x1n−1) =
n−1∑i=0
a1i · x1
i ⊕ s1
dann gilt
A1E((x1
0, . . . , x1n−1)⊕K1) =
∑i∈[1..n−1]
a1i · (x1
i ⊕K1[i]) ⊕ s1
=∑
i∈[0..n−1]
a1i · x1
i ⊕∑
i∈[0..n−1]
a1i ·K1[i] ⊕ s1
=∑
i∈[0..n−1]
a1i · x1
i ⊕ k1 ⊕ s1
fur ein Korrekturbit k1 =∑n−1
i=0 a1i · K1[i] ∈ {0, 1} . Beachte, dass k1 unabhangig von der Eingabe
ist. Wir definieren daherA1
E := A1E + k1 .
Ferner definieren wirπA1
E(x10, . . . , x1
n−1) = A1E(π(x1
0, . . . , x1n−1))
und nennen wir die Approximationen (A0E , A0
A) und (A1E , A1
A) konsistent, wenn
A0A = πA1
E
ist. Sind zwei Approximationen (A0E , A0
A) und (A1E , A1
A) zueinander konsistent, dann ist im zusam-mengefassten System die Approximation (A0
E , A1A) genau fur die Werte x0
0, . . . , x0n−1, y
00 , . . . , y0
n−1, y10 ,
. . . , y1n−1 erfullt, fur die entweder
A0E(x0
0, . . . , x0n−1) = A0
A(y00 , . . . , y0
n−1) und πA1E(y0
0 , . . . , y0n−1) = A1
A(y10 , . . . , y1
n−1)
oder
A0E(x0
0, . . . , x0n−1) 6= A0
A(y00 , . . . , y0
n−1) und πA1E(y0
0 , . . . , y0n−1) 6= A1
A(y10 , . . . , y1
n−1)
gilt.
Wir wollen nun die Wahrscheinlichkeit p(A0E , A1
A) untersuchen. Hierbei mussen wir jedoch folgendesbeachten: Sind die Ereignisse (A0
E , A0A) ist erfullt und (πA1
E , A1A) ist erfullt nicht unabhangig, dann
54

konnen wir aus den Wahrscheinlichkeiten p(A0E , A0
A) und p(πA1E , A1
A) keine Aussage uber die Wahr-scheinlichkeit p(A0
E , A1A) herleiten. Wir nennen (A0
E , A0A) und (πA1
E , A1A) unabhangig, wenn die
Ereignisse (A0E , A0
A) ist erfullt und (πA1E , A1
A) ist erfullt unabhangig sind.
Aus p(AiE , Ai
A) = 12 ± εi folgt unmittelbar p(πAi
E , AiA) = 1
2 ± εi . An Stelle von p(AiE , Ai
A) = 12 ± εi
konnen wir fur ein geeignetes s ∈ {0, 1} auch p(AiE , Ai
A) = 12 + (−1)s · εi schreiben.
Wir gehen nun von der Annahme aus, dass (A0E , A0
A) und (πA1E , A1
A) unabhangig sind, dann gilt furgeeignete Werte s0, s1 ∈ {0, 1} :
p(A0E , A1
A) = p(A0E , A0
A) · p(πA1E , A1
A) + (1− p(A0E , A0
A)) · (1− p(πA1E , A1
A))
=(
12
+ (−1)s0 · ε0
)·(
12
+ (−1)s0 · ε0
)+(
12− (−1)s0 · ε0
)·(
12− (−1)s1 · ε1
)=
14
+(−1)s0 · ε0
2+
(−1)s1 · ε1
2+ (−1)s1+s2 · ε0 · ε1
+14− (−1)s0 · ε0
2− (−1)s1 · ε1
2+ (−1)s1+s2 · ε0 · ε1
=12
+ (−1)s1+s2 · 2 · ε0 · ε1 .
Analog zu dieser Analyse konnen wir auch mehr als zwei Runden zusammenfassen. Wir erhalten:
Lemma 7 Sei p(AiE , Ai
A) = 12 ± εi fur alle i ∈ [0..k − 1] und sei (πAi
E , AiA) unabhangig von
(A0E , Ai−1
A ) , dann gilt fur die Konkatenation der k Runden∣∣∣∣p(A0E , Ak−1
A )− 12
∣∣∣∣ = 2k−1 ·∏
j∈[0..k−1]
εj .
Beweis: Der Beweis folgt uber eine vollstandige Induktion uber k . Die jeweiligen Schritte erfolgenanalog zu unserer Analyse bei der Zusammenfassung der ersten beiden Runden.
4.5.3 Angriff auf den letzten Rundenschlussel fur ein SPN-Kryptosystem
Eine affin-lineare Approximation (AE , AA) nennen wir dominant, wenn ihre Wahrscheinlichkeitp(AE , AA) deutlich großer ist als alle anderen affin-lineare Approximationen.
Zur Vereinfachung betrachten wir wieder ein SPN-Kryptosystem, welches in jeder Runde nur eineS -Box besitzt. Da S -Box-Operationen injektiv sind, konnen wir jede einzelne S -Box-Operationinvertieren. Wir erhalten den folgenden Algorithmus:
Lineare Kryptoanalyse — Algorithmus fur ein SPN:
Gegeben eine dominante affin-lineare Approximation (A0E , Ak−2
A ) fur die ersten k − 1 Runden. SeiN die Anzahl der Plaintext-Ciphertext-Paare (xj , yj) , die wir benutzen.
1. Bestimme eine zufallige Menge an Testschlussel K fur die letzte Runde.
55

2. Bestimme N zufallige Plaintext-Ciphertext-Paare (xj , yj) ( j ∈ [0..N − 1] ).
3. Fur jeden Schlussel K` ∈ K sei e(K`) die Anzahl der Plaintext- Ciphertext-Paare (xj , yj) furdie A0
E(xj) = Ak−2A (S−1(yj)⊕K`) gilt.
4. Sei p(A0E , Ak−2
A ) = 12 + ε , dann ist die erwartete Anzahl der Paare, die die Approximation
(A0E , Ak−2
A ) erfullen, bei N zufalligen Plaintext-Ciphertext-Paaren (xj , yj) gleich N ·(
12 + ε
).
Der Schlussel K` ∈ K , fur den der Wert e(K`) am nahsten an N · ( 12 + ε) liegt, ist mit großer
Wahrscheinlichkeit der richtige Rundenschlussel.
Ein guter Uberblick uber die differentielle und uber die lineare Kryptoanalyse wird von Knudsen inseinem Survey [K98] gegeben. Eine Einfuhrung uber dieses Thema anhand eines Beispiels wird in[M03] gegeben.
Aufgabe 16 Stellen Sie das DES-Kryptosystem als SPN-Kryptosystem mit einer S -Box dar. Be-schreiben Sie die S -Box-Operation, die Permutation und den Algorithmus zur Generierung der Run-denschlussel. Um die Eingabe und Ausgabe in eine geeignet Form zu bringen, durfen Sie vor und nachder Verschlusselung jeweils eine lineare Transformation einsetzen.
Aufgabe 17 Betrachten Sie die folgenden beiden S -Boxen:
x 000 001 010 011 100 101 110 111S0(x) 000 010 100 110 011 111 101 001S1(x) 111 011 010 101 000 001 100 110
1. Zeigen Sie, dass die dazugehorigen Operationen nicht linear sind.
2. Bestimmen Sie die einzelnen Eingabe-/Ausgabedifferenzen und deren Ubergangswahrscheinlich-keiten p(Si;∆E ,∆A) .
3. Bestimmen Sie die affin-lineare Approximation mit dem maximalen Bias fur diese S -Boxen.Bestimmen ferner Sie die affin-lineare Approximation der Konkatenation dieser Boxen, wenndiese parallel auf zwei unabhangigen Blocken ausgefuhrt werden, sowie die dazu gehorige Wahr-scheinlichkeit.
4.6 Advanced Encryption Standard (AES)
Aufgrund der Schwachen von DES kam es 1998 zu der Ausschreibung fur einen neuen Standard, demAES. Hierbei sollte das neue Verfahren die folgenden Kriterien erfullen:
• Gesucht war ein symmetrischer Algorithmus, genauer ein Blockchiffre.
• Das Verfahren sollte Blocke von 128 Bits verwenden und Schlussel von 128, 192 und 256 BitLange einsetzen konnen.
• Der neue Standard sollte leicht in Hard- und Software zu implementieren sein und eine uber-durchschnittliche Performance haben.
• Fur den Einsatz in Smartcards sollten nur geringe Ressourcen erforderlich sein (d.h. kurze Co-delange, niedriger Speicherbedarf).
56

• Der Algorithmus musste frei von patentrechtlichen Anspruchen sein und von jedermann unent-geltlich genutzt werden konnen.
• AES sollt allen bekannten Methoden der Kryptoanalyse widerstehen konnen.
Als Gewinner der Ausschreibung im Oktober 2000 der nach seinen Entwicklern Joan Daemen undVincent Rijmen benannte Rijndael-Algorithmus [FIPS01] bekanntgegeben.
4.6.1 Mathematische Grundlagen
Die Basiseinheit fur Berechnungen im AES stellt das Byte dar, daher sind viele Operationen im AESim GF (28) definiert. Um den Wert eines Byte darzustellen benutzen wir entweder die Binarzahl-, dieHexadezimalzahl- oder die Polynomreprasentation. Betrachten wir die Polynomreprasentation einesBytes, so benutzen wir im AES das irreduzible Polynom
m(x) = x8 + x4 + x3 + x + 1 .
Zur Erinnerung:
• Die Addition ⊕ entspricht dem Bitweisen xor, bzw. dem xor der korrespondierenden Koeffizi-enten der Polynome.
• Die Multiplikation · entspricht der Polynommultiplikation modulo m(x) .
Die Multiplikation kann mit Hilfe der iterierten Multiplikation eines Polynoms mit x und dem be-dingten Subtrahieren (bzw. Addieren) von m(x) ) implementiert werden. Auf dem Bitlevel bedeutetdieses:
• Fuhre einen Linksshift aus.
• Erhalten wir einen Uberlauf, so xor-e das Resultat mit 100011011 .
• Ubernehme nur die hinteren 8 Bits.
Diese Operation nennen wir xtime () .
Um die Operationen in GF (28) zu verdeutlichen, hier ein paar Beispiele.
• Beispiel fur die Addition:
100111002 ⊕ 110001112 = 010110112
oder aquivalent
(x7 + x4 + x3 + x2) ⊕ (x7 + x6 + x2 + x1 + 1) = x6 + x4 + x3 + x1 + 1 .
57

• Beispiel fur die Multiplikation:
(x6 + x4 + x2 + x + 1) · (x7 + x + 1)= x13 + x11 + x9 + x8 + 2 · x7 + x6 + x5 + x4 + x3 + 2 · x2 + 2 · x + 1= x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 + 1≡ (x13 + x11 + x9 + x8 + x6 + x5 + x4 + x3 + 1)⊕ (x5 ·m(x))≡ (x11 + x4 + x3 + 1)⊕ (x3 ·m(x))≡ x7 + x6 + 1 mod m(x) .
• Beispiel fur xtime () :
xtime(x7 + 1) = 1000000102 ⊕ 1000110112 = 000110012 ≡ x4 + x3 + 1 .
Das multiplikative Inverse p−1(x) zu einem Polynom p(x) , d.h.
p(x) · p−1(x) ≡ 1 mod m(x)
konnen wir mit Hilfe des erweiterten Algorithmus von Euklid bestimmen.
Mit Hilfe dieses Verfahrens konnen wir fur zwei Polynome p(x) und m(x) zwei Polynome p(x) undm(x) bestimmen, so dass
p(x) · p(x) + m(x) · m(x) = 1
ist. Wir erhalten somitp−1(x) = p(x) mod m(x) .
Abhangig von der Operation, benutzt man beim AES verschiedene Darstellungen der Werte der ein-zelnen Bytes. Ist b7b6 . . . b0 die Darstellung eines Bytes in Binardarstellung, dann erhalten wir diePolynomdarstellung uber
(b7b6 . . . b0)2 = b7 · x7 + b6 · x6 + b5 · x5 + b4 · x4 + b3 · x3 + b2 · x2 + b1 · x + b0 .
Um die Binardarstellung in Hexadezimal Darstellung umzuwandeln, benutzen wir fur b7b6b5b4 undb3b2b1b0 die folgende Tabelle
00002 = 016
00012 = 116
00102 = 216
00112 = 316
01002 = 416
01012 = 516
01102 = 616
01112 = 716
10002 = 816
10012 = 916
10102 = A16
10112 = B16
11002 = C16
11012 = D16
11102 = E16
11112 = F16
Polynome mit Koeffizienten in GF (28)
Neben den Polynomen zur Darstellung der Werte in GF (28) benutzen wir beim AES noch Polynomenvom Grad 3, deren Koeffizienten wiederum Elemente des endlichen Korpers (GF (28) ) darstellen. Ver-schiedene Operationen im AES konnen wir mit Hilfe von Addition und Multiplikation dieser Polynomedefinieren. Diese Polynome selbst, bilden jedoch keinen endlichen Korper. Sei
a(x) = a3 · x3 + a2 · x2 + a1 · x + a0
58

ein solches Polynom, dann benutzen wir auch die Schreibweise
[a0, a1, a2, a3] .
Seien
a(x) = a3 · x3 + a2 · x2 + a1 · x + a0
b(x) = b3 · x3 + b2 · x2 + b1 · x + b0
zwei solche Polynome, dann definieren wir
• die Addition + uber
a(x) + b(x) = (a3 ⊕ b3) · x3 + (a2 ⊕ b2) · x2 + (a1 ⊕ b1) · x + (a0 ⊕ b0)
• und die Multiplikation ⊗ uber die Polynommultiplikation modulo x4 + 1 .
Es giltxi mod (x4 + 1) = xi mod 4
somit konnen wir die Multiplikation ⊗ wie folgt vereinfachen: Sei
d(x) = d3 · x3 + d2 · x2 + d1 · x + d0 = a(x)⊗ b(x)
dann erhalten wir d0
d1
d2
d3
=
a0 a3 a2 a1
a1 a0 a3 a2
a2 a1 a0 a3
a3 a2 a1 a0
·
b0
b1
b2
b3
.
Die Multiplikation ⊗ mit einem festen Polynom a(x) ist nicht fur alle Polynome a(x) invertierbar.Im AES wir jedoch ein Polynom benutzt welches ein multiplikatives Inverses besitzt:
a(x) = 0316 · x3 + 0116 · x2 + 0116 · x + 0216
a−1(x) = 0B16 · x3 + 0D16 · x2 + 0916 · x + 0E16 .
Wahlen wira(x) = 0116 · x3,
d.h. a3 = 0116 und a2 = a1 = a0 = 0016 , dann erhalten wir uber die Operation ⊗ eine Rotationnach links:
[0016, 0016, 0016, 0116] ⊗ [b0, b1, b2, b3] = [b1, b2, b3, b0] .
4.6.2 Zustand des AES
Die Basiseinheit fur Berechnungen im AES stellt das Byte dar. Sei a0 . . . a7 die folge der Bits imSpeicher, dann benutzen wir die Darstellungen
(a7 . . . a0)2
unda7 · x7 + . . . + a1 · x + a0 .
59

Die Blocklange beim AES betragt 128 Bits, d.h. 16 Byte. Abhangig vom Grad der Sicherheit, benutztdas AES Schlussel der Lange 128, 192 oder 256 Bit, bzw. 16, 24 oder 32 Byte. Ist x ein Blockbestehend aus n Bytes, dann bezeichnen wir im Folgenden mit x[i] das i -te Byte.3
Den Zustand des AES konnen wir Byteweise mit Hilfe eines 4× 4 -Arrays beschreiben:
Inputin0 in4 in8 in12
in1 in5 in9 in13
in2 in6 in10 in14
in3 in7 in11 in15
−→
Zustands0,0 s0,1 s0,2 s0,3
s1,0 s1,1 s1,2 s1,3
s2,0 s2,1 s2,2 s2,3
s3,0 s3,1 s3,2 s3,3
−→
Outputout0 out4 out8 out12out1 out5 out9 out13out2 out6 out10 out14out3 out7 out11 out15
Um ein 1-dimensionales Feld aus 16 Bytes in eine 2-dimensionale 4×4 -Matrix umzuwandeln definierenwir die Funktion Square : ({0, 1}8)16 → ({0, 1}8)4×4 . Sei
s = (si,j)i,j∈[0..3] = Square(x)
fur x ∈ ({0, 1}8)16 , dann gilt fur alle i, j ∈ [0..3]
si,j = x[i + 4 · j] .
Die Funktion InvSquare : ({0, 1}8)4×4 → ({0, 1}8)16 gibt die Umkehrfunktion von Square () an,d.h. fur
x = InvSquare(s)
giltx[i + 4 · j] = si,j .
Sei s = (si,j)i,j∈[0..3] und s′ = (s′i,j)i,j∈[0..3] , dann definieren wir
s⊕ s′ = (si,j ⊕ s′i,j)i,j∈[0..3]
als die elementweise Addition in GF (28) und somit als das bitweises Xor der Matrizen.
4.6.3 Die Unterfunktionen des AES
Die einzelnen Verschlusselungsschritte des AES lassen sich mit Hilfe von 4 individuellen Unterfunk-tionen und deren Umkehrfunktionen aufbauen:
• AddRoundKey () und InvAddRoundKey ()
• ShiftRows () und InvShiftRows ()
• MixColumns () und InvMixColumns ()
• SubBytes () und InvSubBytes ()
1. AddRoundKey () und InvAddRoundKey () :
Bei AddRoundKey () sind Funktion und Umkehrfunktion identisch:
3Allgemein bezeichnen wir mit x[i] das i -te Element in der Zeichenkette x . An anderer Stelle beziehen wir unshierbei oft auf ein Bit. Zur Vereinfachung der Darstellung werden wir beim AES mit x[i] das i -te Byte in x bezeichnen.
60

• Eingabe: eine 4× 4 -Byte-Matrix s und ein 16-Byte Rundenschlussel Ki
• Ausgabe: die 4× 4 -Byte-Matrix s⊕ Square(Ki) .
Die einzelnen Rundenschlussel K0, . . . ,Kr−1 werden mit Hilfe der Funktion KeyExpansion () ausdem Schlussel K generiert. Die 4× 4 -Byte-Matrix s gibt den aktuellen Zustand des Rundentextesan.
s′2,2
Ki[0] Ki[1] Ki[2] Ki[3]
s0,0 s0,1 s0,2 s0,3
s1,0 s1,2 s1,3
s2,0 s2,1 s2,2 s2,3
s3,0 s3,1 s3,2 s3,3
s1,1
s′0,0 s′0,1 s′0,2 s′0,3
s′1,3s′1,2s′1,1s′1,0
s′2,0 s′2,1 s′2,3
s′3,3s′3,2s′3,1s′3,0
Ki[4] Ki[5] Ki[6] Ki[7] Ki[8] Ki[9] Ki[10]Ki[11]Ki[12]Ki[13]Ki[14]Ki[15]
⊕
2. ShiftRows () und InvShiftRows () :
ShiftRows () fuhrt einen zyklischen Shift auf die einzelnen Zeilen einer 4×4 -Byte-Matrix aus. Hierbeiwird die i -te Zeile um i Positionen geshifted.
• Eingabe: eine 4× 4 -Byte-Matrix s .
• Ausgabe: die 4× 4 -Byte-Matrix s′ mit
s′i,j = si,(j+i) mod 4 .
Fur die Umkehrfunktion InvShiftRows () erhalten wir:
• Eingabe: eine 4× 4 -Byte-Matrix s .
• Ausgabe: die 4× 4 -Byte-Matrix s′ mit
s′i,(j+i) mod 4 = si,j .
s′0,0
s′2,3
s′3,3s′3,2s′3,1s′3,0
s0,0 s0,1 s0,2 s0,3
s1,0 s1,2 s1,3
s2,0 s2,1 s2,2 s2,3
s3,0 s3,1 s3,2 s3,3
s1,1
s′0,1 s′0,2 s′0,3
s′1,3s′1,2s′1,1s′1,0
s′2,0 s′2,1 s′2,2
ShiftRows ()
61

3. MixColumns () und InvMixColumns () :
MixColumns () interpretiert jede Spalte der 4× 4 -Byte-Matrix als ein Polynom
sj = s3,j · x3 + s2,j · x2 + s1,j · x + s0,j
mit Koeffizienten aus GF (28) und Multipliziert (⊗ ) dieses mit dem Polynom
p(x) = 0316 · x3 + 0216 · x2 + 0116 · x + 0116
• Eingabe: eine 4× 4 -Byte-Matrix s .
• Ausgabe: die 4× 4 -Byte-Matrix s′ mits′0,j
s′1,j
s′2,j
s′3,j
=
0216 0316 0116 0116
0116 0216 0316 0116
0116 0116 0216 0316
0316 0116 0116 0216
·
s0,j
s1,j
s2,j
s3,j
bzw.
s′0,j := (0216 · s0,j)⊕ (0316 · s1,j)⊕ s2,j ⊕ s3,j
s′1,j := (0216 · s1,j)⊕ (0316 · s2,j)⊕ s3,j ⊕ s0,j
s′2,j := (0216 · s2,j)⊕ (0316 · s3,j)⊕ s0,j ⊕ s1,j
s′3,j := (0216 · s3,j)⊕ (0316 · s0,j)⊕ s1,j ⊕ s2,j
fur alle j ∈ [0..3] .
s′1,3
s′3,2s′3,1s′3,0
s0,0 s0,1 s0,2 s0,3
s1,0 s1,2 s1,3
s2,0 s2,1 s2,2 s2,3
s3,0 s3,1 s3,2 s3,3
s1,1
s′0,0 s′0,1 s′0,2 s′0,3
s′1,2s′1,1s′1,0
s′2,0 s′2,1 s′2,2 s′2,3
s′3,3
p(x)⊗ sj(x)
Die Umkehrfunktion InvMixColumns () erhalten wir uber die Multipliziert (⊗ ) des Spalten-Polynomsmit
p−1(x) = 0B16 · x3 + 0D16 · x2 + 0916 · x + 0E16
• Eingabe: eine 4× 4 -Byte-Matrix s .
• Ausgabe: die 4× 4 -Byte-Matrix s′ mits′0,j
s′1,j
s′2,j
s′3,j
=
0E16 0B16 0D16 0916
0916 0E16 0B16 0D16
0D16 0916 0E16 0B16
0B16 0D16 0916 0E16
·
s0,j
s1,j
s2,j
s3,j
62

bzw.
s′0,j := (0E16 · s0,j)⊕ (0B16 · s1,j)⊕ (0D16 · s2,j)⊕ (0916 · s3,j)s′1,j := (0E16 · s1,j)⊕ (0B16 · s2,j)⊕ (0D16 · s3,j)⊕ (0916 · s0,j)s′2,j := (0E16 · s2,j)⊕ (0B16 · s3,j)⊕ (0D16 · s0,j)⊕ (0916 · s1,j)s′3,j := (0E16 · s3,j)⊕ (0B16 · s0,j)⊕ (0D16 · s1,j)⊕ (0916 · s2,j)
fur alle j ∈ [0..3] .
4. SubBytes () und InvSubBytes () :
SubBytes () ist eine elementweise Transformation einer 4 × 4 -Byte-Matrix mit Hilfe einer nicht-linearen invertierbaren S -Box.
• Eingabe: eine 4× 4 -Byte-Matrix s .
• Ausgabe: die 4× 4 -Byte-Matrix s′ mit
s′i,j = Eintrag in der u-ten Zeile und v-ten Spalteder S-Box Tabelle
wobei si,j = uv mit u, v ∈ {0, 1}4 ist.
Fur die Umkehrfunktion InvSubBytes () erhalten wir:
• Eingabe: eine 4× 4 -Byte-Matrix s .
• Ausgabe: die 4× 4 -Byte-Matrix s′ mit
s′i,j = Eintrag in der u-ten Zeile und v-ten Spalteder inversen S-Box Tabelle
wobei si,j = uv mit u, v ∈ {0, 1}4 ist.
Die folgende Tabelle gibt die S -Box fur das AES wieder:
0 1 2 3 4 5 6 7 8 9 A B C D E F
0 63 7C 77 7B F2 6B 6F C5 30 01 67 2B FE D7 AB 761 CA 82 C9 7D FA 59 47 F0 AD D4 A2 AF 9C A4 72 C02 B7 FD 93 26 36 3F F7 CC 34 A5 E5 F1 71 D8 31 153 04 C7 23 C3 18 96 05 9A 07 12 80 E2 EB 27 B2 754 09 83 2C 1A 1B 6E 5A A0 52 3B D6 B3 29 E3 2F 845 53 D1 00 ED 20 FC B1 5B 6A CB BE 39 4A 4C 58 CF6 D0 EF AA FB 43 4D 33 85 45 F9 02 7F 50 3C 9F A87 51 A3 40 8F 92 9D 38 F5 BC B6 DA 21 10 FF F3 D28 CD 0C 13 EC 5F 97 44 17 C4 A7 7E 3D 64 5D 19 739 60 81 4F DC 22 2A 90 88 46 EE B8 14 DE 5E 0B DBA E0 32 3A 0A 49 06 24 5C C2 D3 AC 62 91 95 E4 79B E7 C8 37 6D 8D D5 4E A9 6C 56 F4 EA 65 7A AE 08C BA 78 25 2E 1C A6 B4 C6 E8 DD 74 1F 4B BD 8B 8AD 70 3E B5 66 48 03 F6 0E 61 35 57 B9 86 C1 1D 9EE E1 F8 98 11 69 D9 8E 94 9B 1E 87 E9 CE 55 28 DFF 8C A1 89 0D BF E6 42 68 41 99 2D 0F B0 54 BB 16
63

s′1,3
s′3,2s′3,1s′3,0
s0,0 s0,1 s0,2 s0,3
s1,0 s1,2 s1,3
s2,0 s2,1 s2,2 s2,3
s3,0 s3,1 s3,2 s3,3
s1,1
s′0,0 s′0,1 s′0,2 s′0,3
s′1,2s′1,1s′1,0
s′2,0 s′2,1 s′2,2 s′2,3
s′3,3
S -Box
Die Tabelleneintrage der S -Box knnen wie folgt berechnet werden: Sei si,j ein Byte, welches wir mitHilfe der S -Box transformieren wollen, dann verfahren wir wie folgt:
• Bestimme das multiplikative Inverse s−1i,j von si,j in GF (28) . Fur si,j = 00 wahlen wir s−1
i,j =00 .
• Seien s−1i,j [i] die Bits von s−1
i,j , d.h.
s−1i,j = s−1
i,j [7]s−1i,j [6]s−1
i,j [5]s−1i,j [4]s−1
i,j [3]s−1i,j [2]s−1
i,j [1]s−1i,j [0]
dann erhalten wir die Bits des Ergebnisses
s′i,j = s′i,j [7]s′i,j [6]s′i,j [5]s′i,j [4]s′i,j [3]s′i,j [2]s′i,j [1]s′i,j [0]
uber
s′i,j [i] = s−1i,j [i]⊕ s−1
i,j [i + 4 mod 8]⊕ s−1i,j [i + 5 mod 8]
⊕s−1i,j [i + 6 mod 8]⊕ s−1
i,j [i + 7 mod 8]⊕ c[i]
wobei c = c[7]c[6]c[5]c[4]c[3]c[2]c[1]c[0] = 011000112 ist.
Alternativ konnen wir die Tabelleneintrage auch uber die folgende affin-lineare Transfromation ausdem multiplikative Inverse s−1
i,j von si,j bestimmen:
s′i,j [0]s′i,j [1]s′i,j [2]s′i,j [3]s′i,j [4]s′i,j [5]s′i,j [6]s′i,j [7]
=
1 0 0 0 1 1 1 11 1 0 0 0 1 1 11 1 1 0 0 0 1 11 1 1 1 0 0 0 11 1 1 1 1 0 0 00 1 1 1 1 1 0 00 0 1 1 1 1 1 00 0 0 1 1 1 1 1
·
s−1i,j [0]
s−1i,j [1]
s−1i,j [2]
s−1i,j [3]
s−1i,j [4]
s−1i,j [5]
s−1i,j [6]
s−1i,j [7]
+
11000110
64

Die folgende Tabelle gibt die inverse S -Box fur das AES wieder:
0 1 2 3 4 5 6 7 8 9 A B C D E F
0 52 09 6A D5 30 36 A5 38 BF 40 A3 9E 81 F3 D7 FB1 7C E3 39 82 9B 2F FF 87 34 8E 43 44 C4 DE E9 CB2 54 7B 94 32 A6 C2 23 3D EE 4C 95 0B 42 FA C3 4E3 08 2E A1 66 28 D9 24 B2 76 5B A2 49 6D 8B D1 254 72 F8 F6 64 86 68 98 16 D4 A4 5C CC 5D 65 B6 925 6C 70 48 50 FD ED B9 DA 5E 15 46 57 A7 8D 9D 846 90 D8 AB 00 8C BC D3 0A F7 E4 58 05 B8 B3 45 067 D0 2C 1E 8F CA 3F 0F 02 C1 AF BD 03 01 13 8A 6B8 3A 91 11 41 4F 67 DC EA 97 F2 CF CE F0 B4 E6 739 96 AC 74 22 E7 AD 35 85 E2 F9 37 E8 1C 75 DF 6EA 47 F1 1A 71 1D 29 C5 89 6F B7 62 0E AA 18 BE 1BB FC 56 3E 4B C6 D2 79 20 9A DB C0 FE 78 CD 5A F4C 1F DD A8 33 88 07 C7 31 B1 12 10 59 27 80 EC 5FD 60 51 7F A9 19 B5 4A 0D 2D E5 7A 9F 93 C9 9C EFE A0 E0 3B 4D AE 2A F5 B0 C8 EB BB 3C 83 53 99 61F 17 2B 04 7E BA 77 D6 26 E1 69 14 63 55 21 0C 7D
4.6.4 Die Rundenschlussel beim AES
Um den Rundenschlussel zu bestimmen benotigen wir noch einige einfache Hilfsfunktionen, die aufeinem 4-Byte Wort w = w[0]w[1]w[2]w[3] arbeiten:
RotWord ()
• fuhrt einen zyklischen Shift um ein Byte nach links aus:
RotWord(w[0]w[1]w[2]w[3]) = w[1]w[2]w[3]w[0] .
SubWord ()
• wendet einen S -Box-Operation auf jedes Byte an:
SubWord(w[0]w[1]w[2]w[3]) = S(w[0])S(w[1])S(w[2])S(w[3]) .
Rcon (i)
• fur i ∈ N mit i > 0 istRcon(i) = ci001600160016,
wobei wir die Rundenkonstante ci wie folgt uber die Operationen in GF (28) und der Poly-nomdarstellung bestimmen
ci = xi−1 (modm(x)) .
Alle diese Operationen konnen wir auch mit Hilfe der Multiplikation ⊗ und Addition + von Poly-nomen mit Koeffizienten in GF (28) darstellen.
65

Algorithm 1 KeyExpansion (K)Eingabe: 4 · k -Byte Schlussel KAusgabe: Folge der Rundenschlussel (K0, . . . ,K`)1: ` := 6 + k2: for i = 0 to k − 1 do hi := K[4i]K[4i + 1]K[4i + 2]K[4i + 3] end for3: for i = k to 4 · ` do4: t := hi−1
5: if (i mod k) = 0 then6: t := SubWord(RotWord(t))⊕ Rcon(i/k)7: else8: if k = 8 ∧ (i mod k) = 4 then t := SubWord(t) end if9: end if
10: hi := hi−k ⊕ t11: end for12: for i = 0 to ` do Ki := h4ih4i+1h4i+2h4i+3 end for13: Return ((K0, . . . ,K`))
Die folgenden beiden Grafiken illustrierten die Arbeitsweise von KeyExpansion (K) bei einer Schlussellangevon 16 und 24 Byte bzw. 128 und 192 Bit, d.h. k = 4 bzw. k = 6 :
⊕
⊕ ⊕
⊕
⊕
Rcon (1)
⊕
⊕
h1 h2 h3 h4 h5 h6 h7h0 h8
SubWord ()
RotWord ()
SubWord ()
RotWord ()
Rcon (2)
⊕
h1 h2 h3 h4 h5 h6h0 h7 h8 h9 h10 h11 h12
⊕⊕
⊕⊕
⊕
SubWord ()
RotWord ()
Rcon (1)
⊕
⊕
SubWord ()
RotWord ()
Rcon (2) ⊕
66

Und die folgende Grafik schlielich illustriert die Arbeitsweise von KeyExpansion (K) bei einer Schlussellangevon 32 Byte bzw. 256 Bit, d.h. k = 8 :
⊕
⊕
SubWord () SubWord ()
⊕
h1 h2 h3 h4 h5 h6h0 h7 h8 h9 h10 h11 h12 h13 h14 h15 h16
⊕⊕
⊕⊕
⊕⊕
RotWord ()
Rcon (1)
⊕
SubWord ()
RotWord ()
Rcon (2) ⊕
4.6.5 Der AES-Algorithmus
Der AES-Algorithmus verschlusselt einen Plaintext von 16 Byte in mehreren Runden. Die Anzahl derRunden hangt hierbei von der Schlussellange ab. Es gilt:
• bei 16-Byte Schlussel betragt die Rundenzahl 10,
• bei 24-Byte Schlussel betragt die Rundenzahl 12 und
• bei 32-Byte Schlussel betragt die Rundenzahl 14.
Die Beschreibung von AES in Federal Infomation Processing Standards Publication 197 erlaubt auchdie Benutzung großerer Blocke und Schlussel. Auf die hierbei benotigten relativ einfachen Modifika-tionen werden wir jedoch nicht eingehen.
Algorithm 2 AES-Verschlusselung (x,K)Eingabe: 16-Byte Plaintext x und 4 · k -Byte Schlussel KAusgabe: 16-Byte Ciphertext y
1: (K0, . . . ,K`) := KeyExpansion (K)2: s := Square (x)3: s := AddRoundKey (s,K0)4: for i = 1 to `− 1 by +1 do5: s := SubBytes (s) ; s := ShiftRows (s)6: s := MixColumns (s) ; s := AddRoundKey (s,Ki)7: end for8: s := SubBytes (s)9: s := ShiftRows (s)
10: s := AddRoundKey (s,K`)11: Return ( InvSquare (s))
67

Algorithm 3 AES-Entschlusselung (y, K)Eingabe: 16-Byte Ciphertext y und 4 · k -Byte Schlussel KAusgabe: 16-Byte Plaintext x
1: (K0, . . . ,K`) := KeyExpansion (K)2: s := Square (y)3: s := AddRoundKey (s,K`)4: for i = `− 1 to 1 by −1 do5: s := InvShiftRows (s) ; s := InvSubBytes (s)6: s := AddRoundKey (s,Ki) ; s := InvMixColumns (s)7: end for8: s := InvShiftRows (s)9: s := InvSubBytes (s)
10: s := AddRoundKey (s,K`)11: Return ( InvSquare (s))
68

5 Public Key Kryptographie
Bei den bisher betrachteten Kryptosystemen handelt es sich um Zwei-Wege Kryptosysteme, d.h. umeine Nachricht sicher zu ubertragen, mussten zunachst der Schlussel sicher ubertragen werden. ImAnschluss konnte dann mit Hilfe dieses Schlussels die Nachricht ubertragen werden. Diesen zusatzli-chen sicheren Transport benotigen wir nicht mehr, wenn ein Public Key Kryptosystem benutzt wird.In einem solchen System teilen wir die beiden Aufgaben eines Schlussels in Zwei-Wege Kryptosy-steme, d.h. Verschlusseln und Entschlusseln, auf zwei Schlussel auf: einen offentlichen Schlussel zurVerschlusselung der Nachricht und einen privaten Schlussel zur Entschlusselung. Diese Idee geht aufDiffie und Hellman (1976) [DH76] zuruck, und hat seit dem die Kryptographie wesentlich beeinflusst.
5.1 Das generelle Schema
Das generelle Szenario fur ein Public Key System hat die folgende Gestalt: Gegeben sind ` PersonenA1, . . . , A` . Jede dieser Personen Ai generiert einen offentlichen Schlussel wi und einen privatenSchlussel wi . Die offentlichen Schlussel sammeln wir in einer Liste. Mochte Ai an Aj eine Nachrichtx senden, so verschlusselt Ai diese Nachricht mit Hilfe von wj und sendet die Nachricht an Aj . Aj
entschlusselt die Nachricht mit Hilfe von wi .
Damit dieses Verfahren sicher ist, mussen die folgenden Eigenschaften erfullt sein:
1. Der Schlussel wi darf nur mit großem Aufwand aus wi (oder irgendwelchen Plaintext-CiphertextPaaren) zu berechnen sein.
2. Die Verschlusselung eines Plaintextes muss einfach sein.
3. Die Entschlusselung ohne Kenntnis von wi muss sehr schwer sein.
Diese Voraussetzungen fuhren uns zu sogenannten One-Way Funktionen:
Definition 22 Seien X, Y zwei nicht-leere Mengen. Eine One-Way Funktion f ist eine injektiveFunktion f : X → Y , so dass f(x) in polynomieller Zeit in der Lange von x fur alle x ∈ X bere-chenbar ist, aber die Umkehrfunktion f−1(y) fur jeden interessanten Anteil der Werte y ∈ Range(f)nicht effizient berechenbar ist.
Aufgabe 18 Beweisen Sie: Ist P = NP , so gibt es keine One-Way Funktionen.
Aufgabe 19 Betrachten Sie die folgende Attacke auf einen Ciphertext y ∈ Zm,n , der durch einPublic-Key Verfahren A mit offentlichem Schlussel w generiert wurde:
Wahle einen Text x ∈ Zm,n . Bestimme den Ciphertext y′ fur x unter Verwendung desSchlussels w . Ist y′ = y , so nennen wir die Wahl von x erfolgreich.
Zeigen Sie: Gilt fur alle Polynome q
Pr(die Wahl von x ist erfolgreich) <1
q(n),
dann ist die Wahrscheinlichkeit, einen Wert x auch bei einer polynomiell haufigen Wiederholungdieser Attacke erfolgreich zu wahlen, kleiner 1
q(n) fur alle Polynome q .
69

Aufgabe 20 Zeigen Sie wie mit Hilfe eines Public-Key Verfahrens ein Authentifizierungsverfahrenimplementiert werden kann.
Bisher konnte der Beweis fur die Existenz von One-Way Funktionen noch nicht erbracht werden.Zwar scheint die Beantwortung dieser Frage mit der Problematik, ob P gleich NP ist, im Zusam-menhang zu stehen. Um jedoch eine fur die Kryptographie anwendbare One-Way Funktion zu finden,mussen noch einige weitere Kriterien erfullt sein, welche uber die klassischen Worst-Case Bedingungenhinausgehen:
1. Probleme mit hoher Worst-Case Komplexitat konnen auf den meisten Eingabeinstanzen einfachgelost werden. Zudem existieren keine nicht-linearen unteren Schranken fur die meisten NP -vollstandigen Probleme.
2. Fur praktische Anwendungen genugt es, wenn wir f−1 randomisiert effizient berechnen konnen.Somit schließt die nicht effiziente Berechenbarkeit von f−1 auch die polynomielle randomisierteBerechenbarkeit von f−1 aus. Selbst aus dem Wissen, dass es keinen effizienten deterministi-schen Algorithmus fur f−1 gibt, konnen wir jedoch nicht schließen, dass es keinen effizientenrandomisierten Algorithmus gibt.
3. Da die meisten relevanten Eingaben fur die Kryptoanalyse von beschrankter Lange sind, durfenwir uns bei der nicht effizienten Berechenbarkeit von f−1 nicht auf uniforme Komplexitats-klassen beschranken. Vielmehr mussen wir fordern, dass f−1 auch nicht durch nicht-uniformkonstruierbare Schaltkreisfamilien polynomieller Große berechnet werden kann.
4. Selbst, wenn alle oben beschriebenen Voraussetzungen erfullt sind, und f−1 auf fast allen Ein-gaben nicht effizient berechnet werden kann, ist es moglich, dass die wenigen Eingaben, aufdenen eine Invertierung von f effizient moglich ist, alle interessanten Eingaben umfasst, wiezum Beispiel alle Eingaben der Lange ≤ 2210
.
Trotz dieser demotivierenden Einschrankungen gibt es dennoch einige vielversprechende Kandidatenfur One-Way Funktionen:
1. die modulare Exponentiation mit der Umkehrfunktion des diskreten Logarithmus,
2. das Produkt von Primzahlen mit der Umkehrfunktion der Primzahlzerlegung und
3. berechne M =∑n
i=0 xi · ai mit ai ∈ N und xi ∈ {0, 1} . Die Umkehrfunktion dieser Funktionstellt eine Verallgemeinerung des Rucksackproblems dar.
Es bleibt jedoch zu klaren, wie wir eine One-Way Funktion einsetzen konnen, um ein Public-KeyVerfahren zu bekommen. Hierfur greifen wir auf sogenannte Trap-Door Funktionen zuruck. In derfolgenden Definition gibt Ko die Menge der offentlichen und Kp die Menge der privaten Schlusselan.
Definition 23 Eine Funktion f : Pt × Ko → Ct nennen wir Trap-Door Funktion, wenn die dreinachfolgenden Bedingungen erfullt sind:
1. Two(·) = f(·, wo) ist eine One-Way Funktion fur alle wo ∈ Ko .
2. Es existiert ein Polynom p , so dass Two(x) in deterministischer (bzw. randomisierter) Zeitp(|x|) fur alle wo ∈ Ko berechnet werden kann.
70

3. Es existiert eine One-Way Funktion d : Kp → Ko und eine in polynomieller Zeit berechenbareFunktion g : Kp × Ct → Pt , so dass
∀x ∈ Pt ∀y ∈ Ct ∀wo ∈ Ko : y = f(x,wo) =⇒ x = g(d−1(wo), y) .
Wie gefahrlich es ist, sich bei der Auswahl einer Trap-Door Funktion auf ein NP -vollstandiges Pro-blem zu verlassen, zeigt das folgende Beispiel (vergleiche hierzu [K86]).
5.2 Das Merkle-Hellman Kryptosystem
Das Merkle-Hellman Kryptosystem basiert auf dem Rucksack-Problem. Hierfur stellen wir den Plain-text als eine binare Zeichenkette x = (x0, . . . , xn−1) ∈ {0, 1}n dar. Ferner sei w = (w0, . . . , wn−1) ∈Nn ein Rucksack-Vektor, d.h. eine Instanz des Rucksack-Problems, mit Rucksackvolumen
y = w · xT =n−1∑i=0
wi · xi .
Das Resultat y ist eine Zahl zwischen 0 und∑n−1
i=0 wi und gibt (aufgefullt mit fuhrenden Nullen)den Ciphertext der Lange ` = dlog2(1 +
∑n−1i=0 wi)e wieder. Damit die Entschlusselung erfolgreich
durchgefuhrt werden kann, mussen wir die Werte von w geschickt wahlen. Im Folgenden wollen wirzunachst auf die Konstruktion von w eingehen. Im Anschluss stellen wir das Entschlusselungsverfah-ren fur diese Kryptosystem vor, um dann abschließend die Attacke von Shamir [S82] zu diskutieren.
5.2.1 Konstruktion des offentlichen Schlussels
Die Hintertur zum Merkle-Hellman Verfahren besteht aus einem Paar (k, m) ∈ N × N , deren Wertehinreichend groß gewahlt werden und die die Bedingung
k < m und ggT(k, m) = 1 (3)
erfullen. Wir wahlen nun n Werte w = (w0, . . . , wn−1) , so dass
m >
n−1∑i=0
wi und ∀i ∈ {1, . . . , n− 1} : wi >
i−1∑j=0
wj (4)
ist. Um ein Public-Key Verfahren zu bekommen, wahlt die entsprechende Person die Werte k, m, w so,dass die Bedingungen (3) und (4) erfullt sind. Anschließend berechnet sie w = (w0, . . . , wn−1) , wobeiwi = (k · wi) mod m ist. Die Werte k, m, w stellen den privaten und der Vektor w den offentlichenSchlussel dar.
5.2.2 Entschlusselungsverfahren
Sei y der empfangene Ciphertext. Wir berechnen zunachst y = (k−1 · y) mod m . Da m und kTeilerfremd sind, konnen wir das multiplikative Inverse zu k modulo m eindeutig bestimmen. Fur
71

y gilt:
y = (k−1 · y) mod m = (n−1∑i=0
k−1 · wi · xi) mod m
= (n−1∑i=0
k−1 · k · wi · xi) mod m =n−1∑i=0
wi · xi .
Wir bestimmen nun den Plaintext x = (x0, . . . , xn−1) wie folgt: Sei yn = y , dann gilt fur i =n− 1, . . . , 0
yi = yi+1 mod wi und xi =⌊
yi+1
wi
⌋.
5.2.3 Attacke von Shamir
Gegeben sei eine Instanz des Merkle-Hellman Systems, d.h.
k, m,w = (w0, . . . , wn−1), w = (w0, . . . , wn−1) .
Der Kryptoanalytiker kennt von dieser Instanz nur den offentlichen Schlussel w = (w0, . . . , wn−1) . DasZiel des Kryptoanalytikers ist es, ein teilerfremdes Paar k, m zu berechnen, so dass fur die Sequenzw = (w0, . . . , wn−1) mit wi ≡ wi · k mod m die Bedingung 4 erfullt sind, d.h.
m >
n−1∑i=0
wi und ∀i ∈ {1, . . . , n− 1} : wi >
i−1∑j=0
wj . (5)
Es ist einfach zu erkennen, dass die Werte k, m,w auf die gleiche Art und Weise zur Entschlusselungvon y benutzt werden konnen, wie die Werte k, m, w . Das Verfahren von Merkle und Hellman hatsomit mehrere Hinterturen.
Dividieren wir die Werte wi durch m , so erhalten wir
wi
m≡ wi ·
k−1
mmod 1 und
n−1∑i=0
wi ·k−1
mmod 1 < 1 .
Zur Vereinfachung wahlen wir r = k−1
m , d.h.
n−1∑i=0
wi · r mod 1 < 1 . (6)
Der Verlauf der Funktion (wi · r) mod 1 ist in Abbildung 5 dargestellt.
Wir suchen zunachst einen Punkt r0 auf der r -Achse, so dass dieser Wert die Bedingung (6) erfullt.
Wir konnen nun die folgende Beobachtungen anstellen:
• Die pi -te Nullstelle der Sagezahnkurve (wi · r) mod 1 ist pi/mi .
• Damit das Merkle-Hellman Kryptosystem einen Plaintext gut verschlusselt, sollten die Werte wi
moglichst gross sein, d.h. die Langen der Binardarstellungen diese Werte liegen nahe bei Langeder Binardarstellung von m .
72

1
1
0
(wi · r) mod 1
r1
wi0 2
wi
3wi
pi
wi
pi+1wi
wi−1wi
Abbildung 5: Verlauf der Funktion fi(r) = (wi · r) mod 1 .
• Somit ist die Lange der Binardarstellung von wi = fi(r) kleiner als die Lange der Binardarstel-lung von wi und daher muss r in der Nahe einer Nullstelle pi von fi liegen.
Aufbauend auf diesen Beobachtungen konnen wir das folgende System von Ungleichungen aufstellen:
1 ≤ p1 ≤ w1 − 1, −ε2 ≤ p1w1− p2
w2≤ ε′2
1 ≤ p2 ≤ w2 − 1, −ε3 ≤ p1w1− p3
w3≤ ε′3
......
1 ≤ pn ≤ wn − 1, −εn ≤ p1w1− pn
wn≤ ε′n,
(7)
wobei die Werte von εi, ε′i akzeptable Abweichungen zwischen den Differenzen p1
w1− pi
widarstellen.
Diese Abweichungen sollen moglichst klein gewahlt werden. In vielen Fallen ist es ausreichend einekonstante Anzahl von diesen Ungleichungen zu losen. Das System von Ungleichungen (7) kann mitHilfe von Lenstra’s Integer-Programming Algorithmus gelost werden [L81].
Seien p1 ein Wert, der als Losung fur unser oben angegebenes Ungleichungssystem bestimmt wurdeund r1, . . . , rh aufsteigende Werte mit
p1
w1≤ r1 < r2 < . . . < rh <
p1 + 1w1
.
Diese Werte konnen wir so wahlen, dass zwischen jedem Paar von Werten rt, rt+1 alle Kurven r ·wi mod 1 linear sind. Sei qt
i die Anzahl der Minima von r ·wi mod 1 im Intervall (0, rt) , dann giltfur r ∈ [rt, rt+1)
r · wi mod 1 = r · wi − qti .
Fur r ∈ [rt, rt+1) konnen wir somit die notigen Voraussetzungen fur r neu formulieren:
n−1∑i=0
(r · wi − qti) < 1 und ∀i ≤ n− 1 :
i−1∑j=0
(r · wj − qtj) < (r · wi − qt
i) .
Dieses Gleichungssystem beinhaltet genau eine Variable. Die Losung dieses Systems ergibt ein Teilin-tervall It von [rt, rt+1) , so dass fur alle r und fur alle Werte k, m mit r = k
−1
m das Paar k, m einEntschlusselungssystem fur jeden Ciphertext der untersuchten Instanz des Merkle-Hellman Systemsbereitstellt.
73

5.3 Probleme aus der Zahlentheorie
Wir werden uns nun verschiedene Kryptosysteme, die auf Problemen aus der Zahlentheorie basieren,naher ansehen. Zuvor mussen wir uns jedoch mit verschiedenen Problemen aus der Zahlentheoriebeschaftigen. Die meisten der folgenden Punkte sollten schon bekannt sein. Um keine Missverstandnisseaufkommen zu lassen, werden wir auf einige Punkte aus der Zahlentheorie hier eingehen.
Zunachst ein paar Notationen. Seien m ∈ N und a, b ∈ Z , dann gilt
• a ≡ b mod m gdw. m|(a− b) , d.h. m teilt (a− b)
• [a]m = {x ∈ Z|a ≡ x mod m}
• Zm = {[0], [1], . . . , [m− 1]} und
• Z∗m = {[a] ∈ Zm|ggT(a,m) = 1} .
Es gilt[a] · [b] = [a · b] und [a] + [b] = [a + b] .
Somit sind (Zm,+) und (Z∗m, ·) zwei Gruppen. Der Einfachheit halber identifizieren wir Zm undZ∗m mit diesen Gruppen. Wir lassen die Klammern um die Elemente der Mengen Zm und Z∗m weg.
Ferner definiert (Zm,+, ·) einen kommutativen Ring.
Um innerhalb eines Restklassenringes rechnen zu konnen, fassen wir noch einige einfache Ergebnissezusammen:
Beobachtung 7 Seien m ∈ N+ , n ∈ N und a, b, c, d ∈ Z , dann gilt
a ≡ b mod m und c ≡ d mod m =⇒ a + c ≡ b + d mod m
a ≡ b mod m und c ≡ d mod m =⇒ a− c ≡ b− d mod m
a ≡ b mod m und c ≡ d mod m =⇒ a · c ≡ b · d mod m
a ≡ b mod m =⇒ an ≡ bn mod m .
Da wir in einem Restklassenring nicht mit der gebrauchlichen Division arbeiten konnen, benutzen wirdas modulare Inverse als Umkehrfunktion der Multiplikation. a−1 ∈ Zm nennen wir das modulareInverse zu a modulo m , wenn a · a−1 ≡ 1 mod m ist. Es gibt jedoch nicht zu jedem Paar a,m dasmodulare Inverse von a . Wie wir schon gesehen haben gilt:
Beobachtung 8 Die Aquivalenz a ·x ≡ 1 mod m hat genau dann eine Losung, wenn ggT(a,m) = 1ist. Wenn eine Losung von a · x ≡ 1 mod m existiert, so ist diese eineindeutig.
Von besonderer Bedeutung fur verschiedene Kryptosysteme ist die Eulersche ϕ -Funktion,
ϕ(m) = |Z∗m| = m ·∏
Primzahlen p<m mit ggT(p,n) 6=1
(1− 1
p
).
Beobachtung 9 Fur die Eulersche ϕ -Funktion gilt:
74

1. ϕ(m · n) = ϕ(m) · ϕ(n) fur ggT(m,n) = 1 ,
2. ϕ(pα) = pα−1(p− 1) fur Primzahlen p und
3. ϕ(p) = p− 1 fur Primzahlen p .
Zahlen a werden wir im Weiteren immer als Binarzahlen darstellen. Mit n = 1+ blog2 ac bezeichnenwir im Allgemeinen die Lange der Binarzahl.
5.3.1 Grundlegende Probleme
Definition 24 Großter gemeinsamer Teiler (ggT)Gegeben: Zwei Zahlen a, b ∈ N .Problem: Bestimme die großte Zahl, die sowohl a als auch b teilt.
Um den großten gemeinsamer Teiler zu finden, konnen wir auf den erweiterten Euklidischen Algorith-mus zuruckgreifen.
Algorithm 4 ErwEuklidEingabe: a, b ∈ N mit a > bAusgabe: d ∈ N , x, y ∈ Z mit d = ggT(a, b) und d = a · x + b · y1: x0 = 1, x1 = 0, y0 = 0, y1 = 1 und r0 = a, r1 = b2: for i = 1, 2, . . . bis ri+1 = 0 do3: qi = b ri−1
ric
4: ri+1 = ri−1 − qi · ri
5: xi+1 = xi−1 − qi · xi
6: yi+1 = yi−1 − qi · yi
7: end for8: Ausgabe ri, xi, yi
Fur diesen Algorithmus gilt:
Theorem 7 Algorithmus 4 berechnet den großten gemeinsamen Teiler zweier Zahlen a, b , indem ermaximal 1, 5 · log2 max{a, b} + O(1) Divisionen von Zahlen kleiner gleich max{a, b} ausfuhrt.
Beweis: Der Beweis erfolgt, indem wir die folgenden Lemmata zeigen:
Lemma 8 Algorithmus 4 berechnet den großten gemeinsamen Teiler zweier Zahlen a, b korrekt.
Beweis: Zunachst zeigen wir uber eine vollstandige Induktion uber i , dass r0 · xi + r1 · yi = ri ist.Fur i = 0 und i = 1 erhalten wir
r0 · x0 + r1 · y0 = r0 · 1 + r1 · 0 = r0 und r0 · x1 + r1 · y1 = r0 · 0 + r1 · 1 = r1 .
Wir betrachten nun die Hypothese, dass die Aussage fur alle i′ ≤ i erfullt ist. Aus dem Algorithmuswissen wir, dass
xi+1 = xi−1 − qi · xi und yi+1 = yi−1 − qi · yi
75

ist. Somit gilt:
r0 · xi+1 + r1 · yi+1 = r0 · xi−1 − r0 · qi · xi + r1 · yi−1 − r1 · qi · yi
= r0 · xi−1 + r1 · yi−1 − qi · (r0 · xi + r1 · yi)= ri−1 − qiri = ri+1 .
Die erste Aussage ist somit bewiesen.
Es gilt fur alle i ≥ 1ri+1 + ri ≤ ri−1 . (8)
Nach Konstruktion gilt ri−1 − qiri = ri+1 und somit ri+1 + ri = ri−1 − (qi − 1)ri . Da wir durch denAlgorithmus sicherstellen, dass ri+1 = ri−1 mod ri < ri ist, gilt qi ≥ 1 und somit ri+1 + ri ≤ ri−1 .
Da die Werte ri nicht negativ sind, gibt es ein n ∈ N , so dass rn+1 = 0 ist. Es verbleibt zu zeigen,dass rn = ggT(a, b) ist.
Sei d = ggT(a, b) . Da rn = r0 · xn + r1 · yn = a · xn + b · yn ist, muss rn ein Vielfaches von d sein.Da rn+1 = 0 ist, gilt rn−1 = qn · rn . Somit teilt rn den Wert rn−1 . Induktiv konnen wir nun furalle i = n − 2, . . . , 0 zeigen, dass rn den Wert ri = qi+1ri+1 + ri+2 teilt. Inbesondere teilt rn dieWerte r0 = a und r1 = b . Somit gilt rn = d .
Lemma 9 Algorithmus 4 benotigt maximal 1, 5·log2 max{a, b} +O(1) Divisionen von Zahlen kleinergleich max{a, b} .
Beweis: Algorithmus 4 benotigt genau eine Division pro Schleifendurchlauf. Die Anzahl der Schleifen-durchlaufe ist jedoch maximal, wenn wir den jeweiligen Wert ri pro Durchlauf nur um einen moglichstkleinen Wert reduzieren. Somit erhalten wir eine moglichst lange Folge bei ri+1 + ri = ri−1 fur allei ≥ 1 . Drehen wir die Zahlrichtung um, so erhalten wir die Folge ai = ai−1 + ai−2 und Startwertea0 = a1 = 1 , d.h. wir erhalten die Folge der Fibonacci-Zahlen, wobei a = an die n -te und b = an−1
die (n− 1) -te Fibonacci-Zahl ist.
Fur diese Zahlenfolge gilt
an =1√5·
(1 +√
52
)n+1
−
(1−
√5
2
)n+1 .
Da | 1−√
52 | < 0, 62 ist, gilt
limn→∞
(1−
√5
2
)n+1
= 0 .
Das asymptotische Wachstumsverhalten von an wird somit durch(
1+√
52
)n+1
bestimmt. Es gilt
n + 1 ≈ log 1+√
52
an .
Die Behauptung des Lemmas folgt unmittelbar.
Theorem 7 folgt unmittelbar aus diesen beiden Lemmata.
76

Definition 25 Modulare InverseGegeben: Zwei Zahlen a,m ∈ N .Problem: Bestimme a−1 ∈ Zm , so dass a−1 ·a ≡ 1 mod m ist, sofern dieser Wert existiert. a−1 = 0 ,wenn kein Wert a−1 mit a−1 · a ≡ 1 mod m existiert.
Das modulare Inverse kann mit Hilfe des erweiterten Euklidischen Algorithmus berechnet werden.
Theorem 8 Das modulare Inverse kann auf Eingabe von a,m in Zeit O(max{log2 a, log2 m}2) be-rechnet werden.
Aufgabe 21 Fuhren Sie das Merkle-Hellman Kryptoverfahren (Ver- und Entschlusselung) fur dieWerte n = 5 , m = 8443 , k = 2550 und w = (171, 196, 457, 1191, 2410) durch. Tip: k−1 =3950 mod m .
Aufgabe 22 Beweisen Sie die Korrektheit des Entschlusselungsverfahrens zum Merkle-Hellman Kryp-tosystem.
Aufgabe 23 Beweisen Sie die Korrektheit der Null-Teiler Eigenschaft fur n ∈ N mit n ≥ 2 :Die Aussage
∀k ∈ N∀` ∈ N : k · ` ≡ 0 mod n =⇒ ` ≡ 0 mod n oder k ≡ 0 mod n
ist genau dann gultig, wenn n eine Primzahl ist.
Aufgabe 24 Beweisen Sie die Korrektheit des Kurzungsgesetzes fur n ∈ N mit n ≥ 2 :Die Aussage
∀k, `, j ∈ N : j 6≡ 0 mod n und j · ` ≡ j · k mod n =⇒ ` ≡ k mod n
ist genau dann gultig, wenn n eine Primzahl ist.
Theorem 9 Chinesischer Restklassen Satz Seien m1, . . . ,mr r Zahlen, die paarweise relativprim zueinander sind, d.h. fur alle i, j ∈ {1, . . . , r} mit i 6= j gilt ggT(mi,mj) = 1 , und seim =
∏ri=1 mi . Ferner seien a1 ∈ Zm1 , . . . , ar ∈ Zmr . Dann existiert genau eine eindeutig bestimmte
Zahl y ∈ Zm mit y ≡ ai mod mi fur alle i ∈ {1, . . . , r} . Ferner kann y in polynomieller Zeit in derLange der Eingabe berechnet werden.
Beweis: Fur jedes i sei ni = mmi
. Da die Werte m1, . . . ,mr alle paarweise relativ prim zueinandersind, gilt ggT(mi, ni) = 1 . Somit existiert auch das modulare Inverse n−1
i von ni bezuglich mi .Wir wahlen
y =t∑
i=1
ni · n−1i · ai und y = y mod m .
Da nj von mi fur alle i 6= j ein Vielfaches ist, gilt
y ≡ y ≡ ni · n−1i · ai ≡ ai mod mi .
Somit erfullt y die erwunschten Bedingungen bezuglich der Restklassenzugehorigkeit.
77

Es verbleibt noch zu zeigen, dass dieser Wert eindeutig ist. Dieser Beweis erfolgt uber eine Wider-spruchsannahme. Sei x 6= y ein Wert in Zm , welcher die Voraussetzungen, d.h. x ≡ ai mod mi furalle i erfullt. Dann gilt x− y ≡ 0 mod mi fur alle i . Folglich teilt mi die Differenz x− y . Da dieWerte m1, . . . ,mr alle paarweise relativ prim zueinander sind, teilt auch das Produkt m =
∏ri=1 mi
die Differenz x − y . Da beide Werte x und y aus Zm gewahlt wurden, folgt dass x − y = 0 undsomit x = y ist – ein Widerspruch.
Die Laufzeitschranke folgt unmittelbar aus der Formel zur Berechnung von y und y .
Definition 26 Modulare ExponentiationGegeben: m ∈ N , m ≥ 2 , x ∈ N und a ∈ Z∗m .Problem: Bestimme y ∈ Zm mit y ≡ ax mod m
Der folgende Algorithmus lost das Problem der modularen Exponentiation:
Algorithm 5 ModExpEingabe: m ∈ N , m ≥ 2 , x = x` . . . x0 ∈ N und a ∈ Z∗mAusgabe: y ∈ Zm mit y ≡ ax mod m
1: y = 12: for i = ` to 0 by −1 do3: if xi = 1 then4: y := y2 · a mod m5: else6: y := y2 mod m7: end if8: end for9: Ergebnis y
Aus der Analyse dieses Verfahrens folgt:
Theorem 10 Algorithmus 5 lost das Problem der modularen Exponentiation in Zeit O(max{log2 a,log2 m, log2 x}3) .
Die Umkehrfunktionen der modularen Exponentiation geben zwei gute Kandidaten fur Trap-DoorFunktion ab: die diskrete Wurzel, bzw. die Faktorisierung, und der diskrete Logarithmus:
Definition 27 Diskrete WurzelGegeben: m ∈ N , m ≥ 2 , r ∈ N und a ∈ Z∗m .Problem: Bestimme x ∈ Zm mit a ≡ xr mod m , wenn ein solcher Wert x existiert. Existiert keinesolche Losung, so gebe Es existiert keine Losung aus.
Um ein besseres Verstandnis fur das Problem der diskreten Wurzel zu erhalten, mussen wir auf dieStruktur der multiplikativen Gruppe Z∗m naher eingehen.
Theorem 11 Ist p eine Primzahl, so ist Z∗p eine zyklische Gruppe der Ordnung p− 1 .
78

Beweis: Fur Primzahlen p haben wir bereits gesehen, dass |Z∗p| = ϕ(p) = p−1 ist. Um zu erkennen,dass Z∗p zyklisch ist, werden wir zeigen, dass ein Element x der Ordnung p− 1 in Z∗p existiert, d.h.|{xi mod p|i ∈ N}| = p− 1 . Hierfur werden wir alle Elemente aus Z∗p verschiedener Ordnung zahlen.Sei d ∈ N , d > 0 , mit d|p− 1 , dann definieren wir
Sd = { a ∈ Z∗p | a ist von der Ordnung d } .
Es ist einfach zu erkennen, dass die Mengen Sd paarweise disjunkt sind. Es ist bekannt, dass dieseMengen Z∗p partitionieren. Es gilt somit∑
d mit d|p−1
|Sd| = |Z∗p| = p− 1 .
Es gilt:
Lemma 10 Sei p eine Primzahl und f(x) = a0 · xn + · · · + an−1 · x + an eine Polynom mit f 6≡0 mod p , dann hat f(b) ≡ 0 mod p maximal n unterschiedliche Losungen.
Wir wollen nun folgendes Lemma zur Bestimmung der Kardinalitt der Mengen Sd zeigen:
Lemma 11 Sei d ein Wert mit d|p− 1 , dann ist entweder |Sd| = 0 oder |Sd| = ϕ(d) .
Beweis: Sei Sd eine nicht leere Menge und a ∈ Sd , dann sind die Werte a mod p, a2 mod p, . . . , ad modp alle paarweise unterschiedlich, und jedes Element dieser Folge ist eine Losung von xd ≡ 1 mod p .Wir kennen somit d Losungen fur xd ≡ 1 mod p .
Unter der Voraussetzung, dass Sd nicht leer ist, folgt aus Lemma 10:
Sd ⊆ { ai | i ∈ {1, . . . , d} } .
Wir betrachten nun ein festes k ∈ {1, . . . , d} . Ist ggT(k, d) = ` > 1 , dann gilt (ak)d/` = ak/`·d ≡1 mod p . Somit ist ak von einer kleineren Ordnung als d .
Wir betrachten nun den Fall, dass ggT(k, d) = 1 ist, dann existiert ein modulares Inverses ` zu k ,d.h. ` · k ≡ 1 mod d , und somit ist ak·` ≡ a mod p . Folglich gilt fur alle e ∈ {1, . . . , d− 1}
((ak)e)` ≡ (ak·`)e ≡ ae 6≡ 1 mod p.
Somit ist |{(ak)e|e ∈ N}| = d und ak ist ein Element der Ordnung d , d.h. ak ∈ Sd .
Fassen wir zusammen, so erkennen wir:
Sd = { ak | 1 ≤ k ≤ d, ggT(k, d) = 1 } und |Sd| = ϕ(d).
Unter der Annahme, dass fur einige Werte d mit d|p− 1 die Menge Sd leer ist, gilt∑d|p−1
|Sd| <∑
d|p−1
ϕ(d) .
Um die rechte Seite dieser Ungleichung abzuschatzen, benutzen wir das folgende Lemma:
79

Lemma 12 Fur alle positiven ganzen Zahlen gilt∑d|n
ϕ(d) = n .
Beweis: Sei n eine positive ganze Zahl und d ein Wert mit d|n , dann definiere
Rd = { m · i | m = n/d und i ∈ Z∗d } .
Zunachst gilt Rd ⊂ {1, . . . , n} und |Rd| = ϕ(d) .
Sei x ∈ {1, . . . , n} , m = ggT(x, n) , d = n/m und i = x/m . Da x = m · i , n = m · d undm = ggT(x, n) ist, gilt ggT(i, d) = 1 und folglich gilt x ∈ Rd . Wir betrachten nun die Frage, ob xauch in einer anderen Menge Re vorkommen kann, also, ob die Mengen Rd paarweise disjunkt sind.Sei e ein entsprechender Wert, d.h. e|n und x ∈ Re . Dann gibt es Werte i und m mit x = m · i ,n = m · e und ggT(e, i) = 1 . Es gilt
n
e· i = m · i = x = m · i =
n
d· i
und somit d · i = e · i . Da jedoch ggT(e, i) = 1 ist, erhalten wir e|d , und da ggT(d, i) = 1 ist,erhalten wir d|e . Somit gilt e = d — ein Widerspruch. Folglich gehort jedes Element x ∈ {1, . . . , n}zu genau einer Menge Rd und es gilt∑
d|n
|Rd| =∑d|n
ϕ(d) = n .
Es gilt demnach ∑d|p−1
|Sd| <∑
d|p−1
ϕ(d) = p− 1 .
Diese Ungleichung widerspricht jedoch der Beobachtung, dass die Mengen Sd eine Partitionierungder Menge Z∗p darstellen. Folglich ist fur jeden Wert d mit d|p− 1 die Menge Sd nicht leer, diesesgilt insbesondere fur d = p− 1 .
Ein Element x ∈ Z∗p , welches die ganze Gruppe Z∗p aufspannt, d.h.
Z∗p = { xi | i ∈ {1, . . . , p} }
nennen wir Generator von Z∗p .
Definition 28 Diskreter LogarithmusGegeben: m ∈ N , m ≥ 2 , a ∈ Z∗m und x ∈ Z∗m .Problem: Bestimme r ∈ Zm mit a ≡ xr mod m , wenn ein solcher Wert x existiert. Existiert keinesolche Losung, so gebe Es existiert keine Losung aus. Wir nennen diesen Wert r den diskretenLogarithmus von a zur Basis x und schreiben r = dlogx(a) .
Fur eine Primzahl p konnen wir folgende naheliegende Beobachtung zeigen:
Beobachtung 10 Fur eine Primzahl p und einen Generator x von Z∗p gilt xp−1 ≡ 1 mod p .
80

Diese Beobachtung konnen wir in einem ersten Schritt wie folgt generalisieren:
Theorem 12 Kleiner Satz von FermatFur alle Primzahlen p und alle x ∈ Z∗p gilt xp−1 ≡ 1 mod p .
Beweis: Fur alle Elemente x ∈ Z∗p gilt:
Beobachtung 11 Fur alle Primzahlen p und alle x ∈ Z∗p gilt
{x mod p, 2 · x mod p, . . . , (p− 1) · x mod p} = Z∗p .
Beweis: Der Beweis erfolgt uber eine Widerspruchsannahme. Sei x ∈ Z∗p mit {x mod p, 2 · x modp, . . . , (p−1)·x mod p} ⊂ Z∗p , dann existieren c1, c2 ∈ Z∗p mit c1 ·x ≡ c2 ·x mod p und c1 6≡ c2 mod p .Da p eine Primzahl ist, gilt ggT(x, p) = 1 . Somit existiert das multiplikative Inverse x−1 von x .Es gilt
c1 · x ≡ c2 · x mod p =⇒ c1 · x · x−1 ≡ c2 · x · x−1 mod p =⇒ c1 ≡ c2 mod p
im Widerspruch zu c1 6≡ c2 mod p .
Aus dieser Beobachtung folgt
xp−1 · (p− 1)! ≡p−1∏i=1
i · x ≡p−1∏i=1
i ≡ (p− 1)! mod p .
Da p eine Primzahl ist, gilt ggT(p, (p − 1)!) = 1 und somit existiert das multiplikative Inverse((p− 1)!)−1 von (p− 1)! . Es gilt
xp−1 · (p− 1)! ≡ (p− 1)! mod p =⇒ xp−1 ≡ 1 mod p .
Eine Verallgemeinerung vom kleinen Satz von Fermat auf beliebige positive ganze Zahlen p ist auchals der Satz von Euler bekannt.
Theorem 13 Satz von EulerSei n ∈ N mit n ≥ 2 , dann gilt fur alle x ∈ Z∗n
xϕ(n) ≡ 1 mod n .
Beweis: Wir beweisen dieses Theorem zunachst fur Primzahlpotenzen n = p` . Der Beweis erfolgtuber eine Induktion uber ` . Fur ` = 1 folgt die Behauptung unmittelbar aus dem kleinen Satz vonFermat.
Sei ` > 1 , dann gilt ϕ(p`) = (p− 1) · p`−1 = p` − p`−1 = p · (p`−1 − p`−2) und somit
xϕ(p`) ≡ xp·(p`−1−p`−2) ≡(xp`−1−p`−2
)p
mod p` .
Da ϕ(p`−1) = p`−1 − p`−2 ist, folgt aus der Induktionshypothese
xp`−1−p`−2≡ 1 mod p`−1 .
81

Folglich giltxp`−1−p`−2
= 1 + c · p`−1
fur eine geeignete Konstante c ∈ N . Zur Vereinfachung setzen wir z = c ·p`−1 . Aus dem Binomialsatzerhalten wir
(1 + z)p =p∑
i=0
(p
i
)· 1i · zp−i .
Da(pi
)fur i ≥ 1 ein Vielfaches von p ist, gilt fur alle i ∈ {1, . . . , p− 1}(
p
i
)· 1i · zp−i ≡ 0 mod p`
und somit, da p · (`− 1) ≥ ` ist,
xϕ(p`) ≡ 1 + zp ≡ 1 + cp · pp·(`−1) ≡ 1 mod p` .
Dieses beweist den Satz von Euler fur Primzahlpotenzen.
Wir betrachten nun diesen Satz fur beliebige n ∈ N mit n ≥ 2 . Sei n = p`11 ·p
`k
k die Primzahlzerlegungvon n . Zunachst gilt
xϕ(n) ≡ 1 mod p`ii .
Die Behauptung folgt nun unmittelbar aus folgender Beobachtung:
Beobachtung 12 Seien m1,m2 ∈ N mit m1,m2 ≥ 1 und x1, x2 ∈ N , dann gilt
x1 ≡ x2 mod m1 und x1 ≡ x2 mod m2 =⇒ x1 ≡ x2 mod m1 ·m2 .
Abschließend noch ein paar Bemerkungen zur Komplexitat von der Berechnung der diskreten Wur-zel. Fur den Fall, dass m eine Primzahl ist, existiert ein polynomial zeitbeschrankter Las-VegasAlgorithmus zur Berechnung der diskreten Wurzel [AMM77, B70]. Ist die Primzahlzerlegung von mbekannt, so konnen wir diskreten Wurzeln mit Hilfe der Darstellung der Wurzel in der ChinesischenRestklassendarstellung bestimmen.
5.4 Das RSA-Kryptosystem
Das RSA-Kryptosystem ist heute wohl das bekannteste Public-Key Kryptoverfahren. Benannt istdieses Verfahren nach dessen Entwicklern Rivest, Shamir und Adleman [RSA78], die 2002 fur dessenEntwicklung den Turing Award erhielten.
Sei A ein Teilnehmer an dem Public-Key-Kryptoverfahren, dann verfahrt A wie folgt, um den offent-lichen Schlussel wo und den privaten Schlussel wp zu generieren.
1. A wahlt zwei große Primzahlen pA und qA (von zumindest 200 Bits, wobei die Anzahl derBits in pA großer ist als die Anzahl der Bits in qA ).
2. Sei nA = pA · qA und ϕ(nA) = ϕ(pA) · ϕ(qA) = (pA − 1) · (qA − 1) = nA − pA − qA + 1 .
82

3. Wahle eine zufallig Zahl eA ∈ {1, . . . , ϕ(nA)} mit ggT(eA, ϕ(nA)) = 1 und berechne dA =e−1A mod ϕ(nA) .
4. Veroffentliche wo = (nA, eA) und verwahre wp = (pA, qA, dA) .
Zur Verschlusselung eines Plaintextes x berechnet B y = xeA mod nA und sendet den Ciphertexty an A . Zur Entschlusselung berechnet A ydA mod nA .
83

Literatur
[AMM77] L. Adleman, K. Mander, G. Miller, On Taking Roots in Finite Fields, 18th FOCS, 1977, S.175-177.
[B94] F. L. Bauer, Kryptologie, Springer-Verlag, 1994.
[B70] E. R. Berlekamp, Factoring Polynomials over Large Finite Fields, Mathematics of Computations24, 1970, S. 713–735.
[B81] M. Blum, Coin Flipping per Telephon: A Protocol for Solving Problems Impossible, SIGACTNews 15, 1981, 23-27.
[B88] G. Brassard, Modern Cryptology, Springer-Verlag, 1988.
[BCC88] G. Brassard, D. Chaum, C. Crepeau, Minimum Disclosure Proofs of Knowledge, Journal ofComputer and System Science, Vol. 37, No. 2, 1988, 156-189.
[BSW95] A. Beutelspacher, J. Schwenk, K.-D. Wolfenstetter, Moderne Verfahren der Kryptographie,Vieweg 1995.
[C94] D. Coppersmith, The Data Encryption Standard (DES) and Its Strength against attacks, IBMJ. Res. Dev. 38, No. 2, 1994, 243-250.
[CLRS01] T. H. Cormen, C. E. Leiserson, R. L. Rivest, C. Stein, Introduction to Algorithms (secondedition), MIT Press, 2001.
[DH76] W. Diffie, M. E. Hellman, New Directions in Cryptography, IEEE Transactions on InformationTheory, IT-22 No. 6, 1976, S. 644–654.
[EP91] European Patent Application 0 428 252 A2, A System for Controlling Access to BroadcastTransmissions, 1991.
[F68] W. Feller, An Introduction to Probability Theory and its Applications, Vol. 1, 3. Auflage, Wiley,1968.
[FIPS99] Federal Information Processing Standards Publication 46-3, Data Encryption Standard,1999.
[FIPS01] Federal Information Processing Standards Publication 197, Announcing the ADVANCEDENCRYPTION STANDARD (AES), 2001.
[GGM86] O. Goldreich, S. Goldwasser, S. Micali, How to Construct Random Functions, Journal ofthe ACM, Vol. 33, No. 4, 1986, 210-217.
[GK96] O. Goldreich, H. Krawczyk, On the Composition of Zero-Knowledge Proof Systems, SIAMJournal on Computing, Vol. 25, No. 1, 1996, 169-192.
[GMR85] S. Goldwasser, S. Micali, R. Rackoff, The Knowledge Complexity of Interactiv Proof Systems,SIAM J. Comput. 8(1), 1989, 186-208; siehe auch Proc. 17. STOC, 1985, 291-304.
[GMW86] O. Goldreich, S. Micali, A. Wigderson, Proofs that Yield Nothing but their Validity and aMethodology of Cryptographic Protocol Design, Proc. 27 FOCS, 1986, 171-185.
[J02] A. Jakoby, Skript zur Vorlesung: Interaktive Protokolle: Arthur-Merlin-Spiele und andere, Uni-versitat zu Lubeck, Institut fur Theoretische Informatik, Sommersemester 2002.
[K67] D. Kahn, The Codebreakers: The Strory of Secret Writing, Macmillan, 1967.
84

[K98] L. Knudsen, Block Ciphers – A Survey, State of the Art in Applied Cryptography, LNCS 1528,1998, 18-48.
[K87] N. Koblitz, A Course in Number Theory and Cryptology, Springer-Verlag, 1987.
[K86] E. Kranakis, Primality and Cryptography. Wiley-Teubner Series in Computer Science, 1986.
[L81] H. W. Lenstra, Integer Programming with a Fixed Number of Variables, University of Amster-dam, Department of Mathematics, TR 81-03, 1981.
[L86] L. A. Levin, Average Case Complete Problems, SIAM Journal on Computing, Vol. 15, 1986,285-286.
[L68] C. L. Liu, Introduction to Combinatorial Mathematics, McGrawHill, New York, 1968.
[M03] R. Matthes, Algebra, Kryptologie und Kodierungstheorie, Fachbuchverlag Leipzig, 2003.
[N91] M. Naor, Bit Commitment Using Pseudorandomness, Journal of Cryptology, 1991, 151-158.
[NPS99] M. Naor, B. Pinkas, R. Sumner, Privacy Preserving Auctions and Mechanism Design, 1stACM Conference on Electronic Commerce, 1999, S. 129-139.
[RSA78] R. Rivest, A. Shamir und L. Adleman, A Method for Obtaining Digital Signatures and Public-Key Cryptosystems, Communications of the ACM 21, 1978, S. 120-126.
[S90] A. Salomaa, Public-Key Cryptology, Springer-Verlag, 1990.
[S96] J. Schwenk, Conditional Access, in: taschenbuch der telekom praxis 1996, B. Seiler, VerlagSchiele & Schon, Berlin.
[S79] A. Shamir, How to Share a Secret, Communications of the ACM 22, 1979, S. 612-613.
[S82] A. Shamir, A Polynomial Time Algorithm for Breaking the Merkle-Hellman Cryptosystem, 23rdFOCS, 1982, S. 145-152.
[S49] C. E. Shannon, Communication Theory of Secrecy Systems, Bell Syst. Tech. J. 28, 1949, S.379-423.
[Y82] A. Yao, Theory and applications of trapdoor functions, 23rd FoCS, 1982, S. 80–91.
[Y86] A. Yao, How to Generate and Exchange Secrets, 27rd FoCS, 1986, S. 162–167.
85

![C. Bourauel - ukbonn.de · 2019. 12. 17. · 100 GPa 400 ε= 0,2 200 σ = σ = [MPa] Diamant 1.200.000 Elastizitätsmoduln versch. Materialien Aluminiumoxid 380.000 Edelstahl 200.000](https://static.fdokument.com/doc/165x107/60a9d1c49f16a214c0195088/c-bourauel-2019-12-17-100-gpa-400-02-200-f-f-mpa-diamant-1200000.jpg)
![Κελαιο 4 Σ ]εδαση Βσε ν Δεδομννusers.sch.gr/delistavrou/.dimiourgies/DBepalK4/k4theoria.pdf · Απρίλιος 2015 Δελησταύρου Κωνσταντίνος](https://static.fdokument.com/doc/165x107/6124e351b37eca4dab68d671/-4-f-f-usersschgrdelistavroudimiourgiesdbepalk4.jpg)