Christopher Beck 28. Dezember 2018 - ETG Kurzschluss€¦ · Vorwort LiebeLeser,...

Formelsammlung

Formelsammlung Elektrotechnik

Christopher Beck

28. Dezember 2018

Beck

Formelsammlung Elektrotechnik

Christopher Beck

28. Dezember 2018

Diese Formelsammlung ist noch nicht vollendet und steht daher unter ständigerWeiterentwicklung und Verbesserung. Bei Fragen zum aktuellen Stand oder nach einer

neueren Version, einfach per E-Mail melden.

Auflage: 0, Version: 0.1.7 Stand: 28. Dezember 2018Diese Formelsammlung erhebt keinen Anspruch auf Richtigkeit und Vollständigkeit.

Verbesserungsvorschläge sowie gefundene Fehler nehme ich aber gerne entgegen.eMail: [email protected]

GPG-Fingerprint: AE1A C931 2BAF C5A1 F0BE 2083 3117 1121 2F9D 4F14

2

VorwortLiebe Leser,

Ihr haltet nun eine (noch unvollständige) Formelsammlung in den Händen, die wäh-rend der Prüfungsvorbereitung in diversen Fächern an der Friedrich-Alexander-UniversitätErlangen-Nürnberg entstanden ist. Die Idee für die Formelsammlung entstand in derVorlesung zu GET1, da zu dieser Prüfung alle Unterlagen erlaubt waren und war an-fangs nur für den Eigengebrauch gedacht. Ein herzlicher Dank geht hier an Anne Sacher,die diese Formelsammlung ebenfalls zur Prüfungsvorbereitung nutzte und viele sinnvolleAnregungen lieferte. Nachdem auch ein Teil für die Folgevorlesung GET2 hinzugefügtwurde und die Formelsammlung auch von anderen Kommilitonen genutzt wurde, lag esauf der Hand, diese weiter zu führen.

Der momentane Stand dieser Formelsammlung ist noch weitab vom Zustand ”Aus-gereift“ entfernt, was bedeutet, dass viele Teile unvollständig sind und sicherlich vieleFehler enthalten sind. Ich bin sehr bemüht, diese Missstände zu beheben, doch reicht dieZeit neben der Arbeit hierfür oft nicht aus. Deswegen bin ich auf Eure Mithilfe angewie-sen: Gebt mir Feedback! Sowohl bei gefundenen Fehlern, als auch bei Wünschen oderÄnderungsvorschlägen. Ich werde mich bemühen, diese einzuarbeiten und diese Formel-sammlung so weiter zu verbessern. Schreibt mir einfach eine E-Mail und gebt dabei bittedie Version und das Datum der Ausgabe an. Vielen Dank!

Christopher Beck

3

DankeFür Feedback, gefundene Fehler und Verbesserungsvorschläge danke ich

Cornelia Speidel, Bastian Bauer

Ein besonders großer Dank geht an ...... Anne Sacher, die, wie im Vorwort bereits erwähnt, in der Anfangszeit viele Verbes-

serungsvorschläge lieferte.... Frau Ingrid Ullmann, die im weiterem Verlauf viel durch Diskussion beigetragen

und einige Fehler gefunden und verbessert hat.... Stefan Walter, der viel zu den Hamiltonzahlen beigetragen hat.

i

Inhaltsverzeichnis

1. Grundlagen der Elektrotechnik 31.1. GET1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3

1.1.1. Elektrostatik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31.1.2. Stationäres Strömungsfeld . . . . . . . . . . . . . . . . . . . . . . 61.1.3. Einfache elektrische Netzwerke . . . . . . . . . . . . . . . . . . . 81.1.4. Das stationäre Magnetfeld . . . . . . . . . . . . . . . . . . . . . . 91.1.5. Das zeitlich veränderliche elektromagnetische Feld . . . . . . . . . 121.1.6. Wechselspannung und Wechselstrom . . . . . . . . . . . . . . . . 141.1.7. Energie und Leistung bei Wechselspannung . . . . . . . . . . . . 16

1.2. GET2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171.2.1. Quelle und Last . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171.2.2. Berechnung einfacher Schaltungen . . . . . . . . . . . . . . . . . 181.2.3. Netzwerkanalyse . . . . . . . . . . . . . . . . . . . . . . . . . . . 201.2.4. Zweipole . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231.2.5. Mehrpolige Netzwerke . . . . . . . . . . . . . . . . . . . . . . . . 251.2.6. Zweitore . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 251.2.7. Fourier-Reihen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27

1.3. GET3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 311.3.1. Laplace-Transformation . . . . . . . . . . . . . . . . . . . . . . . 311.3.2. Nichtlineare Bauelemente . . . . . . . . . . . . . . . . . . . . . . 341.3.3. Einschwingvorgänge . . . . . . . . . . . . . . . . . . . . . . . . . 351.3.4. Fehlerrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 361.3.5. Operationsverstärker (OpAmps) . . . . . . . . . . . . . . . . . . . 371.3.6. Messschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . 37

2. Halbleiterbauelemente 392.1. Grundlagen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39

2.1.1. Intrinsischer Halbleiter . . . . . . . . . . . . . . . . . . . . . . . . 392.1.2. Dotierter Halbleiter . . . . . . . . . . . . . . . . . . . . . . . . . 392.1.3. Ladungsträger im Halbleiter in elektrischem Feld . . . . . . . . . 402.1.4. Halbleiterdioden . . . . . . . . . . . . . . . . . . . . . . . . . . . 412.1.5. Metall-Isolator-Halbleiter-Kondensator . . . . . . . . . . . . . . . 412.1.6. MOSFET . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 432.1.7. Optoelektronik . . . . . . . . . . . . . . . . . . . . . . . . . . . . 44

iii

Inhaltsverzeichnis

3. Schaltungstechnik 453.1. Grundlegende Bauelemente . . . . . . . . . . . . . . . . . . . . . . . . . 45

3.1.1. Diode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 453.1.2. Bipolartransistpr . . . . . . . . . . . . . . . . . . . . . . . . . . . 45

4. Maxwellsche Gleichungen 474.1. Integrale Darstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 474.2. Differentielle Form . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 484.3. Maxwellgleichungen im Frequenzbereich . . . . . . . . . . . . . . . . . . 494.4. Randbedingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 504.5. Magnetisches Vektorpotential und Eichungen . . . . . . . . . . . . . . . 51

5. Elektromagnetische Felder 535.1. Theorie elektromagnetischer Felder . . . . . . . . . . . . . . . . . . . . . 53

5.1.1. Elektrostatik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 535.1.2. Stationäres Strömungsfeld . . . . . . . . . . . . . . . . . . . . . . 575.1.3. Stationäres Magnetfeld . . . . . . . . . . . . . . . . . . . . . . . . 575.1.4. Elektrodynamik . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60

6. Hochfrequenztechnik 616.1. PB . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61

6.1.1. Wellenausbreitung . . . . . . . . . . . . . . . . . . . . . . . . . . 626.1.2. Bauteile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 676.1.3. Leitungstheorie . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71

6.2. HF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 786.2.1. Streuparameter . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78

6.3. Antennen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 806.3.1. Antennentypen . . . . . . . . . . . . . . . . . . . . . . . . . . . . 80

7. Photonik 817.1. Akives Medium . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 817.2. Gauß-Strahl . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 837.3. Resonatoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 837.4. Gaslaser . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 857.5. Laserdioden . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 857.6. Lichtwellenleiter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 857.7. Photonik 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86

7.7.1. Polarisation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 86

8. Regelungstechnik 878.1. Regelungstechnik A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87

8.1.1. Modellbildung . . . . . . . . . . . . . . . . . . . . . . . . . . . . 878.1.2. Stabilitätskriterien und Systemtheorie . . . . . . . . . . . . . . . 888.1.3. Reglerentwurf . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90

iv

Inhaltsverzeichnis

8.1.4. Regelkreise . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93

A. Anhang 95A.1. Geometrische Zusammenhänge . . . . . . . . . . . . . . . . . . . . . . . 95A.2. (Natur)konstanten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95A.3. Einheiten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 95A.4. Vektorrechnung und Koordinatensysteme . . . . . . . . . . . . . . . . . . 96

A.4.1. Allgemeine Definitionen . . . . . . . . . . . . . . . . . . . . . . . 96A.4.2. Karthesische Koordinaten . . . . . . . . . . . . . . . . . . . . . . 96A.4.3. Zylindrische Koordinaten . . . . . . . . . . . . . . . . . . . . . . 96A.4.4. Kugelkoordinaten . . . . . . . . . . . . . . . . . . . . . . . . . . . 96

A.5. Mathematik GET1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 97A.5.1. Geometrische Formeln . . . . . . . . . . . . . . . . . . . . . . . . 97A.5.2. Wichtige Stammfunktionen . . . . . . . . . . . . . . . . . . . . . 97A.5.3. Komplexe Zahlen . . . . . . . . . . . . . . . . . . . . . . . . . . . 97

A.6. Mathematik GET2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98A.6.1. Mathematische Methoden . . . . . . . . . . . . . . . . . . . . . . 98A.6.2. Diverses . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98

A.7. Laplace . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99A.7.1. Laplace-Korrespondenzen . . . . . . . . . . . . . . . . . . . . . . 99A.7.2. Laplace-Sätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100

A.8. Smith-Chart . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101A.9. Mathematik RT-A . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 102A.10.Vektoranalysis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 103

A.10.1. Umformungen grad . . . . . . . . . . . . . . . . . . . . . . . . . . 103A.10.2. Umformungen div . . . . . . . . . . . . . . . . . . . . . . . . . . 103A.10.3. Umformungen rot . . . . . . . . . . . . . . . . . . . . . . . . . . . 103A.10.4. Laplace-Operator . . . . . . . . . . . . . . . . . . . . . . . . . . . 104A.10.5. Integralsätze . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104

Literaturverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105Stichwortverzeichnis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106

v

Abbildungsverzeichnis1.1. Stern-Dreieck-Umwandlung . . . . . . . . . . . . . . . . . . . . . . . . . 191.2. Stern-Dreieck-Umwandlung . . . . . . . . . . . . . . . . . . . . . . . . . 201.3. Kondensator mit Anfangswertgenerator . . . . . . . . . . . . . . . . . . . 321.4. Spule mit Anfangswertgenerator . . . . . . . . . . . . . . . . . . . . . . . 321.5. Dezibel Werte (20 lg (·)) . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

6.1. Brechung und Fresnelgesetze . . . . . . . . . . . . . . . . . . . . . . . . . 666.2. HF-ESB Widerstand . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 676.3. HF-ESB Kondensator . . . . . . . . . . . . . . . . . . . . . . . . . . . . 686.4. HF-ESB Spule . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 696.5. Lecherleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 74

8.1. Ortskurve . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 928.2. Bode-Diagramm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 928.3. Strecke im Regelkreis . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 938.4. allg. Zwei-Freiheitsgrade-Regelung . . . . . . . . . . . . . . . . . . . . . . 938.5. Zwei-Freiheitsgrade-Regelung mit Störgrößenaufschaltung . . . . . . . . . 938.6. Kaskadierte Zwei-Freiheitsgrade-Regelung . . . . . . . . . . . . . . . . . 93

1

1. Grundlagen der ElektrotechnikEs werden Kenntnisse von Vektorrechnung und verschiedenen Koordinatensystemenvorrausgesetzt. Eine Übersicht dazu findet sich in Anhang A.4

1.1. GET1

1.1.1. Elektrostatik

Coulombsches Gesetz ()

~F =QQ14π�0

~r

r3Es gilt für den Ortsvektor ~r: ~r = ~rP −~rQ.

~E-Feld der Punktladung (1-1.3)

~E =Q

4π�

~r

r3

~E =Q

4π�r2~eρ

Q

~E

Bekommt man auch durch In-tegration um eine Punktladung Q heraus(dielektrische Flussdichte)

Kraft auf eine Ladung im ~E-Feld (1-1.2)

~F = Q~E

Linienladungsdichte λ ()

λ =dQ

d l

Q =

ˆ

l

λ d l

3

1. Grundlagen der Elektrotechnik

Flächenladungsdichte σ ()

σ =dQ

dA

Q =

¨

A

σ dAσ entspricht ~D bei leitenden Oberflächen.

Raumladungsdichte ρ ()

ρ =dQ

dV

Q =

˚

Vk

ρ0 dV

Meist wird die so erhaltene Ladung mir derberechneten Ladung aus dem elektrischemFluss gleichgesetzt. Man betrachte hier dieMaxwellgleichungen. Auf diese Weise erhältman das ~E-Feld.

Permittivität ()

� = �0�r

�r = (1 + χe)

Flussdichte ()

~D = � ~E� = �r�0. �0 ist eine Naturkonstante.

Elektrischer Fluss I ()

ψ =

¨

AK

~D · d ~A ψ bezeichnet den elektrischen Fluss aus derFläche A.

Elektrischer Fluss II ()

Q =

‹

AK

~D · d ~A = ψ

Es wird nun das Hüllflächenintegral berech-net. ψ bezeichnet den elektrischen Fluss ausder Fläche A. Nimmt man Q an, integiert dienur von ρ abhängige Flussdichte über A sokann man nach dem Feld der Punktladungauflösen.

4

1.1. GET1

Elektischer Fluss im Raum ()

‹~D · d ~A = 0

Umläuft man eine geschlossene Fläche (nichtüber einen elektisch geladenen Körper!) soist ψ = 0. Also was reingeht geht auch raus.

Flussdichte auf leitenden Oberflächen ()

Dn = ~n · ~D = �~n · ~E = σ

Heißt auf ner leitenden Oberfläche ent-spricht die Flussdichte der Flächenladungs-dichte

Elektrische Spannung ()

U12 = ϕ12 =

P2ˆ

P1

~E · d~s = ϕ1 − ϕ2

0 =

˛~E · d~s

Aus letzerem folgt die Maschenregel. Dervermeindliche Vorzeichenfehler (Obergrenze- Untergrenze) begründet sich aus der Defi-

nition des Potentials ϕ1 = −P1´P0

~E · d~s.

Kapazität eines Kondensators ()

C =Q

U=

�‚AK

~E · d ~A´s

~E · d~s

~E wird durch den elektrischen Fluss be-stimmt. Danach setzt man C = Q´

s

~E·d~smit

dem zuvorberechneten ~E. Dies setzt aller-dings Kenntniss der Feldverteilung vorraus.

Energie im Kondensator ()

W =1

2CU2 =

1

2QU

=1

2

˚~E ~D dV

Dies folgt durch Integration. Letzteres ausder Energiedichte

Energiedichte (I-1.101)

we =1

2~E · ~D

Kondensatorbauformen

Achtung! Hier finden sich teilweise Näherungsformeln!

5


Parallelschaltung

Cges =∑

CK

Reihenschaltung1

Cges=∑ 1

Ck

Plattenkondensator

C =�A

d

Kugelkondensator

C = 4π�ba

b− aZylinderkondensator

C =2π�l

ln(

dida

)

Paralleldrahtleitung

C =π�l

ln(

a+√a2−d2d

)

Horizontaler Draht

C =2π�l

ln(4hd

)vertikaler Draht

C =2π�l

ln(

2ld

√4h+l4h+3l

)

1.1.2. Stationäres Strömungsfeld

Elektrischer Strom ()

I =dQ

dt

I = −dQdt

Ladung pro Zeit. Für die Erklärung des Vor-zeichens siehe Anhang ??

Ohmsches Gesetz ()

κ~E = ~J

U = RI

Letztere Form erhällt man durch Integrati-on. κ ist die spezifische Leitfähigkeit

Elektrischer Widerstand ()

R =l

κA

κ ist eine Materialkonstante (die spezfischeLeitfähigkeit)

6

1.1. GET1

Leitwert ()

G =1

R

Spezifischer Widerstand ()

ρR =1

κρR(T ) = ρR,20◦C(1 + α∆T )

ρR(T ) = ρR,20◦C(1 + α∆T + β(∆T )2)

In Letzteren Formeln wird die Änderung vonρ durch die Temperatur approximiert.

Stromdichte ()

¨~J · d ~A = I

‹~J · d ~A = 0

Aus letzterem folgt die Knotenregel (wasreinfließt muss auch wieder raus). Achtung:Es gibt auch die Kontinuitätsgleichung I =‚A

~J · d ~A, welche für Elektroden untersch.

Potentials gilt.

Elektrische Leistung ()

P = I2R =U2

R= UI

Elektrische Energie ()

WE =

ˆ

t

P d t

Verlustleistungsdichte (I-2.53)

P =

˚

V

pv dV =

˚V

~E · ~J dV

7


1.1.3. Einfache elektrische Netzwerke

Maschenregel ()

∑Masche

U = 0 Folgt aus¸C

~E d~s = 0

Knotenregel ()

∑Knoten

I = 0 Folgt aus‚A

~J d ~A = 0

Spannungsteiler ()

U1U2

=R1R2

U = U1 + U2 I = I1 = I2

U1 = UR1

R1 +R2

Stromteiler ()

I1I2

=R2R1

U = U1 = U2 I = I1 + I2

I1 = IR2

R1 +R2

Leistungsanpassung ()

RL = Ri

PLmax =U204Ri

Bei der Spannungsquelle mit U0 mit dem In-nenwiderstand Ri und dem LastwiderstandRL

Wirkungsgrad η ()

η =PLPges

· 100%

8

1.1. GET1

Reihenschaltung von R

Rges =∑

Rk

Parallelschaltung von R

1

Rges=∑ 1

Rk

Parallelschaltung zweier Widerstände ()

Rges =R1R2R1 +R2

1.1.4. Das stationäre Magnetfeld

Magnetische Flussdichte ()

~B = µ ~H

[B] =V s

m2

[H] =A

m

Oersted’sches Gesetz ()

˛~Hd~s = I

Das Gesetz gilt für einen Leiter. Umkreistman mehrere Leiter enthällt man statt Idie Durchflutung Θ. Im Dauermagneten giltin Folge des nicht vorhandenen Stromes¸~Hd~s = 0. Achtung beim Dauermagneten!

Durchflutung Θ ()

˛~H(ρ)d~s = Θ =

¨

A

~Jd ~A

Θ =∑n

In = NI

Bei Spulen: N ist die Wicklungszahl

9


Kraft auf einen Leiter im Magnetfeld ()

~F = I

ˆ[d~r × ~B(~r)]

• Leiter zeigt in Richtung ~er

• ~B bestimmen

• Kreuzprodukt berechnen

• auf Leiterlänge integrieren

Lorentzkraft ()

~F = q~v × ~B

Magnetischer Fluss ()

Φ =

¨

A

~B · d ~A

Integrieren um einen Magneten ()

‹

A

~B · d ~A = 0Das beweist, dass es keine magnetischen Mo-nopole gibt

magnetische Spannung ()

Vm12 =

P2ˆ

P1

~H · d~s

Vm = RMΦ = Θ

Analoge Behandlung wie im elektrischemFall

magnetischer Widerstand (Reluktanz) ()

Rm =l

µA

10

1.1. GET1

magnetischer Leitwert ()

Λm =1

Rm= AL

L = N2AL, wenn perfekt gekoppelt

Feldstärke eines Linienleiters ()

~H =I

2πρ~eφ außerhalb

~H =Iρ

2πa2~eφ innerhalb

Man erhällt sie durch Anwendung des Oer-stedschen Gesetztes

Durchflutung einer Spule ()

Θ = NI

Induktivität ()

L =

N˜A

~B · d ~A

I=NΦAI

= N2AL

Φ = NΦA. ΦA ist der Fluss in einer Leit-erschleife mit d ~A als Kernquerschnittsfläche.Bei symmetrischen Anordnungen nimmtman I an, berechnet ~H und daraus dannΦ. Letztlich kürzt sich dann I wieder weg(analog zur Kapazität)

Gegeninduktivität ()

M =Φ21i1

= N1N2AL

Analog zur Induktivität, nur dass der Flussder Wicklung 2 der durch die Wicklung 1fließt genommen wird sowie der Strom derWicklung 1.

Induktivität einer Doppelleitung (1-5.68)

L = lµ0π(1

4+ ln

b

a)

Länge l, Abstand b und Leiterradius a

Spulen

Achtung! Hier finden sich teilweise Näherungsformeln!

11


Toroidspule

~H = ~eϕNi

2πρ

Zylinderspule

~H = ~exNi

l

Induktivitäten versch. Anordnungen

Ringspule

L = µN2A

2πrm

Zylinderspule

L = µN2A

l

Koaxialleitung1

L = µl

2πln

(DaDi

)

Paralleldrahtleitung

L ≈ µ lπln

(2a

D

)

Kreiswindung

L = µ0D

2

[ln

(D

d

)+ 0, 08

]

1.1.5. Das zeitlich veränderliche elektromagnetische Feld

Bewegter Leiter im ~B - Feld ()

E = vxB

U12 = lvxB = −dΦ

dt

Faraday’sches Induktionsgesetz ()

˛

C

~E ′ · d~s = − ddt

¨

A

~B · d ~A

u(t) = Ri(t) = −dΦdt

= −N dΦAd t

Die Fläche A umschließt die Kontur C. ~E ′ =~E bei ruhender Kontur. ~A und C sind rechts-händig miteinander verknüpft

1Achtung, die Innere Induktivität des Innenleiters bleibt hier unberücksichtigt!

12

1.1. GET1

Koppelfaktoren ()

KL =Φ21Φ11

=µ

L11

k =M√L11L22

Gegenindiktivität einer Doeppelleitung (1-6.38)

Φ21r =

¨

A2

~B · d ~A = µ0i12π

l lnb

a

Φ21l = −µ0i12π

l lnd

c

Φ21 =µ0i12π

l lnbc

ad

L21 =Φ21i1

=µ0l

2πlnbc

ad

Seite 255. Erhällt man durch stures ausin-tegrieren mit dem Megnetfeld einer Doppel-leitung ~H = ~eϕ−i12πρ

Energiegehalt des Feldes (6.56)

Wm =1

2L11I

21 +MI1I2 +

1

2L22I

22

Dies gilt für einen Trafo mit 2 Wicklungen.Für eine einfache Spule entfallen die Kom-ponenten mit L22 und M .

Energiedichte (I-6.63 I-6.66)

wm =

B̂

0

H · dB

=1

2~H · ~B

Wm =

˚V

wm dV =1

2

˚V

~H · ~B dV

Daher hat man dann auch die Hysteresever-luste

13


Das Übersetzungsverhältniss beim idealen Übertrager (I-6.99)

upus

=isip

= ü

ü =NpNs

upip = usis

Dies gilt beim idealem Übertrager.

Die Widerstandstransformation (I-6.100)

Re =upip

= üusü

is= ü2R2

Hier wird der Widerstand R2 der Sekundär-seite als Re ersetzt, also währe Re statt desÜbertragers angeschlossen.

Trafogleichung (1-6.80)

u0 = R1i1 + L11d i1d t

−M d i2d t

u3 = R2i2 −Md i1d t

+ L22d i2d t

Bei Last ohne Quelle an der Sekundärseitegilt u3 = 0.

Trafogleichung mit Ersatzschaltbild (1-6.86)

u0 = R1i1 + (L11 −M)d i1d t

−M d(i2 − i1)d t

0 = R2i2 −Md(i1 − i2)

d t+ (L22 −M)

d i2d t

Da kommt man drauf, wenn man das Induk-tionsgesetz einfach mal anwendet und zu denzwei Gleichungen, die entstehen, ein ESB zubaut.

Zusammenhänge zwischen Strom und Spannung

Bauteil Widerstand Spule KondensatorZeitabhängig u(t) = Ri(t) uL = Ld iLd t iC = C

duCd t

Zeitunabhängig U = RI UL = 0 IC = 0

1.1.6. Wechselspannung und Wechselstrom

Da dieses Kapitel in [3] und der Vorlesung GET II vertieft wird, ist es ratsam sich Ka-pitel 1.2 ebenfalls anzuschauen.

14

1.1. GET1

Gleichrichtwert (2-1.9)

|u| = 1T

t0+Tˆ

t=t0

|u(t)| d t Mittelwert aus dem Betrag

Effektivwert ()

XEff =

√√√√√ 1T

T̂

0

x2(t) d t

=|X̂|√2

Für eine beliebige Größe x(t). Letztere For-mel gilt für Komplexe Größen

Die Komplexe Spannung ()

u(t) = Re(u(t)) + jIm(u(t))

= û[cos (ωt+ ϕU) + j sin (ωt+ ϕU)]

= ûejϕU ejωt

Die Größe u kann als komplexe Größ u ge-schrieben werden. TODO: Da des Zeigerdia-grambild rein

Schwingkreise ()

ω0 =1√LC

Dies ist die Resonanzfrequenz sowohl für denParallelschwingkreis als auch für den Seri-enschwingkreis. Hier verschwindet beim Se-rienschwingkreis =(Z) und beim Parallel-schwingkreis =(Y )

Schwingkreisgüte ()

Qs =1

R

√L

C

Die Güte taucht ebenfalls in der KomplexenFrequenz s auf.

Bauteil Impedanz AdmittanzWiderstand Z = R Y = 1

R

Spule Z = jωL Y = 1ωL

Kondensator Z = 1jωC

Y = ωC

15


Allgemeines ()

û = Zî∑m

ûm = 0∑k

îk = 0

Z =1

Y

Es gelten die gleichen Gesetzten wie in Kap.3. Die Phase des Stromes zur Spannung än-dert sich bei Z = R nicht.

Berechnungsschritte

• Gleichung nach Tabelle 2.1 [2, S.33] mit den größen aus obiger Tabelle aufstellen.

• auf gesuchte größe Auflößen

• Größe in Polarform bringen

• Zeitabhängige Phase eωt anmultiplizieren

• Zahl auf |z|(cosωt+ ϕ+ sinωt+ ϕ) bringen

•

1.2. GET2

Wirkleistung ()

P =U2effRL

= I2effRL =1

2ûî cos (ϕu − ϕi)︸︷︷︸

γ

γ wird Leistungsfaktor genannt und vor al-lem bei Antriebsmaschinen angegeben.

Blindleistung ()

Q =1

2ûî sin (ϕu − ϕi)

1.2. GET2Beachten Sie bitte, dass sich in [3] die verwendeten Symbole geändert haben. Auchbezieht sich dieser Teil noch auf die Vorlesung GET2 von Prof. Schmidt und dessenLehrbuch.

Größe Buch 1-2 Buch 3komplexe Spannung û U

komplexer Strom î I

1.2.1. Quelle und Last

Umrechnung von Quellen ([3], Formel 1.6)

U q = Iq · Zi

Zi =1

Y i

Umrechnung einer realen Spannungs- undStromquelle ineinander.

Leistungsanpassung ([3], Formel 1.14)

Pmax =1

8

|U q|2

Re(Zi)für ZL = Z∗i

Pmax =1

8

|Iq|2

Re(Y i)für Y L = Y ∗i

Dies gilt entsprechend der Leistungsanpa-sung für Gleichstrom und -spannung für dasKomplexe.

17


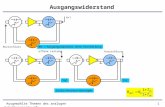
Ersatzquellen ([3], Formel 1.18-1.20)

I = 0 → U = ULL = U q =IqY i

U = 0 → I = IKS = Iq =U qZi

Impedanzbestimmung → −UI

= Zi =1

Y i

• Leerlaufspannung bestimmen

• Kurzschlussstrom bestimmen

• Impedanz bestimmen

2 dieser Fälle müssen ausgeführt werden,letzterer klappt nicht bei gesteuertenQuellen. Es langt da die direkt aneinanderleigenden Widerstände zu nehmen.

Wirkungsgrad ()

η =PLPWV

=4RLRi

(Ri +RL)2 + (Xi +XL)2

Damit kann man einiges abürzen

1.2.2. Berechnung einfacher Schaltungen

Ähnlichkeitssatz ([3], Formel 2.13)

InUq

=InSU qS

In = U qInSU qS

• Annahme eines Stromes InS

• Rückrechnung zur Quellspannung U qS

• Berechnung von In

Achtung: dies gilt nur für linear abhängigeNetzwerke. Bei mehreren Quellen musseinzeln berechnet und überlagert werden.

Zu Quellenversatz und -substitution siehe [3, S. 35ff].

18

1.2. GET2

Satz von Miller (Admittanz) ([3], Formel 2.16)

V U =U2U1

Y p1 =I ′1U1

= Y p(1− V U)

Y p2 =I ′2U2

= Y p(1−1

V U)

Siehe [3, S. 38f], dort wird das durch die Bil-der klar

Satz von Miller (Impedanz) ([3], Formel 2.16)

V U =I2I1

Zs1 =U ′1I1

= Zs(1 + V I)

Zs2 =U ′2I2

= Zs(1 +1

V I)

Siehe [3, S. 39f], dort wird das durch die Bil-der klar

Stern-Dreieck-Umwandlung ([3], Abb. 2.17)

Y 12 =Y 10Y 20∑

Y

Y 13 =Y 10Y 30∑

Y

Y 23 =Y 20Y 30∑

Y

Y10

Y30

Y20

Y12Y13

Y23

Abbildung 1.1.: Stern-Dreieck-Umwandlung

Gilt nur bei konstanter Frequenz!

19


Dreieck-Stern-Umwandlung ([3], Abb. 2.18)

Z10 =Z12Z13∑

Z

Z20 =Z12Z23∑

Z

Z30 =Z13Z23∑

Z

Z10

Z30

Z20

Z12 Z13

Z23

Abbildung 1.2.: Stern-Dreieck-Umwandlung

Gilt nur bei konstanter Frequenz!

Theorem von Tellegen ([3, S. 51])

UT · I = IT ·U = 0UT · I∗ = (I∗)T ·U = 0

Dies besagt, dass die Summe aller Zweiglei-stungen im eingeschwungenen stationäremZustand im zeitlichen Mittel null sind.

Reziprozitäts-Theorem ([3], Formel 2.46)

U1bI1a + U2bI2a = U1aI1b + U2aI2bDes heißt auch Umkehrsatz. Siehe [3, S. 53].

1.2.3. Netzwerkanalyse

Maschenstromverfahren

Achtung: Das Maschenstromverfahren funktioniert nur bei Spannungsquellen, Strom-quellen sind nach Kap. 1.2.1 umzurechnen!

20

1.2. GET2

Vorgehensweise

• Maschen und Maschenströme wählen

• Beziehungen zw. Maschen- und Zweigströmen aufstellen (Inzidenzmatrix)

• Maschenregel anwenden (Gleichung mit Impedanzmatrix, [3], Formel 3.8)

• Gleichungssystem lösen

• Zweigströme mit Inzidenzmatrix berechnen

• Zweigspannungen ermitteln

Inzidenzmatrix ([3], Formel 3.3)

A

Jedes Element aij enthällt das Vorzeichendes die Impedanz i durchfließenden Ma-schenstromes (Spalte j).

Impedanzmatrix ()

∑ZM1 · · ·

∑ZM1|Mn

... . . . ...∑ZMn|M1 · · ·

∑ZMn

= ZM

• In den Hauptdiagonalen die Summeder in der Masche Mn vorkommendenImpedanzen.

• Die Elemente außerhalb werden durchdie Summe der Impedanzen gebildetdie von den angrenzenden Maschen-strömen gemeinsam durchflossen wer-den.

Impedanzmatrix-Gleichung ([3], Formel 3.8)

ZM ·

IM1...IMn

=∑U qM1...∑U qMn

Das Vorzeichen der in einer Masche vorhan-denen Spannungsquellen UqMn ist entspre-chend des Zählpfeilsystems zu wählen.

21


Zweigströme ([3], Formel 3.3)

I1...In

= A ·IM1...IMn

I = A · IM

IMn sind die Maschenströme.

Knotenpotentialverfahren

Achtung: Das Knotenpotentialverfahren funktioniert nur bei Stromquellen, Spannungs-quellen sind nach Kap. 1.2.1 umzurechnen!

Vorgehensweise

• Referenzknoten und K − 1 Knotenspannungen festlegen

• Beziehungen zwischen Knoten- und Zweigspannungen aufstellen (Inzidenzmatrix)

• Kirchhoffsche Knotenregel auf K − 1 Knoten anwenden mit Knotenspannungenals Variablen

• Lineares Gleichungssystem lösen

• Zweigspannungen über Inzidenzmatrix aus den Knotenspannungen berechnen

• Zweigströme ermitteln

Inzidenzmatrix ()

Vom Knoten weg: −1, zum Knoten hin +1.

Admittanzmatrix ()

∑Y K1 · · · −

∑Y K1|Kn

... . . . ...−∑Y Kn|K1 · · ·

∑Y Kn

= YK

• In den Hauptdiagonalen stehen dieSummen der an den jeweiligen Knotenangrenzenden Admittanzen

• In die anderen Elemente wird die ne-gative Summe der sich zwischen denjeweiligen Knoten befindenden Admit-tanzen eingetragen

22

1.2. GET2

Admittanzmatrix-Gleichung ()

YK ·

UK1...UKn

=∑IqK1...∑IqKn

Vorzeichen der Quelle: Zum Knoten +, vomKnotrn −Knotenspannungen ()

1.2.4. Zweipole

Komplexe Frequenz ([3], Formel 4.9)

s = σ + ω

σ = − ω02Q0

σ bezeichnet die Dämpfungskonstante.

Mithilfe der komplexen Frequenz lassen sich Impedanz und Admittanz nach folgenderTabelle schreiben:

R L CImpedanz R sL 1

sC

Admittanz 1R

1sL

sC

23


Komplexe Impedanzfunktion

Man Bildet von einer Schaltung am einfachsten die Kettenbruchfunktion. Aus dieserlässt sich der Aufbau der Schaltung auch leicht ablesen.

Realisierbarkeit einer Impedanzfunktion als Schaltung

• Pol- und Nullstellen wechseln sich ab

• Alle koeffizienten sind positiv und reel

• Die Grade des Zählers und Nenners unterscheiden sich um maximal ±1

• Polstellen müssen einfach sein

Normierung ([3], Formel 4.71)

sn =s

ω0

Ln =ω0L

R0Cn = ω0CR0

Diese Normierung führt man als Rechen-erleichterung bei der Anwendung des Fo-ster’schen Theorems durch

Normierte Impedanzfunktion durch Partialbruchzerlegung Z(s) ()

Zn(s) = a∞s+n∑

i=1

Ais

s2 + p2i+A0s

nachdem man die Impedanzfunktion auf die-se Form gebracht hat kürzt man die Mittel-teile mit deren Zähler und erhällt eine Formaus der man den Schaltungsaufbau heraus-lesen kann

24

1.2. GET2

Beispiel zur Impedanzfunktion ()

Z(s) =1

as+

11ds

+ 11bs+ 1

cs

Dies stellt die normierte komplexe Impe-danzfunktion zu folgender Schaltung dar:

1.2.5. Mehrpolige Netzwerke

1.2.6. Zweitore

Tabellen für die Matrizen finden sich in [3, S. 126-132 / 144-146].

Betriebsverhalten von Zweitoren

Transmittanz / Betriebsübertragungsfaktor ([3], Formel 6.131)

S21 = 2 ·√R1R2

· U2U q1

Betriebsdämpfung ([3], Formel 6.137)

adBB = 20 log1

|S21|dB

= 10 log

(PWVPraus

)dB

25


Symmetrisches Zweitor ([3], Formel 6.39)

Z11 = Z22 =1

2(Za + Zb)

Z12 = Z21 =1

2(Za − Zb)

Za ermittelt man durch die Gleichtaktanre-gung (Leerlauf hinten)Zb ermittelt man durch die Gegentaktanre-gung (Kurzschluss hinten)S. 139

Weitere Bedingungen: Y 11 = Y 22, Y 12 = Y 21 und A11 = A22, detA = 1.

Rückwirkungsfreies Zweitor ([3], Formel 6.24, 6.25)

Y 21 6= Y 12; Z21 6= Z12; H12 6= −H21Y 12 = 0; Z12 = 0; H12 = 0

S. 135

Spannungsübertragungsfaktor ([3], Formel 6.143)

U1U2

=1

ÜU= A11 +

A12R2

Stromübertragungsfaktor ([3], Formel 6.145)

I1I2

=1

Ü I= −A22 − A21 ·R2

Serienschaltung ()

Zges = Z1 + Z2Schaltbild S. 155 Abb 6.26

Parallelschaltung ()

Yges = Y1 +Y2Schaltbild S. 158 Abb 6.30

Kettenschaltung ()

Ages = A1 ·A2Schaltbild S. 164 Abb 6.39

26

1.2. GET2

1.2.7. Fourier-Reihen

Sinus-Cosinus-Darstellung ()

f(t) = a0 +∞∑k=1

(âk cos (kωt) + b̂k sin (kωt))Dies ist die Sinus-Cosinus-Darstellung einerFourier-Reihe

Amplituden-Phasen-Darstellung ()

f(t) = c0 +∞∑k=1

ĉk cos (kωt− ϕk)Dies ist die Amplituden-Phasen-Darstellungeiner Fourier-Reihe

Komplexe Darstellung ()

f(t) =∞∑

k=−∞

dkejkωt

Dies ist die Komplexe Darstellung einerFourier-Reihe

Fourier-Koeffizienten ()

a0 =1

T

t+Tˆ

t

f(t′) d t′

âk =2

T

t+Tˆ

t

f(t′) cos (kωt′) d t′

b̂k =2

T

t+Tˆ

t

f(t′) sin (kωt′) d t′

dk =1

T

t+Tˆ

t

f(t′) · e−jkωt′ d t′

Mit k = 1, 2, 3, ...

27


Umrechnung Trigonometrisch - Amplituden/Phasendarstellung ()

c0 = a0

ĉk =

√â2k + b̂

2k

ϕk =

{arctan ( b̂k

âk), für âk > 0

arctan ( b̂kâk) + π, für âk < 0

âk = ĉk cosϕk

b̂k = ĉk sinϕk

Umrechnung Komplex - Amplituden/Phasendarstellung ()

ĉk = 2|dk|ϕk = arg(d

∗k)

d−k = d∗k

Sollte rel. fix gehn

Umrechnung Komplex - Trigonometrisch ()

a0 = d0âk = 2

1.2. GET2

Scheitelfaktor ()

ξ =Û√

∞∑k=1

U2k,eff

Formfaktor ()

F =

√∞∑k=1

U2k,eff

|U |

|U | ist der Gleichrichtwert

Klirrfaktor ()

k =

√√√√√√√∞∑k=2

U2k,eff

∞∑k=1

U2k,eff

Eigentlich haut man oben den ersten Vor-kommenden Koeffizienten weg und untennicht.

Klirrkoeffizient ()

kµ =Uµ,eff√∞∑k=1

U2k,eff

Grundschwingungsgehalt ()

g = k1 =U1,eff√∞∑k=1

U2k,eff

29


Welligkeit ()

w =

√∞∑k=1

U2k,eff

U0

Momentanleistung ()

p(t) = u(t) · i(t)Wenn das gefragt ist ausrechnen. Additions-theoreme sind dann meist gegeben

Wirkleistung in Amplituden-Phasen-Darstellung ()

Pw = U0I0 +∞∑k=1

1

2ÛkÎk cos (ϕu − ϕi)

= U0I0 +∞∑k=1

Uk,effIk,effk cos (ϕu − ϕi)

Scheinleistung ()

PS = UeffIeff =

√√√√U20 + ∞∑k=1

U2k,eff ·

√√√√I20 + ∞∑k=1

I2k,eff

Sonderfälle und Symmetrien

Gerade Funktion Eine Funktion f(t) ist gerade, wenn gilt: f(t) = f(−t). Einfachstegerade Funktion ist der Kosinus. Ein Gleichanteil kann ebenfalls vorhanden sein.

Ungerade Funktion Eine Funktion f(t) ist ungerade, wenn gilt: f(t) = −f(−t). Ein-fachste ungerade Funktion ist der Sinus. Ein Gleichanteil ist nicht vorhanden.

Alternierende Funktion Eine Funktion f(t) ist alternierend, wenn gilt: f(t) = −f(t+T/2). Ein Gleichanteil ist nicht vorhanden.

30

1.3. GET3

T/2-periodische Funktion Eine Funktion f(t) ist T/2-periodisch, wenn gilt: f(t) =f(t+ T/2).

Fourier-Koeffizienten bei geraden Funktionen ()

b̂k = 0

ĉk = |âk|, ϕ

1.3. GET3

1.3.1. Laplace-Transformation

Es sei hier auf die Korrespondenztabellen aus Anhang A.7 sowie in [4, S. 35 / 38] und[2, S. 253ff] verwiesen.

Einseitige Laplace-Transformation ([4], Formel 3.39)

F (s) = L{f(t)} =∞̂

0

f(t) · e−st d t

Dies ist die Definitionsgleichung der einsei-tigen Laplace-Transformation. Sie kann fürkausale Signale anstalle der beidseitigen ver-werndet werden.

Widerstandsgleichung ([4], Formel 3.145)

UR(s) = RIR(s)

31


Kondensatorgleichung ([4], Formel 3.149)

IC(s) = sC

[UC(s)−

uC(0−)

s

]UC(s) =

IC(s)

sC+uC(0

−)

s

[IC(s)] =A

Hz[UC(s)] =

V

Hz

Abbildung 1.3.: Kondensator mit Anfangs-wertgenerator

Spulengleichung ([4], Formel 3.153)

UL(s) = sL

[IL(s)−

iL(0−)

s

]IL(s) =

UL(s)

sL+iL(0

−)

s

[UL(s)] =V

Hz[IL(s)] =

A

Hz

Abbildung 1.4.: Spule mit Anfangswertge-nerator

Anfangswerttheorem ([4], Formel 3.107)

limt→0

f(t) = f(0+) = lim

1.3. GET3

Berechnung des Amplitudenbetrags in dB ([4], Formel 3.235)

|G(jω)| = 20 · lg |G(jω)|dB

Residuensatz ()

lims→s0

(s− s0)F (s) = Res

Das Residuum entsprich hier dem Koffizi-enten A bei der Partialbruchzerlegung derForm A

s−s0

Wert dB2 6

Wert dB0, 5 −6

Wert dB Wert dB

Abbildung 1.5.: Dezibel Werte (20 lg (·))

Bode-Diagramme

Amplitudengang

1. Lage und Vielfachheit von Polen und Nullstellen bestimmen

2. Achsen zeichnen und Eckfrequenzen eintragen

3. Bei ω → 0 beginnen:(a) weder Pol noch Nullstelle bei s = 0: Steigung 0dB / Dekade(b) pro Pol bei s = 0: Steigung −20dB / Dekade(c) pro Nullstelle bei s = 0: Steigung +20dB / Dekade

4. Gerade Linie bis zu nächsten Eckfrequenzen

5. Für jeden Pol Steigung um 20dB/Dekade verringern, für jede Nullstelle erhöhen.

6. Beschriftung der Vertikalen Achse durch ausrechnen von |G(jω)| in einem waag-rechten Bereiches des Bode-Diagramms

7. Ecken um 3dB pro Pol/Nullstelle abrunden

[4, S. 65]

33


Phasengang Man Beachte: Ein negatives Vorzeichen dreht die Phase um π!

1. Achsen zeichnen und Eckfrequenzen eintragen

2. Bei ω → 0 beginnen:(a) weder Pol noch Nullstelle bei s = 0: Phase 0◦

(b) pro Pol bei s = 0: Phase −90◦

(c) pro Nullstelle bei s = 0: Phase +90◦

3. Gerade Linie bis 0, 1· nächste Eckfrequenz

4. Jeder Pol subtrahiert 90◦, jede nullstelle addiert 90◦ über einen Bereich von 0, 1·Eckfrequenz bis 10· Eckfrequenz verteilt. A schwach gedämpfter Komplexer Polhüpft direkt um 180◦.

5. Phasenskizze Glätten, so dass arctan-Verläufe entstehen. Abrundungen ca. 6◦ proPol bzw. Nullstelle bei 0, 1· Eckfrequenz und 10· Eckfrequenz.

1.3.2. Nichtlineare Bauelemente

Es ist hier zu beachten, dass hier einige Prinzipien wie man sie von Linearen Netzwerkenher kennt nicht mehr gelten.

Berechnung mit Ersatzquellen

Diese Methode funktioniert gut wenn keine Einschwingvorgänge untersucht werden undbis auf das Nichtlineare Bauelement die restliche Schaltung zu einer Ersatzquelle um-transformiert werden kann. Man beachten hierzu auch das Kapitel 1.2.1.

34

1.3. GET3

Berechnung durch Ersatzspannungsquelle

1. Übriges Netzwerk zu einer Ersatzspannungsquelle umtransformieren

2. Zwischen den Anschlussklemmen des Nichlinearen Bauelements eine Hilfsspannungeinführen

3. Die Gleichung des Bauelements auf die i(u) auflösen

4. Einen Maschenumlauf über die Hilfsspannung bilden

5. i(u) des Bauelements in die Gleichung einsetzten

6. Lösen

1.3.3. Einschwingvorgänge

Kondensator ()

i(t) = Cdu

d t

Bei der Lösung von DGLs ist nach Trennungder Variablen von u(t = 0) bist u(t) zu inte-grieren.Beim Kondensator ist die Spannung immerstetig, der Strom kann springen.

Spule ()

u(t) = Ld i

d t

Bei der Lösung von DGLs ist nach Trennungder Variablen von i(t = 0) bist i(t) zu inte-grieren.Bei der Spule ist der Strom immer stetig, dieSpannung kann springen.

Anfangswerte

Bauteil Mit Quelle verbunden Von Quelle getrenntKondensator uC(0) = uc uC(0) = 0

Spule iL(0) = iL iL(0) = 0

35


Vorgegensweisen

Vorgehen im Zeitbereich

1. Differentialgleichung aufstellen (durch Maschenumläufe o.Ä.)

2. Anfangswerte bestimmen (Nach Kapitel 1.3.3)

3. DGL lösen

Vorgehen im Laplacebereich

1. Gleichung aufstellen (durch Maschenumläufe o.Ä. wie in Kapitel 1.3.1)

2. Anfangswerte bestimmen (Nach Kapitel 1.3.3)

3. Auf gesuchte Größe auflösen

4. Rücktransformieren in den Zeitbereich

1.3.4. Fehlerrechnung

Absoluter Fehler ([4], Formel 5.1)

F = A−WHier bezeichnet F den Fehler, A den ange-zeigten Wert und W den wahren Wert

Relativer Fehler ([4], Formel 5.2)

f =A−WW

· 100%

=F

W· 100%

Hier bezeichnet f den relativen Fehler, Fden absoluten Fehler, A den angezeigtenWert und W den wahren Wert

Fortpflanzung des Systematischen Absoluten Fehlers ([4], Formel 5.11)

∆y =n∑

i=1

∣∣∣∣ ∂y∂xi∆xi∣∣∣∣ Die zu messende Größe wird hier nach denfehlerhaften Größen abgeleitet

36

1.3. GET3

1.3.5. Operationsverstärker (OpAmps)

Idealer Opamp ([4], Formel 7.1, 7.2)

uA = V0uD = V0(uP − uN︸︷︷︸uD

)

uD = 0 ∧ uP = uN , für V0 → ∞iN = iP = 0

1.3.6. Messschaltungen

Abgleichbedingung Brücke ([4], Formel 9.46)

Z2Z3 = Z1Z4 ⇒ UD = 0Bild...

äquivalente Abgleichbedingungen einer Brücke ([4], Formel 9.50, 9.51)

Zi = Ri + jXi

R2R3 −X2X3 = R1R4 −X1X4X2R3 +R2X3 = X1R4 +R1X4

Bei unteren Gleichungen müssen erfüllt sein.Es müssen somit 2 unabhängig voneinanderabgleichbare Elemente vorhanden sein.

Diagonalspannung bei der Brücke ([4], Formel 9.21)

UD = UE

(R2

R1 +R2− R4R3 +R4

)= UE

R2R3 −R1R4(R1 +R2)(R3 +R4)

Das Schaltbild ist in [4, S. 242]

37

2. Halbleiterbauelemente

2.1. Grundlagen

2.1.1. Intrinsischer Halbleiter

Intrinsische Ladungsträgerkonzentration ()

ni =√NC ·NV exp

(− Eg2kT

)n2i = n0 · p0

Intrinsisches Ferminiveau ()

EFi =EC + EV

2+

1

2kT · ln

(NVNC

)Effektive Zustandsdichten Elektronen/Löcher ()

NC = 2

(2πm∗ekT

h2

); NV = 2

(2πm∗hkT

h2

)

2.1.2. Dotierter Halbleiter

Ladungsträgerkonzentrationen ()

n = NC · exp(EF − EC

kT

)= ni · exp

(EF − EFi

kT

)p = NV · exp

(EV − EF

kT

)= ni · exp

(−EF − EFi

kT

)

39


Ferminiveau ()

EF = EFi + kT ln

(n

ni

)bzw. EF = EFi − kT ln

(p

ni

)

2.1.3. Ladungsträger im Halbleiter in elektrischem Feld

Driftstromdichte ()

JDrift = q(pµp + nµn)E = σE

Elektrischer Widerstand ()

R =l

σA

Diffusionskonstante ()

Dn/p =kT

qµn/p

Dielektrische Relaxation ()

τd =�0�rσ

Diffusionslänge ()

Lp/n =√Dp/nτp/n

Debye-Länge ()

LD =

√�0�rkT

q2p

40

2.1. Grundlagen

2.1.4. Halbleiterdioden

Diffusionsspannung ()

UDiff =kT

qln

(NANDn2i

)

Weite der Raumladungszone ()

wRL = xn + xp =

√2�0�HLUDiff

q

(1

NA+

1

ND

)mit xpNA = xnND und x2pNA + x2nND =2�0�HLUDiff

q

Weite der Raumladungszone bei abruptem pn-Übergang ()

wRL = xn + xp =

√2�0�HLUDiffqNA/D

Sperrschichtkapazität ()

CS =�0�HLwRL

· A

Sperrsättigungsstromdichte ()

JS = qn2i

(DnLnNA

+Dp

LpND

)= qn2i

(LnτnNA

+LpτpND

)

2.1.5. Metall-Isolator-Halbleiter-Kondensator

Bulkpotential ()

ΦB =EFi − EF

q= kT · ln

(NAni

)bzw. kT · ln

(niND

)

41


Austrittsarbeit des Halbleiters ()

qΦHL = qχHL +Eg2

+ qΦB

Austrittsarbeitsdifferenz ()

qΦMHL = q(ΦM − ΦHL)

Flachbandspannung ()

UFB = ΦMHL −QIsCIs

Weite der Raumladungszone ()

wRL =

√−2�0�HL

qNDΦS bzw.

√2�0�HLqNA

ΦS

Maximale Weite der Raumladungszone ()

wRL,max =

√−4�0�HL

qNΦB

Einsatzspannung ()

UTh = UFB + 2ΦB −QHLCIs

Ladung im Halbleiter(flächenbezogen!) ()

QHL = ±√

4�0�HLqN |ΦB| (+ : n− HL;− : p− HL)

Isolatorkapazität (flächenbezogen!) ()

CIs =�0�IsxIs

42

2.1. Grundlagen

Gesamtkapazität des Kondensators ()

Cges =CIsCHLCIs + CHL

2.1.6. MOSFET

Kanalwiderstand ()

RC = ρl

xCW

Drainstrom (n-Kanal: + ; p-Kanal: -) ()

ID = ±β(UG − UTh)UD linearer Bereich

ID = ±β((UG − UTh)UD −

UD2

)Triodenbereich

ID = ±β(UG − UTh)2 Sättigungsbereich

Transkonduktanz ()

β = µp/nCIsW

L

Substratstreufaktor ()

γ = ∓√2�0�HLqN

CIs(p-Kanal: -, N = ND; n-Kanal: +, N = NA)

Ladung im Halbleiter bei angelegter Sperrspannung ()

QHL,Sp. = ±√2�0�HLqN |2ΦB − UB| (p-Kanal: +; n-Kanal: -)

Durchbruchspannung bei angelegter Sperrspannung ()

UTh,Sp. = UFB + 2ΦB + γ√

|2ΦB| − UB

43


2.1.7. Optoelektronik

Wellenlänge ()

λ =c

ν

Energie ()

Eph = h · ν

Absorptionsbedingung ()

Eph ≥ Eg

Impuls ()

pph =h

ν

44

3. SchaltungstechnikDieses Kapitel befasst sich mit analogen Schaltungen der Elektrotechnik und derenGrundlagen

3.1. Grundlegende Bauelemente3.1.1. DiodeSchaltbild...

Stromkennlinie ()

ID = IS

(e

UDn·UT − 1

)ID: Strom durch die DiodeIS:UD:n:UT :Hierbei ist der Bahnwiderstand nicht be-rücksichtigt, denn die Gleichung wäre sonstnicht auf den Diodenstrom auflösbar.

Spannungskennlinie ()

UD = n · UT lnIDIS

+ IDRB

Vereinfachtes Modell ()

Dies stellt eine sehr stark vereinfachte Nä-herung dar. Für analytische Lösungen wirddiese gerne verwendet, da durch die e-Funktion nichtlineare Gleichungen entste-hend, die nur noch numerisch gelöst werdenkönnen.

3.1.2. Bipolartransistpr

45

4. Maxwellsche Gleichungen

Zur Übersicht sind hier die Maxwellschen Gleichungen mit ihrer prinzipiellen Bedeutungin verschiedenen Formen angegeben.

4.1. Integrale Darstellung

Maxwell 1 (Induktionsgesetz) (Schmidt 3.1)

˛

C

~E(t) d~s = − ∂∂t

¨

A

~B(t) d ~A� +

˛

C

(~v × ~B) d~s

Dies ist auch als Induktionsgesetz bekannt.Zu beachten ist, dass die Kurve C auch imVakuum / in irgend einem Medium umlau-fen werden kann. Somit besagt diese Glei-chung dass ein Zeitlich veränderliches Ma-gnetfeld immer mit einem zeitlich veränder-lichen E-Feld in Verbindung ist und gemein-sam auftritt.

Maxwell 2 (Amperesches Gesetz) (Schmidt 3.2)

˛

C

~H(t) d~s =

¨

A

~J(t) d ~A� +∂

∂t

¨

A

~D(t) d ~A�︸︷︷︸Verschiebungsstrom

Dies ist aus GET1 bekannt. Allerdings isthier noch der sog. Verschiebungsstrom zufinden. Seine Bedeutung ist leicht am Bei-spiel des Kondensators zu erkennen: Lässtman einen Kondensator von einer Wechsel-stromquelle speißen, so fließt Strom obwohlder Ideale Kondensator perfekt Isoliert. Die-ser Stromfluss geschiet durch das ~E-Feld inForm des Verschiebungsstroms.

Maxwell 3 (Coulombsches Gesetz) (Schmidt 3.3)

‹

A

~D(t) d ~A� =

˚

V

ρ(t) dV

47


Maxwell 4 (Schmidt 3.4)

‹

A

~B(t) d ~A� = 0

Da sich der magnetische Fluss schließt, istdas Hüllflächenintegral über diesen 0. Diesbedeutet, dass das Magnetfeld ein Quellen-freies Feld ist.

Kontinuitätsgleichung ()

‹~J d ~A� = −

∂Q

∂t

I = −∂Q∂t

Fließt ein Strom von einem geladenen Kör-per weg, so verschwinden auf diesem La-dungen. Mann kan sich dies vorstellen, dassder geladene Körper ein voller Eimer Was-ser ist und die Wassermolekühle Ladungenrepräsentieren. Schüttet man den Eimer aus,entsteht ein Wasserstrom und das Wasserim Eimer verschwindet. Achtung: Da hier-bei Ladungen vom Körper wegtransportiertwerden, ist das Hüllflächenintegral über ~Jnicht 0!

4.2. Differentielle FormDiese Darstellung erhällt man durch Anwendung des Satzes von Stokes und Gauß


rot ~E(t) = − ∂∂t~B(t)

= − ∂∂t

rot ~A(t)

~A bezeichnet das magnetische Vektorpoten-tial. Es gilt: ~B = rot ~A.


rot ~H(t) = ~J(t) +∂

∂t~D(t)︸︷︷︸

Verschiebungsstromdichte


div ~D(t) = ρ(t)

Das elektrische Feld ist ein Quellenfeld. DieQuellen des elektrischen Felds sind Ladun-gen.

48

4.3. Maxwellgleichungen im Frequenzbereich


div ~B(t) = 0Das magnetische Feld ist ein Quellen freiesFeld.

Kontinuitätsgleichung ()

div ~J = − ∂∂tρ

Sagt aus, dass bei einem fließenden Strom,Ladungen bewegt werden.

4.3. Maxwellgleichungen im Frequenzbereich

Dies gilt nur allerdings nur für zeitharmonische Größen! Für allgemein zeitabhängigeGrößen, sind die integralen und differentiellen Formen zu verwenden.


rot ~E(ω) = −jω~B(ω)


rot ~H(ω) = ~J(ω) + jω~D(ω)︸︷︷︸Verschiebungsstromdichte


div ~D(ω) = ρ(ω)


div ~B(ω) = 0

49


4.4. Randbedingungen

~E-Feld an der Grenzfläche ()

~n · (~E2 − ~E1) =σ

�

~n · (~D1 − ~D2) = 0~n× (~E2 − ~E1) = 0

Man beachte die Entsprechenden kompo-nenten (tangential und normal) der Feld-stärke / Flussdichte.

~H-Feld an der Grenzfläche ()

~n · (~B2 − ~B1) = 0~n× (~H2 − ~H1) = ~K

Achtung: Einheitsvektoren beachten durchdas Kreuzprodukt!

Dirichlet Randbedingung Als Dirichlet Randbedingung werden Randbedingungen be-zeichnet, bei denen der Randwert direkt als Potentialgröße gegeben ist.

ϕe = Wert (4.1)~A = Wert (4.2)

Von Neumann Randbedingung Als Von Neumann Randbedingung werden Randbe-dingungen bezeichnet, bei denen der Randwert als Ableitung der Potentialgröße gegebenist.

∂ϕe∂n

= Wert (4.3)

Dies entspricht der Vorgabe von ~D oder ~E bzw. ~H oder ~B. Man beachte, dass dies eineAbleitung nach der Normalen n ist.

50

4.5. Magnetisches Vektorpotential und Eichungen

4.5. Magnetisches Vektorpotential und Eichungen

Magnetisches Vektorpotential ()

~B = rot ~A

Allerdings ist ~A nicht eindeutig definiert:~A′ = ~A+ grad(ψ) würde wegen rot grad(ψ)genau das selbe liefern. Also ist ψ als Frei-heitsgrad vorhanden.

Coulomb-Eichung ()

div ~A = 0

Lorenz-Eichung ()

div ~A+ �µ∂

∂tΦ = 0

Eichtransformation ()

~A′ = ~A+ grad(V )

Φ′ = Φ− ∂V∂t

V bezeichnet hierbei die Eichfunktion. Je-des beliebige V , welches diese Bedingungenerfüllt, kann zur Eichung des magnetischenVektorpotentials verwendet werden.

51

5. Elektromagnetische Felder

5.1. Theorie elektromagnetischer Felder

5.1.1. Elektrostatik

Es empfiehlt sich hier in GET1 nachzulesen.Die elektrische Feldstärke (2.11)

~E = − gradϕe

⇒˛

C

~E d~s = 0

rot ~E = 0

Feld und Potential einer Raumladung (2.18, 2.19)

ϕr(~rP ) =1

4π�0

˚

V

1

rρ(~rQ) dVQ

~E(~rP ) =1

4π�0

˚

V

~r

r3ρ(~rQ) dVQ

Man geht hier von bekannter Raumladungρ aus. Am Punkt ~rP kann man dann dasPotential / die Feldstärke berechnen indemmal ρ stur über das Volumen aufintegriert.

Ergibigkeit (Divergenz) des E-Feldes (2.13)

‹

A

~D d ~A =

˚

V

div ~D dV =

˚

V

ρ dV

⇒ div ~D = ρ‹

A

(−�∇ϕe) d ~A = 0

Dies ist das Coulombsche Gesetz

53


Poisson- / Laplace-Gleichung (2.14, 2.15)

∆ϕe = −ρ

�0, Poisson-Gleichung

∆ϕe = 0, Laplace-Gleichung

Die Poisson-Gleichung findet Anwendungbei vorhandener Raumladung. Ist man au-ßerhalb dieses Bereichs, so verwendet mandie Laplace-Gleichung als Sonderfall. Siewird oft auch einfach als Feldgleichung be-zeichnet.

Feld / Potential eines Dipols (2.54-2.56)

~Me = ~eMe = ~eQs

ϕe(~rP ) =1

4π�0r2P

~rPrP

· (~rQ1Q1 +~rQ2Q2)

=~eQs

4π�0r2P

~rPrP

=1

4π�0~Me ·

~rPrP

~E = − grad(ϕe)

Hierbei zeigt ~e von der negativen Ladungzur positiven Ladung. Man kann es fürräumlich dicht beieinanderliegenden Ladun-gen anwenden.

Komplexes Feld / Potential einer Linienladung ()

~E = ~eρλ02π�0

l

ρ, Reelles Feld

~E = ~eρλ02π�0

1

ρe−jϕ︸︷︷︸1/z∗

, Komplexes Feld

ϕe(ρ) = −λ02π�0

ln(ρc

), Reelles Potential

p(z) = − λ02π�0

ln

(ρejϕ

c

)︸︷︷︸

z/c

, Komplexes Potential

= ϕe − jψ

�0l

54


Lösungsverfahren

Verfahren I Felder bei symmetrischen LadungsverteilungenDieses Verfahren ist bereits aus GET1 bekannt. Man kann es immer bei symmetrischenGeometrien verwenden. Bedingung hierfür ist u.A., dass die Flussdichte auf einer ent-sprechenden Oberfläche, welche die Anordnung vollständig umschließt, einen konstantenWert haben muss (z.B. Kugel: Hier ist ~D unabhängig von ρ, es kann also ~D angegebenwerden, wenn man Q annimmt). Auch bei symmetrischen Ladungsverteilungen ist esmöglich.

1. Über den Fluss das elektrische Feld allg. bestimmten

2. Falls Raumladungen vorhanden: Aus diesen allg. die Ladung bestimmen

3. Ladung und Fluss gleichsetzen und auf das Feld auflösen

Verfahren II Integration über die LadungsverteilungDieses Verfahren kann genuttz werden, wenn die Ortsverteilung der Ladungsträger be-kannt ist und der Raum überall gleiche Materialeigenschaften besitzt.

1. ~r = ~rP −~rQ angeben

2. r angeben

3. Integrationsgrenzen bestimmen

4. In die entsprechende Formel für ~E oder ϕ einsetzen

Verfahren III Vergleich mit bekannten FeldbildernHierfür werden Äquipotentialflächen benötigt. Man geht von einer einfachen Anordnungaus, z.B. eine Linienladung, setzt Äquipotentialflächen dran und kann so z.B. das Feldeines dicken Drahtes berechnen.

Verfahren IV SpiegelungsverfahrenHierfür wird eine Ebene benötigt, auf der das Potential den Wert 0 (jaja, ich weiß, esgeht nur im Bezug auf irgendwas, aber ihr wisst schon, wie ichs meine ;)) hat. Dann kannman die Anordnung spiegeln, so dass diese Bedingung erfüllt ist und die Feldverteilungangeben.

55


Teilkapazitäten

Maxwellsche Potentialkoeffizienten (2.160)

ϕe1ϕe2...ϕen

=p11 p12 . . . p1np21 p22 . . . p2n... ... . . . ...pn1 pn2 . . . pnn

·Q1Q2...Qn

Nachdem ϕe ∼ Q gilt, kann man die Max-wellchen Potentialkoeffizienten pik einfüh-ren. Dieses Gleichungssystem kann man nunnach den den Ladungen auflösen

Maxwellsche Kapazitätskoeffizienten (2.165)

Q1Q2...Qn

=k11 k12 . . . k1nk21 k22 . . . k2n... ... . . . ...kn1 kn2 . . . knn

·ϕe1ϕe2...ϕen

Dies ist das nach den Ladungen aufgelösteGleichungssysten von oben mit k = p−1

Teilkapazitäten (2.168)

Cii =n∑

k=1

kik

Cik = −kik

Da noch a Bildle nei

Bestimmung der Teilkapazitäten Man kann entweder die Potentiale annehmen oderdie Ladungen und dann rumrechnen. Über die Ladungen ist es meist einfacher.

Ladungen (Achtung!! Hierbei wird der Abstand der Teile zueinander als sehr groß ange-nommen, da so das Potential des Körpers alleine näherungsweise gilt!):

1. Q annehmen

2. ϕei berechnen (wie üblich)

3. Jetzt hat man schon die Potentialkoeffizienten

4. Gleichungssystem auf Q auflösen

5. Die Kapazitätskoeffizienten durch Vergleichen oder Lösen des LGS bestimmen

6. Die Teilkapazitäten ausrechnen

56


5.1.2. Stationäres Strömungsfeld

Ohmsches Gesetz (3.9)

− gradϕe = ~E =1

κ~J

Dies ist aus GET1 bekannt

Randbedingungen (3.18)

0 = ~n×(

1

κ2~J2 −

1

κ1~J1

)0 = ~n ·

(~J2 − ~J1

) Folgt direkt aus den Randbedingungen deselektrischen FeldsFeldgleichung ([5], Formel 3.11, 3.12)

div ~J = 0

∆ϕe +1

κgradκ · gradϕe = 0, für κ = κ(~r)

∆ϕe = 0, für κ = const.

5.1.3. Stationäres Magnetfeld

Oersted’sches Gesetz ()

˛

C

~H · d~s = I

rot ~H = ~J

An Stellen nicht veschwindende Stromdichteweißt das Magnetfeld Wirbel auf (zur Veran-schaulichung betrachte man sich den Strom-durchflossenen Draht mit dem in ϕ gerich-teten Magnetfeld)

57


magnetische Flussdichte (4.93)

Φ =

¨

A

~B · d ~A =˛

C

~A d~s

div ~B = 0‹

A

~B · d ~A =˚

V

div ~B dV = 0

Magnetische Flussdichte ist Quellenfrei (imGegensatz zur elektrischen Flussdichte)

magnetisches Vektorpotential (4.8, 4.23)

~B = rot ~A

∆~A = −µ0~J

~A(~rP ) =µ

4π

˚

V

1

r~J(~rQ) dVQ

~A(~rP ) =µ

4π

¨

A

1

r~K(~rQ) dAQ

Nicht mit der Fläche ~A verwechseln! ~K isthierbei der Strombelag

magnetisches Skalarpotential (4.15)

~H = − gradVm

Dies ist das analogon zum elektrostatischenPotential ϕe und ist auch aus GET1 bereitsbekannt.

Biot-Savart ([5], Formel 4.22, 4.26)

~H(~rP ) =1

4π

˚

V

~J(~rQ)×~r

r3

~H(~rP ) =I

4π

˛

C

(d~sQ ×

~r

r3

)~H(~rP ) =

1

4π

¨

A

~K(~rQ)×~r

r3dAQ

• ~r für die Kurve allg. bestimmen

• ~s entlang der Kurve allg. bestimmen

• r bestimmen (geht aus ~r)

• Ausrechnen (wird oft mathematischhässlich)

58


Feld einer dünnen Leiterschleife (4.25, 4.26)

~A(~rP ) =µI

4π

˛

C

1

rd~sQ

~H(~rP ) =I

4π

˛

C

(d~sQ ×

~r

r3

)

Vm(~rP ) =I

4π

¨

A

~r

r3· d ~AQ

magnetischer Dipol (4.49, 4.50)

~Mm = ~nMm = ~nIA

Vm(~rP ) =1

4π~Mm ·

~rPr3P

~A(~rP ) =µ04π

(~Mm ×

~rPr3

)~H(~rP ) = −

1

4π

(~Mm · grad

) ~rPr3P

letzteres Folg als Spezialfall aus der kreisför-migen, sehr dünnen und kleinen Leiterschlei-fe (also so ne gaaaanz putzige). Des vom Di-pol hervorgerufene Feld hängt nur von derumschlossenen Fläche, nicht von der Geome-trie der Stromschleife ab. Man kann auch beieiner gegebenen Stromdichte die Fläche pa-rametriesieren und I durch Integration derStromdichte bestimmen.

komplexes magnetisches Potential (4.76)

Pm(z) = −µI

2πlnz

c

= −µI2π

lnρ

c︸︷︷︸=A(ρ)

+j(−µI ϕ

2π

)︸︷︷︸

=Pmi

Die Herleitung erfolgt analog wie im elek-trostatischen Fall. Man sieht hier sehr gut,dass das alles das selbe ist, nur anders ;).Pmi = µVm

Energie des Magnetfelds ([5], Formel 4.119)

wm =1

2~H · ~B

Wm =

˚

V

wm dV =1

2

˚

V

~Am · ~J(~rQ) dVQMuss über V = V∞ integriert werden

59


Induktivitäten räumlicher Massivleiter ([5], Formel 4.136, 4.138)

Lik =

˚

V

~JiIi

·~AikIk

dV

=µ04π

˚

V

˚

V

1

rik

~JiIi

·~JkIk

dV dV

Induktivität einer dünnen Leiterschleife ([5], Formel 4.145)

Li =µl

8π

Im Üblichen nur proportional zu l, nicht vonwas andrem Abhängig. Daher kann das auchfür andere Leiterschleifen und Leiteranord-nungne, die entsprechend lang sind übertra-gen werden.

Induktivitätsmatrix ([5], Formel 4.147)

Φ1Φ2...Φn

=L11 L12 . . . L1nL21 L22 . . . L2n

... ... . . . ...Ln1 Ln2 . . . Lnn

·I1I2...In

Lik wird oft auch als Mik geschrieben.

5.1.4. ElektrodynamikBisher waren alle Größen von der Zeit unabhängig, d. h. es galt, dass alle zeitlichenAbleitungen zu 0 werden.

Elektrisches Feld ()

~E = − grad(ϕe)−∂

∂t~A

Jetzt muss zusätzlich ein Feldanteil durchInduktion berücksichtigen.

60

6. Hochfrequenztechnik

6.1. PB

Leistungsbilanz im EM-Feld

Energiedichte im E/M-Feld ()

we(t) =dWe(t)

dV=

1

2�0E

2(t)

wm(t) =dWm(t)

dV=

1

2µ0H

2(t)

Leistungsbilanz im Frequenzbereich ()

‹

A

1

2(~E× ~H∗) d ~A

︸︷︷︸Pps+jPps

− jω∗˚

V

�0�∗r

2

∣∣∣~E∣∣∣2 dV︸︷︷︸

Ppe+jPpe

+ jω

˚

V

µ0µr2

∣∣∣~H∣∣∣2 dV︸︷︷︸

Ppm+jPpm

+

˚

V

1

2σ∣∣∣~E∣∣∣2 dV

︸︷︷︸Pv

+

˚

V

1

2~E · ~J∗Q dV︸︷︷︸

PpQ+jPpQ

= 0

61


Frequenzabhähnige Leistungsanteile ()

Pe + Pm = (�′′

rω′ − �′rω

′′)

˚

V

�02

∣∣∣~E∣∣∣2 dV︸︷︷︸

dielektrische Verluste

+ (µ′′

rω′ − µ′rω

′′)

˚

V

µ02

∣∣∣~H∣∣∣2 dV︸︷︷︸

magnetische Verluste

− j�′rω′˚

V

�02

∣∣∣~E∣∣∣2 dV︸︷︷︸

elektrische Feldleistung

+ jµ′

rω′˚

V

µ02

∣∣∣~H∣∣∣2 dV︸︷︷︸

magnetische Feldleistung

Man erhällt diese Leistungsanteile durcheinsetzten der komplexen Materialparame-ter µr und �r ind die frequenzabhähnigenLeistungsanteile der Leistungsbilanz.Die elektrische und magnetische Feldlei-stung pendelt (sie geht gegenseitig ineinan-der über). Die dielektrischen Verluste entste-hen z.B. dadurch, dass Dipole bei der Um-polung umkippen (Mikrowellenherd!).

6.1.1. Wellenausbreitung

Helmholtz-Gleichung ()

∇2~E− µ� ∂2

∂t2~E = 0

∇2 ~H− µ� ∂2

∂t2~H = 0

Dies folt aus den Maxwellgleichungen. Be-schrieben ist das auf Seite 18 im Skript.

Wellezahl k ([6], Formel 4.27)

k =ω√�µ

Phasengeschwindigkeit einer EM-Welle ()

vPh =1

√�µ

ω

k

µ wurde experimentell bestimmt und legtzusammen mit c0 den Wer von �0 fest. Hier-mit ist auch die Wellenzahl verknüpft.

62

6.1. PB

Skintiefe ([6], Formel 4.86)

δ =1√

πfµ(ω)σ(ω)

Wellenlänge ()

λ0 = wπf =c0f

Gilt im Vakuum.

Wellenlänge ()

λ =λ0√�r

=λ0n

Gilt im Medium. Hiebei bezeichnet n denBrechungsindex.

Flächenwiderstand ([6], Formel 4.93)

R� =l

σ(ω) δ(ω)l︸︷︷︸A

=1

σ(ω)δ(ω)

Hochfrequenzwiderstand ()

RHF =l

σδb

=l

σδπd, Draht m. Durchmesser d

Feldwellenwiderstand ([6], Formel 4.02)

ZF = (1 + j)R�, leitendes Medium

=

√µ

�, nichtleitendes Medium

Man muss also aufpassen wo sich die Welleausbreitet. Im Vakuum gilt Z0 = 120πΩ

63


Snellius’sches Brechungsgesetz ()

sinα

sin β=n2n1

=

√�2�1

= nFür die Bezeichnungen betrachte man Abb.6.1.

Winkel der Totalreflexion ()

sin (αT ) =n2n1

=

√�r1�r2

Tritt nur auf, wenn die Welle vom optischdichten ins optisch dünne Medium fällt. An-gewendet wird dies u.A. in Glasfasern.

Brewsterwinkel ()

αB = arctann2n1

=

√�r1�r2

Das paralell polarisierte Licht wird unterdiesem Winkel nicht reflektiert

E-Feld einer linear polarisierten EM-Welle ()

Ex(t) =

6.1. PB

Magnetfeld einer EM-Welle Um das Magnetfeld einer EM-Welle zu berechnen, be-dient man sich der Maxwellgleichungen:Aus

−∂~B

∂t= ∇× ~E

folgt im Frequenzbereich

~H(ω) =j

ωµ

[(∂Ez∂y

− ∂Ey∂z

)~ex +

(∂Ex∂z

− ∂Ez∂x

)~ey +

(∂Ey∂x

− ∂Ex∂y

)~ez

]Nun folgt die Berechnung des H-Feldes (hier am Beispiel einer sich in ~ez-Richtung aus-breitenden linear polarisierten EM-Welle, deren E-Feld in richtung ~ex zeigt).

~H(ω) =j

ωµ

[(∂Ex∂z

)~ey +

(−∂Ex∂y

)~ez

]=

j

ωµ

[(∂(E+0xe

−jkz + E−0xe+jkz)

∂z

)~ey +

(−∂(E

+0xe


∂y

)~ez

]= ~ey

k

ωµ(E+0xe


mit kωµ

= 1ZF

folgt z.B. für die Hinlaufende Welle:

~H+ = ~eyE+0xe

−jkz

ZF

Hierraus lässt sich der Pointing-Vektor berechnen.

Pointing-Vektor ()

~S± =1

2~E± ×

(~H±)∗

= ±~ezE±0,z(H±0,z

)∗= ±1

2~ez

∣∣E±0,z∣∣2ZF

= ±12~ezZF

∣∣H±0,z∣∣2Der Pointing-Vektor zeigt in Ausbreitungs-richtung der EM-Welle und ist ein Maß fürdie transportierte Leistung. Er stellt eineFlächenleistungsdichte dar.

65


Fresnelgesetze ()

Er||Ee||

=tan (α− β)tan (α + β)

Er⊥Ee⊥

= −sin (α− β)sin (α + β)

Eg||Ee||

=2 cosα sin β

sin (α + β) cos (α− β)Eg⊥Ee⊥

=2 cosα sin β

sin (α + β)

αα

β

Abbildung 6.1.: Brechung und Fresnelgeset-ze

senkrechter Einfall ([6], Formel 4.61 4.62)

Er||Ee||

= −Er⊥Ee⊥

=n2 − n1n2 + n1

= r

Eg||Ee||

= −Eg⊥Ee⊥

=2n1

n2 + n1= g

Dies stellt den Sonderfall der Fresnelgesetzefür α = 0 dar. Bei Leistungsverhältnissen istdies zu quadrieren.

Antireflexschicht ()

�AF =√�r1 · �r2 =

√n1 · n2

d =λ

4=

λ04√�AR

=λ0

4nAR

66

6.1. PB

6.1.2. Bauteile

Widerstand

CK

CW

LZ LW RN

Abbildung 6.2.: Ersatzschaltbild des Widerstands mit allen Verlusten [6, S. 47 Abb. 5.7]

Hierbei gilt:LZ : Induktivität des ZuleitungsdrahtesLW : Induktivität der WicklungenCK : Kapazität der KontaktkappenCW : Kapazität der WicklungenRN : Nennwiderstand

Temperaturabhähngigkeit ([6], Formel 5.8 - 5.10)

R(T ) =RN +dR(T )

dT|T=TN + · · ·

≈RN [1 + TKR(T − TN)]

TKR =dR(T )

RN dT|T=TN

Der Temperaturkoeffizient TKR hat die oftdie Einheit [TKR] = ppmK .

67


Kondensator

LZ RZ RK

C

RD Riso

Abbildung 6.3.: Ersatzschaltbild des Kondensators mit allen Verlusten [6, S. 69 Abb.6.15]

Hierbei gilt:LZ : Induktivität des ZuleitungsdrahtesRZ : Widerstand des ZuleitungsdrahtesRK : Widerstand der KontakteRD, Riso: Widerstände im DielektrikumC: Nennkapazität


C(T ) =CN +dC(T )

dT|T=TN + · · ·

≈CN [1 + TKC(T − TN)]

TKC =dC(T )

CN dT|T=TN

Der Temperaturkoeffizient TKC hat die oftdie Einheit [TKR] = ppmK .

Verlustwinkel d. Dielektrikums ()

tan δ� =�′′r

�′r=GPBP

=GPωC ′

Komplexwertige Dielektrizitätszahl ()

�r = �r(1− j tan (δ�))

68

6.1. PB

Güte des Dielektrikums ()

Q� =

∣∣∣∣PqPv∣∣∣∣ = �′r�′′r = 1tan δ�

Güte des Kondensators ()

QC =

∣∣∣∣PqPv∣∣∣∣ = 1R1ωC ′(1 + tan2 δ�) + tan δ�

Spule

RH RW RCu RWW L

CW

RD

Abbildung 6.4.: Ersatzschaltbild der Spule mit allen Verlusten [6, S. 102 Abb. 7.24]

Hierbei gilt:RH : HystereseverlusteRW : WirbelstromverlusteRCu: Widerstand des ZuleitungsdrahtesRWW : Wirbelstromverluste in der WicklungCW : WicklungskapazitätRD: Verschiebungsstromverluste der WicklungskapazitätL : Nenninduktivität

69



µA(T ) =µA,N +dµA(T )

dT|T=TN + · · ·

≈µA,N [1 + TKµ(T − TN)]

TKµ =dµA(T )

µA,N dT|T=TN

L(T ) =LN +dL(T )

dT|T=TN + · · ·

≈LN [1 + TKL(T − TN)]

TKL =dL(T )

LN dT|T=TN

Der Temperaturkoeffizient TKL hat oft dieEinheit [TKR] = ppmK .

Verlustwinkel und Güte der Spule ()

tan δL =tan δH + tan δW︸︷︷︸tan δµ

+

tan δWW + tan δC︸︷︷︸=0 ohne Streufelder

+tan δCu

QL =1

tan δL

Man beachte für diese ganzen Verlustwinkel[6, S. 101ff].

Permeabler Verlustwinkel δµ ([6], Formel 7.75)

tan δµ =µ

′′r

µ′r=RSXS

=RSωL′

δµ beinhalltet die Hystereseverluste (RH)sowie die Wirbelstromverluste (RW ). Alsohauptsächlich die Verluste im Spulenkern.

Hystereseverlustfaktor ([6], Formel 7.78)

tan δH =

∣∣∣∣Pv,HPq∣∣∣∣ = RHωL

70

6.1. PB

Wirbelstromverlustfaktor ([6], Formel 7.79)

tan δW =µ

′′A

µ′A

=sinhx− sinxsinhx+ sinx

mit x = s

√f

fw

Zuleitungsverlustfaktor ([6], Formel 7.81)

tan δCu =RCuωL

Man beachte, dass bei hohen Frequenzen derSkineffekt bei der Bestimmung von RCu zubeachten ist.

Flussverdrängung und Wirbelströme Wenn ein elektrisch leitfähiges Medium voneinem magnetischen Wechselfeld durchflossen wird, bilden sich Wirbelströme aus.Grundlegend gilt:

Wirbelströme ()

∇× ~E(t) = − ∂∂t~B(t)

~E(t) = ρ~J(t)

∇× ~J(t) = −1ρ

∂

∂t~B(t)

Hier besagt das Induktionsgesetz nichts an-deres als dass ein zeitlich veränderliches Ma-gnetfeld die Rotation einer Stromdichte her-vorruft.

6.1.3. Leitungstheorie

Reflexionsfaktor ([6], Formel 9.30, 9.31)

rx =Rx − Z`Rx + Z`

rL bezeichnet den Reflexionsfaktor an derLeitung, ri den an der Quelle und rA den ander Last. Anstatt der Resistanzen könnenauch Impedanzen stehen.

Wellenwiderstand ([6], Formel 9.57)

Z` =

√R′ + jωL′

G′ + jωC ′

Man kann also einen bestimmten Wellenwi-derstand einer Leitung durch die entspre-chenden, eig. nur von der Geometrie abhän-gigen Größen auslegen.

71


Dämpfungsmaß ([6], Formel 9.59)

α =

(R

′

2√L′/C ′

+G

′

2

√L′

C ′

)· 1cosh

(δR−δG

2

)Phasenmaß ([6], Formel 9.60)

β = ω√L′C ′ cosh

(δR − δG

2

)

Phasengeschwindigkeit ([6], Formel 9.61)

v =ω

β=

1√L′C ′

· 1cosh

(δR−δG

2

)Wellenwiderstand ([6], Formel 9.62)

Z` =

√L′/C ′

cosh δG·[cosh

(δR + δG

2

)− j sinh

(δR − δG

2

)]

Leistungstransport der allg. Leitung ()

P (`) = P (0)e−2α`Für hin und rücklaufende Welle.

Reflexionsfaktor ([6], Formel 10.21)

r(d) = rAe−2γd

r(l − z) = rAe−2α(l−z)e−j2β(l−z)Mit d = l − z.

72

6.1. PB

Verlustarme Leitung Hier gelten mit der Näherung cosh(δR−δG

2

)≈ 1 folgende

Formeln:


α ≈ R′

2√L′/C ′

+G

′

2

√L′

C ′

Phasenmaß ([6], Formel 9.64)

β ≈ ω√L′C ′

Phasengeschwindigkeit ([6], Formel 9.65)

v =ω

β≈ 1√

L′C ′

Wellenwiderstand ([6], Formel 9.66)

Z` ≈√L′

C ′

Die Lecherleitung

Die Lecherleitung stellt ein wirkungsvolles Instrument zur Impedanzanpassung dar undkann bei sehr hohen Frequenzen als reaktives Bauelement fungieren.

73


(a) Schema der LecherleitungI1 R

′dz L

′dz

G′dz C

′dz

I2

U1 U2

(b) ESB der inifinitesimal kurzen Lecherleitung

Abbildung 6.5.: Lecherleitung

Wellenwiderstand ()

Z` =

√R′ + jωL′

G′ + jωC ′

Eingangsimpedanz ([6], Formel 10.24)

ZE =U1I1

=ZA + Z` tanh γ`

Z` + ZA tanh γ`Z`

ZA: Abschlussimpedanz (Lastimpedanz)Z`: Leitungsimpedanz`: Leitungslänge

Stehwellenverhälltnis ([6], Formel 11.24)

VSWR =|Umax||Umin|

=1 + |rA|1− |rA|

Das Stehwellenverhältnis kann gemessenwerden.

Reflexionsfaktor und Eingangsimpedanz bei lmin ()

Die Abkürzug steht für Voltage StandingWave Ratio.

74

6.1. PB

Berechnung der Abschlussimpedanz einer Leitung Aufgrund der Messung vonVSWR kann man die Abschlussimpedanz an einer Messleitung bestimmen.

1. VSWR bestimmen

2. rE(lmin) eintragen (geht über ZE(lmin))

3. um lminλ

zurückdrehen.

Strom- und Spannungsextrema einer Leitung ()

Imax =Uminm · Z`

Imin =Umax

VSWR · Z`

Aus U = RI (ab Diagramm veranschaulich-ten!) folgt Imax aus Umin und umgekehrt. Be-achtet man nun mal die Achsenbeschriftungdes SD, welche ja VSWR wiederspiegeln, sowird deutlich dass diese Formeln nichts an-deres sind als die Entnormierung von R usw.

Leistung an der Lastimpedanz ()

PW =1

2

|Umax|2

VSWR · Z`

=1

2

|Umin|2

m · Z`, mit m = 1

VSWR

So benötigt man ZA nicht bestimmen um dieLeistung daran zu berechnen.

Der Rechteckhohlleiter

cutoff-Frequenz ()

fc =c0

2π√µr�r

qH

qH = π

√(ma

)2+(nb

)2Für den Hmn Feldtyp. Die E-Feld Moden be-rechnen sich analog. Es gibt hier aber keineEm0 und E0n Moden.

Dämpfungsmaß des verlustlosen Hohlleiters ()

αH = qH√1− Ω2 , mit Ω = f

fc

Dies gilt im Fall er Wellenausbreitung, nichtim Dämpfungsfall!!

75


H10-Welle im Rechteckhohlleiter ([6], Formel 12.129ff, S. 185)

λH10λ

=1√

1−(

λ2a

) Am besten dortn nachschaun. Die Wellen-länge wird halt oft gebraucht.Wirkleistung der H10-Welle ([6], Formel 12.141f)

P10 =ab

4

∣∣∣Ey (x = a2

)∣∣∣2 1ZFH10

=ab

4

∣∣∣Hx (x = a2

)∣∣∣2 ZFH10An der Stelle x = a

2ist das Maximum des

Feldes.

Dämpfung durch Wandverluste ([6], Formel 12.152)

αWand,H10 =R�ZF

·Ω2 + 2 b

a

bΩ√Ω2 − 1

Mit Ω = ffc,H10

. Sack mühsam zu tippen...grml.

Koaxialleitung

[6, S. 192ff].Transportierte Wirkleistung ([6], Formel 13.111)

P =1

2Û Î =

1

2

Û2

Z`=

1

2Î2Z`

Phasengeschwindigkeit ()

vPh =c0√�rµr

Ganz normal wie im Dielektrikum

Phasenmaß ([6], Formel 13.14)

β =2π

λ=ω

c0

√�rµr

76

6.1. PB

Induktivitätsbelag ([6], Formel 13.15)

L′=µ0µr2π

lna

b

Kapazitätsbelag ([6], Formel 13.16)

C′=

2π�r�0ln a

b

Leitungswellenwiderstand ([6], Formel 13.17)

Z` = 60Ω

√µr�r

lna

bFolgt aus Z` =

√L′

C′.


α ≈ R′

2Z`+G

′Z`2

= αL + αD

Gilt für geringe Verluste.αL: LeitungsverlusteαD: dielektrische Verluste

Das Smith-Diagramm

Ein paar Grundregeln Sozusagen die Verkehrsregeln, wie man da mit dem Zirkel drauf-rumschrubben darf.

• Alle Impedanzen und Admittanzen werden normiert!

• Durch Spiegelung am Ursprung wandelt man eine Impedanz in eine Admittanzum (und umgedreht)

• Umaufrichtung füerLeitungen is von Last zur Quelle im Uhrzeigersinn

• Beim Impedanzdiagramm wird I von rechts aufgetragen, U von links. Entspre-chend umgedreht gilt das beim Admittanzdiagramm

• VSWR wird vom 0-Punkt aus gemessen und oben angetragen.

• Die Reflexionsfaktoren werden vom Mittelpunkt des SD gemessen und oben ange-tragen

77


6.2. HF

6.2.1. Streuparameter

Wellengrößen ()

ai =1

2

(Ui√ZLi

+√ZLiIi

)bi =

1

2

(Ui√ZLi

−√ZLiIi

) ai: hinlaufende Wellebi: zurücklaufende WelleStreuparametermatrix ()

(b1b2

)=

(S11 S12S21 S22

)·(a1a2

)=

(T12T22

det(T )T22

1T22

−T21T22

)·(a1a2

) für Zweitor

Transmissionsparametermatrix ()

(b1a1

)=

(T11 T12T21 T22

)·(a2b2

)=

(− det(S)

S21

S11S21

−S22S21

1S21

)·(a2b2

) Achtung: a und b kann jeweils auch ver-tauscht werden, dann müssen die Indicesebenfalls vertauscht werden.

Reflexionskoeffizient ()

Sii =ZiE − ZLiZiE + ZLi

= riE

Abschluss eines Zweitores mit angepasstemAbschlusswiderstand. Das gibt dann an, wasdas Zweitor an und für sich reflektiert

Reflexionsfaktortransformation ()

r1E = S11 + r2S12S21

1− r2S22r2 =

Z2 − ZL2Z2 + ZL2

Wenn das Zweitor mit Z2 statt ZL2 abge-schlossen ist, gibt sich eine Reflexion amEnde mit dem Reflexionsfaktor r2. DieserTransformiert sich über das Zweitor als r1E.

78

6.2. HF

Transmissionsparameter ()

Streuparameter einiger HF-Komponenten

Wellenquelle ()

Leitung ()

S =

(0 e−γl

e−γl 0

)Dämpfungsglied ()

S =

(0 s12s21 0

)|s21| = |s12| ≤ 0

a = 20 lg1

|221|dB

Phasenschieber ()

S =

(0 ejβl

ejβl 0

)Richtungsleitung ()

S =

(0 0ejϕ 0

)Asymmetrischer Phasenschieber ()

79


Dreitorzirkulator ()

Richtkoppler ()

Wilkinson-Leistungsteiler ()

6.3. Antennen

Feldstärkerichtcharakteristik ()

CE,H(ϑ, ϕ) =

∣∣∣∣Et(ϑ, ϕ)Et,max∣∣∣∣ = ∣∣∣∣Ht(ϑ, ϕ)Ht,max

∣∣∣∣Leistungsdichterichtcharakteristik ()

CS(ϑ, ϕ) =

∣∣∣∣S(ϑ, ϕ)Smax∣∣∣∣

6.3.1. AntennentypenPatchantennen

Inset feed und so kram...

80

7. Photonik

Energie ()

E = hν = hc

λ= h · f

Kennt mer ja. Die Energier von Photonenist hier gequantelt, d. h. es ist hier jeweilsdie Energie eines einzelnen Photons.

Phasenmaß ()

β =2π

λ

7.1. Akives Medium

Besetzungsdichtenverhältnis ()

NνNµ

= e−Wν−Wµ

kT

Das ist im Endeffekt die Boltzmann-Verteilung

Natürliche Linienbreite ()

∆fn =1

2π

(1

τ1+

1

τ2

) τ bezeichnet hier die Lebensdauer der Zu-stände

Druckverbreiterung ()

∆fn =1

2π

(1

τ1+

1

τ2

)=

1

πτs

∆fn =

√3

4mkTd2p

Hierbei ist τs = τ1 = τ2 als mittlere Zeitzwischen zwei Stößend: Durchmesser des Mikrosystemsp: Gasdruck / Partialdruckm: Masse des Mikrosystems

81

7. Photonik

Lorenzprofil ()

γL(t) =2

π∆fL

(∆fL/2)2

(f − f0)2 + (∆fL/2)2∆fL: Linienbreite

Dopplerverbreiterung ()

∆fD =2fcc

√2kT ln 2

m

m: Masse des Mikrosystemsfc: Mittenfrequenz

Gauß-Profil ()

γG(t) =2√

ln(2)√π∆fG

e− (f−f0)

2

(∆fG/2)2 ln(2) ∆fG: Linienbreite

Ratengleichung ()

− dd t

[N2(t)−N20] = A12 [N2(t)−N20]

N10:N1:N20:N2:A12 =

1τ12

:

Absorbtion ()

dN1d t

= R21N1 = −σ21N1φ

dN1d t

=dΦ

d t=

dφ

dxmit Φ = φ

c

Φ: Photonen pro Volumenφ: Photononen pro Zeit und Fläche. Photo-nenflussdichte

Optische Leistungsdichte ()

I = hfφ

Beer-Lambertsches Absorbtionsgesetz ()

d I

dx|Abs. = −σ21N1I = −aI

α = 2a muss ich nochmal nachschaun...

82

7.2. Gauß-Strahl

7.2. Gauß-Strahl

Divergenzwinkel ()

Θ =λ

πw0=w0zR

Einheit mrad

Krümmungsradius ()

R(z) = zR,x,y

(z

zR,x,y+zR,x,yz

)Rayleight-Länge ()

zR =2πw20x,0y

λ

Strahlparameterprodukt ()

SPP = w0Θ =λ

π

Gilt für den Grundmode.[SPP ] = mm mrad

SPP höherer Moden ()

w0x,m = w0x√2m+ 1

Θx,m = Θx√2m+ 1

w0y,n = w0y√2n+ 1

Θy,n = Θy√2n+ 1

Und dann ins SPP des Grundmodes einset-zen

7.3. ResonatorenBei sphärischen Spiegeln gilt:

L: Länge des Resonatorsρ1, ρ2: Krümmungsradien der Spiegelz1, z2: Spiegelabstände zum Tallienortw0, w1, w2: Tallienradius, Radius der Spiegel

83

7. Photonik

g-Parameter ()

g1 = 1−L

ρ1

g2 = 1−L

ρ2

Strahlweite ()

w21 =

√(λρ1π

)2ρ2 − Lρ1 − L

(L

ρ1 + ρ2 − L

)=Lλ

π

√g2

g1(1− g1g2)

Andersrum einfach Idices vertauschen. Giltfür Strahlradius am Ort vom Spielgel 1

Taillenradius ()

w20 =Lλ

π

√g1g2(1− g1g2)

(g1 + g2 − 2g1g2)2

Kleinsignalverstärkung ()

gks = (N20 −N10)λ2

8πτspontγ(t)

γ(t): LinienprofilfunktionN20−N10: anfängliche Besetzugsdichtediffe-renz

()

Gks = egks2La

Anschwingbedingung ()

GksV = R1R2T egks2La ≥ 1

Da kann mit Kleinsignalverstärkung gerech-net werden

Stabilitätsbedingung ()

0 ≤ g1 · g2 ≤ 1Ansonsten kommt in der Wurzel was nega-tives

84

7.4. Gaslaser

7.4. Gaslaser

Puh...

7.5. Laserdioden

So funktionsweise und Aufbauten...DFB. Also mit dem lambda / 2... Schaff ich jetzt nur nimmer... Sorry!

7.6. Lichtwellenleiter

Maximaler Einkopplungswinkel ()

Θi,c = arcsin1

n0

√n2k − n2M

Numerische Apertur ()

NA = sinΘi,c =1

n0

√n2k − n2M

Faserparameter V ()

V =2πρ

λNA

Multimodig ab V ≥ 2, 405. Anzahl der Mo-den M ≈ V 2

2

Dispersion und Dispersionskonstante ()

∆T = D · L ·∆λ

D =d β1dλ

= −2πcλ2

β2

[D] = ps/nmkm

85

7. Photonik

7.7. Photonik 27.7.1. Polarisation

Stokes-Vektor ()

~S =

S0S1S2S3

=

2P02P1 − 2P02P2 − 2P02P3 − 2P0

S0: GesamtleistungS1: Linear H-VS2: Linear ±45◦S3: RZP - LZPBildung der Leistungen: Die Leistung wirdauf vier Pfade aufgeteilt. P0 ist 50% ge-dämpfte Gesamtleistung, P1 ist die Leistungdes linear horizontal Polarisierten Lichts, P2die des um +45circ polarisierten und P3 diedes rechtszirkular polarisierten.Wird meist auf S0 normiert.

Polarisationsgrad ()

DOP =√S21 + S

22 + S

23

S0

Poincare-Kugel ()

Fasst man den Stokes Vektor auf als ~S3D =~exS1 + ~eyS2 + ~ezS3 und spannt damit einKoordinatensystem auf, so entsteht diesePoincare-Kugel.

86

8. Regelungstechnik

8.1. Regelungstechnik A

Es empfiehlt sich, SiSy und GET3 nochmal anzuschauen. Die Beiblätter ( ) sind eben-falls nützlich.

Prinzipielles Vorgehen:

1. Beschreibung des Systems im Frequenzbereich

2. Darstellen als System und Linearisierung gemäß Kapitel 8.1.1

3. Untersuchung auf Stabilität gemäß Kapitel 8.1.2

4. Herauslesen von Anforderungen an den Regler aus den Stabilitätsbedingungen

5. Wahl eines Reglers und Auslegung gemäß Kapitel 8.1.3

8.1.1. ModellbildungEs sind grob folgende Schritte zu tun:

1. Bestimmen der beschreibenden Gleichungen und Zeichnen des Struckturbildes

2. Bestimmung des Betriebspunktes

3. Angeben der Betriebspunktabweichungen in der Form ∆x = x(t)− xB

4. Linearisierung aller nichtlinearen Gleider (also alles wie multiplizierer und nichtli-neare Fkts) des Systems im Betriebspunkt (Taylorreihe)

5. Zeichnen des neuen, linearisierten StruckturbildesEinfaches ersetzen der Funktionalen Glieder durch die linearisierten Funktio-

nenBeachten der linearisiert Gleichung der Multiplizierer: Diese werden zu Sum-

men. Hierzu die Gleichungen vergleichen

87

Universität Erlangen-Nürnberg Lehrstuhl für Regelungstechnik

Prof. Dr.-Ing. Günter Roppenecker

Regelungstechnik A

Beiblatt 1/1

Christopher Beck 28. Dezember 2018 - ETG Kurzschluss€¦ · Vorwort LiebeLeser,...

Documents

Transcript of Christopher Beck 28. Dezember 2018 - ETG Kurzschluss€¦ · Vorwort LiebeLeser,...