Differentialquotient dy/dx := lim y/ x D D D für x -> 0c) y(x) = ex => y(x)'= ex: Der Anstieg der...

© J. & H-T. Tomiska 2010: Mathematikskizzen Teil 3 1

3. Differentialrechnung

3.1. Differentialquotient, Ableitung und Differential

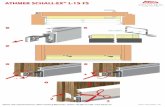
Differentialquotient dy/dx := lim y/ x D D Dfür x -> 0

x = x + x0 D Werteachse x

Winkel a

y(x + x)0 D

a

Bildachse y

Sekante:

D D D Dy/ x := [y(x + x) - y(x )]/ x0 0

Funktion y = f(x )

x0

y(x )0

Tangente in x0

o Die Sekante wird im Grenzfall (Δx 0) zur Tangente im Punkt (x0, y(x0)).

o Kurvenanstieg im Punkt (x0, y(x0)) ist per def. der Anstieg der Tangente in (x0, y(x0)).

o Differentialquotient: per def. der Limes der Differenzquotienten:

lim Δy(x) / Δx = [y(x) - y(x0)] / [x - x0]

= lim [y(x0+ Δx) - f(x0)]/ Δx

:= d [y(x0)] / dx

= [d/dx] y(x0)

:= y’(x0).

Der Differentialquotient d[y(x0)]/dx heißt auch „Ableitung“ der Funktion y(x) im Punkte

(x0, y(x0)).

o Differential: per def. die Änderung der Tangentenordinate: dy(x) := y’(x) . dx.

o Differenzierbar: Eine Funktion y(x) ist im Punkt (x0, y(x0)) differenzierbar, wenn sie in

der Umgebung ε dieses Punktes definiert ist (also in ε stetig ist) und der linksseitige

Limes = den rechtsseitigen Limes ist. Ist eine Funktion in allen Punkten eines Inter-

valls differenzierbar, dann ist sie „In diesem Intervall differenzierbar“.


3.2. Die Ableitungsregeln

3.2-1 Die 3 grundlegenden Ableitungsregeln

a) y(x) = Const => y(x)' = 0:

Der Graph einer konstanten Funktion ist eine Gerade mit Anstieg 0.

b) y(x) = x => y(x)’ = 1:

Der Graph der identischen Funktion ist eine Gerade mit Anstieg 1.

c) y(x) = ex => y(x)'= ex:

Der Anstieg der Exponentialfunktion ist in jedem Punkt gleich dem Funktionswert (ei-

ne weitere Besonderheit des „exponentiellen Wachstums“). Mit genau dieser Voraus-

setzung wurde die Zahl e als natürliche Basis der Exponentialfunktionen erhalten. Die

rigorose Herleitung dieses Ergebnisses erfordert allerdings tiefere Kenntnisse der

Operationen an Folgen und Reihen („gleichmäßige Konvergenz“).

Aus diesen drei grundlegenden Ableitungsregeln können wir alle anderen Regeln für das

Ableiten aller analytischen Funktionen herleiten.

3.2-2 Ableitungsregeln II. Für Funktionen, die sich als Summe, Differenz, Produkt oder

Quotient von anderen Funktionen darstellen, gibt es Regeln, welche die Ableitung der Ge-

samtfunktion auf die Ableitungen ihrer Teile zurückführen. Diese Regeln bilden drei Grup-

pen:

a) Summe: [f+g]’(x) = f’(x) + g’(x)

b) Vielfaches: [c.f]’(x) = c.f’(x)

c) Produkt: [f . g]’(x) = f’(x) . g(x) + f(x) + g’(x)

[f1 . f2 . f3 . ...]’(x) = f1’(x) . f2(x) . f3(x) . ... + f1(x) . f2’(x) . f3(x) . ... + ...

c-1) Potenz: (xn)’ = n.xn-1.

c-2) Quotient: [f(x) /g(x)]’ = [f’(x) . g(x) - f(x) . g’(x)] / [g(x)]²

Die Quotientenregel sollte allerdings nur dann verwendet werden, wenn wir

viele solcher Ableitungen berechnen müssen. Ansonsten ist es besser,

f(x)/g(x) = f(x) . g(x)-1 zu schreiben, und die Produktregel zu benützen.


Beispiele: ______________________________________________________________

________________________________________________________________________

3.2-3 Ableitung von zusammengesetzten Funktionen.

o Kettenregel: [f°g]’(x) = [f(g(x))]’ = [df(u)/du] . [du(x)/dx] mit u = g(x).

o Fortgesetzte Kettenregel: [f°g°...°h]’(x) = df/dg . dg/dh . ... . dh/dx

Beispiele: _________________________________________________________

________________________________________________________________________


3.2-4 Ableitungen von elementaren Funktionen. Alle Ableitungen können im Prinzip auf

die drei fundamentalen Bausteine zurückgeführt werden. Es ist jedoch einfacher, beim Diffe-

renzieren mit dem erweiterten Bausteinsatz der Ableitungen aller elementaren Funktionen zu

arbeiten. Diese sind in der folgenden Tabelle zusammengestellt (aus Bartsch, S 443f).

f(x) f’(x) Bedingungen

ax ax.ln a*) a>0

ln x 1/x x>0

alog x 1/(x.ln a) a1, x>0

sin x cos x

cos x -sin x*2)

tan x 1/cos² x = 1 + tan² x*3) x(2k+1)/2, k = Z

cot x -1/sin² x = -(1+cot²x) xk, k = Z

*) ax = (exp (ln a))x; Substituieren u := x.ln a => ax = eu;

=> d(eu)/dx = d(eu)/du . du/dx = eu . ln a = (exp (ln a))x . ln a = ax . ln a

*2) Dies folgt aus der e-Potenzdarstellung von sin x und cos x:

sin x = [eix - e-ix] / (2i) => sin’ x = [i. eix - (-i). e-ix] / (2i) = [ieix + e-ix] / 2 = cos x.

*3) tan’ x = (sin x / cos x)’ = sin’ x / cos x + sin x . (1 / cos x)’ = 1 + (sin x/cos² x).sin x

wegen 1 + tan² x = cos²/cos² + sin²/cos² = 1 / cos² = tan’ x.


3.2-5 Ableitung der Umkehrfunktionen y = f(x) <=> x = f-1(y) = g(y).

Die Umkehrfunktion x = f-1(y) = g(y) einer differenzierbaren Funktion y = f(x) ist in y differen-

zierbar, wenn y’ = f’(x) 0. Die Ableitung von dx/dy = dg(y)/dy = df-1(y)/dy ist der Kehrwert

der Ableitung von y = f(x).

dx/dy = dg(y)/dy = 1/f’(x) = 1/[df(x)/dx] = 1/[dy/dx].

=> dx/dy = 1/[dy/dx].

Beispiel: ______________________________________________________________

f(x) =y = tan x => g(y) = x = arctan y.

f’(x) = 1+ tan² x => g’(y) = 1/f’ = 1/(1+ tan² x)

wegen tan x = y => dg(y)/dy = 1/(1+y²).

________________________________________________________________________


3.3 „Höhere Ableitungen“

Ist f'(x) eine differenzierbare Funktion, so kann sie selbstverständlich ebenfalls abgeleitet

werden:

d [f(x)’] / dx := f’’(x); f’’(x=x0) heißt 2. Ableitung von f im Punkt x0.

Manchmal auch:

Analog werden die 3. Ableitung f’’’(x) und alle höheren Ableitungen f(n)(x ) (die n-ten Ablei-

tungen) gebildet - sofern sie existieren. Eine Funktion f(x) heißt n-mal differenzierbar, wenn

ihre n-te Ableitung existiert.

Beispiele: ______________________________________________________________

(i)

(ii)

(iii) Höhere Ableitungen von Potenzen

Die Potenzfunktionen xn, nЄN, können genau (n+1)-mal abgeleitet werden, die n-te Ablei-

tung ist eine Konstante, die (n+1)-te Ableitung ist identisch 0.

(iv)

_______________________________________________________________________


3.4 Kurvencharakteristika

3.4-1 (Erste) Ableitung: Anstieg der „Kurven“. Hat eine differenzierbare Funktion f(x) in

x0 ein (lokales) Extremum, so verschwindet dort die 1. Ableitung, f’(x0) = 0. Dieser Satz ist

aber nicht umkehrbar, denn bei f’(x0) = 0, muss keineswegs ein Extremwert vorliegen, es

kann hier auch ein Wendepunkt mit horizontaler Wendetangente vorliegen.

Beispiele: ______________________________________________________________

f(x) = x³:

__________________________________________________________________

3.4-2 Zweite Ableitung: Krümmung und Wendepunkte.


Beispiele: ______________________________________________________________

3.4-3 Globale (absolute) Extremwerte. Das globale oder absolute Maximum (Minimum)

einer Funktion ist der größte bzw. der kleinste Wert, der von der Funktion auf ihrem Definiti-

onsbereich oder auf einem einschränkenden Intervall angenommen wird. Solch ein Wert

muss nicht existieren! Über globale Extrema kann man jedoch einige ganz allgemeine Aus-

sagen machen. Auf einem abgeschlossenen Intervall [a, b] haben stetige Funktionen ein

globales Maximum und ein globales Minimum (Satz vom Maximum und vom Minimum). An

der Stelle eines absoluten Extremwertes verschwindet entweder die 1. Ableitung oder aber

ist sie nicht existent! (Etwa an den Randpunkten eines geschlossenen Intervalls).


Die tatsächlichen globalen Extrema findet man mittels einer Wertetabelle, die jeweils sämtli-

che Kandidaten enthält (bei offenen Intervallen zum Vergleich auch die Grenzwerte in den

Randpunkten).

3.4-4 Kurvendiskussion. Die Ermittlung der qualitativen Eigenschaften einer gegebenen

Funktion f und die anschauliche Deutung der Eigenschaften ihres Graphen, der Kurve y -

f(x)=0, heißt Kurvendiskussion. Die dazu nötigen Daten umfassen vor allem die Nullpunkte,

kritischen (stationären) Punkte, Wendepunkte und Ausnahmepunkte und das asymptotische

Verhalten der Funktion. Eine Kurvendiskussion ist vollständig, wenn der Verlauf des Gra-

phen zweifelsfrei skizziert werden kann.

(i) Definitionsbereich: Erlaubte Werte für x

(ii) Periodizität: f(x) = f(x+ a.T)

(iii) Symmetrie: f(x) = f(-x); f(x) = -f(-x)

(iv) Unendlichkeitsstellen (Pole): f(x) mit vertikalen Asymptoten

(v) Verhalten im Unendlichen: f(x) , Asymptoten

(vi) Differenzierbarkeit: f’(x), f’’(x), ... f(n)(x)

(vii) Nullstellen: f(xN) = 0

(viii) Extrempunkte: f’(xE) = 0 und f’’(xE) 0;

f’(xE) = f’’(xE) = ... = f(2k-1)(xE) = 0 und f(2k)(xE) 0

(ix) Wendepunkte: f’’(xW) = 0 und f’(xW) 0;

f’(xW) = f’’(xW) = ... = f(2k)(xW) = 0 und f(2k+1)(xW) 0

(x) Wertebereich: Mögliche Werte von f(x)

(xi) Graph

Beispiel: f(x) = x4 - 4x³ + 4x² ___________________________________

Parabel (Polynom) 4-ten Grades

(i) Definitionsbereich: R

(ii) Periodizität: keine

(iii) Symmetrie: weder gerade noch ungerade

(iv) Unendlichkeitsstellen (Pole): keine

(v) Verhalten im Unendlichen: höchste Potenz entscheidend: f()

keine Asymptoten


(vi) Differenzierbarkeit: 4-mal

f’(x) = 4x3 - 12x² + 8x = 4x(x² - 3x + 2)

f’’(x) = 12x² - 24x + 8 = 4(3x² - 6x + 2)

(vii) Nullstellen: f(xN) = xN4 - 4xN³ + 4xN² =

= xN²(xN² - 4xN +4) = xN²(xN-2)² = 0

=> xN1,2 = 0; xN3,4 = 2

(viii) Extrempunkte: f’(xE) = 4xE(xE² - 3xE +2) = 0

=> xE1 = 0; xE2 = 1; xE2 = 2;

f’’(0) = 8 > 0 => Minimum;

f’’(1) = -4 < 0 => Maximum;

f’’(2) = 8 > 0 => Minimum;

(ix) Wendepunkte: f’’(xW) = 4(3xW² - 6xW + 2) = 0 => xW1,2 = 1 ± 1/3

=> xW1 = 0.423; xW2 = 1.577;

(x) Wertebereich:

x: 0 1 2 0.423 1.577 3 4 -1 -2

y: 0 1 0 0.444 0.444 9 64 9 64

(xi) Graph


Beispiel: y = f(x) = x / [1 - x²] ___________________________________

Im Prinzip eine Hyperbel, die in der Nähe des Ursprungs gestört wird.

(i) Definitionsbereich: R \ Polstellen

(ii) Periodizität: keine

(iii) Symmetrie: gespiegelt am Ursprung, ungerade

(= sowohl an x- als auch an y-Achse)

(iv) Unendlichkeitsstellen (Pole): 1-x² = 0 => xP1,2 = ±1

(v) Verhalten im Unendlichen: f(-∞) +0; f(∞) → -0, Asymptote = x-Achse

(vi) Differenzierbarkeit: f’(x) = [1+x²] /[1-x²]²

f’’(x) = 2x[3+x²] /[1-x²]³

(vii) Nullstellen: f(xN) = 0: Zähler = x = 0 => xN = 0

(viii) Extrempunkte: f’(xE) = 0: Zähler = 1+x² = 0 => keiner

(ix) Wendepunkte: f’’(xW) = 0: Zähler = 2x[3+x²] = 0 => xW = 0

(x) Wertebereich:

(xi) Graph

2 Polstellen; links und rechts Hyperbelähnlich; insgesamt zusammengesetzt.


3.5 Optimierungsaufgaben

Minimums- und Maximumsbestimmung, die Frage nach dem größten oder kleinsten Wert

einer Variablen, nach ihrem Maximum und Minimum, und unter welchen Bedingungen diese

erreicht werden, ist eines der wesentlichen Probleme in Wissenschaft, Technik und Ökono-

mie. Sie betrifft die Optimierung von Prozessen und Resultaten, und ist eine der wichtigsten

Anwendungen der Mathematik.

Beispiel: ______________________________________________________________

Der Wärmeverlust eines Körpers ist umso größer, je größer seine Oberfläche ist. Wir lösen

nun folgendes Optimierungsproblem: Ein Quader mit quadratischer Grundfläche und vorge-

gebenem Volumen V soll möglichst wenig Wärmeverlust aufweisen. Wie ist das Verhältnis

von Seitenlänge a und Höhe h zu wählen?

Die Oberfläche F ergibt sich als Summe aus der doppelten quadratischen Grundfläche a²

und dem Vierfachen der Fläche a.h eines Mantelrechtecks:

(1) F = 2a² + 4a.h.

Die Frage ist die nach dem Minimum der Oberfläche F bei gegebenem Volumen

(2) V = a².h.

Gl.(2) erlaubt uns, entweder a durch h oder - völlig gleichwertig - umgekehrt h durch

a auszudrücken. Ein Blick auf Gl.(1) zeigt, dass wir weniger Rechenaufwand haben,

wenn wir h = V/ a² setzen.

In Gl.(1) eingesetzt, erhalten wir: F = 2a² + 4a.V/a² = 2a² + 4V/a.

Damit ist F’(a) = 4a - 4V/a² = 0 zu lösen.

=> aE³ = V; => h = aE³/aE² = aE, also ein Würfel.

Prüfung, ob der Würfel tatsächlich die minimale Oberfläche F besitzt:

F’’(aE) = 4 + 8V/aE³ > 0 ?

Immer, denn beide Summanden sind positiv definit (ausgerechnet: F’’(aE) = 4+8aE³/aE³ = 12).

__________________________________________________


3.6 Unbestimmte Werte und die Regeln von de l’Hospital

Die Regeln von de l’Hospital sind Anleitungen zur Behandlung von unbestimmten Ausdrü-

cken der Form 0/0 und /. Andere unbestimmte Ausdrücke wie 0., 00, 0, 1,... lassen

sich durch Umformung auf eine der beiden Standardformen überführen.

Regel von de l’Hospital: Sind f(x) und g(x) in der Umgebung U(x0) von x0 differenzierbare

Funktionen und ist g(x) 0 in U(x0)\{x0}, dann gilt:

Bei der Regel von de l’Hospital müssen wir den Zähler f(x) und den Nenner g(x) un-

abhängig voneinander differenzieren, und danach erst den Bruch [f’(x) / g’(x)] bilden (Keine

Quotientenregel anwenden!).

Ist dieser Ausdruck für x x0 wiederum ein unbestimmter, dann ist erneut die Regel

von de l’Hospital anzuwenden (vorher gegebenenfalls immer umformen)... Abbruch, sobald

sich als Limes kein unbestimmter Ausdruck ergibt.

Beispiele: ____________________________________________________


3.7 Näherungsweise Lösungen von Gleichungen

Die Mehrzahl der Gleichungen vom Typ g(x) = h(x) kann nicht analytisch gelöst werden. Eine

Möglichkeit zur Bestimmung der Lösungen ist die grafische Methode: man konstruiert die ei-

den Graphen und bestimmt deren Schnittpunkte. In der Praxis greift man aber besser auf

numerische Näherungslösungen zurück. Wenn auch manche Probleme durch den Einsatz

von Papier und Bleistift zu knacken sind (und vormals auch so geknackt wurden), so stellen

diese numerischen Verfahren doch typische Computeranwendungen dar.

Es ist vorteilhaft, die Lösung der Gleichung als Nullstellenbestimmung anzusetzen,

indem man die Hilfsfunktion f = g – h definiert und die Gleichung f(x) = 0 löst.

o Nullstellenbestimmung. Eine effiziente Methode zur numerischen Nullstellenbe-

stimmung ist das Newton-Verfahren. Es beruht auf folgender Beobachtung:

Ist f eine auf ( a, b ) differenzierbare Funktion mit Nullstelle x0(a, b), und ist x1 eine

Näherungslösung zu f(x) = 0, für die eine der beiden Bedingungen

(a) f’(x1) > 0 und f’’(x1) > 0; oder (b) f’(x1) < 0 und f’’(x1) < 0,

gilt, so ist

x2 = x1 - f(x1) / f’(x1)

eine bessere Näherungslösung als x1, d.h., x2 liegt näher an der Nullstelle x0 als x1 (|x2 - x0| <

|x1 - x0|). Die Methode wird mit x2 als neuem Startwert fortgesetzt, und iterativ immer weiter

mit

xn+1 = xn - f(xn) / f’(xn),

bis die gewünschte Lösungsgenauigkeit erfüllt ist, wie etwa ( = 10-k, kN):

|f(xn+1)| < ,

oder

|xn+1 - xn| < .


Bild: Geeignete und ungeeignete Startwerte für das Newton-Verfahren.

Links: Konvergenz durch geeigneten Startwert x1. Rechts: Ungeeigneter Startwert x1.

Es ist meist eine günstige Strategie, den Startwert x1 zunächst durch Intervallteilung

und Vorzeichentest einzuengen. Das Newton-Verfahren ist eine weitere Anwendung der li-

nearen Approximation: der Graph wird zur Nullstellenbestimmung jeweils durch eine Tan-

gente ersetzt.

Beispiel: Numerische Näherungslösung der Gl. ln x = sin x. ______________________

nur Bedingung (a) erfüllt ist, sondern der Funktionswert des Startwerts ebenfalls schon sehr klein ist

(0.033).


_________________________________________________________________

Differentialquotient dy/dx := lim y/ x D D D für x -> 0c) y(x) = ex => y(x)'= ex: Der Anstieg der...

Documents

Transcript of Differentialquotient dy/dx := lim y/ x D D D für x -> 0c) y(x) = ex => y(x)'= ex: Der Anstieg der...