PARABELN KREISE TANGENTEN · 2013-02-12 · - 1 - 5 5 10 15 x 8 6 4 2 2 4 6 8 y Scheitelkreis...

5 5 10 15 x

8

6

4

2

2

4

6

8

y

Scheitelkreis

Tangente t

Normale n

Achse a

Leitgerade

Scheiteltangente

l

p = 6 cm

M

B = Berührpunkt

S

Brennpunkt F

L

PARABELN

KREISE

TANGENTEN

UND

NORMALEN

11. Klasse, 2013

© Jens Möller

Owingen

Tel 07551-68289

[email protected]

FÜR INHALT

UND PERSÖNLICHE NOTIZEN

- 1 -

5 5 10 15 x

8

6

4

2

2

4

6

8

y

ScheitelkreisTangente t

Normale n

Achse a

Leitgerade

Scheiteltangente

l

p = 6 cm

MB = Berührpunkt

S

Brennpunkt F

L

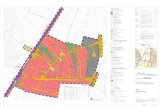
DIE PARABEL ALS GEOMETRISCHE ORTSLINIE

EIGENSCHAFTEN UND GESETZE

Die Parabel ist der geometrische Ort aller Punkte, die von einer festen Geraden (Leitgerade)

und einem festen Punkt F (Brennpunkt) gleichen Abstand haben. Der Abstand des

Brennpunktes von der Leitgeraden heißt Parameter p, dieser ist bestimmend für die Form der

Parabel.

Man kann beliebige Punkte der Parabel konstruieren, indem man den Brennpunkt F mit einem

beliebigen Punkt L (auf der Leitgeraden) verbindet, dann auf der Strecke FL das Mittellot t

errichtet und dieses anschließend mit einem achsenparallelen Strahl durch L schneidet. So

erhält man einen Parabelpunkt B, der gleichzeitig Berührpunkt für die Tangente t ist.

Errichtet man in B das Lot auf der Tangente t, so erhält man die sogenannte Normale n. Diese

verläuft parallel zur Strecke FL. Die Steigung der Normale kann man erhalten, indem man die

Steigung der Strecke FL bestimmt.

Der Scheitelkreis berührt die Parabel im Scheitelpunkt S, sein Mittelpunkt M liegt auf der

Parabel-Achse und sein Radius ist so groß wie der Parameter: r p .

Parallel zur Parabel-Achse einfallende Lichtstrahlen werden so reflektiert, dass diese sich im

Brennpunkt F treffen. Mit einem Parabolspiegel und Sonnenlicht kann man ein Feuer

entzünden.

- 2 -

AUFGABE A

Gegeben ist eine Parabel durch die Leitgerade y = 6 und den Brennpunkt F(0/0). Der

Parameter ist also p = 6.

Bestimme den Scheitelpunkt der Parabel, finde die beiden Punkte (Quadratecken), die von F

und der Leitgeraden den Abstand p haben. Konstruiere den Parabelpunkt B(8/...) und die

entsprechende Parabeltagente t. Konstruiere auch die NORMALE n in B.

Mache eine Zeichnung mit 1LE = 1cm.

Bestimme die Gleichung der Parabel.

[Ansatz: ²y a x c , setze zwei Punkte mit bekannten Koordinaten ein.]

Bestimme die Gleichung der Normale n in B.

[Suche in der Zeichnung ein geeignetes Steigungsdreieck, dann verwende: ( )1 1y y m x x .]

Bestimme die Gleichung der Tangente t in B.

[Steigung der Tangente: n

t m

1m ]

Die Tangente t, die Normale n und die y-Achse spannen ein Dreieck auf. Bestimme den

Flächeninhalt des Dreiecks mithilfe der Formel 2

hgA

Wie lautet die Gleichung des Scheitelkreises?

[Die allgemeine Kreisgleichung lautet: ²r)²yy()²xx( MM ]

Bestimme die Schnittpunkte des Scheitelkreises mit der x-Achse.

[Setze 0y in die Kreisgleichung ein, benutze die binomischen Formeln und löse die

quadratische Gleichung.]

Bestimme die Schnittpunkte der Parabel mit der Geraden 7 24 0x y .

Bestimme die Schnittpunkte des Scheitelkreises mit der Geraden 3 0y x .

- 3 -

-5 5 10 15

x

8

6

4

2

-2

-4

-6

-8

y

Scheitelkreis

a = Achse

Normale n

Leitgerade

Scheiteltangente

Tangente t

p = 6 cm

R

MB

S

F

L

LÖSUNGEN A

Gleichung der Parabel:

Ansatz [wegen Symmetrie] c²axy

Scheitelpunkt S(0/3) → 3cca03

Spezieller Punkt Q(6/0) → 121a3a360 [Q = Quadratecke]

Die Parabelgleichung lautet: 112: ² 3P y x

Gleichung der Normale n in B(8/...):

Aus dem Dreieck FLR mit R(8/0) erhält man: 43

86

nm

Aus der Parabelgleichung erhält man: 31

121

B 2364y

Mit )xx(myy 11 ergibt sich: )8x(2y 43

31 → 3 1

4 3: 8n y x

Gleichung der Tangente t in B:

Steigung der Tangente: 34

43

nt

1

m

1m

Mit )xx(myy 11 ergibt sich: )8x(2y 34

31 → 4 1

3 3: 8t y x

- 4 -

Flächeninhalt des Dreiecks aus t, n und y-Achse:

FE664162

8)88(

2

hgA 3

2323

131

Gleichung des Scheitelkreises?

Ansatz: ²r)²yy()²xx( MM | mit M(0/-3) und r = 6

²6)²3y()²0x(

: ² ( 3)² 36K x y

Schnittpunkte des Scheitelkreises mit der x-Achse:

Setze y = 0 in die Kreisgleichung ein:

/² ( )² ² ² ,1 2x 0 3 36 x 9 36 x 27 x 27 5 2

1 2(5, 2 / 0) ( 5, 2 / 0)N und N

Schnittpunkte der Parabel mit der Geraden 7x + 24y = 0:

3²xyundxy 121

247 gleichsetzen: 072x7²x23²xx 12

1247

)1/5,4(Bund)2/8(B 165

231

1

Schnittpunkte des Scheitelkreises mit der Geraden y + x – 3 = 0:

3xy einsetzen in die Kreisgleichung:

0x12²x23636x12²x²x36)²6x(²x36)²3y(²x

( ) 1 22x x 6 0 x 0 und x 6

( / ) ( / )1 2A 0 3 und A 6 3

- 5 -

AUFGABE B [WIEDERHOLUNG]

Gegeben ist eine Parabel durch die Leitgerade y = 6 und den Brennpunkt F(0/2).

Der Parameter ist also p = 4.

Bestimme den Scheitelpunkt der Parabel, finde die beiden Punkte Q (Quadratecken), die von

F und der Leitgeraden den Abstand p haben. Konstruiere den Parabelpunkt B(6/...) und die


a) Mache eine Zeichnung mit 1LE = 1cm.

b) Bestimme die Gleichung der Parabel.


c) Bestimme die Gleichung der Normale n in B.

[Suche in der Zeichnung ein geeignetes Steigungsdreieck, dann verwende:

( )1 1y y m x x ]

d) Bestimme die Gleichung der Tangente t in B.


t m

1m ]

e) Die Tangente t, die Normale n und die y-Achse spannen ein Dreieck auf. Bestimme den


hgA

f) Wie lautet die Gleichung des Scheitelkreises?


g) Bestimme die Schnittpunkte des Scheitelkreises mit der x-Achse.



h) Bestimme die Schnittpunkte der Parabel mit der Geraden 32 4y x .

i) Bestimme die Schnittpunkte des Scheitelkreises mit der Geraden 32 4y x .

- 6 -

x

y

t

n

B

L

Q

S

F

1

1

LÖSUNGEN B

a)

b) 18(0 / 2) (0 / 4) (4 / 2) ² ² 4F S Q y ax c y x

c) 18 6² 4 0,5 (6 / 0,5)By B und 4 2

6 3FLm

( )B By y m x x 2 23 3: 0,5 ( 6) 4,5n y x y x

d) 32: 8,5t y x

e) 12 (8,5 4,5) 6 39A FE

f) : ² ² 16K x y

g) 1/ 20 ² 16 ( 4 / 0)y x N

h) 318 2² 4 4 | 8 ² 32 12 32 ² 12 64 0x x x x x x

1 2(4 / 2) ( 16 / 28)S Q und S

i) 3 92 4² ( 4)² 16 ² ² 12 16x x x x x 16 13

40 ² 12 0 | 4x x

481 2 1313 ² 48 0 | (13 48) 0 0x x ausklammern x x x x

1 2(0 / 4) (3,692../1,538..)S und S [Zur Kontrolle zeichne die Gerade ein.]

- 7 -

AUFGABE C-1

Gegeben ist eine Parabel durch die Leitgerade 4y und den Brennpunkt F(0/1). Der










)xx(myy 11 ]



t m

1m ]


Flächeninhalt des Dreiecks mit Hilfe der Formel 2

hgA






h) Bestimme die Schnittpunkte der Parabel mit der Geraden 12 3,5y x .

i) Bestimme die Schnittpunkte des Scheitelkreises mit der Geraden 43 3,5y x .

- 8 -

x

y

n

t

D

C

Q

B

S

M

F

1

L

A

LÖSUNGEN C-1

a)

b) 110(0 /1) (0 / 1,5) (5 /1) ² ² 1,5 ( )F S Q y ax c y x nach oben geöffnet

c) 5 110 2(10 / 8,5) ( )n B BB und m y y m x x 1

2: 13,5n y x

d) (10 / 8,5) 2 ( )t B BB und m y y m x x : 2 11,5t y x

e) 12 (13,5 11,5) 10 125A FE

f) 2: ² ( 3,5) 25K x y

g) 1/20 ² 12,25 25 ( 3,57 / 0)y x N

h) 1 110 2² 1,5 3,5 | 10 ² 15 5 35 ² 5 50 0x x x x x x

1 2( 5 /1) (10 / 8,5)S A und S B

i) 43² ( 3,5 3,5x x 2 16

9) 25 ² ² 25 | 9 9 ² 16 ² 225 ² 9 |x x x x x

1 2( 3 / 0,5) (3 / 7,5)S D und S C [Zur Kontrolle zeichne die Gerade ein.]

- 9 -

AUFGABE C-2

Gegeben ist eine Parabel durch die Leitgerade 3y und den Brennpunkt F(0/1). Der




entsprechende Parabeltagente t. Konstruiere auch die Normale n in B.






)xx(myy 11 ]



t m

1m ]



hgA






h) Bestimme die Schnittpunkte der Parabel mit der Geraden 12 3y x .

i) Bestimme die Schnittpunkte des Scheitelkreises mit der Geraden 7y x .

- 10 -

x

y

C

L

B

F

1

D

A

LÖSUNGEN C-2

a)

b) 18(0 /1) (0 / 1) (4 /1) ² ² 1 ( )F S Q y ax c y x nach oben geöffnet

c) 4 26 3(6 / 3,5) ( )n B BB und m y y m x x 2

3: 7,5n y x

d) 32(6 / 3,5) ( )t B BB und m y y m x x 3

2: 5,5t y x

e) 12 (7,5 5,5) 6 39A FE

f) 2: ² ( 3) 16K x y

g) 1/20 ² 9 16 ( 2,65 / 0)y x N

h) 1 18 2² 1 3 | 8 ² 8 4 24 ² 4 32 0x x x x x x

1 2( 4 /1) (8 / 7)S A und S

i) 2² ( 7 3) 16 ² ² 8 16x x x x x 16 2 ² 8 0 (2 8) 0x x x x

1 2(0 / 7) ( 4 / 3)S C und S D [Zur Kontrolle zeichne die Gerade ein.]

- 11 -

AUFGABE D [WIEDERHOLUNG DREIECK UND PARABEL]

Ein Dreieck ist gegeben durch die drei Punkte A(-2/0), B(8/2) und C(2/8).

a) Zeichne das Dreieck (1LE = 1cm) mit allen drei Höhen und dem Höhenschnittpunkt H.

b) Bestimme die Gleichungen der Höhen ha und hb.

c) Berechne den Höhenschnittpunkt.

d) Stelle die Gleichung der Parabel auf, die durch die Punkte A, B und C geht.

e) Zeichne die Parabel mit der Gleichung 0,3 ² 2 5,2y x x in das vorhandene

Koordinatensystem ein.

WERTETABELLE Ergänze die fehlenden y-Werte

x -2 -1 0 1 2 3 4 5 6 7 8

y 0 8 2

f) Wo schneidet die Parabel die x-Achse?

g) In welchen Punkten schneidet die Gerade g mit der Gleichung y = 2x + 4 die Parabel?

- 12 -

x

y

H

C

B

A

1

1

LÖSUNGEN D

a)

b) 12: 2 : 6 : 5 18a b ch y x h y x h y x

c) 2 23 3(2 / 4 )H

d) PARABELGLEICHUNG

ANSATZ ycbx²ax

A → 0cb2a4

B → 2cb8a64 lasse zuerst c herausfallen

C → 8cb2a4 (zweimal)

Ergebnis: 0,3 ² 2 5,2y x x

e) Wertetabelle:

x -2 -1 0 1 2 3 4 5 6 7 8

y 0 2,9 5,2 6,9 8 8,5 8,4 7,7 6,4 4,5 2

Zeichnung der Parabel

Mitternachtsformel: a2

ac4²bbx 2/1

f) Nullstellen: )0/2(N1 und )0/8(N 32

2

g) Schnittpunkte: )0/2(S1 und )8/2(S2

- 13 -

-10 -5 5 10

x

4

2

-2

-4

-6

y

p p = 6 cm

Q(p/0)

S

F

L

PARABEL UND BRENNPUNKT

Kann man aus einer Parabelgleichung auf die Größe des Parameters p und auf die Lage des

Brennpunktes F schließen?

Zunächst soll eine Parabel untersucht werden, deren Brennpunkt F im Koordinatenursprung

und dessen Scheitel S auf der y-Achse liegt. So eine Parabel hat die Gleichung c²axy ,

wobei die Koeffizienten a und c sowohl positive als auch negative Werte haben können.

Folgende Angaben sind bekannt

Brennpunkt: F(0/0)

Scheitelpunkt: S(0/- 2p ), die Parabel soll nach oben geöffnet sein.

Spezieller Punkt auf der x-Achse: Q(p/0) hat gleichen Abstand zur Leitgeraden und zu F.

Daraus ergibt sich

S(0/- 2p ) einsetzen: → c²axy → c02

p → 2pc

Q(p/0) einsetzen: → 2p²axy → 2

p²ap0 → p21a

→ 2p

p21 ²xy für nach oben geöffnete Parabeln.

Entsprechend → 2p

p21 ²xy für nach unten geöffnete Parabeln.

MERKE → 12 pa

- 14 -

Beispiel

Untersuche die Parabel mit der Gleichung 3²xy 121 . Bestimme den Parameter p, den

Scheitelpunkt S und den Brennpunkt F.

Lösung Aus p21a folgt: p2

1121 → p = -6 nach unten geöffnet

Aus c = 3 folgt: → S(0/3)

Aus c = 3 und 32p folgt: → F(0/0)

Beispiel



Lösung p21

81 → p = 4 nach oben geöffnet

c = -6 → S(0/-6)

c = -6 und 22p → F(0/-4)

Beispiel



Lösung p21

52 → 25,1p 4

5 nach oben geöffnet

c = -3 → S(0/-3)

c = -3 und 85

2p → )2/0(F 8

3

- 15 -

AUFGABE E

Gegeben ist eine Parabel mit der Gleichung 3²xy 81 .

Bestimme den Parameter p, den Scheitelpunkt S und den Brennpunkt F.

Zeichne die Parabel im Bereich 6x6 mithilfe einer Wertetabelle.

Wertetabelle: Ergänze die fehlenden y-Werte

x 0 ±1 ±2 ±3 ±4 ±5 ±6

y

Bestimme in B(6/...) die Gleichung der Normale n.

Bestimme in B(6/...) die Gleichung der Tangente t.


Flächeninhalt des Dreiecks mithilfe der Formel 2hgA

.

Stelle die Gleichung der Geraden g auf, die durch F und B geht. In welchem Punkt

schneidet die Gerade FB die Parabel noch einmal?

Bestimme einen Kreis, der die y-Achse, den nach oben verlängerten Brennstrahl BL

und den Strahl BF berührt. Wo liegt sein Mittelpunkt, wie groß ist sein Radius, wie

lautet die Kreisgleichung?

Bestimme im Dreieck FBL auf einfache Weise den Höhenschnittpunkt (Sonderfall).

- 16 -

-5 5

x

8

6

4

2

-2

-4

-6

y

n

p = 4 cm

B

S

F

L

HC

LÖSUNGEN E

Aus p21a folgt: p2

181 → p = +4 Die Parabel ist nach oben geöffnet.

Aus c = -3 folgt: → S(0/-3)

Aus c = -3 und 22p folgt: → F(0/-1)

Wertetabelle

x 0 ±1 ±2 ±3 ±4 ±5 ±6

y -3 -2,875 -2,5 -1,875 -1 0,125 1,5

Parabel zeichnen, Tangente und Normale zeichnen

5,1336y 81

B

( / , )B 6 1 5

n: 5,5xy 32

t: 5,7xy 23

2hgA

= 39 FE

g: 1xy 125 mit der Parabel gleichsetzen → )2/2(C 9

132

Mittelparallele: x = 3 geschnitten mit n (Winkelhalb.) ergibt: M(3/3,5)

Kreisgleichung: K: 9)²5,3y()²3x(

Höhenschnittpunkt: Schneide t mit 1y → H(4 31 /-1)

- 17 -

AUFGABE F


Bestimme den Parameter p, den Scheitelpunkt S und den Brennpunkt F.

Zeichne die Parabel im Bereich 12x6 mithilfe einer Wertetabelle. Wähle fürs

Zeichnen 1LE = 1cm.

Wertetabelle: Ergänze die fehlenden y-Werte

x 0 ±2 ±4 ±6 8 10 12

y

Bestimme in B(10/...) die Gleichung der Normale n.

Bestimme in B(10/...) die Gleichung der Tangente t.


Flächeninhalt des Dreiecks mithilfe der Formel 2hgA

.

Stelle die Gleichung der Geraden g auf, die durch F und B geht. In welchem Punkt C

schneidet die Gerade FB die Parabel noch einmal?

Bestimme einen Kreis, der die y-Achse, den nach oben verlängerten Brennstrahl BL

und den reflektierten Strahl BF berührt. Wo liegt sein Mittelpunkt, wie groß ist sein

Radius, wie lautet die Kreisgleichung?

Bestimme einen Kreis, der die y-Achse, den nach unten verlängerten Brennstrahl BL

und den Strahl BF berührt. Wo liegt sein Mittelpunkt, wie groß ist sein Radius, wie


Bestimme im Dreieck FBL auf einfache Weise den Höhenschnittpunkt (Sonderfall).

Bestimme den Flächeninhalt des Dreieckes FBL (Sonderfall).

Bestimme die Nullstellen der Parabel.

Wo schneidet der untere Kreis die x-Achse?

Wo schneidet der untere Kreis die Leitgerade der Parabel?

Welchen Abstand haben die beiden Kreise voneinander? Die Lösung ergibt sich aus der

Zeichnung.

Der untere Kreis schneidet die Parabel in zwei Punkten. Bestimme einen dieser beiden

Punkte durch Rechnung, der andere Schnittpunkt ist durch elementares Rechnen

zunächst nicht bestimmbar.

Bitte unbedingt alle Ergebnisse an der Zeichnung überprüfen!!

MITTERNACHTSFORMEL a2

ac4²bbx 2/1

- 18 -

LÖSUNGEN F

Parabel: 2²xy 121

Aus p21a folgt: p2

1121 → p = +6 → Die Parabel ist nach oben geöffnet

Aus c = -2 folgt: → S(0/-2)

Aus c = -2 und 32p folgt: → F(0/1)

Wertetabelle

x 0 ±2 ±4 ±6 8 10 12

y -2 -1,67 -0,67 1 3,33 6,33 10

Die Parabel, Tangente und Normale zeichnen.

31

121

B 62100y → B(10/6 31 )

n: 31

53 12xy

t: 31

35 10xy

2hgA

= 113,3 FE

Die Steigung von g erhält man aus den Punkten F und B mithilfe der Formel: 12

12xxyym

g: 1xy 158 mit der Parabel gleichsetzen → )92,0/6,3(C

Mittelparallele: x = 5 geschnitten mit n (Winkelhalb.) ergibt: → M1(5/9 31 ) und r = 5

Kreisgleichung K1: 25)²9y()²5x( 31

Mittelparallele: x = 5 geschnitten mit t (Winkelhalb.) ergibt: → M2(5/-2) und r = 5

Kreisgleichung K2: 25)²2y()²5x(

Höhenschnittpunkt: Schneide t mit y = 1 → H(6,8/1)

Flächeninhalt: FE56A 32

2hg

Nullstellen der Parabel: setze y = 0 N1(-4,9/0) und N2(4,9/0)

Schnittstellen des Kreises mit der x-Achse: 25²2)²5x(

215x 2/1

Schnittpunkte mit der Leitgeraden:

S1(1/-5) und S2(9/-5)

Abstand der beiden Kreise: d = 1 31

Schnitt Parabel / Kreis:

- 19 -

-5 5 10

x

12

10

8

6

4

2

-2

-4

-6

y

n

t

H

B

S

F

L

C

D

( )² ( ² )²

( )² ( ²)²

²

² |

( )

112

112

41144

41144

31144

x 5 x 2 2 25

x 5 x 25

x 10x 25 x 25

x 10x x 0 x ausklammern

x x 10 x 0 Nullprodukt x 0

Daraus ergibt sich S(0/-2).

- 20 -

-5 5 10 15

x

14

12

10

8

6

4

2

-2

-4

-6

y

a

p

x

t

n

p = 6 cm

B(x /...)

F

L

PARABEL UND STEIGUNG DER TANGENTE

Um die Tangente an irgendeinem Parabelpunkt bestimmen zu können, benötigt man die

Koordinaten des Berührpunktes und die Steigung der Parabel am Berührpunkt.

Zunächst soll die Steigung an einer Parabel untersucht werden, die symmetrisch zur y-Achse

liegt und die Gleichung ²axy + c hat.

Zur Veranschaulichung kann man c = 0 wählen, da die Konstante c die Kurve nur verschiebt,

nicht aber ihre Steigung ändert.

Aus dem markierten Steigungsdreieck bekommt man die Steigung der Normale: xp

nm

Durch Kehrwertbildung erhält man die Steigung der Tangente: px

xp

nt

1

m

1m

Aus p21a folgt, a2p

1 . Damit ergibt sich die Tangentensteigung: ax2m px

t

MERKE

Die Tangentensteigung am Parabelpunkt B(x /...) beträgt: 2tm ax .

- 21 -

Beispiel:

Gegeben ist die Parabelgleichung: 2²xy 121 und der Parabelpunkt B(9/4,75)

Gesucht ist die Tangentengleichung in B.

121a und xB = 9 und yB = 4,75 → 5,192ax2m 12

18121

t

Tangentengleichung: )xx(myy BB → t: )9x(5,175,4y

→ t: 75,8x5,1y

AUFGABE G-1


Bestimme den Parameter p, den Scheitel S und den Brennpunkt F der Parabel. Wie ist

die Parabel geöffnet?

Berechne die beiden Nullstellen der Parabel.

Bestimme die Gleichung der Tangente in B(8/...) nach dem neuen Verfahren (siehe

vorige Seite). Zeichne die Tangente.

Bestimme die Gleichung der Tangente in A(-4/...) nach dem neuen Verfahren (siehe

vorige Seite). Zeichne die Tangente.

Ergänze die fehlenden y-Werte und zeichne die Parabel für 8x8 :

x 0 ±2 ±4 ±6 ±8

y

Die Tangenten schneiden sich in einem Punkt C. Bestimme die Koordinaten von C.

Verbindet man die Punkte A und B miteinander, so erhält man die Gerade c. Bestimme

die Gleichung von c.

Bestimme den Flächeninhalt vom Dreieck ABC. (Formel: siehe Formelsammlung)

Konstruiert man eine Parallele zur y-Achse durch A, so erhält man einen Brennstrahl,

verbindet man A mit F, so erhält man den reflektierten Brennstrahl. Konstruiere die

Winkelhalbierende w zwischen den beiden Strahlen und bestimme ihre Gleichung.

Es gibt einen Kreis K1, der die x-Achse und den Brennstrahl parallel zur y-Achse

berührt und dessen Mittelpunkt auf der Winkelhalbierenden w liegt. Wie lautet seine

Gleichung?

Wie lautet die Gleichung des Kreises, dessen Mittelpunkt M(-1/-3) ist und die Parabel

im Punkt A berührt? Wie groß ist der Radius?

In welchen 4 Punkten schneidet der Kreis K2 die Koordinatenachsen?

- 22 -

x

yLeitgerade

tB

tA

c

C

M

AS

BF

LÖSUNGEN G-1

Parabel: 4²xy 161

Aus p21a folgt: p2

1161 → p = - 8 → Die Parabel ist nach unten geöffnet.

Aus c = +4 folgt: → S(0/+4)

Aus c = +4 und 42p folgt: → F(0/0)

Nullstellen: Gleichung der x-Achse: y = 0 → 4²x0 161 → N1/2( 8/0)

Tangentensteigung: 161a und xB = 8 und yB = 0 →

18)(2xa2m 1616

161

BB

Tangentengleichung: )xx(myy BB → t: )8x(1y

→ t: 8xy

Tangentensteigung: 161a und xA = -4 und yB = 3 →

21

168

161

AA )4()(2xa2m

Tangentengleichung: ( ) ( )1 1A A 2 2y y m x x y 3 x 4 y x 5

- 23 -

Wertetabelle

x 0 ±2 ±4 ±6 ±8

y 4 3,75 3 1,75 0

Schnittpunkt C: ( / )12x 8 x 5 C 2 6

Steigung c: 2 1

2 1

y y 1m

x x 4

Verbindungsgerade c: ( ) : 11 1 4y y m x x c y x 2

Dreiecksfläche: ( ) ( ) ( ) .......1A B C B C A C A B2A x y y x y y x y y 27 FE

Winkelhalbierende konstruieren:

Die Normale zur Tangente t ist die Winkelhalbierende. Die Steigung der Normale erhält man

durch Kehrwertbildung:

( / ) ( ) :1 1m 2 und A 4 3 y y m x x w y 2x 5

Kreis 1K :

Der Mittelpunkt muss einerseits auf der Geraden :g y x 4 (Winkelhalbierende

zwischen x-Achse und Brennstrahl) andererseits auf der Geraden :w y 2x 5 liegen.

Der Schnittpunkt der beiden Geraden ist M(-1/-3). Der Abstand zur x-Achse ist r = 3.

Damit ergibt sich die Kreisgleichung : ( )² ( )²1K x 1 y 3 9 .

Kreis 2K :

Radius = Abstand von M nach A: 2r 45

: ( )² ( )²2K x 1 y 3 45 mit r 45

Schnitt mit der x-Achse,

setze ( )² ²y 0 x 1 3 45 ² ²x 2x 1 9 45 x 2x 35 0

( / ) ( / )1 2N 7 0 und N 5 0

Schnitt mit der y-Achse,

setze x = 0: rechne ebenso / , / ,1 2S 0 3 63 und S 0 9 63

- 24 -

AUFGABE G-2 [WIEDERHOLUNG]


Bestimme den Parameter p, den Scheitel S und den Brennpunkt F der Parabel. Wie ist

die Parabel geöffnet?

Berechne die beiden Nullstellen der Parabel.

Bestimme die Gleichung der Tangente in B(4/...) nach dem neuen Verfahren (siehe

Musteraufgabe). Zeichne die Tangente.

Bestimme die Gleichung der Tangente in A(-8/...) nach dem neuen Verfahren (siehe

Musteraufgabe). Zeichne die Tangente.

Ergänze die fehlenden y-Werte und zeichne die Parabel für 8x8 :

x 0 ±2 ±4 ±6 ±8

y

Die Tangenten schneiden sich in einem Punkt C. Bestimme die Koordinaten von C.

Bestimme im Punkt B die Gleichung der Normale n.

Es gibt einen Kreis K1, der die Parabel im Punkt B berührt und dessen Mittelpunkt M

auf der x-Achse liegt. Wie lautet die Kreisgleichung?

Bestimme die Schnittpunkte dieses Kreises mit der y-Achse.

Es gibt einen zweiten Kreis K2, der die Parabel im Punkt A berührt und außerdem durch

die Punkte ( 8 / 8)P und (0 /8)Q geht. Bestimme den Mittelpunkt. Wie lautet die

Kreisgleichung?

Bitte alle Ergebnisse an der Zeichnung prüfen.

- 25 -

10

8

6

4

2

-2

-4

-6

-8

-10 -5 5 10

K2

K1

x

y

n

Q

M2

M1

B

A

C

P

LÖSUNGEN G-2

1

2

: ( 2)² ² 8

: ( 4)² ( 6)² 20

K x y

K x y

- 26 -

DIE STEIGUNG EINER BELIEBIGEN PARABEL

Die allgemeine Parabelgleichung lautet: 2y a x b x c

Die Gleichung besteht aus folgenden Teilen:

(1) dem quadratischen Teil: 2y a x

(2) dem linearen Teil: y b x

(3) dem konstanten Teil: y c

Jedem Teil kann man seine spezielle Steigung m zuordnen:

(1) Der quadratische Teil besitzt die Steigung einer Parabel: m 2a x

(2) Der lineare Teil besitzt die Steigung einer Geraden: m b

(3) Der konstante Teil besitzt die Steigung einer Waagerechten: m 0

ZUSAMMENFASSUNG

Die allgemeine Parabel 2y a x b x c

besitzt die Steigung m 2a x b 0

Beispiel 1: ²1

y x 3 x 54

2 1

m x 3 m x 34 2

Beispiel 2:

Gegeben ist die Parabel mit der Gleichung ² ,1

y x 1 5x 210

.

Bestimme die Tangenten in den Punkten A(5/...) und B(15/...) durch Rechnung.

Anschließend zeichne die Tangenten und die Parabel. Wo liegt der Scheitelpunkt?

- 27 -

5 10 15

12

10

8

6

4

2

-2

y

x

A

B

S

LÖSUNG

Funktionswert ² , ( / )A

1y 5 1 5 5 2 7 A 5 7

10

Steigung ,1

m x 1 55

( ) , , ,A

1m 5 1 5 1 1 5 0 5

5

( ) , ( )A Ay y m x x y 7 0 5 x 5

: , ,At y 0 5 x 4 5

Ebenso erhält man für

B(15/2) die Tangente: : , ,Bt y 1 5 x 24 5

BESTIMMUNG DES PARABELSCHEITELS

MERKE

Am Scheitel ist die Steigung m = 0, weil die Scheiteltangente waagerecht verläuft.

, , , ( , / , )15m 0 x 1 5 0 x 7 5 x 7 5 S 7 5 7 625

- 28 -

AUFGABE H

Gegeben ist die Parabel mit der Gleichung ² ,1

y x 2 5 x 34

.

Bestimme die Tangentengleichung im Punkt A(2/...). Zeichne die Tangente.

Bestimme die Tangentengleichung im Punkt B(6/...). Zeichne die Tangente.

Bestimme den Scheitelpunkt der Parabel. (siehe Musteraufgabe auf der vorigen Seite).


In welchem Punkt schneidet die Parabel die y-Achse?

Zeichne die Parabel im Bereich 0 x 10 . Mache eine Wertetabelle

x 0 1 2 3 4 .......... 10

y

Berechne den Schnittpunkt C der beiden Tangenten.

Bestimme die Geradengleichung von AB = c.

Bestimme die Gleichung des Lotes von C auf die gegenüberliegende Seite c.

Wo schneidet dieses Lot die x-Achse?

Die Gerade c, die Tangente in B und die y-Achse schließen eine dreieckige Fläche ein.

Bestimme die Größe der Dreiecksfläche.

Ein Kreis K berührt die Gerade c im Punkt Q(3/1,5). Der Mittelpunkt M des Kreises

liegt auf der x-Achse. Bestimme die Koordinaten von M. Bestimme den Radius. Wie


Wo schneidet der Kreis die x-Achse?

Wo liegt der Brennpunkt der Parabel?

Wie lautet die Gleichung des Scheitelkreises?

- 29 -

2 4 6 8 10

7

6

5

4

3

2

1

-1

-2

y

x

tB

tA

cQ

B

AM

F

S

C

LÖSUNGEN H

: 3A 2t y x 2 :

1B 2t y x 6

S(5/3,25) N1(1,4/0) und N2(8,6/0)

Y(0/-3) C(4/4)

: 12c y x

:Lot y 2x 12

( / )Lotfußpunkt auf der x Achse y 0 L 6 0

g hA 18 FE

2

: ,Lot in Q y 2x 7 5

( , / )Lotfußpunkt auf der x Achse y 0 M 3 75 0

Radius = MQ = 1,677..

: ( , )² ² ,1K x 3 75 y 2 8125

N1(3,75-1,677/0) = (2,073/0) und N2(3,75+1,677/0) = (5,427/0)

Parameter p = -2, F(5/2,25),

: ( )² ( , )²2K x 5 y 1 25 4

- 30 -

AUFGABE I [WIEDERHOLUNG]

Gegeben ist die Parabel mit der Gleichung ²1

y x x 212

.

Bestimme die Steigung der Parabel: m = . . . .

Bestimme die Tangentengleichung im Punkt A(0/...). Zeichne die Tangente.

Bestimme die Tangentengleichung im Punkt B(10/...). Zeichne die Tangente.

Bestimme den Scheitelpunkt der Parabel. (siehe Musteraufgabe).

Wo liegt der Brennpunkt F der Parabel? Zeichne F ein.


Zeichne die Parabel im Bereich 12x0 . Mache eine Wertetabelle

x 0 1 2 3 4 5 6 .......... 12

y

Berechne den Schnittpunkt C der beiden Tangenten.

Bestimme die Geradengleichung von AB = c.

Die Gerade c, die Tangente in B und die y-Achse schließen eine dreieckige Fläche ein.

Bestimme die Größe der Dreiecksfläche.

Bestimme die Gleichung der Normale in B.

Ein Kreis K1 berührt die beiden Brennstrahlen (FB und den Parallelstrahl zur y-Achse)

und die Parabelachse a. Bestimme die Kreisgleichung.

Ein zweiter Kreis K2 hat denselben Mittelpunkt wie K1 und berührt die Parabel im

Punkt B. Bestimme den Radius. Wie lautet die Kreisgleichung?

Wo schneidet K2 die x-Achse?

- 31 -

-2 2 4 6 8 10 12

x

9

8

7

6

5

4

3

2

1

-1

-2

y

K2K1

n

tc

a

M

F

S

B

A

LÖSUNGEN I

Steigung: 1

m x 16

:At y x 2 :1

B 3

2t y x 6

3

Scheitelpunkt:

Setze m = 0 → S(6/-1)

Parameter: p = 6 → F(6/2)

Nullstellen: N1(2,54/0) und N2(9,46/0)

Schnittpunkt: C(5/-3)

:1

c y x 26

23

g hA 41 FE

2

Normale: 13

3y x 15

2

1. Kreis: Normale geschnitten mit x = 8 → M(8/3 31 )

: ( )² ( )²11 3K x 8 y 3 4

2. Kreis: r = MB = 13

K2: : ( )² ( )²12 3K x 8 y 3 13

Schnittpunkte: S1(6,63/0) und S2(9,37/0)

- 32 -

10

8

6

4

2

-2

y

5 10

x

C

A

B

PARABEL AUS DREI PUNKTEN

Gegeben ist eine Parabel durch die drei Punkte A(-2/0), B(8/2) und C(2/8). Bestimme die

Parabelgleichung. Wo schneidet die Parabel die x-Achse? Wie lautet die Tangentengleichung

im Punkt A?

Ansatz: ycbx²ax

(I) A(-2/0) einsetzen: 0cb2a4

(II) B(8/2) einsetzen: 2cb8a64

(III) C(2/8) einsetzen: 8cb2a4 |·(-1) zuerst lasse c herausfallen.

Kombiniere (I) mit (III):

(I) 0cb2a4

(III) 8cb2a4

8b4 | :(-4)

b = 2

Ebenso kombiniere (II) mit (III):

(II): 2cb8a64

(III) 8cb2a4

1ba10

6|:6b6a60

b = 2 einsetzen in 1ba10 : → 3,0a12a10 103

a und b einsetzen in Gleichung (I) oder (II) oder (III):

(I): 2,5c0c22)3,0(4

Die Gleichung der Parabel lautet: 2,5x2²x3,0y

Nullstellen: )0/2(N1 und )0/8(N 32

2

Tangente in A: 4,6x2,3y

- 33 -

2 4 6 8 10 12 14 16 18

x

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

-1

-2

-3

y

M

B

S

F

A

AUFGABE J-1

Gegeben ist eine Parabel durch die drei Punkte A(2/1,25), B(4/0) und C(8/-1). Bestimme die

Parabelgleichung.

[Rechnung auf der folgenden Seite. Zwischenergebnis: ²1

y x x 316

]



Bestimme den Scheitelpunkt der Parabel.

Bestimme den Brennpunkt F der Parabel?

Bestimme die Gleichung des Scheitelkreises.

Bestimme die Gleichungen der Parabeltangenten in den beiden Nullstellen.

LÖSUNGEN J-1

Steigung: 1xm 81

Nullstellen: )0/4(N1 und )0/12(N2

Scheitel: m = 0 → S(8/-1)

Brennpunkt: p = 8 → F(8/3) und M(8/7)

Scheitelkreis: 64)²7y()²8x(

Tangenten: 6xy 21 2xy 2

1

- 34 -

PARABELGLEICHUNG BESTIMMEN

Ansatz: ycbx²ax

(I) A(2/1,25) einsetzen: 25,1cb2a4

(II) B(4/0) einsetzen: 0cb4a16 |·(-1)

(III) C(8/-1) einsetzen: 1cb8a64 zuerst lasse c herausfallen.

Kombiniere (I) mit (II):

(I) 25,1cb2a4

(II) 0cb4a16

25,1b2a12 (*)

Ebenso kombiniere (II) mit (III):

(II): 0cb4a16

(III) 1cb8a64

5,0b2a24

2|:1b4a48

(**)

Man hat zwei neue Gleichungen (*) und (**) erhalten und lässt nun b herausfallen:

5,0b2a24

25,1b2a12

161a75,0a12 einsetzen in (**) →

1b2b25,0b25,15,0b21624

a und b einsetzen in Gleichung (I) oder (II) oder (III):

(I): 325,0225,1c25,1c)1(24 161

Die Gleichung der Parabel lautet: 3x²xy 161

- 35 -

AUFGABE J-2

Ein Parabolspiegel ist nach oben geöffnet und besitzt den Parameter p = 10. In den Punkten

A(2/2,8) und B(10/1,2) ist der Spiegel befestigt. Wie lautet die Gleichung der Parabel?

[Rechnung auf der folgenden Seite. Zwischenergebnis: ² , ,1

y x 0 8 x 4 220

]


Bestimme den Scheitelpunkt der Parabel.

Wo liegt der Brennpunkt F der Parabel?

Bestimme den Scheitelkreis der Parabel.

Bestimme die Schnittpunkte P und Q des Scheitelkreises mit der y-Achse?

Bestimme den Mittelpunktswinkel PMQ.

Welchen Flächeninhalt besitzt das Dreieck PMQ?

Bestimme die Parabeltangenten in A und B.

Wo schneiden sich die Tangenten?

- 36 -

-2 2 4 6 8 10 12 14 16

x

18

17

16

15

14

13

12

11

10

9

8

7

6

5

4

3

2

1

1

y

c

Q

P

A

M

BS

F

LÖSUNGEN J-2

Ansatz wegen p = 10: ²1

y x bx c20

A(2/2,8) → , ,0 2 2b c 2 8

B(10/1,2) → ,5 10b c 1 2

Zuerst lasse c herausfallen,

man erhält ,b 0 8 ,

dann setze b ein, man erhält ,c 4 2

² , ,1

y x 0 8 x 4 220

Steigung: ,1

m x 0 810

S(8/1) F(8/6) M(8/11) Kreis: : ( )² ( )²K x 8 y 11 100

P(0/5) und Q(0/17) Fläche = 48 FE

Winkel: tan , ... ,3

36 869 73 742 4 2

Tangenten: 3

y x 45

,1

y x 0 85

C(6/0,4)

- 37 -

1. VORÜBUNG ZUR KLASSENARBEIT

Gegeben ist die Parabel mit der Gleichung 1 8

² 410 5

y x x

1. Bestimme die Steigung der Parabel: m = . . . . 1 P

2. Bestimme den Parameter p. 1 P

3. Wo hat die Parabel ihren Scheitelpunkt? 2 P

4. Bestimme die Nullstellen der Parabel. 2 P

5. Wie lautet die Gleichung der Tangente in A(2/1,2) ? 2 P

6. Wie lautet die Gleichung der Tangente in B(16/4) ? 2 P

7. In welchem Punkt C schneiden sich die beiden Tangenten? 2 P

8. Welche Gleichung hat die Verbindungsgerade AB = c? 2 P

9. Bestimme die Gleichung des Scheitelkreises K1. 2 P

10. Bestimme die Nullstellen des Scheitelkreises. 2 P

11. Welchen Flächeninhalt besitzt der Scheitelkreis? 1 P

12. Welchen Umfang besitzt der Scheitelkreis? 1 P

13. Wie groß ist die Fläche vom Dreieck ABC? 2 P

14. Zeichne die bekannten Punkte A, B, S, Nullstellen, Tangenten und den Scheitelkreis in

ein Koordinatensystem ein. Skizziere den Verlauf der Parabel möglichst genau im

Bereich 16x0 . Wähle 1LE = 1cm. 2 P

15. Ein zweiter Kreis K2 hat den Mittelpunkt M(2/-4) und geht durch den Ursprung.

Bestimme die Kreisgleichung. 2 P

16. In welchen Punkten schneidet K2 die y-Achse? 2 P

17. Welchen Winkel bildet die Tangente in B mit der Waagerechten? 2 P

= 30 P

- 38 -

8

6

4

2

-2

-4

-6

-8

5 10 15

x

y

M

C

1

1

A

B

S

ZUSATZAUFGABE

Der Bogen einer Brücke ist parabelförmig. Die Punkte D(0/1), E(2/3) und F(6/3) sind

bekannt.

18. Stelle die Parabelgleichung auf. [Kontrolle: 16 ² ............y x ] 6 P

19. Bestimme den Scheitel der Parabel. Bestimme die Nullstellen. 3 P

20. Welchen Winkel bildet der Parabelbogen mit der y-Achse? 1 P

- 39 -

LÖSUNGEN

Parabelgleichung: 8110 5² 4y x x

Steigung der Parabel: 815 5m x

Parameter: p = +5

Scheitelpunkt: m = 0 → 815 5 0x → x = 8 → S(8/-2,4)

Nullstellen: 8110 5² 4 0x x → ² 16 40 0x x →

1/2 8 64 40x N1(3,1/0) und N2(12,9/0)

Tang. in A und B: tA: 65 3,6y x tB: 8

5 21,6y x

Schnittpunkt: 6 85 53,6 21,6 | 5x x → 14 126x → C(9/-7,2)

Verb.gerade c: 4 1,2 2,8 116 2 14 50,2m 1

5: 0,8c y x

Mittelpunkt: M(8/-2,4 + 5) → M(8/2,6) und r = p = 5

Scheitelkreis: 1 : ( 8)² ( 2,6)² 25K x y

Nullstellen: ( 8)² 6,76 25x → 1/2 8 18, 24x N1(3,73/0) N2(12,27/0)

Fläche: 2 25A r

Umfang: 2 10U r

Dreiecksfläche: 68,6A FE

Zeichnung: darf nicht fehlen

Radius: ² (2 0)² ( 4 0)² 20r 4,47r

Zweiter Kreis : 2 : ( 2)² ( 4)² 20K x y P(0/0) und Q(0/-8)

Winkel: 185tan 1,6 | tan 58

Zusatzaufgabe: 1 46 3² 1y x x 2

3(4 / 3 )S N1(-0,7/0) N2(8,7/0)

13,53tanm 34

34

)0( → Winkel mit der y-Achse: 87,3690

- 40 -

4

3

2

1

-1

2 4 6 8

x

y

A

S

BESTIMMUNG EINER WURFPARABEL

Ein Mann steht an der Stelle x = 2 auf dem Erdboden und stößt eine Kugel unter der Richtung

m = 0,5 so weit, dass diese bei B(8/0) auf dem Boden auftrifft. Der Abstoßpunkt ist A(2/1,5).

Bestimme die Gleichung der Wurfparabel. Wo hat diese ihren Scheitelpunkt?

Wie lautet die Gleichung der Tangente in A?

Ansatz: cbx²axy )x(

bax2m )x(

(I) A(2/1,5) → 5,1cb2a4 |·(-1)

(II) B(8/0) → 0cb8a64

(III) m(2) = 0,5 → 5,0ba4 zuerst lasse c herausfallen.

Kombiniere (I) mit (II):

(I) 5,1cb2a4

(II) 0cb8a64

)6(|:5,1b6a60

(*) 25,0ba10

Kombiniere (*) mit (III):

(*) 25,0ba10

(III) 5,0ba4

81a

)6(|:75,0a6

81a einsetzen in (III): 1b5,0b48

1

a und b einsetzen in Gleichung (I) oder (II):

(I): 0c5,1c12)(4 81

Gleichung der Parabel: x²xy 81

Steigung der Parabel: 1xm 41

Scheitelpunkt: m = 0 → )2/4(S4x1x0 41

Tangente in A: 5,0xy 21

- 41 -

5 10 15

14

12

10

8

6

4

2

-2

-4

x

y

M

C

A

B

S

AUFGABE K

Ein Feuerwehrmann spritzt mit einem Wasserstrahl unter der Richtung m = 2 so weit, dass

dieser bei B(12/8) auf ein brennendes Haus trifft. Der Anfangspunkt des Wasserstrahles ist

A(0/2).

Bestimme die Gleichung der Wasserparabel.

Wo hat diese ihren Scheitelpunkt?


Wie lautet die Gleichung der Tangente in B?

In welchem Punkt C schneiden sich die beiden Tangenten?

Welche Gleichung hat die Verbindungsgerade AB = c?

Wo trifft der Wasserstrahl die x-Achse?

Bestimme die Gleichung des Scheitelkreises K1.

Liegt M1 auf der Geraden c? Mache die Punktprobe.

Ein zweiter Kreis K2 berührt die Parabel im Punkt A und hat seinen Mittelpunkt auf der

x-Achse. Bestimme M2 und r2 und die Kreisgleichung.

In welchen Punkten schneidet K2 die Parabelachse?

Welchen Winkel bildet die Tangente

in A mit der Waagerechten?

Rechne mit: mtan .

- 42 -

LÖSUNGEN K

Ansatz: cbx²axy )x(

bax2m )x(

(I) A(0/2) → 2c

(II) B(12/8) → 8cb12a144

(III) m(0) = 2 → 2b

c und b in (II) einsetzen: 144 24 2 8a

18144 18a a

Gleichung der Parabel: 2x2²xy 81

Steigung der Parabel: 2xm 41

Scheitelpunkt: m = 0 → )10/8(S8x2x0 41

Tangenten in A und B: 2x2y 20xy → C(6/14)

Gerade c: 2xy 21

Nullstelle: N(16,94/0)

Scheitelkreis: K1: 16)²6y()²8x(

Punktprobe für M(8/6): M in c einsetzen: stimmt66

286 21

Normale in A: 2xy 21 Normale geschnitten mit der x-Achse ergibt: M2(4/0)

Radius: 20)²20()²04(²r

Kreis : K2: 20²y)²4x( P(8/2) und Q(8/-2)

Winkel:

4,63

tan|2tan 1

- 43 -


Ein Stein wird vom Punkt A(-2/4) aus mit der Richtung m = 1 geworfen, so dass dieser

im Punkt B(16/1,75) auf einem Betonklotz landet.

Bestimme die Gleichung der Wurfparabel.

[Kontrolle: 3116 4² 5,75y x x ]








Wo schneidet der Scheitelkreis die y-Achse?

Zeichne die bekannten Punkte A, B, S, Nullstellen, Tangenten und den Scheitelkreis in


Bereich 6 18x . Wähle 1LE = 0,5cm.

Welchen Winkel bildet die Tangente in B mit der Waagerechten?

Die Punkte A(-2/4), B(16/1,75), D(16/0) und E(-2/0) bilden ein Viereck. Bestimme den

Flächeninhalt des Vierecks ABDE.


y-Achse. Bestimme M2 und r2 und die Kreisgleichung.

In welchen Punkten schneidet K2 die y-Achse?

ZUSATZAUFGABE

Der Bogen einer Brücke ist parabelförmig. Die Punkte A(0/- 0,9), B(4/3,9) und C(5/4,6)

sind bekannt.

Stelle die Parabelgleichung auf.

[Kontrolle: 110 ² ............y x ]

Bestimme den Scheitel der Parabel. Bestimme die Nullstellen.

Welchen Winkel bildet der Parabelbogen mit der y-Achse?

- 44 -

K2

K1

x

y

D

C

S

A

1

1E

B

S

LÖSUNGEN

Parabel: 3116 4² 5,75y x x

Steigung: 318 4m x

Scheitel: 0 (6 /8)m S

Nullstellen: 1 20 ( 5,31/ 0) (17,31/ 0)y N und N

Tangenten: : 6At y x und 54: 21,75Bt y x

Schnittpkt: C(7/13)

Gerade: 18: 3,75c y x

Scheitelkreis: 1 : ( 6)² ² 64K x y

Schnittstellen: 1 20 (0 / 5,29) (0 / 5,29)x S und S

Winkel mit x-Achse: 54tan 51,34

Trapez: 4 1,75

18 51,752

A FE

Kreis: 2 : ² ( 2)² 8K x y

Schnittstellen: 1 20 (0 / 4,82) (0 / 0,82)x S und S

- 45 -

LÖSUNG ZUSATZAUFGABE

Parabel: 8 9110 5 10²y x x (8 / 5,5)S

Nullstellen: 1 20 (0,58 / 0) (15,42 / 0)y N und N

Winkel mit y-Achse: 1(0) 52 ( ) 0m 8

5 tan 1,6 58 32


Ein Stein wird vom Punkt A(2/8) aus mit der Richtung m = 1 geworfen, so dass dieser

im Punkt B(14/2) auf einem Misthaufen landet.

1. Bestimme die Gleichung der Wurfparabel. 6 P

[Kontrolle: 18 ² 1,5 5,5y x x ]

2. Wo hat diese ihren Scheitelpunkt? 2 P

3. Bestimme die Nullstellen der Parabel. 2 P

4. Wie lautet die Gleichung der Tangente in A? 2 P

5. Wie lautet die Gleichung der Tangente in B? 2 P

6. In welchem Punkt C schneiden sich die beiden Tangenten? 2 P

7. Welche Gleichung hat die Verbindungsgerade AB = c? 2 P

8. Bestimme die Gleichung des Scheitelkreises K1. 2 P

9. Liegt 1M auf der Geraden c? Mache die Punktprobe. 2 P

10. Zeichne die bekannten Punkte A, B, S, Nullstellen, Tangenten und den Scheitelkreis in


Bereich 16x0 . Wähle 1LE = 1cm. 2 P

11. Ein zweiter Kreis K2 berührt die Parabel im Punkt A und hat seinen Mittelpunkt auf der

y-Achse. Bestimme M2 und r2 und die Kreisgleichung. 2 P

12. In welchen Punkten schneidet K2 die y-Achse? 2 P

13. Welchen Winkel bildet die Tangente in B mit der Waagerechten? 2 P

….= 30 P

- 46 -

5 10 15

14

12

10

8

6

4

2

-2

y

x

c

M

S

C

B

A

1

1

ZUSATZAUFGABE

Der Bogen einer Brücke ist parabelförmig. Die Punkte A(0/ 2 ), B(4/2 ) und C(5/2 712 ) sind

bekannt.

14. Stelle die Parabelgleichung auf. [Kontrolle: ............²xy 121 ] 6 P

15. Bestimme den Scheitel der Parabel. Bestimme die Nullstellen. 3 P

16. Welchen Winkel bildet der Parabelbogen mit der y-Achse? 1 P

LÖSUNGEN

1. Ansatz: ²ax bx c y

2ax b m

(I) A(2/8) → 4 2 8 | ( 1)a b c

(II) B(14/2) → 196 14 2a b c

(II) minus (I): 192 12 6a b

(III) m(2) = 1 → 4 1a b | ( 12)

192 12 6a b

48 12 12a b

Kombiniere (*) mit (III): 144 36a

→ 36 1144 8a

Die Größen b und c ergeben sich durch Einsetzen.

- 47 -

Parabelgleichung: 18 ² 1,5 5,5y x x 4mit p

Steigung der Parabel: 14 1,5m x

2. Scheitelpunkt: m = 0 → S(6/10)

3. Nullstellen: 1 2( 2,94 / 0) (14,94 / 0)N und N

4. Tangente in A: : 6At y x

5. Tangente in B: : 2 30Bt y x

6. Schnittpunkt: C(8/14)

7. Verb.gerade: 12: 9c y x

8. Scheitelkreis: K1: ( 6)² ( 6)² 16x y

9. Punktprobe für M(6/6): M in c einsetzen: 126 6 9

6 6 .stimmt

10. Zeichung:

11. Normale in A: : 10An y x

:An y Achse 2 (0 /10)M

Radius: ² (10 8)² (0 2)² 8r

Kreis: 2 : ² ( 10)² 8K x y

12. Schnittpunkte: P(0/12,83) und Q(0/7,17)

13. Winkel: 1tan 2 | tan

63, 43

100%

LÖSUNGEN ZUSATZAUFGABE

1 412 3² 2y x x S(8/3 1

3 ) N1(1,67 / 0) N2(14,33 / 0)

13,53tanm 34

34

)0( → Winkel mit der y-Achse: 87,3690

33%

- 48 -

6

4

2

2

5 10 15

Brücke

x

y

d

A

C

B

S

N

AUFGABE L-1

Der Bogen einer Brücke ist parabelförmig. Die Punkte A(0/0), B(2/1,75) und C(4/3)

bestimmen die Parabel (Angaben jeweils in Metern).

Stelle die Parabelgleichung auf.

[Kontrolle: x²xy 161 ]

Bestimme den Scheitel der Parabel.

Eine Autostraße führt in 5m Höhe parallel zur x-Achse über die Brücke. Wie lautet ihre

Gleichung? Wie groß ist der Abstand zwischen dem Scheitelpunkt und dieser Geraden?

In welchen Punkten schneidet die Parabel die x-Achse?

LÖSUNGEN L-1

x²xy 161

1xm 81 m = 0 S(8/4)

Abstand: d = 1m

A(0/0) und N(16/0)

- 49 -

-4 -2 2 4 6 8 10 12 14

x

12

11

10

9

8

7

6

5

4

3

2

1

-1

-2

-3

-4

y

cA

C

M

B

S

F

AUFGABE L-2

Gegeben ist eine Parabel mit der Gleichung 45

43

161 x²xy .

Bestimme die Steigung der Parabel m = . . . . . .

Wo hat die Parabel ihren Scheitelpunkt?


Wie lautet die Gleichung der Tangente in A(-2/...)?

Wie lautet die Gleichung der Tangente in B(12/...)?



Bestimme die Gleichung des Scheitelkreises K.

Zeichne die Parabel mithilfe der bekannten Punkte A, B, S, Nullstellen, Tangenten und

Scheitelkreis.

In welchen Punkten schneidet K die y-Achse?

Die beiden Tangenten tA und tB und die y-Achse bestimmen ein Dreieck. Wie groß ist

der Flächeninhalt?

LÖSUNGEN L-2

45

43

161 x²xy

43

81 xm m = 0

S(6/-1)

Nullstellen: N1(2/0) und

N2(10/0)

Tangenten: 1xy

75,7xy 43

Schnittpunkt: C(5/-4)

Gerade c: 75,2xy 81

Scheitelkreis: : ( )² ( )²K x 6 y 7 64

Zeichnung:

Schnitt

mit y-Achse: P(0/1,7..) und Q(0/12,3)

Fläche: A = 21,875 FE

- 50 -

2 4 6 8 10 12 14

x

12

11

10

9

8

7

6

5

4

3

2

1

-1

y

c

A

C

M

B

S

F

AUFGABE L-3

Ein Stein wird vom Punkt A(2/6) aus mit der Richtung m = 1 so weit geworfen, dass dieser

bei B(14/0) auf den Boden trifft.

Bestimme die Gleichung der Wurfparabel.

[Kontrolle: 5,3x5,1²xy 81 ]








Liegt M1 auf der Geraden c? Mache die Punktprobe.


x-Achse. Bestimme M2 und r2 und die Kreisgleichung.

In welchen Punkten schneidet K2 die y-Achse?

Welchen Winkel bildet die Tangente in A mit der Waagerechten? Rechne mit:

mtan .

- 51 -

LÖSUNGEN L-3

Ansatz: ²ax bx c y

2ax b m

(I) A(2/6) → 6cb2a4

(II) B(14/0) → 0cb14a196

(III) m(2) = 1 → 1ba4

Rechne (II) minus (I): → (*)1b2a32

)6(|:6b12a192

Kombiniere (*) mit (III): 3a24

→ 81

243a

Die Größen b und c ergeben sich durch Einsetzen:

Parabelgleichung: 5,3x5,1²xy 81 p = -4

Steigung der Parabel: 5,1xm 41

Scheitelpunkt: m = 0 → S(6/8)

Nullstellen: N(-2/0) und B(14/0)

Tangenten in A und B: 4xy 28x2y → C(8/12)

Gerade c: 7xy 21

Scheitelkreis: K1: 16)²4y()²6x(

Punktprobe für M(6/4): M in c einsetzen: stimmt44

764 21

Normale in A: 8xy Normale geschnitten mit der x-Achse ergibt: M2(8/0)

Radius: 72)²60()²28(²r

Kreis : K2: 72²y)²8x( P(0/2,8) und Q(0/-2,8)

Winkel:

45

tan|1tan 1

- 52 -

AUFGABE M [LOOPINGBAHN]

Eine Kugel rollt eine parabelförmige Loopingbahn hinunter. Sie durchläuft dabei die

Punkte ( 4 /12,4)B und ( 2 /8)C , wobei die Tangente in C die Richtung 2m hat.

Bestimme die Gleichung der Parabelbahn.

[Kontrolle: 20,1 1,6 4,4y x x ]

In welchem Punkt durchstößt die Parabel die y-Achse?

In welchen Punkten durchstößt die Parabel die x-Achse?

Bestimme den Scheitelpunkt der Parabel?

Bestimme die Gleichung der Parabeltangente im Punkt C?

Die Parabelbahn hat ihren Anfang im Punkt A auf der Höhe y = 17,6. Bestimme die

Koordinaten von A.

Bestimme die Gleichung des Scheitelkreises 1K .

Bestimme die Nullstellen des Scheitelkreises.

Der Scheitelkreis hat im Punkt (12 / 0)D eine Tangente Dt . Bestimme die

Tangentengleichung des Kreises.

Bestimme den Schnittpunkt der Tangenten Ct und Dt .

Bestimme die Gleichung der Verbindungsgerade CD = c.

Welchen Winkel bildet Dt mit der x-Achse.

Ein zweiter Kreis 2K berührt die Parabel im Punkt C und hat seinen Mittelpunkt auf der

y-Achse. Bestimme die Kreisgleichung. Wo schneidet 2K die y-Achse?

Zeichne die bekannten Punkte A, B, C, S, Nullstellen, die Tangenten in C und D und

den Scheitelkreis der Parabel in ein Koordinatensystem ein. Skizziere den Verlauf der

Parabel möglichst genau im Bereich 6 12x .

* * *

Nachdem die Kugel im Scheitelpunkt der Parabel angekommen ist, durchläuft sie

einmal den Scheitelkreis, macht also einen Looping und verlässt danach im Punkt

(12 / 0)D tangential die Loopingbahn, fliegt auf einer Wurfparabel weiter und landet

schließlich auf einem Heuhaufen im Punkt (18/ 2)H .

Bestimme die Parabelgleichung. [Kontrolle: 2 1616 3 40y x x ]

- 53 -

K2K1

x

y

tD

tC

n

H

E

C

A

B

D

S

1

1

freiwillig

Eine Parabel mit Scheitelpunkt bei 9x geht durch den Punkt (3/ 3)P und hat dort

die Steigung 83m . Bestimme die Parabelgleichung. Welche Koordinaten besitzt der

Brennpunkt?

- 54 -

LÖSUNGEN M

GLEICHUNG DER PARABELBAHN

2 2y ax bx c m ax b

( 2)

( 4 /12, 4) 16 4 12, 4

( 2 / 8) 4 2 8 | ( ) 12 2 4, 4

2 4 2 4 2 | 2

B a b c

C a b c a b

m a b a b

4 0,4 0,1a a

4 0,1 2 1,6 ......... 4,4b b c

(0 / 4,4)yS Die Gleichung der y-Achse lautet: x = 0

1 2(3,528 / 0) (12,472 / 0)N und N Die Gleichung der x-Achse lautet: y = 0

0, 2 1,6 0 (8 / 2)m x m S

: 2 4Ct y x

17,6 6 ( 6 /17,6)y einsetzen in Parabelgleichung x A

2 21110 5 (8 / 3) : ( 8) ( 3) 25a p M K x y

Nullstellen: 1 2(4 / 0) (12 / 0)N und N D

43: 16Dt y x (6 / 8)C Dt t E

647 7: 6c y x

43tan 53,13 [Kontrolle durch Nachmessen]

2 22 : ( 9) 5K x y 1 20 (0 / 9 5) (0 / 9 5)x S und S

Bedingungen: 4(12) 3(12 / 0) (18 / 2)D und m und H

freiwillig: 219 2 4y x x ( 9 / 10,75)F

- 55 -

EXTRAAUFGABEN

AUFGABE 1

Eine Parabel besitzt die Tangenten : 3At y x und : 2 15Bt y x und die

Scheiteltangente 3y . Bestimme die Gleichung der Parabel.

[Hinweis: Nimm die Grundkonstruktion auf Seite 1 zur Hilfe und beachte, dass jede

schräg verlaufende Tangente die Gerade FL auf der Scheiteltangente senkrecht

schneidet. So findet man den Brennpunkt F. Alles Weitere ergibt sich dann.]

Bestimme die Koordinaten des Scheitelpunktes.

Bestimme die Koordinaten der Berührpunkte A und B:

Bestimme die Gleichung der Geraden c = AB.

Bestimme den Schnittpunkt C der beiden Tangenten.

Die Parabel und die Gerade c schließen eine Fläche ein. Diese beträgt 2/3 der Fläche

des Dreieckes ABC. Bestimme die Fläche zwischen Parabelbogen und der Geraden c.

Bestimme die Gleichung der Tangente im Parabelpunkt D(0 / … ).

Ein Strahl mit der Richtung m = 3 wird im Punkt D an der Parabel reflektiert. Welche

Gleichung hat der einfallende Strahl?

Welche Gleichung hat das Lot in D?

Bestimme die Richtung des reflektierten Strahles in D mit Hilfe der Formel

2 1

2 1

tan1

m m

m m

. Dazu berechne zunächst den Tangenswert zwischen dem

einfallendem Strahl und dem Lot. Dann verwende die Formel nochmals, um die neue

Richtung zu bestimmen. Wie lautet die Gleichung des reflektierten Strahles?

Der Strahl wird im Punkt E nochmals an der Parabel reflektiert. Welche Koordinaten

hat der Punkt E?

Wie lautet die Gleichung des in E reflektierten Strahles?

Der ursprünglich einfallende Strahl und der zuletzt reflektierte Strahl kreuzen sich in

einem Punkt G. Welche Koordinaten hat G?

- 56 -

x

y

c

D

G

F

1

1

B

A

E

LÖSUNGEN 1

1 14 2: ² 2 1 2P y x x m x

12 2 0 (4 / 3)m x S

22 1 (4 / 2)pp F

( 2 / 6)AP t A

(8 /1)BP t B

12: 5c y x (3 / 9)A Bt t C

2362,5 41ParA FE A FE

: 2 1Dt y x

: 3 1Strahl y x 12: 1DLot y x

12 1

312

11

mm

m

Reflektierter Strahl in D: 13 1y x

2 23 9(6 / 1 )P Strahl E

Reflektierter Strahl in E: 13 119 278y x

13 11 29 27 38 3 1 (1 / 6)x x G

- 57 -

AUFGABE 2

Gegeben ist eine Parabel mit der Gleichung 218y x . Bestimme den Brennpunkt F.

Die Gerade 34: 2c y x schneidet die Parabel in den beiden Punkten A und B.

Bestimme die Koordinaten von A und B.

Bestimme die Tangenten in A und B.

Bestimme den Schnittpunkt C der beiden Tangenten.

Zeige, dass sich die Tangenten senkrecht schneiden.

Bestimme den Abstand, den die Gerade : 8g y x von der Parabel hat.

Ein Kreis mit Mittelpunkt M(0/2) berührt die x-Achse. Bestimme die Gleichung.

Ein weiterer Kreis berührt den ersten Kreis und die x-Achse. Bestimme den

geometrischen Ort, auf dem alle Mittelpunkte des zweiten Kreises liegen.

Wie lautet die Gleichung der Parabel, die im Punkt D(-4/2) zur gegebenen Parabel den

Abstand 18 hat? Es gibt zwei Lösungen.

Verlaufen die drei Parabeln parallel zueinander? Begründung?

WEITERE AUFGABEN

Gegeben ist die Parabel 132 ²y x . Gesucht ist die Tangente im Punkt P(x > 0 / 8 ).

: 8t y x

Gegeben ist die Parabel 1532 ²y x . Gesucht ist die Tangente im Punkt P(3,2 / .. ).

: 3 4,8t y x

Gegeben ist die Parabel 21201 ( 3)y x . Wo liegt der Scheitelpunkt? Wie lautet die

Tangentengleichung im Punkt P(5 / .. ).

15(3 / 1) ; : 0, 2S t y x

Gegeben ist die Parabel 5 ² 40 12 40 0x x y . Tangente im Punkt P( 2 / .. ) ?

53: 5t y x

- 58 -

x

y

B

C

F

1

1

A

D

E

G

LÖSUNGEN 2

(0 / 2)F

Kürzester Abstand = 3 2 18

Geometrischer Ort aller KREISMITTELPUNKTE ( / )M x y :

2 2( 2) 2y y x | 2 , die Wurzel isolieren

2 22 ( 2)y y x 2| (...)

2 2 22 4 ( 2)y y y x

2y 4 4y 2y 4 4y 2x

28y x |: 8

18 ²y x

Zwei neue Parabeln:

Ansatz: 2 2y ax c und m ax

Bedingungen: ( 7) ( 7)1 1y und m , wegen Punkt E(-7/-1) mit Steigung m = -1

2 21 114 24,5 4,5y x und y x

Die Parabeln sind nicht parallel zueinander, weil der Abstand am Scheitel größer ist.

- 59 -

AUFGABE 3

DER SKISPRINGER

Für einen Skispringer soll eine parabelförmige Schanze gebaut werden, die folgende

Bedingungen erfüllt:

a) Die Absprungstelle liegt bei x = 8 auf der Tangente Bt mit der Gleichung

0,5 3y x .

b) Der Startpunkt liegt bei A(0 /9).

Bestimme die Parabelgleichung.

Wo hat die Parabel ihren tiefsten Punkt?

Am Absprungpunkt folgt der Springer einer Flugparabel so, dass er am Punkt C(10/-2)

am Hang auftrifft. Bestimme die Gleichung der Flugparabel.

Wo hat die Flugparabel ihren höchsten Punkt?

Wie lautet die Tangentengleichung im Punkt C?

Wie lautet die Gleichung der Hangparabel, die die Flugparabel in C berührt und den

Parameter p = 20 hat?

Wo hat die Hangparabel ihren tiefsten Punkt?

Bestimme den Schnittpunkt der Tangente Bt mit der Tangente Ct .

Zwischen den beiden Tangenten gibt es eine Winkelhalbierende mit positiver Steigung.

Bestimme die Steigung mit Hilfe der Tangensformel.

Wie lautet die Gleichung der Winkelhalbierende?

Bestimme einen Kreis, der den Radius 32 besitzt und beide Tangenten berührt.

- 60 -

x

y

M: (12,88, -2,88)

M

1

1

LÖSUNGEN 3

316 ² 2,5 9y x x

2 23 3(6 / )TP

Flugparabel: 2116 1,5 7y x x

(12 / 2)HP

: 18Ct y x

Hangparabel: 140 ² 2 28y x x

(40 / 12)TP

(14 / 4)D

2 1

2 1

3 101 1

m m m mm

m m m m

Winkelhalbierende: 3 10 ( 4) 14y x

Parallele zu Ct mit Abstand 32 : : 10p y x

(12,88/ 2,88)p w M

: ( 2,88)² ( 12,88)² 32K x y

- 61 -

5 x

6

4

2

y

Steigung = 2

5

b = 3

5

2

31

FORMELSAMMLUNG

MITTELPUNKT einer Strecke: 1 22

x xM

1 22

y y

SCHWERPUNKT eines Dreieckes: 1 2 33

x x xS

1 2 33

y y y

LÄNGE einer Strecke: 2 2 2 22 1 2 1( ) ( )AB x y x x y y

STEIGUNG einer Geraden: 2 1

2 1

y yym

x x x

GERADENGLEICHUNGEN

Allgemeine Geradengleichung: 0Ax By C

Achsenabschnittsform: 1x y

a b

Zwei-Punkte-Form: 1 2 1

1 2 1

y y y y

x x x x

Punkt-Richtungs-Form: 1 1( )y y m x x

Normalform

y m x b

m Steigung

b Schnittstelle mit der y Achse

Gerade durch den Ursprung: y m x

Gleichung der x-Achse: 0y

Parallele zur x-Achse: y b

Gleichung der y-Achse: 0x

Parallele zur y-Achse: x a

SENKRECHT STEHEN (orthogonal sein): 1 2 1m m oder 21

1m

m

WINKEL Gerade mit Gerade 2 1

2 1

tan1

m m

m m

Gerade mit der x-Achse tan m

- 62 -

DREIECKSFLÄCHE 11 2 3 2 3 1 3 1 22 [ ( ) ( ) ( )]A x y y x y y x y y

2

g hA

[Sonderfall]

MITTELPUNKT DES UMKREISES Schnittpunkt der Mittellote

SCHERUNG EINES DREIECKES Die Dreiecksspitze wird parallel zur Basis

verschoben, der Flächeninhalt bleibt dabei gleich

groß.

ROTATIONSVOLUMEN 2x SV A y und 2y SV A x

ROTATIONSOBERFLÄCHE 2x SO y und 2y SO x

PUNKTPROBE Punkt in Geradengleichung einsetzen und prüfen,

ob die Gleichung erfüllt ist.

NORMALPARABELN

nach oben geöffnet

² 1y x p x q mit Faktor

nach unten geöffnet

² 1y x p x q mit Faktor

SCHEITELFORM

2

2

( )

( )

S S

S S

y y x x

oder

y x x y

Scheitel bei /S SS x y .

ALLGEMEINE PARABELN

Scheitel ist nicht ablesbar. ²y a x b x c

Scheitel bei (0 / )S c . ²y a x c mit Scheitel auf der y Achse

KREISGLEICHUNG 2 2 2M Mx x y y r

BINOMISCHE FORMELN

2 2 2

2 2

a b a 2ab b

a b a b a b

P-Q-FORMEL 2

1/2 2 2

p px q

MITTERNACHTSFORMEL 2

1/2

4

2

b b acx

a

- 63 -

PARABEL - GESETZMÄSSIGKEITEN

PARABELGLEICHUNG ²y a x b x c

PARABELSTEIGUNG ( )xm 2a x b

SCHEITELPUNKT S m 0

PARAMETER =

ABSTAND BRENNPUNKT – LEITGERADE p

ABSTAND VON S NACH F p

SF2

FORMFAKTOR DER PARABEL a

ZUSAMMENHANG p und a 1

2 p a a2 p

RADIUS DES SCHEITELKREISES MS p r

NULLSTELLEN y 0 setzen

SCHEITELPUNKT m 0 setzen

NULLPRODUKTE A B 0

A 0 oder B 0

Durch Ausklammern kann man eine Summe / Differenz in ein Produkt verwandeln.

Beispiele

Bei quadratischen Gleichungen ohne konstantes Glied kann man x ausklammern:

( )

2 2

1 2

2x 8x 0 x x 0 x x 4 0

x 0 oder x 4 0 x 4

Im folgenden Beispiel kann man (sin x) ausklammern:

( )

π

2

2

1 2

sin x sin x 0 sin x sin x 1 0

sin x 0 oder sin x 1 x 0 oder x

PARABELN KREISE TANGENTEN · 2013-02-12 · - 1 - 5 5 10 15 x 8 6 4 2 2 4 6 8 y Scheitelkreis...

Documents

Transcript of PARABELN KREISE TANGENTEN · 2013-02-12 · - 1 - 5 5 10 15 x 8 6 4 2 2 4 6 8 y Scheitelkreis...