Thermodynamik: 1. Hauptsatz - theochem.uni-due.de · Thermodynamik: 2. Hauptsatz Entropie ist eine...

Thermodynamik: 1. Hauptsatz

• Energieerhaltung:Arbeit plus Warmeentwicklung gleich Anderung der inneren Energie

∆E = w + q

• kein Perpetuum Mobile der 1. Art(also: keine Maschine verrichtet Arbeit ohne Brennstoff)

• differentielle Form:

dE = dw + dq∮dE = 0

Energie ist eine Zustandsfunktion

E. Spohr, Theoretische Chemie, Masterstudium SS 2017. Universitat Duisburg-Essen 1


• Entropie ist eine Zustandsfunktion

• Warme kann nicht 100%ig in Arbeit umgewandelt werden

• kein Perpetuum Mobile der 2. Art

• differentielle Form:

dS =dqrev

T∮dS = 0

dabei ist T die Temperatur und qrev die bei reversibler Prozessfuhrung ausgetauschteWarme


Thermodynamik

Kombination von 1. und 2. Hauptsatz:

dE = dq + dw = dqrev + dwrev (weil E eine Zustandsfunktion ist)

dE = TdS − pdV (in einem abgeschlossenen Einkomponentensystem)

dE = TdS − pdV + µdN (in einem offenen Einkomponentensystem)

dE = TdS − pdV +∑iµidNi (in einem Mehrkomponentensystem)

(Druck p, Volumen V , chemisches Potential µ und Teilchenzahl N )


Thermodynamik

Da die Energie eine Zustandsfunktion ist, ist dE ein exaktes Differential. Außerdemsind S, p und N Zustandsvariablen. Deshalb gilt

dS =1

TdE +

p

TdV −

µ

TdN

was wiederum bedeutet, daß aus S(N,V,E) alle anderen Zustandsvariablen berechnetwerden konnen, gemaß

1

T=

∂S∂E

V,N

p

T=

∂S∂V

E,N

µ

T= −

∂S∂N

E,V



wir haben dabei implizit angenommen, daß die Integrationskonstante trivial ist, d.h., daßfur T → 0 die Entropie gegen einen trivialen konstanten Wert geht.

Normalerweile setzt man diese Konstante gleich null.

Man bezeichnet die Tatsache, daß die Entropie am absoluten Nullpunkt gegen Null geht,allgemein als 3. Hauptsatz der Thermodynamik.


Grundlagen der Statistischen Mechanik: Isoliertes System

weder Energie- noch Materieaustausch mit der Umgebung

makroskopisch:

U,V,N1, N2, . . .

wohldefinierte innere Energie U , Volumen V und Teilchenzahl(en) Ni

Prozesse laufen so ab, daß S maximiert wird.Endzustand aller Prozesse ist der Gleichgewichtszustand.



mikroskopisches Bild:

klassisch quantenmechanisch

V, N1, N2, . . .~qi~pi

V, N1, N2, . . .ψj, εj,nj

(i: Partikelindex) (j: Zustandsindex)



klassisch:

System ist eindeutig durch Angabe der Koordinaten ~qi und Impulse ~pi der Atome (Elek-tronen, Molekule, “Teilchen”) i definiert.

Die innere Energie ist gleich des Wertes der klassischen Hamiltonfunktion H , die vonden Koordinaten und Impulsen abhangt.

E = U = H(~qi, ~pi)

Hier istH = Ekin(~qi, ~pi) + Epot(~qi)

Die potentielle Energie Epot beschreibt die intermolekularen oder interatomaren Wech-selwirkungen. Sie heißt konservativ, wenn Epot keine Funktion der Impulse ~pi ist.

Die kinetische Energie Ekin =1

2

∑i

~p2i

mi

kann (z. B. in kurvilinearen Koordinatensyste-

men) auch von den ~qi abhangen.



quantenmechanisch:

System ist eindeutig durch Angabe der Zustande ψj, deren Energieniveaus εj und Be-setzungszahlen nj bestimmt.

εjψj = Hψj H = (H)(qi, pi)

E =∑jnjεj

H = H(qi, pi) ist der Hamiltonoperator(das quantenmechanische ‘Aquivalent’ der Hamiltonfunktion)

V und Ni gehen bereits in die Berechnung der Energieeigenwerte des Systems ein.


Isoliertes System: quantenmechanische Zustande

Interpretationsmoglichkeiten fur die ψj

• als Vielteilchenzustande des Gesamtsystems:also: alle nj = 0 außer nk = 1, d.h., das System befindet sich zu einem Zeitpunktt1 im Zustand ψk.Da das System mikroskopisch zeitabhangig ist, befindet es sich zu einem spaterenZeitpunkt t2 in einem anderen Zustand, z. B. ψl. Dann ist nl = 1.Es gibt sehr viele dieser Zustande k und l. Sie besitzen alle die gleiche Energie, dasSystem besitzt also viele energetisch entartete Zustande. Ein Weg ware nun, die ψjalle zu berechnen.Dies ist fur N ≈ 1023 unmoglich!!!!.



• Man nimmt an, daß die Molekule naherungsweise voneinander unabhangig sind (z. B.in verdunnten Gasen),oder daß sich kollektive Quasi-Teilchen definieren lassen, wie z. B. Phononen (in pe-riodischen Festkorpern),oder daß sich das System in einer anders gearteten Weise (naherungsweise) in Un-tersysteme zerlegen lasst,so daß eine Einteilchennaherung moglich ist.Es gibt dann z.B. eine große Zahl von molekularen Energieniveaus, deren Beset-zungszahlen > 1 sein konnen (analog eine große Zahl von Phononenniveaus, derenBesetzung 0 oder 1 ist).



In jedem Fall gibt es mehr als ein nj, dessen Wert von 0 verschieden ist.

Es gilt also allgemein

E =∑jnjεj und N =

∑jnj

Man wird in jedem Fall zu einer Verteilung von Besetzungszahlen fur einen gegebenenZustand des Gesamtsystems gelangen. Die vielen entarteten Zustande zeichnen sichjeder durch einen speziellen Wert des Vektors

~n = n1, n2, n3, . . .

aus!

Wenn das Einteilchensystem sehr viel mehr Zustande als Teilchen besitzt, wird ni sehrselten großer als 1 sein.


Isoliertes System: klassische Zustande

Jede Systemkonfiguration, bei der alle Teilchen sich im Volumen V befinden und dieSumme aus kinetischer und potentieller Energie gleich der Gesamtenergie ist, stellt einenmikroskopischen Zustand dar.

Anmerkung: Frage: wie groß darf δq oder δp sein, damit das System sichin zwei “wirklich” unterschiedlichen Konfigurationen befindet?

Antwort: großenordnungsmaßig δqδp ≥ h/2genaue Rechnung: δqδp = h


Klassische Dynamik: Newton’sche Bewegungsgleichungen

Kraft = Masse mal Beschleunigung F = m · a = m · q

q =p

mp = F

wobei q die Teilchenposition und p der Teilchenimpuls ist.


Klassische Dynamik: Hamilton’scheBewegungsgleichungen

• das System verhalte sich hamiltonisch, d. h., es sei durch eine HamiltonfunktionH = V(qk) + T (qk, pk) beschrieben, aus der sich die Hamiltonschen Be-wegungsgleichungen ableiten lassen:

∂H∂qi

= −pi∂H∂pi

= qi

• in kartesischen Koordinaten hangt die kinetische Energie nur von den pk ab:

T = T (pk) =∑k

pk2

2mkdie Bewegungsgleichungen lauten dann:

∂H∂qi

=∂V∂qi

= −pi∂H∂pi

=∂T∂pi

=pi

mi

= qi =⇒ miqi = −∂V∂qi

(Aquivalenz der Newtonschen und Hamiltonschen Bewegungsgleichungen)


Klassische statistische Mechanik

Im folgenden seien folgende Annahmen erfullt:

• das System verhalt sich klassisch

• hinreichend gut isoliertes System

• Wechselwirkungen zwischen den Atomen / Molekulen konnen durch eine Potential-funktion beschrieben werden

Die Newtonsche Dynamik (Bewegungsgleichungen) beschreiben also die Evolution desSystems durch die Trajektorie qi(t), pi(t) in einem (6N-dimensionalen) Phasenraum.

Punkte in diesem 6N-dimensionalen Phasenraum (3N Freiheitsgrade fur die Koordinatenqi der N Atome 3N Freiheitsgrade fur die Impulse pi der N Atome) bezeichnet manhaufig durch das Symbol Γ.

das System ist dynamisch: Γ = Γ(t)

die Trajektorie des Systems durchlauft nacheinander die fur ein bestimmtes System inFrage kommenden Punkte Γ (die Mikrozustande)


Klassische statistische MechanikMakroskopische Eigenschaften

Makroskopische Observable OMakro sind dann offensichtlich(?) zeitliche Mittelwerte Ouber die Trajektorie wahrend der Beobachtungszeit T

OMakro = O =1

T

∫TO(Γ(t))dt

fur T → ∞ erwartet man, daß die Trajektorie alle moglichen Zustande des Systemsdurchlauft.


Klassische statistische MechanikMakroskopische Eigenschaften

vergessen wir die zeitliche Abfolge der Zustande und nehmen wir an, daß zu irgendwelchenZeitpunkten ti stichprobenartig Zustande Γi herausgegriffen werden

Dann ist in einem isolierten System folgendes plausibel

Postulat der gleichen a priori Wahrscheinlichkeiten

Das System befindet sich mit gleicher Wahrscheinlichkeit ineinem beliebigen der mit dem vorgegebenen Makrozustandkompatiblen Mikrozustande

Das Postulat bildet das Ruckgrat der statistschen Mechanik!!

Die Gesamtzahl der moglichen Mikrozustande ist eine systemabhangige Große

Ω(N,V,E)


Entropie und Mikrozustande

Betrachtet man das thermodynamische Gleichgewicht als den wahrscheinlichsten Ma-krozustand, so ist ebenfalls plausibel, daß der makroskopische Gleichgewichtszustanddadurch charakterisiert ist, daß die Zahl Ω maximal ist.

Makroskopisch ist der Gleichgewichtszustand auch durch die Forderung, daß die Entropiemaximal wird, charakterisiert.

Offensichtlich muß also S eine monoton steigende Funktion von Ω sein!

Welche?


Entropie und Mikrozustande

S ist eine extensive Große.Bringt man also zwei isolierte Systeme 1 und 2 zusammen, so ist S = S1 + S2.

Die Zahl der mikroskopischen Zustande ist Ω = Ω1 · Ω2, da fur jede Konfiguration(Mikrozustand) des Systems 1 alle Ω2 Zustande des Systems 2 moglich sind.

miteinander vereinbar ist dies nur, wenn gilt S ∝ ln Ω.

nach Boltzmann gilt: S = k · ln Ω

Boltzmannkonstante k = 1.38 · 10−23JK−1

Anmerkung: S = 0⇐⇒ Ω = 1


Ensembletheorie

Def.: Die Gesamtheit aller Mikrozustande, die mit den makroskopischen Systemgroßenkompatibel ist, bilden ein Ensemble

Die einzelnen Mikrozustande nennt man Ensemblemitglieder; sie sind gedankliche Kopiendes Systems.

2 Betrachtungsweisen:

1. Die einzelnen Ensemblemitglieder stellen den Zustand des Systems zu verschiede-nen Zeiten ti dar. Wenn die Zeiten ti nach aufsteigender Zeit geordnet werden,dann spiegeln sie also die zeitliche Evolution des Systems wieder. Sie stellen eineDiskretisierung der Phasenraumtrajektorie dar.

2. Die einzelnen Ensemblemitglieder stellen den Zustand vieler aquivalenter Systeme(zum gleichen Zeitpunkt t) dar. Dies ist der Standpunkt der Ensembletheorie.


Ensembletheorie: Ergodenhypothese

Ist die Ensembleinterpretation nutzlich?

ja, wenn folgendes wahr ist:

Ergodenhypothese: (Boltzmann 1981)Ein System ist ergodisch, wenn die ungestorte Bewegung desSystems — uber einen beliebig langen Zeitraum verfolgt — letz-tendlich jeden Punkt im Phasenraum, der mit einem bestimmtenWert der Energie E vereinbar ist, durchlauft.


Ensembletheorie: Quasiergodenhypothese

wegen der kontinuierlichen Natur der klassichen Variablen ist dies nur naherungsweiseerfullt. =⇒

Quasiergodenhypothese:Ein System ist quasiergodisch, wenn die ungestorte Bewegungdes Systems — uber einen beliebig langen Zeitraum verfolgt —letztendlich die Nachbarschaft jedes Punktes im Phasenraum,der mit einem bestimmten Wert der Energie E vereinbar ist,durchlauft.

nicht beweisbar

man nimmt oft an, daß, wenn sich das System hinreichend ergodisch verhalt, die Un-termenge der (wie auch immer) generierten Ensemblemitglieder reprasentativ fur dasgesamte Ensemble ist, was in der Praxis oft, jedoch nicht immer, erfullt ist.

Dies ist haufig ein heikler Punkt fur die Bewertung der erhaltenen Simulationsergebnisse!!


Ensembletheorie: Mittelwerte

Konsequenz:

In einem ergodischen System ist der Ensemblemittelwert 〈O〉 zu irgendeiner Zeit t gleichdem Langzeitmittelwert O irgendeines Ensemblemitgliedes.

O = limt→∞

1

t

t∫0O(t′)dt′

〈O〉 =1

Ω

∑iO(Γi(t))

O = 〈O〉(Meßgroße) (Theorie: statistische Mechanik)

Die Zahl der Mikrozustande in einem System mit N Atomen ist von der Großenordnung10N , also 101023

. Es ist also offensichtlich unmoglich, ein komplettes Ensemble zugenerieren.


Ensembletheorie: Computersimulation

man benotigt also:

• analytische Verfahren, um uber alle Ensemblemitglieder mitteln zu konnen.(Domane der “traditionellen” statistischen Mechanik)

• numerische Verfahren, die Ensemblemitglieder generieren, uber deren Eigenschaftengemittelt werden kann.(Domane der Computersimulation)

Problem: es konnen nur endlich viele, z. B. 107 – 1010 statt 101023Zustande

generiert werden.

Computersimulationen stellen eine Methode dar, um reprasentativeEnsemblemitglieder zu generieren!

Computersimulationen mussen reprasentative Ensemblemitglieder gener-ieren!


Ensembletheorie: Charakterisierung eines Ensembles

• die makroskopischen Großen (“kompletter” Satz von thermodynamischen Variablenzur Beschreibung des Systems)

• eine Dichtefunktion im Phasenraum ρ(Γ)ρ(Γ)dΓ ist die Zahl der Ensemblemitglieder im Phasenraumbereich

[Γ; Γ + dΓ] =

x1, x1 + dx1

y1, y1 + dy1

z1, z1 + dz1

. . .zN , zN + dzNpx1, px1 + dpx1

. . .pzN , pzN + dpzN


Ensembletheorie: Charakterisierung eines Ensembles

• eine Zustandssumme Z (zur Normierung der Dichtefunktion)

• ein dazugehoriges thermodynamisches Potential Φ

Φ = − lnZ

wobei gelten muß, daß Φ im Gleichgewicht minimal ist.

Die Ensembletheorie geht auf Gibbs zuruck (1902)


Liouville-Theorem

Das Liouville-Theorem schrankt die Wahl der Dichtefunktionen fur stationare Ensemblessehr stark ein.

Stationare Ensembles∂ρ

∂t= 0 sind solche, die Systeme im thermodynamischen Gleich-

gewicht beschreiben.(Ein System im Ggw. hat naturgemaß keine zeitabhangige Dichteverteilung!)

Liouville-Theorem: 0 =dρ(qi, pi, t)

dt

Der Phasenraum eines Systems ist inkompressibel (sein “Volumen” ist constant).


Liouville-Theorem

dρ

dt=∂ρ

∂t+

N∑i=1

∂ρ

∂qi·∂qi

∂t+

N∑i=1

∂ρ

∂pi·∂pi

∂t

dρ

dt=∂ρ

∂t+

N∑i=1

∂ρ

∂qi·∂H

∂pi−

N∑i=1

∂ρ

∂pi·∂H

∂qi(Hamiltonsche Bewegungsgleichungen (aquivalent zu Newtonschen Bewegungsgleichungen))

dρ

dt=∂ρ

∂t+ ρ,H

=⇒ ρ,H =3N∑i=1

∂ρ∂qi·∂H

∂pi−∂ρ

∂pi·∂H

∂qi

muß also im Gleichgewicht gleich Null sein.

Dies ist zum Beispiel dann erfullt, wenn ρ eine explizite Funktion von H , nicht aber vonden qi und pi ist.


Mikrokanonisches Ensemble

• beschreibt isoliertes System: U = E = const ,N = const, V = const

• Dichtefunktion ρ(Γ) = ρ0δ(H − E)(erfullt Liouville-Theorem)

• Zustandssumme Z = Ω = 1/ρ0

• thermodynamisches Potential Φ = −S

k(aus S = k ln Ω; wird in der Tat minimal, da im isolierten System S im Ggw.maximal wird)

• Ensemblemittelwert einer Observablen: 〈O〉 =1

N

∑iO(Γi)


Kanonisches Ensemble

• beschreibt geschlossenes System: T = const, N = const, V = const

• Dichtefunktion ρ(Γ) = ρ0 exp

− EkT

(“Boltzmannfaktor”)

• Zustandssumme Z = QNV T =∑i

exp

− EkT

• thermodynamisches Potential Φ = −A

kT

(also freie Helmholtz-Energie A = −kT lnQNV T )

• Ensemblemittelwert einer Observablen: 〈O〉 =

∑iO(Γi) exp

(− EkT

)∑iexp

(− EkT

)


Großkanonisches Ensemble

• beschreibt offenes System: T = const, µ = const, V = const

• Dichtefunktion ρ(Γ) = exp

− EkT

+µN

kT

• Zustandssumme Z = QµV T = Ξ =∑N

exp

µNkT

·QNV T

• thermodynamisches Potential Φ = −PV

KT

(also pV = kT lnQµV T )


∑iO(Γi) exp

(−E(Γi)

kT+ µN(Γi)

kT

)∑iexp

(− EkT

+ µN(Γi)kT

)


Isobar-isothermes Ensemble

Mikrokanonisches, kanonisches, und großkanonisches Ensemble sind die am haufigstenverwendeten.Daneben wird noch das isotherm-isobare Ensemble verwendet:

• T = const, P = const, N = const

• Dichtefunktion ρ(Γ) = exp

− EkT

+−pVkT

• Zustandssumme Z = QNPT = Ξ =∫V

exp

−pVkT

·QNV T

• thermodynamisches Potential Φ = −G

KT

(also freie Gibbs-Energie G = −kT lnQNPT )


∑iO(Γi) exp

(−E(Γi)

kT− pV (Γi)

kT

)∑iexp

(− EkT− pV (Γi)

kT

)


Zustandssummen

Wir haben die Zustandssumme als “Summe uber Zustande” eingefuhrt

z.B. im kanonischen Ensemble: Z = QNV T =∑i

exp

−Ei(qk, pk)kT

Diese Definition birgt keine Probleme fur eine quantenmechanische Beschreibung desSystems in einem festen Volumen V , da dort die Zustande diskret und damit abzahlbarsind.

In der Praxis sind auch in einem quantenmechanisch beschriebenen System mitmakroskopischem Volumen V die Translationszustande quasikontinuierlich:

Teilchen im Kasten mit Lange V 1/3: Ei =h2

2mV 2/3i2 = εi2

fur ein Proton in V = 1cm3: ε = [6.625 · 10−34]2/[2 · 1.008 · 1.6605 · 10−27 · 10−4] ≈1.3 · 10−36J

E. Spohr, Theoretische Chemie, Masterstudium SS 2017, Universitat Duisburg-Essen 1

Zustandssummen

andererseits ist bei 298 K: kT ≈ 4.1 · 10−21J

d. h., kT/ε ≈ 3 · 1015 =⇒ i ≈ 5 · 107

maW: bei Raumtemperatur gibt es ungefahr 106 Translationszustande pro Kelvin undFreiheitsgrad.D. h., mit experimentell handhabbarer Temperaturkontrolle kann man bei Raumtem-perature selbst fur ein einzelnes Proton die diskrete Natur der Translation kaum fest-stellen.

fur

• ein großeres Volumen

• großere Atommasse

• und besonders: eine große Anzahl von Atome

wird die Zustandsdichte noch wesentliche großer


Zustandssummen

bei einer klassischen Beschreibung sind die Zustande des Systems durch die Angabealler Koordinaten und Impulse qk, pk kontinuierlich beschrieben. Man geht dahervon der Summe uber Zustande zum Integral uber den Phasenraum uber :

im kanonischen Ensemble:

Z = QNV T =∑i

exp

−Ei(qk, pk)kT

−→ Z = ω∫

dΓ exp

−Ei(qk, pk)kT

mit dΓ = dq1dq2 . . . dq3Ndp1dp2 . . . dp3N ;

∫ist ein 6N-dimensionales Integral


Zustandssummen

Wie groß ist der Proportionalitatsfaktor ω ? Antwort: ω =1

N !h3N

Die Argumentation ist komplex, jedoch kann man die Richtigkeit der Formel z. B.durch die statistisch-mechanische Behandlung des idealen Gases verifizieren.

vereinfacht: N ! ist eine Konsequenz der Ununterscheidbarkeit der Atomeh3N ist eine Konsequenz der Unscharferelation


Die freie Energie des idealen Gases

Kann man mit dem ganzen Formalismus irgendetwas ausrechnen?Ja, z. B. die Eigenschaften des idealen Gases

man startet von der Beziehung

A = −kT lnQ

= −kT ln

1

N !h3N∫ ∫

dΓ exp

−E(qk, pk)kT

fur das ideale Gas gilt: E(qk, pk) = E(pk) =N∑i=1

~p 2i

2mi=

3N∑α=1

pα2

2mα

das ideale Gas befinde sich im Volumen V , also gilt:

∫dq1dq2 . . . dq3N =

N∏i=1

(∫Vdxi dyi dzi) = V N

alle Teilchen mogen die gleiche Masse mi = m haben



also gilt: A = −kT ln

1

N !h3NV N

∫. . .

∫exp

− 3N∑α=1

pα2

2mkT

3N∏α=1

dpα

= −kT ln

1

N !h3NV N 3N∏

α=1

∫ dpα exp(− pα2

2mkT)

= −kT ln

1

N !h3NV N

∫ dp exp(− p2

2mkT)

3N

= −kT ln 1

N !h3NV N

(√2mkT

∫dx exp(−x2)

)3N

= −kT ln 1

N !h3NV N

(√2mkT

√π)3N

= −kT ln

1

N !V N

2πmkT

h2

3N/2

= −kT ln 1

N !V NΛ3N

mit der de Broglie’schen (“thermischen”) Wellenlange Λ =√2πmkT/h2



also:

A = −kT ln 1

N !V NΛ3N

= kT [ln(N !)−NkT lnV − 3N ln Λ] (Stirlingsche Formel: ln(N !) ≈ N lnN −N)

= NkT [− lnV − 3 ln Λ + lnN − 1]

Partielle Ableitungen von A

P := −∂A∂V

N,T

= +NkT1

V=⇒ Zustandsgleichung: pV = NkT

S := −∂A∂T

N,V

= −Nk [− lnV − 3 ln Λ + lnN − 1] + 3NkT∂ ln Λ

∂T

= −Nk [− lnV − 3 ln Λ + lnN − 1] + 3NkT1

2T

= −Nk [− lnV − 3 ln Λ + lnN − 1] +3

2Nk



Ferner gilt A = U − TS oder

U = A + TS

= NkT [− lnV − 3 ln Λ + lnN − 1]

−NkT [− lnV − 3 ln Λ + lnN − 1] +3

2NkT

=3

2NkT kT/2 pro Freiheitsgrad


Die innere Energie

mikroskopisch:

U = A + TS

= A− T ·∂A∂T

N,V

= −kT lnQ− T−k lnQ− kT

∂ lnQ

∂T

N,V

= kT 2∂ lnQ

∂T

N,V

= kT 2 1

Q

∂Q∂T

N,V

= kT 2 1

Q

1

N !h3N∫ ∫

dΓE(qk, pk)

kT 2exp

−E(qk, pk)kT

=

∫dΓE(qk, pk) exp

[−E(qk,pk)

kT

]∫dΓ exp

[−E(qk,pk)

kT

] = 〈E〉

die innere Energie ist ein einfacher Mittelwert (im kanonischen Ensemble)E. Spohr, Theoretische Chemie, Masterstudium SS 2017, Universitat Duisburg-Essen 9

Zustandssummen

fur das ideale Gas war die Separierung der Zustandssumme in Zustandssummen proFreiheitsgrad vollstandig, maW:

∫dΓ =

∫dq1dq2 . . . dq3Ndp1dp2 . . . dp3N

= (∫

dq1) · (∫

dq2) . . . (∫

dq3N) · (∫

dp1) . . . (∫

dp3N)

fur konservative Systeme in kartesischen Koordinaten kann man generell kinetische undpotentielle Beitage separieren:

E(qk, pk = T (pk) + V(qk)

und damit auch die Zustandssumme


Zustandssummen

Q =1

N !h3N∫

dΓ exp

−E(qk, pk)kT

=1

N !h3N∫

dΓ exp

−T (pk) + V(qk)kT

=1

N !h3N∫

dq1dq2 . . . dq3Ndp1dp2 . . . dp3N exp

−T (pk) + V(qk)kT

=1

N !h3N∫

dq1dq2 . . . dq3N∫

dp1dp2 . . . dp3N exp

−T (pk)kT

· exp

−V(qk)kT

=1

N !h3N

∫ dq1 . . . dq3N exp

−V(qk)kT

·

∫ dp1 . . . dp3N exp

−T (pk)kT

=1

N !h3N

∫ dq1 . . . dq3N exp

−V(qk)kT

·

∫ dp1 . . . dp3N exp

− 3N∑k=1

pk2

2mkT

=1

N !

∫ dq1dq2 . . . dq3N exp

−V(qk)kT

· Λ3N


Konfigurationsintegral

Man nennt

ZN =∫

dq1∫

dq2∫. . .

∫dq3N exp

−V(qk)kT

Konfigurationsintegral

Fur das ideale Gas kann man ZN ausrechnen und erhalt V N .

Die analytische Berechnung des Konfigurationsintegrals ist im allgemeinen Fall nichtoder nur naherungsweise moglich.

Das Konfigurationsintegral ist der “nichttriviale”, das kinetische Energieintegral der“triviale” Beitrag zur Zustandssumme


Dichtefunktion und Mittelwerte

Die Dichtefunktion im Phasenraum ist mit

ρ(qk, pk) =1

Q· 1

N !h3Nexp

−E(qk, pk)kT

so definiert, dass∫

dq1dq2 . . . dq3Ndp1dp2 . . . dp3Nρ(qk, pk) = 1

Ein Ensemblemittelwert einer Observablen O(qk, pk) ist definiert als:

〈O〉 =∫

dq1dq2 . . . dq3Ndp1dp2 . . . dp3Nρ(qk, pk)O(qk, pk)

=

∫dq1dq2 . . . dq3Ndp1dp2 . . . dp3NO(qk, pk) exp

[−E(qk,pk)

kT

]∫dq1dq2 . . . dq3Ndp1dp2 . . . dp3N exp

[−E(qk,pk)

kT

]


Ensemblemittelwerte

hangt O nur von den qk ab, so kann man wieder kinetische und potentielle Beitrageseparieren

〈O〉 =

∫dq1dq2 . . . dq3Ndp1dp2 . . . dp3NO(qk) exp

[−E(qk,pk)

kT


[−E(qk,pk)

kT

]

=

(∫dp1dp2 . . . dp3N exp

[−T (pk)kT

])·(∫

dq1dq2 . . . dq3NO(qk) exp[−V(qk)kT

])(∫

dp1dp2 . . . dp3N exp[−T (pk)kT

])·(∫

dq1dq2 . . . dq3N exp[−V(qk)kT

])

=

(∫dq1dq2 . . . dq3NO(qk) exp

[−V(qk)kT

])(∫


])

=1

ZN

∫ dq1dq2 . . . dq3NO(qk) exp

−V(qk)kT

Es wurde “uber die Impulse integriert” (gemittelt).E. Spohr, Theoretische Chemie, Masterstudium SS 2017, Universitat Duisburg-Essen 14

Ensemblemittelwerte

hangt O nur von den pk ab, gilt analog:

〈O〉 =

∫dq1dq2 . . . dq3Ndp1dp2 . . . dp3NO(pk) exp

[−E(qk,pk)

kT


[−E(qk,pk)

kT

]

=

(∫dp1dp2 . . . dp3NO(pk) exp

[−T (pk)kT

])·(∫


])(∫


])·(∫


])

=


[−T (pk)kT

])(∫


])

Es wurde “uber die Koordinaten integriert” (gemittelt).


Mittelwert der kinetischen Energie

O(qk, pk) = O(pk) = T (pk) =3N∑i=1

pi2

2mi

also

〈T 〉 =


[−T (pk)kT

])(∫


])

=

∫ dp1dp2 . . . dp3N3N∑i=1

pi2

2miexp

[−T (pk)kT

](∫


])

=

3N∑i=1

(∫dp1dp2 . . . dp3N

pi2

2miexp

[−T (pk)kT

])(∫


])

von den 3N Integralen im Zahler und im Nenner sind jeweils 3N − 1 paarweise gleich,lediglich die Integrale

∫dpi sind voneinander verschieden:


Mittelwert der kinetischen Energie

also

〈T 〉 =

3N∑i=1

(∫dp1dp2 . . . dp3N

pi2

2miexp

[−T (pk)kT

])(∫


])

=

3N∑i=1

(∫dpi

pi2

2miexp

[− pi

2

2mikT

])(∫

dpi exp[− pi2

2mikT

])

= . . .

= 3N2 kT Aquipartitionstheorem


Mittelwert der inneren Energie

wir hatten gesehen, daß

U = A + TS

=

∫dΓE(qk, pk) exp

[−E(qk,pk)

kT

]∫dΓ exp

[−E(qk,pk)

kT

]

=

∫dΓ (T (pk) + V(qk)) exp

[−T (pk+V(qk)kT

]∫dΓ exp

[−T (pk+V(qk)kT

]

= 〈T 〉 +

∫dq1dq2 . . . dq3NV(qk) exp

[−V(qk)kT

]

ZN

= 〈T 〉 + 〈V〉 =3N

2kT + 〈V〉

Wenn V = 0, erhalten wir wieder die Formel fur das ideale Gas!


Andere Mittelwerte

• man kann fragen: Wie groß ist die Wahrscheinlichkeit, daß ein bestimmtes Atom keinen bestimmten Impuls in, z. B. x-Richtung besitzt, unabhangig von seinem Ort,und unabhangig von den Orten und Impulsen der anderen Atome?

=⇒ Maxwellsche Geschwindigkeitsverteilung p(vx)

es handelt sich um eine Mittelung uber alle 3N Koordinaten und uber 3N − 1Impulse

•Wie groß ist die Wahrscheinlichkeit, daß ein bestimmtes Atom k an einem bes-timmten Ort (x, y, z) ist?

=⇒ Einteilchendichte ρ(x, y, z)(wg. der Homogenitat ist in einer Flussigkeit ρ = const., nicht aber an einerGrenzflache oder in einem Festkorper)

Mittelung uber 3N Impulse und 3N − 3 Koordinaten


Andere Mittelwerte

•Wie groß ist die Wahrscheinlichkeit, ein bestimmtes Atom k in einem Abstand zvon der Oberflache, unabhangig von seiner x und y-Position uber der Oberflachezu finden?

=⇒ Dichteprofil ρ(z)

Mittelung uber 3N Impulse und 3N − 1 Koordinaten

•Wie groß ist die Wahrscheinlichkeit, daß in einer atomaren Flussigkeit, z. B. Argon,zwei Atome k und m einen Abstand r voneinander besitzen?

Koordinatentransformation: (xk, yk, zk, xm, ym, zm) −→ (xk, yk, zk, r, θ, φ)mit dem Abstand r =

√(xm − xk)2 + (ym − yk)2 + (zm − zk)2 und θ und φ zwei

(Euler)Winkeln, die die Orientierung des Verbindungsvectors ~xm− ~xk beschreiben.

=⇒ Paarkorrelationsfunktion g(r)

Mittelung uber 3N Impulse und 3N − 1 Koordinaten(d. h. uber alle Koordinaten außer uber r)


Andere Mittelwerte

•Wie sieht die Konformationsverteilung Butan, gelost in DMSO, aus?

Koordinatentransformation:(kart. Koordinaten der C-Atome in Butan)−→ (interne Koordinaten mit Torsionswinkel φ)

=⇒ Verteilung der Torsionswinkel p(φ)unabhangig von allen anderen internen Koordinaten und Geschwindigkeiten

Mittelung uber 3N Impulse und 3N − 1 Koordinaten(d. h. uber alle Koordinaten außer uber φ)

man kann dann als nachstes definieren, welche Bereiche der φ-Koordinate einer“trans”-Konfiguration entspricht und welche Bereiche einer “gauche”-Konfigurationentspricht.

Integration von p(φ) uber die entsprechenden Bereiche ergibt dann Anteile vontrans und gauche-Konfigurationen

Beispiel fur ein grundsatzliches Problem: die Definition z. B. der der trans-Konformation zugeordneten Bereiche ist bis zu einem gewissen Grad arbitrar!


Andere Mittelwerte

• “Reaktionswahrscheinlichkeit” fur die Umwandlung von Sessel- in Wannenform vonCyclohexan in flussiger Phase?

=⇒ Ratenkonstanten der Reaktionskinetik

kompliziertere Verteilungsfunktionen / Mittelwerte−→ (vielleicht spater)

Computersimulationen konnen zur Berechnung solcher Mittelwerte herangezogenwerden, in der Regel ohne daß die Zustandssummen explizit ausgewertet werdenmussen


Simulationsmethoden

deterministisch ←→ stochastisch

MolekulardynamikBrownscheDynamik

LangevinDynamik

Force-biasMonte Carlo

Monte Carlo

E. Spohr, Master-Vorlesung Theoretische Chemie SS 2008. Universitat Duisburg-Essen 1

Molekulardynamik

• das System verhalte sich hamiltonisch, d. h., es sei durch eine HamiltonfunktionH = V(qk) + T (qk, pk) beschrieben, aus der sich die Hamiltonschen Bewe-gungsgleichungen ableiten lassen:

∂H∂qi

= −pi∂H∂pi

= qi

• in kartesischen Koordinaten hangt die kinetische Energie nur von den pk ab:

T = T (pk) =∑k

pk2

2mkdie Bewegungsgleichungen lauten dann:

∂H∂qi

=∂V∂qi

= −pi∂H∂pi

=∂T∂pi

=pimi

= qi =⇒ miqi = −∂V∂qi

(Aquivalenz der Newtonschen und Hamiltonschen Bewegungsgleichungen)


Molekulardynamik

• Ein Hamiltonsches System besitzt konstante Energie E = H, also stellt die Trajek-torie von N Teilchen in einem Volumen V (oder aquivalent: der Dichte ρ = N/Veine Serie von Zustanden des Mikrokanonischen Ensembles dar.

• wir nehmen an, daß die Zustande reprasentativ sind, daß also der Trajektorienmit-telwert einer Observablen O

M(O) =1

N

N∑i=1O(Γ(ti)) =

1

N

N∑i=1O(ti) =

1

N

N∑i=1O(t0 + i ·∆t)

eine gute Naherung fur den Ensemblemittelwert darstellt.M(O) ist eine Stichprobe im statistischen Sinne.

• Annahme der Ergodizitat: limN→∞

M(O) = 〈O〉 = O

also: ein kurzes Stuck der Trajektorie sei eine gute Naherung.


Molekulardynamik

• ∆t ist dabei die Diskretisierung, die festlegt, in wieviele Intervalle die Trajektoriezum Zweck der Mittelwertbestimmung zerlegt wird.

• ∆t ist nicht frei wahlbar:

• es muß gewahrleistet sein, daß 2 aufeinander folgende Zeitpunkte hinreichend ver-schiedene Zustande darstellen.

• insbesondere ist ∆t nicht gleich der Lange des Integrationszeitschrittes (s.u.).

• “hinreichend verschieden” wird spater so definiert, daß keine Korrelationen zwischenden Eigenschaften der Zustande existieren.

• m.a.W: hat man N Zeitschritte simuliert, so heißt dies nicht, daß man uber einestatistische Stichprobe aus N Einzelmessungen verfugt.


Endliche Differenzmethoden

eine Standardmethode zur Losung gewohnlicher Differentialgleichungen wie z. B.

miqi ==∂V(qk)

∂qii = 1, . . . , N

basiert auf der Approximation der Differentialquotientent durch endliche Differenzen-quotienten, z. B.

qi =dqidt≈ δqi

δtwobei δt ein kleines aber endliches Zeitintervall, δqi die dazugehorige Differenz der Ortedes Teilchens ist, also

q ≈ q(tend)− q(tan)

tend − tanWahl von δt:

• deutlich kleiner als die Zeit, in der sich das Atom um eine Lange vergleichbar seinesDurchmessers bewegt.

• deutlich kleiner als die Periode der schnellsten Schwingung (Bewegungsmode), ander das Atom beteiligt ist


Der Verlet-Algorithmus

Zweck: Losung einer oder mehrerer gekoppelter Differentialgleichungen 2. Ordnungvom Typ y(x) = f (y), also eines Spezialfalles der allgemeinen DGL y(x) = f (y, y, x)

Mit y → qi (qi sei eine Koordinate, z. B., x1, y3, z137) und x→ t laßt sich das Verfahrenauf die Newtonschen EOMs (“equations of motion”) anwenden.

In diesem Falle ist fi(qi) die auf die Koordinate qi wirkende Kraft, die sich aus demWechselwirkungspotential V ergibt

miqi(t) = fi(qi) = −∂V(qk)∂qi


Verlet-Algorithmus

Taylorentwicklung fur kurzes Zeitinkrement δt:

vorwarts: qi(t + δt) = qi(t) + qi(t) · δt +1

2qi(t) · (δt)2 ± . . .

ruckwarts: qi(t− δt) = qi(t) + qi(t) · (−δt) +1

2qi(t) · (−δt)2 ± . . .

Aufaddieren: qi(t + δt) + qi(t− δt) = 2qi(t) + qi(t) · (δt)2

Nach Umformen erhalt man: qi(t + δt) = 2qi(t)− qi(t− δt) + qi(t) · (δt)2

hat man qi(t+ δt) auf diese Weise bestimmt, so laßt sich daraus qi(t+ 2δt) berechnen:

mit t′ := t + δt wird qi(t + δt)→ qi(t′) und qi(t)→ qi(t

′ − δt),was man wieder in die Gleichung einsetzen kann.


Verlet-Algorithmus

Startproblem (t = 0): Normalerweise gibt man bei einem Anfangswertproblem im Falleeiner DGL 2. Ordnung zwei Großen vor, hier: qi(0) und qi(0).

Der Algorithmus verlangt stattdessen qi(0− δt)!Es ist also ein Startschritt erforderlich:

t = 0 : qi(δt) = qi(0) + qi(0) · δt +1

2fi(qk(0))

Danach: qi(2δt) = P(qi(δt), qi(0))und allgemein qi(t + δt) = P(qi(t), qi(t− δt))

mit P(xk, xk−1) = 2xk − xk−1 + f (xk)(δt)2

Bestimmung der Geschwindigkeiten durch Subtraktion der beiden Taylorentwicklungenqi(t + δt)− qi(t− δt) = 2qiδt

also qi =qi(t + δt)− qi(t− δt)

2δt(“zentrale Differenz”)


Verlet-Algorithmus

Datenfluss

δ tt+t− δ t

q.

t

q

f

δ tt+t− δ t

q.

t

q

f

δ tt+t− δ t

q.

t

q

f

δ tt+t− δ t

q.

t

q

f

t+2 δt

Vorzuge Nachteilezeitlich umkehrbar Geschwindigkeiten werden “asynchron” berechneteinfach Fehler von q ist 2. Ordnung in δt


Monte Carlo Methoden

(entwickelt wahrend des II. Weltkriegs von von Neumann, Ulam, und Metropolis zurUntersuchung der Diffusion von Neutronen in spaltbaren Materialien )

• Name ruhrt daher, daß massiver Gebrauch von Zufallszahlen gemacht wird

• es gibt eine Vielzahl verschiedener Monte Carlo-Schemata, die vorstellbar und/odergetestet sind.

• wichtigstes: Metropolis Monte Carlo Methode

• Zweck: Generierung einer Trajektorie im Phasenraum, die Stichproben eines ge-wahlten statistisch-mechanischen Ensembles erstellt.

• maW: die Wahrscheinlichkeit, einen Punkt im Phasenraum entlang dieser Trajek-torie zu finden, muß konsistent mit der Dichteverteilung ρ des Ensembles sein

• letztendlich ist die Trajektorie weniger interessant als die Mittelwerte von Obser-vablen, die makroskopisch meßbar sind:=⇒ Berechnung von multidimensionalen Integralen vom Typ 〈O〉 =

∫E(Γ)ρ(Γ)dΓ

• nichttriviale Aufgabe, MC ist die einzige Methode fur vieldimensionale IntegraleE. Spohr, Master-Vorlesung Theoretische Chemie SS 2008. Universitat Duisburg-Essen 10

Monte Carlo Integration: “hit and miss” Algorithmus

x

y

x

x

x

x

Problem: numerische Abschatzung der Flache desEinheitskreises oder, dazu aquivalent, numerischeBestimmung von π

• zunachst generiert man einen Satz von Paarenunabhangiger Zufallszahlen, die von einer uni-formen (gleichformigen) Verteilung von Zufalls-zahlen auf dem Interval [0; 1] “gezogen” werden.Jedes Paar von Zufallszahlen bestimmt einenPunkt in der (x,y)-Ebene.

• als nachstes berechnet man den Abstand r =√x2 + y2 vom Ursprung

• Vergleiche r mit 1:wenn r ≤ 1, dann hat der “Versuchsschuß” den Kreis getroffen;wenn r > 1, dann hat er ihn verfehlt.


Monte Carlo Integration: “hit and miss” Algorithmus

• das Ergebnis ist statistischer Natur: jeder Punkt (x) hat die gleiche Wahrschein-lichkeit.

• man registriert die Zahl τshot der Schusse und die Zahl τhit der Treffer im rotenGebiet.

• offensichtlich gilt:

τhitτshot

≈ Flache des Einheitsviertelkreises

Flache des Einheitsquadrates=π

4=⇒ π ≈ 4τhit

τshot

• Die Grundlage des Algorithmus ist die Generierung von 2τshot Zufallszahlen (s.u.)

• Schatzwert fur π hangt von der Zahl der Schusse ab, der Fehler ist von der Gro-ßenordnung 1/

√τshot [O(τshot

−1/2]

• =⇒ fur 108 Versuche kann man eine Genauigkeit von 1/104, also 4 Stellen erwarten(z. B. 3.14173 statt 3.14159. . .)


Monte Carlo Integration: “Sample Mean Integration”

• allgemeiner anwendbar als der “hit and miss”-Algorithmus

• genauerer Schatzwert fur das Integral

• man betrachte dazu das Integral F =x2∫x1

dxf (x) =x2∫x1

dxρ(x)

f (x)

ρ(x)

mit einer beliebigen Wahrscheinlichkeitsverteilungsfunktion ρ.

• es werde eine Anzahl Versuche τ gemacht, wovon jeder darin besteht, eine Zufalls-zahl ζτ aus der Verteilung ρ(x) im Intervall [x1;x2] zu ziehen.

• offensichtlich gilt: F =⟨f (ζτ)

ρ(ζτ)

⟩V ersuche

〈. . .〉V ersuche ist der Mittelwert uber alle Versuche



• in unserem Beispiel:π

4=

1∫0

dx√

1− x2, also f (x) =√

1− x2.

• einfachste Anwendung: ρ(x) ist uniform

ρ(x) =

1

x2−x1wennx1 ≤ x ≤ x2

0 andernfalls

• dann kann F abgeschatzt werden durch

F =⟨f(ζτ )ρ(ζτ )

⟩=

1

τmax

τmax∑τ=1

f (ζτ)

ρ(ζτ)

= 1τmax

τmax∑τ=1

f(ζτ )1

x2−x1=x2 − x1τmax

τmax∑τ=1

f (ζτ)

= x2−x1τmax

τmax∑τ=1

√1− ζτ2

(vgl. Simpson-Regel)E. Spohr, Master-Vorlesung Theoretische Chemie SS 2008. Universitat Duisburg-Essen 14


• naturlich ist das Verfahren fur eine einfache 1-dimensionale Integration nicht kon-kurrenzfahig zur normalen numerischen Integration (mit Hilfe der Simpson-Regeloder der Trapezregel)

• mit Hilfe der Simpson-Regel wurden z. B. schon 104 Schritte ausreichen, um π auf 7Stellen zu berechnen (im Ggs. zu 108 Schritten fur eine Genauigkeit von 4 Stellen)



• aber:fur die vieldimensionalen Integrale der statistischen Mechanik ist die “Sample MeanIntegration” die einzige sinnvolle Methode, eine vernunftige Wahl von ρ(x)vorausgesetzt.

• man betrachte z. B. das Konfigurationsintegral ZNV T =∫

d~r exp(−βV(qk) furein System aus nurN = 100 Atomen in einem Wurfel der Kantenlange L (V = L3).

• d~r reprasentiert eine 300-dimensionale Integration!eine extrem ungenaue Integration mit der Simpson-Regel wurde 10 Funktionsaus-wertungen in jeder “Richtung” erfordern, um den Bereich [0;L] vernunftig aufzu-spannen=⇒ 10300 Funktionsauswertungen unmoglich

• außerdem wurde der Integrand fur die uberwaltigende Mehrzahl der Funktionsaus-wertungen aufgrund eines ungunstigen Boltzmannfaktors (ungunstige Uberlappungvon Atomen, sogenannte “bad contacts”) praktisch gleich Null sein und nur wenigePunkte (Konfigurationen) wurden signifikant zum Integral beitragen



Das “Sample-mean Integration” Verfahren sahe also folgendermaßen aus:

• wahle eine zufallige Konfiguration (Punkt im 300-dimensionalen Konfigurations-raum), indem 300 Zufallszahlen im Bereich [0;L], als Tripel zusammengefasst, dieKoordinaten jedes Atoms bestimmen

• berechne potentielle Energie V(τ ) und den Boltzmannfaktor

• wiederhole diese beiden Schritte viele Male.

• das Konfigurationsintegral kann dann abgeschatzt werden mittels

ZNV T =V N

τmax

τmax∑τ=1

exp[−βV(τ )]

• man kann erwarten, daß man weniger als 10300 Konfigurationen fur eine vernunftigeSchatzung benotigt

• aber wieder wurde die uberwaltigende Mehrzahl der Konfigurationen zu einemBoltzmannfaktor ≈ 0 fuhren (“unnotige Arbeit”)



• =⇒ fur dichte Flussigkeiten ubersteigt der Rechenzeitbedarf der Methode die Fa-higkeiten heutiger (und wohl auch zukunftiger) Computer

• Die Methode wurde angewandt auf die Untersuchung der strukturellen Eigenschaf-ten von Fluiden aus harten Kugeln bei niedriger Dichte (Alder et al, 1955)

• die Probleme mit den vieldimensionalen Integralen der statistischen Mechanik kom-men daher, daß die Verteilung extrem scharfe Maxima der Dichtefunktionbesitzt und riesige Regionen die Dichte ρ ≈ 0 besitzen!

• Analoge Probleme treten bei der Berechnung von Ensemblemittelwerten auf:

〈A〉NV T =∫d~rA exp(−βV(~r)∫d~r exp(−βV(~r)

≈τmax∑τ=1A(τ ) exp(−βV(τ ))

τmax∑τ=1

exp(−βV(τ ))

• fur realistische Dichten kann das Problem gelost werden, indem die Zufallskoordi-naten von einer nichtgleichformigen Verteilung ermittelt werden.

• =⇒ Importance Sampling (Metropolis-Sampling)


Importance Sampling

Zufallszahlen werden von einer nichtgleichformigen Verteilung ρ(x) ausgewahlt, wo-durch die Funktionsauswertungen auf die Regionen im Phasenraum konzentriert wer-den, die die wichtigen (“important”) Beitrage zur Zustandssumme machen:

〈A〉NV T =∫

dΓρNV T (Γ)A(Γ)

mit ρNV T (Γ) =1

ZNV Texp[−βV(Γ)]. Der Integrand lautet also A(Γ)ρNV T (Γ).

Sammelt man nun Konfigurationen von einer (frei wahlbaren) Verteilung ρ, so kannman das Integral abschatzen als

〈A〉NV T = 〈AρNV Tρ〉V ersuche

Fur die meisten Funktionen A(Γ) ist der Integrand ρNV TA nur dort signifikant, woρNV T signifikant ist. In diesem Falle sollte also die Wahl ρ = ρNV T eine akkurateAbschatzung des Integrals ermoglichen.(funktioniert meistens, nicht immer!)


Metropolis Monte Carlo

• im Falle ρ = ρNV T gilt also 〈A〉NV T = 〈A〉V ersuche• wir haben das Problem nur neu formuliert, jedoch nicht gelost!

• Das Problem lautet nun:Wie kann ich eine kanonische Verteilung generieren?

• Ein solches Verfahren wurde von Metropolis et al. (1953) entwickelt.

• die Schwierigkeit:Wie findet man eine Methode, die eine Sequenz von zufalligen Zustanden so ge-neriert, daß nach Ende der Simulation jeder Zustand mit der adaquaten Wahr-scheinlichkeit vorkam?

• Dies ist moglich, und sogar so, daß man nie den Normierungsfaktor von ρNV T , alsodie Zustandssumme selbst, berechen muß.

• die Methode:Generierung einer Markov-Kette


Markov-Ketten

Definition: Eine Markov-Kette ist eine Sequenz von Versuchen (“Versuchskonfigura-tionen”), die folgenden zwei Bedingungen genugt:

a) Das Ergebnis jedes Versuchs gehort zu einer endlichen Menge moglicher Ergeb-nisse, Γ1,Γ2,Γ3, . . . ,Γm, . . . ,Γn, . . ., dem Zustandsraum.

b) Das Ergebnis jedes Versuchs hangt allein vom unmittelbar vorhergehendenZustand ab.

• 2 Zustande Γm und Γn sind uber eine Ubergangswahrscheinlichkeit Πmn

verknupft, die die Wahrscheinlichkeit fur den Ubergang vom Zustand Γm nach Γn(kurz m nach n) darstellen.

• in einem endlichen Zustandsraum, kann man die Verteilungsfunktion ρ als Vektor~ρ = (ρ1, ρ2, . . . , ρn) charakterisieren

• die Πmn sind dann die Elemente einer Matrix Π


Markov-Ketten

• man startet mit einer Anfangsverteilung ~ρ (1).

• die Verteilungsfunktion

nach einem Schritt: ~ρ (2) = Π · ~ρ (1)

nach 2 Schritten: ~ρ (3) = ~ρ (2) ·Π = ~ρ (1) ·Π ·Π. . . ~ρ (4) = ~ρ (1) ·Π ·Π ·Π

and so on

• schließlich wird dies zu einer Grenzverteilung ~ρ konvergieren:

~ρ = limτ→∞ ~ρ

(1)Πτ

• die Wahrscheinlichkeit, daß ein Ubergang vom Zustand m in irgendeinen Zustand(des endlichen Zustandsraumes) passiert, inkl. des Ubergangs m→ m (kein Uber-gang), ist gleich 1 (100%).

• eine solche Matrix Π mit∑n

Πmn = 1 heißt stochastische Matrix (da ihre Zeilen

sich zu 1 addieren).


Markov-Ketten

•Wenn also die Grenzverteilung existiert, dann muß offensichtlich folgende Eigen-wertgleichung gelten:

~ρ ·Π = ~ρ = ~ρ · 1oder ∑

mρmΠmn = ρn

• Perron-Frobenius-Theorem: In einer irreduziblen Markovkette (eine, in der jederZustand von jedem anderen Zustand aus erreicht werden kann) gibt es einen links-seitigen Eigenwert 1, fur den der Eigenvektor gleich der Grenzverteilung ist.Die anderen Eigenwerte sind kleiner als 1 und bestimmen die Konvergenzrate.

• ρ ist unabhangig von der Anfangsverteilung ~ρ (1)

• Dies ist eine extrem wichtige Eigenschaft:Konsequenz: thermodynamische Ergebnisse hangen nicht von der Wahl des An-fangszustand ab!


Beispiel fur eine Markovkette

Zuverlassigkeit des Rechenzentrums:Man beobachtet:

•Wenn heute alles funktioniert, dann wird es auch morgen mit 60%iger Wahrschein-lichkeit funktionieren!

•Wenn heute nichts geht, dann ist die Wahrscheinlichkeit 70%, daß morgen auchnichts funktioniert!

Der Zustandsraum hat 2 Zustande (1. Zustand: ↑ 2. Zustand: ↓)

Π =

0.6 0.40.3 0.7

Wie sehen die Aussichten aus, in den nachsten Tagen arbeiten zu konnen?



Fall I: Heute funktioniert der Rechner (good news?)

also: ~ρ (1) = (1, 0)

morgen? ~ρ (2) = ~ρ (1) ·Π = (0.6, 0.4)ubermorgen? ~ρ (3) = ~ρ (2) ·Π = (0.48, 0.52)

~ρ (4) = ~ρ (3) ·Π = (0.444, 0.556)~ρ (5) = ~ρ (4) ·Π = (0.4332, 0.5668)

. . .~ρ = lim

τ→∞ ~ρ(1) ·Πτ =(0.4286,0.5714)

= (3/7, 4/7)



Fall II: Heute funktioniert der Rechner nicht (bad news?)

also: ~ρ (1) = (0, 1)

morgen? ~ρ (2) = ~ρ (1) ·Π = (0.3, 0.7)ubermorgen? ~ρ (3) = ~ρ (2) ·Π = (0.39, 0.61)

~ρ (4) = ~ρ (3) ·Π = (0.417, 0.583)~ρ (5) = ~ρ (4) ·Π = (0.4251, 0.5749)

=⇒ In vier Tagen sind unsere Chancen, arbeiten zu konnen, praktisch unabhangig vonder heutigen Situation!



• fur das kanonische Ensemble kennen wir die stochastische Matrix der Ubergangs-wahrscheinlichkeiten nicht

• stattdessen kennen wir aber die Grenzverteilung

ρnρm

=exp(−βVn)

exp(−βVm)= exp[−β(Vn − Vm)]

• es gibt viele Moglichkeiten, dies zu erreichen. =⇒ Wahlfreiheit

• insbesondere konnen wir die unnotig strenge Bedingung der mikroskopischenReversibilitat fordern:

ρmΠmn = ρnΠnm ⇐⇒ ρnρm

=Πmn

Πnm

das bedeutet, daß das Verhaltnis der direkten Ubergangswahrscheinlichkeiten zwi-schen den beiden Zustanden gleich ρm/ρn ist: die anderen Ubergange mussen alsodas korrekte Verhaltnis nicht erzwingen.



Die Wahl von Metropolis et al.:

Πmn = αmn wenn ρn ≥ ρm und m 6= n

Πmn = αmn(ρn/ρm) wenn ρn < ρm und m 6= n (also Πmn < αmn)

Πmm = 1− ∑n6=m

Πmn

αmn ist eine symmetrische stochastische Matrix: αmn = αnm

meist wird αmn = const. gewahlt.



Beweis:

• nach Voraussetzung ist αmn eine stochastische Matrix, also ∑mαmn = 1

• daher gilt: ∑m6=n

Πmn < 1,

weil der Faktor ρn/ρm nur dann benutzt wird, wenn er kleiner als 1 ist.

• also Πmn < αmn fur alle m 6= n.

• man definiert Πnn := 1− ∑m6=n

Πmn,

also ist Π eine stochastische Matrix.

• wenn ρn > ρm, dann ist Πmn = αmn und Πnm = αnm(ρm/ρn)

• also: Πnmρn = αnmρm = αmnρm = Πmnρm

• und damit ist auch die mikroskopische Reversibilitat erfullt und jeder Zustanderscheint mit der korrekten kanonischen Wahrscheinlichkeit


Metropolis Monte Carlo: Implementation

• starte von einem Zustand m, definiert durch Angabe aller Atomkoordinaten.

• * suche zufallig ein Atom aus

• ziehe 3 Zufallszahlen aus dem Intervall [0; 1] und verschiebe das ausgewahlte Atomentsprechend dieser Zufallszahlen innerhalb eines Volumens (2δrmax)

3 um die Po-sition des gewahlten Atoms

nach der Verschiebung befindet sich das Atomirgendwo (mit gleicher Wahrscheinlichkeit) in derschraffierten Region

rδ max



• dieser Schritt definiert α:

αmn = 1/NR wenn die Endposition innerhalb des schraffierten Bereichesαmn = 0 andernfallsNR ist die große (aber, wegen der endlichen Genauigkeit der Zahlendarstellungim Rechner, immer endliche) Zahl der Zustande mit dem Atom i irgendwo in derschraffierten Region.

• δrmax ist ein geeignet gewahlter Parameter

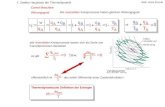
• berechne (Vn − Vm) und daraus ρn/ρm

• Fall α wenn ρn > ρm, dann akzeptiere die Verschiebung und gehe zuruck zu *

• wenn ρm ≥ ρn, dann akzeptiere die Verschiebung mit einer Wahrscheinlichkeitρn/ρm = exp[−β(Vn − Vm)] folgendermaßen:a) berechne exp[−β(Vn − Vm)] (< 1 und > 0)b) ermittle eine Zufallszahl im Intervall [0; 1].



• Fall β wenn die Zufallszahl kleiner als exp[−β(Vn−Vm)] ist, dann akzeptiere dieVerschiebung und gehe zuruck zu *

• Fall γ wenn nicht, dann akzeptiere die Verschiebung nicht, man andere also dieKoordinaten von Atom i nicht, zahle den Zustand m noch einmal und gehezuruck zu * (Πmm-Fall!)

Monte Carlo Simulation: dieser Zyklus wird millionen- oder milliardenfach wiederholt


Bemerkungen

• δrmax wird normalerweise so gewahlt, daß die mittlere Akzeptanzrate ungefahr 50% betragt:– sehr hohe Akzeptanz bedeutet geringe Energieunterschiede und damit langsameBewegung durch den Konfigurationsraum (δrmax ist klein!)– sehr niedrige Akzeptanz bedeutet, daß die meisten Energieanderungen sehr un-gunstig sind, weil δrmax zu groß ist und daher haufig eine signifikante Uberlappungdes Atoms i mit anderen Atomen zustande kommt

• eine typische Simulation dauert 105 bis 106 Durchgange(1 Durchgang (“pass”) = eine versuchte Verschiebung / Atom)

• Akzeptanzrate von 0.5 ist nicht notwendigerweise das Optimum. Dies hangt vonSystemgroße, Wechselwirkungsenergie, Temperatur, Dichte etc. ab.

• Man kann die zugrundeliegende stochastische Matrix α auch verandern, z. B. so,daß mehrere oder alle Atome gleichzeitig verschoben werden.


Bemerkungen

• man kann nicht uber alle Zustande summieren=⇒ ZNV T ist nicht direkt berechenbar

• Konsequenz: es gibt kein direktes Verfahren, um die thermodynamischen Großen“statistischer Natur” wie A, S und µ zu berechnen.

• dies gelingt mit Hilfe anderer Techniken wieThermodynamische IntegrationUmbrella SamplingGroßkanonische Monte Carlo-Methoden


Thermodynamik: 1. Hauptsatz - theochem.uni-due.de · Thermodynamik: 2. Hauptsatz Entropie ist eine...

Documents

Transcript of Thermodynamik: 1. Hauptsatz - theochem.uni-due.de · Thermodynamik: 2. Hauptsatz Entropie ist eine...