Einstieg in die Integralrechnung. Frage: Wie groß ist der Flächeninhalt der markierten Fläche ? A...
-
Upload
hulderich-kempter -
Category
Documents
-
view
107 -
download
3
Transcript of Einstieg in die Integralrechnung. Frage: Wie groß ist der Flächeninhalt der markierten Fläche ? A...

Einstieg in die Integralrechnun
g

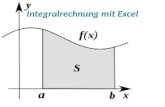
Frage: Wie groß ist der Flächeninhalt der markierten Fläche ?
A = ?

Wodurch ist die Größe der Fläche festgelegt ?
A = ?
Graph der Funktion x-AchseIntervalllänge

A (x) = ?
Gesucht ist eine Funktionsvorschrift A(x), die den Inhalt der Fläche liefert, die vom Graphen einer Funktion mit
der x–Achse im Intervall [0;x] eingeschlossen wird.
x0
Präzisierung der Aufgabe :

Betrachten wir zunächst einfache Beispiele:
x0
Durch elementare Rechnung erhält man: A(x) = 3·x
A(x) = 3·x
3)x(f

Beispiel 2:
Die Fläche des entstehenden Dreiecks berechnet sich zu:
0 x
x·32
)x(f
²x·31
x·x·32·
21
)x(A
²x·31
)x(A

Beispiel 3:
Die Fläche des Trapezes berechnet sich zu:
0
2x·31
)x(f
x2²x·61
x)·2x·31
·(221
)x(A
x
x2²x·61
)x(A

Zusammenstellung
2x·31
)x(f x2²x·61
)x(A
3)x(f A(x) = 3·x
x·32
)x(f ²x·31
)x(A
Lässt sich ein Zusammenhang zwischen Flächenfunktion und Ausgangsfunktion finden ?

Zusammenstellung
2x·31
)x(f x2²x·61
)x(A
Feststellung: Leitet man die Flächenfunktion ab, so erhält man die Ausgangsfunktion
3)x(f A(x) = 3·x
x·32
)x(f ²x·31
)x(A

Zusammenstellung
2x·31
)x(f x2²x·61
)x(A
3)x(f A(x) = 3·x
²x·41
)x(f ?)x(A
Falls dies richtig sein sollte, wie könnte dann die Funktionsvorschrift der Flächenfunktion zu f mit
²x·41
)x(f lauten ?
²x·31
)x(A x·32
)x(f

Zusammenstellung
2x·31
)x(f x2²x·61
)x(A
3)x(f A(x) = 3·x
²x·41
)x(f
Falls dies richtig sein sollte, wie könnte dann die Funktionsvorschrift der Flächenfunktion zu f mit
²x·41
)x(f lauten ?
?? ³x·121
)x(A
x·32
)x(f ²x·31
)x(A

Zusammenstellung
2x·31
)x(f x2²x·61
)x(A
3)x(f A(x) = 3·x
²x·41
)x(f ?? ³x·121
)x(A
Nur eine Vermutung !!
Doch Grund genug, sich den Differenzenquotienten der Flächenfunktion einmal anzuschauen
x·32
)x(f ²x·31
)x(A

h)x(A)hx(A
00
Betrachten wir also den Term:
Bzw. zunächst mal nur den Zähler :
)x(A)hx(A00
Wir verdeutlichen am Einstiegsbeispiel, was durch diese Differenz ausgedrückt wird

A (x0)
0 x0
)x(A)hx(A00
A(x0) ist der Inhalt der Fläche, die vom Graphen einer Funktion mit der x–Achse im Intervall [0;x0]
eingeschlossen wird.

A (x0+h)
0 x0+h
)x(A)hx(A00
A(x0+h) ist der Inhalt der Fläche, die vom Graphen einer Funktion mit der x–Achse im Intervall [0;x0+h]
eingeschlossen wird.

0 x0+h
)x(A)hx(A00
Obíge Differenz drückt also den Flächeninhalt der grün markierten Fläche aus.
x0

0 x0+h
)x(A)hx(A00
Obíge Differenz drückt also den Flächeninhalt der grün markierten Fläche aus.
x0

0 x0+h
)x(A)hx(A00
Wir versuchen, die Größe der Fläche nach oben und nach unten abzuschätzen:
x0
Sicherlich ist der Flächeninhalt größer als der Flächeninhalt der folgenden Rechteckfläche:

0 x0+h
)x(A)hx(A00
Diese hat den Flächeninhalt:
x0
f(x0)h

0
)x(A)hx(A00
Diese hat den Flächeninhalt:
f(x0)
h

0
)x(A)hx(A00
Diese hat den Flächeninhalt:
f(x0)
h
h)·x(f0
Es gilt also: h)·x(f0

0
)x(A)hx(A00
Schätzen wir nun die grüne Fläche durch folgendes Rechteck nach oben hin ab:
h
h)·x(f0
f(x0+h)

0
)x(A)hx(A00
Das Rechteck hat den Flächeninhalt:
h
h)·x(f0
f(x0+h)
h)·hx(f0
Es folgt: h)·hx(f 0

0
)x(A)hx(A00
h)·x(f0
h)·hx(f 0
Damit ist der obige Term sinnvoll nach oben und unten abgeschätzt

)x(A)hx(A00
h)·x(f0
h)·hx(f 0
Dividiert man die gesamte Ungleichung durch h, erhält man in der Mitte den
Differenzenquotienten der Flächenfunktion !
: h
)x(f0
h
)x(A)hx(A00
)hx(f 0

)x(A)hx(A00
h)·x(f0
h)·hx(f 0 : h
)x(f0
h
)x(A)hx(A00
)hx(f 0
h)x(A)hx(A
lim 00
0h
)hx(f lim 00h
)x(flim 00h
Bildet man den Limes aller Terme für h gegen Null, erhält man:

)x(A)hx(A00
h)·x(f0
h)·hx(f 0 : h
)x(f0
h
)x(A)hx(A00
)hx(f 0
h)x(A)hx(A
lim 00
0h
)hx(f lim 00h
)x(flim 00h
Bzw.: )x(f0
)x('A 0
)x(f 0

)x(A)hx(A00
h)·x(f0
h)·hx(f 0 : h
)x(f0
h
)x(A)hx(A00
)hx(f 0
h)x(A)hx(A
lim 00
0h
)hx(f lim 00h
)x(flim 00h
Diese Ungleichung ist nur erfüllbar, wenn gilt:
)x(f0
)x('A 0
)x(f 0
)f(x )x('A 00
Liefert der Term A(x) also den Inhalt der betrachteten Fläche, so gilt: A‘(x) = f(x)

Man beachte die in dieser Herleitung enthaltenen Vereinfachungen:
-Die Fläche liegt gänzlich oberhalb der x – Achse
-In den Beweis geht ein, dass f im betrachteten Intervall monoton wachsend ist
- f ist im betrachteten Intervall stetig