Numerische Mathematik I · Dieses Skript basiert auf einer Vorlesungsmitschrift der Vorlesung "Einf...
Transcript of Numerische Mathematik I · Dieses Skript basiert auf einer Vorlesungsmitschrift der Vorlesung "Einf...

Numerische Mathematik I
Olaf IppischInstitut fur Mathematik
TU ClausthalErzstr. 1
D-38678 Clausthal-ZellerfeldE-mail: [email protected]
Peter BastianInterdisziplinares Zentrum furWissenschaftliches Rechnen
Universitat HeidelbergIm Neuenheimer Feld 368
D-69120 HeidelbergE-mail: [email protected]
9. Marz 2016
i

Dieses Skript basiert auf einer Vorlesungsmitschrift der Vorlesung ”Einfuhrung in die Numerik”von Prof. Peter Bastian, Universitat Heidelberg, die von Stefan Breunig angefertigt wurde.
Beiden sei hiermit herzlich fur die zur Zurverfugungstellung des Materials gedankt.

Inhaltsverzeichnis
1 Einfuhrung 11.1 Modellbildung und Simulation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31.2 Ein einfaches Beispiel: Das Fadenpendel . . . . . . . . . . . . . . . . . . . . . . 41.3 Eine Geothermieanlage . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 101.4 Schadstoffausbreitung im Boden . . . . . . . . . . . . . . . . . . . . . . . . . . 111.5 Inhaltsubersicht der Vorlesung . . . . . . . . . . . . . . . . . . . . . . . . . . . 12
2 Fließkommazahlen 152.1 Zahlendarstellung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
2.1.1 Zahlenbereich . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192.1.2 Abstande zwischen Fließkommazahlen . . . . . . . . . . . . . . . . . . . 202.1.3 Praxis: IEEE754/IEC559 Standard . . . . . . . . . . . . . . . . . . . . . 20
2.2 Runden und Rundungsfehler . . . . . . . . . . . . . . . . . . . . . . . . . . . . 212.2.1 Rundungsfehler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.3 Fließkommarithmetik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 232.4 Fehleranalyse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 252.5 Ausloschung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3 Motivation zur Losung linearer Gleichungssysteme 313.1 Lineare Ausgleichsrechnung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 313.2 Randwertproblem . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
4 Notwendige Grundlagen aus der linearen Algebra 334.1 Skalarprodukt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 334.2 Vektornormen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 344.3 Matrixnormen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 364.4 Eigenwerte und Eigenvektoren . . . . . . . . . . . . . . . . . . . . . . . . . . . 384.5 Die Spektralnorm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
5 Konditionierung der Losung linearer Gleichungssysteme 415.1 Losbarkeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 415.2 Storungstheorie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
6 Eliminationsverfahren zur Losung linearer Gleichungsysteme 476.1 Dreieckssysteme (auch: gestaffelte Systeme) . . . . . . . . . . . . . . . . . . . . 476.2 Gauß-Elimination . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 476.3 LR-Zerlegung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
6.3.1 Permutation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 566.4 Rundungsfehleranalyse der LR-Zerlegung (GEM) . . . . . . . . . . . . . . . . . 586.5 Pivotisierung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 646.6 Spezielle Systeme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 67
6.6.1 Symmetrisch positiv definite Matrizen . . . . . . . . . . . . . . . . . . . 676.6.2 Diagonaldominante Matrizen . . . . . . . . . . . . . . . . . . . . . . . . 706.6.3 Bandmatrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 70
6.7 Spezielle Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 716.7.1 Nachiteration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 71
iii

6.7.2 Rangbestimmung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
6.7.3 Berechnung der Inversen . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
7 Irregulare Systeme 737.1 Least Squares Losung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 73
7.2 QR-Zerlegung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
8 Polynominterpolation 838.1 Approximation und Interpolation . . . . . . . . . . . . . . . . . . . . . . . . . . 83
8.2 Polynominterpolation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
8.2.1 Lagrange-Interpolation . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
8.2.2 Newton-Polynome . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 88
8.2.3 Interpolationsfehler . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
8.2.4 Horner Schema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 92
8.3 Anwendungen der Polynominterpolation . . . . . . . . . . . . . . . . . . . . . . 92
8.3.1 Numerische Differentation . . . . . . . . . . . . . . . . . . . . . . . . . . 92
8.3.2 Extrapolation zum Limes . . . . . . . . . . . . . . . . . . . . . . . . . . 95
8.4 Splines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
9 Trigonometrische Interpolation 1099.1 Trigonometrische Polynome . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
9.2 Diskrete Fourier-Transformation (DFT) . . . . . . . . . . . . . . . . . . . . . . 110
9.3 Schnelle Fourier-Transformation (FFT) . . . . . . . . . . . . . . . . . . . . . . . 113
9.4 Anwendung der Diskreten Fouriertransformation . . . . . . . . . . . . . . . . . 115
9.4.1 Spektralanalyse . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115
9.4.2 Spektren einiger Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . 115
10 Approximation von Funktionen 12110.1 Bernsteinpolynome . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 121
10.2 Gauß-Approximation . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 124
10.2.1 Approximation mit Orthonormalbasen . . . . . . . . . . . . . . . . . . . 127
10.2.2 Fehlerkontrolle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
10.3 Adaptive Approximation mit Haar-Wavelets . . . . . . . . . . . . . . . . . . . . 129
10.3.1 Definition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 129
10.3.2 Eigenschaften von Haar-Wavelets . . . . . . . . . . . . . . . . . . . . . . 130
10.3.3 Datenkompression mit Wavelets . . . . . . . . . . . . . . . . . . . . . . 133
11 Numerische Integration 13511.1 Newton-Cotes Formeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
11.2 Summierte Quadraturformeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
11.2.1 Fehlerkontrolle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 143
11.3 Quadraturen hoherer Ordnung . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
11.3.1 Romberg-Integration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 145
11.3.2 Gauß-Integration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
11.4 Ausblick . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
11.4.1 Adaptive Quadratur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 148
iv

11.5 Vergleich verschiedener Verfahren hoherer Ordnung . . . . . . . . . . . . . . . . 15011.5.1 Mehrdimensionale Quadratur . . . . . . . . . . . . . . . . . . . . . . . . 15211.5.2 Gebietszerlegung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15311.5.3 Fluch der Dimension . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 154
12 Iterative Losung von Gleichungsystemen 15512.1 Intervallschachtelung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15512.2 Newton Verfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15512.3 Fixpunktiteration . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16012.4 Iterationsverfahren zur Losung linearer Gleichungsysteme . . . . . . . . . . . . 162
v


1 Einfuhrung
Organisatorisches
Ubungen
• Ubung
– Donnerstags, 15-17 Uhr, Raum 310 (Institut fur Mathematik)
– Anmeldung uber Stud.IP
– Korrektur abgegebener Ubungsblatter (verpflichtend).
– Abgabe
∗ Mittwoch zu Beginn der Vorlesung
– Ruckgabe in der Ubung
• Programmieraufgaben in Python.
– Pythoneinfuhrung am 29. Oktober, 15-17 Uhr, Horsaal B
– Wir empfehlen als Python-Entwicklungsumgebung das kostenlose PyCharm Edu.Installationsanleitung fur Windows, MacOS, Linux unter https://www.jetbrains.com/pycharm-edu/quickstart/installation.html
Intensive Beteiligung an den Ubungen ist essentiell fur den Lernerfolg (und fur das Bestehender Klausur)
Klausur
• Termin wird noch bekannt gegeben.
• Erlaubte Hilfsmittel: 1 eigenhandig beschriebenes (nicht kopiertes) DIN A4 Blatt. Vorder-und Ruckseite durfen verwendet werden.
• Taschenrechner wird nicht notig (und damit erlaubt) sein
Literatur
• Vorlesungsmitschrift
– wird wahrend der Vorlesung erstellt
– enthalt den Tafelanschrieb
– erhaltlich uber Stud.IP
• Literatur:
– Wikipedia
– Barwolf, G.: “Numerik fur Ingenieure, Physiker und Informatiker: fur Bachelor undDiplom”, Spektrum Akademischer Verlag
1

– Dahmen, W. und Reusken, A.: “Numerik fur Ingenieure und Naturwissenschaftler”,Springer, 2. korr. Aufl. 2008
– Freund, R. W. und Hoppe, R. H. W.: “Stoer/Bulirsch: Numerische Mathematik 1:Numerische Mathematik 1”, Springer, 10. Auflage
– Hanke-Bourgeois, M.: “Grundlagen der Numerischen Mathematik und des Wissen-schaftlichen Rechnens”, Vieweg+Teubner Verlag, 3. akt. Aufl. 2009
– Plato, R.: “Numerische Mathematik kompakt: Grundlagenwissen fur Studium undPraxis”, Vieweg+Teubner Verlag, 4. Aufl. 2010
– Schwarz, H. R.: “Numerische Mathematik”, Vieweg+Teubner Verlag, 8. akt. Aufl.2011
Studentenbeteiligung
Zur Vorlesung
• Ruckmeldung uber Tutoren
• Mail an mich: [email protected]
Zu den Ubungen
• Ruckmeldung uber Tutoren
• Mail an mich: [email protected]
Computer (1949)
Quelle: Dryden Flight Research Center Photo Collection, NACA (NASA)
Supercomputer (2012)
2

Quelle: Julich Supercomputing Center (JSC)
1.1 Modellbildung und Simulation
Die Wissenschaftliche Methode
• Experiment: Beobachte was passiert.
• Theorie: Versuche die Beobachtung mit Hilfe von Modellen zu erklaren.
• Theorie und Experiment werden sukzessive verfeinert und verglichen, bis eine akzeptableUbereinstimmung vorliegt.
• In Naturwissenschaft und Technik liegen Modelle oft in Form mathematischer Gleichun-gen vor.
• Oft konnen die Modellgleichungen nicht geschlossen (mit Papier und Bleistift oder Ma-thematica . . . ) gelost werden.
Simulation
• Simulation: Gleichungen numerisch losen.
– Undurchfuhrbare Experimente werden moglich (z. B. Galaxienkollisionen).
– Teuere Experimente werden eingespart (z. B. Modelle im Windkanal).
– Parameterstudien schneller durchfuhrbar.
– (Automatische) Optimierung von Prozessen.
• Vielfaltiger Einsatz in Naturwissenschaft, Technik und Industrie: Stromungsberechnung(Klimasimulation), Festigkeit von Bauwerken . . .
• Grundlage fur alle diese Anwendungen sind numerische Algorithmen!
Die prinzipielle Herangehensweise im Wissenschaftlichen Rechnen zeigt Abbildung 1. Dieerfolgreiche Durchfuhrung einer Simulation erfordert die interdisziplinare Zusammenarbeit vonPhysikern oder Ingenieuren mit Mathematikern und Informatikern.
3

mathematisches Modellkonzeptionelles Modell
numerisches ModellComputerprogramm
Realität
wesentliche Prozesse
WellenausbreitungTransport von Materie
ReaktionPhasenübergänge...
algebraische GleichungenDifferentialgleichungenWahrscheinlichkeiten
Funktionen, ...Objekte: reelle Zahlen,
Näherungsverfahrenzur Lösung oben genannter Gleichungen
Komplexe SWSW−Engineering, Qualität
High Performance Comp.Visualisierung
?
SimulationEffizienz ("Teraflop")
Abbildung 1: Prinzipielles Vorgehen im Wissenschaftlichen Rechnen.
FehlerquellenUnterschiede zwischen Experiment und Simulation haben verschiedene Grunde:
• Modellfehler: Ein relevanter Prozess wurde nicht oder ungenau modelliert (Temp. kon-stant, Luftwiderstand vernachlassigt, . . . )
• Datenfehler: Messungen von Anfangsbedingungen, Randbedingungen, Werten fur Para-meter sind fehlerbehaftet.
• Abschneidefehler: Abbruch von Reihen oder Iterationsverfahren, Approximation vonFunktionen
• Rundungsfehler: Reelle Zahlen werden im Rechner genahert dargestellt.
Untersuchung von Rundungsfehlern und Abschneidefehler ist ein zentraler Aspekt der Vor-lesung!
1.2 Ein einfaches Beispiel: Das Fadenpendel
Pisa, 1582Der Student Galileo Galilei sitzt in der Kirche und ihm ist langweilig. Er beobachtet den
langsam uber ihm pendelnden Kerzenleuchter und denkt:”Wie kann ich nur die Bewegung
dieses Leuchters beschreiben?“.
4

Konzeptionelles Modell
Welche Eigenschaften (physikalischen Prozesse) sind fur die gestellte Frage relevant?
• Leuchter ist ein Massenpunkt mit der Masse m.
• Der Faden der Lange ` wird als rigide und masselos angenommen.
• Der Luftwiderstand wird vernachlassigt.
Nun entwickle mathematisches Modell.
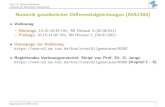
length
phi
FT FN
F
origin
m
Abbildung 2: Das Fadenpendel.
Abbildung 2 zeigt das Fadenpendel, welches aus dem sogenannten konzeptionellen Modellresultiert.
Krafte
• Pendel lauft auf Kreisbahn: Nur Tangentialkraft ist relevant.
• Tangentialkraft bei Auslenkung φ:
FT (φ) = −mg sin(φ)
• Also etwa:
FT (0) = −mg · 0 = 0
FT (π/2) = −mg · 1 = −mg.
• Vorzeichen kodiert Richtung.
5

Weg, Geschwindigkeit, Beschleunigung
• Fur den zuruckgelegten Weg (mit Vorzeichen!) gilt s(t) = `φ(t).
• Fur die Geschwindigkeit
v(t) =d s(φ(t))
dt=
d `φ(t)
dt= `
dφ(t)
dt
• und fur die Beschleunigung
a(t) =d v(φ(t))
dt= `
d2φ(t)
dt2.
Bewegungsgleichung
• Einsetzen in das 2. Newton’sche Gesetz
ma(t) = F (t)
⇒ m`d2φ(t)
dt2= −mg sin(φ(t)) ∀t > t0.
• Ergibt gewohnliche Differentialgleichung 2. Ordnung fur die Auslenkung φ(t):
d2φ(t)
dt2= −g
`sin(φ(t)) ∀t > t0. (1.1)
• Eindeutige Losung erfordert zwei Anfangsbedingungen (t0 = 0):
φ(0) = φ0,dφ
dt(0) = u0. (1.2)
Allgemeine Gleichung fur das Pendel ist schwer”analytisch“ zu losen.
Genahertes Modell: kleine Auslenkung
• Fur kleine Winkel φ gilt
sin(φ) ≈ φ, z.B. sin(0, 1) = 0, 099833417.
• Diese Naherung reduziert die Gleichung auf
d2φ(t)
dt2= −g
`φ(t).
• Ansatz φ(t) = A cos(ωt) liefert mit φ(0) = φ0, dφdt (0) = 0 dann die bekannte Formel
φ(t) = φ0 cos
(√g
`t
)(1.3)
6

Volles Modell, Numerisches Verfahren 1
• Lose das volle Modell mit zwei numerischen Verfahren.
• Ersetze Gleichung zweiter Ordnung durch zwei Gleichungen erster Ordnung:
dφ(t)
dt= u(t),
d2φ(t)
dt2=
du(t)
dt= −g
`sin(φ(t)).
• Ersetze Ableitungen durch Differenzenquotienten:
φ(t+∆t)− φ(t)
∆t≈ dφ(t)
dt= u(t),
u(t+∆t)− u(t)
∆t≈ du(t)
dt= −g
`sin(φ(t)).
• Mit φn = φ(n∆t), un = u(n∆t) erhalt man Rekursion (Euler):
φn+1 = φn +∆tun φ0 = φ0 (1.4)
un+1 = un −∆t g`
sin(φn) u0 = u0 (1.5)
Volles Modell; Verfahren 2
• Nahere zweite Ableitung mit zentralem Differenzenquotienten
φ(t+∆t)− 2φ(t) + φ(t−∆t)∆t2
≈ d2φ(t)
dt2= −g
`sin(φ(t)).
• Auflosen nach φ(t+∆t) ergibt Rekursionsformel (n ≥ 2):
φn+1 = 2φn − φn−1 −∆t2 (g/`) sin(φn) (1.6)
mit der Anfangsbedingung
φ0 = φ0, φ1 = φ0 +∆tu0. (1.7)
(Die zweite Bedingung kommt aus dem Eulerverfahren von oben).
Abbildung 3 zeigt Ergebnisse mit dem genaherten Modell und dem Eulerverfahren. Furfesten Zeitpunkt t und ∆t → 0 konvergiert das Verfahren. Fur festes ∆t und t → ∞ nimmtdie Abweichung von der genaherten Losung immer weiter zu.
Abbildung 4 zeigt zum Vergleich die Ergebnisse mit dem zentralen Verfahren. Im Unter-schied zum Eulerverfahren scheint der Fehler bei festem ∆t und t→∞ nicht unbeschrankt zuwachsen. Dieses Verfahren ist anscheinend robuster.
Ein Vergleich der numerischen Losung aus dem zweiten Verfahren fur das volle Modell mitdem vereinfachten Modell zeigt die Auswirkungen der Annahme sinφ ≈ φ auf das Ergebnis(Abbildung 5). Bei 28.6 Auslenkung ist die Ubereinstimmung noch einigermaßen passabel,aber die numerische Losung konvergiert bereits gegen eine andere Losung. Fur großere Aus-lenkungen weichen das vereinfachte Modell und die (konvergente) numerische Losung immerstarker voneinander ab. Die Form der Schwingung ist kein Kosinus mehr, da sich die Schwin-gung oben immer starker verlangsamt.
7

-0.2
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0.2
0 0.5 1 1.5 2 2.5 3 3.5 4
Aus
lenk
ung
Zeit
Konvergenz Differenzenquotient (Euler), phi=0.1
vereinfachtes Modelldt=0.2dt=0.1
dt=0.01dt=0.001
Abbildung 3: Simulation des Fadenpendels (volles Modell) bei φ0 = 0.1 ≈ 5.7 mit demEulerverfahren.
-0.15
-0.1
-0.05
0
0.05
0.1
0.15
0 0.5 1 1.5 2 2.5 3 3.5 4
Aus
lenk
ung
Zeit
Konvergenz zentriertes Verfahren, phi=0.1
vereinfachtes Modelldt=0.2dt=0.1
dt=0.01dt=0.001
Abbildung 4: Simulation des Fadenpendels (volles Modell) bei φ0 = 0.1 ≈ 5.7 mit dem zen-tralen Verfahren.
8

-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0 0.5 1 1.5 2 2.5 3 3.5 4
Aus
lenk
ung
Zeit
Zentriertes Verfahren, phi=0.5
vereinfachtes Modelldt=0.01
dt=0.0001
-4
-3
-2
-1
0
1
2
3
4
0 0.5 1 1.5 2 2.5 3 3.5 4
Aus
lenk
ung
Zeit
Zentriertes Verfahren, phi=3.0
vereinfachtes Modelldt=0.0001
-4
-3
-2
-1
0
1
2
3
4
0 2 4 6 8 10
Aus
lenk
ung
Zeit
Zentriertes Verfahren, phi=3.14
vereinfachtes Modelldt=0.0001
Abbildung 5: Vergleich von vollem und vereinfachtem Modell (jeweils in rot) bei den Winkelnφ = 0.5, 3.0, 3.14 gerechnet mit dem zentralen Verfahren.
9

VorlaufRuecklauf
Wasserstrom
Waermestrom
Abbildung 6: Schematischer Aufbau einer Geothermieanlage.
1.3 Eine Geothermieanlage
Wir betrachten die Modellierung und Simulation einer Geothermieanlage. Den schematischenAufbau zeigt die Abbildung 6. Kaltes Wasser fließt in einer Bohrung nach unten, wird erwarmtund in einem isolierten Innenrohr wieder nach oben gefuhrt.
• Grundwasserstromung gekoppelt mit Warmetransport.
• Welche Leistung erzielt so eine Anlage?
Modell fur eine Geothermieanlage
• Stromung des Wassers in und um das Bohrloch (stationare Grundwasserstromung)
∇ · jw = qw,
jw = −Kµ
(∇p− ρwg)
• Transport der Warme durch Konvektion und Warmeleitung
∂(Ctot ρtotT )
∂t+∇ · jh + Cwρwqw T = 0,
jh = Cwρw jwT − λ∇T
in Abhangigkeit diverser Parameter: Bodendurchlassigkeit K, Viskositat µ, spezifischeWarmekapazitat Cw, Ctot, Dichte ρw, ρtot, Warmeleitfahigkeit λ, Pumprate qw sowieRand- und Anfangsbedingungen. Gesucht werden die Verteilung von Druck p und Tem-peratur T .
Abbildung 6 zeigt die Entzugsleistung so einer Anlage fur die ersten hundert Tage Betriebs-zeit. Dabei wurden plausible Werte fur die Modellparameter gewahlt.
10

300000
400000
500000
600000
700000
800000
900000
1e+06
1.1e+06
1.2e+06
1.3e+06
0 10 20 30 40 50 60 70 80 90 100
En
tzu
gsle
istu
ng
[W
att
]
Zeit [Tage]
Entzugsleistung im kalibrierten System
Abbildung 7: Entzugsleistung der Geothermieanlage uber die Zeit fur bestimmteSystemparameter.
1.4 Schadstoffausbreitung im Boden
Als weiteres Beispiel nennen wir die Modellierung und Simulation einer Schadstoffausbreitungim Boden, siehe Abbildung 8. Der Schadstoff wird hier als mit Wasser mischbarer idealer Tracerangenommen (also ein Stoff, der nicht am Boden sorbiert, wie z.B. Chlorid).
Transportgleichungen
• Stromung des Wassers im (ungesattigten) Boden (instationare Richardsgleichung)
∂θw(ψm)
∂t−∇ ·
[K kr(θw)
µ(∇ψm − ρwg)
]+ qw = 0
• Transport des gelosten Stoffes (Konvektions-Dispersionsgleichung)
∂ (θw(ψm) cs)
∂t−∇ · [D(θw)∇cs − cs jl] + qs = 0
Hier sind das Matrixpotential ψm im Boden und die Konzentration cs des gelosten Stoffesgesucht. Dabei gehen mehrere Materialfunktionen ein, z.B. die Bodenwassercharakteri-stik θw(ψm), die relative Leitfahigkeit kr(θw) und der Diffusionskoeffizient D(θw) (sieheAbb. 9)
.
Mit heutigen Parallelrechnern lassen sich auch Fließprozesse in stark heterogenen Syste-men mit hoher Auflosung simulieren (Abb. 10). Das Beispiel zeigt eine Rechnung mit 1024×
11

Abbildung 8: Potential- und Wassergehaltsverteilung am Beginn der Simulation. Insbesondereder Wassergehalt spiegelt die Heterogeneitat des Bodenblocks (10× 10× 6.5 m)wieder. Dabei sind Fahrspuren im gepflugten Oberboden ebenso zu erkennen wieTonlinsen im Unterboden.
1024 × 810 ≈ 850 · 106 Gitterzellen. Die Rechenzeit fur den Wassertransport betrug mit 1024Computenodes (4096 Kernen) des ehemals schnellsten deutschen Parallelrechners JUGENE(Bluegene/P) 17 Tage und fur den Stofftransport mit 128 Computenodes (4096 Prozessen) desNachfolgemodells JUQUEEN (Bluegene/Q) 18.7 Stunden.
1.5 Inhaltsubersicht der Vorlesung
Wir werden in dieser Vorlesung die folgenden Themengebiete behandeln:
• Grundbegriffe, Fließkommazahlen, Fließkommaarithmetik
• Direkte Methoden zur Losung linearer Gleichungssysteme
• Interpolation und Approximation
• Numerische Differentiation
• Numerische Integration
• Iterationsverfahren zur Losung linearer und nichtlinearer Gleichungssysteme
12

1
10
100
1000
0 0.1 0.2 0.3 0.4 0.5
ψ [
cm
]
θ [-]
Bodenwassercharakteristik
OberbodenSandLehmlinsen
PflugsohleSaatbett
1e-06
1e-05
0.0001
0.001
0.01
0.1
1
10
100
1 10 100 1000
K [
cm/h
]ψ [cm]
Hydr. Leitfähigkeitsfunktion
OberbodenSandLehmlinsen
PflugsohleSaatbett
Abbildung 9: Materialfunktionen: Zusammenhang zwischen Matrixpotential und Wasserge-halt (Bodenwassercharakteristik, links) sowie zwischen Matrixpotential undLeitfahigkeit (rechts).
Abbildung 10: Potential- und Wassergehaltsverteilung nach 225 Stunden simulierter Zeit(links) und Stoffkonzentration nach 499 Stunden simulierter Zeit (rechts).
13


2 Fließkommazahlen
Im Computer gibt es verschiedene Typen zur Reprasentation von Zahlen. In C/C++/Java z.B.
unsigned int, unsigned short, unsigned long N0
int, short, long Zfloat, double Rcomplex<float>, complex<double> C
und in Python:
int, long Zfloat Rcomplex C
Diese sind Realisierungen der Zahlenmengen N0,Z,R,C.Ganzzahlen (z.B. unsigned int, int . . . ) sind exakt, haben aber einen endlichen Wertebe-
reich.Bei Fließkommazahlen (z.B. float und double) konnen auch innerhalb des erlaubten Be-
reichs liegenden Zahlen nur naherungsweise dargestellt werden.Welche Folgen hat das fur die Genauigkeit von Berechnungen?
Beispiel 2.1Potenzreihe fur ex
• ex lasst sich mit einer Potenzreihe berechnen (siehe IngMathe I):
ex =∞∑
n=0
xn
n!= 1 +
∞∑
n=1
xn
n!= 1 +
∞∑
n=1
yn.
• Dies formulieren wir rekursiv:
Anfangswerte:
y1 = x, S1 = 1 + y1.
Rekursion:
yn =x
nyn−1, Sn = Sn−1 + yn.
• Probiere verschiedene Genauigkeiten und Werte von x.
• Wir testen zunachst positive Argumente.
Fur x = 1 und float-Genauigkeit erhalten wir:
1.000000000000000e+00 1 2.000000000000000e+00
2 5.000000000000000e-01 2 2.500000000000000e+00
1.666666716337204e-01 3 2.666666746139526e+00
4 4.166666790843010e-02 4 2.708333492279053e+00
8.333333767950535e-03 5 2.716666936874390e+00
6 1.388888922519982e-03 6 2.718055725097656e+00
1.984127011382952e-04 7 2.718254089355469e+00
15

8 2.480158764228690e-05 8 2.718278884887695e+00
2.755731884462875e-06 9 2.718281745910645e+00
10 2.755731998149713e-07 10 2.718281984329224e+00
0.000000000000000e+00 100 2.718281984329224e+00
12 ex 2.718281828459045e+00
also 7 gultige Ziffern.
Fur x = 5 . . .
9.333108209830243e-06 21 1.484131774902344e+02
2 ex 1.484131591025766e+02
ebenfalls 7 gultige Ziffern.
• Nun testen wir negative Argumente.
Fur x = −1 und float-Genauigkeit erhalten wir:
2.755731998149713e-07 10 3.678794205188751e-01
2 -2.505210972003624e-08 11 3.678793907165527e-01
2.087675810003020e-09 12 3.678793907165527e-01
4 ex 3.678794411714423e-01
also 6 gultige Ziffern.
Fur x = −5
-5.000000000000000e+00 1 -4.000000000000000e+00
2 1.250000000000000e+01 2 8.500000000000000e+00
-2.083333396911621e+01 3 -1.233333396911621e+01
4 2.604166793823242e+01 4 1.370833396911621e+01
-2.333729527890682e-02 15 1.118892803788185e-03
6 7.292904891073704e-03 16 8.411797694861889e-03
1.221854423194557e-10 28 6.737461313605309e-03
8 0.000000000000000e+00 100 6.737461313605309e-03
ex 6.737946999085467e-03
nur noch 4 gultige Ziffern!
Fur x = −20 und float-Genauigkeit sind . . .
-2.000000000000000e+01 1 -1.900000000000000e+01
2 2.000000000000000e+02 2 1.810000000000000e+02
-1.333333374023438e+03 3 -1.152333374023438e+03
4 6.666666992187500e+03 4 5.514333496093750e+03
-2.666666796875000e+04 5 -2.115233398437500e+04
6 -2.611609750000000e+06 31 -1.011914250000000e+06
1.632256125000000e+06 32 6.203418750000000e+05
8 -9.892461250000000e+05 33 -3.689042500000000e+05
5.819095000000000e+05 34 2.130052500000000e+05
10 -3.325197187500000e+05 35 -1.195144687500000e+05
1.847331718750000e+05 36 6.521870312500000e+04
16

12 -4.473213550681976e-07 65 7.566840052604675e-01
1.355519287926654e-07 66 7.566841244697571e-01
14 -4.046326296247571e-08 67 7.566840648651123e-01
1.190095932912527e-08 68 7.566840648651123e-01
16 ex 2.061153622438557e-09
keine Ziffern mehr gultig. Das Ergebnis ist um 8 Großenordnungen daneben!
Wir konnen die Genauigkeit verbessern indem wir mit mehr Ziffern rechnen. Fur x = −20und double-Genauigkeit erhalt man
-1.232613988175268e+07 27 -5.180694836889297e+06
2 8.804385629823344e+06 28 3.623690792934047e+06
1.821561256740375e-24 94 6.147561828914626e-09
4 -3.834865803663947e-25 95 6.147561828914626e-09
ex 2.061153622438557e-09
Immer noch um einen Faktor 3 daneben! Erst mit”vierfacher Genauigkeit“ erhalt man
1 7.0937168371834023136209731491427e-42 118 2.0611536224385583392700458752947e-09
ex 2.0611536224385578279659403801558e-09
also 15 gultige Ziffern (bei ca 30 Ziffern”Rechengenauigkeit“).
Die Berechnungen mit vierfacher Genauigkeit wurden mit den Paketen qd und arprec (beidehttp://crd.lbl.gov/~dhbailey/mpdist/) durchgefuhrt. qd erlaubt bis zu vierfache double
Genauigkeit, arprec beliebige Genauigkeit. Die GNU multiprecision library (http://gmplib.org/) ist eine Alternative.
Um dieses Verhalten zu verstehen, mussen wir uns zunachst mit der Darstellung von Zahlenauf dem Computer beschaftigen.
2.1 Zahlendarstellung
Die Darstellung einer Zahl
±mn . . .m2m1m0,m−1m−2 . . .m−k
ist in einem Stellenwertsystem1 die Kurzschreibweise fur
x = ±mnβn + . . .+ m2β
2 +m1β +m0 +m−1β−1 +m−2β
−2 + . . .+m−kβ−k
dabei ist
• ± das Vorzeichen (ein Bit genugt)
• β ∈ N, β ≥ 2 heißt Basis
• mi ∈ 0, 1, 2, . . . , β − 1 heißen Ziffern
Geschichte: (D. E. Knuth. The Art of Computer Programming. Addison–Wesley, 3. edition,1998, Band 2, Seite 195ff)
1Es geht auch ganz anders, siehe z.B. die romischen Zahlen.
17

• Babylonier (≈ 1750 v. Chr.): β = 60
• Basis 10 erstmals verwendet in Indien (≈ 600 v. Chr.), in Europa ab ca. 1585
• Blaise Pascal (1623-1662): Jedes β ≥ 2 moglich
Heute gebrauchlich:
• Binarzahlen (Basis 2): (101010)2
• Oktalzahlen (Basis 8): (52)8
• Dezimalzahlen (Basis 10): (42)10
• Hexadezimalzahlen (Basis 16): (2A)2
Festkommazahlen: Wahle minimalen und maximalen Exponenten
x = ±n∑
i=−kmiβ
i
Problem: Wissenschaftliche Anwendungen brauchen Zahlen sehr unterschiedlicher Große:Plancksches Wirkungsquantum: 6, 626093 · 10−34 JsRuhemasse des Elektrons: 9, 11 · 10−28 gAvogadrokonstante: 6, 021415 · 1023mol−1
Bei β = 2 wurde man fur 2n+k ≈ 1023+34 mindestens n+ k = 57log 2 ≈ 190 Stellen brauchen.
Definition 2.2 (normierte Fließkommazahlen)Sei β, r, s ∈ N und β ≥ 2. F(β, r, s) ⊂ R besteht aus den Zahlen mit folgenden Eigenschaften:
1. ∀x ∈ F(β, r, s) gilt x = m(x) · βe(x) mit
m(x) = ±r∑
i=1
miβ−i, e(x) = ±
s−1∑
j=0
ejβj , mi, ej ∈ 0, 1, . . . , β − 1
m heißt Mantisse, e Exponent.
2. ∀x ∈ F(β, r, s) gilt m1 6= 0 falls x 6= 0.
m1 6= 0 heißt Normierung. Diese Bedingung macht die Fließkommadarstellung eindeutig.
ist x ∈ F(β, r, s) und x 6= 0, dann gilt wegen 2.
β−1 ≤ |m(x)| < 1 und damit βe(x)−1 ≤ |x| ≤ βe(x). (2.1)
Beispiel 2.31. F(10, 3, 1) besteht aus Zahlen der Form:x = ±(m1 · 0, 1 +m2 · 0, 01 +m3 · 0, 001) · 10±e0
mit m1 6= 0 ∨ (m1 = 0 ∧m2 = 0 ∧m3 = 0)z.B. 0, 999 · 101, 0, 123 · 10−1, 0, aber nicht 0, 000000000014 = 0, 140 · 10−10, da Exponentzu klein.
18

2. F(2, 2, 1) besteht aus Zahlen der Form:
x = ±(m1
1
2+m2
1
4
)
︸ ︷︷ ︸0, 1
2, 34
· 2±e0︸︷︷︸2−1,20,21= 1
2,1,2
⇒ F(2, 2, 1) =
−3
2,−1
︸ ︷︷ ︸− 3
4,− 1
2·2
, −3
4,−1
2︸ ︷︷ ︸− 3
4,− 1
2·1
−3
8,−1
4︸ ︷︷ ︸− 3
4,− 1
2· 1
2
, 0,1
4,3
8,1
2,3
4, 1,
3
2
.
−32
−1 −34 −1
2−38−1
40 1
438
12
34
1 32
Lucken wegen Normalisierung
Der Abstand zwischen zwei Fließkommazahlen ist in diesem Beispiel bei großen Zahlen1/2, bei kleinen 1/8. In der Nahe der Null ist der Abstand allerdings 1/4, was an derNormierung liegt.
Losung: Nehme fur |x| < 14 (= β−β
s) die nicht normalisierten Zahlen dazu.
2.1.1 Zahlenbereich
Großte/kleinste darstellbare Zahl in F(β, r, s):
X+/− = ±großte Ziffer︷ ︸︸ ︷(β − 1)
(β−1 + . . .+ β−r
)︸ ︷︷ ︸
=1−β−r
· β
=βs−1︷ ︸︸ ︷(β − 1)(βs−1 + . . .+ 1) = ±(1− β−r) · ββs−1
Kleinste positive/großte negative Zahl in F(β, r, s):
x+/− = ± β−1
︸︷︷︸kleinste Mantisse (Normierung)
· β
=−(βs−1)︷ ︸︸ ︷−(β − 1)(βs−1 + . . .+ 1) negativ! = ±β−βs
Damit ist die Untermenge D der reellen Zahlen aus der Fließkommazahlen in der Basis β mitr Stellen Mantisse und s Stellen fur den Exponenten dargestellt werden konnen:
F(β, r, s) ⊂ D(β, r, s) := [X−, x−] ∪ 0 ∪ [x+, X+] ⊂ R.
19

2.1.2 Abstande zwischen Fließkommazahlen
Festkommazahlen: Abstand zwischen Zahlen konstant β−k.Fließkommazahlen: Abstand von x ∈ F zum nachsten x′ ∈ F hangt von x ab:
βe−1 = 0, 10 . . . 0 · βenachste Zahl: 0, 10 . . . 1 · βe
Abstand: β−rβe = βe−r
...
vorrige Zahl: = 0, (β − 1)(β − 1) . . . (β − 1) · βe
βe = 0, 10 . . . 0 · βe+1
Abstand: β−rβe = βe−r
nachste Zahl: 0, 10 . . . 1 · βe+1
Abstand: β−rβe+1 = βe+1−r
⇒ Im Intervall [βe−1, βe] betragt der absolute Abstand zwischen zwei Zahlen βe−r.Der relative Abstand liegt zwischen β−r und β−r+1, schwankt also um den Faktor β−1 je
nach Große von |x|. Dieser Faktor heißt wobble.Konsequenz: Kleine β sind besser, weil die Zahlen dann gleichmaßiger verteilt sind.
2.1.3 Praxis: IEEE754/IEC559 Standard
Verabschiedet: 1985, Ziel: Portabilitat.β = 2 mit 4 Genauigkeitsstufen und normierter Darstellung (single-ext wird in der Praxiskaum verwendet).
Format
single single-ext double double-ext
emax 127 ≥ 1024 1023 ≥ 16384emin −126 ≤ −1024 −1022 ≤ −16381
Bit Expon. 8 ≥ 11 11 ≥ 15
Bits total 32 ≥ 43 64 ≥ 79
Beispiel double:
• 64 Bit insgesamt
• 53 Bit fur Mantisse, davon 1 Bit Vorzeichen, bleiben 52 Nachkommastellen.Wegen β = 2 und Normierung ist immer m1 = 1⇒ erste Ziffer braucht nicht gespeichertwerden (hidden bit). Damit erhalt man r = 53.
• 11 Bit fur Exponenten. Der Exponent e wird vorzeichenlos als Zahl c ∈ [1, 2046] gespei-chert. Setze e = c− 1023⇒ e ∈ [−1022, 1023]
• Die Werte c ∈ 0, 2047 werden anderweitig genutzt.
c = 0 ∧ m = 0 kodiert die Zahl x=0
c = 0 ∧ m 6= 0 kodiert die denormalisierte Darstellung (evtl. langsam, abschaltbar bei SSE2)
c = 2047 ∧ m 6= 0 kodiert NaN:”not a number“
c = 2047 ∧ m = 0 kodiert Wert ±∞ (Uberlauf)
20

2.2 Runden und Rundungsfehler
Um x ∈ R in F(β, r, s) zu approximieren brauchen wir eine Abbildung
rd: D(β, r, s)→ F(β, r, s). (2.2)
Achtung: rd setzt voraus, dass x im darstellbaren Zahlenbereich liegt!Im Falle eines Uber-/Unterlaufes muss die Anzahl der Stellen fur Mantisse und Exponenten
erhoht werden.Sinnvollerweise verlangen wir:
|x− rd(x)| ≤ miny∈F|x− y| ∀x ∈ D (Bestapproximation).
Mit
| | |
`(x) = maxy ∈ F : y ≤ x x ∈ D r(x) = miny ∈ F : y ≥ x
gilt dann:
rd(x) =
`(x) falls |x− `(x)| < |x− r(x)|r(x) falls |x− `(x)| > |x− r(x)|? falls |x− `(x)| = |x− r(x)|
Im letzten Fall ist eine zusatzliche Rundungsregel erforderlich! Dafur gibt es verschiedeneMoglichkeiten.
Sei x = sign(x) ·(∑∞
i=1miβ−i) · βe die exakte normierte Darstellung von x ∈ D.
Naturliche Rundung (das was jeder kennt)
rd(x) =
`(x) = sign(x) ·(∑r
i=1miβ−i) · βe falls 0 ≤
nachste Stelle︷ ︸︸ ︷mr+1 < β
2
r(x) = `(x) + sign(x) · βe−r︸︷︷︸Wertigkeit der letzten Stelle
falls β2 ≤ mr+1 < β
Gerade Rundung (nur falls β gerade):
rd(x) =
`(x) falls (|x− `(x)| < |x− r(x)|) ∨ (|x− `(x)| = |x− r(x)| ∧mr gerade)
r(x) sonst
Wahrend bei der naturlichen Rundung systematisch immer in eine Richtung gerundet wird,wird bei der geraden Rundung genauso oft auf- wie abgerundet, was systematische Fehlervermeidet.
Beispiel 2.4
x = 110→ x′ ∈ F(4, 3, 2)
21

1. Exponent
log4(110) =log10(110)
log10(4)=
ln(110)
ln(4)= 3, 39
Aufrunden damit Mantisse < 1⇒ Exponent 4 (bzw. 10 im 4er-System)
2. Mantisseteile x durch 4 hoch Exponent minus eins, also 43.
y1 =110
43= 1, 71875⇒ m1 = 1
y2 = (y1 −m1) · 4 = 2, 875⇒ m2 = 2
y3 = (y2 −m2) · 4 = 3, 5⇒ m3 = 3
y4 = (y3 −m3) · 4 = 2, 0⇒ m4 = 2
⇒ x in Basis 4 ist 0, 1232 · 410.Runden mit gerader Rundung:⇒ x′ = 0, 130 · 410
Kontrolle:(0, 130 · 410
)4
= (112)10(0, 123 · 410
)4
= (108)10
2.2.1 Rundungsfehler
Definition 2.5Sei x′ ∈ R eine Naherung von x ∈ R. Dann heißt
∆x = x′ − x absoluter Fehler
und fur x 6= 0
εx′ =∆x
xrelativer Fehler.
Umformen liefert: x′ = x+∆xx 6=0= x
(1 + ∆x
x
)= x (1 + εx′).
Der relative Fehler ist in der Praxis geeigneter um z.B. Messfehler zu quantifizieren.
Beispiel 2.6Sei ∆x = x′ − x = 100km.Fur x = Entfernung Erde – Sonne ≈ 1, 5 · 108 km ist
εx′ ≈ 6, 6 · 10−7
relativ klein. Fur x = Entfernung Clausthal-Zellerfeld – Berlin ≈ 300 km ist
εx′ = 0, 3
dagegen relativ groß.
22

Lemma 2.7 (Rundungsfehler)Bei der Rundung in F(β, r, s) gilt fur den absoluten Fehler
|x− rd(x)| ≤ 1
2βe(x)−r (2.3)
und fur den relativen Fehler (x 6= 0)
|x− rd(x)||x| ≤ 1
2β1−r
Beweis: Sei x = m(x) ·βe(x) die normierte, Darstellung von x (mit moglicherweise unendlichvielen Mantissenstellen).
Wie oben (Abschnitt 2.1.2) gezeigt gilt
|r(x)− `(x)|︸ ︷︷ ︸zwei aufeinanderfolgende
Zahlen in F,`(x)∈[βe(x)−1,βe(x)]
= βe(x)−r.
Der maximale Fehler tritt auf fur x = `(x)+r(x)2
|x− rd(x)| ≤∣∣∣∣`(x) + r(x)
2− `(x)
∣∣∣∣ =1
2|r(x)− `(x)| = 1
2βe−r
Fur den relativen Fehler (x 6= 0) gilt
|x− rd(x)||x| ≤
12β
e(x)−r
|m(x)| · βe(x)=
1
2
1
|m(x)|︸ ︷︷ ︸|m(x)|≥β−1
β−r ≤ 1
2β−r+1
eps := 12β−r+1 heißt Maschinengenauigkeit (u in MATLAB, von “unit roundoff”). Dies ist
der maximale Fehler, der bei der Rundung der Mantisse auftreten kann.
2.3 Fließkommarithmetik
Wir benotigen eine Arithmetik auf F
~ : F× F→ F mit ~ ∈ ⊕,,,,
die den bekannten Operatoren ∗ ∈ +,−, ·, / auf R entspricht.
Problem: In der Regel ergibt sich x, y ∈ F⇒ x ∗ y 6∈ F.
Somit ist das Ergebnis x~ y wieder zu runden. Wir definieren
x~ y = rd(x ∗ y) ∀x, y ∈ F. (2.4)
Man sagt ~ ist “exakt gerundet”. Dies ist nicht trivial! (implizite Annahme: x ∗ y ∈ D!)
23

Beispiel 2.8Es sei F(10, 3, 1), x = 0, 215 · 108 und y = 0, 125 · 10−5
Betrachte: x y = rd(x− y)
1. x− y : x = 0, 215 000 000 000 000 0 · 108
y = 0, 000 000 000 000 0︸ ︷︷ ︸13 Nullen
12 5 · 108 ← Schiebe y auf gleichen Exponenten
(x− y) = 0, 214 999 999 999 987 5 · 108
2. Runden
x y = rd(0, 2149 . . . · 108) = 0, 215 · 108
Problem: Schritt 1 erfordert extrem hohe Stellenzahl in der Großenordnung von βs!
Geht es einfacher?
Runde y z.B. schon nach dem Schieben, d.h. betrachte x y = rd(x)− rd(y). Dies liefert imobigen Fall das gleiche Ergebnis.
Im Allgemeinen ist das gefahrlich
x = 0, 101 · 101 −−−−−−−−−−−→ 0, 101 · 101
y = 0, 993 · 100 schieben u. runden−−−−−−−−−−−→ 0, 099 · 101
rd(x)− rd(y) = 0, 002 · 101
relativer Fehler im Ergebnis
(x y)− (x− y)
(x− y)=
0, 02− 0, 017
0, 017≈ 0, 176 ≈ 35 eps
(mit eps =
1
210−3+1 = 0, 005
)
⇒ Fehler ist 35 mal großer als erwartet.
Eine Stelle mehr im Addierer (also r + 1) liefert hier das exakte Ergebnis!
Mit einer zusatzlichen Stelle erhalt man im Allgemeinen:
∣∣∣∣(x y)− (x− y)
(x− y)
∣∣∣∣ ≤ 2 eps
Mit zwei Stellen erreicht man exakte Rundung!
Die zusatzlichen Stellen nennt man “guard digits”.
Zusatzliche Probleme bei der Arithmetik ~ : F× F→ F
• Assoziativ- und Distributivgesetz gelten nicht, es kommt also auf die Reihenfolge derOperationen an!
• ∃ y ∈ F so dass x⊕ y = x
• Allerdings gilt das Kommutativgesetz.
24

• Es gelten folgende einfache Regeln:
(−x) y = −(x y)
1 x = x,
x y = 0⇒ (x = 0) ∨ (y = 0)
(x z ≤ y z) ∧ (z > 0) ⇐⇒ (x ≤ y).
Falls x y < β−βs, gibt es eine sog. Underflow-Exception und es wird eine denormierte
Zahl zuruckgegeben. Ist x y < β−(βs+r−1)), dann ist diese auch Null.
2.4 Fehleranalyse
Wir wollen die Fortpflanzung von Rundungsfehlern in Berechnungen untersuchen.Sei f : Rm → Rn, in Komponenten
f(x) =
f1(x1, . . . , xm)...
fn(x1, . . . , xm)
.
Zur Berechnung von f im Rechner nutze numerische Realisierung
f ′ = Fm → Fn.
f ′ wird durch einen Algorithmus realisiert, d.h. aus
• endlich vielen (=Terminierung)
• elementaren (=bekannten) Rechenoperationen ϕi
f ′(x) = ϕ`(. . . ϕ2(ϕ1(x)) . . .).
Wichtig:
1. Zu einem f gibt es in der Regel viele Realisierungen im Sinne unterschiedlicher Reihen-folgen, z.B.
(a⊕ b)⊕ c 6= a⊕ (b⊕ c)
2. Jedes ϕi steuert einen unbekannten Fehler bei.
3. Im Prinzip kann die Rechengenauigkeit beliebig gesteigert werden, d.h. eigentlich gibt eseine Folge
f (k) : (F(k))m → (F(k))n
mit wachsender Mantissenlange k.
Der auftretende Fehler ist
f(x)︸︷︷︸exaktes Ergebnis
− f ′( rd(x)︸ ︷︷ ︸Eingabe runden
) =
︸ ︷︷ ︸numerische Auswertung
f(x)− f(rd(x))︸ ︷︷ ︸À Konditionsanalyse von f
+ f(rd(x))− f ′(rd(x))︸ ︷︷ ︸Á Rundungsfehleranalyse
. (2.5)
25

Die Konditionsanalyse untersucht also die Fehlerverstarkung des Eingabefehlers in exakterArithmetik, die Rundungsfehleranalyse den Rundungsfehler bei Berechnungen in Fließkom-maarithmetik fur gleiche Eingaben.
À Differentielle Konditionsanalyse
Sei f : Rm → Rn zweimal stetig differenzierbar. Nach dem Satz von Taylor gilt fur dieKomponentenfunktion fi:
fi(x +∆x) = fi(x) +m∑
j=1
∂fi∂xj
(x) ∆xj +Rf (x, ∆x). (2.6)
Definition 2.9 (Landausche Symbole)Man schreibt
g(t) = O(h(t)) (t→ 0)
falls es t0 > 0 und c0 ≥ 0 gibt, so dass fur alle t ∈]0, t0] die Abschatzung
|g(t)| ≤ c0 · |h(t)|
gilt. Sprechweise: “g(t) geht wie h(t) gegen 0”.
Weiter bedeutet
g(t) = o(h(t)) (t→ 0),
dass es t0 > 0 und eine Funktion c(t) mit limt→0 c(t) = 0 gibt, so dass fur alle t ∈]0, t0]
|g(t)| ≤ c(t) · |h(t)|.
Man sagt “g(t) geht schneller als h(t) gegen 0” (falls h(t)→ 0).
Entsprechend definiert man fur t→∞.
Beispiel 2.101.
g(t) = at2 + bt+ c = c+ bt+O(t2)
= c+O(t)
fur t→ 0.
2.
g(t) = at2 + bt+ c = O(t2) fur t→∞.
Fur das Restglied der Taylorformel (2.6) gilt wegen der zweimaligen stetigen Differenzier-barkeit:
Rfi(x, ∆x) = O(‖∆x‖2)
26

und damit
fi(x +∆x)− fi(x) =m∑
j=1
∂fi∂xj
(x) ∆xj
︸ ︷︷ ︸“fuhrende (erste) Ordnung”
+ O(‖∆x‖2)︸ ︷︷ ︸hohere Ordnung
.
Oft lasst man die Terme hohrerer Ordnung weg und schreibt “.=” statt “=”.
Sprechweise: “ist in erster Naherung gleich”.
Definition 2.11 ((relative) Kondition)Sei fi(x) 6= 0 und xj 6= 0 ∀ 0 < j < m. Wir nennen
fi(x +∆x)− fi(x)
fi(x)
.=
m∑
j=1
(∂fi∂xj
(x)xjfi(x)
)
︸ ︷︷ ︸Verstarkungs-faktor κij(x)
·(∆xjxj
)
︸ ︷︷ ︸relativer
Eingabefehler
(2.7)
die (relative) Kondition von f und κij die Konditionszahl von fi bezuglich der Variablen xj .Die Auswertung von y = f(x) heißt “schlecht konditioniert” im Punkt x, falls ein |κij(x)|
1, andernfalls “gut konditioniert”.Bei |κij(x)| < 1 spricht man von Fehlerdampfung, bei |κij(x)| > 1 von Fehlerverstarkung.
Man betrachtet die relative Kondition, da∣∣∣∣∆xjxj
∣∣∣∣ =
∣∣∣∣xj − rd(xj)
xj
∣∣∣∣ ≤ eps
gerade den relativen Eingabefehler beschreibt.
Beispiel 2.121. Addition: f(x1, x2) = x1 + x2
∂f∂x1
= 1 ∂f∂x2
= 1
Nach obiger Formel
f(x1 +∆x1, x2 +∆x2)− f(x1, x2)
f(x1, x2)
.= 1 · x1
x1 + x2︸ ︷︷ ︸κ1=
x1x1+x2
· ∆x1
x1︸︷︷︸| . | ≤eps
+ 1 · x2
x1 + x2︸ ︷︷ ︸κ2=
x2x1+x2
∆x2
x2︸︷︷︸| . | ≤eps
⇒ Fur x1 → −x2 gehen beide Verstarkungsfaktoren gegen ∞ (falls |x1|, |x2| > 0).Schlecht konditioniert fur x1 ≈ −x2.
2. f(x1, x2) = x21 − x2
2∂f∂x1
= 2x1∂f∂x2
= −2x2
f(x1 +∆x1, x2 +∆x2)− f(x1, x2)
f(x1, x2)= 2x1 ·
x1
x21 − x2
2︸ ︷︷ ︸κ1=2
x21x21−x
22
∆x1
x1︸︷︷︸| . | ≤eps
−2x2x2
x21 − x2
2︸ ︷︷ ︸κ2=−2
x22x21−x
22
∆x2
x2︸︷︷︸| . | ≤eps
Schlecht konditioniert fur |x1| ≈ |x2|.
27

Á RundungsfehleranalyseWir betrachten f(x)− f ′(x) mit x ∈ Fm.f ′ ist “zusammengesetzt” aus Einzeloperationen ~ ∈ ⊕,,,.Wegen (2.4) (exakt gerundete Arithmetik) und Lemma 2.7 (relativer Fehler) gilt:
(x~ y)− x ∗ yx ∗ y = ε mit |ε| ≤ eps .
Vorsicht: ε ist abhangig von x und y, d.h. fur jede Operation verschieden!Damit gilt:
x~ y = (x ∗ y)(1 + ε) fur ein |ε(x, y)| ≤ eps =1
2β−r+1.
Wir fuhren wieder eine Analyse in”erster Naherung“ durch.
Beispiel 2.13
f(x1, x2) = x21 − x2
2 mit den zwei Realisierungen
fa(x1, x2) = (x1 x1) (x2 x2)
fb(x1, x2) = (x1 x2) (x1 ⊕ x2)
1.
u = x1 x1 = (x1 · x1)(1 + ε1)
v = x2 x2 = (x2 · x2)(1 + ε2)ε1 6= ε2 aber |εi| ≤ eps
fa(x1, x2) = u v = (u− v)(1 + ε3)
=(x2
1(1 + ε1)− x22(1 + ε2)
)(1 + ε3)
= x21 − x2
2︸ ︷︷ ︸=f(x1,x2)
+ ε1x21 − ε2x
22 + ε3x
21 − ε3x
22︸ ︷︷ ︸
erste Ordnung
+ ε1ε3x21 − ε2ε3x
22︸ ︷︷ ︸
zweite Ordnung
relativer Fehler:
fa(x1, x2)− f(x1, x2)
f(x1, x2)
.=
x21
x21 − x2
2
|ε1+ε2|≤2 eps︷ ︸︸ ︷(ε1 + ε3) +
x22
x22 − x2
1
|ε2+ε3|≤2 eps︷ ︸︸ ︷(ε2 + ε3)
Wir erhalten vergleichbare Verstarkungsfaktoren wie in Beispiel 2.13.
2.
u = x1 x2 = (x1 − x2)(1 + ε1)
v = x1 ⊕ x2 = (x1 + x2)(1 + ε2)
fb(x1, x2) = u v = (u · v)(1 + ε3)
= [(x1 − x2)(1 + ε1) · (x1 + x2)(1 + ε2)] (1 + ε3)
= (x1 − x2)(x1 + x2) (1 + ε1)(1 + ε2)(1 + ε3)
= (x21 − x2
2)(1 + ε1 + ε2 + ε3 + . . .+ ε1ε2ε3)
28

Relativer Fehler:
fb(x1, x2)− f(x1, x2)
f(x1, x2)
.=
(x21 − x2
2)(ε1 + ε2 + ε3)
x21 − x2
2
= ε1 + ε2 + ε3.
|ε1 + ε2 + ε3| ≤ 3 eps ⇒ Verstarkungsfaktor maximal 3, besser als vorher.
Definition 2.14Wir nennen einen Algorithmus “numerisch stabil”, wenn die im Lauf der Rechnung akkumu-lierten Rundungsfehler aus Á den unvermeidbaren Problemfehler aus der Konditionsanalyse À
nicht ubersteigen.
2.5 Ausloschung
Obige Beispiele 2.12 und 2.13 enthalten das Phanomen der Ausloschung. Dieses tritt auf bei
• Addition x1 + x2 falls x1 ≈ −x2,
• Subtraktion x1 − x2 falls x1 ≈ x2.
Anmerkung 2.15Bei der Ausloschung werden vor der entsprechenden Addition bzw. Subtraktion eingefuhrteFehler extrem verstarkt.
Sind x1, x2 ∈ F Maschinenzahlen, so gilt wie oben gezeigt:
∣∣∣∣(x1 x2)− (x1 − x2)
x1 − x2
∣∣∣∣ ≤ eps
Also kein Problem. Das Problem tritt erst auf, wenn x1, x2 selbst schon mit Fehlern behaftetsind.
Beispiel 2.16Berechne ∇T ≈ T2−T1
h mit T1 = 273.58762 K und T2 = 273.44891 K. Betrachte die Subtraktionim Zahler:
F = F(10, 4, 1)
T1 = 0, 27358762 · 103 → rd(T1) = 0, 2736 · 103
T2 = 0, 27344891 · 103 → rd(T2) = 0, 2734 · 103
T1 − T2 = 0, 00013871 · 103 rd(T1)− rd(T2) = 0, 0002 · 103
= 0, 13871 · 100 = 0, 2 · 100
Das Ergebnis hat keine gultige Ziffer!
relativer Fehler:
0, 2− 0, 13871
0, 13871≈ 0, 44 ≈ 883 · 1
210−3
︸ ︷︷ ︸=eps
Betrachte folgende Situation:
29

rd(x1) x1 x2 rd(x2)
mit | rd(x2)− rd(x1)| = 2 eps, d. h. rd(x1) und rd(x2) sind zwei aufeinanderfolgende Fließkom-mazahlen und |x2 − x1| = δ. Dann kann der relative Fehler 2 eps−δ
δ beliebig groß werden!Hier: Fehler durch Rundung der Eingangsgroßen, aber: Herkunft der Fehler ist egal, tritt
ebenso auf, wenn x1, x2 mit Fehlern vorhergehender Rechenschritte behaftet sind.
Allerdings: Hatten wir in Celsius gerechnet, dann ware das Ergebnis T1−T2 = 0.5876 ·100−0.4489 · 100 = 0.1387 · 100 also exakt gerundet.
Anmerkung 2.17Regeln:
• Setze potentiell gefahrliche Operationen moglichst fruh in einen Algorithmus ein (sieheBeispiel 2.13).
• Vermeide konstante Offsets bei Rechengroßen. Verwende z.B. Temperaturunterschiederelativ zu einer Referenztemperatur statt absoluter Temperatur.
30

3 Motivation zur Losung linearer Gleichungssysteme
3.1 Lineare Ausgleichsrechnung
Finde eine Parabel y(x) = ax2 +bx+c, die die Daten P1(x1, y1), . . . , Pm(xm, ym) approximiert,d.h. die Summe der quadratischen Abweichungen minimiert:
φ(a, b, c) =m∑
i=1
(yi − y(xi))2
Finde
mina,b,c
φ(a, b, c)
⇒ ∇φ(a, b, c) = 0 ⇐⇒ ∂φ
∂a=∂φ
∂b=∂φ
∂c= 0
1.
∂φ
∂c=
m∑
i=1
2 (yi − y(xi)) ·(−∂y(xi)
∂c
)= −2
m∑
i=1
(yi − y(xi)) · 1 != 0
⇒ −2
m∑
i=1
yi −(ax2
i + bxi + c)
= 0
⇒m∑
i=1
ax2i + bxi + c =
m∑
i=1
yi
⇒ a ·m∑
i=1
x2i + b ·
m∑
i=1
xi +mc =m∑
i=1
yi
2.
∂φ
∂b= −2
m∑
i=1
(yi − y(xi)) · xi != 0
⇒a ·m∑
i=1
x3i + b ·
m∑
i=1
x2i + c ·
m∑
i=1
xi =m∑
i=1
yixi
3.
∂φ
∂a= −2
m∑
i=1
(yi − y(xi)) · x2i
!= 0
⇒a ·m∑
i=1
x4i + b ·
m∑
i=1
x3i + c ·
m∑
i=1
x2i =
m∑
i=1
yix2i
Dies entspricht dem linearen Gleichungssystem:∑x4i
∑x3i
∑x2i∑
x3i
∑x2i
∑xi∑
x2i
∑xi m
︸ ︷︷ ︸A
·
abc
︸ ︷︷ ︸x
=
∑yix
2i∑
yixi∑yi
︸ ︷︷ ︸b
31

3.2 Randwertproblem
Gegeben:
• Schnur, befestigt an Ihren Endpunkten
0 1
• Krummung der Schnur
∂2y
∂x2= sin (πx)
• Randbedingungen
y(0) = 0, y(1) = 0
Wahle Punkte xi = i · h, i = 0, . . . , n und h = 1n mit yi = y(xi).
Nahere
∂2y
∂x2≈ yi+1 − 2yi + yi−1
h2zentraler Differenzenquotient
Fur Punkt xi gilt:
yi+1 − 2yi + yi−1 = sin(πxi) i = 1, . . . , n− 1
Auch dies ist ein lineares Gleichungssystem:
1 0 0 0 0 . . . . . . . . . . . . 01 −2 1 0 0 . . . . . . . . . . . . 00 1 −2 1 0 . . . . . . . . . . . . 0...
. . .. . .
. . .. . .
. . ....
.... . .
. . .. . .
. . . 00 . . . . . . . . . . . . . . . 0 1 −2 10 . . . . . . . . . . . . . . . 0 0 0 1
︸ ︷︷ ︸A
·
y0
y1
y2
...
yn−1
yn
︸ ︷︷ ︸y
=
0h2 sin(πx1)h2 sin(πx2)
...
h2 sin(πxn−1)0
︸ ︷︷ ︸b
A ist eine Tridiagonalmatrix. Lasst man die erste und letzte Gleichung weg und setzt die Rand-werte direkt in die zweite und vorletzte Gleichung ein, dann ist die Matrix auch symmetrisch.
32

4 Notwendige Grundlagen aus der linearen Algebra
Im folgenden steht K fur einen Korper (vgl. Mitschrift IngMathe I, Def. 2.2). Dabei ist entwederK = R (d.h. der Korper der reellen Zahlen), oder K = C (d.h. der Korper der komplexenZahlen).
4.1 Skalarprodukt
Definition 4.1 (Skalarprodukt auf reellem Vektorraum)Ein Skalarprodukt oder inneres Produkt auf einem reellen Vektorraum ist eine positiv definite,symmetrische Bilinearform 〈·, ·〉 : V ×V→ R, d.h. fur u,v,w ∈ Rn und λ ∈ R gilt:
1. bilinear
〈u + v,w〉 = 〈u,w〉+ 〈v,w〉 (4.1)
〈u,v + w〉 = 〈u,v〉+ 〈u,w〉 (4.2)
〈u, λv〉 = λ〈u,v〉 = 〈λu,v〉 (4.3)
2. symmetrisch
〈u,v〉 = 〈v,u〉 (4.4)
3. positiv definit
〈u,u〉 ≥ 0 und 〈u,u〉 = 0 ⇐⇒ u = 0 (4.5)
Satz 4.2 (Skalarprodukt im Rn)Seien x,y ∈ Rn, dann ist das Skalarprodukt gegeben durch
〈x,y〉 := xT · y =
n∑
i=1
xi · yi
Insbesondere gilt im Rn:
〈ATx,y〉 =(ATx
)Ty = xAy = 〈x,Ay〉
Definition 4.3 (Skalarprodukt auf komplexen Vektorraum)Ein Skalarprodukt oder inneres Produkt auf einem komplexen Vektorraum ist eine positivdefinite, hermitesche Sesquilinearform 〈·, ·〉 : V ×V→ C, d.h. fur u,v,w ∈ V und λ ∈ C gilt:
1. sesquilinear
〈u + v,w〉 = 〈u,w〉+ 〈v,w〉 (4.6)
〈u,v + w〉 = 〈u,v〉+ 〈u,w〉 (4.7)
〈u, λv〉 = λ〈u,v〉 (4.8)
〈λu,v〉 = λ〈u,v〉 (4.9)
semilinear im ersten und linear im zweiten Argument.
33

2. hermitesch
〈u,v〉 = 〈v,u〉 (4.10)
3. positiv definit
〈u,u〉 ≥ 0 und 〈u,u〉 = 0 ⇐⇒ u = 0 (4.11)
Satz 4.4 (Skalarprodukt im Cn)Seien x,y ∈ Cn, dann ist das Skalarprodukt gegeben durch
〈x,y〉 := xT · y =
n∑
i=1
xi · yi,
wobei x der komplex konjugierte Vektor zu x ist.
Im Cn gilt damit:
〈x,Ay〉 = 〈ATx,y〉
4.2 Vektornormen
Definition 4.5Eine Norm ist eine Abbildung, die jedem Element v aus einem Vektorraum V (hier V = Kn)eine nicht-negative reelle Zahl zuweist.
|| · || : V→ R+0 , x 7→ ||x||
Diese muss fur alle x,y ∈ V und alle λ ∈ R folgende Eigenschaften haben:
||x|| = 0 ⇐⇒ x = 0 (sonst ||x|| > 0) (4.12)
||λ · x|| = |λ| · ||x|| (4.13)
||x + y|| ≤ ||x||+ ||y|| (4.14)
Beispiel 4.6Haufig verwendete Normen sind:
‖x‖2 =(∑n
i=1 |xi|2) 1
2 euklidische Norm, `2-Norm‖x‖∞ = max1≤i≤n |xi| Maximumnorm, `∞-Norm‖x‖1 =
∑ni=1 |xi| `1 Norm
Die euklidische Norm wird durch ein Skalarprodukt induziert:
‖x‖2 =√〈x,x〉 x ∈ Kn.
Es gilt die Cauchy-Schwarz-Ungleichung:
|〈x,y〉| ≤ ‖x‖2 · ‖y‖2.
34

Eine wichtige Folgerung aus (4.14) ist
‖x− y‖ ≥∣∣∣∣‖x‖ − ‖y‖
∣∣∣∣ x,y ∈ Kn (4.15)
Beweis:
‖x‖ = ‖x− y + y‖(4.14)
≤ ‖x− y‖+ ‖y‖ ⇒ ‖x− y‖ ≥ ‖x‖ − ‖y‖‖y‖ = ‖y − x + x‖ ≤ ‖y − x‖+ ‖x‖ ⇒ ‖x− y‖ ≥ ‖y‖ − ‖x‖︸ ︷︷ ︸
−(‖x‖−‖y‖)
Satz 4.7 (Aquivalenz aller Normen)Auf Kn sind alle Normen im folgenden Sinne aquivalent:
Zu ‖ · ‖, ‖ · ‖′ gibt es Zahlen m,M > 0 aus R so dass gilt:
m‖x‖′ ≤ ‖x‖ ≤M‖x‖′ ∀x ∈ Kn
Beweis: Um ∃M ∈ R mit ‖x‖ ≤ M‖x‖′ zu beweisen, genugt es, dies fur ‖ · ‖′ = ‖ · ‖∞zu zeigen. Dann kann man eine entsprechende Beziehung fur zwei beliebige Normen uber denUmweg der Beziehung der Normen zur Unendlichnorm herleiten.
Seien e1, . . . , en die kartesischen Einheitsvektoren. Jedes x ∈ Kn hat dann die Darstellung
x =
n∑
i=1
xiei
Damit ist
‖x‖ =
∥∥∥∥∥n∑
i=1
xiei
∥∥∥∥∥ ≤n∑
i=1
|xi| ‖ei‖ ≤(
max1≤i≤n
|xi|)
︸ ︷︷ ︸=‖x‖∞
n∑
i=1
‖ei‖ ≤ ‖x‖∞n∑
i=1
‖ei‖︸ ︷︷ ︸
γ
= γ‖x‖∞
wegen ‖x‖ ≤ γ‖x‖∞ ist ‖ · ‖ stetig bezuglich komponentenweiser Konvergenz.
Beweise nun ∃m ∈ R,m > 0, mit m‖x‖′ ≤ ‖x‖. Definiere dazu Punktmenge:
S ≡ x ∈ Kn : ‖x‖∞ = 1 ⊂ Kn
S ist
• beschrankt bezuglich ‖ · ‖, da ‖x‖ ≤ γ
• abgeschlossen, d.h. Grenzwerte von Folgen aus S sind in S (da Kn metrischer Raum)
35

damit ist S kompakt. Die Funktion ‖ · ‖ : S → R+ ist auf S stetig und nimmt daher auf S ihrMinimum und Maximum an (Satz 10.22, IngMathe II), d.h. es gibt x, x ∈ S:
0 < ‖x‖︸ ︷︷ ︸da 0 6=S, x∈S und (4.12)
≤ ‖x‖ ≤ ‖x‖ ≤ γ ‖x‖∞︸ ︷︷ ︸=1, da x∈S
= γ ∀x ∈ S
Nun sei y ∈ Kn \ 0 beliebig. Dann ist y‖y‖∞ ∈ S und damit
‖x‖ ≤∥∥∥∥
y
‖y‖∞
∥∥∥∥(4.13)
=1
‖y‖∞‖y‖ ≤ ‖x‖
⇐⇒ ‖x‖︸︷︷︸m
‖y‖∞ ≤ ‖y‖ ≤ ‖x‖︸︷︷︸M
‖y‖∞
m, M hangen i.d.R. von der Dimension n ab. Vorsicht bei Beweisen mit n→∞!
Konvergenz und NormenWie man leicht uberlegt gilt fur die Konvergenz einer Folge von Vektoren x(t) gegen x, dass:
x(t) → x (t→∞) ⇐⇒ ∀ i = 1, . . . , n : x(t)i → xi (t→∞) ⇐⇒ ‖x(t)−x‖∞ → 0 (t→∞)
Konvergenz der Norm der Abweichungen ist aquivalent zu komponentenweiser Konvergenz.Satz 4.7 zeigt dann, dass man auch eine beliebige Norm nehmen darf.
Aus (4.15) folgt:
‖x(t) − x‖ → 0 (t→∞) ⇒ ‖x(t)‖ → ‖x‖ (t→∞)
4.3 Matrixnormen
Die Menge aller m×n Matrizen uber dem Korper K, also Km×n, ist ein Vektorraum und kannmit dem Kmn identifiziert werden (also einem Raum von Vektoren mit m · n Eintragen).
Damit definiert jede Norm auf Kmn auch eine Norm auf A ∈ Km×n.
A(t) → A (t→∞) meint dann a(t)ij → aij (t→∞) ∀ i, j ∈ 1, . . . ,m × 1, . . . , n.
Es zeigt sich, dass folgende Eigenschaften hilfreich sind:
Definition 4.8Eine Norm auf Kn×n heißt vertraglich mit einer Vektornorm ‖ · ‖ auf Kn, falls gilt:
‖Ax‖ ≤ ‖A‖ · ‖x‖ x ∈ Kn,A ∈ Kn×n
Sie heißt Matrixnorm, wenn sie submultiplikativ ist:
‖AB‖ ≤ ‖A‖ · ‖B‖ A,B ∈ Kn×n
Beispiel 4.9 (Frobeniusnorm)
‖A‖Fr =
n∑
i, j=1
|aij |2
12
ist eine Matrixnorm, die vertraglich mit der euklidischen Norm ist.
36

Definition 4.10 (Zugeordnete Matrixnorm)Es sei ‖ · ‖ ein beliebiger Vektorraum auf Kn. Dann heißt
‖A‖ := supx∈Kn\0
‖Ax‖‖x‖ = sup
‖x‖=1x∈Kn
‖Ax‖
die ‖·‖ zugeordnete (oder naturliche) Matrixnorm, d.h. ‖·‖ ist vertraglich und submultiplikativ.
Fur naturliche Matrixnormen gilt:
‖I‖ = supx∈Kn\0
‖Ix‖‖x‖ = 1.
Satz 4.11Die zugeordneten Matrixnormen zu ‖ · ‖∞ und ‖ · ‖1 sind:
‖A‖∞ = max1≤i≤n
n∑
j=1
|aij | Zeilensummennorm
‖A‖1 = max1≤j≤n
n∑
i=1
|aij | Spaltensummennorm
Beweis: siehe Rannacher, Numerische Mathematik 0, S. 104. Auszuge:
1. Vertraglichkeit
‖Ax‖∞ = maxi=1...n
∣∣∣∣∣∣
n∑
j=1
aijxj
∣∣∣∣∣∣≤ max
i=1...n
n∑
j=1
|aij ||xj |
≤ maxi=1...n
n∑
j=1
|aij |(
maxk=1...n
|xk|)
︸ ︷︷ ︸=‖x‖∞
= ‖x‖∞ maxi=1...n
n∑
j=1
|aij |︸ ︷︷ ︸
=‖A‖∞
= ‖A‖∞‖x‖∞
2. Somit
sup‖x‖∞=1
‖Ax‖∞(1.)
≤ sup‖x‖∞=1
‖A‖∞ ‖x‖∞︸ ︷︷ ︸=1
= ‖A‖∞
3. Zu zeigen ist nun noch
sup‖x‖∞=1
‖Ax‖∞ ≥ ‖A‖∞
Dies geschieht konstruktiv indem man einen Vektor y mit ‖y‖∞ = 1 angibt, fur den gilt‖Ay‖∞ ≥ ‖A‖∞. Wegen sup‖x‖∞=1 ‖Ax‖∞ ≥ ‖Ay‖∞ folgt dann die Behauptung(→ Rannacher, Numerische Mathematik 0).
37

4.4 Eigenwerte und Eigenvektoren
Definition 4.12Eine Zahl λ ∈ K heißt Eigenwert der Matrix A ∈ Kn×n, wenn es wenigstens einen Vektorx ∈ Kn, x 6= 0 gibt mit
A · x = λ · x.
Jeder Vektor x 6= 0, der diese Gleichung erfullt, heißt Eigenvektor von A zum Eigenwert λ.(λ,x) heißt auch
”Eigenpaar“.
Definition 4.13χA = det(A− λI) heißt charakteristisches Polynom.χA = 0 heißt charakteristische Gleichung.
Satz 4.14λ ∈ K ist genau dann ein Eigenwert der Matrix A ∈ Kn×n, wenn λ eine Nullstelle des charak-teristischen Polynoms χA ist, d.h. det(A− λI) = 0.
Beweis: Fur einen Eigenvektor gilt
A · x = λ · x = λ · I · x⇐⇒ A · x− λ · I · x = 0
⇐⇒ (A− λ · I) · x = 0 (4.16)
4.16 hat nicht triviale Losungen nur, falls
det(A− λI) = 0
(da sonst nur genau eine Losung x = 0 existiert) Das charakteristische Polynom χA(λ) hat genau n Nullstellen in C (Vielfachheit mitgezahlt).Zu jedem Eigenwert λ gibt es mindestens einen Eigenvektor x.
Mit den Normregeln folgt fur ein Eigenpaar (λ,x) mit ‖x‖ = 1:
|λ| ‖x‖=1= |λ| ‖x‖ = ‖λx‖ = ‖Ax‖ ≤ ‖A‖ ‖x‖︸︷︷︸
=1
= ‖A‖ (4.17)
Also liegen alle Eigenwerte λ ∈ C innerhalb eines Kreises um 0 mit Radius ‖A‖.Wahlt man z.B. ‖A‖∞, erhalt man so eine konkrete Abschatzung fur den großten Eigenwert.
Definition 4.15 (Spezielle Matrizen)Zu A ∈ Km×n heißt AT ∈ Kn×m transponierte Matrix und es ist
(AT)ij
= (A)ji.
Zu A ∈ Km×n heißt A ∈ Km×n die konjugiert komplexe Matrix mit (A)ij = (A)ij (diekonjugiert komplexe Zahl zu (A)ij).
1. A ∈ Kn×n heißt hermitesch, falls A = AT
, d.h. (A)ij = (A)ji.
Manche Autoren schreiben auch AH fur AT
.Reelle hermitsche Matrizen heißen symmetrisch (dann ist A = AT ).
38

2. Eine komplexe Matrix A ∈ Cn×n mit
AAT = ATA heißt normal,
AAT = ATA = I, also A−1 = AT heißt unitar .
3. Eine reelle Matrix A ∈ Rn×n mit
AAT = ATA = I, also A−1 = AT heißt orthogonal.
Fur ein euklidisches Skalarprodukt und eine hermitesche Matrix A gilt damit:
A = AT ⇐⇒ 〈Ax,y〉 = 〈x,Ay〉 ∀x,y ∈ Kn.
4.5 Die Spektralnorm
Definition 4.16 (Spektralnorm)Die der euklidischen Norm zugeordnete Matrixnorm ‖A‖ heißt Spektralnorm.
Satz 4.171. Fur die Spektralnorm einer hermiteschen Matrix A gilt:
‖A‖2 = max |λ| : λ ist Eigenwert von A
2. Fur jede beliebige Matrix A ∈ Kn×n gilt:
‖A‖2 = max|λ| 12 : λ ist Eigenwert von ATA
Beweis:
1. Sei A hermitesch. Dann hat A n reelle Eigenwerte und einen vollstandigen Satz vonorthonormalen Eigenvektoren
w1, . . . ,wn ⊂ Kn : Awi = λiwi, 〈wi,wj〉 = δij ∀ i, j = 1, . . . , n
Dabei ist δij das sogenannte Kronecker-Delta mit δij =
1 i = j
0 sonst.
Jedes x ∈ Kn lassst sich in der Basisw1, . . . ,wn
darstellen:
x =
n∑
i=1
αiwi αi = 〈x,wi〉
Und es gilt:
‖x‖22 = 〈x,x〉 = 〈n∑
i=1
αiwi,
n∑
j=1
αjwj〉 =
n∑
i=1
n∑
j=1
αiαj 〈wi,wj〉︸ ︷︷ ︸=δij
=n∑
j=1
|αi|2
‖Ax‖22 = 〈Ax,Ax〉 = 〈n∑
i=1
Aαiwi
︸ ︷︷ ︸=αiλiwi
,n∑
j=1
Aαjwj
︸ ︷︷ ︸=αjλjwj
〉
=n∑
i=1
n∑
j=1
αiλiαjλj 〈wi,wj〉︸ ︷︷ ︸=δij
=
n∑
i=1
λ2i︸︷︷︸
wg. λi=λi
|αi|2
39

Also
‖A‖22 = supx∈Kn\0
‖Ax‖22‖x‖22
=
∑ni=1 λ
2i |αi|2∑n
i=1 |αi|2≤ max
1≤i≤nλ2i
Andererseits folgt aus (4.17) ‖A‖ ≥ |λ| fur jede Norm und jeden Eigenwert, daher mussdie Gleichheit erfullt sein:
‖A‖2 = max1≤i≤n
|λi|.
2. Sei A ∈ Kn eine beliebige Matrix. Dann gilt:
‖Ax‖22 = 〈Ax,Ax〉 = (Ax)T
(Ax) = xT AT (Ax) = xT (ATAx) = 〈x, ATAx〉.
ATA ist hermitesch und hat damit wieder n reelle Eigenwerte λi, sowie orthonormaleEigenvektoren wi (wie oben).
‖Ax‖22 = 〈n∑
i=1
αiwi,
n∑
j=1
AAαjwj〉 =
n∑
i=1
n∑
j=1
αiλjαj 〈wi,wj〉︸ ︷︷ ︸=δij
=n∑
i=1
λi|αi|2
und damit
‖A‖22 = supx∈Kn\0
‖Ax‖22‖x‖22
=
∑ni=1 λi|αi|2∑ni=1 |αi|2
≤ max1≤i≤n
|λi|
Mit (4.17) folgt die Behauptung.
Satz 4.18Fur A ∈ Kn×n gilt:
‖A‖ ≤√‖A‖1 · ‖A‖∞
ohne Beweis
40

5 Konditionierung der Losung linearer Gleichungssysteme
5.1 Losbarkeit
Sei A ∈ Km×n eine Matrix und b ∈ Km ein Vektor.
A =
a11 . . . a1n...
. . ....
am1 . . . amn
b =
b1...bm
Ein Vektor x ∈ Kn ist eine Losung des linearen Gleichungssystems A · x = b, falls gilt
n∑
j=1
aij · xj = bi ∀ 1 ≤ i ≤ m (5.1)
Es gibt mindestens eine Losung, falls
Rang(A) = Rang(A|b) = Rang
a11 . . . a1n...
. . ....
am1 . . . amn
∣∣∣∣∣∣∣
b1...bm
Fur quadratische Matrizen A ∈ Kn×n sind folgende Aussagen aquivalent:
1. A · x = b ist fur jedes b eindeutig losbar.
2. Rang(A) = n
3. det(A) 6= 0
4. A hat keinen Eigenwert Null.
5. A ist invertierbar.
Eine solche Matrix nennt man auch regular.
5.2 Storungstheorie
Wir wollen nun die Kondition der Losung linearer Gleichungssysteme fur kleine Storungen inden Eingaben untersuchen.
Definition 5.1 (normweise relative Kondition)Sei f : Km → Kn sowie ‖f(x)‖ 6= 0 und ‖x‖ 6= 0. Die normweise relative Kondition von f imPunkt x ist gegeben durch :
κrel = sup
‖f(x + δx)− f(x)‖‖f(x)‖
‖δx‖‖x‖ : δx 6= 0
. (5.2)
Sei A ∈ Kn×n invertierbar und x,b ∈ Kn.
f(A,b) = A−1b ist der Losungsoperator zur Gleichung g(x) = Ax− b = 0.
41

Betrachte die (normweise) relative Kondition von f , wobei wir zunachst nur Anderungen inb zulassen wollen:
‖f(A,b + δb)− f(A,b)‖‖f(A,b)‖ · ‖b‖‖δb‖ =
‖A−1(b + δb)−A−1b‖‖A−1b‖ · ‖
=I︷ ︸︸ ︷AA−1 b‖‖δb‖
≤︸︷︷︸‖·‖ sei vertraglich
und submultiplikativ
‖A−1‖ · ‖δb‖‖A−1b‖ · ‖A‖ · ‖A
−1b‖‖δb‖ = ‖A−1‖ · ‖A‖
Definition 5.2Die Zahl
cond(A) = ‖A‖ · ‖A−1‖
fur irgendeine vertragliche und submultiplikative Matrixnorm heißt Konditionszahl von A.Der genaue Wert der Kondition hangt von der verwendeten Norm ab.
Wenn die exakte Losung x = A−1b ist, erhalten wir also fur den Fehler δx bei einer Storungb:
‖δx‖‖x‖ ≤ cond(A) · ‖b‖‖δb‖
Fur die Kondition einer hermiteschen Matrix bei Verwendung der Spektralnorm (die soge-nannte Spektralkonditionszahl) gilt:
cond2(A) =max |λ| : λ ist Eigenwert von Amin |λ| : λ ist Eigenwert von A .
Nun wollen wir auch Anderungen in A selbst zulassen. Sei A ∈ Kn×n regular.Frage: Wann ist A + δA regular?
Satz 5.3B ∈ Kn×n habe die Norm ‖B‖ < 1. Dann ist I + B regular und es gilt
‖(I + B)−1‖ ≤ 1
1− ‖B‖Beweis:
1. ∀x ∈ Kn gilt:
‖x‖ = ‖x + Bx−Bx‖ ≤ ‖(I + B)x‖+ ‖Bx‖⇐⇒ ‖(I + B)x‖ ≥ ‖x‖ − ‖Bx‖ ≥︸︷︷︸
‖Bx‖≤‖B‖·‖x‖
‖x‖ − ‖B‖ · ‖x‖
= (1− ‖B‖) · ‖x‖
Damit gilt fur x 6= 0, dass (I + B) · x 6= 0 also I + B regular.
42

2.
1 = ‖I‖ = ‖(I + B)(I + B)−1‖ = ‖(I + B)−1 + B(I + B)−1‖≥ ‖(I + B)−1‖ − ‖B‖ · ‖(I + B)−1‖ = ‖(I + B)−1‖ · (1− ‖B‖)
> 0︸︷︷︸da ‖B‖<1 nach Vor.
Daraus folgt die Behauptung.
Satz 5.4 (Storungssatz)A ∈ Kn×n sei regular und ‖δA‖ < 1
‖A−1‖ . Dann ist A = A + δA ebenfalls regular und es gilt
fur den relativen Fehler in der Losung des gestorten Systems (A + δA)(x + δx) = (b + δb):
‖δx‖‖x‖ ≤
cond(A)
1− cond(A) · ‖δA‖‖A‖
·‖δb‖‖b‖ +
‖δA‖‖A‖
Beweis:
1.
A + δA = A · (I + A−1δA︸ ︷︷ ︸”B“
) und ‖A−1δA‖ ≤ ‖A−1‖ · ‖δA‖ < ‖A−1‖ · 1‖A−1‖ = 1
Nach Satz 5.3 ist A + δA damit regular (da Produkt regularer Matrizen regular).
2.
(A + δA)(x + δx) = (b + δb)
⇐⇒ Ax︸︷︷︸b
+δAx + (A + δA)δx = b + δb
⇐⇒ (A + δA)δx = δb− δAx
⇐⇒ δx = (A + δA)−1(δb− δAx)
‖δx‖ ≤ ‖(A + δA)−1‖ · ‖δb‖+ ‖δA‖ · ‖x‖= ‖(A · (I + A−1δA))−1‖ · ‖δb‖+ ‖δA‖ · ‖x‖≤ ‖(I + A−1δA)−1‖︸ ︷︷ ︸
5.3
·‖A−1‖ · ‖δb‖+ ‖δA‖ · ‖x‖
≤ ‖A−1‖1− ‖A−1δA‖ · ‖δb‖+ ‖δA‖ · ‖x‖
≤ ‖A−1‖ · ‖A‖ · ‖x‖1− ‖A−1‖ · ‖δA‖ · ‖A‖ · ‖A‖−1
︸ ︷︷ ︸=1
·
‖δb‖‖A‖ · ‖x‖︸ ︷︷ ︸
‖b‖=‖Ax‖≤‖A‖·‖x‖
+‖δA‖‖A‖
≤ ‖x‖ · cond(A)
1− cond(A)‖δA‖‖A‖
‖δb‖‖b‖ +
‖δA‖‖A‖
43

Beispiel 5.5Es sei ‖δA‖‖A‖ ≈ 10−k und ‖δb‖‖b‖ ≈ 10−k sowie cond(A) ≈ 10s mit s, k > 0.
Weiter sei 10s · 10−k 1, also z.B. s− k ≤ −3.
Dann gilt:
‖δx‖‖x‖ ≤
10s
1− 10s · 10−k︸ ︷︷ ︸1︸ ︷︷ ︸
Nenner ≈1
· 2 · 10−k ≈ 10s−k = 10−(k−s)
⇒ Man verliert s Stellen an Genauigkeit!
Wahrend der Eingabefehler in der k-ten Nachkommastelle ist, hat das Ergebnis einen Fehlerin der k − s-ten Stelle.
Beispiel 5.61. Betrachte die 2× 2 Matrix
A =
(−1 1
1− ε −1
), |ε| < 1
⇒ A−1 =1
ε
(−1 −1
−(1− ε) −1
), ε = det(A),
Wegen |ε| < 1 gilt:
‖A‖∞ = max(2, 2− ε), ‖A−1‖∞ =1
|ε| max(2, 2− ε)
4
|ε| ≤ cond∞(A) ≤ (2 + |ε|)2
|ε|
Die Kondition geht also gegen Unendlich fur ε→ 0.
Hier gilt offensichtlich cond∞(A) = O(
1det(A)
).
2. Gibt es also immer einen Zusammenhang zwischen cond∞(A) und (det(A))−1 ?
Wir betrachten dazu
B =
(10−10 0
0 10−10
)B−1 =
(1010 0
0 1010
)
cond∞(B) = ‖B‖∞ · ‖B−1‖∞ = 10−10 · 1010 = 1, aber det(B) = 10−20 !
3. cond(εA) = cond(A) ∀ ε 6= 0, aber det(εA) = εn det(A)
44

Beispiel 5.7
A =
(d1 00 d2
), A−1 =
(d−1
1 0
0 d−12
), d1, d2 6= 0
cond2(A) = ‖A‖2 · ‖A−1‖2 A sym.=
max(|d1|, |d2|)min(|d1|, |d2|)
d.h. cond2
(1010 0
0 1
)= 1010 !
(Fur Diagonalmatrizen gilt ubrigens, wie man leicht uberlegt, cond1(A) = cond2(A) = cond∞(A))
Andererseits sind alle Gleichungen in Ax = b unabhangig und xi = bi/di ist gut konditio-niert.
Das Problem liegt hier in der Verwendung von Normen, die Abschatzung fur einzelne Kom-ponenten ist relativ schlecht.
Man lernt: schlechte Kondition muss nicht unbedingt Probleme beim Losen des LGS bewir-ken, es ist jedoch “wahrscheinlich”.
45


6 Eliminationsverfahren zur Losung linearer Gleichungsysteme
6.1 Dreieckssysteme (auch: gestaffelte Systeme)
Sei A ∈ Kn×n von oberer Dreiecksgestalt. Zu losen ist dann:
a11 · x1 + a12 · x2 + · · · + a1n · xn = b10 a22 · x2 + · · · + a2n · xn = b2...
. . .. . .
......
0 . . . 0 ann · xn = bn
Das System ist regular genau dann, wenn alle aii 6= 0 i = 1, . . . , n.
Losen durch ruckwarts einsetzen:
xn =bnann
xi =1
aii
bi −
n∑
j=i+1
aijxj
, i = n− 1, . . . , 1
Die notwendige Anzahl an Rechenoperationen ist:
NDreieck(n) =n−1∑
i=0
(2i+ 1) =n∑
i=1
(2i− 1) = n2
Analog: Unteres Dreieckssystem und vorwarts einsetzen.
6.2 Gauß-Elimination
Sei A ∈ Kn×n regular gegeben. Bringe nun Ax = b durch aquivalente Umformungen auf(obere) Dreiecksgestalt.
Dazu benutzt man
1. Vertauschen zweier Gleichungen,
2. Addition des Vielfachen einer Gleichung zu einer anderen.
Verwende als Abkurzung fur die erweiterte Koeffizientenmatrix
[A,b] =
a11 · · · a1n...
. . ....
an1 · · · ann
∣∣∣∣∣∣∣
b1...bn
∈ Kn×(n+1)
Das Gaußsche Eliminationsverfahren erzeugt eine Folge von Matrizen
[A(0),b(0)
]= [A,b] ,
[A(1),b(1)
], . . . ,
[A(n−1),b(n−1)
]
sodass nach n− 1 Schritten A(n−1) obere Dreiecksgestalt hat.
47

Schritt 1 :[A(0),b(0)
]→[A(1),b(1)
]: (k = 1)
1.[A(0),b(0)
]→[A(0), b(0)
](nach Zeilenvertauschung)
Bestimme ein r ∈ 1, . . . , n, sodass a(0)r1 6= 0. Dieses existiert wegen der Regularitat von
A. Vertausche Zeilen 1 und r, womit a(0)11 6= 0.
2.[A(0), b(0)
]→[A(1),b(1)
]
Fur i ∈ 2, · · · , n :
À qi1 =a(0)i1
a(0)11
, a(0)11 heißt Pivotelement.
Á Subtrahiere das qi1-fache der Zeile 1 von Zeile i:
∀ j ∈ 1, . . . , n : a(1)ij = a
(0)ij − qi1a
(0)1j , b
(1)i = b
(0)i − qi1b
(0)1 .
Wegen a(1)i1 = a
(0)i1 −
a(0)i1
a(0)11
· a(0)11 = 0 fur i ≥ 2 gilt:
[A(1),b(1)
]=
a(0)11 a
(0)12 · · · a
(0)1n b
(0)1
0 a(1)22 · · · a
(1)2n b
(1)2
......
. . ....
...
0 a(1)n2 · · · a
(1)nn b
(1)n
Dies fuhrt man nun rekursiv fur die (n− k)× (n− k + 1) Untermatrizen fort.
Schritt k :[A(k−1),b(k−1)
]→[A(k),b(k)
]1 ≤ k < n
[A(k−1),b(k−1)
]=
a(k−1)11 ∗
. . .
0 a(k−1)k−1 k−1
∗ ∗
0
a(k−1)kk · · · a
(k−1)kn
.... . .
...
a(k−1)nk · · · a
(k−1)nn
b(k−1)k
...
b(k−1)n
À[A(k−1),b(k−1)
]→[A(k−1), b(k−1)
]
Bestimme r ∈ k, · · · , n sodass a(k−1)rk = 0.
Tausche Zeilen k und r.
Á[A(k−1), b(k−1)
]→[A(k),b(k)
]
Fur i ∈ k + 1, · · · , n:
48

• qik =a(k−1)ik
a(k−1)kk
• ∀ j ∈ k, . . . , n : a(k)ij = a
(k−1)ij − qika(k−1)
kj
• b(k)i = b
(k−1)i − qik b(k−1)
k
Nach insgesamt n− 1 Schritten hat An−1 obere Dreiecksgestalt.
Algorithmus 6.1
Input: A ∈ Kn×n, b ∈ Kn (werden uberschrieben)Output: x ∈ Kn
System in oberer Dreiecksgestalt [A(n−1),b(n−1)] gespeichert in A,b
for (k = 1; k < n; k = k + 1) doFinde r ∈ k,...,n so dass ark 6= 0; sonst Fehlerif (r 6= k) then tausche Zeile k mit Zeile r
for (j = k; j ≤ n; j = j + 1) dot = akj ; akj = arj ; arj = t;
end fort = bk; bk = br; br = t;
end iffor (i = k + 1; i ≤ n; i = i+ 1) do Update der unteren Zeilenq = aik/akk;for (j = k + 1; j ≤ n; j = j + 1) doaij = aij − q · akj ;
end forbi = bi − q · bk;
end forend forfor (k = n; k ≥ 1; k = k − 1) do Ruckwartseinsetzent = 0;for (j = k + 1; j ≤ n; j = j + 1) dot = t+ akj · xj ;
end forxk = (bk − t)/akk
end for
Beispiel 6.2Hier sind keine Zeilenvertauschungen notwendig. Das Pivotelement ist jeweils durch einen
49

Kasten gekennzeichnet.
2 4 6 8 4016 33 50 67 3304 15 31 44 167
10 29 63 97 350
→
2 4 6 8 40
0 1 2 3 100 7 19 28 870 9 33 57 150
→
2 4 6 8 400 1 2 3 10
0 0 5 7 170 0 15 30 60
→
2 4 6 8 400 1 2 3 100 0 5 7 170 0 0 9 9
Schließlich liefert Ruckwartseinsetzen:
x4 = 9/9 = 1 , x3 = (17− 7 · 1)/5 = 2 ,
x2 = (10− 2 · 2− 3 · 1)/1 = 3 , x1 = (40− 4 · 3− 6 · 2− 8 · 1)/2 = 4 .
Lemma 6.3Der Aufwand der Transformation einer Matrix A ∈ Kn×n auf obere Dreiecksgestalt betragt
NGauß(n) =2
3n3 +O(n2)
Beweis:
NGauß(n) =n−1∑
k=1
[(n− k)︸ ︷︷ ︸# Zeilen
·(
1︸︷︷︸Berechnung
der qik
+ (n− k)︸ ︷︷ ︸# Spalten
· 2︸︷︷︸1 Mult1 Add
+ 2︸︷︷︸b
)]
= 2n−1∑
k=1
(n− k)2 + 3n−1∑
k=1
(n− k)
umnumme-rieren= 2
n−1∑
k=1
k2 + 3
n−1∑
k=1
k
= 2 · (n− 1) · n · (2n− 1)
6+ 3 · (n− 1)n
2
=2
3n3 +O(n2)
6.3 LR-Zerlegung
Voruberlegung: Abstrakte Formulierung der Gauß-Elimination mit Matrixmultiplikationen.
Fur Schritt À (Zeilenvertauschung) definieren wir die sog. Permutationsmatrizen
Prs ∈ Kn×n, 1 ≤ r, s ≤ n, r 6= s
50

mit
(Prs)ij =
1 (i 6= r, s) ∧ (i = j)
1 (i = r ∧ j = s) ∨ (i = s ∧ j = r)
0 sonst
Hilfssatz 6.4
Die Matrizen Prs haben die folgenden Eigenschaften:
i) A = PrsA ist A mit Zeilen r und s vertauscht
ii) A = APrs ist A mit Spalten r und s vertauscht
iii) Prs = PTrs
iv) P−1rs = Prs ⇒ P−1
rs = PTrs (orthogonal)
Beweis:
i) aij =∑n
k=1 (Prs)ik · akj(Prs)ik 6= 0 nur fur genau ein k:
Falls i 6= r ∧ i 6= s aij = aij
i = r ( k = s) arj = asj ∀ji = s ( k = r) asj = arj ∀j
ii) analog
iii) folgt aus Definition von Prs
iv) PrsPrs = I wegen i), also P−1rs = Prs
Fur Schritt Á definieren wir sog. Frobeniusmatrizen.
Definition 6.5 (Frobeniusmatrizen)
Eine Matrix Gk ∈ Kn×n, 1 ≤ k < n mit der Eigenschaft
Gk = I + G′k(G′k)ij
= 0 fur (j 6= k) ∨ (i ≤ k)
heißt Frobeniusmatrix.
51

Hilfssatz 6.6Die Frobeniusmatrizen haben folgende Eigenschaften:
i) Fur A = GkA gilt:
aij =
aij i ≤ kaij + gikakj i > k
ii) G′kG′k = 0
iii) G−1k = I−G′k
iv) G1G2 · · ·Gk = I +∑k
j=1 G′j, analog: G−11 · · ·G−1
k = I−∑kj=1 G′k
v) ∀ k < α ≤ β : PαβGk = (I + PαβG′k)︸ ︷︷ ︸
I+PαβG′k ist
eine geanderteFrobeniusmatrix
Pαβ
Beweis: Wird alles mit der Nullstruktur von G begrundet.
i) aij =∑n
s=1(Gk)isasj =
aij i ≤ kgikakj + aij sonst
ii)
G′kG′k =
(0 00 Bk
)(0 00 Bk
)=
0 00 BkBk︸ ︷︷ ︸
=0
da:
BKBk =
(0 0∗ 0
)(0 0∗ 0
)=
(0 00 0
)
iii) (I + G′k)(I−G′k) = I−G′k + G′k −G′kG′k︸ ︷︷ ︸
=0
= I
iv) Per Induktion:
k = 1 : G1 = I + G′1 hat die geforderte Gestalt
k − 1→ k : Es sei also G1 · · ·Gk−1 = I +
k−1∑
j=1
G′j bereits gezeigt.
G1 · · ·Gk−1Gk =
I +
k−1∑
j=1
G′j
(I + G′k
)= I +
k−1∑
j=1
G′j + G′k +
k−1∑
j=1
G′j
G′k
52

da einer der beiden Faktoren im Zeilen–Spalten (Skalar-)produkt immer Null ist.
v) Nach Voraussetzung ist k < α ≤ β.
PαβGk = Pαβ(I + G′k)
= Pαβ + PαβG′k
= Pαβ + PαβG′k︸ ︷︷ ︸
nur Spalte k6=0
Pαβ︸︷︷︸tauscht zwei
Spalten α,β>kDiese sind Null!
= ( I + PαβG′k︸ ︷︷ ︸
Wieder eineFrobeniusmatrix!
)Pαβ
Wir definieren das Produkt von Matrizen:
b∏
i=a
Bi := Bb · · ·Ba+1Ba
Satz 6.7 (LR-Zerlegung)Sei A ∈ Kn×n regular. Dann gibt es eine Zerlegung
PA = LR
wobei
L =
1 0
l21. . .
.... . .
ln1 · · · ln,k−1 1
R =
r11 · · · r1n
. . ....
0 rnn
und
P =n−1∏
k=1
Pk,rk
ein Produkt von Permutationsmatrizen mit rk ≥ k.
Im Fall P = I ist die Zerlegung eindeutig.
Beweis:
53

a) Wir behandeln zunachst P = I, d.h. ohne Zeilentausch.
Ax = b
Schritt 1: G1Ax = G1b mit Frobeniusmatrix (G1)i1 = −qi1 = −a(1)i1
a(1)11
Schritt 2: G2G1Ax = G2G1b...
nach n− 1 Schritten : Gn−1 · · ·G1A︸ ︷︷ ︸x = Gn−1 · · ·G1b mit (Gk)ik = −qik aus GEM
Ergebnis der GEM: Gn−1 · · ·G1A = R
mit Hilfssatz 6.6: A = G−11 · · ·G−1
n−1R(iii)= (I−G′1) · · · (I−G′n−1)︸ ︷︷ ︸R
(iv)=
(I−
n−1∑
i=1
G′j
)
︸ ︷︷ ︸=:L
R
b) Nun mit Zeilenvertauschungen: GEM liefert
Gn−1Pn−1,rn−1 · · ·G2P2,r2G1P1,r1A = R
rk ist der im Schritt k bestimmte Vertauschungsindex rk ≥ k.
Wende nun sukzessive Hilfssatz 6.6 v) an:
Gn−1Pn−1,rn−1 · · ·G2P2,r2G1P1,r1A
= Gn−1Pn−1,rn−1 · · ·P3,r3G2(I + P2,r2G′1)P2,r2P1,r1A
= Gn−1Pn−1,rn−1 · · ·P4,r4G3(I + P3,r3G′2)(I + P3,r3P2,r2G
′1)P3,r3P2,r2P1,r1A
...
=n−1∏
k=1
(I +
(n−1∏
α=k+1
Pα,rα
)G′k
)
︸ ︷︷ ︸nach rechts bringen
n−1∏
k=1
Pk,rk
︸ ︷︷ ︸=:P
A = R
⇐⇒ PA =
1∏
k=n−1
(I−
(n−1∏
α=k+1
Pα,rα
)G′k
)
︸ ︷︷ ︸=:L
R
c) Eindeutigkeit. Es ist P = I, also A = LRAngenommen es gibt zwei Zerlegungen: A = L1R1 = L2R2 der geforderten Gestalt.
I = AA−1 = L1R1︸ ︷︷ ︸A
R−12 L−1
2︸ ︷︷ ︸A−1
⇐⇒ L−11 L2 = R1R
−12 = I
• Inverse von Li (Ri) ist wieder untere (obere)Dreiecksmatrix.
• Produkt ebenso.
Das geht nur fur L−11 L2 = R1R
−12 = I.
54

Wo ist L?
Aus dem Beweis:
L =1∏
k=n−1
(I−
(n−1∏
α=k+1
Pα,rα
)G′k
)
Hilfssatz 6.6 v)= I−
n−1∑
k=1
(n−1∏
α=k+1
Pα,rα
)G′k mit (G′k)ik = −qik aus GEM.
• Die Nicht-Nullelemente von L nehmen gerade den Platz der im Schritt k zu eliminieren-
den Eintrage a(k)ik von A ein ⇒ kein zusatzlicher Speicher notwendig (A wird ohnehin
uberschrieben). Die Diagonalelemente von L sind alle 1 und brauchen deshalb nicht ge-speichert zu werden.
• Geht auch mit Zeilenvertauschungen zum Finden eines Pivotelementes ungleich Null. BeiZeilenvertauschungen nehmen die Eintrage in L an allen spateren Zeilenvertauschungenebenso teil, wie der Rest von A(k+1) (also die Eintrage von R) ⇒ ganze Zeile tauschen!
Wozu das Ganze?
Losen von Ax = b mittels LR-Zerlegung:
Ax = b
⇐⇒ PAx = Pb
⇐⇒ L Rx︸︷︷︸=:y
= Pb
⇐⇒
Ly = Pb vorwarts einsetzen
Rx = y ruckwarts einsetzen
).
also
À Berechne LR-Zerlegung von A sowie P
Á fur gegebenes b berechne b′ = Pb
 Lose Ly = b′
à Lose Rx = y
Aufwand
Beobachtung: Transformation auf obere Dreiecksgestalt mittels GEM ist aquivalent zu LR-Zerlegung berechnen und Ly = Pb losen.
Somit: Der Aufwand zur Berechnung der LR-Zerlegung ist
NLR(n) =2
3n3 +O(n2).
LR-Zerlegung ist insbesondere interessant, wenn Ax = bi zu mehreren rechten Seiten bi zulosen ist, da der Aufwand fur das Ruckwartseinsetzen nur O(n2) ist.
55

6.3.1 Permutation
P = Pn−1,rn−1 · · ·P2,r2P1,r1 mit rk ≥ kspeichert man nicht als Matrix sondern man speichert nur die Zahlen r1, . . . , rn−1 in einemVektor (Feld).
Algorithmus 6.8 (LR-Zerlegung und Losung von Ax = b)
Input: A ∈ Kn×n, b ∈ Kn (werden uberschrieben)Output: L ∈ Kn×n in aij , j < i, (lii = 1 wird nicht gespeichert)
R ∈ Kn×n in aij , j ≥ ip : 1, . . . , n → 1, . . . , nx ∈ Kn
for (k = 1; k < n; k = k + 1) doFinde r ∈ k,...,n so dass ark 6= 0; sonst Fehlerif (r 6= k) then tausche Zeile k mit Zeile r
for (j = 1; j ≤ n; j = j + 1) dot = akj ; akj = arj ; arj = t;
end forend ifpk = r; merke Permutationfor (i = k + 1; i ≤ n; i = i+ 1) do Update der unteren Zeilenaik = aik/akk;for (j = k + 1; j ≤ n; j = j + 1) doaij = aij − aik · akj ;
end forend for
end forfor (k = 1; k < n; k = k + 1) do Permutation von b
if (pk 6= k) thent = bk; bk = bpk ; bpk = t;
end ifend forfor (k = 1; k ≤ n; k = k + 1) do Vorwartseinsetzent = 0;for (j = 1; j < k; j = j + 1) dot = t+ akj · yj ;
end foryk = bk − t;
end forfor (k = n; k ≥ 1; k = k − 1) do Ruckwartseinsetzent = 0;for (j = k + 1; j ≤ n; j = j + 1) dot = t+ akj · xj ;
end forxk = (yk − t)/akk;
end for
56

Algorithmus 6.9 (LR-Zerlegung und Losung von Ax = b mit verbesserter Permutation)
Input: A ∈ Kn×n, b ∈ Kn (werden uberschrieben)Output: L ∈ Kn×n in aij , j < i, (lii = 1 werden nicht gespeichert)
R ∈ Kn×n in aij , j ≥ ip : 1, . . . , n → 1, . . . , nx ∈ Kn
for (k = 1; k ≤ n; k = k + 1) do Initialisiere Permutationsindicespk = k;
end forfor (k = 1; k < n; k = k + 1) do
Finde r ∈ k,...,n so dass ark 6= 0; sonst Fehlerif (r 6= k) then tausche Zeile k mit Zeile r
for (j = 1; j ≤ n; j = j + 1) dot = akj ; akj = arj ; arj = t;
end fort = pk; pk = pr; pr = t;
end iffor (i = k + 1; i ≤ n; i = i+ 1) do Update der unteren Zeilenaik = aik/akk;for (j = k + 1; j ≤ n; j = j + 1) doaij = aij − aik · akj ;
end forend for
end forfor (k = 1; k ≤ n; k = k + 1) do Permutation von byk = bpk ;
end for
for (k = 1; k ≤ n; k = k + 1) do Vorwartseinsetzent = 0;for (j = 1; j < k; j = j + 1) dot = t+ akj · xj ;
end foryk = yk − t;
end forfor (k = n; k ≥ 1; k = k − 1) do Ruckwartseinsetzent = 0;for (j = k + 1; j ≤ n; j = j + 1) dot = t+ akj · xj ;
end forxk = (yk − t)/akk;
end for
57

6.4 Rundungsfehleranalyse der LR-Zerlegung (GEM)
Definition 6.10 (Absolutwertnotation)Sei A ∈ Rm×n dann ist
B = |A| ⇒ bij = |aij | 1 ≤ i ≤ m, 1 ≤ j ≤ n
(analog definiert: |x|)
Die Abbildung rd : R→ F erweitern wir entsprechend auf Rn,Rm×n.
Definition 6.11Seien A, ∆A ∈ Rm×n und A ∈ Fm×n. A sei die Fließkommadarstellung von A mit
A = rd(A) = A +∆A mit |∆A| ≤ |A| eps︸ ︷︷ ︸dies sind m·n Ungleichungen!
,
bzw:
aij = rd(aij) = aij(1 + εij) = aij + εijaij︸ ︷︷ ︸∆aij
|∆aij | ≤ |aij | eps
fl-NotationSei f eine Formel (d.h. z.B. f = ax+by+· · · ) dann bezeichnet fl(f) die Auswertung der Formelf in Fließkommaarithmetrik. Dabei wird die Ausfuhrungsreihenfolge meist offensichtlich sein(von links nach rechts, Punkt vor Strich, Klammern), sonst ist sie anzugeben.
Somit ist zum Beispiel:
fl( A + B︸ ︷︷ ︸A,B∈Fm×n
) = (A + B)︸ ︷︷ ︸exakte Rechnung
+ H mit |H| ≤ eps ·|A + B|
(folgt aus fl(aij + bij) = aij ⊕ bij = (aij + bij)(1 + εij) = (aij + bij) + εij(aij + bij))
Man kann auch schreiben: fl(√x) oder fl(sinx) schreiben.
VorwartsanalyseBisher haben wir die sogenannte
”Vorwartsanalyse“ der Rundungsfehler betrieben, z.B. gilt
fur das Skalarprodukt xTy:
| fl(xTy)− xTy| ≤ n eps |xT | · |y|+O(eps2) (absolut)
oder
|fl(xTy)− xTy||xTy| ≤ n eps
|xT | · |y||xTy| +O(eps2) (relativ).
Eine Alternative ist die sog.”Ruckwartsanalyse“.
Dabei versucht man das Ergebnis der Fließkommarechnung als exaktes Ergebnis eines modifi-zierten Ausdrucks zu schreiben.
58

Beispiel 6.12Betrachte Losung des LGS Ax = b. Die GEM berechnet die numerische Losung x.
Vorwartsanalyse: ‖x− x‖ ≤ F (n, eps,A,b)Ruckwartsanalyse: (A + E) · x = b mit |E| ≤ F ′(n, eps,A)
Storungssatz 5.4 (bei Storungen nur in A):
‖δx‖‖x‖ ≤
cond(A)
1− cond(A) · ‖δA‖‖A‖
· ‖δA‖‖A‖
Kondition der Rundung:
rd(A) = A + δA, |δA| ≤ |A| eps
Verwende Unendlichnorm: ‖A‖∞ = ‖ |A| ‖∞
‖δA‖∞‖A‖∞
=‖ |δA| ‖∞‖A‖∞
≤ ‖A‖∞ eps
‖A‖∞= eps
⇒ ‖x− x‖∞‖x‖∞
≤ cond(A)
1− cond(A) · eps· eps
Fur E aus Ruckwartsanalyse:
‖x− x‖∞‖x‖∞
≤ cond(A)
1− cond(A) · ‖ |E| ‖∞‖A‖∞
· ‖ |E| ‖∞‖A‖∞︸ ︷︷ ︸
noch abzuschatzenideal ware
‖ |E| ‖∞≤np eps ‖A‖∞
⇒ Direkter Vergleich mit Konditionsanalyse moglich.
Ruckwartsanalyse des Skalarprodukts:
Hilfssatz 6.13Es gilt fur x,y ∈ Fn
s = fl(xTy) = (x + f)Ty |f | ≤ n · eps |x|+O(eps2)
Beweis: Induktion uber n
n = 1 : s1 = fl(x1y1) = x1y1(1 + δ1) = (x1 + x1δ1︸︷︷︸=:f1
) · y1
also |f1| = |δ1| · |x1| ≤ eps |x1|
59

n ≥ 2 : sn = fl(xTy) = fl(xT y + xnyn) mit x =
(xxn
), y =
(yyn
)
=[fl(xT y) + fl(xnyn)
]· (1 + εn)
=[(x + f)T · y + xnyn(1 + δn)
]· (1 + εn)
= (x + f)T · y · (1 + εn) + xnyn · [1 + (δn + εn) + δnεn]
= (x + f + εnx + εnf)T · y + [xn + (δn + εn) · xn + δnεnxn] · yn
=
(xxn
)+
(f + εnx + εnf
(δn + εn) · xn + δnεnxn
)
︸ ︷︷ ︸=:f
(yyn
)
mit |f + εnx + εnf | ≤ (n− 1) eps |x|+ eps |x|+O(eps2)
= n · eps |x|+O(eps2)
und |(δn + εn)xn + δnεnxn| ≤ 2 eps |xn|+O(eps2)
wegen n ≥ 2 gilt also
|f | ≤ n eps |x|+O(eps2)
Anmerkung 6.14n eps in Hilfssatz 6.13 ist der schlechteste Fall und sehr pessimistisch. Die Rundungsfehler ineiner Operation hangen von den Argumenten ab und konnen sich auch wegheben (positiv/ne-gativ!). Besser ware eine statistische Betrachtung.
Satz 6.15 (Losen von Dreieckssystemen)Es seien x bzw. y die numerischen Losungen der unteren bzw. oberen Dreickssysteme Lx = bund Ry = c. Dann gilt:
(L + F) · x = b |F| ≤ n eps |L|+O(eps2)
(R + G) · y = c |G| ≤ n eps |R|+O(eps2)
Beweis: [Als Ubungsaufgabe]
Satz 6.16 (Ruckwartsanalyse der LR-Zerlegung)Sei A ∈ Fn×n. Es werde die LR-Zerlegung von A ohne Pivotisierung (Zeilentausch) berechnet.
Dann gilt fur die numerisch berechneten L, R:
LR = A + H mit |H| ≤ 3 (n− 1) eps(|A|+ |L| |R|
)+O(eps2)
60

Beweis: (aus Golub/van Loan: Matrix Computations, Theorem 3.3.1)
n = 1 : Es ist l11 = 1 und r11 = a11 und somit |H| = 0.
n ≥ 2 : Schreibe
A =
[α wT
v B
]
mit v,w ∈ R(n−1) und B ∈ R(n−1)×(n−1).
Dann macht die LR-Zerlegung im 1. Schritt:
a) z = fl(vα
)
b) A1 = fl(B− zwT
)
c) Berechne LR-Zerlegung von A1
Betrachte Teilschritte:
a) Fehler in z:
z =v
α+ f (1) mit |f | ≤ eps
|v||α|
b) Fehler in A1:
A1 = fl(B− zwT
)
= B− fl(zwT
)+ G mit |G| ≤ eps
∣∣B− fl(zwT
)∣∣= B− (zwT + G′) + G︸ ︷︷ ︸
=:F
mit |G′| ≤ eps∣∣zwT
∣∣ ≤ eps |z| |w|T
A1 = B− zwT + F (2)
mit
|F| = | −G′ + G| ≤ |G′|+ |G|≤ eps |z| |w|T︸ ︷︷ ︸
|G′|
+ eps |B− zwT −G′|
≤ eps |z| |w|T + eps(|B|+ |z| |w|T
)+ eps2 |z| |w|T
≤ 2 eps(|B|+ |z| |w|T
)+O(eps2)
c) Nun wird A1 LR-zerlegt und es gilt die Induktionsannahme:
L1R1 = A1 +H1 (3) mit |H1| ≤ 3 (n−2) eps(|A1|+ |L1| |R1|
)+O(eps2)
61

also ist die Blockform der LR-Zerlegung von A:
LR =
(1 0
z L1
)(α wT
0 R1
)=
α wT
αz zwT + L1R1︸ ︷︷ ︸=A1+H1
(1),(2),(3)einsetzen=
α wT
α(vα + f
)zwT + (B− zwT + F)︸ ︷︷ ︸
A1
+H1
=
[α wT
v B
]
︸ ︷︷ ︸=A
+
[0 0αf H1 + F
]
︸ ︷︷ ︸=:H
Damit hat man schon mal die Form LR = A + H. Bleibt noch H abzuschatzen.
In H steckt H1 + F, in |H1| steckt |A1|, also:
|A1| = |B− zwT + F| ≤ |B|+ |z| |w|T + |F|≤ |B|+ |z| |w|T + 2 eps
(|B|+ |z| |w|T
)+O(eps2)
≤ (1 + 2 eps)(|B|+ |z| |w|T
)+O(eps2)
|H1 + F| ≤ |H1|+ |F|Indukt.
annahme≤ 3(n− 2) eps[|A1|+ |L1| |R1|
]+ 2 eps
(|B|+ |z| |w|T
)+O(eps2)
≤ 3(n− 2) eps[(1 + 2 eps)
(|B|+ |z| |w|T
)+ |L1| |R1|
]
+ 2 eps(|B|+ |z| |w|T
)+O(eps2)
≤ 3(n− 1) eps[|B|+ |z| |w|T + |L1| |R1|
]+O(eps2)
und damit
|H| =(
0 0|αf | |H1 + F|
)
≤(
0 0
eps |v| 3(n− 1) eps[|B|+ |z| |w|T + |L1| |R1|
])
+O(eps2)
≤ 3(n− 1) eps
(0 0
|v| |B|+ |z| |w|T + |L1| |R1|
)+O(eps2)
≤ 3(n− 1) eps
[(|α| |w|T|v| |B|
)
︸ ︷︷ ︸|A|
+
( |α| |w|T|z| |α| |z| |w|T + |L1| |R1|
)]
= 3(n− 1) eps
[|A|+
(1 0
|z| |L1|
)
︸ ︷︷ ︸|L|
(|α| |w|T0 |R1|
)
︸ ︷︷ ︸|R|
]
Terme in rot wurden eingefugt um das System in die gewunschte Form zu bringen.
62

Nun sind noch die Dreieckssysteme aufzulosen.
Satz 6.17Seien L und R die numerisch berechnete LR-Zerlegung aus Satz 6.16. Sei weiter y ∈ Fn
die numerisch berechnete Losung von Ly = b und schließlich x die numerische Losung vonRx = y. Dann gilt fur x die Beziehung
(A + E) · x = b
mit
|E| ≤ n eps(
3 |A|+ 5 |L| |R|)
+O(eps2)
Beweis: Wegen (6.15) gilt:
(L + F) y = b |F| ≤ n eps |L|+O(eps2)
(R + G) x = y |G| ≤ n eps |R|+O(eps2)
Einsetzen liefert(L + F
)y =
(L + F
)(R + G
)x =
(LR︸︷︷︸
=A+H
+FR + LG + FG)
x = b
Wegen Satz 6.16 gilt
LR = A + H mit |H| ≤ 3 (n− 1) eps(|A|+ |L| |R|
)+O(eps2)
also
(A + E) x = b mit E = H + FR + LG + FG︸︷︷︸O(eps2)
und
|E| ≤ |H|+ |F| |R|+ |L| |G|+O(eps2)
≤ 3(n− 1) eps(|A|+ |L| |R|
)
︸ ︷︷ ︸|H|
+n eps |L|︸ ︷︷ ︸|F|
|R|+ n eps︸ ︷︷ ︸ |L| |R|︸︷︷︸︸ ︷︷ ︸|G|
+O(eps2)
≤ 3n eps |A|+ 5n eps |L| |R|+O(eps2)
⇐⇒ |eij | ≤ n eps
(3|aij |+ 5
n∑
k=1
|lik| |rkj |)
+O(eps2) ∀1 ≤ i, j ≤ n
63

FolgerungNach Satz 6.17 ist x die exakte Losung des modifizierten Systems
(A + E) x = b
Mit dem Storungssatz gilt dann in der ‖ · ||∞-Norm (Beachte: ‖B‖∞ = ‖ |B| ‖∞):
‖x− x‖∞‖x‖∞
≤︸︷︷︸‖E‖∞‖A‖∞
1
cond∞(A) ·(
3n eps‖A‖∞‖A‖∞︸ ︷︷ ︸
=1︸ ︷︷ ︸vergleichbar
mit Rundungs-‖ rd(A)‖∞‖A‖∞O.K.
+5n eps‖L‖∞‖R‖∞‖A‖∞︸ ︷︷ ︸
evtl. Problem!
+O(eps2)
)
• Erster Term vergleichbar mit dem aus der Konditionsanalyse
• Zweiter Term ist moglicherweise problematisch. L enthalt Eintrage der Formaijaii
, also
proportional zu 1Pivotelement .
|Pivotelement| klein ⇒ ‖L‖ groß ⇒ großer Rundungsfehler!
• Dies kann trotz guter Kondition von A passieren!Beispiel:
A =
(ε 11 0
)A−1 =
(0 11 −ε
)
⇒ Gauß-Elimination ist in dieser Form nicht numerisch stabil!
6.5 Pivotisierung
Die Rundungsfehleranalyse in Satz 6.17 fuhrt auf den unvorteilhaften Term |L| |R|.Mit der Wahl des Zeilenindex r im Gauß-Algorithmus, so dass∣∣∣a(k)rk
∣∣∣ ≥∣∣∣a(k)ik
∣∣∣ ∀ k ≤ i ≤ n
(mache betragsmaßig großtes Element zum Pivotelement) gilt
|lij | ≤ 1 und damit ‖L‖∞ ≤ n
Diese Wahl nennt man”Spaltenpivotisierung“
Beispiel 6.18a)
Ax =
(−10−5 1
2 1
)(x1
x2
)=
(10
)= b
A−1 =−1
10−5 + 2
(1 −1−2 −10−5
)
cond∞(A) = ‖A‖∞‖A−1‖∞ ≈ 3 · 1 = 3
64

GEM in exakter Arithmetik:
(−10−5 1
0 1 + 2 · 105
)(x1
x2
)=
(1
2 · 105
)
Losung: x1 = −0, 4999975, x2 = 0, 999995
GEM in F(10, 4, 1):
q21 = (0, 2 · 101) (−0, 1 · 10−4) = −0, 2 · 106
a(1)22 = (0, 1 · 101) (−0, 2 · 106) (0, 1 · 101)
= (0, 1 · 101)⊕ (0, 2 · 106) = 0, 2 · 106
︸ ︷︷ ︸(auf 4 Stellen
gerundet
)b(1)2 = 0 (−0, 2 · 106) (0, 1 · 101) = 0, 2 · 106
Losung:
x2 = b(1)2 a
(1)22 = 0, 2 · 106 0, 2 · 106 = 0, 1 · 101 = 1
x1 =[(0, 1 · 101) (0, 1 · 101) (0, 1 · 101)
] (−0, 1 · 10−4) = 0
keine richtige Stelle!
a22 wird ignoriert. Tatsachlich gelost wird
(−10−5 1
2 0
)(x1
x2
)=
(10
)
Mit Spaltenpivotisierung:
(2 1
−10−5 1
)(x1
x2
)=
(01
)
q21 = (−0, 1 · 10−4) (0, 2 · 101) = −0, 5 · 10−5
a(1)22 = (0, 1 · 101) (−0, 5 · 10−5) (0, 1 · 101)
= (0, 1 · 101)⊕ 0, 5 · 10−5 = 0, 1 · 101
︸ ︷︷ ︸(auf 4 Stellen
gerundet
)b(1)2 = (0, 1 · 101) (−0, 5 · 10−5) 0 = 0, 1 · 101
x2 = (0, 1 · 101) (0, 1 · 101) = 1
x1 =[0 (0, 1 · 101) (0, 1 · 101)
] (0, 2 · 101) = −0, 5
⇒ Ergebnis exakt gerundet in F(10, 4, 1).
65

b) Aber Spaltenpivotisierung nicht immer ausreichend:
(−10 106
2 1
)(x1
x2
)=
(106
0
)
(1. Spalte von A mit 106 multipliziert)
Keine Vertauschung durch Spaltenpivotisierung⇒ gleiche Rundungsfehler wie bei A.
Diese Probleme kann man durch eine Skalierung des Gleichungssystems vermindern (“Aquilibrierung”):
Ax = b → D−1Ax = D−1b mit dii =n∑
j=1
|aij | (also ‖A‖∞ = 1)
⇐⇒ Ax = b
Rundungsfehleranalyse bei PivotisierungAnalog zu Satz 6.17 zeigt man, dass fur die Losung x bei Spaltenpivotisierung gilt:
(A + E) x = b mit |E| ≤ n eps(3 |A|+ 5 PT |L| |R|) +O(eps2)
Nach Konstruktion ist ‖L‖∞ ≤ n und mit der Definition des”Wachstumsfaktors“ ρ
ρ = maxi,j,k
|a(k)ij |
‖A‖∞(Einflusse aus |R|)
folgt
‖R‖∞ ≤ nρ‖A‖∞
und damit zeigt man (Golub/van Loan: Matrix Computations, Seite 115)
‖E‖∞ ≤ 8n3‖A‖∞ρ eps +O(eps2)
In der Praxis ist ρ ≈ 10.Der schlechteste Fall bei Spaltenpivotisierung ist ρ = 2n−1!
Mit totaler Pivotisierung erreicht man in exakter Arithmetik (Golub/van Loan: Matrix Com-putations, Seite 119):
|a(k)ij | ≤ k
12 ·√
2 · 3 12 · . . . · k 1
k−1 · max1≤i,j≤n
|aij |
also deutlich ein kleineres Wachstum (z.B. |a(100)ij | ≤ 806 · max1≤i,j≤n |aij |).
Totale PivotisierungWahle r, s ∈ k, . . . , n sodass
|a(k)rs | ≥ |a(k)
ij | ∀ k ≤ i, j ≤ n
und erreiche durch Zeilen- und Spaltenvertauschung, dass
a(k)kk = a(k)
rs
66

In Matrixform:
Schritt 1:G1Pr1APs1 Ps1x︸ ︷︷ ︸ = G1Pr1b
Schritt 2:G2Pr2G1Pr1APs1Ps2Ps2Ps1x = G2Pr2G1Pr1b
...Schritt n-1:
G′n−1 · · ·G′1 Prn−1 · · ·Pr1︸ ︷︷ ︸=:P
A Ps1 ·Psn−1︸ ︷︷ ︸=:QT
︸ ︷︷ ︸R
Q︷ ︸︸ ︷Psn−1 · · ·Ps1 x︸ ︷︷ ︸
z
= G′n−1 · · ·G′1Prn−1 · · ·P1b
und damit
PAQT z = Pb
PAQT = LR z = Qx
Losen des LGS gelingt dann mit
b′ = Pb
Ly = b′
Rz = y
x = QT z
Bei einer totalen Pivotisierung erhalt man also am Ende der LR-Zerlegung und des Vorwarts-und Ruckwartseinsetzens mit der entsprechend der Zeilenvertauschungen umsortierten rechtenSeite b einen vertauschten Losungsvektor z. Dieser muss wieder zuruckgetauscht werden. EineMoglichkeit ist es, zusatzlichem zum Vektor p fur die Zeilenvertauschungen mit einen Vektorq mit fortlaufendem Index 1 . . . n zu starten und diese bei Zeilen- bzw. Spaltenvertauschungenjeweils mit zu vertauschen. Dann gilt
xqi = zi.
Aufwand der Pivotisierung:
• O(n2
2 ) Vergleiche bei Spaltenpivotisierung
• O(n3
3 ) Vergleiche bei totaler Pivotisierung
Da Speicherzugriffe teurer als eigentliche Rechnung⇒ Verdopplung des Zeitbedarfs bei totalerPivotisierung.Praktische Erfahrung zeigt keine Vorteile fur Rundungsfehler bei totaler PivotisierungSpaltenpivotisierung mit Zeilenskalierung ist effizient und numerisch stabil.
6.6 Spezielle Systeme
6.6.1 Symmetrisch positiv definite Matrizen
Definition 6.19Eine Matrix A ∈ Kn×n heißt positiv definit in K wenn
R 3 〈x,Ax〉 > 0 ∀x ∈ Kn \ 0
67

Lemma 6.20Fur A ∈ Cn×n gilt: A ist hermitesch genau dann, wenn 〈x,Ax〉 ∈ R ∀x ∈ Cn \ 0.
Beweis: Ubungen
Positiv definite Matrizen in Cn×n sind also immer hermitesch. Da diese Aussage im Beweisauf dem Verschwinden des Imaginarteils basiert, gibt es fur positiv definite Matrizen in Rn×ndiese Einschrankung nicht. Diese sind also nicht notwendigerweise symmetrisch.
Lemma 6.21Eine hermitesche Matrix A ist genau dann positiv definit, wenn alle ihre (reellen) Eigenwertepositiv sind. Alle Hauptdiagonalelemente sind (reel und) positiv.
Beweis:
• A sei hermitesch mit lauter positiven Eigenwerten. Dann hat A eine orthonormale Basisaus Eigenvektoren wi. Ein beliebiges x ∈ Kn hat die Darstellung x =
∑ni=1 αiw
i, wobeiwi ein Eigenvektor zum Eigenwert λi ist.
〈x,Ax〉 =n∑
i,j=1
αiλjαj〈wi,wj〉 =n∑
i=1
λi|αi|2 > 0
• A sei hermitesch und positiv definit. A hat also Eigenpaare (λi,wi) mit λi ∈ R. Zu
zeigen ist, dass λi > 0 ∀ i.
0 < 〈wi,Awi〉 = 〈wi, λiwi〉 = λi 〈wi,wi〉︸ ︷︷ ︸
=1
= λi
• Sei ei der i-te karthesische Einheitsvektor mit eij = δij . Dann gilt: 0 < 〈ei,Aei〉 = aii ∈ R
Die Aussage gilt naturlich auch fur reelle symmetrische und positiv definite Matrizen.
Speziell fur reelle Matrizen gilt:
Lemma 6.22Sei A ∈ Rn×n symmetrisch und positiv definit. Dann liegt das betragsmaßig großte Elementauf der Hauptdiagonalen.
Beweis: Sei ei der i-te kartesische Einheitsvektor und aij , j 6= i das betragsmaßig großteElement. Dann zeigt man durch Widerspruch:
0 <〈(ei − sign(aij)e
j)),A(ei − sign(aij)e
j))〉
A=AT
= 〈ei,Aei〉︸ ︷︷ ︸aii
−2 sign(aij) 〈ei,Aej〉︸ ︷︷ ︸aij
+ sign(aij)2〈ej ,Aej〉︸ ︷︷ ︸ajj
= aii − 2|aij |+ ajj ≤ 0, da |aij | ≥ akk > 0 ∀ 1 ≤ k ≤ n
68

Satz 6.23Eine symmetrisch positiv definite Matrix A ∈ Rn×n ist stets ohne Pivotisierung LR-zerlegbar.Fur die Diagonalelemente der im Eliminationsprozess auftretenden Matrizen gilt:
a(k)ii ≥ λmin(A) > 0 k ≤ i ≤ n
Beweis: Betrachte einen Schritt der LR-Zerlegung:
1. A =
(α vT
v B
)mit v,w ∈ R(n−1) und B ∈ R(n−1)×(n−1), α > 0.
Elimination der Spalte v liefert:
(1 0−vα I
)
︸ ︷︷ ︸G1
(α vT
v B
)
︸ ︷︷ ︸A
=
(α vT
0 B− 1αvvT
)=
(α 00 B− 1
αvvT
)(1 vT
α0 I
)
mit
(1 vT
α0 I
)−1
=
(1 −vT
α0 I
)folgt:
⇐⇒(
1 0−vα I
)
︸ ︷︷ ︸xT
(α vT
v B
)
︸ ︷︷ ︸A
(1 −v
α0 I
)
︸ ︷︷ ︸X
=
(α 00 B− 1
αvvT
)
︸ ︷︷ ︸=:A
X hat vollen Rang, A ist symmetrisch positiv definit nach Voraussetzung⇒ XTAX = Aist symmetrisch positiv definit.
B− 1αvvT ist Hauptuntermatrix von A und somit auch auch symmetrisch positiv definit.
2. Es gilt: (Rayleigh-Quotient)
〈x,Ax〉 =
n∑
i=1
αiλjαj〈wi,wj〉 =
n∑
i=1
λi|αi|2 ≥ λmin(A)〈x,x〉
und damit fur x = ei:
aii = 〈ei,Aei〉 ≥ λmin(A) 〈ei, ei〉︸ ︷︷ ︸=1
= λmin(A)
Fur die Diagonalelemente von B− 1αvvT gilt mit ei =
(0ei
)
(B− 1
αvvT )ii = 〈ei, Aei〉 = 〈ei,XTAXei〉 = 〈Xei,AXei〉
≥ λmin(A) 〈Xei,Xei〉
mit
(1 −vT
α0 I
)
︸ ︷︷ ︸X
(0ei
)
︸ ︷︷ ︸ei
=
(−viαei
)
= λmin(A)
(1 +
v2i
α2
)≥ λmin(A)
69

Dies zeigt, dass die Pivotelemente bei der Gaußelimination echt nach unten beschrankt bleiben.
Die Pivotelemente, die bei der LR-Zerlegung auftreten sind nach 6.21 stets positiv.
Mit D = diag(R) gilt:
A = LR = LD D−1R︸ ︷︷ ︸U
= LDU
U ist eine obere Dreiecksmatrix mit uii = 1. Wegen der Symmetrie von A gilt U = LT , also
A = LDLT .
Da dii > 0 ist die Matrix”D
12 “
(D
12
)ii
=√dii
wohldefiniert und es gilt:
A = LD12︸ ︷︷ ︸
L
D12 LT︸ ︷︷ ︸LT
= LLT
Dies ist die sogenannte Cholesky-Zerlegung einer symmetrisch positiv definiten Matrix A.
Ausnutzung der Symmetrie erlaubt die Berechnung der Cholesky-Zerlegung in n3
3 + O(n2)Operationen (also um den Faktor 2 schneller) sowie eine Halbierung des Speicherbedarfs.
6.6.2 Diagonaldominante Matrizen
Definition 6.24Eine Matrix A ∈ Kn×n heißt (strikt) diagonaldominant, falls
n∑
j=1,j 6=i|aij |
(<)
≤ |aii| i = 1, . . . , n.
Satz 6.25Diagonaldominante, regulare Matrizen erlauben eine LR-Zerlegung ohne Pivotisierung.
Beweis: Ubungen
6.6.3 Bandmatrizen
Definition 6.26Eine Matrix A ∈ Kn×n heißt Bandmatrix vom Bandtyp (ml,mr) mit 0 ≤ ml,mr ≤ n − 1,wenn gilt
ajk = 0 falls (k < j −ml) ∨ (k > j +mr) 1 ≤ j, k ≤ n
Die Große m = ml +mr + 1 heißt Bandbreite.
Beispiel: Tridiagonalmatrix: ml = mr = 1
70

Definition 6.27A ∈ Kn×n heißt Tridiagonalmatrix falls
aij = 0 fur |i− j| > 1 1 ≤ i, j ≤ n
Satz 6.28Ist A ∈ Kn×n eine Bandmatrix vom Typ (ml,mr), fur die das Gauß’sche Eliminationsver-fahren ohne Zeilenvertauschungen durchfuhrbar ist, dann sind auch alle reduzierten MatrizenBandmatrizen desselben Typs und die Faktoren L und R der Dreieckszerlegung von A sindBandmatrizen vom Typ (ml, 0) bzw. (0,mr).
ohne Beweis.
Der Aufwand fur die Berechnung der LR-Zerlegung einer Bandmatrix vom Typ (ml,mr) ist
N =2
3nmlmr +O(n (ml +mr))
Tridiagonalmatrix:Falls die LR-Zerlegung einer Tridiagonalmatrix ohne Pivotisierung durchfuhrbar ist, berechnetsie sich nach (Thomas-Algorithmus):
li,i−1 · ri−1,i + rii = aii ⇒ rii = aii − li,i−1ri−1,i
li,i−1 · ri−1,i−1 = ai,i−1 ⇒ li,i−1 =ai,i−1
ri−1,i−1
1 · ri−1,i = ai−1,i ⇒ ri−1,i = ai−1,i
Der Aufwand ist dabei O(3n) und fur die Losung eines linearen Gleichungssystems O(8n).
6.7 Spezielle Anwendungen
6.7.1 Nachiteration
Sei e der Fehler der numerischen Losung x des linearen Gleichungssystems Ax = b mit A ∈Kn×n und x,b ∈ Kn, also e = x− x. Dann gilt
Ax− b = A (x + e)− b = Ax + Ae− b = Ae.
d = Ax− b nennt man auch den Defekt. Berechnet man numerisch d und lost dann
Ae = d,
als e, dann erhalt man durch x(1) = x − e eine verbesserte numerische Losung des linearenGleichungssystems. Dies nennt man Nachiteration. Wenn eine LR-Zerlegung von A bereitsberechnet ist, lasst sich die Korrektur in O(n2) berechnen. Das Ganze lasst sich naturlich auchwiederholt anwenden.
Damit die Nachiteration gut funktioniert, sollte der Defekt mit erhohter Genauigkeit berech-net werden. Zum Beispiel kann man A, b und x mit einfacher Genauigkeit speichern und auchdie LR-Zerlegung mit einfacher Genauigkeit berechnen. Fur die Berechnung von d verwendetman dann doppelte Genauigkeit.
Schon wenige Iterationen fuhren zu einer deutlich verbesserten Losung.
71

6.7.2 Rangbestimmung
Sei A ∈ Kn×n. Gilt nach k-Schritten der Gauß-Elimination
A(k) =
(R(k) ∗
0 0
)
mit R(k) ∈ Kk×k mit r(k)ii 6= 0, so ist der Rang(A) = k.
• Kann die GEM zu Ende gefuhrt werden, so gilt k = n, mithin Rang(A) = n.
• Die Rangbestimmung erfordert totale Pivotisierung, da die erste Spalte der (n−k)×(n−k)Restmatrix 0 sein kann, was aber nicht Rang(A) = k bedeutet!
6.7.3 Berechnung der Inversen
Zur Berechnung der Inversen geht man wie folgt vor:
• Berechne LR-Zerlegung von A. Der Aufwand bei Spaltenpivotisierung ist dabei
2
3n3 +O(n2)
• Fur i = 1, . . . , n lose Ax(i) = ei.Aufwand: n · 2n2 fur das Losen der Dreieckssysteme.
• A−1 =(x(1), . . . ,x(n)
)besteht spaltenweise aus den x(i).
• Gesamtaufwand:
2
3n3 +O(n2) + 2n3 =
8
3n3 +O(n2)
72

7 Irregulare Systeme
Es sei nun A ∈ Rm×n, b ∈ Rm sowie Rang(A) beliebig. Ax = b hat dann genau eine, unendlichviele oder gar keine Losung.
Einige Grundbegriffe aus der linearen Algebra:
• Bild(A) = y ∈ Rm : y = Ax fur ein x ∈ Rn
• Kern(A) = x ∈ Rn : Ax = 0
• Rang(A) = dim(Bild(A)) = Rang(AT ) = dim(Bild(AT ))
• Orthogonales Komplement:Bild(A)⊥ = y ∈ Rm : 〈y,y′〉 = 0 ∀y′ ∈ Bild(A)Es gilt:
〈y,y′〉 = 0 y′ ∈ Bild(A)
⇐⇒ 〈y,Ax〉 = 0 ∀x ∈ Rn
⇐⇒(ATy
)Tx = 0 ∀x ∈ Rn
⇐⇒ y ∈ Kern(AT )
und damit: Bild(A)⊥ = Kern(AT ) .
Dies zeigt dann
dim(Bild(A))︸ ︷︷ ︸=Rang(A)
+ dim(Kern(AT )) = m
︷ ︸︸ ︷dim(Bild(AT )) + dim(Kern(A)) = n
7.1 Least Squares Losung
Den Losungsbegriff fur lineare Gleichungssysteme kann man in folgender Weise erweitern:
Satz 7.1 (Least Squares Losung)a) Es existiert ein x∗ ∈ Rn sodass
‖Ax∗ − b‖2 = minx∈Rn
‖Ax− b‖2
b) Diese Bedingung ist aquivalent dazu, dass x∗ eine Losung von
ATAx∗ = ATb,
der sogenannten”
Normalengleichung“ ist.
c) Falls Rang(A) = n (dann ist m ≥ n), ist x∗ eindeutig bestimmt, sonst hat jede weitereLosung die Form x∗ + y mit y ∈ Kern(A).
73

Beweis:b) ⇒ a):x∗ sei Losung der Normalengleichung. Fur beliebiges x ∈ Rn gilt dann:
‖Ax− b‖22 = ‖A(x− x∗ + x∗)− b‖22= 〈Ax∗ − b + A(x− x∗),Ax∗ − b + A(x− x∗)〉= 〈Ax∗ − b,Ax∗ − b〉+ 2〈 Ax∗ − b︸ ︷︷ ︸
∈Bild(A)⊥
=Kern(AT ) da
AT (Ax∗−b)=0
,A(x− x∗)︸ ︷︷ ︸∈Bild(A)
〉+ 〈A(x− x∗),A(x− x∗)〉
= ‖Ax∗ − b‖22 + ‖A(x− x∗)‖22︸ ︷︷ ︸≥0
≥ ‖Ax∗ − b‖22Damit erfullt x∗ die Minimalitatsbedingung.
a) ⇒ b)Setze f : Rn → R, f(x) = ‖Ax− b‖22.
Notwendige Bedingung fur ein Minimum von f ist
∇f(x∗) = 0 ⇐⇒ ∂f
∂xk(x∗) = 0 ∀k = 1, . . . , n.
∂f
∂xk(x∗) =
∂
∂xk〈Ax− b,Ax− b〉
∣∣∣∣x=x∗
=∂
∂xk
m∑
i=1
n∑
j=1
aijxj
− bi
2∣∣∣∣∣∣x=x∗
=
m∑
i=1
2
n∑
j=1
aijxj
− bi
aik
∣∣∣∣∣∣x=x∗
= 2
m∑
i=1
(AT )ki
[( n∑
j=1
aijx∗j
)−bi
︸ ︷︷ ︸(Ax∗−b)i
]
= 2(AT (Ax∗ − b)
)k.
Damit ist
∇f(x∗) = 2AT (Ax∗ − b)!
= 0 ⇐⇒ ATAx∗ = ATb
c) Losbarkeit der Normalengleichung
Rm = Bild(A)⊕ Bild(A)⊥
d.h. jedes b ∈ Rm besitzt eine eindeutige Zerlegung
b = s + r mit s ∈ Bild(A), r ∈ Bild(A)⊥ = Kern(AT )
74

Zu s ∈ Bild(A) gibt es ein x∗ ∈ Rn mit Ax∗ = s. Fur dieses gilt dann
ATAx∗ = AT s = AT s + AT r︸︷︷︸=0
= ATb
also lost dieses x∗ auch die Normalengleichung. Sei Rang(A) = n und damit m ≥ n (daRang(A) ≤ min(m,n)).
Betrachte ATAx = 0, also Kern(ATA).
ATAx = 0 ⇐⇒ ATy = 0 ∧ y = Ax
Nun ist aber Kern(AT )⊥Bild(A), d.h. Kern(AT ) ∩ Bild(A) = 0.Somit ist ATA regular.(Alternative: ATA ist symmetrisch und positiv definit wegen maximalem Rang.)
Sei Rang(A) < n:Sei x1 eine weitere Losung der Normalengleichung (also ATAx1 = ATb), dann gilt:
b = Ax1︸︷︷︸∈Bild(A)
+ (b−Ax1)︸ ︷︷ ︸∈Kern(AT ),
da AT (b−Ax1)
=ATb−ATAx1=0
Da die Zerlegung Rm = Bild(A)⊕ Bild(A)⊥ eindeutig ist, muss
Ax1 = Ax∗
sein und damit
A(x1 − x∗) = 0, also x1 − x∗ ∈ Kern(A)
ATA ist symmetrisch und positiv semidefinit. Die Losung ist damit prinzipiell mit der Cholesky-Zerlegung moglich (oder mit einer normalen LR-Zerlegung). Die Normalenmatrix ist jedochhaufig schlecht konditioniert, insbesondere wenn mehrere Messpunkte nahe beieinander liegen.Deshalb wahlt man in der Praxis einen anderen Losungsweg, die QR-Zerlegung.
7.2 QR-Zerlegung
Satz 7.2Zu jeder Matrix A ∈ Rm×n mit m ≥ n und Rang(A) = n existiert eine orthogonale MatrixQ ∈ Rm×m und eine obere Dreiecksmatrix R ∈ Rm×n, so dass
A = QR.
Die ersten n Spaltenvektoren von Q bilden eine orthonormale Basis von Bild(A).
Beweis: Im folgenden durch Konstruktion.
Satz 7.3Seien A ∈ Rm×n und b ∈ Rm.
75

a) Die Losung des Least-Squares-Problems“Finde x∗ ∈ Rn mit ρLS = ‖Ax∗ − b‖2 = minx∈Rn ‖Ax− b‖2”,ist invariant unter orthogonaler Transformation, d.h. fur eine orthogonale MatrixQ ∈ Rm×m gilt:
‖Ax∗ − b‖2 = ‖QTAx∗ −QTb‖2.
b) Ist Q eine orthogonale Matrix mit A = QR und setzen wir
QTA = QTQR = R =
(R1
0
)und QTb =
(cd
)
mit R1 ∈ Rn×n und c ∈ Rn, d ∈ Rm−n, dann ist x∗ die Losung des linearen Gleichungs-systems R1x
∗ = c und ρLS = ‖d‖2 das Residuum des Least-Squares-Problems.
Beweis:
a)
‖Ax∗ − b‖22 = 〈Ax∗ − b,Ax∗ − b〉= 〈Ax∗ − b,QQT
︸ ︷︷ ︸=I
(Ax∗ − b)〉
= 〈QT (Ax∗ − b),QT (Ax∗ − b)〉= ‖QTAx∗ −QTb‖22
b)
QT (Ax∗ − b) = QTAx∗ −QTb = QT QR︸︷︷︸A
−QTb
= Rx−QTb
mit c =
(c0
), d =
(0d
)⇒ c + d = QTb
‖Ax∗ − b‖22 = 〈Rx∗ − c− d,Rx∗ − c− d〉
=(
(Rx∗ − c)− d)T (
(Rx∗ − c)− d)
= (Rx∗ − c)T (Rx∗ − c)− (Rx∗ − c)T d︸ ︷︷ ︸=0
− dT (Rx∗ − c)︸ ︷︷ ︸=0
+dT d
= ‖R1x∗ − c‖22︸ ︷︷ ︸=0
+‖d‖22
= ‖d‖22
76

Definition 7.4Eine Matrix S ∈ Rn×n der Form
S = I− 2vvT
vTv
mit v ∈ Rn \ 0 heißt Householder Transformation.
Satz 7.5Eine Householder-Transformation
S = I− 2vvT
vTv
ist symmetrisch und orthogonal.
Beweis:
• S symmetrisch:
ST =
(I− 2
vvT
vTv
)T= I− 2
(vvT
)T
(vTv)T= I− 2
vvT
vTv
• S orthogonal, zu zeigen: ST · S = S · S = I
S · S =
(I− 2
vvT
vTv
)·(
I− 2vvT
vTv
)= I− 4
vvT
vTv+ 4
1
(vTv)2
(vvT
) (vvT
)
I− 4vvT
vTv+ 4
1
(vTv)2 v(vTv
)vT = I− 4
vvT
vTv+ 4
1
vTvvvT = I
Hilfssatz 7.6Das Produkt zwischen einer Householder Transformation Si ∈ Rn×n und einem Vektor x ∈ Rnmit v = x± ‖x‖2 · ei hat die Form Si · x = ∓‖x‖2 · ei.Beweis:
Si · x =
(I− 2
vvT
vTv
)· x = x− 2v
vTx
vTv
vTx = (x± ‖x‖2 · ei)T · x = xTx± ‖x‖2 · xi = ‖x‖22 ± ‖x‖2 · xivTv = (x± ‖x‖2 · ei)T · (x± ‖x‖2 · ei) = xTx± 2‖x‖2 · xi + ‖x‖22
= 2(‖x‖22 ± ‖x‖2 · xi
)
Si · x = x− 2 · ‖x‖22 ± ‖x‖2 · xi
2(‖x‖22 ± ‖x‖2 · xi
) · (x± ‖x‖2 · ei)
= ∓‖x‖2 · ei
77

QR-Zerlegung einer MatrixZu Beginn des k-ten Schritts haben wir die Matrix
A(k−1) =
r11 . . . . . . . . . . . . . . . . . . r1n
. . .
0 rk−1,k−1 . . . . . . . . . . . . rk−1,n
0 z(k)
a(k−1)k,k+1 . . . . . . . . . a
(k−1)k,n
.... . .
...
a(k−1)n,k+1 . . . . . . . . . a
(k−1)n,n
mit z(k)i = a
(k−1)i+(k−1),k
Multipliziere nun mit Householder-Matrix
Sk = I− 2v(k)v(k)T
v(k)Tv(k)
mit
v(k) =
0...0
z(k)1 + sign(z
(k)1 ) · ‖z(k)‖2
z(k)2...
z(k)m−k
also
A(k) = Sk ·A(k−1)
⇒ die ersten (k − 1) Zeilen bleiben unverandert, die Spalte k unterhalb der Diagonalen istNull.
Nach n-Schritten: A(n) = R ist obere Dreiecksmatrix.
Sn · Sn−1 · · ·S1︸ ︷︷ ︸QT
A = R ⇐⇒ A = Q ·R
Da alle Si orthogonal ⇒ Q orthogonal.Damit ist Satz 7.2 bewiesen.
Anmerkung 7.7• Faktorisierte Speicherung von Q:
Q muss nicht explizit gespeichert werden. Man speichert stattdessen die Householder-Vektoren. Wenn man v(k) normalisiert zu
v(k) =1
z(k)1 + sign(z
(k)1 ) · ‖z(k)‖2
· v(k)
⇒ v(k)k = 1, v
(k)i = 0 fur i < k.
78

v(k)k+1, . . . , v
(k)m konnen in der Spalte k von A(k) unter der Diagonalen gespeichert werden.
Man nennt dies auch den essentiellen Teil der Matrix Sk.
• Effiziente Multiplikation mit der Householder Matrix:
A(k) =
(I− 2
v(k)v(k)T
v(k)Tv(k)
)·A(k−1) = A(k−1) − 2
v(k)Tv(k)· v(k)v(k)TA(k−1)
⇒À Berechne Skalarprodukt (dabei sind die ersten k−1 Terme Null und konnen ignoriert
werden)
‖v(k)‖22 = v(k)Tv(k)
und Gewichtungsfaktor
β =2
‖v(k)‖22
Á Berechne Matrix Vektor Produkt
wT = β v(k)TA(k−1)
 Berechne Outer-Product Update
A(k) = A(k−1) − v(k)wT
Á und  mussen nur fur die Untermatrix
A(k−1) =a
(k)ij : (k < i ≤ m) ∧ (k < j ≤ n)
durchgefuhrt werden.
Analog wird fur QTb = (∏ni=1 Si) b das b nach und nach mit den jeweiligen Househol-
dermatrizen Si multipliziert.
Householder Least-Squares Algorithmus
À Berechne QTA = R mit Householdertransformationen. Speichere QT in faktorisierter
Form und R1 ∈ Rn×n aus R =
(R1
0
).
Á Berechne
b = QTb =
(cd
), c ∈ Rn,d ∈ Rm−n
 Residuum: ρLS = ‖d‖2à x durch Ruckwartseinsetzen R1x = c.
79

Algorithmus 7.8 (Least-Squares mit Householder-Algorithmus)
Input: A ∈ Rm×n, b ∈ RmOutput: x ∈ Rn
ρLS ∈ Rn Vektoren v(k) ∈ Rm in aij , j < i, v
(k)1 = 1 implizit
R ∈ Rm×n in aij , j ≥ iHouseholderVektor(x) Berechne Householder Vektorµ = ‖x‖2;v = x;if (µ 6= 0) thenβ = 1/(x1 + sign(x1) · µ);v = β · v;v1 = 1;
elseFehler!
end ifreturn v;
HouseholderMatrix(x) Berechne Householder Matrixi = length(x)v = HouseholderVektor(x)H = I ∈ Ri×iH− = 2/‖v‖22 · v · vTreturn H;
HouseholderQR(A)Berechne QR-Zerlegungm = lines(A), n = columns(A);Q = I ∈ Rm×m;for k = 1; k ≤ n; k = k + 1 do
H = I ∈ Rm×m;H[k:m,k:m]=HouseholderMatrix(A[k:m,k]);Q = Q ·H;A = H ·A;
end forreturn Q,A;
HouseholderLeastSquares(A, b)m = lines(A), n = columns(A);Q,R=HouseholderQR(A)b = QT · bρLS = ‖b[n+ 1 : m]‖2; Residuumx = b[1:n];for (k = n; k ≥ 1; k = k − 1) do Ruckwartseinsetzen
for (j = k + 1; j ≤ n; j = j + 1) doxk− = rkj · xj ;
end forend forreturn x, ρLS ;
80

Algorithmus 7.9 (Schneller Least-Squares mit Householder-Algorithmus)
Input: A ∈ Rm×n, b ∈ RmOutput: x ∈ Rn
ρLS ∈ Rn Vektoren v(k) ∈ Rm in aij , j < i, v
(k)1 = 1 implizit
R ∈ Rm×n in aij , j ≥ iHouseholderVektor(x) Berechne Householder Vektorµ = ‖x‖2;v = x;if (µ 6= 0) thenβ = 1/(x1 + sign(x1) · µ);v = β · v;v1 = 1;
elseFehler!
end ifreturn v;
HouseholderMult(A, v)β = −2/(vTv);w = βATv;A = A + v ·wT ;return A;
HouseholderQRFast(A)Berechne QR-Zerlegungm = lines(A), n = columns(A);for k = 1; k ≤ n; k = k + 1 do
v = HouseholderVector(A[k:m,k]);A[k:m,k:n] = HouseholderMult(A[k:m,k:n],v);A[k+1:m,k]=v[1:m-(k+1)];
end forreturn A;
HouseholderLeastSquaresFast(A, b)m = lines(A), n = columns(A);A=HouseholderQRFast(A)for k = 1; k ≤ n; k = k + 1 do Wende Q auf b an
v= A[k:m,k]; v1 = 1;b[k:m] = HouseholderMult(b[k:m],v)
end forρLS = ‖b[n+ 1 : m]‖2; Residuumx = b[1:n];for (k = n; k ≥ 1; k = k − 1) do Ruckwartseinsetzen
for (j = k + 1; j ≤ n; j = j + 1) doxk− = akj · xj ;
end forend forreturn x, ρLS ;
81

Vergleich mit der NormalengleichungKonditionsanalyse der Losung des linearen Gleichungssystems liefert:
‖x− x‖2‖x‖2
≈ eps ·(cond(A) + ρLS cond(A)2
)
Householder Normalengleichung
Rechenaufwand O(2n2 ·(m− n
3
)) O(n2 ·
(m+ n
3
))
Rundungsfehler ‖x−x‖2‖x‖2 ≈ eps ·
(cond2(A) + ρLS cond2(A)2
) ‖x−x‖2‖x‖2 ≈ eps · cond2(A)2
aus Golub/van Loan: Matrix Computations, Seiten 224, 226 und 230
⇒ Householdertransformation stabiler bei kleinem Residuum und schlechter Kondition, aberaufwandiger. Bei großem Residuum und schlechter Kondition sind beide Verfahren vergleichbarschlecht.
Bei nahezu irregularen und daher sehr schlecht konditionierten Matrizen verwendet man diesogenannte Singularwertzerlegung.
82

8 Polynominterpolation
8.1 Approximation und Interpolation
Approximation von Funktionen ist notwendig fur die Darstellung von Funktionen im Rechner.
Anwendungen
• Rekonstruktion eines funktionalen Zusammenhangs aus”gemessenen“ Funktionswerten
fur z.B. Auswertung an Zwischenstellen
• Teuer auszuwertende Funktionen effizienter auswerten
• Darstellung von Fonts (Zeichensatzen, 2D), Korpern (3D) im Rechner. Voraussetzungfur Simulationen und Visualisierung, Szenen in der Computergraphik
• Losen von Differential- und Integralgleichungen, Diskretisierungsverfahren fur gewohnlicheund partielle Differentialgleichungen
• Datenkompression
Wir beschranken uns weitgehend auf Funktionen in einer Variablen, z.B.
f ∈ C[a, b]
C[a, b] ist ein unendlich dimensionaler (Vektor-)raum von Funktionen. Im Rechner betrachtenwir Funktionenklassen, die durch eine endliche Zahl von Parametern bestimmt sind (mussenkeine Teilraume sein!).
Beispiele
• p(x) = a0 + a1x+ · · ·+ anxn (Polynome)
• r(x) = a0+a1x+···+anxnb0+b1x+···+bmxm (rationale Funktionen)
• t(x) = 12a0 +
∑nk=1 [ak cos(kx) + bk sin(kx)] (trigonometrische Funktionen)
• e(x) =n∑k=1
ak exp(bkx) (Exponentialsumme)
Grundaufgabe der ApproximationGegeben sei eine Menge von Funktionen P (siehe oben) sowie eine Funktion f (z.B. f ∈ C[a, b]).Finde g ∈ P , sodass der Fehler f − g in geeigneter Weise minimiert wird.Mogliche zu minimierende Zielgroßen sind z.B.:
•(
b
a(f − g)2dx
)→ min
• maxa≤x≤b
|f(x)− g(x)| → min
• maxi=0,...,n
|f(xi)− g(xi)| → min fur a ≤ xi ≤ b, i = 0, . . . , n
83

Man spricht von Interpolation, falls g durch
g(xi) = yi := f(xi) i = 0, . . . , n
festgelegt wird. Dies ist ein Spezialfall der Approximationsaufgabe.
8.2 Polynominterpolation
Pn sei die Menge der Polynome uber R vom Grad kleiner gleich n ∈ N0:
Pn :=
p(x) =
n∑
i=0
aixi : ai ∈ R
Pn ist ein n+ 1-dimensionaler Vektorraum.Die Monome 1, x, x2, . . . , xn bilden eine Basis von Pn. Abbildung 11 zeigt die Monome bis zumGrad 6.
0
0.2
0.4
0.6
0.8
1
1.2
0 0.2 0.4 0.6 0.8 1
y
x
i=0i=1i=2i=3i=4i=5i=6
Abbildung 11: Die Monome bis zum Grad 6.
Zu n+ 1 gegebenen, paarweise verschiedenen Stutzstellen x0, x1, . . . , xn ist die Interpolations-aufgabe
p ∈ Pn : p(xi) = yi := f(xi) i = 0, . . . , n
aquivalent zu dem linearen Gleichungssystem
1 x0 x20 · · · xn0
1 x1 x21 · · · xn1
......
.... . .
...1 xn x2
n · · · xnn
︸ ︷︷ ︸V [x0,...,xn]
a0
a1...an
=
y0
y1...yn
• V [x0, . . . , xn] heißt Vandermonde Matrix
84

• falls xi = xj ⇒ Zeile i = Zeile j ⇒ V nicht regular
• Fur paarweise verschiedene xi ist V [x0, . . . , xn] regular! (siehe unten)
• V ist schlecht konditioniert fur große n:
– cond∞(V ) = O(2n) fur xi positiv
– cond∞(V ) = O(2n/2)fur xi ∈ R symmetrisch um den Ursprung (Gautschit+Inglese, 88).
8.2.1 Lagrange-Interpolation
Definition 8.1Zu den paarweise verschiedenen Stutzstellen xi, i = 0, . . . , xn definiere die sogenannten Lagrange-Polynome:
L(n)i (x) =
n∏
j=0j 6=i
x− xjxi − xj
i = 0, . . . , n
Abbildung 12 zeigt die Lagrange-Polynome vom Grad 6 bei aquidistanten Stutzstellen auf[0, 1].
-1.5
-1
-0.5
0
0.5
1
1.5
0 0.2 0.4 0.6 0.8 1
y
x
i=0i=1i=2i=3i=4i=5i=6
Abbildung 12: Die Lagrange-Polynome L(6)i (x) vom Grad 6.
Diese Polynome haben folgende Eigenschaften:
1. L(n)i hat Grad n, da
n∏j=0i 6=j
(x− xj) gerade n Faktoren hat.
2. Es gilt:
L(n)i (xk) = δik =
1 i = k
0 sonst
85

i 6= k : Im Produkt
n∏
j=0i 6=j
(xk − xj) kommt j = k 6= i vor,
und damit der Faktor (xk − xk) = 0
i = k : L(n)i (xi) =
n∏
j=0j 6=i
xi − xjxi − xj︸ ︷︷ ︸
=1
= 1
3. Die L(n)i bilden eine Basis von Pn:
• L(n)k ist das einzige Polynom unter den L
(n)i , i = 0 . . . n mit Li(xk) 6= 0, daher ist es
linear unabhangig von den anderen Lagrange-Polynomen L(n)i , i 6= k.
• Da Pn ein n+ 1 dimensionaler Vektorraum ist, bilden die n+ 1 linear unabhangigen
Lagrange-Polynome L(n)i , i = 0, . . . , n eine Basis von Pn.
4. Fur gegebene (xi, yi), i = 0, . . . , n erfullt
p(x) =
n∑
i=0
yi L(n)i (x)
die Interpolationsaufgabe:
p(xk) =n∑
i=0
yi L(n)i (xk)︸ ︷︷ ︸δik
= yk
Beispiel 8.2Zu interpolieren sei die folgende Wertetabelle mit 4 Eintragen:
xi yi
0 1.00002 0.45467 0.093810 -0.0544
Abbildung 13 zeigt das zugehorige Interpolationspolynom sowie die skalierten Lagrange-
Polynome yiL(3)i .
Satz 8.3 (Eindeutigkeit der Polynominterpolation)Zu gegebenen paarweise verschiedenen Stutzstellen x0, . . . , xn gibt es genau ein Polynom vomGrad n mit
p(xi) = yi i = 0, . . . , n, yi ∈ R
Beweis:
86

-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0 2 4 6 8 10
y
x
py0*L0y1*L1y2*L2y3*L3Daten
Abbildung 13: Interpolationspolynom zur Wertetabelle aus Beispiel 8.2.
1. Kurze Variante: p =n∑i=0
yi L(n)i (xi) interpoliert die gegebenen Werte. Da die L
(n)i eine
Basis von Pn bilden, ist diese Darstellung eindeutig.
2. p =n∑i=0
yi L(n)i (xi) zeigt konstruktiv die Existenz des Interpolationspolynoms.
Eindeutigkeit: Angenommen es gibt zwei verschiedene Polynome p1, p2 mit p1 6= p2, aberp1(xi) = p2(xi) = yi i = 0, . . . , n.
p := p1 − p2 ∈ Pn (Differenzpolynom) erfullt p(xi) = 0 i = 0, . . . , n, hat also n + 1Nullstellen ⇒ p ≡ 0 wegen des
Satz von Rolle: u(x) sei auf [a, b] stetig und auf ]a, b[ differenzierbar sowie u(a) =u(b) = 0. Dann existiert mindestens ein x ∈]a, b[ mit u′(x) = 0
a b
Angenommen p sei nicht das Nullpolynom, also p = αmxm+. . . mit 0 ≤ m ≤ n αm 6= 0.
Dann gilt:
p = p(0) = αmxm + . . . hat n+ 1 Nullstellen
p′ = p(1) = αmmxm−1 + . . . hat n Nullstellen (Satz v. Rolle)
p′′ = p(2) = αmm(m− 1)xm−2 + . . . hat n− 1 Nullstellen...
p(m) = αmm! hat n+ 1−m ≥ 1 Nullstellen (da m ≤ n)
Dies geht nur fur αm = 0 im Widerspruch zur Annahme!
87

-3
-2
-1
0
1
2
3
4
5
6
7
0 0.2 0.4 0.6 0.8 1
y
x
Lagrange Polynome mit steigendem Grad
i=2, n=4i=3, n=6i=4, n=8
i=5, n=10
-200
-150
-100
-50
0
50
100
0 0.2 0.4 0.6 0.8 1
y
x
Lagrange Polynome mit steigendem Grad
i=5, n=10i=6, n=12i=7, n=14i=8, n=16
Abbildung 14: Die Lagrange-Polynome L(n)n/2 fur n = 4, 6, 8, 10, 12, 14, 16.
Anmerkung 8.4 (Konditionierung der Lagrange-Interpolation)p(x,y) bezeichne das Interpolationspolynom zu den Ordinatenwerten y = (y0, . . . , yn)T und
festen Abszissenwerten x = (x0, . . . , xn)T .
p(x,y +∆y)− p(x,y)
p(x,y)=
∑ni=0 (yi +∆yi) L
(n)i (x)−∑n
i=0 yi L(n)i (x)
p(x,y)
=
n∑
i=0
L(n)i (x) yip(x,y)︸ ︷︷ ︸
Verstarkungs-faktor
· ∆yiyi︸︷︷︸
relativerEingabefehler
Bei steigendem Polynomgrad n wachsen die Lagrange-Polynome L(n)i (x) weit weg von der
Stutzstelle x mit L(n)i (x) = 1 sehr stark an, dann ist die Interpolationsaufgabe schlecht kondi-
tioniert!. Abbildung 14 zeigt dies am Beispiel des Lagrange-Polynoms L(n)n/2 mit einer steigen-
den Anzahl aquidistanter Stutzstellen auf dem Interval [0, 1]. Am Rand wachst der Maximal-/Minimalwert des Lagrange-Polynoms exponentiell.
8.2.2 Newton-Polynome
Nachteil der Lagrange-Polynome:
• Hinzufugen einer neuen Stutzstelle andert alle bisherigen Basispolynome.
• Eignet sich nicht zur “inkrementellen” Erstellung des Interpolationspolynoms.
Besser ist die Newton-Darstellung mit den Basispolynomen:
N0(x) = 1
Ni(x) =i−1∏
j=0
(x− xj) fur i = 1, . . . , n.
88

1. Ni(x) ist ein Polynom vom Grad i.
2. N0, . . . , Nn bilden eine Basis von Pn
3. Ni(xk) = 0 fur alle i > k, denn (x− xk) kommt in Ni fur i > k vor.
Dies erlaubt die gestaffelte Berechnung:
p(xk) =n∑
i=0
aiNi(xk) =k∑
i=0
aiNi(xk)!
= yk k = 0, . . . , n
also
k = 0 a0 = y0
k > 0 ak =1
Nk(xk)
(yk −
k−1∑
i=0
aiNi(xk)
)
Alternativ lassen sich die Koeffizienten auch folgendermaßen berechnen:
Satz 8.5 (Dividierte Differenzen)Man definiert rekursiv die sogenannten
”dividierten Differenzen”.
∀ i = 0, . . . , n y[xi] := yi (die n+ 1 Werte an den Stutzstellen)
∀ k = 1, . . . , n− i y[ xi, . . . xi+k︸ ︷︷ ︸k+1 Argumente
] :=y[
k Argumente︷ ︸︸ ︷xi+1, . . . , xi+k]− y[
k Argumente︷ ︸︸ ︷xi, . . . , xi+k−1]
xi+k − xi
Dann gilt:
p(x) =n∑
i=0
y[x0, . . . , xi︸ ︷︷ ︸=ai
]Ni(x)
Beweis: Rannacher, Numerische Mathematik 0, Satz 2.2.
Die dividierten Differenzen ordnet man in folgendem Tableau an:
y0 =:
a0︷ ︸︸ ︷y[x0] →
a1︷ ︸︸ ︷y[x0, x1] →
a2︷ ︸︸ ︷y[x0, x1, x2] . . .
an−1︷ ︸︸ ︷y[x0, . . . , xn−1] →
an︷ ︸︸ ︷y[x0, . . . , xn]
y1 =: y[x1] → y[x1, x2] →
y[x1, x2, x3] . . . y[x1, . . . , xn]
y2 =: y[x2] → y[x2, x3] →
...
... → y[xn−2xn−1, xn]
... → y[xn−1, xn]
yn =: y[xn]
Diese Berechnung der Koeffizienten der Newton-Darstellung ist numerisch stabiler.Effiziente und numerisch stabile Auswertung des Interpolationspolynoms an einzelnen Stellen
(also p(x) an einer Stelle x) gelingt mit der Methode von Neville.siehe: Rannacher, Numerische Mathematik 0, Seite 27.
89

8.2.3 Interpolationsfehler
yi = f(xi) i = 0, . . . , n sei die Auswertung einer Funktion f an n+1 paarweise verschiedenenStutzstellen. p(x) sei das Polynom vom Grad n welches (xi, yi), i = 0, . . . , n interpoliert.
Die Differenz f(x)− p(x) erfullt
f(x)− p(x) =
0 x = xi
? x 6= xi
Frage: Wie groß kann die Differenz werden?
Satz 8.6Sei f(x) ∈ Cn+1 auf [a, b] und sei a ≤ x0 < x1 < · · · < xn ≤ b (lasst auch Extrapolation
zu). Dann gibt es zu jedem x ∈ [a, b] ein ξx ∈ ]x0, . . . , xn, x[ (=kleinstes Intervall, welches allePunkte enthalt), so dass
f(x)− p(x) =f (n+1)(ξx)
(n+ 1)!
n∏
j=0
(x− xj).
Beweis:
x ∈ x0, . . . , xn liefertn∏j=0
(x − xj) = 0, somit ist ξx beliebig wahlbar. Sei also x ∈ [a, b] \
x0, . . . , xn. Zu diesem x definiere die Funktion
Fx(t) = f(t)− p(t)− f(x)− p(x)
l(x)︸ ︷︷ ︸eine Zahl
abhangig von x
l(t) mit l(t) =n∏
j=0
(t− xj)
Fx(t) hat die n+ 2 Nullstellen x0, . . . , xn︸ ︷︷ ︸n+1
, x, denn
i = 0, . . . , n : Fx(xi) = f(xi)− p(xi)︸ ︷︷ ︸=0
−f(x)− p(x)
l(x)l(xi)︸︷︷︸
=0
= 0
x : Fx(x) = f(x)− p(x)− f(x)− p(x)
l(x)
l(x) = 0
Satz von Rolle:Fx(t) hat n+ 2 Nullstellen (mindestens) (nach t ableiten!)
F(1)x (t) hat n+ 1 Nullstellen (mindestens)
F(n+1)x (t) hat 1 Nullstelle (mindestens)
Zusatzlich gilt: Diese Nullstellen sind in (x0, . . . , xn, x).
Nenne die Nullstelle von F(n+1)x (t) ξx ∈ (x0, . . . , xn, x) und es gilt:
F (n+1)x (ξx) = f (n+1)(ξx)− p(n+1)(ξx)︸ ︷︷ ︸
=0, da pvom Grad n
−f(x)− p(x)
l(x)l(n+1)(ξx)︸ ︷︷ ︸l(t)=tn+1+...
n+1 mal differenzierenl(n+1)(t)=(n+1)!
= f (n+1)(ξx)− f(x)− p(x)
l(x)(n+ 1)!
!= 0
90

Auflosen nach f(x)− p(x) liefert die Behauptung.
Diskussion des InterpolationsfehlersBetrag bilden:
|f(x)− p(x)| ≤ |f(n+1)(ξx)|(n+ 1)!
n∏
j=0
|x− xj | fur ein ξx.
Die Stutzstellen seien aquidistant gewahlt: |xi − xi+1| = h und x0 ≤ x ≤ xn:l sei die Anzahl der Punkte links von x auf dem Zahlenstrahl, r die Anzahl der Punkte rechts
von x ⇒ l + r = n+ 1 (Gesamtzahl der Punkte) und damit
n∏
j=0
|x− xj | ≤ lh · · · 2h · 1h︸ ︷︷ ︸links von x
· 1h · 2h · · · rh︸ ︷︷ ︸rechts von x
= l! r! hn+1
also
|f(x)− p(x)| ≤ |f (n+1)(ξx)| l! r!
(n+ 1)!︸ ︷︷ ︸≤1 da
l+r=n+1
hn+1
Fur |f (n+1)| beschrankt und n→∞ geht |f(x)− p(x)| → 0.Allerdings sind die hoheren Ableitungen auch einfacherer Funktionen fur n → ∞ oft nicht
beschrankt, sondern wachsen sehr schnell.Runges Gegenbeispiel (Rannacher, Numerische Mathematik 0, S. 32):
f(x) =1
1 + x2|f (n+1)(x)| ≈ 2n n!O
(1
|x|n+2
)
Anmerkung 8.7Approximationssatz von Weierstrass: Jede Funktion f ∈ C[a, b] kann beliebig gut gleichmaßigauf [a, b] mit Polynomen approximiert werden. Obige Behauptung ist kein Widerspruch, denn:
• Approximation muss nicht durch Interpolation erfolgen (Der Beweis nutzt sogenannteBernstein-Polynome).
• Bei nicht aquidistanter Wahl der Stutzstellen wird es auch schon sehr viel besser.
Anmerkung 8.8Allgemein gilt fur Methoden hoher (Polynom-)Ordnung, dass entsprechende Differenzierbarkeitvon f vorliegen muss.
Beispiel 8.9
Beim Sinus bleiben auch hohere Ableitungen immer beschrankt, daher lasst er sich auch beiaquidistanten Stutzstellen sehr gut mit Polynomen interpolieren. Abbildung 15 (links) zeigtdies fur sin(2x). Ganz anders ist dies bei der rationalen Funktion 1
1+x2(Abbildung 15, rechts).
Hier treten Schwingungen auf, die mit steigendem Polynomgrad zunehmen.
91

-2.5
-2
-1.5
-1
-0.5
0
0.5
1
1.5
2
2.5
0 1 2 3 4 5 6
y
x
Polynominterpolation von f(x) = sin(2x)
sin(2*x)n=4n=5
n=12-4
-3.5
-3
-2.5
-2
-1.5
-1
-0.5
0
0.5
1
-4 -2 0 2 4
y
x
Polynominterpolation von f(x) = 1/(1+x*x)
1.0/(1.0+x*x)n=4n=8
n=12
Abbildung 15: Interpolation der Funktionen sin(2x) (oben) und 11+x2
(unten) mit aquidistanten
Stutzstellen und verschiedenen Polynomgraden.
8.2.4 Horner Schema
Der Vollstandigkeit halber sei noch die numerisch stabile Auswertung von Polynomen erwahnt.
Fur n = 3 konnte man den Wert des Polynoms an der Stelle x folgendermaßen ausrechnen:
p(x) = a3x3 + a2x
2 + a1x+ a0
= (a3x+ a2)x2 + a1x+ a0
= ((a3x+ a2)x+ a1)x+ a0 .
Allgemein erhalten wir die folgende Rekursion zur Bestimmung von p(x)
bn = an
bk = ak + xbk+1 k = n− 1, . . . , 0
p(x) = b0.
Dies nennt man das Horner2 Schema.
8.3 Anwendungen der Polynominterpolation
8.3.1 Numerische Differentation
Problem: Berechne die Ableitung (der Ordnung k) einer tabellarisch gegebenen Funktionoder einer im Rechner als Programm gegebenen Funktion.
Idee: Erstelle Interpolationspolynom zu bestimmten Stutzstellen, leite dieses ab und wertees aus.
Zunachst: Ableitungsordnung = Polynomgrad
2William George Horner, 1786-1837, brit. Mathematiker.
92

Lagrange-Polynome:
L(n)i (x) =
n∏
j=0j 6=i
(x− xj)(xi − xj)
=
n∏
j=0j 6=i
1
(xi − xj)
︸ ︷︷ ︸=:λi∈R
xn + αn−1xn−1 + · · ·+ α0
n-maliges differenzieren liefert:
dn
dxnL
(n)i (x) = λin! (konstant, unabhangig von x)
Damit gilt fur die n-te Ableitung eines Interpolationspolynoms vom Grad n:
dn
dxn
(n∑
i=0
yiL(n)i (x)
)
︸ ︷︷ ︸p(x)
= n!
n∑
i=0
yiλi. (unabhangig von x)
Eine Aussage uber den Fehler liefert:
Satz 8.10Sei f ∈ Cn[a, b] und a = x0 < x1 < · · · < xn = b. Dann gibt es ein ξ ∈]a, b[, so dass furdie durch Interpolation mit einem Polynom vom Grad n an den Stutzstellen xi bestimmte n-teAbleitung mit den Koeffizienten λi =
∏nj=0j 6=i
(xi − xj)−1 gilt:
f (n)(ξ) = n!n∑
i=0
yiλi
Beweisskizze: n-malige Anwendung des Satzes von Rolle auf g(x) = f(x)− p(x).
Damit muss sich die Ableitung beliebig gut annahern lassen, wenn die Stutzstellen immer naheran die Stelle x heranrucken, an der die Ableitung bestimmt werden soll.
Um einfachere Formeln zu bekommen verwenden wir nun aquidistante Stutzstellen, d.h.
xi = x0 + ih, 0 ≤ i ≤ n.
Damit ist
λi =1
(xi − x0)︸ ︷︷ ︸ih
. . . (xi − xi−1)︸ ︷︷ ︸h︸ ︷︷ ︸
i Faktoren positiv
(xi − xi+1)︸ ︷︷ ︸−h
. . . (xi − xn)︸ ︷︷ ︸x0+ih−x0−nh=−(n−i)h︸ ︷︷ ︸
n−i Faktoren negativ
=1
hn (−1)n−i i! (n− i)! =(−1)n−i
hn n!
(n
i
)
︸︷︷︸Binominal-koeffizient)
93

und damit
f (n)(x) ≈ dn
dxn
(n∑
i=0
yiL(n)i
)=
1
hn
n∑
i=0
(−1)n−i(n
i
)yi.
Insbesondere:
f (1)(x) ≈ y1 − y0
h
f (2)(x) ≈ y2 − 2y1 + y0
h2
f (3)(x) ≈ y3 − 3y2 + 3y1 − y0
h3
Bisher: n-te Ableitung aus Polynom vom Grad n
Alternativ: m-te Ableitung aus Polynom vom Grad n > m Der Naherungswert hangt dannvon der Auswertestelle x ab.
Beispiel: m = 1, n = 2. Aquidistante Stutzstellen x0, x1 = x0 + h, x2 = x0 + 2h.
⇒ p′(x1) =y2 − y0
2h ”zentraler Differenzenquotient“
Taylorreihenentwicklung zeigt:
f ′(x) =f(x+ h)− f(x− h)
2h+O(h2) fur f ∈ C3
f ′′(x) =f(x+ h)− 2f(x) + f(x− h)
h2+O(h2) fur f ∈ C4
Beispiel 8.11Wir wollen die zweite Ableitung von f(x) = sinh(x) fur x = 0.6 mit dem zweiten Differenzen-quotient ermitteln:
d2
dx2sinh(x) ≈ sinh(x+ h)− 2 sinh(x) + sinh(x− h)
h2
Es gilt:
sinh(x) =1
2(ex − e−x),
d
dxsinh = cosh =
1
2(ex + e−x),
d2
dx2sinh(x) = sinh(x).
Mit doppelter Genauigkeit erhalt man den Wert
sinh(0.6) = 6, 366535821482 · 10−1.
Dagegen liefert die numerische Differentiation die folgende Tabelle:
94

h Differenzenquotient
1 · 10−1 6.371 ·10−1
1 · 10−2 6.3665888 ·10−1
1 · 10−3 6.366536352 ·10−1
1 · 10−4 6.3665358540 ·10−1 Ausloschung1 · 10−5 6.3665017 ·10−1 Ausloschung1 · 10−6 6.3671 ·10−1 Ausloschung...1 · 10−10 1.1102 ·104 vollig falsch !
Anmerkung 8.12• Numerische Differentation ist sehr anfallig gegenuber Rundungsfehlern.
• Mogliche Abhilfe bietet die”Extrapolation“.
• Eine gute Schrittweite sollte man proportional zur Wurzel der Maschinengenauigkeit epswahlen, z.B.
∆x =√
epsx+√eps.
8.3.2 Extrapolation zum Limes
Eine Große a(h) sei im Rechner fur h > 0 berechenbar, nicht jedoch fur h = 0. Man mochte
a(0) = limh→0
a(h)
mit guter Genauigkeit berechnen.
Beispiel 8.131.
a(0) = limx→0
cos(x)− 1
sin(x)(= 0)
2. Numerische Differentiation
f ′(x) = limh→0
f(x+ h)− f(x)
h(fur kleine h tritt Ausloschung ein)
3. Numerische Integration:
ˆ b
af(x)dx = lim
N→∞
N∑
i=1
b− aN
f
(a+ (i− 1/2) · b− a
N
)= lim
N→∞
N∑
i=1
h f
(a+
2i− 1
2h
)mit h :=
b− aN
h→ 0 nicht moglich wegen Aufwand →∞.
4. Numerische Losung des Anfangswertproblems:
y′(t) = f(t, y(t)), y(0) = y0
berechne y(T ) ≈ yN mit yn = yn+1 + hf(t, yn−1) mit h :=T
N
h→ 0 bedeutet N →∞ und damit Aufwand →∞.
95

Idee der Extrapolation:Zu h0 > h1 > · · · > hn > 0 bestimme Interpolationspolynom vom Grad n sodass
p(hi) = a(hi) i = 0, . . . , n
und berechne a(0) ≈ p(0) (Extrapolation, da 0 /∈ [h0, hn])
Beispiel 8.14
a(h) =cos(h)− 1
sin(h)
h0 = 18 a(h0) = −6.258151 · 10−2
h1 = 116 a(h1) = −3.126018 · 10−2
h2 = 132 a(h2) = −1.562627 · 10−2
halbiert sich jeweils,da h halbiert
wird
und bei Extrapolation mit einem Polynom vom Grad 2:
a(0) ≈ p2(0) = −1.02 · 10−5
also sehr viel besser!
Warum funktioniert das so gut?
Die Funktion a(x) sei n + 1-mal stetig differenzierbar in einer genugend großen Umgebungvon x = 0. Dann gibt es zu jedem h > 0 (in dieser Umgebung) ein ξh ∈ [0, h], so dass:(Taylorreihe):
a(h)︸︷︷︸Fur h>0
numerischberechenbar
= a(0 + h) = a(0) + a′(0)h+a′′(0)
2h2 + · · ·+ a(n)(0)
n!hn
︸ ︷︷ ︸Polynom in h vom Grad n
Koeffizienten hangen NICHT von h ab!
+a(n+1)(ξh)
(n+ 1)!︸ ︷︷ ︸abhangig
von h!
hn+1
Idee: Fur verschiedene hi bilde Linearkombinationen:
n∑
i=0
cia(hi) =n∑
i=0
ci
n∑
j=0
ajhji
+
n∑
i=0
cia(n+1)(ξhi)
(n+ 1)!hn+1i
=n∑
j=0
aj
(n∑
i=0
cihji
)+ Fehler
!= a(0) + Fehler (klein wegen hn+1
i ),
wahle die ci so, dass
n∑
i=0
cihji =
1 j = 0
0 sonst
96

Als Gleichungssystem lauten die Bestimmungsgleichungen:
VT c = e0
mit e0 = (1, 0, . . . , 0)T
und V = V[h0, . . . , hn] der Vandermonde-Matrix
Die Auswertung mit diesen Koeffizienten ist dann:
A :=n∑
i=0
ci a(hi)︸ ︷︷ ︸=yi
=(V−Te0︸ ︷︷ ︸
=c
)Ty = eT0 V−1y.
Fur den Fehler gilt dann:
|A− a(0)| =∣∣∣∣∣n∑
i=0
cia(n+1)(ξi)
(n+ 1)!hn+1i
∣∣∣∣∣
≤︸︷︷︸wahlehi:=hr
i
z.B. r=1/2
n∑
i=0
∥∥V−Te0
∥∥∞|a(n+1)(ξi)|
(n+ 1)!hn+1ri(n+1)
≤∥∥V−T
∥∥∞ ‖e0‖∞︸ ︷︷ ︸
=1
max0≤i≤n
|a(n+1)(ξi)| ·hn+1
(n+ 1)!
n∑
i=0
ri(n+1)
︸ ︷︷ ︸=rn+1+1
(geom. Reihe)
≤ ‖V−T ‖∞ max0≤i≤n
|a(n+1)(ξi)|︸ ︷︷ ︸beschrankt
hn+1
(n+ 1)!(1 + rn+1)︸ ︷︷ ︸≤ 5
4fur r≤ 1
2∧n≥1
Nun betrachte das Interpolationspolynom
p(hi) =n∑
j=0
bjhji
!= a(hi) = yi
und somit Vb = y fur dessen Koeffizienten. Auswerten an der Stelle Null bedeutet
p(0) = b0 = eT0 b = eT0 V−1y = A von oben!
Die oben beschriebene Elimination der Fehlerterme entspricht also genau der Extrapolations-methode!
Es geht sogar noch besser:
Beispiel 8.15
Betrachte Naherung fur f ′(x) mit zentralem Differenzenquotienten und geradem Polynom-grad 2n:
a(h) :=f(x+ h)− f(x− h)
2h
97

f(x+ h) = f(x) + hf (1)(x) +h2
2f (2)(x) +
h3
3!f (3)(x) + · · ·+ h2n+1
(2n+ 1)!f (2n+1)(x) +
h2n+2
(2n+ 2)!f (2n+2)(ξ+)
f(x− h) = f(x)− hf (1)(x) +h2
2f (2)(x)− h3
3!f (3)(x) + · · · − h2n+1
(2n+ 1)!f (2n+1)(x) +
h2n+2
(2n+ 2)!f (2n+2)(ξ−)
f(x+ h)− f(x− h) = 2hf ′(x) +2h3
3!f (3)(x) + · · ·+ 2h2n+1
(2n+ 1)!f (2n+1)(x) +
h2n+2
(2n+ 2)![f (2n+2)(ξ+)+f (2n+2))(ξ−)]
a(h) = f ′(x) +h2
3!f (3)(x) + · · ·+ h2n
(2n+ 1)!f (2n+1)(x) +
h2n+1
(2n+ 2)!
[f (2n+2)(ξ+) + f (2n+2)(ξ−)
]
Da alle ungeraden Terme in der Fehlerdarstellung”von selbst“ wegfallen, kann man mit der
gleichen Anzahl von Auswertungen doppelt so viele Fehlerterme eliminieren! Dazu wahlt manein Interpolationspolynom in h2
i
Naturlich muss f dazu entsprechend oft differenzierbar sein.
8.4 Splines
Bis jetzt:
• Polynomgrad + 1 = Anzahl Stutzstellen
• Viele Stutzstellen ⇒ Großer Polynomgrad ⇒ eventuell starke Abweichungen zwischenden Stutzstellen
Idee: Nehme stuckweise Polynome niedrigen Grades
Definition 8.16Sei X = (x0, x1, . . . , xn) mit a = x0 < x1 < xn = b eine Zerlegung des Intervalles [a, b] und seim ∈ N. Die Menge
Sm(X) =s ∈ Cm−1[a, b] : s|[xi,xi+1] ∈ Pm([xi, xi+1]), 0 ≤ i < n
heißt Spline-Raum vom Grad m uber der Zerlegung X
Beispiel 8.17S1(X) bedeutet:
• s ∈ S1(X) ist Polynom vom Grad 1 auf jedem Teilintervall [xi, xi+1]
• S1(X) ⊂ C0[a, b], also s ∈ S1(X) stetig
• Stetigkeit ⇒ s ∈ S1(X) ist eindeutig durch Werte in den Stutzstellen beschrieben.
DimS1(X) = DimX.
98

Kubische Splines
In der Praxis ist S3(X) sehr beliebt. S3(X) heißt Raum der kubischen Splines.
Geschichte:
”Straklatte“ (englisch spline) zur Konstruktion glatter Kurven im Schiffs- und Flugzeugbau.
Nagel
biegt sich unter”Energieminimierung“
dunnes Balsaholz
ˆ b
a
|y′′(t)|21 + |y′(t)|2 dt
︸ ︷︷ ︸totale Krummung
|y′(t)|1≈
ˆ b
a|y′′(t)|2 dt→ min
Konstruktion s ∈ S3(X). Die Funktion setzt sich stuckweise aus n Polynomen zusammen.
s(x) =
pi(x) x ∈ [xi−1, xi[, i ∈ 1, . . . , npn(x) x = xn
Fur die Polynome pi gelten folgende Bedingungen:
a) Interpolationsbedingung (Stetigkeit):
i = 1, . . . , n :pi(xi−1) = yi−1
pi(xi) = yi
2n Bedingungen
b) Stetigkeit der ersten und zweiten Ableitung an den inneren Punkten:
i = 1, . . . , n− 1:p′i(xi) = p′i+1(xi)p′′i (xi) = p′′i+1(xi)
2(n− 1) = 2n− 2 Bedingungen
⇒ zusammen 4n− 2 Bedingungen
Pro Polynom pi (vom Grad 3) hat man 4, also insgesamt 4n Freiheitsgrade.
Die fehlenden zwei Bedingungen erhalt man durch Randbedingungen an den Stellen x0
und xn.
99

c) Randbedingungen. Eine der folgenden Varianten:
(i) Naturliche Randbedingungen: p′′1(x0) = 0 p′′n(xn) = 0
(ii) Hermite-Randbedingungen: p′1(x0) = f ′(x0) p′n(xn) = f ′(xn)
(iii) Periodische Randbedingungen: p′1(x0) = p′n(xn) p′′1(x0) = p′′n(xn)
Wir behandeln im folgenden nur die naturlichen Randbedingungen.
Satz 8.18 (Berechnung kubischer Splines)Wir schreiben die Teilpolynome des Splines fur x ∈ [xi−1, xi[ in der Form
pi(x) = a(i)0 + a
(i)1 (x− xi) + a
(i)2 (x− xi)2 + a
(i)3 (x− xi)3 i = 1, . . . , n
Die a(i)2 sind dann die Losung des linearen Gleichungssystems der Dimension n− 1:
hia(i−1)2 + 2(hi + hi+1)a
(i)2 + hi+1a
(i+1)2 = 3
(yi+1 − yihi+1
− yi − yi−1
hi
), i = 1, . . . , n− 1,
(8.1)
wobei a(0)2 = a
(n)2 = 0 (naturliche Randbedingung!) und hi := xi − xi−1.
Die restlichen Koeffizienten ergeben sich zu:
a(i)0 = yi (8.2)
a(i)1 =
yi − yi−1
hi+hi3
(2a
(i)2 + a
(i−1)2
)(8.3)
a(i)3 =
a(i)2 − a
(i−1)2
3hi(8.4)
Beweis:
(i) Berechne Ableitungen der Teilpolynome
p′i(x) = a(i)1 + 2a
(i)2 (x− xi) + 3a
(i)3 (x− xi)2 (8.5)
p′′i (x) = 2a(i)2 + 6a
(i)3 (x− xi) (8.6)
(ii) Interpolationsbedingung nutzen: Einsetzen von xi, yi:
yi = pi(xi) = a(i)0 ⇒ a
(i)0 = yi i = 1, . . . , n. (8.7)
Das ist (8.2).
Einsetzen von xi−1:
yi−1 = pi(xi−1) = a(i)0︸︷︷︸
=yi
+a(i)1 (−hi) + a
(i)2 h2
i + a(i)3 (−h3
i ) i = 1, . . . , n
⇔ yi−1 − yi = −hia(i)1 + h2
i a(i)2 − h3
i a(i)3 (8.8)
100

(iii) Randbedingungen einsetzen. Wir behandeln nur naturliche:
0 = p′′1(x0) = 2a(1)2 − 6a
(1)3 h1 (8.9)
0 = p′′n(xn) = 2a(n)2 ⇒ a
(n)2 = 0 (8.10)
(iv) Stetigkeit der ersten Ableitung
p′i(xi) = p′i+1(xi) i = 1, . . . , n− 1
⇔ a(i)1 = a
(i+1)1 − 2a
(i+1)2 hi+1 + 3a
(i+1)3 h2
i+1 (8.11)
(v) Stetigkeit der zweiten Ableitung
p′′i (xi) = p′′i+1(xi) i = 1, . . . , n− 1
⇔ 2a(i)2 = 2a
(i+1)2 − 6a
(i+1)3 hi+1 (8.12)
(vi) Drucke a(i)3 durch a
(i)2 aus. Fur i = 2, . . . , n lose (8.12) nach a
(i+1)3 auf:
a(i+1)3 =
a(i+1)2 − a(i)
2
3hi+1i = 1, . . . , n− 1
umnummerieren:
⇔ a(i)3 =
a(i)2 − a
(i−1)2
3hii = 2, . . . , n− 1 (8.13)
Fur i = 1 erhalt man das Gleiche aus (8.9), damit gilt die Formel also fur i = 1, . . . , n.
Das ist (8.4).
(vii) a(i)1 durch a
(i)2 ausdrucken. Dazu lose (8.8) nach a
(i)1 auf und setze (8.13) ein:
a(i)1 =
yi − yi−1
hi+ hia
(i)2 − h2
i a(i)3 i = 1, . . . , n
(8.13)=
yi − yi−1
hi+ hia
(i)2 − h2
i
(a
(i)2 − a
(i−1)2
3hi
)
a(i)1 =
yi − yi−1
hi+hi3
(2a
(i)2 + a
(i−1)2
)i = 1, . . . , n
Das ist (8.3).
(viii) Nun setze a(i)1 und a
(i)3 in die verbleibende Gleichung (8.11) ein:
yi − yi−1
hi+hi3
(2a
(i)2 + a
(i−1)2
)
=yi+1 − yihi+1
+hi+1
3
(2a
(i+1)2 + a
(i)2
)− 2a
(i+1)2 hi+1 + 3h2
i+1
(a
(i+1)2 − a(i)
2
3hi+1
)i = 1, . . . , n− 1
⇐⇒ hia(i−1)2 + a
(i)2 (2hi − hi+1 + 3hi+1) + a
(i+1)2 (−2hi+1 + 6hi+1 − 3hi+1)
= 3
(yi+1 − yihi+1
− yi − yi−1
hi
)i = 1, . . . , n− 1
101

-2
0
2
4
6
8
10
0 0.2 0.4 0.6 0.8 1
y
x
DatenPolynom Grad 6
LinearKubischer Spline
Abbildung 16: Vergleich der Interpolation mit Polynomen, stuckweise linearen Funktionen undkubischen Splines.
⇐⇒ hia(i+1)2 + 2 (hi + hi+1) a
(i)2 + hi+1a
(i+1)2 = 3
(yi+1 − yihi+1
− yi − yi−1
hi
)i = 1, . . . , n−1
Und das ist (8.1). Beachte, dass in (iii) und (vi) a(0)2 = a
(n)2 = 0 gesetzt wurde (naturliche
Randbedingungen).
Anmerkung 8.19 (Zur Losung des Gleichungssystems)• Das Gleichungssystem ist symmetrisch und strikt diagonaldominant⇒ stabile LR-Zerlegung
ohne Pivotisierung.
• Das LGS ist tridiagonal, daher verwende Thomas-Algorithmus mit O(n) Aufwand ⇒sehr schnell.
Beispiel 8.20Es sei folgende Wertetabelle zu interpolieren:
x 0 0.1 0.2 0.25 0.5 0.7 1.0y 1 -1 -1 -0.5 0 0 5
Abbildung 16 zeigt die Interpolation mit Polynomen, stuckweise linearen Funktionen undkubischen Splines (mit naturlichen Randbedigungen) anhand eines Beispiels. Deutlich zu er-kennen ist der starke
”Uberschwinger“ bei der Polynominterpolation.
102

Satz 8.21 (Fehlerabschatzung)Sei f ∈ C4[a, b]. Erfullt der kubische Spline Hermite-Randbedingungen so gilt
maxa≤x≤b
|f(x)− s(x)| ≤ h4 maxa≤x≤b
|f (4)(x)|
fur
h := max1≤i≤n
|xi − xi−1|
Beweis: Schaback/Wendland: Numerische Mathematik, 5. Auflage, Satz 11.13.Selbst unter (wesentlich) schwacheren Voraussetzungen konvergiert die Spline-Interpolation
gleichmaßig gegen f .
Beispiel 8.22 (Zur Konvergenzordnung stuckweiser Polynome)Wir betrachten die Interpolation der folgenden drei Funktionen (Abbildung 17):
f1(x) = exp(−x2) in [−10, 10], (8.14)
f2(x) =
cos2(x) |x| < π
20 |x| ≥ π
2
in [−π, π], (8.15)
f3(x) =
−1 x < 1
2+1 x ≥ 1
2
in [0, 1], (8.16)
mittels Polynomen, S1,0h und S3,2
h (mit naturlichen Randbedingungen, alle Funktionen fi erfullen(naherungsweise) f ′′i = 0 an den Randpunkten).
0
0.2
0.4
0.6
0.8
1
-10 -5 0 5 10
y
x
f1(x)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
-4 -3 -2 -1 0 1 2 3 4
y
x
f2(x)
-1
-0.5
0
0.5
1
0 0.2 0.4 0.6 0.8 1
y
x
f3(x)
Abbildung 17: Die Funktionen f1(x) (links), f2(x) (Mitte) und f3(x) (rechts)
Die Abbildung 18 zeigt die Interpolation der Funktion f1(x).Die Abbildung 19 zeigt die Interpolation der Funktion f2(x).Die Abbildung 20 zeigt die Interpolation der Funktion f3(x).Wir lernen:
• Interpolation mit Polynomen steigenden Grades an aquidistanten Stutzstellen schlagt inallen Fallen fehl, d. h. der Interpolationsfehler steigt mit dem Grad an.
• Kubische Splines konvergieren und liefern einen glatten Verlauf. Allerdings kommt es zumoglicherweise
”unphysikalischen“ Unter- bzw. Uberschwingern. Diese sind aber im Falle
von f3(x) um die Sprungstelle lokalisiert.
• Stuckweise lineare Funktionen haben diesen Defekt nicht.
103

Wir wollen nun den Interpolationsfehler noch experimentell bestimmen.Fehler bei Interpolation der Funktion f1(x) = e−x
2:
n S1,0h S3,2
h pn
4 6.045 · 10−1 7.420 · 10−1 8.038 · 10−1
6 4.447 · 10−1 5.612 · 10−1 9.999 · 10−1
8 3.002 · 10−1 3.918 · 10−1 2.31110 1.774 · 10−1 2.464 · 10−1 5.94916 1.060 · 10−1 2.753 · 10−2
32 6.946 · 10−2 7.083 · 10−3
64 2.241 · 10−2 3.316 · 10−4
128 5.974 · 10−3 1.918 · 10−5
256 1.517 · 10−3 1.173 · 10−6
512 3.809 · 10−4 7.289 · 10−8
1024 9.533 · 10−5 4.549 · 10−9
2048 2.383 · 10−5 2.842 · 10−10
Angegeben ist der maximale Fehler an einem Punkt. Polynome konvergieren nicht.Stuckweise linear konvergiert mit h2 (d. h. e2n/en = (1/2)2), kubische Splines mit h4 (d. h. e2n/en =
(1/2)4).In beiden Fallen gilt dies nur, wenn n genugend groß, man spricht von
”asymptotischer“
Konvergenz.
Fehler bei Interpolation der Funktion f2(x) =
cos2(x) x < π/2
0 x ≥ π/2:
n S1,0h S3,2
h
4 1.052 · 10−1 1.649 · 10−1
8 1.052 · 10−1 4.498 · 10−2
16 3.518 · 10−2 8.434 · 10−3
32 9.423 · 10−3 1.945 · 10−3
64 2.396 · 10−3 4.764 · 10−4
128 6.015 · 10−4 1.184 · 10−4
256 1.505 · 10−4 2.958 · 10−5
512 3.764 · 10−5 7.394 · 10−6
1024 9.412 · 10−6 1.848 · 10−6
In diesem Fall konvergiert der maximale Fehler auch im Falle kubischer Splines nur mit h2.Dies liegt daran, dass f ′′2 (x) unstetig am Punkt x = π/2 ist (springt von 2 auf 0).Die dritte Ableitung existiert nicht mehr.
Anmerkung 8.23 (Regel)Fur die Interpolation mit stuckweisen Polynomen merken wir uns:
• Je hoher der (abschnittsweise) Polynomgrad umso schneller konvergiert das Verfahren.Im allgemeinen erhalt man O(hk+1) Konvergenz fur Polynome vom Grad k.
• Dies gilt allerdings nur dann, wenn die zu interpolierende Funktion genugend oft diffe-renzierbar ist. Ist dies nicht der Fall so lohnt also auch die Verwendung von Polynomenhohen Grades nicht.
104

-2.5
-2
-1.5
-1
-0.5
0
0.5
1
-10 -5 0 5 10
y
x
f(x) = exp(-x*x), Polynom
exp(-x*x)n= 4n= 6n= 8
-0.2
0
0.2
0.4
0.6
0.8
1
-10 -5 0 5 10
y
x
f(x) = exp(-x*x), stueckweise linear
exp(-x*x)n= 4n= 8
n=16
-0.2
0
0.2
0.4
0.6
0.8
1
-10 -5 0 5 10
y
x
f(x) = exp(-x*x), kubischer Spline
exp(-x*x)n= 4n= 8
n=16
Abbildung 18: Interpolation der Funktion f1(x) mit Lagrange-Polynomen, stuckweise linearenFunktionen und kubischen Splines.
105

0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
-4 -3 -2 -1 0 1 2 3 4
y
x
f(x) = cos(x)*cos(x), stueckweise linear
n= 4n= 8
n=16n=16
-0.2
0
0.2
0.4
0.6
0.8
1
-4 -3 -2 -1 0 1 2 3 4
y
x
f(x) = cos(x)*cos(x), kubischer Spline
n= 4n= 8n=16n=16
Abbildung 19: Interpolation der Funktion f2(x) mit Lagrange-Polynomen, stuckweise linearenFunktionen und kubischen Splines.
106

-4
-2
0
2
4
6
8
0 0.2 0.4 0.6 0.8 1
y
x
Sprungfunktion, Polynom
n= 4n= 6n= 8
n=10
-1
-0.5
0
0.5
1
0 0.2 0.4 0.6 0.8 1
y
x
Sprungfunktion, stueckweise linear
n= 4n= 8
n=16n=32
-1
-0.5
0
0.5
1
0 0.2 0.4 0.6 0.8 1
y
x
Sprungfunktion, kubischer Spline
n= 4n= 8
n=16n=32
Abbildung 20: Interpolation der Funktion f3(x) mit Lagrange-Polynomen, stuckweise linearenFunktionen und kubischen Splines.
107


9 Trigonometrische Interpolation
9.1 Trigonometrische Polynome
Ziel: Interpolation periodischer Funktionen, d.h. es gebe ein ω ∈ R, ω > 0, sodass
f(x+ ω) = f(x) ∀x ∈ R
Statt Polynome nehme (periodische) trigonometrische Funktionen als Ausgangspunkt. Wirerhalten als Interpolationsfunktion:
tn(x) =a0
2+
m∑
k=1
(ak cos (kx) + bk sin (kx))
die sogenannte”trigonometrische Summe“. tn(x) ist 2π-periodisch. Durch Substitution x = 2πx
ωkonnen wir jede periodische Funktion mit Periode ω auf dieses Intervall abbilden.tn(x) hat 2m + 1 Parameter. Wir setzen als Abkurzung n := 2m und wahlen wieder
aquidistante Stutzstellen:
xk =2πk
n+ 1k = 0, . . . , n
Es zeigt sich: Die Interpolationsaufgabe tn(xk) = yk := f(xk) k = 0, . . . , n ist einfacherim Komplexen zu losen! Dazu betrachten wir das komplexe trigonometrische Polynom:
t∗n(x) =
m∑
k=0
ck eikx =
m∑
k=0
ck(eix)k.
Dabei ist i =√−1 die imaginare Einheit, ck ∈ C sind die komplexen Koeffizienten.
Die Beziehung zur trigonometrischen Summe ergibt sich mit φ = kx wegen:
eiφ = cosφ+ i sinφ φ ∈ R
Wir untersuchen zunachst die Eigenschaften der komplexen Exponentialfunktion:
Hilfssatz 9.1 (Komplexe Einheitswurzeln)Setze
wk := eixk = ei2πkn+1
fur alle k ∈ Z und gegebenes n ∈ N. wk ∈ C heißt”
k-te Einheitswurzel“ und hat folgendeEigenschaften:
a) wn+1k − 1 = 0 ∀ k ∈ Z,
d.h. die wk sind Losungen der Gleichung wn+1 − 1 = 0 in C.
Beweis:
wn+1k =
(ei
2πkn+1
)n+1= ei2πk = cos(2πk)︸ ︷︷ ︸
=1
+i sin(2πk)︸ ︷︷ ︸=0
= 1.
109

b) wjk = wkj ∀ j, k ∈ Z
Beweis:
wjk =(ei
2πkn+1
)j= ei
2πjkn+1 =
(ei
2πjn+1
)k= wkj
c) w−jk = w−kj ∀ j, k ∈ Z
Beweis wie b)
d) wjk = wj mod (n+1)k = wjk mod (n+1) = w
j mod (n+1)k mod (n+1) ∀j, k ∈ Z
zeige nur die erste Identitat Rest analog:
Sei j = r(n+ 1) + s mit 0 ≤ s ≤ n:
wjk = ei2πkn+1 = ei
2πk[r(n+1)+s]n+1 = e
i2πkr(n+1)
n+1︸ ︷︷ ︸1
·ei 2πksn+1 = wj mod (n+1)k
e)∑n
j=0wjk =
n+ 1 k mod (n+ 1) = 0
0 sonst
O.B.d.A. sei k < n+ 1 (sonst setze k = k mod (n+ 1), siehe d)).Sei k = 0 : wj0 = ei0 = 1 ∀ j, also
∑nj=0 1 = n+ 1.
k 6= 0: wk ist nach a) Losung von
wn+1 − 1 = (w − 1)(wn + wn−1 + · · ·+ w + 1
)= 0
Fur k 6= 0 ist wk 6= 1 als wk−1 6= 0 somit muss der zweite Faktor, also∑n
j=0wjk = 0 sein.
9.2 Diskrete Fourier-Transformation (DFT)
Satz 9.2 (Komplexe trigonometrische Interpolation)Zu gegebenen Zahlen y0, . . . , yn ∈ C gibt es genau eine Funktion der Gestalt
t∗n(x) =n∑
k=0
ckeikx
die den Interpolationsbedingungen
t∗n(xj) = yj j = 0, . . . , n xj =2πj
n+ 1
genugt. Die komplexen Koeffizienten sind bestimmt durch
ck =1
n+ 1
n∑
j=0
yj e−ijxk︸ ︷︷ ︸=e−i 2πjkn+1 =w−jk
∀ k = 0, . . . , n. (9.1)
110

Beweis: Mit der Abkurzung w = eix gilt
t∗n(x) =n∑
k=0
ckeikx =
n∑
k=0
ck( eix︸︷︷︸:=w
)k =n∑
k=0
ckwk = pn(w)
Da die Transformation w = eix auf [0, 2π[ eindeutig ist, entspricht jedem t∗n also ein komplexesPolynom vom Grad n mit den Interpolationsbedingungen
t∗n(xj) = pn(eixj ) = pn(wj) = yj j = 0, . . . , n
Da die Polynominterpolation zu paarweise verschiedenen Stutzstellen (auch im Komplexen)eindeutig ist, gibt es genau ein solches Polynom pn und damit t∗n.
Die Koeffizienten ck ergeben sich (wie bei reellen Polynomen) durch das Losen des linearenGleichungssystems
pn(eixj ) =
n∑
l=0
cl · (eixj )l =
n∑
l=0
clei 2πljn+1 =
n∑
l=0
clwlj
!= yj j = 0, . . . , n
mit n+ 1 (komplexen) Gleichungen fur die n+ 1 (komplexen) Unbekannten.In diesem Fall kann man das Gleichungssystem explizit auflosen. Fur ein k ∈ 0, . . . , n:
n∑
j=0
w−jk
(n∑
l=0
clwlj
)
︸ ︷︷ ︸=yj
=n∑
l=0
cl
n∑
j=0
wl−kj
︸ ︷︷ ︸n∑
j=0
wjl−k =
n+ 1 l − k = 0
0 l − k 6= 0
=n∑
j=0
w−jk yj
und damit
ck(n+ 1) =n∑
j=0
yjw−jk ⇐⇒ ck =
1
n+ 1
n∑
j=0
yje−ijxk .
Damit ist auch die reelle Interpolationsaufgabe gelost, wenn man yj ∈ R annimmt.
Satz 9.3 (Reelle Diskrete Fouriertransformation)Fur n ∈ N0 gibt es zu gegebenen reellen Zahlen y0, . . . , yn genau ein trigonometrisches Polynomder Form
tn(x) =a0
2+
m∑
k=1
(ak cos(kx) + bk sin(kx)) +θ
2am+1 cos((m+ 1)x)
mit tn(xj) = yj , j = 0, . . . , n, xj = 2πjn+1 , sowie
n gerade: θ = 0, m =n
2→ a0, . . . , am, b1, . . . , bm
n ungerade: θ = 1, m =n− 1
2→ a0, . . . , am+1, b1, . . . , bm
111

(n gerade: 2 · n2 + 1 = n+ 1, n ungerade: 2 · (n−1)2 + 2 = n+ 1).
Die Koeffizienten sind bestimmt durch:
ak =2
n+ 1
n∑
j=0
yj cos(jxk), bk =2
n+ 1
n∑
j=0
yj sin(jxk)
Beweis:[Skizze]Man bestimmt die Koeffizienten ck des komplexen trigonometrischen Polynoms zu reellen
Daten yj ∈ R und setzt dann
a0 = 2c0
ak = ck + cn+1−k k = 1, . . . ,m
bk = i(ck − cn+1−k) k = 1, . . . ,m
am+1 = 2cm+1 n = 2m+ 1(n ungerade)
Dann rechnet man nach, dass t∗n(xj) = tn(xj) = yj ∈ R.Wir wollen nachrechnen, dass die ak reell sind:
ak = ck + cn+1−k
=1
n+ 1
n∑
j=0
yj
(e−ijxk + e−ijxn+1−k︸ ︷︷ ︸
e−i 2πj(n+1)−k
n+1 =ei2πjkn+1 =eijxk
)
=1
n+ 1
n∑
j=0
yj(e−ijxk + eijxk
)
=1
n+ 1
n∑
j=0
yj
(cos(−jxk)︸ ︷︷ ︸
=cos(jxk)
+ i sin(−jxk)︸ ︷︷ ︸− sin(ixk)
+ cos(jxk) + i sin(jxk))
=1
n+ 1
n∑
j=0
yj2 cos(jxk)
Anmerkung 9.4Die trigonometrische Interpolation kann man als Naherung der Fourierreihe einer 2π-periodischenFunktion f : R→ R betrachten:
∞∑
k=−∞cke
ikx
Die Koeffizienten sind dabei:
ck =1
2π
ˆ π
−πf(x)e−ikx dx
Diese konvergiert unter gewissen Voraussetzungen (f ist eine stetig differenzierbare, 2π-periodischeFunktion oder f ist eine quadratintegrable Funktion auf dem Intervall [−π, π]) gleichmaßig ge-gen die Funktion f . Die Koeffizienten der DFT erhalt man, wenn man die Integrale numerischmit der summierten Trapezregel berechnet.
112

Andererseits kann man die trigonometrische Interpolation auch als eine Diskretisierung derFouriertransformation sehen, man spricht deshalb auch von diskreter Fourier-Transformation(DFT). Fur eine Funktion f : R→ C berechnet sich die Fourier-Transformierte Ff als
(Ff)(ω) =
∞
−∞
e−iωx · f(x) dx, ω ∈ R.
Die Fourier-Transformierte ist nicht mehr eine Funktion des Ortes (oder der Zeit) sondern eineFunktion der Kreisfrequenz ω (bzw. der Frequenz). Man spricht daher auch von einer Trans-formation vom Orts- in den Frequenzraum. Die Fourier-Transformierte gibt Auskunft uberdas (kontinuierliche) Spektrum einer Funktion (also den Anteil von bestimmten Frequenzenin einem Signal) man spricht deshalb auch von der Spektralfunktion wahrend die DFT eindiskretes Spektrum liefert.
9.3 Schnelle Fourier-Transformation (FFT)
Einer der beruhmtesten Algorithmen der angewandten Mathematik/Informatik!Entwickelt von James Cooley und John Tukey 1965.Zuruck zur komplexen trigonometrischen Interpolation:
ck =1
N
N−1∑
j=0
yje−i 2πjk
N fur k = 0, . . . , N − 1 (Hintransformation) (9.2)
yj =N−1∑
j=0
ckei 2πjkN fur j = 0, . . . , N − 1 (Rucktransformation)
• Hier wurde N = n+ 1 gesetzt.
• Die Berechnung yj aus den ck ist schlicht die Definition des komplexen trigonometrischenPolynoms
• (9.2) bezeichnet man als diskrete Fouriertransformation.
• Der Aufwand fur die Hin- und Rucktransformation ist O(N2) (N -malige Auswerten vonvon N Summentermen).
Betrachte (9.2) ck mit ck = 1N ck. Es sei N = 2n gerade, dann lassen sich die Summen fur
die Koeffizienten in zwei Teilsummen aufspalten:
ck =2n−1∑
j=0
yje−2πi2n
jk =n−1∑
j=0
y2je−2πi2n
2jk
︸ ︷︷ ︸gerader Teil
+n−1∑
j=0
y2j+1e−2πi2n
(2j+1)k
︸ ︷︷ ︸ungerader Teil
mit ygj = y2j , cgk = c2k, y
uj = y2j+1, cuk = c2k+1 ergibt sich:
ck =
n−1∑
j=0
ygj · e−2πinjk
︸ ︷︷ ︸:=cgk
+e−2πi2nkn−1∑
j=0
yuj e− 2πi
njk
︸ ︷︷ ︸:=cuk
113

Wegen der n = N2 -Periodizitat der Einheitswurzeln e−
2πink gilt:
cgk+N
2
= cgk und cuk+N
2
= cuk k = 0, . . . ,N
2− 1.
⇒ Das Problem lasst sich auf die Berechnung von zwei Fourier Transformierten der Lange N/2reduzieren.
• cgk und cuk fur k = 0, . . . , N2 − 1 berechnen sich durch eine DFT der Lange N2 .
• Daraus berechnet man die ursprunglich gesuchten Koeffizienten
ck = cgk + e−i2πkN cuk 0 ≤ k < N
2
ck = cgk−N
2
+ e−i2πkN cu
k−N2
N
2≤ k < N
(9.3)
• Falls N2 wieder gerade ist, kann man das Prinzip rekursiv fortsetzen.
• Ist N = 2d eine Zweierpotenz, erhalt man schließlich eine DFT der Lange 1, die gleichdem Eingangswert ist.
Beispiel 9.5 (N=8)
”Abstiegsphase“ der Rekursion: Umsortieren der Eingabedaten. Am besten schreibt man die
Indizes zur Basis 2.
Die dabei auftretende Permutation der Indizes (bd−1, . . . , b0)→ (b0, b1, . . . , bd−1)2 heißt”bit-
reversal“.
”Aufstiegsphase“: Rekombination der Koeffizienten nach (9.3).
Dieses Verknufpungsmuster nennt man”perfect shuffle“.
114

Aufwand der FFTfur N = 2d (Zweierpotenz ⇒ d = log2N)
A(N) = 2A
(N
2
)
︸ ︷︷ ︸2 Transf. der
Lange N/2 ber.
+ c ·N︸︷︷︸Aufwand fur (9.3)
)
= 2 [2 ·A(N
4
)+ c
N
2] + c ·N
= 4 ·A(N
4
)+ c ·N + c ·N (d-mal . . . )
= 2d︸︷︷︸=N
A(1)︸︷︷︸≤c
+ cN + · · ·+ cN︸ ︷︷ ︸d−1 Summanden
≤ d · c ·N = O(N log2N)
Deutlich schneller fur große N im Vergleich zur O(N2)-Komplexitat der DFT.
9.4 Anwendung der Diskreten Fouriertransformation
9.4.1 Spektralanalyse
Mit der Diskreten Fourier-Analyse kann man ein periodisches Signal durch Sinus und Kosi-nusschwingungen unterschiedlicher Frequenzen darstellen. Die Koeffizienten ak, bk bilden dasSpektrum des Signals. Man spricht auch von Zeit- und Frequenzbereich.
Dies hat unzahlige Anwendungen in der sog. Signalverarbeitung. So arbeitet das JPEGVerfahren zur Bildkompression mit einer diskreten Kosinustransformation (eine Variante derdiskreten Fourier-Analyse, die nur mit reellen Werten rechnet) und Abschneiden im Frequenz-bereich.
Einen Spektrumanalysator hat vielleicht auch schon jeder mal an einem Verstarker oderMP3-Player gesehen.
9.4.2 Spektren einiger Funktionen
Wir wollen uns nun die Spektren zu einigen einfachen Signalen sowie ihre trigonometrischeInterpolation anschauen.
Abbildung 21 zeigt einige Beispiele fur Spektren. Die Konstante im Zeitbereich hat einen Pulsals Spektrum. Umgedreht hat ein Puls im Ortsbereich ein konstantes Spektrum. Schließlichwird noch das Spektrum eines Dreiecks- bzw. Rechtecksignals gezeigt.
Abbildung 22 zeigt die Interpolation von Dreick- bzw. Rechtecksignal bei Vorgabe von jeweilsacht Datenpunkten.
Abbildung 23 illustriert die Verbesserung der Annaherung an die zu interpolierende Funktionfur ein Dreiecks- und Rechteckssignal bei steigender Anzahl aquidistanter Stutzstellen.
Der Fehler direkt an der Sprungstelle des Rechtecks nimmt jedoch mit steigender AnzahlStutzstellen nicht ab. Das bezeichnet man als Gibbssches3 Phanomen.
3Josiah Willard Gibbs, 1839-1903, amerik. Physiker.
115

Man kann zeigen, dass die Fourier-Reihe an einer Sprungstelle ζ gegen den Wert
1
2
(limx→ζ+
f(x) + limx→ζ−
f(x)
)
konvergiert.Schreibt man diesen Mittelwert an der Sprungstelle vor, erhalt man eine wesentlich bes-
sere Approximation wie Abbildung 24 fur ein Rechteckssignal zeigt. Wir verwenden einmaln = 15 (Sprungstelle ist Interpolationspunkt, Mittelwert wird vorgeschrieben) und n = 16(Sprungstelle ist kein Interpolationspunkt).
116

0
0.2
0.4
0.6
0.8
1
0 1 2 3 4 5 6
y
x
Konstante
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0 10 20 30 40 50 60
y
x
Konstante Spektrum
0
0.2
0.4
0.6
0.8
1
0 1 2 3 4 5 6
y
x
Delta Peak
0
0.005
0.01
0.015
0.02
0 10 20 30 40 50 60
y
x
Deltafunktion Spektrum
-1
-0.5
0
0.5
1
0 1 2 3 4 5 6
y
x
Dreieck
1e-05
1e-04
0.001
0.01
0.1
1
0 10 20 30 40 50 60
y
x
Dreieck Spektrum
-1
-0.5
0
0.5
1
0 1 2 3 4 5 6
y
x
Rechteck
1e-05
1e-04
0.001
0.01
0.1
1
0 10 20 30 40 50 60
y
x
Rechteck Spektrum
Abbildung 21: Signal (links) und Frequenzspektrum (rechts) zu einer konstanten Funktion(oben), einem Delta-Peak (Mitte oben), einem Dreieck (Mitte unten) und einemRechteckssignal (unten). Man beachte die logarithmische Darstellung.
117

-1
-0.5
0
0.5
1
0 1 2 3 4 5 6 7
y
x
DreieckDreieck n=7
Datenpunkte
-1
-0.5
0
0.5
1
0 1 2 3 4 5 6 7
y
x
RechteckRechteck n=7Datenpunkte
Abbildung 22: Trigonometrische Interpolation von Dreiecks- (links) und Rechtecksignal(rechts) mit jeweils acht Datenpunkten.
-1
-0.5
0
0.5
1
0 1 2 3 4 5 6 7
y
x
Dreieck n= 3Dreieck n= 7Dreieck n=15Dreieck n=31
-1.5
-1
-0.5
0
0.5
1
1.5
0 1 2 3 4 5 6 7
y
x
Rechteck n= 3Rechteck n= 7Rechteck n= 15Rechteck n= 31Rechteck n= 63
Rechteck n=127
Abbildung 23: Approximation von Dreiecks- (links) und Rechteckssignal (rechts) bei steigenderAnzahl aquidistanter Stutzstellen.
118

-1.5
-1
-0.5
0
0.5
1
1.5
0 1 2 3 4 5 6 7
y
x
n= 15n= 16
Daten n=15Daten n=16
Abbildung 24: Approximation eines Rechteckssignals mit n = 15 (Sprungstelle ist Interpola-tionspunkt, Mittelwert wird vorgeschrieben) und n = 16 (Sprungstelle ist keinInterpolationspunkt) aquidistanten Stutzstellen.
119


10 Approximation von Funktionen
10.1 Bernsteinpolynome
Wir gehen nun uber von der Interpolation zur Approximation. Speziell geeignet fur Kurven,d.h. Funktionen u(t) : [a, b]→ Rd (d = 2, 3) haben sich Bernstein-Polynome bewahrt.
Definition 10.1 (Bernstein-Polynome)Die Polynome
B(n)i (t) =
(n
i
)(1− t)n−i ti i = 0, . . . , n
vom Grad n heißen Bernstein-Polynome auf [0, 1].
• n = 1 : • n = 2 :
Mittels der Transformation ϕ : [a, b] → [0, 1], ϕ(u) = u−ab−a , definiert man die Bernstein-
Polynome auf einem allgemeinen Intervall [a, b]:
B(n)i,[a,b] = B
(n)i (ϕ(u))
=
(n
i
)(1− u− a
b− a
)n−i(u− ab− a
)i
=
(n
i
)1
(b− a)n(b− u)n−i(n− a)i.
Satz 10.2 (Eigenschaften der Bernstein-Polynome)1.
n∑
i=0
B(n)i (t) = 1
Beweis: bionomischer Lehrsatz:
1 = ((1− t) + t)n =n∑
i=0
(n
i
)(1− t)n−i ti
︸ ︷︷ ︸=B
(n)i (t)
2. t = 0 ist i-fache Nullstelle von B(n)i
121

3. t = 1 ist n− i-fache Nullstelle von B(n)i
⇒ t = 0, t = 1 sind die einzigen Nullstellen.
4. Symmetrie: B(n)i (t) = B
(n)n−i(1− t)
5. Positivitat:
0 ≤ B(n)i (t) ≤ 1 fur t ∈ [0, 1]
B(n)i (t) > 0 fur t ∈]0, 1[
6. B(n)i hat in [0, 1] genau ein Maximum im Punkt i
n .Beweis:
d
dtB
(n)i (t) =
(n
i
)[−(n− i)(1− t)n−i−1 ti + i(1− t)n−i ti−1
]
=
(n
i
)(1− t)n−i−1 ti−1
[(1− t) i− (n− i) t︸ ︷︷ ︸
i−it−nt+it
]
=
(n
i
)(1− t)n−i−1
︸ ︷︷ ︸n−i−1-fache
Nullstellebei t=1
ti−1︸︷︷︸
i−1-facheNullstellebei t=0
[(1− t) i− (n− i) t︸ ︷︷ ︸
Nullstellebei t=i/n
]
Da die Ableitung ein Polynom vom Grad n− 1 ist, sind dies alle Nullstellen. Aus 2., 3.und 5. folgt, dass bei i/n ein Maximum vorliegt.
7. DieB
(n)i : 0 ≤ i < n
sind linear unabhangig und bilden eine Basis von Pn.
Beweis:zu zeigen:
n∑
i=0
αiB(n)i (t) = 0 ∀ t⇒ αi = 0 fur i = 0, . . . , n
Betrachte Ableitungen:
dj
dtj
n∑
i=0
αiB(n)i (t) =
n∑
i=0
αidj
dtjB
(n)i (t)
!= 0 ∀ t ∈ R
Setze j = 0, t = 0 Es ist nur B(n)0 6= 0, alle anderen haben dort Nullstelle ⇒ α0 = 0
j = 1, t = 0 Es ist nur ddtB
(n)1 6= 0 ⇒ α1 = 0
u.s.w.
8. Die B-Polynome erlauben folgende rekursive Darstellung uber den Grad n:
B(n)i (t) =
(1− t)B(n−1)0 (t) i = 0
tB(n−1)i−1 (t) + (1− t)B(n−1)
i (t) 0 < i < n
tB(n−1)n−1 (t) i = n
122

Beweis:i = 0, n sieht man durch einsetzen.
0 < i < n
t
(n− 1
i− 1
)(1− t)n−1−i−1t(i−1) + (1− t)
(n− 1
i
)(1− t)n−1−iti
=
(n− 1
i− 1
)(1− t)n−iti +
(n− 1
i
)(1− t)n−1ti
=[(n− 1
i− 1
)+
(n− 1
i
)
︸ ︷︷ ︸=(ni)
](1− t)n−iti
9. Fur die erste Ableitung gilt:
d
dtB
(n)i (t) =
−nB(n−1)0 (t) i = 0
n[B
(n−1)i−1 (t)−B(n−1)
i (t)]
0 < i < n
nB(n−1)n−1 (t) i = n
Satz 10.3Fur eine auf dem Intervall [0, 1] stetige Funktion f : [0, 1] → R konvergiert die Folge ihrer
Bernsteinpolynome B(n)(f) mit
B(n)(f)(t) =
n∑
i=0
B(n)i (t) · f
(i
n
)
gleichmaßig gegen f .
ohne Beweis.
Man beachte, dass dies ganz anders ist, als bei den Interpolationspolynomen, bei denenzwischen den aquidistanten Stutzstellen große (und mit steigendem Grad wachsende) Abwei-chungen auftreten konnen.
Definition 10.4 (Bezier-Kurve)Fur gegebene Punkte b0, . . . ,bn ∈ Rd heißt das vektorwertige Polynom
x(t) =n∑
i=0
biB(n)i (t)
Bezier-Kurve. Die Verbindung der Punkte bi nennt man Bezier-Polygon.
Es gelten folgende Eigenschaften:
• Das Bezier-Polynom liegt in der konvexen Hulle der Bezier-Punkte, da x(t) =∑n
i=0 biB(n)i (t)
wegen 0 ≤ B(n)i (t) ≤ 1 und
∑ni=0B
(n)i (t) = 1 eine Konvexkombination ist.
• Es ist x(0) = b0,x(1) = bn.
123

• Die Ableitung (=Tangente an die Kurve) hat in den Endpunkte die Richtung (b1 − b0)bzw. (bn − bn−1).
Beispiel 10.5
Betrachte:
b0 =
(00
),b1 =
(13−1
),b2 =
(23−1
),b3 =
(11
)
Die zugehorige Bezier-Kurve ist:
x(t) =
(t
t3 + 3t2 − 3t
)
Eine effiziente und numerisch stabile Auswertung einer Bezierkurve erlaubt der Algorithmusvon de Casteljau.
10.2 Gauß-Approximation
Wir betrachten die Approximation von Funktionen in sogenannten Prahilbertraumen:
Definition 10.6Ein Vektorraum von Funktionen uber R oder C, auf dem ein Skalarprodukt definiert ist, heißtPrahilbertraum.
Beispiele
1. Raum der stetigen Funktionen C[a, b] mit dem Skalarprodukt
〈f, p〉 =
bˆ
a
f(x)g(x) dx
2. Raum der quadratintegrierbaren bzw. quadratintegrablen Funktionen
L2[a, b] =
f :
bˆ
a
|f(x)|2dx <∞
124

Dabei ist´ ba dx das sogenannte
”Lebesgue-Integral“ (→ Funktionalanalysis).
Im Gegensatz zu C[a, b] ist L2[a, b] vollstandig (d.h. jede Cauchy-Folge konvergiert)bezuglich der Norm
‖f‖ =√〈f, f〉
und damit ein Hilbertraum. L2[a, b] ist das Analogon des Rn fur Funktionenraume.
3. Gegeben Ψ = ψ1, . . . , ψN, ψi ∈ L2[a, b]
S = SpanΨ =
f : f =
N∑
i=1
ciψi
ist ein endlich dimensionaler Prahilbertraum.
Im folgenden sei H ein Prahilbertraum und S ⊆ H ein endlich dimensionaler Teilraum.
Wir betrachten folgende Aufgabe: Zu f ∈ H finde g ∈ S, sodass
‖f − g‖ → min (10.1)
wobei ‖f‖ =√〈f, f〉 die durch das Skalarprodukt induzierte Norm ist.
Satz 10.7 (Allgemeine Gauß-Approximation)Die Aufgabe (10.1) hat genau eine Losung g ∈ S. Diese ist charakterisiert durch:
〈g, ϕ〉 = 〈f, ϕ〉 ∀ϕ ∈ S (10.2)
Beweis:
1. Sei ‖f − g‖ minimal fur g ∈ S
Fϕ(t) := ‖f − (g + tϕ)‖2 t ∈ R
ist fur beliebiges ϕ ∈ S eine stetig differenzierbare Funktion mit Minimum bei t = 0.
Fur ein Minimum muss gelten:
d
dtFϕ(t)
∣∣t=0
=d
dt〈f − g − tϕ, f − g − tϕ〉
∣∣t=0
=d
dt
[〈f − g, f − g〉 − 2t〈f − g, ϕ〉+ t2〈ϕ,ϕ〉
] ∣∣t=0
= [−2〈f − g, ϕ〉+ 2t〈ϕ,ϕ〉]|t=0
= −2〈f − g, ϕ〉 != 0
⇒ 〈f − g, ϕ〉 = 0 fur alle ϕ ∈ S
Dies ist (10.2). Geometrisch: Der”Fehler“ f − g ist orthogonal zu allen ϕ ∈ S.
125

2. Sei nun 〈f − g, ϕ〉 = 0 ∀ϕ ∈ S. Fur beliebiges g′ ∈ S gilt dann:
‖f − g′‖2 = ‖f − g + g − g′︸ ︷︷ ︸=:ϕ
‖2 = ‖f − g − ϕ‖2 = 〈f − g − ϕ, f − g − ϕ〉
= 〈f − g, f − g〉 − 2 〈f − g, ϕ〉︸ ︷︷ ︸=0 nach Vor.
+〈ϕ,ϕ〉
= ‖f − g‖2 + ‖ϕ‖2 ≥ ‖f − g‖2 also ist g Minimum
Damit ist die Aquivalenz gezeigt:
‖f − g‖ → min ⇐⇒ 〈f − g, ϕ〉 = 0 ⇐⇒ 〈g, ϕ〉 = 〈f, ϕ〉 ∀ϕ ∈ S
3. Eindeutigkeit des Minimums:
Angenommen es gabe zwei Minima g1 und g2 mit g1 6= g2. Dann ist
‖f − g1‖2 = ‖f − g2 + g2 − g1︸ ︷︷ ︸=:ϕ
‖2
= ‖f − g2‖2 + ‖g2 − g1‖2︸ ︷︷ ︸>0 da g1 6=g2
> ‖f − g2‖ zu g1 Minimum
4. Existenz des Minimums: Dies zeigen wir konstruktiv und erhalten damit auch einenAlgorithmus zur Berechnung von g.
Da S endlich-dimensional ist, gibt es eine Basis Ψ = ψ1, . . . , ψN mit N = DimS. Dasgesuchte Element g hat die Darstellung
g =N∑
j=1
cjψj .
Einsetzen der Basisdarstellung in (10.2) liefert
〈g, ϕ〉 = 〈f, ϕ〉 ∀ϕ ∈ S
⇐⇒ 〈N∑
j=1
cjψj , ψi〉 = 〈f, ψi〉 i = 1, . . . , N
⇐⇒N∑
j=1
cj〈ψj , ψi〉 = 〈f, ψi〉 i = 1, . . . , N
⇐⇒ A · c = b
mit (A)ij = 〈ψj , ψi〉 Massenmatrix oder Gramsche Matrix
(b)i = 〈f, ψi〉
A ist symmetrisch und positiv definit, denn
a) (A)ij = 〈ψj , ψi〉 = 〈ψi, ψj〉 = (A)ji
126

b)
cTAc =
N∑
i=1
ci
N∑
j=1
(A)ij cj
=
N∑
i=1
ci
N∑
j=1
〈ψj , ψi〉 cj
=
N∑
i=1
ci
〈
N∑
j=1
cjψj , ψi〉
= 〈
N∑
j=1
cjψj
︸ ︷︷ ︸=:g
,
N∑
i=1
ciψi
︸ ︷︷ ︸=:g
〉
= 〈g, g〉 > 0 da g 6= 0 ⇐⇒ c 6= 0.
(Wir nehmen hier K = R an, sonst hermitesch).
Da A symmetrisch positiv definit ist, hat das LGS A ·c = b genau eine Losung fur jedesb. Nach 1. bis 3. ist
∑cjψj die eindeutig bestimmte Bestapproximation.
10.2.1 Approximation mit Orthonormalbasen
Besonders einfach wird die Losung der Approximationsaufgabe, wenn Ψ eine Orthonormalbasisist, d.h. 〈ψi, ψj〉 = δij .
Dann gilt:
N∑
j=1
cj 〈ψj , ψi〉︸ ︷︷ ︸=δij
= ci = 〈f, ψi〉 i = 1, . . . , N
und somit
g =N∑
j=1
cjψj =N∑
j=1
〈f, ψj〉 ψj
Beispiel 10.8 (Fourierreihe)Fur N = 2m+ 1, m ∈ N ist
ΨF =
1√2π,
1√π
cosx, . . . ,1√π
cos(mx),1√π
sinx, . . . ,1√π
sin(mx)
eine Orthonormalbasis auf [−π, π]. Damit gilt dann
g(x) =a0
2+
m∑
k=1
(ak cos(kx) + bk sin(kx))
ak =1
π
ˆ π
−πf(x) cos(kx) dx k = 0, . . . ,m
bk =1
π
ˆ π
−πf(x) sin(kx) dx k = 1, . . . ,m
Fur unendlich viele Glieder (m = ∞) nennt man die Reihe Fourier-Reihe. Diese konvergiertgegen ein Element aus L2[−π, π].
127

Beispiel 10.9 (Finite-Elemente-Diskretisierung)Die numerische Losung der partiellen Differentialgleichung
∂2u
∂x2+∂2u
∂y2= f in Ω Poisongleichung
mit Hilfe der Methode der Finiten-Elemente fuhrt auf die Aufgabe:Finde u ∈ S (ein geeigneter Raum von Ansatzfunktionen), sodassˆ
Ω
∇u · ∇ϕdx =
ˆ
Ω
fϕdx ∀ϕ ∈ S
10.2.2 Fehlerkontrolle
Bisher: S ⊂ H fest gewahlt, Berechnung des”optimalen“ g. Der Fehler ‖f−g‖ wird akzeptiert.
Bei der Fourierreihe z.B. sollte ‖f − g‖ fur m→∞ immer kleiner werden.Verfeinerung der Approximationsaufgabe:
Finde S ⊂ H mit DimS moglichst klein, so dass
‖f − g‖ ≤ TOL (= vorgegebene Zahl)
Mittels Orthonormalbasen lasst sich der Fehler recht einfach messen.Sei SN ∈ H, N ∈ N eine Folge von Approximationsraumen mit DimSN = N . Oft gilt sogarSN ⊂ SN+1.Sei nun gN die Bestapproximation von f in SNWeiter sei ΨN eine Orthonormalbasis von SN (oft gilt ΨN ⊂ ΨN+1).Dann gilt fur den Fehler:
0 ≤ ‖f − gN‖2 = 〈f − gN , f − gN 〉 = 〈f, f〉 − 2〈f, gN 〉 − 〈gN , gN 〉Basis
einsetzen= 〈f, f〉 − 2〈f,N∑
i=1
〈f, ψi〉︸ ︷︷ ︸=ci
ψi〉+ 〈N∑
i=1
〈f, ψi〉ψi,N∑
j=1
〈f, ψj〉ψj〉
= 〈f, f〉 − 2N∑
i=1
〈f, ψi〉〈f, ψi〉+N∑
i=1
N∑
j=1
〈f, ψi〉〈f, ψj〉 〈ψi, ψj〉︸ ︷︷ ︸=δij
= 〈f, f〉 − 2
N∑
i=1
〈f, ψi〉2 +
N∑
i=1
〈f, ψi〉2
= 〈f, f〉 −N∑
i=1
〈f, ψi〉2
Wir wollen
‖f − gN‖2 = 〈f, f〉 −N∑
i=1
〈f, ψi〉2 ≤ TOL · 〈f, f〉︸ ︷︷ ︸relative Toleranz
⇐⇒N∑
i=1
〈f, ψi〉2 ≥ (1− TOL) 〈f, f〉 (10.3)
128

Anmerkung 10.101. 〈f, f〉 sei berechenbar (zumindest mit ausreichender Genauigkeit).
2. Falls ΨN ⊂ ΨN+1 (hierarchische Basis) sind einfach so viele Basisfunktionen hinzuzufugenbis (10.3) erreicht ist.
3. Fur die Fourierreihe gilt ΨN ⊂ ΨN+1
4. Aus der obigen Fehlerdarstellung folgt bei ΨN ⊂ ΨN+1 unmittelbar
‖f − gN+1‖2 = 〈f, f〉 −N+1∑
i=1
〈f, ψi〉2 = 〈f, f〉 −N∑
i=1
〈f, ψi〉2
︸ ︷︷ ︸‖f−gN‖2
−〈f, ψN+1〉2︸ ︷︷ ︸≥0
=≤ ‖f − gN‖2
Der Fehler nimmt also hochstens ab!
10.3 Adaptive Approximation mit Haar-Wavelets
10.3.1 Definition
Wir mochten jetzt eine Funktion mit moglichst wenigen Basisfunktionen gut genug approxi-mieren. Die zu approximierenden Funktionen variieren haufig nur lokal sehr stark, z.B. beilokalen Sprungen. Man mochte dann die Funktion lokal besser nahern konnen, ohne den Restder Approximation zu beeinflussen.
Definition 10.11Der Support (oder Trager) einer Funktion ist die kleinste abgeschlossene Teilmenge der Defi-nitionsmenge D einer Funktion f : D → R, in der alle Punkte liegen, an denen die FunktionWerte ungleich Null annimmt:
supp(f) = x ∈ D : f(x) 6= 0
Fur die (orthogonale) Fourier-Basis gilt zum Beispiel:
supp(ψ) = [−π, π] = D fur ψ ∈ ΨF
Die Basisfunktionen haben also alle einen globalen Trager. Um z.B. eine Sprungfunktion gutanzunahern, braucht man daher sehr viele Basisfunktionen.
Wir suchen nun orthogonale Basisfunktionen ψi ∈ ΨN aus einem quadratintegrablen Unter-raum ΨN , die nur einen kleinen Trager haben. Insbesondere mochten wir folgende Eigenschaf-ten:
1. 〈ψi, ψj〉 = δij ⇒ orthonormale Basis
2. ΨN ⊂ ΨN+1 ⇒ hierarchische Basis, erlaubt adaptive Verfeinerung
3. Die Lange des Tragerintervalls einer Basisfunktion wird immer kleiner, je weiter untendie Basisfunktion in der Hierarchie steht.
129

1
-1 10 2
1
-1
-1/2 1/20 1
Abbildung 25: Die Indikatorfunktion χ(x) (links) und das daraus abgeleitete Haar-Wavelet derStufe 0.
Eine Klasse von Funktionen mit diesen Eigenschaften heißt Waveletfunktionen. Wir betrachtenhier das Haar-Wavelet4
Definition 10.12 (Haar-Wavelet)Sei χ(x) die charakteristische Funktion bzw. Indikatorfunktion des Intervalls ]0, 1] (Abbildung25, links):
χ(x) =
1 0 < x ≤ 1
0 sonst.
Wir definieren damit das sogenannte “mother wavelet” (Abbildung 25, rechts) als
ψ(x) = χ(2x)− χ(2x− 1) =
1 0 < x ≤ 1
−1 1 < x ≤ 2
0 sonst
.
Zur Konstruktion einer Waveletbasis setzen wir ψ00(x) := χ(x) und ψ1
0(x) := ψ(2x). Auf derStufe k ∈ N gibt es insgesamt 2k−1 Haar-Waveletfunktionen. Das i-te Haar-Wavelet (1 ≤ i <2k−1) der Stufe k ist gegeben durch
ψki (x) = 2k−12 · ψ(2kx− 2i).
Der Vorfaktor ergibt sich aus der Normierung.Die Haar-Waveletbasis der Stufe k ∈ N0 setzt sich als Vereinigungsmenge aller Wavelet-
Funktionen bis zur Stufe k mit der Indikatorfunktion zusammen:
Ψk =ψ0
0
∪
k⋃
j=1
2k−1⋃
i=0
ψji
= χ ∪
k⋃
j=1
2k−1⋃
i=0
ψji
10.3.2 Eigenschaften von Haar-Wavelets
• Das Wavelet ψki (k > 0) ist ein Haar-Wavelet, das nur die Breite 2−(k−1) hat und nurauf dem Intervall ]i · 2−(k−1), (i+ 1) · 2−(k−1)] ungleich Null ist. Auf jeder Stufe wird derSupport um den Faktor 2 verkleinert.
4Das Haar-Wavelet wurde erstmals 1909 von dem Mathematiker Alfred Haar vorgeschlagen.
130

Abbildung 26: Baumstruktur von Haar-Wavelets bis zur Stufe 3.
• Die Wavelets bilden eine Baumstruktur bezuglich der Inklusion ihres Supports, d.h.
supp(ψki ) = supp(ψk+12i ) ∪ supp(ψk+1
2i+1).
Der Support von ψki und ψk−lj uberschneidet sich nur, wenn i mod 2l = j ist. Tragt man
die ψki als binaren Baum auf, dann ist in diesem Fall ψki ein Blatt an einem von ψk−lj
ausgehendem Ast (Abbildung 26).
• Die Wavelets sind zueinander orthogonal, d.h. 〈ψki , ψlj〉 = δij · δkl
i = j ∧ k = l :
k = 0 : 〈ψ00, ψ
00〉 = 〈χ, χ〉 =
ˆ 1
01 dx = 1
k > 0 : 〈ψji , ψji 〉 =
ˆ 2−(k−1)·(i+1)
2−(k−1)·i
2
k−12 ψ(2kx− 2i)︸ ︷︷ ︸
=±1
2
dx
=
ˆ 2−(k−1)·(i+1)
2−(k−1)·i2k−1 dx =
1
2k−1· 2k−1 = 1
k = l ∧ i 6= j : supp(ψki ) ∩ supp(ψlj) = 0⇒ 〈ψki , ψlj〉 = 0
k 6= l :
o.B.d.A. sei l > k ⇒ l > 0⇒ ψki = c = const auf supp(ψlj)
〈ψlj , ψki 〉 = c
ˆ 2−(l−1)·(j+1)
2−(l−1)·jψlj dx = 0, da ψlj ungerade Funktion.
131

• Offensichtlich erfullt die Konstruktion
Ψk ⊂ Ψk+1,
da immer nur Basisfunktionen hinzugenommen werden. Damit sind alle geforderten Ei-genschaften erfullt.
• Veranschaulichung: Wir definieren die Funktionen
φk1(x) =
1 i · 2−k < x ≤ (i+ 1) · 2−k0 sonst
k ∈ N0, 0 ≤ i < 2k
Φk =2k−1⋃
i=0
φki
Sk = SpanΦk ist der Raum der stuckweise konstanten Funktionen auf dem Intervall ]0, 1]mit der Intervallbreite 2−k. Es gilt
SpanΨk = SpanΦk = Sk
• Wenn eine Funktion f(x) in einer Waveletbasis gegeben ist, lasst sich diese Naherungsehr effizient auswerten. Sei cji der Koeffizient zur Basisfunktion ψji . Zu berechnen istdann
f(x) = c00ψ
00 +
k∑
j=1
2j−1−1∑
i=0
cjiψji .
Allerdings sind wegen des lokalen Supports nur sehr wenige Basisfunktionen an der Stellex ∈]0, 1] ungleich Null.
Algorithmus 10.13f = c0
0 · ψ00(x)
j = 1, i = 0while true dof = f + cji · ψ
ji (x)
if j = k thenbreak
end ifif x ≤ (2i+ 1) · 2−(j+1) theni = 2i
elsei = 2i+ 1
end ifj = j + 1
end while
132

10.3.3 Datenkompression mit Wavelets
Die Anwendung von Gleichung (10.3) aus Abschnitt 10.2.2 erlaubt eine Datenkompression mitvorgegebener Toleranz mit Hilfe orthogonaler Wavelets.
Durch die Indizes I ⊆
(i, k) : k ∈ N0, 0 ≤ i < 2k−1
sei eine beliebige Menge von Wavelet-basen charakterisiert.
Algorithmus 10.14
Gegeben: Darstellung von f ∈ Sk in Basis Ψk.Gesucht: Teilraum S ⊂ Sk, sodass ‖f − f‖ ≤ TOL〈f, f〉 und S moglichst klein.
I = (0, 0)e = 〈f, ψ0
0〉 Fehler der Approximationwhile s < (1− TOL · 〈f, f〉) do
wahle Kind (k, l + 1) einer Basisfunktion (i, l) ∈ I mit 〈f, ψl+1k 〉2 maximal.
I = I ∪ (k, l + 1) Fuge Basisfunktion mit maximalem Fehler hinzue = e+ 〈f, ψl+1
k 〉2end while
133


11 Numerische Integration
auch:”numerische Quadratur“
Wir behandeln die numerische Berechnung bestimmter Integrale in einer Raumdimension:
I[a,b] =
ˆ b
af(x) dx
Alle hier behandelten Verfahren fuhren auf folgende Form
I[a,b](f) = (b− a)n∑
i=0
wif(xi) + Fehler
Hierbei sind
wi ∈ R die Gewichte
und xi ∈ R die Stutzstellen.
Fur f ≡ 1 gilt
ˆ b
a1 dx = b− a = (b− a)
n∑
i=0
wi · 1 ⇐⇒n∑
i=0
wi = 1.
11.1 Newton-Cotes Formeln
Als erstes betrachten wir sog. Newton-Cotes5 Formeln, die ein Spezialfall interpolatorischerQuadraturformeln sind.
Idee: Stelle Interpolationspolynom p zu gewissen Stutzstellen auf, und berechne das Intergraluber p exakt.
Formel:Interpolationspolynom in Lagrangebasis zu Stutzstellen (xi, f(xi)), i = 0, . . . , n:
pn(x) =n∑
i=0
f(xi)L(n)i (x) L
(n)i (x) =
n∏
j=0j 6=i
(x− xj)(xi − xj)
Integral:
I[a,b](f) ≈ I(n)[a,b](f) =
ˆ b
apn(x) dx =
n∑
i=0
(f(xi)
ˆ b
aL(n)(x) dx
)(11.1)
Newton-Cotes-Formeln verwenden aquidistante Stutzstellen. Es gibt zwei Varianten:
a) Abgeschlossene Formeln: a, b Stutzstellen
xi = a+ i · h i = 0, . . . , n, h =b− an
5Roger Cotes, 1682-1716, engl. Mathematiker
135

b) Offene Formeln: a, b keine Stutzstellen
xi = a+ (i+ 1) · h i = 0, . . . , n, h =b− an+ 2
Stutzpunkte der abgeschlossenen Formeln fur n = 5 (unten) und der offenen Formeln furn = 3 (oben):
0 1
0
2
1
3
2
4
3
5
Beachte: Die offenen Formeln benutzen Werte des Interpolationspolynoms außerhalb des In-tervalls der Stutzstellen, d.h. Extrapolation. Das kann problematisch sein.
Berechnung der Gewichte (abgeschlossene Formeln):
I(n)[a,b](f)
(11.1)=
n∑
i=0
f(x)
ˆ b
aL
(n)i (x) dx = (b− a)
n∑
i=0
(1
b− a
ˆ b
aL
(n)i (x) dx
)
︸ ︷︷ ︸=:wi
· f(xi)
Mittels Substitution x = g(s) = a+ sh, h = b−an , g′(s) = h ergibt sich:
wi =1
b− a
ˆ b
aL
(n)i (x) dx =
1
b− a
ˆ g−1(b)
g−1(a)L
(n)i (a+ sh) g′(s)︸︷︷︸
=h
ds
=1
b− ab− an︸ ︷︷ ︸
=h
ˆ n
0
n∏
j=0j 6=i
[a+ sh− (a+ jh)]
[a+ ih− (a+ jh)]ds =
1
n
ˆ n
0
∏
j=0j 6=i
s− ji− j ds.
Berechnet man diese Gewichte, so erhalt man:
a) Abgeschlossene Formeln: n = 1, 2, 3, h = b−an
I(1)[a,b](f) =
b− a2
[f(a) + f(b)] Trapezregel
I(2)[a,b](f) =
b− a6
[f(a) + 4f
(a+ b
2
)+ f(b)
]Simpsonregel / Keplersche Faßregel
I(3)[a,b](f) =
b− a8
[f(a) + 3f(a+ h) + 3f(b− h) + f(b)]3
8-Regel
b) Offene Formeln n = 0, 1, 2, h = b−an+2
I(0)[a,b](f) = (b− a)f
(a+ b
2
)Mittelpunktsregel, Tangenten-Trapez, Rechteckregel
I(1)[a,b](f) =
b− a2
[f(a+ h) + f(b− h)]
I(2)[a,b](f) =
b− a3
[2f(a+ h)− f
(a+ b
2
)+ 2f(b− h)
]
136

Anmerkung 11.1Ab n = 7 fur abgeschlossene und n = 2 fur offene Formeln treten negative Gewichte wi auf.Dies ist ungunstig, weil
• Fur f(x) ≥ 0 garantieren positive wi, dass auch I(n)(f) ≥ 0, sonst nicht.
• Erhohte Gefahr von Ausloschung
• Kondition wird schlechter:
Sei f(xi) = f(xi) +∆yi |∆yi| ≤ ε so gilt:
I(n)(f) = (b− a)n∑
i=0
f(xi)wi = (b− a)n∑
i=0
(f(xi) +∆yi)wi = I(n)(f) + (b− a)n∑
i=0
wi∆yi
also
∣∣∣I(n)(f)− I(n)(f)∣∣∣ =
∣∣∣∣∣(b− a)
n∑
i=1
wi∆yi
∣∣∣∣∣ ≤ ε (b− a)
n∑
i=0
|wi|
Sind alle wi positiv, so gilt∑n
i=0 |wi| =∑n
i=1wi = 1. Gibt es auch Elemente mit umge-kehrtem Vorzeichen wird die Kondition schlechter.
Satz 11.2 (Restglieder)Den begangenen Fehler kann man folgendermaßen abschatzen:
1. Trapezregel:
I(f)− b− a2
[f(a) + f(b)] = −(b− a)3
12f ′′(ξ) f ∈ C2[a, b], ξ ∈ [a, b]
2. Simpson-Regel:
I(f)− b− a6
[f(a) + 4f
(a+ b
2
)+ f(b)
]= −(b− a)5
2880f (4)(ξ) f ∈ C5[a, b], ξ ∈ [a, b]
3. Mittelpunktregel
I(f)− (b− a) f
(a+ b
2
)=
(b− a)3
24f ′′(ξ) f ∈ C2[a, b], ξ ∈ [a, b].
Beweis:
ˆ b
af(x)− pn(x) dx
Inter-polations-
fehler=
ˆ b
a
f (n+1)(η(x))
(n+ 1)!
n∏
j=0
(x− xj) dx
Speziell fur die Trapezregel gilt (n = 1):
I(f)− I(1)(f) =1
2
ˆ b
af ′′(η(x)) (x− a)(x− b)︸ ︷︷ ︸
=:g(x)≤0
dx
Mittelwert-satz derIntegral-rechnung
=1
2f ′′(ξ)
ˆ b
a(x− a)(x− b) dx = −(b− a)3
12f ′′(ξ), ξ ∈ [a, b]
137

• Die Fehlerabschatzung fur die Mittelpunktsregel liefert den halben Fehler der Trapezregelbei nur einer Auswertung von f .
• Die Restglieder haben immer die typische Form: c (b− a)m+1 f (m)(ξ).
Definition 11.3 (Ordnung einer Quadratur)Eine Quadraturformel I(n)(f) hat mindestens die Ordnung m, wenn sie Polynome vom Gradm− 1 exakt integriert.
Anmerkung 11.4• n+ 1 Stutzstellen ⇒ Interpolationspolynom vom Grad n exakt⇒ Ordnung mindestens n+ 1.
• Aus den Restgliedern sieht man: Trapezregel hat mindestens die Ordnung 2 (da fur einelineare Funktion die zweite Ableitung Null ist), die Simpsonregel mindestens die Ordnung4.
• Bei geschickter Wahl der Stutzstellen und Gewichte maximal Ordnung 2n+ 2 bei n+ 1Stutzstellen.
11.2 Summierte Quadraturformeln
Erhohen des Polynomgrades ist wenig sinnvoll, da
• negative Gewichte auftreten
• die Lagrange-Interpolation nicht gleichmaßig konvergiert
• entsprechende Differenzierbarkeit von f gegeben sein muss.
Idee:
• Unterteile [a, b] in N Teilintervalle
[xi, xi+1] xi = a+ ih, i = 0, . . . , N − 1, h =b− aN
• wende eine der obigen Formeln I(n)(f) in jedem Teilintervall [xi, xi+1] an
• Das Ergebnis nennt man”summierte Quadraturformel“
Satz 11.5 (Restglied fur summierte Quadraturen)Fur die je Teilintervall verwendete Quadraturformel gelte
I[xi,xi+1](f)− I(n)[xi,xi+1](f) = αnh
m+2f (m+1)(ξi) ξi ∈ [xi, xi+1], f ∈ C(m+1)
Dann gilt fur die summierte Quadraturformel:
I(f)− I(n)h (f) = αn(b− a)hm+1f (m+1)(ξ) ξ ∈ [a, b], f ∈ C(m+1).
138

Trapezregel: n = 1,m = 1, also O(h2). Die Ordnung ist (mindestens) 2 (dies motiviert dieDefinition der Ordnung).Simpsonregel: n = 2,m = 3, also O(h4). Die Ordnung ist mindestens 3 (Polynom vom Grad2).
Beweis:Zwischenwertsatz:Sei g(x) stetig auf [α, β], dann ∃ zu jedem u ∈ [min(g(α), g(β)),max(g(α), g(β))] ein η ∈ [α, β]so dass g(η) = u.
Aus dem Zwischenwertsatz folgt: Sei ξi ∈ [a, b], i = 0, . . . , N − 1 und g stetig auf [a, b].Dann nimmt g jeden Wert zwischen mini g(ξi) und maxi(g(ξi)) an. Wegen mini g(ξi) ≤
1N
∑N−1i=0 g(ξi) ≤ maxi g(ξi) existiert ξ ∈ [a, b] mit
∑N−1i=0 g(ξi) = Ng(ξ).
Also:
I(f)− I(n)h (f) =
N−1∑
i=0
αnhm+2f (m+1)(ξi) = αnh
m+2N−1∑
i=0
f (m+1)(ξi)
︸ ︷︷ ︸=Nf (m+1)(ξ)
= αnhm+2Nf (m+1)(ξ)
h= b−aN= αnh
m+2 b− ah
f (m+1)(ξ) = αnhm+1(b− a)f (m+1)(ξ)
Beispiele fur summierte Formeln
1. Summierte Trapezregel
I(1)h =
N−1∑
i=0
(xi+1 − xi)︸ ︷︷ ︸=h
1
2[f(xi) + f(xi+1)] = h
[f(a)
2+N−1∑
i=1
f(a+ ih) +f(b)
2
]
I(f)− I(1)h (f) = −b− a
12h2f ′′(ξ) ξ ∈ [a, b], f ∈ C(2)
2. Summierte Simpsonregel
I(2)h (f) =
N−1∑
i=0
(xi+1 − xi)︸ ︷︷ ︸=h
1
6
[f(xi) + 4f
(xi + xi+1
2
)f(xi+1)
]
= h
[f(a)
6+N−1∑
i=1
f(a+ ih)
3+
2
3
N−1∑
i=0
f
(a+
(i+
1
2
)h
)+f(b)
6
]
I(f)− I(2)h (f) = −b− a
2880h4f (4)(ξi) ξ ∈ [a, b], f ∈ C(4)
3. Summierte Mittelpunktregel
I(0)h (f) =
N−1∑
i=0
(xi+1 − xi) · f(xi + xi+1
2
)= h
N−1∑
i=0
f
(a+
(i+
1
2
)h
)
I(f)− I(0)h =
b− a24
h2f ′′(ξ) ξ ∈ [a, b], f ∈ C(2)
139

Anmerkung 11.6Die summierte Simpson-Regel lasst sich aus summierter Trapez- und Mittelpunktregel zusam-mensetzen:
I(2)h (f) =
1
3I
(1)h (f) +
2
3I
(0)h (f).
Die summierte Trapezregel zu dem nachst feineren Gitter erhalt man aus summierter Trapez-und Mittelpunktregel des groberen Gitters:
I(1)h2
=1
2I
(1)h (f) +
1
2I
(0)h (f)
Diese Formeln erlauben eine okonomischere Auswertung bei fortgesetztem Halbieren durchWiederverwendung von Funktionswerten.
Beispiel 11.7 (Beispiele zu Quadraturformeln)Wir betrachten folgende bestimmte Integrale:
(i) Eine einfache, unendlich oft differenzierbare Funktion:
ˆ π/2
0sin(x) dx = 1.
(ii) Eine glatte Funktion aber mit großen hoheren Ableitungen:
ˆ 1
−1
1
10−5 + x2dx = 9.914588332462438 · 102.
(iii) Eine nicht unendlich oft differenzierbare Funktion (Halbkreis):
ˆ 1
−1
√1− x2 dx = π/2.
Summierte Trapezregel fur (i).
I Fehler #Fktausw.
9.480594489685199 ·10−1 5.1941 ·10−2 39.871158009727754 ·10−1 1.2884 ·10−2 59.967851718861696 ·10−1 3.2148 ·10−3 99.991966804850723 ·10−1 8.0332 ·10−4 179.997991943200188 ·10−1 2.0081 ·10−4 339.999498000921015 ·10−1 5.0200 ·10−5 659.999874501175253 ·10−1 1.2550 ·10−5 1299.999968625352869 ·10−1 3.1375 ·10−6 2579.999992156341920 ·10−1 7.8437 ·10−7 513. . .9.999999999995609 ·10−1 4.3909 ·10−13 5242891.000000000003847 3.8467 ·10−12 1048577
140

Fehler viertelt sich jeweils, und das von Anfang an. Weniger als 10−13 wird mit double Ge-nauigkeit nicht erreicht.
Summierte Simpsonregel fur (i).
I Fehler #Fktausw.
1.000134584974194 1.3458 ·10−4 51.000008295523968 8.2955 ·10−6 91.000000516684706 5.1668 ·10−7 171.000000032265001 3.2265 ·10−8 331.000000002016129 2.0161 ·10−9 651.000000000126001 1.2600 ·10−10 1291.000000000007874 7.8739 ·10−12 2571.000000000000491 4.9094 ·10−13 5131.000000000000030 2.9976 ·10−14 10251.000000000000006 5.7732 ·10−15 20491.000000000000002 1.7764 ·10−15 4097
Fehler reduziert sich jeweils um den Faktor 16 = (1/2)4, und das fast von Anfang an.
Summierte Trapezregel fur (ii).
I Fehler #Fktausw.
1.000009999900001 ·105 9.9010 ·104 35.000449983500645 ·104 4.9013 ·104 52.501113751079469 ·104 2.4020 ·104 91.252430268327760 ·104 1.1533 ·104 176.300548144658167 ·103 5.3091 ·103 333.227572909110977 ·103 2.2361 ·103 651.765586982280199 ·103 7.7413 ·102 1291.160976493727309 ·103 1.6952 ·102 2571.003813438906513 ·103 1.2355 ·101 5139.915347090712996 ·102 7.5876 ·10−2 10259.914588358257512 ·102 2.5795 ·10−6 20499.914588331667655 ·102 7.9478 ·10−8 40979.914588332263689 ·102 1.9875 ·10−8 81939.914588332412698 ·102 4.9740 ·10−9 16385
Fehlerverhalten am Anfang unklar, erst spat stellt sich h2 ein.
Summierte Simpsonregel fur (ii).
141

I Fehler #Fktausw.
3.333899978334190·104 3.2348·104 51.668001673605744·104 1.5689·104 98.362024407438566·103 7.3706·103 174.225963298451690·103 3.2345·103 332.203247830595247·103 1.2118·103 651.278258340003273·103 2.8680·102 1299.594396642096787·102 3.2019·101 2579.514257539662473·102 4.0033·101 5139.874417991262286·102 4.0170 10259.914335447439017·102 2.5289·10−2 20499.914588322804369·102 9.6581·10−7 40979.914588332462367·102 7.0486·10−12 81939.914588332462367·102 7.0486·10−12 16385
Bis 4096 Auswertungen ist Simpson schlechter als Trapez.”Asymptotische Konvergenzrate“
stellt sich erst fur genugend kleines h ein. Summierte Trapezregel fur (iii).
I Fehler #Fktausw.
1.000000000000000 5.7080·10−1 31.366025403784439 2.0477·10−1 51.497854534051220 7.2942·10−2 91.544909572178587 2.5887·10−2 171.561626518913870 9.1698·10−3 331.567551211438566 3.2451·10−3 651.569648456389842 1.1479·10−3 1291.570390396198308 4.0593·10−4 2571.570652791478614 1.4354·10−4 5131.570745576359828 5.0750·10−5 10251.570778383269506 1.7944·10−5 20491.570789982705718 6.3441·10−6 40971.570794083803873 2.2430·10−6 81931.570795533774854 7.9302·10−7 16385
Die Konvergenzordnung h2 wird nicht erreicht, sondern nur ein hα mit α < 2 (siehe unten).
Summierte Simpsonregel fur (iii).
142

I Fehler #Fktausw.
1.488033871712585 8.2762·10−2 51.541797577473481 2.8999·10−2 91.560594584887709 1.0202·10−2 171.567198834492299 3.5975·10−3 331.569526108946797 1.2702·10−3 651.570347538040268 4.4879·10−4 1291.570637709467796 1.5862·10−4 2571.570740256572051 5.6070·10−5 5131.570776504653564 1.9822·10−5 10251.570789318906069 7.0079·10−6 20491.570793849184461 2.4776·10−6 40971.570795450836595 8.7596·10−7 81931.570796017098507 3.0970·10−7 16385
Die Simpsonregel zeigt dieselbe Konvergenzordnung wie die Trapezregel!
Anmerkung 11.8 (Zum Begriff der Konvergenzordnung)Satz 11.5 liefert eine Konvergenzabschatzung der Form
|I(f)− I(n)h (f)| ≤ Chm+1.
Fur die summierte Trapezregel gilt m = 1, man spricht von h2-Konvergenz, fur die summierteSimpsonregel gilt m = 3, man hat h4-Konvergenz.
Wir haben gesehen, dass die Konvergenzordnung kleiner als m + 1 sein kann, wenn dieFunktion nicht genugend oft differenzierbar ist. Experimentell konnen wir diese folgendermaßenbestimmen.
Mit dem Ansatz eh = |I(f)− I(n)h (f)| = Chα gilt
eh/2
eh=C(h/2)α
Chα= (1/2)α
und daraus erhalten wir
α = log
(eh/2
eh
)/log
(1
2
).
Das so bestimmte α heißt experimental order of convergence (EOC).
Im letzen Beispiel oben erhalten wir α = 3/2.
11.2.1 Fehlerkontrolle
Idee: Die Simpson-Summe konvergiert schneller als die Trapezsumme (wenn f glatt genugist), hat also fur genugend kleines h einen kleineren Fehler.
Wir wollen den Fehler in der Trapezsumme fur eine Intervallbreite h/2 abschatzen. Dazu
”schieben“ wir die Auswertung der Simpsonsumme dazwischen:
|I(f)− I(1)h2
(f)| = |I(f)− I(2)h (f) + I
(2)h (f)− I(1)
h2
(f)|.
143

Mit der Dreiecksungleichung ergibt sich:
|I(f)− I(1)h2
(f)| ≤ |I(f)− I(2)h (f)|+ |I(2)
h (f)− I(1)h2
(f)|.
Nimmt man an, dass die Simpsonsumme genauer ist als die Trapezsumme: |I(f)− I(2)h (f)| ≤
ω|I(f)− I(1)h2
(f)| mit 0 < ω < 1, lasst sich abschatzen:
|I(f)− I(1)h2
(f)| ≤ ω|I(f)− I(1)h2
(f)|+ |I(2)h (f)− I(1)
h2
(f)|.
Auflosen nach dem Fehler in der Trapezsumme liefert:
|I(f)− I(1)h2
(f)| ≤ 1
1− ω |I(2)h (f)− I(1)
h2
(f)|.
Besonders okonomisch lasst sich die Fehlerkontrolle zusammen mit Anmerkung 11.6 umset-zen (deshalb haben wir die Trapezregel zu h/2 und die Simpsonsumme zu h verwendet). DieFehlerkontrolle lasst sich so ohne zusatzlichen Aufwand erledigen.
Algorithmus 11.9 (Integration mit Fehlerschatzung)
Gegeben: f : Df → RIntegrationsgrenzen a, b ∈ Df
Toleranz ε > 0Faktor ω ∈]0, 1]
h = b− aN = 1I(1) = 0.5 · h · (f(a) + f(b))while (h > ε) doI(0) = 0;for (i = 0, i < N , i = i+ 1) do MittelpunktsummeI(0) = I(0) + h · f(a+ (i+ 0.5) · h)
end forI(2) = 1
3I(1) + 2
3I(0) Simpson-Summe zu h
I(1) = 0.5 · (I(1) + I(0)) Trapez-Summe zu h/2h = 0.5 · hN = 2Nif(
11−ω · |I(2) − I(1)| ≤ TOL
)then
return I(1) Liefere Trapez-Summe zu hend if
end while
11.3 Quadraturen hoherer Ordnung
Wie gesehen ist mit abgeschlossenen Newton-Cotes-Formeln maximal n = 7 (n=2 bei offenen)sinnvoll.
Wie erreicht man hohere Ordnung?
144

11.3.1 Romberg-Integration
(= Extrapolation zum Limes mit Trapezregel)
Mit den summierten Formeln ist man an limh→0 I(n)h (f) interessiert. Man kann also eine
Extrapolation zum Limes anwenden. Dabei hilft folgender Satz:
Satz 11.10 (Euler-MacLaurinsche6 Summenformel)Sei f ∈ C2m+2[a, b] und einmal integrierbar, dann gilt
I(1)h (f)︸ ︷︷ ︸
Trapezsumme
=
bˆ
a
f(x) dx+
m∑
k=1
h2k B2k
(2k)!
(f (2k−1)(b)− f (2k−1)(a)
)
+ h2m+2 B2m+2
(2m+ 2)!(b− a)f (2m+2)(ζ)
︸ ︷︷ ︸Restglied
ζ ∈ [a, b]
(11.2)
mit B0 = 1, B2 = 16 , B4 = − 1
30 , . . . , den Bernoulli-Zahlen7. Diese lassen sich berechnen als
B0 = 1, Bn = − 1
n+ 1
n−1∑
k=0
(n+ 1
k
)Bk.
ohne Beweis.Satz 11.10 bedeutet, dass fur die Trapezsumme folgende Darstellung gilt:
I(1)h (f) = τ0︸︷︷︸´ b
a f(x)dx
+ τ1h2 + τ2h
4 . . .+ τmh2m
︸ ︷︷ ︸unabhangig von h!nur abh. von f, a, b
+αm+1(h)h2m+2 (11.3)
wobei die Konstanten τi nicht von der Schrittweite h abhangen. Diese sog. asymptotische
Entwicklung stellt ein Polynom in y = h2 dar. Bei der”Extrapolation“ kombiniert man I
(1)h
fur verschiedene h so, dass moglichst viele Terme außer τ0 Null werden.Speziell in ihrer Anwendung auf die Berechnung von Integralen mittels Trapezsummen un-
terschiedlicher Schrittweiten heißt dieses Verfahren Romberg-Integration8. Bei Anwendung aufallgemeine Diskretisierungsverfahren spricht man auch von Richardson-Extrapolation9.
Zur praktischen Durchfuhrung eignet sich wieder das Neville-Schema (siehe Ubungen), wel-ches angepasst lautet:
pi,0(h2i ) = I
(1)hi
(f) fur i = 0, . . . , n
pi,k(0) = pi+1,k−1(0) +(0− h2
i+k
) pi+1,k−1(0)− pi,k−1(0)
h2i+k − h2
i
= pi+1,k−1(0)− pi+1,k−1(0)− pi,k−1(0)
1−(
hihi+k
)2 fur k = 1, . . . , n, i = 0, ..., n− k.
pi,i+k interpoliert Stutzstellen h2i bis h2
i+k.
7Jacob Bernoulli, 1655-1705, Schweizer Mathematiker.8Werner Romberg, 1909-2003, deutscher Mathematiker.9Lewis Fry Richardson, 1881-1953, brit. Mathematiker.
145

Verwendet man als Schrittweite hi = h0 · 2−i ergibt sich:
pi,k = pi+1,k−1 +pi+1,k−1 − pi,k−1
22k − 1fur k = 1, . . . , n, i = 0, ..., n− k.
Bei Interpolation von n+1 Werten (h2i , I
(1)hi
(f)), i = 0, . . . , n gilt dann p(0) = I(f)+O(h2n+2).
Aber : Anwendung dieser Methode erfordert dann auch f ∈ C2n+2[a, b].
11.3.2 Gauß-Integration
Frage: Lasst sich die Genauigkeit von Quadraturformeln durch nicht nichtaquidistante Stutzstellenverbessern?
Idee: Wahle wi, xi so, dass Polynome von moglichst hohem Grad exakt integriert werden(Ordnungsmaximierung).
Beispiel 11.11Finde x0, x1 und w0, w1 so, dass p3(x) = a0 + a1x+ a2x
2 + a3x3 in I = [−1, 1] exakt integriert
wird:
1ˆ
−1
p3(x) dx = [1− (−1)] ·1∑
i=0
wip3(xi) = 2 · [w0p3(x0) + w1p3(x1)]
⇔ a0
1ˆ
−1
1 dx
︸ ︷︷ ︸2
+a1
1ˆ
−1
x dx
︸ ︷︷ ︸0
+a2
1ˆ
−1
x2 dx
︸ ︷︷ ︸2/3
+a3
1ˆ
−1
x3 dx
︸ ︷︷ ︸0
=
2w0(a0 + a1x0 + a2x20 + a3x
30) + 2w1(a0 + a1x1 + a2x
21 + a3x
31)
Koeffizientenvergleich (fur die ai) ergibt vier nichtlineare Gleichungen:
2a0 = 2a0(w0 + w1)0a1 = 2a1(w0x0 + w1x1)23a2 = 2a2(w0x
20 + w1x
21)
0a3 = 2a3(w0x30 + w1x
31)
⇒ Losung: w0 = w1 =
1
2x0 =
−1√3, x1 =
1√3.
Damit hat man also mit zwei Stutzstellen eine Quadraturformel mit Ordnung 4 erhalten.
Zum Vergleich: Die Trapezregel erreicht mit zwei Stutzstellen nur Ordnung 2. Newton-CotesFormeln haben allgemein bei n+ 1 Stutzstellen mindestens die Ordnung n+ 1.
Im folgenden beschranken wir uns auf Quadraturformeln fur das Einheitsintervall [−1, 1].Integrale uber [a, b] berechnet man per Transformation.
Man kann folgende Aussage zu nichtaquidistanten interpolatorischen Quadraturformeln zei-gen.
Satz 11.12Die maximale Ordnung einer Quadraturformel mit n+1 Stutzstellen ist 2n+2 (d.h. Polynomevom Grad 2n+ 1 werden exakt integriert).
146

Beweis: Angenommen man konnte Polynome vom Grad 2n+ 2 bei n+ 1 Stutzstellen exaktintegrieren (Ordnung 2n+ 3). Betrachte:
q(x) =
n∏
i=0
(x− xi)2
• q(x) hat Grad 2n+ 2
• q(x) ≥ 0 ∀x und q(x) 6≡ 0 also´ 1−1 q(x) dx > 0
• Andererseits:∑n
i=0 q(xi)︸ ︷︷ ︸=0
wi = 0, d.h. q wird nicht exakt integriert
Die maximal mogliche Ordnung wird mit der Gauß-Quadratur erreicht:
Satz 11.13 (Gauß-Quadratur)Es gibt genau eine interpolatorische Quadraturformel zu n+1 paarweise verschiedene Stutzstellenin [−1, 1] mit der Ordnung 2n + 2. Ihre Stutzstellen sind die Nullstellen λ0, . . . , λn ∈] − 1, 1[des (n+ 1)-ten Legendrepolynoms 10 Ln+1:
L0(x) = 1, L1(x) = x Ln+1(x) =2n+ 1
n+ 1· x · Ln(x)− n
n+ 1Ln−1(x)
Die Gewichte erhalt man mittels
wi =1
2
ˆ 1
−1
n∏
j=0j 6=i
(x− λjλi − λj
)2
dx
ohne Beweis
Die Legendre-Polynome (Abbildung 27) bilden ein Orthogonalsystem in folgendem Sinne:
1ˆ
−1
Ln(x)Lm(x) dx = 0 n 6= m.
Beispiel 11.14Fur n = 1, n = 2 ergibt sich: h = b−a
2 , c = b+a2 und
I(1)(f) =b− a
2
[f(c−
√1/3h
)+ f
(c+
√1/3h
)]Ordnung: 4
I(2)(f) =b− a
18
[5f(c−
√3/5h
)+ 8f(c) + 5f
(c+
√3/5h
)]Ordnung: 6
Hier wurde schon auf das allgemeine Intervall [a, b] transformiert.
Entsprechend lassen sich summierte Formeln definieren.
10Adrien-Marie Legendre, 1752-1833, frz. Mathematiker.
147

-1.5
-1
-0.5
0
0.5
1
1.5
-1 -0.5 0 0.5 1
y
x
i=0i=1i=2i=3i=4i=5i=6
Abbildung 27: Die Legendrepolynome bis zum Grad 6.
11.4 Ausblick
11.4.1 Adaptive Quadratur
Quadratur mit konstanter Schrittweite ist bei manchen Integranden ineffizient. Betrachte z.B.f(x) = 1
10−5+x2.
0
20000
40000
60000
80000
100000
-1 -0.5 0 0.5 1
1/((1e-5)+(x**2))
In so einem Fall mochte man die Schrittweite”adaptiv“, d. h. angepasst an den speziellen
Integranden wahlen.Dazu bedient man sich eines lokalen
”Fehlerschatzers“ (oder Indikators), der angibt, an
welcher Stelle die Schrittweite weiter verkleinert werden muss.
148

Wir betrachten das Prinzip von Archimedes11:
a = xl b
I0
I1
I2
I3
I2 =(f(xm)− f(xl)+f(xr)
2
)(xr − xm + xm − xl)
12
xm xr
gh
h
Wir konnen das Integral (die Flache)”hierarchisch“ zerlegen in die Anteile
I = I0 + I1 + . . .
I0 das Trapez (a, 0), (b, 0), (b, f(b)), (a, f(a)).
I1 das Dreieck (a, f(a)), (b, f(b)), ((a+ b)/2, f((a+ b)/2)).
I2 das Dreieck (a, f(a)), ((a+ b)/2, f((a+ b)/2)), (a+ 1/4(b− a), f(a+ 1/4(b− a))).
usw.Die hierarchischen Zuwachse berechnen sich wie folgt: Seien die Punkte (xl, fl) und (xr, fr)
gegeben, so berechnet sich die Flache des Dreiecks (A = g · h/2) mit (xm, f(xm)), xm =(xl + xr)/2 mittels
I∆ =
(f(xm)− f(xl) + f(xr)
2
)xr − xl
2
Der hierarchische Zuwachs I∆ dient gleichzeitig als lokaler Fehlerindikator. Ist er klein genug,so ist die Funktion dort gut angenahert und das Teilintervall muss nicht weiter verfeinertwerden.
Es bietet sich die Formulierung als rekursive Funktion an:
Algorithmus 11.15 (Adaptive Quadratur nach Archimedes)Archimedes (xl, xr, fl, fr, l) :xm = (xl + xr)/2, fm = f(xm)s = (fm − (fl + fr)/2) · (xr − xl)/2if (s ≥ TOL ∨ l < lmin) then
return s+Archimedes(xl, xm, fl, fm, l + 1)+Archimedes(xm, xr, fm, fr, l + 1)
11Archimedes von Syrakus, 287 v. Chr.-212 v. Chr., griechischer Mathematiker, Physiker und Ingenieur.
149

elsereturn s
end if
Das Integral berechnet sich dann via
I = (b− a)(f(a) + f(b))/2 + Archimedes(a, b, f(a), f(b), 0).
11.5 Vergleich verschiedener Verfahren hoherer Ordnung
Beispiel 11.16 (Beispiel zur numerischen Quadratur hoher Ordnung)Wir betrachten dieselben Funktionen wie in Beispiel 11.7:
(i) Eine einfache, unendlich oft differenzierbare Funktion:
π/2ˆ
0
sin(x) dx = 1.
(ii) Eine glatte Funktion aber mit großen hoheren Ableitungen:
1ˆ
−1
1
10−5 + x2dx = 9.914588332462438 · 102.
(iii) Eine nicht unendlich oft differenzierbare Funktion (Halbkreis):
1ˆ
−1
√1− x2 dx = π/2.
Vergleich verschiedener Quadraturen fur (i):
Methode I Fehler #Fktausw.
Gauss4 9.999101667698898·10−1 8.9833·10−5 49.999944679581383·10−1 5.5320·10−6 89.999996555171785·10−1 3.4448·10−7 169.999999784895880·10−1 2.1510·10−8 32
Gauss6 1.000000118910998 1.1891·10−7 61.000000001828737 1.8287·10−9 121.000000000028461 2.8461·10−11 241.000000000000444 4.4409·10−13 48
Archimedes 9.480594489685199·10−1 5.1941·10−2 39.871158009727754·10−1 1.2884·10−2 59.967851718861697·10−1 3.2148·10−3 99.990131153231707·10−1 9.8688·10−4 159.997876171856270·10−1 2.1238·10−4 31
150

Das Verfahren hoher Ordnung zahlt sich aus.
Vergleich verschiedener Quadraturen fur (ii):
Methode I Fehler #Fktausw.Trapez 1.000009999900001·105 9.9010·104 3
3.227572909110977·103 2.2361·103 651.765586982280199·103 7.7413·102 1291.160976493727309·103 1.6952·102 2571.003813438906513·103 1.2355·101 5139.915347090712996·102 7.5876·10−2 10259.914588358257512·102 2.5795·10−6 2049
Archimedes 1.767335925226728·103 7.7588·102 251.004348965298925·103 1.2890·101 379.946212584262852·102 3.1624 819.922788393957054·102 8.2001·10−1 1739.916266302474447·102 1.6780·10−1 3619.914967844457766·102 3.7951·10−2 7699.914672523966888·102 8.4192·10−3 16259.914606991793892·102 1.8659·10−3 34659.914592092819358·102 3.7604·10−4 7629
Fehlerreduktion mit Archi ist von Anfang an quadratisch, allerdings”uberholt“ die Trapez-
summe dann kraftig.
Vergleich verschiedener Quadraturen fur (iii):
Methode I Fehler #Fktausw.
Gauss4 1.592226038754547 2.1430·10−2 41.570801362699711 5.0359·10−6 10241.570798107100650 1.7803·10−6 20481.570796956200537 6.2941·10−7 40961.570796549318533 2.2252·10−7 8192
Gauss6 1.578036347519909 7.2400·10−3 61.570801237513435 4.9107·10−6 7681.570798062869299 1.7361·10−6 15361.570796940567470 6.1377·10−7 30721.570796543792309 2.1700·10−7 6144
Archimedes 1.366025403784439 2.0477·10−1 51.570774639679624 2.1687·10−5 3651.570791453003758 4.8738·10−6 7651.570795219591928 1.1072·10−6 16051.570796082320714 2.4447·10−7 3433
Hohe Ordnung lohnt sich nicht wegen mangelnder Differenzierbarkeit.
151

11.5.1 Mehrdimensionale Quadratur
Die Welt ist nicht eindimensional. Fur Recheckte (d = 2), Quader (d = 3), . . . lassen sich obigenFormeln leicht erweitern:
dˆ
c
ˆ b
af(x, y) dx dy ≈ (b− a)
n∑
i=0
wi
dˆ
c
f(xi, y) dy
≈ (b− a)(d− c)n∑
i=0
n∑
j=0
wiwj︸ ︷︷ ︸=wij
f(xi, yj)
Dies lasst sich einfach auf d Raumdimensionen verallgemeinern. Allerdings sind nicht alle(zusammenhangenden) Gebiete Rechtecke (anders als in 1D!).
Zur Integration uber komplex berandete Gebiete, die sich durch eine differenzierbare Abbil-dung auf ein Rechteck transformieren lassen, nutzt man den Transformationssatz fur Integrale:
ˆ
Ω
f(x, y) dx dy =
1ˆ
−1
1ˆ
−1
f (ϕ(ξ, η), ψ(ξ, η))
∣∣∣∣∂(ϕ,ψ)
∂(ξ, η)
∣∣∣∣ dξ dη
wobei die Transformation
(ϕ(ξ, η)ψ(ξ, η)
): [−1, 1]× [−1, 1]→ Ω ⊂ R2
das Gebiet [−1, 1]× [−1, 1] auf Ω abbildet.
Weiter ist
∣∣∣∣∂(ϕ,ψ)
∂(ξ, η)
∣∣∣∣ = det
(∂ϕ∂ξ (ξ, η) ∂ψ
∂ξ (ξ, η)∂ϕ∂η (ξ, η) ∂ψ
∂η (ξ, η)
)
︸ ︷︷ ︸(Transponierte Jacobimatrix)
6= 0
die Determinante der (transponierten) Jacobimatrix12 der Transformation.
152

Abbildung 28: Triangulierung eines komplexen zweidimensionalen Gebietes mit Dreiecks- undViereckselementen
11.5.2 Gebietszerlegung
Bei komplizierteren Gebieten Ω zerlegt man Ω in mehrere Teilgebiete und wendet den Trans-formationssatz fur jedes Teilgebiet an.
Die Zerlegung eines Gebietes in Teilgebiete einfacher geometrischer Gestalt (Dreicke, Vier-ecke, Tetraeder, Hexaeder, . . . ) nennt man Triangulierung oder Gittergenerierung. Dies istinsbesondere in drei Raumdimensionen eine schwierige Aufgabe. Dabei tritt ein zusatzlicherGeometriefehler durch die nicht exakte Approximation der Geometrie auf.
Auch in mehr als einer Raumdimensionen kann man hierarchisch adaptiv verfeinern:
Abbildung 29: Links: Adaptives Dreiecks- und Vierecksgitter. Rechts: Adaptives Tetraedergit-ter mit Bisektionsverfeinerung.
12Carl Gustav Jacob Jacobi, 1804-1851, dt. Mathematiker
153

11.5.3 Fluch der Dimension
Ist d sehr groß, so sind die hier behandelten Methoden nicht brauchbar.Betrachte Ω = [0, 1]d. Zerlegt man [0, 1] in zwei Teilintervalle je Richtung so hat man den
d-dimensionalen Wurfel in 2d Teilwurfel zerlegt.⇒ Der Aufwand steigt exponentiell in d an. Dies bezeichnet man als
”Fluch der Dimension“.
Eine Moglichkeit ist dann die Monte-Carlo Integration
I(f) ≈ C
N
N∑
i=1
f(ξi) mit Zufallszahlen ξi ∈ Ω
154

12 Iterative Losung von Gleichungsystemen
In diesem Abschnitt betrachten wir die Losung von algebraischen Gleichungen
f(x) = 0 mit f : Rn → Rn
Zunachst beschranken wir uns dabei auf den Fall n = 1 (skalar).
12.1 Intervallschachtelung
Idee: Angenommen f sei eine stetige Funktion und man kennt ein Teilintervall [a0, b0], sodassf(a0) f(b0) < 0 (unterschiedliche Vorzeichen).
Dann hat f nach dem Zwischenwertsatz mindestens eine Nullstelle in [a0, b0].
Algorithmus 12.1 (Intervallschachtelung)
Input: I0 = [a0, b0] mit f(a0)f(b0) < 0, a0, b0 ∈ RToleranz ε > 0, ε ∈ R
Output: x ∈ R
for (t = 0, 1, . . .) doxt = 1
2(at + bt); Mittelpunkt des Intervallsif (f(xt) = 0) then
break; fertig!end ifif (f(at)f(xt) < 0) thenat+1 = at; bt+1 = xt; Nullstelle in [at, xt]
elseat+1 = xt; bt+1 = bt; f(xt)f(bt) < 0 da sign(xt) = sign(at)!
end ifif (|bt − at| < ε) then
break; Fehler akzeptabelend if
end for
Es gilt at ≤ at+1 < bb+1 ≤ btund |bt+1 − at+1| ≤ 1
2 |bt − at| =(
12
)t+1 |b0 − a0|(solange nicht f(xt) ≡ 0).
Anmerkung 12.2• Konvergenz ist linear mit Rate 1
2 .
• Sehr robust
• Nur fur skalare reelle Funktionen geeignet.
12.2 Newton Verfahren
Eine Funktion f : D → R, D ⊆ R sei (mindestens) einmal stetig differenzierbar.
155

Idee: Gegeben: xt. Da f ∈ C1 gibt es eine”Tangente“
Tt(x) = f ′(xt)(x− xt) + f(xt)
Die Nullstelle der Tangente ist:
Tt(x) = 0⇔ x = xt −f(xt)
f ′(xt)
Dies fuhrt zur Iterationsvorschrift
xt+1 = xt −f(xt)
f ′(xt)
Offensichtlich ist |f ′(xt)| > 0 erforderlich, d.h. wir setzen voraus, dass die Nullstelle einfachist.
Nun untersuchen wir die Konvergenz des Newton-Verfahrens.
Satz 12.3 (Newton-Verfahren)Die Funktion f ∈ C2[a, b] habe in ]a, b[ eine Nullstelle z und es sei
m := mina≤x≤b
|f ′(x)| > 0 M := maxa≤x≤b
|f ′′(x)|
Es sei ρ > 0 so gewahlt, dass
q :=M
2mρ < 1, Kρ(z) := x ∈ R : |x− z| ≤ ρ ⊂ [a, b]
Dann sind fur jeden Startwert x0 ∈ Kρ(z) die Newton-Iterierten xt ∈ Kρ(z) definiert undkonvergieren gegen die Nullstelle z.
Dabei gilt die a-priori Fehlerabschatzung
|xt − z| ≤2m
Mq(2t) t ∈ N
und die a-posteriori Fehlerabschatzung:
|xt − z| ≤1
m|f(xt)| ≤
M
2m|xt − xt−1|2 t ∈ N
(a-priori: nur abhangig von den Voraussetzungen, a-posteriori: auch abhangig von bereits be-rechneten Iterierten.)
Beweis:
Vorbereitungen:
1. Mittelwertsatz der Differentialrechnung liefert fur alle x, y ∈ [a, b], x 6= y
∣∣∣∣f(x)− f(y)
x− y
∣∣∣∣ = |f ′(ξ)|Vor.≥ m ⇐⇒ |x− y| ≤ 1
m|f(x)− f(y)| (12.1)
Die Nullstelle z ist eindeutig, da sonst 0 < |z1 − z2| ≤ 1m |f(z1)− f(z2)| = 0.
156

2. Da f ⊂ C2[a, b] gilt folgende Taylordarstellung (mit Integralrestglied):
f(y) = f(x) + f ′(x)(y − x) +
yˆ
x
(x− t)f ′′(t) dt
︸ ︷︷ ︸=:R(y,x) Restglied
Transformation des Integrals mit
ϕ(s) = x+ s(y − x) ϕ : [0, 1]→ [x, y]
liefert fur das Restglied
R(y, x) =
yˆ
x
(x− t)f ′′(t) dt =
1ˆ
0
(x− ϕ(s)) f ′(ϕ(s))ϕ′(s) ds
=
1ˆ
0
(x− x︸ ︷︷ ︸=0
−s(y − x))f ′′(x+ s(y − x)) (y − x) ds
= −(y − x)2
1ˆ
0
sf ′′(x+ s(y − x)) ds
und damit
|R(y, x)| ≤ (y − x)2
1ˆ
0
s |f ′′(x+ s(y − x))|︸ ︷︷ ︸≤M nach Vor.
ds ≤ M
2|y − x|2
3. Nun setze g(x) := x− f(x)f ′(x) (d.h. xt+1 = g(xt))
Dann gilt:
g(x)− z = x− f(x)
f ′(x)− z = − 1
f ′(x)
(f(x) + (z − x)f ′(x)
)︸ ︷︷ ︸
=−R(z,x)
wegen f(z)︸︷︷︸=0
= f(x) + (z − x)f ′(x) +R(z, x).
Fur x ∈ Kρ(z) gilt dann
|g(x)− z| =∣∣∣∣
1
f ′(x)R(z, x)
∣∣∣∣ ≤1
m
M
2|z − x|2 (12.2)
=M
2m|x− z|︸ ︷︷ ︸
≤ρ da x∈Rρ(z)︸ ︷︷ ︸<1 nach Wahl von ρ
· |x− z|︸ ︷︷ ︸≤ρ da x∈Rρ(z)
< ρ
Somit folgt aus x ∈ Kρ(z), dass auch g(x) ∈ Kρ(z). g bildet die Menge Kρ(z) also aufsich selbst ab.
157

Jetzt konnen wir zum eigentlichen Beweis schreiten: Die Newton-Iterierten sind xt+1 = g(xt).Setze ρt := M
2m |xt − z|. Dann gilt mit der Abschatzung von oben:
ρt :=M
2m|xt − z| =
M
2m|g(xt−1)− z|
(12.2)
≤ M
2m|xt−1 − z|2 = ρ2
t−1
Somit gilt nach t Schritten:
ρt ≤ ρ2t−1 ≤ ρ4
t−2 · · · ≤ ρ(2t)
t− t︸︷︷︸=0
= ρ(2t)0
und damit wegen |xt − z| = 2mM ρt und ρ0 = M
2m |x0 − z|︸ ︷︷ ︸≤ρ
≤ q < 1
|xt − z| =2m
Mρt ≤
2m
Mρ
(2t)0 ≤ 2m
Mq(2t)
was zu zeigen war.Die a-posteriori Abschatzung folgt aus der Taylor-Formel fur xt, xt−1:
f(xt) = f(xt−1) + (xt − xt−1)f ′(xt)︸ ︷︷ ︸=0 nach Konstruktion!
+R(xt, xt−1)
und
|xt − z|(12.1)
≤ 1
m|f(xt)− f(z)︸︷︷︸
=0
| = 1
m|R(xt, xt−1)| ≤ M
2m|xt − xt−1|2.
Beispiel 12.4 (Wurzelberechnung mit Newton-Verfahren)Sei a > 0, n ≥ 1, lose
xn = a ⇐⇒ f(x) = xn − a = 0, f ′(x) = nxn−1.
Also
xt+1 = xt−f(xt)
f ′(xt)= xt−
xnt − anxn−1
t
=nxnt − xnt + a
nxn−1t
=(n− 1)xnt + a
nxn−1t
=1
n
[(n− 1)xt +
a
xn−1t
]
Satz 12.3 behauptet: Die Iteration konvergiert, falls x0 nahe genug an z. Hier gilt jedochsogar: Die Iteration konvergiert global, d.h. fur alle x0 > 0. Aber nicht unbedingt quadratischvon Beginn an.
1. fur xt > z gilt
|xt+1 − z| < |xt − z|,
da f(xt) > 0 und f ′(xt) >f(xt)xt−z .
2. 0 < x0 < zdann ist x1 > z,da f(x0) < 0 und f ′(x0) < −f(x0)
z−x0 .
Man zeigt: fur n = 2 ist fur |x0 −√a| ≤ 2
√a die Konvergenz
quadratisch.
158

Das Newton-Verfahren lasst sich auf Systeme f : Rn → Rn erweitern:Es existiere die Taylorentwicklung von f :
fi(xt +∆x) = fi(xt) +
n∑
j=1
∂fi∂xj
(xt)∆xj + Ri(xt, ∆x) i = 1, · · · , n
oder in vektorieller Schreibweise
f(xt, ∆x) = f(xt) + J(xt)∆x +R(xt, ∆x)
Dabei ist J(x) die Jacobimatrix. Das Ignorieren des Restgliedes entspricht einer Linearisierungvon f . Wir setzen wieder
f(xt) + J(xt)∆x!
= 0
Dies fuhrt zur Iteration
J(xt)∆x = −f(xt)
xt+1 = xt +∆x
Jeder Schritt erfordert die Losung eines linearen Gleichungssystems mit der Jacobimatrix!
Anmerkung 12.5• Das Newton-Verfahren konvergiert nur lokal, d.h. wenn ‖x0 − z‖ ≤ ρ, wenn also x0 im
”Einzugsbereich“ von z liegt, wobei
– ρ in der Regel unbekannt und
– ρ moglicherweise sehr klein ist. Oben: M2mρ < 1⇒ ρ < 2m
M = 2 min f ′
max f ′′
• Das Newton Verfahren konvergiert quadratisch
‖xt − z‖ ≤ c ‖xt−1 − z‖2
Die Intervallschachtelung konvergiert nur linear und ist nur fur skalare Gleichungen an-wendbar.
|xt − z| ≤1
2|xt−1 − z|
• Gedampftes Newton-Verfahren: Verbesserung der Konvergenz außerhalb des Einzugsbe-reichs:
xt+1 = xt + λt∆x λt ∈]0, 1]
mit ∆x = − f(xt)f ′(xt)
im skalaren Fall bzw. J(xt)∆x = −f(xt). Zur Wahl von λt gibt es unter-schiedliche
”Dampfungstrategien“. Eine Moglichkeit ist z.B.
Berechne ∆x als Losung von J(xt)∆x = −f(x).Setze λ = 1
159

while ‖f(x + λ∆x)‖ ≥ f(x) doλ = 0.5 · λ
end while
Alternativ kann man z.B. eine bestimmte Mindestreduktion von f fordern etc.
• Mehrfache Nullstellen:Sei z zunachst zweifache Nullstelle, d.h. f(z) = f ′(z) = 0 und f ′′(z) 6= 0. Wegen
xt+1 = xt −f(xt)
f ′(xt)= xt −
f(xt)− f(z)
f ′(xt)− f ′(z)Erweitern
=
f(xt)−f(z)xt−z
f ′(xt)−f ′(z)xt−z
= xt −f ′(ξt)
f ′′(ηt)
und f ′′(z) 6= 0 bleibt die Iteration fur xt → z (und damit ηt → z) wohldefiniert.
Man zeigt: Fur eine p-fache Nullstelle erhalt man quadratische Konvergenz mit
xt+1 = xt − pf(xt)
f ′(xt)
• Sekanten-Methode
Die Berechnung der Ableitung ist unter Umstanden teueroder schwierig.
Idee: Ersetze Tangente durch eine Sekante:
s(x) = f(xt) + (x− xt)f(xt)− f(xt−1)
xt − xt−1
Der Ansatz s(x)!
= 0 fuhrt auf die Iteration
xt+1 = xt − f(xt)xt − xt−1
f(xt)− f(xt−1)Konvergenz: lokal mit
|xt − z| ≤2m
Mqγt t ∈ N
mit
γ0 = γ1 = 1, γt+1 = γt + γt−1 ”Fibonaccizahlen“
γt ∼ 0.723 · (1.618)t
Konvergenzordnung ist ca. 1,6 also zwischen 1 und 2.
Nur eine Auswertung von f pro Iteration notwendig.
Problem: Ausloschung in xt−xt−1
f(xt)−f(xt−1) .
12.3 Fixpunktiteration
Mit g(x) = x− f(x)f ′(x) hat das Newton-Verfahren die Form
xt+1 = g(xt).
160

Da die Nullstelle z wegen f(z) = 0 ein Fixpunkt der Iteration xt+1 = g(xt) ist, nennt man diesauch eine Fixpunktiteration.
Hier untersuchen wir nun allgemeine Iterationen dieser Art. Die Berechnung von f ′(x) konntez.B. sehr teuer sein und man wertet f ′ nur einmal
”in der Nahe“ von z aus:
xt+1 = x− f(x)
f ′(c).
Frage: Wann konvergiert so eine Iteration? Insbesondere wollen wir auch f : Rn → Rn zulas-sen.
Antwort gibt der sogenannte”Banachsche Fixpunktsatz“.
Definition 12.6 (Lipschitz Stetigkeit)Eine Funktion g : D → D mit D ⊆ Rn heißt Lipschitz-stetig, wenn eine Konstante q existiert,so dass
‖g(x)− g(y)‖ ≤ q · ‖x− y‖ ∀x,y ∈ DHierbei ist ‖ · ‖ eine Vektornorm im Rn.
Satz 12.7 (Banach’scher Fixpunktsatz)Sei D ⊂ Rn eine nicht leere, abgeschlossene Punktmenge und g : D → D Lipschitz-stetig mitKonstante q < 1, dann nennt man g eine
”Kontraktion“ und es existiert genau ein Fixpunkt
z ∈ D von g. Fur jeden Startpunkt x(0) ∈ D konvergiert die Folge der Iterierten x(t+1) = g(x(t))gegen z.
Es gelten die a-posteriori und a-priori Fehlerabschatzungen
‖x(t) − z‖ ≤ q
1− q‖x(t) − x(t−1)‖ ≤ qt
1− q‖x(1) − x(0)‖
(Wir schreiben den Iterationsindex oben in Klammern, damit bei Vektoren unten Platz furden Komponentenindex bleibt).
Beweis:
1. Da g : G→ G ist
x(t) = g(x(t−1)) = g(g(x(t−2))) = · · · = g(· · ·g︸ ︷︷ ︸t mal
(x(0)) · · · )
wohldefiniert.
2. Weiter ist
‖x(t+1) − x(t)‖ = ‖g(x(t))− g(x(t−1))‖ ≤ q‖x(t) − x(t−1)‖ ≤ qt‖x(1) − x(0)‖
3. Zeige nun, dass die x(t) eine Cauchy-Folge bilden. Sei m ≥ 1 und ε > 0 gegeben. Es ist
‖x(t+m) − x(t)‖ = ‖x(t+m) − x(t+m−1)
︸ ︷︷ ︸+ x(t+m−1) − x(t+m−2)
︸ ︷︷ ︸+ · · ·+ x(t+1) − x(t)
︸ ︷︷ ︸ ‖
Dreiecksungl. ≤ ‖x(t+m) − x(t+m−1)‖+ ‖x(t+m−1) − x(t+m−2)‖+ · · ·+ ‖x(t+1) − x(t)‖(2.) ≤ qt+m−1‖x(1) − x(0)‖+ qt+m−2‖x(1) − x(0)‖+ · · ·+ qt‖x(1) − x(0)‖
Ausklammern = (qt+m−1 + qt+m−2 + · · ·+ qt)‖x(1) − x(0)‖
geom. Reihe ≤ qt 1− qm
1− q ‖x(1) − x(0)‖ ≤ ε fur t ≥ t(ε) hinreichend groß
161

Rn ist vollstandig, jede Cauchy-Folge konvergiert. Also existiert z = limt→∞ x(t) undz ∈ G, da G abgeschlossen. Schließlich ist z = g(z). Dies zeigt man so:
‖z− g(z)‖ t bel.= ‖z− x(t) + x(t) − g(z)‖ ≤ ‖z− x(t)‖+ q‖ x(t−1) − z︸ ︷︷ ︸
→0 fur t→∞
‖ → 0.
4. Fehlerabschatzung
‖x(t+m) − x(t)‖ ≤ ‖x(t+m) − x(t+m−1)‖+ · · ·+ ‖x(t+1) − x(t)‖ (wie oben)
≤ qm‖x(t) − x(t−1)‖+ · · ·+ q‖x(t) − x(t−1)‖= (qm + qm−1 + · · ·+ q︸ ︷︷ ︸
absch. durch. geom. Reihe
)‖x(t) − x(t−1)‖ ≤ q
1− q‖x(t) − x(t−1)‖
Fur m→∞ gilt x(t+m) → z rechte Seite ist unabhanging von m, also
‖z− x(t)‖ ≤ q
1− q︸ ︷︷ ︸kann man benutzen um Abstandzur exakten Losung zu schatzen
‖x(t) − x(t−1)‖ ≤ q
1− q qt−1
︸ ︷︷ ︸= qt
1−q
‖x(1) − x(0)‖
Satz 12.8Sei g : D → D mit D ⊂ R eine skalare Funktion. Dann ist
|g′(x)| ≤ q < 1 ∀x ∈ D
eine hinreichende Bedingung dafur, dass g eine Kontraktion ist.
Beweis: Aus dem Zwischenwertsatz folgt:
g(x)− g(y)
x− y = g′(ξ) fur ein ξ ∈ [x, y]⇔ g(x)− g(y) = g′(ξ) · (x− y)
⇒ |g(x)− g(y)| = |g′(ξ)||x− y|
und damit die Lipschitz-Stetigkeit von g mit Lipschitz-Konstante q falls g′(x) ≤ q fur allex ∈ D. Wenn zusatzlich q < 1 ist, dann ist g eine Kontraktion.
12.4 Iterationsverfahren zur Losung linearer Gleichungsysteme
Wir kehren zuruck zur Losung von linearen Gleichungssystemen
Ax = b, A ∈ Rn×n, b ∈ Rn, A regular
Definition 12.9Eine Menge von Matrizen A(n) : n ∈ N heißt dunn besetzt, falls
Dima
(n)ij : a
(n)ij 6= 0
= nnz(A(n))︸ ︷︷ ︸
number ofnon-zerosvon A(n)
= O(n).
162

m
m m
m
Abbildung 30: Eine Matrix, die aus der Diskretisierung partieller Differentialgleichungen miteinem Finite-Differenzen bzw. Finite-Volumen-Verfahren entsteht (links). Dieblauen Elemente sind Eintrage mit Werten ungleich Null. Die roten Elemente(rechts) werden bei der Elimination von Null verschieden (Fill-In). Das gehtnach und nach so, bis nahezu der ganze Bereich zwischen den außeren Diago-nalen gefullt ist.
Die Gauß-Elimination ist fur dunn besetze Matrizen oft schlecht geeignet da hier sogenannterfill-in auftritt (Abbildung 30), was zu einem vergleichsweise hohem Aufwand (verglichen mitder Anzahl von Nicht-Null-Elementen) fuhrt.
Eine Alternative stellen iterative Losungsverfahren dar. Eine Klasse von iterativen Losernsind sogenannte Relaxationsverfahren. Sie konnen wie folgt abgeleitet werden:
Das Losen von Ax = b entspricht einer Suche nach der Nullstelle von f(x) = b−Ax = 0
Wir definieren nun eine Iteration
x(t+1) = g(x(t)) = x(t) + C−1f(x(t)) = x(t) + C−1(b−Ax(t)
)=(I−C−1A
)︸ ︷︷ ︸
=:B”Iterationsmatrix“
x(t) + C−1b
Fur x := A−1b gilt dann
g(x) = (I−C−1A) A−1b︸ ︷︷ ︸x
+C−1b = A−1b−C−1b + C−1b = A−1b = x
also ist x ein Fixpunkt von g. Fur die Lipschitzkonstante der Funktion g gilt (‖ · ‖ sei einevertragliche Matrixnorm)
‖g(x)− g(y)‖ = ‖Bx + C−1b−By −C−1b‖ = ‖B(x− y)‖ ≤ ‖B‖ · ‖x− y‖
Falls ‖B‖ < 1 ist, dann ist g eine Kontraktion auf Rn und das Verfahren konvergiert.
Beispiele fur IterationsverfahrenFur C wahlen wir eine Matrix, die A moglichst ahnlich, aber einfach zu invertieren ist. Setze
163

dazu A = L + D + U. Dabei ist L eine strikte untere Dreiecksmatrix, D eine Diagonalmatrixund U eine obere Dreiecksmatrix.
C = D also x(t+1) = x(t) + D−1(b−Ax(t)
)”Jacobi-Verfahren“
C = L + D also x(t+1) = x(t) + (L + D)−1(b−Ax(t)
)”Gauß-Seidel Verfahren“
In komponentenweiser Darstellung erhalt man dann:
x(t+1)i =
1
aii
bi −
∑
j 6=iaijx
(t)j
”Jacobi-Verfahren“
x(t+1)i =
1
aii
bi −
∑
j<i
aijx(t+1)j −
∑
j>i
aijx(t)j
”Gauß-Seidel-Verfahren“
Iterationsverfahren konvergieren in der Regel nur fur bestimmte Klassen von Matrizen. Hierein Beispiel:
Satz 12.10Das Jacobi-Verfahren konvergiert fur strikt diagonaldominante Matrizen.
Beweis:B = I−D−1A. Zeige ‖B‖∞ < 1 (Zeilensummennorm).
B = I−D−1A = I−D−1(L + D + U) = −D−1(L + U)
‖B‖∞ = ‖D−1(L + U)‖∞ = maxi=1,...,n
∑
i 6=j
∣∣∣∣aijaii
∣∣∣∣
= max
i=1,...,n
1
|aii|∑
i 6=j|aij |
︸ ︷︷ ︸<|aii| n. Vor.
< 1
Es gibt viele weitere solche Aussagen fur symmetrisch positiv definite Matrizen, schwachdiagonaldominanten Matrizen, M-Matrizen, . . .
Aufwand fur Iterationsfahren
1. Der Aufwand fur eine Iteration x(t+1) = x(t) + C−1(b−Ax(t)) sei α(n). Typischerweiseist fur dunn-besetzte Matrizen α(n) = O(n).
2. Da ‖x(t) − x‖ ≤ ‖B‖ ‖x(t−1) − x‖ ist ‖x(t) − x‖ ≤ ‖B‖t ‖x(0) − x‖. Wir brauchen
‖B‖t ≤ ε ⇐⇒ t log ‖B‖︸︷︷︸<1︸ ︷︷ ︸
<0
≤ log ε︸︷︷︸<0
⇐⇒ t ≥ log ε
log ‖B‖︸ ︷︷ ︸>0
Gesamtaufwand: t · α(n) =log ε
log ‖B‖α(n)
‖B‖ ist vom Problem und je nach Verfahren auch von n abhangig. Es gibt Verfahren, dierelevante Probleme in einem (optimalen) Gesamtaufwand von O(n) losen konnen!
164