Triangulation of cross-sectional digital straight segments and

August 23, 2009 17:49 RPS 015-wiederhold

Triangulation of cross-sectional digital straight segments andminimum length polygons for surface area estimation

Petra Wiederholda and Mario Villafuerteb

Department of Automatic Control,Centro de Investigacion y de Estudios Avanzados CINVESTAV - IPNAv. I.P.N. 2508, Col. San Pedro Zacatenco, Mexico 07000 D.F., MexicoE-mail: [email protected], [email protected]

This paper proposes a new heuristic locally determined algorithm for the trian-gulation between points sequences representing serial sections of a surface. More-over, a strategy for surface area estimation based on triangulation of cross sectionalcontours is described, where each contour is represented by its sequence of ver-tices of maximal digital straight segments (DSS), or by its minimal length polygon(MLP). The application of the strategy, using the new triangulation algorithm, isillustrated by examples.

Keywords: surface area estimation, triangulation from contours, triangular mesh,digital straight segments DSS, minimal length polygon MLP, multigrid conver-gence.

1. Introduction

Surface area estimation is an important task within the analysis of 3D objects in

many application areas of digital image analysis. The surface area of a 3D digital

object can be calculated as the sum of the areas of all polygons which are the faces

of a polyhedron approximating the surface. Such a polyhedron can be constructed

by local or global polyhedrization methods. As defined in ([8], [10]), a polyhedriza-

tion method is local if it is based on evaluating local configurations of surface ele-

ments, that means, where each configuration is considered within a neighborhood

of prefixed size of some surface element. Any other polyhedrization method (not

depending on such a neighborhood of prefixed size) is called global. Marching cube

algorithms ([18], [10] sect.8.4, [7]), are examples of local polyhedrization methods.

More simple local methods based on weighted counting of surface elements are

recommended in textbooks ([19] p.545). The polyhedron given as the relative con-

vex hull [23], and digital polygon segments ([10] sect.12.2), are bases of global

polyhedrization methods.

Another approach to the approximation of digital surfaces, widely used for rep-

resentation and visualization purposes, is based on triangulation of serial cross

sections [19],[22]. The supposition that the surface is given as a stack of contours,

Progress in Combinatorial Image Analysis. Editors: Petra Wiederhold and Reneta BarnevaCopyright c© 2009 by Research Publishing Services :: www.rpsonline.com.sg978-981-08-0000-0


2 Petra Wiederhold and Mario Villafuerte

is justified by the practical argument that many image adquisition methods gen-

erate cross-sectional 2D images of an 3D object of interest. Also, from a 3D digital

object or surface already identified, slices parallel to some coordinate plane are

easily obtained. The preparation of a stack of contours (for example 4-contours, or

sequences of particular vertices of 4-contours), in general needs the application of

contour following algorithms to the slices of the 3D object.

The contributions of this paper are the following ones:

1. We propose a new heuristic triangulation algorithm to be performed for two

ordered sequences of points which represent consecutive cross sections of the

surface of a 3D digital object. If the sequences have m and n points, respectively,

the complexity of our algorithm is O(m + n). Our algorithm is based on simple

proximity criteria which are checked by comparisons of coordinates.

2. We propose a general strategy for surface approximation and area estimation

based on triangulation of cross-sectional contours represented by polygons

whose perimeter provides a multigrid convergent curve length estimator. We

apply this strategy and our triangulation algorithm, using DSS (digital straight

segments) polygons and MLP (minimal length polygons) representing the con-

tours, for estimating the surface area. We present experimental examples to

study the multigrid convergent behaviour of the surface area estimators.

In this paper, we suppose a 3D digital object to be a bounded 6-connected subset

of (voxels in) ZZ3; its digital surface is the set of all object voxels which have a 26-

neighbor in the complement of the object. The 3D digital object is given as a stack

of cross sections being 2D digital (4-connected) objects lying in parallel, not nec-

essarily equidistant planes. A digital surface is given as a stack of (Jordan) curves

lying in such parallel planes and represented by sequences of grid points (vox-

els when considered in ZZ3, but pixels when considered within the slicing plane).

As primary input data, we suppose such sequences to be digital Jordan 4-curves;

but we use a more general concept of contour, including any ordered sequence of

grid points, in particular, of DSS vertices, or of MLP vertices. Note that a contour

always forms a polygon in the Euclidean plane, generated by connecting subse-

quently the vertices of the contour. The paper is organized as follows: In section

2, triangulation from serial cross sections is reviewed. Section 3 presents our new

triangulation algorithm and shows examples. Section 4 reviews multigrid conver-

gence for curve length and surface area estimators. Section 5 presents our strategy

for surface approximation and area estimation, section 6 describes experiments

and examples, and section 7 contains conclusions.

2. Triangulation from serial cross sections

The aim of a triangulation algorithm for generating a surface from serial cross

sections is to generate a triangular mesh given as the union of triangulated sur-

face bands spanned by consecutive sections. Problems to be solved to satisfy this


Triangulation of DSS and MLP for surface area estimation 3

aim, include the identification of corresponding contours in two sections, and the

design of methods for the triangulation from-one-to-many or from-many-to-many

contours. These problems are mainly solved by preprocessing of the given con-

tours, and then triangulation is performed between two consecutive contours.

Most triangulation algorithms, to guarantee the triangular mesh generated to rep-

resent a topologically correct surface (without self intersections), require strong

conditions to the contours, as convexity, similarity, alignment, or, they first decom-

pose the contours in parts which satisfy such conditions (and where eventually, the

correspondence problem for these parts has to be solved), see [9],[5],[3],[6].

Optimal or global triangulation algorithms use global information about the given

contours or satisfy global optimization criteria, as for example surface area min-

imization [4] or volume maximization [9], where searching for determining an

optimal path in a weighted graph is applied. The Delaunay triangulation is the

base of other global algorithms [25].

Heuristic triangulation algorithms are applied to the input contours using only

local information in order to generate the triangles [22],[1],[3],[26]. Those algo-

rithms are characterized by simplicity and high computational efficiency. For two

consecutive contours given by sequences of m and n points, respectively, a heuris-

tic algorithm has time complexity O(m + n). Nevertheless, the exact performance

time depends on the criteria used for the decision about the next edge, and this

complexity does not include preprocessings. For example, the local version [5] of

Keppels’s algorithm [9] needs the calculation of sophisticated formulaes and iter-

ative decompositions of the contours into convex and concave parts. A heuristic

triangulation algorithm applied to two consecutive contours, starts with the selec-

tion of an initial pair of points from both contours, and subsequently, whenever

a pair has been selected, the algorithm decides which is the next pair, based on

some local criterion ([22] sect.10.3). The end condition, for a wide class of surfaces,

is having found again the initial pair. Each pair of points defines an edge (line seg-

ment), and each two consecutively detected edges (together with an edge of one

of the two polygons given by the contours) form a triangle of the triangulation of

the surface.

This conference paper only focuses the problem of the triangulation between

two consecutive contours; each slicing plane is supposed to contain only one con-

tour, so, the surface is not allowed to have bifurcations.

3. A new triangulation algorithm

3.1. Suppositions and Notations

Suppose ZZ3 to be represented by a cartesian coordinate system where the x-axis

points to the right, the y-axis points to the front and the z-axis points upwards.

Let the surface be sliced such that each cross section is parallel to the x-y-plane.

Hence, in each such plane (viewed from the top), the x-axis points to the right, and



the y-axis points downwards, as it is common in many image analysis computer

systems.

Assume C(1) = 〈p(1)1 , p

(1)2 , · · · , p

(1)n 〉 and C(2) = 〈p

(2)1 , p

(2)2 , · · · , p

(2)m 〉 to be two

ordered cyclic (p(1)n+1 = p

(1)1 and p

(2)m+1 = p

(2)1 ) sequences of points representing

consecutive contours. Since each contour lies in a plane parallel to the x-y-plane,

all points of C(1) have the same z-coordinate z(1), and those of C(2) have the z-

coordinate z(2). Let us denote the (integer) coordinates of these grid points as fol-

lows: p(1)k = (x

(1)k , y

(1)k , z(1)), 1 ≤ k ≤ n; p

(2)l = (x

(2)l , y

(2)l , z(2)), 1 ≤ l ≤ m.

Without restriction of generality, let (p(1)1 , p

(2)1 ) denote an initial edge of trian-

gulation between C(1) and C(2). The subsequent formulations of our algorithm are

valid under the following conditions:

(i) n ≤ m (contour C(1) has probably fewer points than C(2));

(ii) both sequences follow the contours in the mathematically negative (clock-

wise) sense (when the plane containing the contour is viewed from the top);

3.2. Determination of the initial edge

Our algorithm starts with the determination of an initial edge (pair of points)

(p(1)i , p

(2)j ), using heuristic proximity criteria. We propose a simplified method,

where for a point p fixed from C(1), we search for the nearest point from C(2), but

only within a 3D neighborhood of p of prefixed size, for avoiding the necessity of

tracing the whole(s) contour(s). The neighborhood size should be larger that the

distance between the slices, but it can be small in practice and under the suppo-

sitions of smoothness of the surface, and of a “sufficiently good” digitization res-

olution. In case of slices which are not well aligned or not similar, supposing that

the contours were generated by contour following from 2D objects, the authors

experimented with success to use the vertices of the rectangles or octagons circum-

scribing the 2D object, as a guide for searching for the initial edge: For example, in

each of the two corresponding contours, a neighborhood of the upper left corner

of this rectangle is considered, and the shortest edge is determined as a pair of

points only from these neighorhoods. Circumscribing rectangles or octagons for

2D objects are easily determined during the contour following.

3.3. Intuitive description and main steps

Let us give first an intuitive description of our algorithm: Let (p(1)i , p

(2)j ) denote

an actual edge (the last edge having been determined), we name p(1)i the actual

point on C(1) and p(2)j the actual point on C(2). There are only two possibilities for

the next edge: (p(1)i+1, p

(2)j ) or (p

(1)i , p

(2)j+1), because (p

(1)i+1, p

(2)j+1) will not be allowed

since this would not generate a triangle. The decision about the next edge is taken

purely by comparisons involving the x- and y-coordinates of the contour points.



So, triangulation is completely decided within the x-y-plane, and after this, the

triangulation edges (and triangles) determined there are put up into the 3D space.

In a simplified manner, the following main steps are performed:

Step A. If both contours advance towards the same direction, then the next point

on that contour which advances less, and the actual point on the other

contour, form the next edge.

Step B. Suppose that the condition in step A is not satisfied. Then let the next

point on contour C(2) and the actual point on contour C(1) form the next

edge.

The algorithm has four steps of type A, since it searches subsequently in four

directions, in the following order: to the right, upwards, to the left, downwards.

The condition in step A means more precisely that C(1) advances strictly, and C(2)

advances or keeps constant, towards this direction. For the case “to the right” this

reads: x(1)i+1 > x

(1)i and x

(2)j+1 ≥ x

(2)j . Each time a new edge is found, the algorithm

checks the end conditions (mainly that the initial edge is found again), and in case

of continuation it starts newly with the first step of type A (to the right). Step

B reflects a situation where the triangulation essentially changes its proceeding

direction, and it shows that the sequence C(2) is preferred to provide the proceed-

ing of triangulation; C(2) has more (or an equal number of) points than C(1).

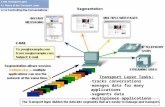
Figure 1 shows an example of the beginning of triangulation, for two consec-

utive non-similar contours C(1) = {A1, A2, · · · , A20}, C(2) = {B1, B2, · · · , B21},

starting with the initial edge (A1, B1). This is a typical example where (purely)

shortest edge criterion based triangulation can fail, as the images on the left illus-

trate, see also [3].

The decisions of our algorithm, made on the base of relative positions of contour

points, all projected into the x-y-plane, guarantee that during the triangulation, no

contour is “advancing much more rapidly than the other one”. A similar idea is

used in the triangulation algorithm in [27], where Yu and Klette triangulate pieces

of cross sections of so called “visible surfaces”. Under the restrictive conditions to

such surfaces, using our coordinate system and orientation of slices as supposed

above, Yu/Klette would consider a pair of consecutive contours as “seen from

the right” (and projected on the y-z-plane), and later on as “seen from the front,

from the left, and from behind”, in order to triangulate the surface band portion

which can be “seen” from each of these orthogonal directions. Each such portion

is a bounded horizontal strip (between two lines containing the contours points),

on which triangulation always proceeds from one end to the other, without any

possibilities of “returns or direction changes”. Triangulation in [27] is more simple,

but it does not provide immediately the triangulated surface band between the

given contours, and the surface has to fulfil much more restrictions than for our

algorithm.



Figure 1. Example of the first edges of triangulation, as projected into the x-y-plane, and

seen in perspective. First image (left): shortest edge triangulation method. Second image

(right): our new algorithm.

3.4. Triangulation algorithm

The following presents a pseudo-code of our algorithm. Recall that n ≤ m, the

y-axis points downwards, and contours are traced clock-wise. The step 01 is not

detailed in this description. In step 03, for the case n = 1, a procedure one-to-many-

points-triangulation connects the unique point of C(1) with each point of C(2).

Triangulation algorithm for two consecutive contours

Input: Ordered cyclic sequences of 3D grid points C(1) = 〈p(1)1 , p

(1)2 , · · · , p

(1)n 〉,

C(2) = 〈p(2)1 , p

(2)2 , · · · , p

(2)m 〉.

Output: Ordered sequence of edges E = 〈e0, e1, e2, · · · , es〉 which define a triangu-

lated surface band between the two input contours.

01 Determination of the initial edge e0 = (p(1)1 , p

(2)1 ).

02 i = 1, j = 1, k = 0, ek = (p(1)1 , p

(2)1 )

03 if n = 1 then go to procedure one-to-many-points-triangulation; endif

04 if x(1)i+1 ≥ x

(2)j then j = j + 1 and go to Line05; else; go to Line24; endif

05 if (x(1)i+1 > x

(1)i AND x

(2)j ≥ x

(2)j−1) then

06 if x(1)i+1 > x

(2)j then go to Line22; else; go to Line23; endif

07 else



08 if (y(1)i+1 < y

(1)i AND y

(2)j ≤ y

(2)j−1) then

09 if y(1)i+1 < y


10 else

11 if (x(1)i+1 < x

(1)i AND x

(2)j ≤ x

(2)j−1) then

12 if x(1)i+1 < x


13 else

14 if (y(1)i+1 > y

(1)i AND y

(2)j ≥ y

(2)j−1) then

15 if y(1)i+1 > y


16 else

17 go to Line22

18 endif

19 endif

20 endif

21 endif

22 ek+1 = (p(1)i , p

(2)j ) new edge found, go to Line25

23 j = j − 1

24 ek+1 = (p(1)i+1, p

(2)j ) new edge found; i = i + 1

25 if (i = n AND j = m) then

26 k = k + 1; ek+1 = (p(1)i+1, p

(2)j ), (ek+1, e0) forms the last triangle; STOP.

27 else; k = k + 1; j = j + 1

28 if j > m then go to Line23

29 else

30 if i < n then go to Line05; else; go to Line22; endif

31 endif

32 endif

Since our triangulation algorithm is locally determined (as well as the algorithm

[27]), and we also base the determination of the initial edge on a local analysis, its

time complexity for the triangulation of the surface spanned between the two con-

tours C(1), C(2), is O(n + m); it needs only one complete traversal of both contours,

and decisions are taken by comparing x- and y-coordinates of points rather than on

calculations. For completing the triangulation of the whole surface, subsequently

each pair of consecutive contours is triangulated.

4. Multigrid convergent estimators

For details related to this section we refer to [8],[10],[11], where multigrid conver-

gence has been established as an important characteristic of estimators of geomet-

ric properties. A surface area estimator is defined to be multigrid convergent, if the

sequence of numbers, calculated due to this estimator, for 3D digital objects which

are the results of digitization of the same Euclidean object (compact subset of IR3



with a measurable surface), but using increasing digitization resolutions, is con-

vergent, and its limit is the value of the surface area of the Euclidean object, the so

called true value. Similarly, if a rectifiable Jordan curve γ in IR2 is digitized using

increasing digitization resolutions, a curve length estimator is multigrid conver-

gent if it provides a sequence of numbers, calculated for the digital curves, which

converges to the (Euclidean) curve length of γ.

Similarly as local estimators of curve length, based on weighted counting of

digital curve elements ([19] p.520), also surface area estimators determined by

local polyhedrization methods, are not multigrid convergent. The perimeter of

a polygon constructed by maximum length digital straight segments (DSS poly-

gon), or of the minimum length polygon (MLP), are multigrid convergent curve

length estimators. Both polygons have vertices which are elements of the given

digital curve, and the perimeter is the sum of the Euclidean lengths of all its

edges (straight line segments). Multigrid convergence for the DSS polygon was

proved in [17] for convex plane curves, and was experimentally shown in [2], [10].

Whereas the DSS polygon depends on the initial (curve) point used in the DSS

determination, the MLP of a digital 4-Jordan curve is uniquely determined, and

coincides with the relative convex hull of the region enclosed by the curve [24].

Multigrid convergent surface area estimators are provided by global polyhedriza-

tion methods as follows:

(a) The estimator is the area of a polyhedron given as the relative convex hull (RCH),

which is contained in the outer Jordan digitization and contains the inner

Jordan digitization of the Euclidean object. This estimator was proved to be

multigrid convergent for any smooth 3D Euclidean object [23]. No efficient

algorithm for the RCH determination has been published. A first idea of an

approximative algorithm was presented in [27].

(b) The estimator is the sum of the areas of digital polygon segments (DPS) with

vertices belonging to the digital surface. Some algorithms have been proposed

for the DPS determination [12],[15]. Both the problem of determination of a

set of initial elements which serve as seeds for the DPS growing process, and

the problem of deciding in which preferred directions the growing process

should proceed, are not solved [15]. Multigrid convergence of this estimator

was experimentally shown in [12], [10], but no proof has been published.

5. A strategy for surface approximation and area estimation

Suppose that a digital surface, which was generated by digitization from a Jor-

dan surface S (in IR3), is represented by a stack of serial cross-sectional contours

{C1, C2, ..., Ck}. Then S can be seen as sliced by Jordan curves {S1, S2, ..., Sk}, lying

in parallel planes, such that each contour Ci is the discrete version of the curve Si,

for i = 1, 2, · · · , k. Now let us represent each contour Ci by a polygon Pi (in IR2,

but whose vertices are elements of the digital space) whose perimeter is a curve



length estimator known to be multigrid convergent to the (Euclidean) length of the

curve Si. An estimator of the surface area of S is constructed as the sum of areas

of all triangles, generated by some triangulation performed between each pair of

consecutive polygons (Pi, Pi+1) (i = 1, 2, · · · , k − 1).

The aims of this strategy is to obtain a triangulation (triangular mesh) of the

surface and a surface area estimator which can serve as a base for the development

of multigrid convergent estimators. The mathematical analysis whether (or, under

which conditions) a multigrid convergent surface area estimator is obtained in this

way, lies outside the scope of this paper.

In this paper, the strategy is illustrated by the application of our new triangula-

tion algorithm to the cases where each contour is represented by a DSS polygon,

or, by its minimal length polygon (MLP). For the special case of using the MLP

as contour representant, the idea of the strategy was published before by Yu and

Klette in [27] where, under strong restrictions imposed to the surface, and using

a simplified version of triangulation of pieces of the surface, the surface area was

estimated, and the estimator was experimentally shown to have multigrid conver-

gence behaviour. The surface area estimator in [27] was proposed as an approx-

imation of the surface area of the RCH (relative convex hull) of the correspond-

ing 3D digital object. The RCH in 3D space is a concept analogous to that of the

MLP in the plane, which coincides with the RCH in 2D space (however, in 3D

space, the RCH does not coincide with a minimal area polyhedron). The relations

between the 3D RCH and the polyhedron generated by triangulation of serial sec-

tions being MLP’s (and similarly, between DPS and the result of triangulation of

cross- sectional DSS’s) are still unknown.

6. Experiments for surface area determination

We illustrate the strategy for surface area estimation, by examples of smooth sur-

faces with known surface area, which were digitized and sliced into parallel cross

sections, equidistant with distance equal to the digitization resolution, to gener-

ate a stack of 4-contours. This is achieved by a rounding procedure we developed

for many surfaces representable by algebraic equations of second grade, which

is not presented in this paper. The idea is to determine all intersection points of

the Euclidean surface with the grid lines within each slicing plane, and then, the

coordinates are rounded “in direction towards the exterior of the surface”. All 4-

contours together form the Outer Jordan digitization of the object enclosed by the

original surface, and all contours are obtained as ordered sequences of points with

the same (clock wise) traversal direction.

From these 4-contours, we generate their MLP applying the algorithm due to

Klette/Yip [14]. For obtaining a DSS polygon for each 4-contour, we use the DSS

algorithm of Kovalevsky [16]. Based on the suppositions that the surface is smooth,

and that the digitization resolution is sufficient to represent all details of the object,

we apply a simple heuristic to decide the initial vertex for the DSS algorithm in

Au

gu

st2

3,2

00

91

7:4

9R

PS

01

5-w

iederh

old

10P

etraW

iederholdand

Mario

Villafuerte

Table 1. Surface area estimation for a sphere.

Radius r Area A A-DSS e-DSS P-DSS t-DSS A-MLP e-MLP P-MLP t-MLP

15 2827 3305 0.17 361 61.37 2798 0.01 568 5.68

20 5027 5982 0.19 696 132.24 5224 0.04 930 37.20

25 7854 8560 0.089 1127 90.16 7879 0.003 1439 4.320

30 11310 12480 0.103 1537 153.70 11390 0.007 1955 13.68

35 15390 16910 0.0987 2119 190.71 15550 0.0103 2641 26.41

40 20110 21670 0.0775 2765 193.55 20290 0.0089 3488 27.90

45 25450 27520 0.0821 3519 281.52 25670 0.0094 4188 37.69

50 31420 33620 0.0700 4291 300.37 31800 0.0120 5215 62.58

55 38010 40710 0.0710 5221 365.47 38510 0.0131 6013 78.78

60 45240 48490 0.0718 6222 441.76 45890 0.0143 7176 100.46

65 53090 56700 0.0679 7344 499.39 53820 0.0137 8663 118.68

70 61580 65990 0.0716 8576 614.04 62410 0.0147 9977 146.66

75 70690 75360 0.0660 9901 653.46 71710 0.0144 11295 162.64

80 80420 85980 0.0691 11442 789.49 81670 0.0155 12812 192.18

82 84500 90090 0.0661 11897 785.20 85750 0.0147 13463 197.91



Figure 2. Relative error and trade off measure for surface estimation of a sphere.

each contour: For the first contour, this initial vertex is selected arbitrary, but for

each other contour, the initial vertex is selected to be near to the initial vertex of

the previous contour, due to the order of the stack. Searching for such near other

point is performed locally, which is possible since for a smooth surface, consecu-

tive cross sections are aligned and similar.

As examples, consider ellipsoids represented by their normal forms x2

a2 + y2

b2 +z2

c2 = 1. (center point coinciding with the origin of the cartesian coordinate system,

all axis aligned with the coordinate axis). In the case of an ellipsoid of revolution

(spheroid), where two of the parameters a, b, c coincide, there are exact formulaes

for the surface area [21]. Supposing b = c, and denoting δ = 1− b2/a2, the surface

area is given by

A = 2πb(a · arcsin√

δ√δ

+ b) for the case a > b (prolate spheroid),

A = 4πa2 for the case a = b (sphere),

A = 2πb(a · arcsinh√−δ√

−δ+ b) for the case a < b (oblate spheroid).

In the two experiments of approximation of ellipsoids, increasing digitization

resolution is modelled by magnifying the object. In the tables, A denotes the true

surface area, A-DSS and A-MLP the surface area estimated as the area of the trian-

gulation generated from DSS cross sections or MLP sections, respectively. e-DSS

and e-MLP are the corresponding relative errors e = |A − Aestimated|/A, and P-

DSS, P-MLP denote the total number of vertices of the triangulation (this equals

Figure 3. Relative error and trade off measure for surface estimation of a prolate spheroid.

Au

gu

st2

3,2

00

91

7:4

9R

PS

01

5-w

iederh

old

12P

etraW

iederholdand

Mario

Villafuerte

Table 2. Surface area estimation for an ellipsoid of revolution (prolate spheroid).

a b A A-DSS e-DSS P-DSS t-DSS A-MLP e-MLP P-MLP t-MLP

10 6 663.17 796.42 0.2008 92 18.48 597.64 0.0988 124 12.25

15 8 1300.82 1527 0.1739 159 27.65 1245 0.0429 198 8.49

20 10 2147.84 2318 0.0792 264 20.92 2073 0.0348 334 11.64

25 13 3509.78 3839 0.0938 413 38.74 3638 0.0365 521 19.03

30 15 4832.65 5099 0.0551 553 30.48 4872 0.0081 670 5.45

35 17 6364.80 6625 0.0409 733 29.97 6194 0.0269 832 22.33



Figure 4. Ellipsoid and truncated cone, triangulated from DSS cross-sections.

Figure 5. Truncated hyperboloid and paraboloid, triangulated from MLP cross-sections.

the total number of the DSS or MLP segments generated in all slices). t-DSS, t-

MLP are the trade off measures of the estimations (efficiency of convergence)

t = e · P, similarly as defined for curve length estimators [13]. An algorithm is

more efficient than another one if t increases slower or decreases faster; t mea-

sures the capability of reducing estimation errors without generating too many

polyhedron vertices. Table 5 contains the results for a sphere, where r denotes the

radius and Figure 2 shows the relative error and trade off measure functions. In

Table 6, a and b denote the two parameters of a prolate spheroid. For both exam-

ples, MLP based trianguation has a better multigrid convergence behaviour (and

efficiency for the first example) than that based on DSS. Figures 4 and 5 present

examples of triangulation of surfaces, generated from DSS or MLP cross-sections.

7. Conclusions

In this paper, we proposed a new heuristic triangulation algorithm to be per-

formed for two ordered sequences of points called contours, which represent con-

secutive cross sections of a digital surface. Our algorithm is based on local prox-

imity criteria which are checked by comparisons of coordinates exclusively within

a plane to which both contours are projected. Hence, the algorithm can be inter-

preted to be performed first within this plane, and later, the coordinates of result-

ing triangulation edges (and triangles) are put back to 3D space. A similar idea



is used for methods based on the Delaunay triangulation constraint to a so-called

parametric domain [25]. Although we formulated the algorithm here for slicing

planes parallel to some coordinate plane, the algorithm in principal does not need

slices to be parallel, and permits non-convex, non-similar or non-aligned input

contours. Nevertheless, the analysis of conditions which guarantee that the algo-

rithm produces topologically correct triangulated surfaces, are not treated in this

paper. The 3D digital object enclosed by the surface to be triangulated, is supposed

to be the digitization of a compact simply connected subset of IR3. Our algorithm

triangulates from one to another contour, so, the surface is not allowed to have

bifurcations. The algorithm needs no preliminary traversal of contours (prepro-

cessing).

Moreover, we proposed a strategy for surface approximation and area estima-

tion based on triangulation of cross-sectional contours represented by polygons

whose perimeter are multigrid convergent curve length estimators. We apply this

strategy and our triangulation algorithm, using DSS polygons and MLP, for gener-

ating triangular meshes and for estimating the surface area of ellipsoide surfaces.

Our triangulation from DSS polygon or from MLP cross sections satisfies the

definition of a global polyhedrization method due to [10] (def.8.7), since the deci-

sion for each digital surface vertex whether it will be a vertex of the triangu-

lation or not, does not depend on a uniformly bounded neighbourhood of this

vertex; the DSS polygon or MLP are determined without such restriction within

each slice (contour). Nevertheless, we consider our polyhedrization method only

as “semi-global”, because our triangle generation is strongly restricted to be per-

formed within two consecutive slices, fact which applies to the method presented

in [27] as well. In order to achieve global polyhedrization (and hence, guarantee

of multigrid convergence of the surface area estimator), intuitively, our triangles

have to be given the chance to “grow over various slices”. Another possibility is

the application of postprocessings to the resulting polyhedron, where triangles of

similar surface normal are unified to form some new polygon. This is a known

method used for the improvement of approximations and representations of sur-

faces [25], which of course can substantially increase the time complexity of the

whole surface area estimation algorithm.

Acknowledgements

This research is supported by CONACYT Mexico, grant No. CB-2007-01-79887.

The authors wish to thank the reviewers for their constructive remarks.

References

1. Christiansen, H.N., Sederberg, T.W.: Conversion of complex contour line definitionsinto polygonal mosaics, Computer Graphics: A Quart. Rep. of SIGGRAPH-ACM 12(1977) 693–702.



2. Coeurjolly, D., Klette, R.: A comparative evaluation of length estimators of digitalcurves, IEEE T-PAMI, 26 (2004) 252–258.

3. Ekoule, A.B., Peyrin, F.C., Odet, C.L.: A triangulation algorithm from arbitrary shapedmultiple planar contours, ACM Trans. on Graphics, 10 (1991) 182–199.

4. Fuchs, H., Kedem, Z.M., Uselton, S.P.: Optimal surface recosntructon from planar con-tours, Comm. of the ACM, 20 (1977) 693–702.

5. Ganapathy, S., Dennehy, T.G.: A new general triangulation method for planar contours,Computer Graphics, 16 (1982) 69–75.

6. Kehtarnavaz, N., Simar, L.R., de Figueiredo, R.J.P., A syntactic/semantic technique forsurface reconstruction from coss-sectional contours (Note), CVGIP 42 (1988) 399–409.

7. Kenmochi, Y., Kotani, K., Imiya, A.: Marching cubes method with connectivity, Proc.of 1999 Int.. Conf. on Image Processing, Vol. 4, 361-365, Kobe au Japan (1999) (0-7803-5467-2/99 1999 IEEE)

8. Kenmochi, Y., Klette, R.: Surface area estimation for digitized regular solids, SPIEVision Geometry IX, SPIE Proc. 4117 (2000) 100–111.

9. Keppel, E.: Approximating complex surfaces by triangulation of contour lines, IBM J.of Res. and Developm., 19 (1975) 2–11.

10. Klette, R., Rosenfeld, A.: Digital Geometry - Geometric Methods for Digital PictureAnalysis, Morgan Kaufman Publ., Elsevier (2004), CA, U.S.A.

11. Klette, R.: Multigrid convergence of geometric features. in: Bertrand, G. et al (Eds.), Dig-ital and Image Geometry: Advanced Lectures, LNCS 2243, Springer, Berlin Germany,(2004), 314–333.

12. R. Klette, H. J. Sun: Digital planar segment based polyhedrization for surface area esti-mation. In: C. Arcelli, L.P. Cordella, G. Sanniti di Baja (Eds.), Visual Form 2001, LNCSSpringer, Berlin, Germany, 2059 (2001) 356–366.

13. Klette, R., Kovalevsky, V., Yip, B.: On the length estimation of digital curves, SPIE Vol.3811 (SPIE Vision Geometry VII, 1999), 52–63 (117–128).

14. Klette, R., Yip, B.: Evaluation of curve length measurements, 15th Int. Conf. on Pat-tern Recognition, Vol. 1 (2000), 1610-1614, and: The length of digital curves, MachineGraphics Vision, 9:673–703 (2000)

15. Kovalevsky, V.A.: Geometry of Locally Finite Spaces, Editing House Dr. BaerbelKovalevski, Berlin, Germany (2008)

16. Kovalevsky, V.A.: New definition and fast recognition of digital straight segments andarcs , ICPR-10, IEEE Comp. Soc. Vol. II (1990) 31–34.

17. Kovalevsky, V.A., Fuchs, S.: Theoretical and experimental analysis of the accuracy ofperimeter estimatates, In: W. Frster, S. Ruwiedel (Eds.), Robust Computer Vision, 218-242, Wichmann, Karlsruhe, Germany, (1992)

18. Lorensen, W.E., Cline, H.E.: Marching cubes - a high-resolution 3D surface constructionalgorithm, Computer Graphics 21 (1987) 163–169.

19. Russ, J.C.: The Image Processing Handbook (2nd ed.), CRC Press Inc., USA (1995)20. Sloboda, F., Stoer, J. On piecewise linear approximation of planar Jordan curves, Journal

of Comp. and Appl. Mathematics 55 (1994) 369–383.21. Tee, G.J.: Surface area and capacity of ellipsoids in n dimensions, New Zealand Journal

of Mathematics, 34 (2005) 165–198.22. Shirai, Y.: Three-Dimensional Computer Vision, Springer Verlag Berlin Heidelberg

(1987)23. Sloboda, F., Zatco, B.: On approximation of Jordan Surfaces in 3D, in: Bertrand et al

(Eds.), Digital and Image Geometry, LNCS 2243 (2001) 365–386.24. Sloboda, F., Zatco, B., Stoer, J.: On approximation of planar one-dimensional continua,

in: Klette, R., Rosenfeld, A., Sloboda, F. (Eds.), Advances in Digital and ComputationalGeometry, Springer, Singapore (1998) 113–160.



25. Wang, D., Hassan, O., Morgan, K., Weatherill, N.: Efficient surface reconstruction fromcontours based on two-dimensional Delaunay triangulation, Int. Jour. for Num. Meth-ods in Enginieering, 65 (2006) 734–751.

26. Wang, Y.F., Aggarwal, J.K.: Surface reconstruction and representaction of 3-D scenes,PR 19 (1986) 197–207.

27. Yu, L., Klette, R.: An approximative calculation of of relative convex hulls for surfacearea estimation, Proc. Image Vis. Computing New Zealand (2001) 69–74.

Triangulation of cross-sectional digital straight segments and

Documents

Transcript of Triangulation of cross-sectional digital straight segments and