Vorlesungsmanuskript ET-EW 2011
Transcript of Vorlesungsmanuskript ET-EW 2011
Energietechnik EnergiewirtschaftAachen Fach Nr. 55610, Jlich 1515
Prof. Dr.-Ing. H. AltStand 30.1.2011
VorlesungsmanuskriptInhaltbersicht der Vorlesung in Stichworten: Elektrische Energieerzeugungssysteme Stoffliche Umwandlungsarten (chem. und kerntechnische) CO2 Emission bei Kohle- und Gasverbrennung Hauptstze der Thermodynamik Dampfkraftwerksprozesse: Kohle und Kernenergie GuD - Anlagen, BHKW's, Brennstoffzellen Regenerative Energieerzeugung (Wasser, Wind, Sonne, Biomasse) Leistungs-Frequenzregelung Leistungsaustausch in Verbundsysteme, UCTE Verfgbarkeit, Erzeugungsprofil und Lastprofil
Energiewirtschaftsgesetz, EU Richtlinie Stromerzeugungskosten, Leistungs- und Arbeitspreise Wirtschaftlichkeitsberechnung, Annuitt Liberalisierter Strommarkt, Undbundling, Strombrse, Stromhandel, Strompreisbildung EEG, KWK-Gesetz, BNA, Emissionshandel Strommix, -Kosten und -Preise Netznutzungsentgelte Kundenwechselprozesse Stromkosten, Stromtarife
Elektrische Energieverteilungssysteme Netzebenen und Netzkosten, TSO, DSO AC, DC bertragungssysteme HD, HG Versorgungsqualitt Netzberechnungen, Strahlen-, Ring-, und Maschennetze Lastflussberechnungen, Praktiker-, Knotenpunkt-Potenzial-Verfahren Kurzschlussstromberechnungen
Energieanwendungen Strom und Spannungsverhltnisse beim Reihenschwingkreis Oberschwingungsentstehung und belastung Wechselstromleistung nicht sinusfrmiger Strme Steinmetzschaltung Kraftwirkungen im elektromagnetischen Feld Transformatoren Elektrische Maschinen, Drehstrom und Gleichstrom
2
1. Stoffliche Umwandlungsarten zur elektrischen Energieerzeugung1.1 Chemische Umwandlungsprozesse 1.1.1 Kohleverbrennung (Oxidation des Kohlenstoffs, Prozesstemperatur 525 C bis 700 C) C + O2 CO2 + 393 kJ/12g C thermische Energie Atomgewichte: 12 + 32 = 44 Daraus folgt: 1kg C ergibt W = 1000g 393kWs = 9,10 kWh bei GCO 2 = 44 kg = 3,67 kg CO2 12 s 12g kg C 3600 h Die energiebezogene CO2-Emission betrgt somit:3,67 g CO 2 = kg CO2 g CO2 kg C = 403 kWh kWh 9,1 kg C
Fr Steinkohle gilt: C + O2 CO2 + 8,14 kWh/kg Kohle Die CO2 Emission bei der Stromerzeugung mit = 50 % betrgt 900 g/kWh 1.1.2 Erdgasverbrennung (Oxidation des Kohlenstoffs und Wasserstoffs, Prozesstemperatur 800 C) CH4 + 2 O2 CO2 + 2 H2O + 886 kJ/16g CH4 therm. Energie Atomgewichte: 16 + 64 = 44 + 36 1kg CH4 ergibt W = 1000g 886kWs = 15,38 kWh bei GCO 2 = 44 kg = 2,75 kg CO2 16 s 16g kg CH 4 3600 h Mit der Dichte von CH4: CH = 0,72 kg folgt: WV = W CH = 11,1 kWh 4 m3 m3 Die energiebezogene CO2-Emission betrgt somit:4
g CO 2
kg CO2 kg CH 4 g CO2 = = 178,8 kWh kWh 15,38 kg CH 4 2,75
Fr Erdgas gilt:
CH4 + 2 O2 CO2 + 2 H2O + 11,0 kWh/m3 CH4
Die CO2 Emission bei der Stromerzeugung mit = 50 %: 393 g/kWh 1.1.3 Brennstoffzelle (umgekehrte Elektrolyse, "kalte Verbrennung", Oxidation des Wasserstoffs in einer PEM - Zelle (Proton Exchange Membran), Prozesstemperatur 80 C) 2 H2 + O2 2 H2O + 572 kJ/4g H2 therm. Energie 1000g 572kWs kWh ohne CO2-Emission 1kg H2 ergibt: W = = 39,72 s 4g kg H 2 3600 h kWh Mit der Dichte von H2: CH = 0,0899 kg folgt: WV = W CH = 3,57 3 4 3 m m Atomgewichte: 4 + 32 = 36 Fr Wasserstoff gilt: 2 H2 + O2 2 H2O + 3,5 kWh/m3 H24
Positive Wasserstoffionen H+ (Protonen) wandern in der Zelle durch eine gasdichte Elektrolytmatrix von der Anode (Wasserstoffzufuhr mit der Anodenreaktion: H2 - 2e- = 2H+) zur Kathode (Sauerstoffzufuhr mit der Kathodenreaktion: 2H+ + 2e- + 1/2 O2 = H2O). Der Ladungsausgleich erfolgt im ueren Stromkreis durch einen Elektronenfluss von der Anode zur Kathode entsprechend einem elektrischen Stromfluss von der Kathode (+ Pol) zur Anode (- Pol). An der Kathode wird Wasser als Reaktionsprodukt abgefhrt. (Zellenspannung 1,23 V). Die langfristige Funktionstchtigkeit der Zelle erfordert sehr reinen Wasserstoff. Fr stationre Anwendungen SOFC (Solid Oxide Fuel Cell) mit keramischem Elektrolyt (O2- Ionen, die von der Kathode zur Anode wandern) und einer Prozesstemperatur von 900 C.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
3
Brennstoffzellen Elektroden - Reaktionen SOFC: Kathode: Anode: Gesamtreaktion: Kathode: Anode: Gesamtreaktion: O2 + 2e- O2O2- + 2 H2 - 2e- 2H2O 2H2 + O2 2H2O + 572 kJ CO2 + O2 + 2e- CO32H2O + CO2 CO32- + H2 - 2e- H2 + CO2 + O2 H2O + CO2 H2 - 2e- 2H+ 2H+ + 2e- + O2 H2O H2 + O2 H2O + 286 kJ O2 + 2e- + H2O 2OH2OH- + H2 - 2e- 2H2O 2(H2 + O2) 2H2O + 572 kJ
MCFC:
PAFC, PEMFC: Anode: Kathode: Gesamtreaktion: AFC: Kathode: Anode: Gesamtreaktion:
572 kJ/Mol = 572 kJ/4gH = 143 kJ/gH = 143 kWs/gH = 39,7 kWh/kg H. Der untere Heizwert von Wasserstoff betrgt: 33 kWh/kg, von Methan 13,9 kWh/kg und von Benzin 12,4 kWh/kg. Das spezifische Gewicht (Wichte) des Wasserstoffs H unter Normalbedingungen (d.h. 0C, 760 mm QS) ist 0,09 kg/m3. Dem unteren Heizwert von 33 kWh/kg entspricht somit 3 kWh/m3, so dass fr die exotherme Wasserstoff - Sauerstoff - Redaktion gilt:
H2 + O2 H2O + 3 kWh/m3 (Hu)Zum Vergleich: Erdgasverbrennung (CH4) ergibt 11,3 kWh/m3. Ohne katalytische Verluste ergeben sich somit einschlielich der Konvertierung und Reformierung des Erdgases rd. 3 kWh elektrische Energie und 8 kWh Wrmeenergie. In der Praxis ist dieses Verhltnis elektrische zu thermische Energie bei Reformierung des Erdgases CH4 mit Wasserdampf zu H2 und CO2 etwa 1:3. Strukturvielfalt der KohlenWasserstoff-Verbindungen:
Netzstruktur
Linearstruktur Zentralstruktur Atombindung Abkrzungen und Brennstoffzellenarten: SOFC: MCFC: PAFC: PEMFC: DMFC: AFC: Solid Oxide Fuel - Cell, Elektrolyt: Keramik (dotiertes Zirkonoxyd) Molten Carbonate Fuel - Cell, Elektrolyt: Karbonatschmelze Phosphoric Acid Fuel - Cell, Elektrolyt: H3PO4 (ortho - Phosphorsure) Proton Exchange Membran Fuel - Cell, Elektrolyt: Direct Methanol Fuel - Cell, Polymermembran (2CH3OH + 4H2O 5H2 + 2H2O + 2CO2) Alcaline Fuel - Cell, Elektrolyt: KOH (Kaliumhydroxid)
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
4 Funktionsweise der Brennstoffzellen Arten:
Elektrischer Strom I
- PolNicht umgesetzter Brennstoff (10-20 %)
UZellenspannung < 1 V Elektrisches Feld
+ PolNicht umgesetzter Oxidant
- SOFC 2 H2O 2 H2 MCFC PAFC PEMFC DMFC AFC CO2 H2O H2 H2 Methanol H2O H2
EO 22O
- O2 CO2 O2 H2O O2 O2 160-200 C 60- 80 C 80-110 C 60-90 C 800-1000 C
CO32HH2O+
600-660 C
H
+
OH- OH-
Brennstoff H2
Elektrolyt Sauerstoff O2, (Luft) PolymereCO2 (Oxidant) Membran Anode Kathode - Anionen + KationenElektrolyt: Keramik (dotiertes Zirkonoxyd) Elektrolyt: Karbonatschmelze Elektrolyt: H3PO4 (ortho - Phosphorsure) Elektrolyt: Polymermembran (2CH3OH + 4H2O 5H2 + 2H2O + 2CO2) Elektrolyt: KOH (Kaliumhydroxid)Luft / Sauerstoff (Wasserdampf) H2O Reformer und Konverter
SOFC: MCFC: PAFC: PEMFC: DMFC: AFC:
Solid Oxide Fuel - Cell, Molten Carbonate Fuel - Cell, Phosphoric Acid Fuel - Cell, Proton Exchange Membran Fuel - Cell, Direct Methanol Fuel - Cell, Alcaline Fuel - Cell,
Erdgas-Brennstoffzelle mit Reformer und Konverter:
CO2
Reformer: CH4 T > 200 C: (Erdgas) CH4 + H2ODampf 3H2+CO - 214 kJ/mol Konverter: T < 500 C: CO + H2ODampf H2+CO2 + 42 kJ/mol
Kz. B.
Brennstoffzelle
K A
Strom
+ -
PEM-FC 0 der Strom eilt der Spannung nach(induktive Last). (Merkregel: I nach dem
~
U
Z
U)
< 0 der Strom eilt der Spannung vor
) ) u j (t + ) 1 u (t ) = u cos(t + ) = e + e j (t + ) = U e jt e j + e jt e j 2 2 1 * u (t ) = U e jt + U e jt 2 ) ) i j (t + ) 1 i (t ) = i cos(t + ) = e + e j (t + ) = U e jt e j + e jt e j 2 2 1 * i (t ) = I e jt + I e jt 2
(kapazitive Last) = 0 Strom und Spannung Phasengleich (ohmsche Last)
[
]
[
]Re
[
]
[
]
[
]
[
]
p(t ) = u (t ) i (t ) = p(t ) =
1 * * * * U I e j 2t + U I + I U + U I e j 2t 2
[
]U I* I
1 * 1 * * * U I + I U + U I e j 2t + U I e j 2t 2 2
[
] [
]U
Der Mittelwert der Leistung ist gleich dem Integralwert ber eine Periode von 0 bis t = 2. Der erste Term ist gleich dem Argument des Terms selbst, der zweite Term ergibt den Integralwert Null.
P
U* I I* U*
1 1 * * P = p(t ) dt = U I + I U T 0 2
T
(
)
j
Q
Diesen Wert der Leistung nennt man Wirkleistung, da der Mittelwert ber eine Periode ungleich Null ist, wenn U > 0 und I > 0 sind. Dieser Mittelwert ist gleich der Hlfte der Summe aus dem Produkte aus der konjugiert komplexen Spannung mal dem komplexen Stromwert und dem konjugiert komplexen Strom mal dem komplexen Spannungswert. Es ist fr die Wirkleistung daher auch zulssig und richtig, eines der beiden Produktwerte zu ermitteln ohne diesen Wert dann zu halbieren. Diese Beliebigkeit hat allerdings eine Auswirkung auf das Vorzeichen der Blindleistung, die man als den imaginren Anteil der komplexen Leistung definiert. * * Man definiert daher die Scheinleistung zu: S = P + jQ = U I oder U I Wir whlen die Form: S = P + jQ = U I , weil dann die induktive Blindleistung als positive Blindleistung in der komplexen Leistungsebene erscheint. Hier wird auch deutlich, dass im physikalischen Sinne die Leistung nur als Wirkleistung existiert, die Blindleistung ist eine Wirkleistung mit der Eigenschaft, dass sie ber eine Periode gemittelt den Wert Null ergibt. In oberschwingungsbehafteten Netzen ist nur die Grundschwingung des Stromes Trger der Wirkleistung. ScheinleistungD:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc*
Blindleistung
Wirkleistung
27 4.4 Leistungsanpassung bei Wechselstrom und komplexen Widerstnden Aus der Gleichstromtechnik ist bekannt, dass die maximale Leistung von einer Quelle an den Abschlusswiderstand abgegeben wird, wenn Ra =Ri ist (Leistungsanpassung).
Ri
I
Zi Ra
I
Pa = Re { a I a U*
{
}
=
U0
P Ua
~
U0
P Ua
Za
* Ua Pa = Re{U a * Za
2 U Pa = Re a * Z a Za U 0 Zi + Za2
Nach der Spannungsteilerregel ist: U a = Mit: U a =
Za U0 , Zi + Za
2 Ua =
2 Za
Zi + Za2
Z 2 U 2 2 0 a U 0 folgt: Pa = Re 2 * Zi + Za Za 2
Z U 2 U2 0 Pa = Re a 0 2 = Re Zi + Za Zi + Za 2 U0 Pa = R 2 (R i + Ra ) + ( X i + X a )2 a
2 U0 Za = Zi + Za
Ra
Notwendige Bedingung fr den relativen Extremwert von Pa ist, dass die partiellen Ableitungen nach Ra und Xa gleich Null sind:
Pa 2 (R + R a ) + ( X i + x a ) 2 (R i + R a ) R a = U0 i =0 2 R a (Ri + Ra )2 + ( X i + x a )22 2
Pa Pa = 0 und =0 R a X a
[
]
2 2 2 R i R a + 2 R a = R i2 + 2 R i R a + R a + ( X i + x a )
2 (R i + R a ) R a = (R i + R a ) + ( X i + x a )2 2 R a = R i2 + ( X i + x a ) 2
2 2
Pa 2 ( X i + X a ) Ra 2 = U0 X a (R i + Ra )2 + ( X i + x a )2
[
]
2
= 0 X a = X i Ra = Ri Z a = Z i
*
Das Leistungsmaximum wird erreicht, wenn Ra = Ri ist und der innere Blindwiderstand durch den ueren Blindwiderstand kompensiert wird. Beispiel Ersatzspannungs-und Ersatzstromquelle: Kompensation durch Reihenresonanz: Kompensation durch Parallelresonanz:
I Ri Xi Zi Pmax Ua Ra Xa=-Xi Za = Zi* Zi Ri Xi
I Xa=-Xi Pmax Ua Ra
~
U0
~
Ik
Za = Zi*
Im Ersatzschaltplan der Kompensation durch Reihenresonanz ergnzen sich die Blindwiderstnde zu Null und im Ersatzschaltplan durch Parallelresonanz zu unendlich, so dass diese im jeweiligen Ersatzschaltplan entfallen und nur noch die Wirkwiderstnde Ri und Ra erscheinen.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
28 4.5 Nachweis fr die Behauptung, dass nur die Grundschwingung des Stromes bei sinusfrmiger Spannung Trger der Wirkleistung ist. Die Spannung sei rein sinusfrmig gegeben als cosinus-Funktion der Zeit mit der Kreisfrequenz :
u (t ) = cos t =
u u e jt + e jt = (cos t + j sin t + cos t j sin t ) 2 2
(
)
Der Strom sei gegeben als eine Summe aus der Grundschwingung mit der Kresfrequenz und den Oberschwingungen wobei = 3, 5, 7,...,2n + 1 ist. Die gradzahligen Oberschwingungen entfallen gem den Gesetzen der Fourier-Analyse bei in t = T/2 bzw t = , spiegelsymmetrischer Kurvenform des Wechselstromes. Damit gilt fr den oberschwingungsbehafteten Strom:
i (t ) = p(t ) = u (t ) i (t ) =
2 n +1=1
2 cos( t ) = 2 (e 2 n +1=1
i
i
j t
+ e j t
)
Die Leistung ergibt sich aus dem Produkt aus Spannung mal Strom:2 n +1 i u e jt + e jt e j t + e j t 2 =1 2 2 n +1 2 n +1 i u i u p(t ) = e jt + e jt e j t + e j t = e jt (1+ ) + e j (1 ) + e jt (1 ) + e j (1+ ) =1 2 2 =1 2 2 i u und I = folgt: Mit U = 2 2 2 n +1 1 1 2n +1 p(t ) = U I e jt (1+ ) + e j (1 ) + e jt (1 ) + e j (1+ ) = U I 2[cos t (1 + ) + cos t (1 )] 2 2 =1 =1
(
)
(
)
(
)(
)
(
)
(
)
p(t ) = U I [cos t (1 + ) + cos t (1 )] =1T
2 n +1
Fr den Mittelwert der Leistung ber eine Periode ergibt sich als Wirkleistung:
P=
1 1 p(t ) dt = T T 0
T
p(t ) d (t ) =0
1 2
2
U I [cos t (1 + ) + cos t (1 )] d (t )0
2 n +1
=1
P= P=
1 21 2
2
U I [cos t (1 + ) + cos t (1 )] d (t ) = 0 fr 10
2 n +1
=1
2
1 U I [cos 2t + 1] d (t ) = 2 U I (2 0) = U I1 1 0
1,
Ergebnis: P = U I1
Beispiel eines reinen Oberschwingungsstromes: i ges = i (sin 3 t + sin 5 t + sin 7 t + sin11 tWechselstrom, -Spannung und -LeistungSpannung Strom 3. Oberschwingung Leistung
)Leistung
Wechselstrom, -Spannung und -LeistungSpannung Strom 5. Oberschwingung Leistung
Wechselstrom, -Spannung und -LeistungSpannung Strom 7. Oberschwingung Leistung
Wechselstrom, -Spannung und -LeistungSpannung Strom 11. Oberschwingung
1,00 0,75 0,50
1,00 0,75 0,50
1,00 0,75 0,50
1,00 0,75 0,50
Funktionswert
Funktionswert
Funktionswert
Funktionswert
0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360
0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360
0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360
0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360
Argument
Argument
Argument
Argument
Wechselstrom, -Spannung und -Leistung
Der Mittelwert der Leistung ist gleich Null. Aber es ist wohl eine Blindleistung als Verzerrungsleistung vorhanden.
Spannung
Strom 3.+5.+7.+11.Oberschwingung
Leistung
1,00 0,75 0,50
Man erkennt die Spiegelsymmetrie des Stromes da gilt:
Funktionswert
0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360
T i (t ) = i t 2 Argument
Die Oberschwingungen lschen sich teilweise gegenseitig aus.
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
29
5. Netzregelung5.1 Primrregelung mit statischer Frequenz-Leistungs-Kennlinie 5.1.1 Drehmoment und Leistung von Strmungsmaschinen Das Drehmoment durch die Kraftwirkung des strmenden Mediums auf die Turbinenschaufeln ist maximal bei Stillstand des Rotors bei = 0 . Es ist gleich Null, wenn die Umfangsgeschwindigkeit gleich der Strmungsgeschwindigkeit des ausstrmenden Mediums ist, da dann keine Kraft mehr auf die Turbinenschaufeln ausgebt wird: = max . Wird fr 0 max ein linearer Zusammhang angenommen, so gilt:
Drehmoment M, Leistung P
Abhngigkeit von der Winkelgeschwindigkeit . Die maximale Leistung ergibt sich durch Differentiation und Null setzen zu:
M = M max 1 Fr die Leistung gilt: P = M max P = M max 1 Dies ist eine quadratische max
Drehmoment- / LeistungsdiagrammM P
2 1,5 1 0,5 0 0 0,5
Werte normiert auf Mn und Pn
1 1 + max max dP =0 = M max 1 2 d max 1 Daraus folgt: = n = max 2 dP = M max d
1
1,5
2
Leistungsk oeffizient
K=
P 1 Pn = f s fn
Strmungsmaschinen werden mit einer Drehzahl betrieben, die der Hlfte der maximal erreichbaren Geschwindigkeit im Leerlauf entspricht. (Durchgangsdrehzahl). 5.1.2 Primrregelung der Kraftwerke durch statische Regelkennlinie:
f fn
tan =
f s P
Ys
Rn P
3
Italien- Blackout am 28. September 2003
Statik
s=
f fn f Pn = P Pn P fn
T KPn P
G3~
blicher Wert s = 4 %
0
0
5.1.3 Sekundrregelung mit dem Netzkennlinienverfahren nach Graner Durch die Sekundrregelung werden die bergabeleistungen an den bergabestellen zu den Nachbarnetzen und die Frequenz wieder auf ihre jeweiligen Sollwerte zurckgefhrt. Sekundrregelung im Verbundbetrieb der Kraftwerke zweier Netzgebiete
PG1
PN1 N1
PN2+PN2 bergabeleistung P Zunahme der Leistung im Netzgebiet N2 um PN2 mit der Folge, dass P um P1 ansteigt N2
PG2
G3~
G3~
Es sei in der Ausgangslage: PG1 =PN1 und PG2 = PN2, dann ist die bergabeleistung P =0 und die Frequenz ist gleich der Nennfrequenz f = 50 Hz. Der Arbeitspunkt liegt im Schnittpunkt der beidenD:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
30 Netzkennlinien (Frequenz-Leistungskennlinien K1 und K2). Die Kraftwerke im Netzgebiet N1 liefern die Leistung PG1 und die Kraftwerke im Netzgebiet N2 liefern die Leistung PG2.
f
f
Leistungsk oeffizient
K=
P 1 Pn = f s fn
f
K2
K1 fn f A2 P2
K2 A P1 PN2 PN2 PG1 PG2 P1 A1 f fn
PG2 P2 PG1
PG1
PG2
Nun soll die Last im Netzgebiet N2 um PN2 zunehmen. Die Folge ist eine Frequenzabsenkung durch die Lastzunahme im Netz 2. Diese betrgt: Infolge der Frequenzabsenkung steigt die Last der Kraftwerke im Netzgebiet N1 um P1 = K 1 f und im Netzgebiet 2 um P2 = K 2 f an. Nun greift die Sekundrregelung ein und bildet die Stellgren: YS1 = K 1f + P und YS 2 = K 2 f + P .
YS1 = K 1f K 1f = 0 ,
YS 2 = K 2 f + K 1f = K f = PN 2
Im Netzgebiet N2 wird die Frequenz-Leistungskennlinie durch Aktivierung von Leistung parallel nach oben verschoben, so dass sich der ursprngliche Arbeitspunkt A wieder einstellt. 5.1.4 Tertirregelung zum Zeitausgleich zwischen astronomischer Zeit tA und der Synchronzeit tS:Hz50,3 50,2
Blackout in Italien am 28.9.2003 um 3.29 Uhr
Frequenz
50,1 50 49,9
Erzeugerleistung > Verbraucherleistung
tS =
f 1 f (t ) dt A , fr f = const . : t S = t A fn 0 fn
TA
49,8 0:00
1:00
2:00
3:00
4:00
5:00
6:00
Auf der Zeitachse lsen die einzelnen Regelverfahren einander ab: Die Primrregelung ist in den ersten 30 Sekunden wirksam, dann folgt die Sekundrregelung in dem verursachenden Netzgebiet, um in den folgenden 15 Minuten den Normalzustand bezglich der Frequenz und Leistungen zu den benachbarten Netzen in allen Netzgebieten wieder herzustellen. Nach Absprache kommt dann ggfs. die Minutenreserveleistung dort zum Einsatz, wo keine ausreichende Regelleistung mehr verfgbar ist, mit entsprechender Anpassung der Sollwerte fr die bergabeleistungen.
Zeit
PrimrRegelung
SekundrRegelung
Minutenreserve - Leistung
30 s50,1 50,05
15 min02.09.2010
1hFrequenzverlauf UCTE Netz Europa50,1 50,05
t02.09.2010
Frequenzverlauf UCTE Netz Europa
Hz
50
Hz06:00:00 12:00:00 18:00:00 00:00:00
50
49,95 49,9 00:00:00
49,95 49,9 06:00:00
Zeit
07:00:00
Zeit
08:00:00
09:00:00
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
31
6. Ausgewhlte Themen der Netzpraxis6.1 Verschiebungs- und Verzerrungsblindleistung Wechselstromleistung nicht sinusfrmiger Strme nach DIN 40110:2 2 2 2 2 Scheinleistung S = U I = U I1 + I2 + I3 + ... + I + ...In
Fr spiegelsymmetrische Funktionen d.h. i (t ) = i t T Oberschwingungen, so dass gilt:
(
2
) entfallen die geradzahligen2 2 2 2 S = U I = U I1 + I3 + I5 + ... + I2 + ...In
Trger der Wirkleistung ist nur die Grundschwingung des Stromes in Verbindung mit der sinusfrmigen Spannung:
P = P1 = U I1 cos1
Fr die Blindleistung Q gilt:
Q = S2 P 2
Die Blindleistung Q setzt sich zusammen aus der Grundschwingungsblindleistung Q1 und der Verzerrungsleistung D:
Q1 = U I1 sin 1
2 2 2 2 D = U I 3 + I 5 + ... + I + ...I n
Fr die Grundschwingungs-Scheinleistung S1 gilt: Fr den Leistungsfaktor als das Verhltnis von Wirkleistung zu Scheinleistung gilt:
S1 = U I1
=
P = g i cos 1 S
mit g i =
I1 I
gi ist der Grundschwingungsgehalt des Stromes. cos1 ist der Grundschwingungs-Leistungsfaktor (auch Verschiebungsfaktor genannt). Fr nichtsinusfrmige Strme gilt: < cos1 Fr die Scheinleistung S gilt:
S 2 = P 2 + Q12 + D 2 ,
2 S = P 2 + Q1 + D 2
Die Verzerrungsblindleistung lsst sich auch mit dem Klirrfaktor k und der Scheinleistung S ausdrcken:
D = S k
In der Nachrichtentechnik werden nichtlineare Verzerrungen durch das Dmpfungsma Dk (Klirrdmpfung) in dB oder als Klirrfaktor k in Prozent angegeben. Auch der englische Ausdruck THD = Total Harmonic Distortion ist fr die Verzerrungsgre Klirrdmpfung blich. Das Dmpfungs-ma Dk ist der Pegelunterschied zwischen Klirranteil (unerwnschte Oberschwigungen) und dem gesamten Signal in dB. Der Klirrfaktor eines Audiogerts gibt an, in welchem Mae einem sinusfrmigen Eingangssignal (Messton) durch nichtlineare Verzerrungen unerwnschte Obertne bzw. Harmonische zugefgt werden. Er ist also ein Ma fr die auftretenden harmonischen Verzerrungen.2 2 2 2 2 2 2 2 2 2 U 2 + U 3 + U 4 + ... + U + ... + U n U 2 + U 3 + U 4 + ... + U + ... + U n k= 100% = 100% 2 2 2 2 2 2 U1 + U 2 + U 3 + U 4 + ... + U + ... + U n U2
THD = Dk = 20dB log10 kZeigerdarstellung der Leistungen:
P S Q1 D Q
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
32 Liniendiagramme verschiedener Oberschwingungsstrme bei sinusfrmiger Spannung:
u = u sin t , i = i sin 3 t
Wechselstrom, -Spannung und -LeistungSpannung Sinus Strom 3. Oberschwingung Leistung
p ( t ) = u sin t i sin tFunktionswert
1,00 0,75 0,50 0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360
p ( t ) = u i sin t sin tP =n
=1
1 p ( t ) dt = P1 T 0 2
T
Argument
P1 =
1 1 u i1 sin 2 t d (t ) = u i1 = U I1 2 2 0T
1 Fr alle ungleich 1 gilt: P = T
p ( t ) dt = 00
Allgemein gilt: Nur die Grundschwingung des Stromes ist Trger der Wirkleistung
i = i [sin t + 1 3 sin(3t ) + 1 5 sin(5t ) + 1 7 sin(7t ) + ...]Oberschwingungsbehafteter Strom bestehend aus Grundschwingung + 3. bis 11. Oberschwingung, Leistungsmaximum = 1,00 p.u. Man erkennt, dass die aus der Summe aller Teilleistungen der Grund- und Oberschwingungen gebildete rote Leistungsflche Flchengleich der allein aus der Grundschwingung des Stromes mit der sinusfrmigen Spannung gebildeten grnen Leistungsflche ist. Stromaufnahme kapazitiver Netzgerte (z. B. Fernseher, Computer, Energiesparlampen, Ladegerte):1,00 0,75 0,50
Wechselstrom, -Spannung und -Leistungsinusfrmige Spannung Grundschwingungsstrom + 3.+5.+7.+9.+11. Oberschwingung Leistung aus Grundschwingungsstrom Leistung aus Synthesestrom Strom als Rechteckfunktion
Funktionswert
0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360 Argument
i ges = i (0,27 sin t 0,19 sin3 t + 0,19 sin5 t 0,13 sin7 t + 0,11sin9 t 0,11sin11 t )
u = u sin tEffektivwert der Spannung:U = u / 2 = 0,707u
Wechselstrom, -Spannung und -Leistungsinusfrmige Spannung (Effektivwert = 0,707 p.u.) Grundschwingungsstrom + 3.+5.+7.+9.+11. Oberschwingung Leistung aus Grundschwingungsstrom Leistung aus Analysestrom Leistungsmittelwert = 0,14 p.u. Effektivwert des Stromes = 0,31 p.u.
Normierung p.u.
u u= =1 U0Leistung:
i i = =1 I0Funktionswert
1,00 0,75 0,50 0,25 0,00 -0,25 -0,50 0 30 60 90 120 150 180 210 240 270 300 330 360
p (t ) = u (t ) i (t )Wechselstrom, -Spannung und -LeistungSpannung Strom Grundschwingung Leistung
1,00 0,75 0,50
Argument
Funktionswert
0,25 0,00 -0,25 -0,50 -0,75 -1,00 0 30 60 90 120 150 180 210 240 270 300 330 360
Argument
-0,75 -1,00
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
33 6.2 Resonanzwirkungen in oberschwingungsbehafteten Netzen 6.2.1 Resonanz zwischen Einspeisetrafo und Blindleistungskompensationsanlage Schaltplan einer Last mit Kompensationskondensator, uk = 4% U = Un R C Ersatzschaltplan: XkWiderstand in Ohm
Blindwiderstand X=XL-XC Reihenresonanz Trafo mit KompensationsanlageXL XC X = XL+XC f Resonanz
0,2 0,0
Un 3
RY
CY
-0,2 -0,4 -0,6 -0,8
RY ist der Phasenwiderstand und CY ist die Phasenkapazitt der Ersatz-Sternschaltung. Zunchst soll der Widerstand RY unbeachtet bleiben. Dann gilt fr die Resonanzfrequenz der Reihenschaltung aus Induktivitt und Kapazitt (Reihenresonanz mit Blindwiderstand X=0) bei der Resonanzfrequenz fR:Frequenz in Hz
50
150
250
350
450
550
650
fR =Mit X k Z k gilt: X k =
QC X 1 1 , Lk = k , CY = 2 2 n n U n Lk CY
Uk u U , Fr die Kurzschlussspannung des Transformators gilt: U k = k n 100 3 In
u k ist die relative Kurzschlussspannung. Sie wird als Prozentwert angegeben. Bei Ortsnetztransformatoren ist z.B. u k = 4% . Bei Hochspannungstransformatoren ist u k = 10 % .Die Kurzschlussspannung ist diejenige Spannung, die bei kurzgeschlossener Unterspannungsseite oberspannungsseitig angeschlossen werden kann, damit der Strom in beiden Wicklungen gleich dem Nennstrom wird. So lsst sich im Prffeld das thermische Verhalten auch bei niedriger Leistung prfen.
Lk CY =
QC QC QC Q Uk u U u u 1 1 1 = k n = k = k 2 C 2 2 n I n n U n 100 3 n I n n U n 100 3 n I n n U n 100 n Sn 100 Sn u k QC2 2 UY U n folgendes: = RY RY
Damit ergibt sich fr die Resonanzfrequenz: fR = fn
Mit Bercksichtigung des Lastwiderstandes RY ergibt sich mit der Last P = 3
Resonanz liegt vor, wenn der Imaginrteil verschwindet, also Im{Z } = 0 wird.
1 jCY RY R (1 jCY RY ) Z = jLk + = jLk + = jLk + Y 2 1 jCY RY + 1 1 + (CY RY ) R+ jCY RY 2 CY RY 2 1 + ( CY RY )
Lk =
2 1 CY RY 2 = 1 + ( CY RY ) 2 = Lk (CY RY )2
C 2 Y RY 1 L k
2 =
1 Lk CY1 Lk CY
L 1 2 k R C Y Y
2 2 L u Un u Un 1 U 2 P U2 , 2 k = k 2 n n = k 4 n n R C 100 n Sn RY 100 n Sn U n QC QC Y Y 2 100 n S n = u QC k
2 =
u P 1 k 100 S Q n C
u P 1 k 100 S Q n C
2 100 S n = n u k QC
u P 1 k 100 S Q n C
Allgemein gilt somit fr die Resonanzfrequenz: fR = fn
100 Sn u k QC
u P 1 k 100 S Q n C
Beispiel: Ortsnetztransformator 630 kVA, uk = 4 %, P = 500 kW, QC=250 kVar:
u P 1 k 100 S Q = 384Hz n C Durch die ohmsche Last wird die Resonanzfrequenz geringfgig um 3,4 % erniedrigt.fR = f n
100 Sn 100 Sn 100 630 = 50Hz = 397Hz , fR = fn u k QC u k QC 4 250
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
34 6.2.2 Verdrosselung der Blindleistungkompensationsanlage
uk = 4%
U = Un LD IL C M
Ersatzschaltplan fr die Oberrschwingungeinspeisung des Stromrichters
IL,h
Xk
Ik,h
LD CY
I K ,h I L,h
=
Z N ,h Z N ,h + Z K ,h
mit der Netzimpedanz: Z N ,50 Hz
2 UN = uk S n,T
u k als per unit -Wert (p.u.)0,8 0,6
fr Oberschwingung h ist die Netzimpedanz: Z N ,h Fr den verdrosselter Kompensationszweig gilt: X K = X LD X C , mit dem Verdrosselungsfaktor p =2 n
U2 = uk N h S n,TIk / IL
Saugwirkung einer verdrosselten Kompensationsanlage fr die 7. Oberschwingung 4 7 14 % p=
0,4 0,2 0,0
X LD 2 = n LD CY folgt: XC2 n
U 1 1 U , fr die Oberschwingung h: X C ,h = X C = , XC = QC h h QC X LD
0,0
0,2
0,4
Qc / Sn,T
0,6
0,8
1,0
2 2 UN Un = p XC = p , fr die Oberschwingung h: X LD,h = p h X C = p h QC QC 2 Un 1 = ph , QC h
X k ,h = X LD,h X C,h
h= , n
QLC
QC U2 U2 = = = X C X LD X C p X C (1 p )
QLC ist die kapazitive Blindleistung der verdrosselten Kompensationsanlage. (s. Grossmann, etz 5/2008) Damit folgt fr das Verhltnis des von der Kompensationsanlage abgesaugten Oberschwingungsstromes zu dem vom Stromrichter emittierten Oberschwingungsstrom der Ordnung h:
I K ,h I L,h
=
Z N ,h Z N ,h + Z K ,h
uk h =
2 Un S n,T
uk =
QC S n,T
u k (1 p ) = u k (1 p )
QLC S n,T
U2 U2 1 uk h n + n p h S n,T QC h
Q 1 uk C + p 2 S n,T h
QLC 1 +p 2 S n,T h
Durch die Verdrosselung wird die Resonanzfrequenz der Kompensationsanlage mit dem Einspeisetransformator zu niedrigeren Werten verschoben: Mit h =
, ergibt sich die Resonanzn
Blindwiderstand X=XL-XC Reihenresonanz Trafo mit KompensationsanlageXL XC X = XL+XC f Resonanz XL+XCD
frequenz, wenn man den Nenner gleich Null setzt, mit = R zu:
0,2
R = n
S nT u k QC
1 1+ p S n,T u k QC
Widerstand in Ohm
0,0
-0,2 -0,4 -0,6 -0,8 50 150 250
Mit den vorstehenden Daten ergibt sich bei p = 7 % fr die Resonanzfrequenz fR = 170,6 Hz gegenber
fR = 396,9 Hz ohne Verdrosselung.
Resonanzfrequenz bei 7 % Verdrosselung350
Resonanzfrequenz ohne Verdrosselung450 550 650
Frequenz in Hz
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
35 6.3 Allgemeine Bestimmungsgleichungen im Drehstromnetz, Stern-Dreieckumwandlung a) fr Dreieck-Stern-Umwandlung I1 Z1
I1
U12 U23
Z12 I2 U31 I 3 Z23Z2 =
-Z31Z0
L1 L2
U1
I2 I3 I0
Z2 Z3 Z0
U2 L3 U3
MpZ 23 Z 12 , Z 12 + Z 23 + Z 31 Z3 = Z 31 Z 23 Z 12 + Z 23 + Z 31
Z1 =
Z 12 Z 31 , Z 12 + Z 23 + Z 31
b) fr Stern-Dreieck-Umwandlung
L1 L2
I1 U1 I2 I3 I0
Z1 Z2 Z3 Z0
I1
-
U12 U23
Z12 I2 U31 I 3 Z23 Z31
U2 L3 U3
MpZ Z Z1 Z 2 Z 23 = Z 2 + Z 3 + 2 3 , , Z3 Z1 Leiterstrme im Dreileitersystem: Z 12 = Z 1 + Z 2 + Z 31 = Z 3 + Z 1 + Z 3 Z1 Z2
In einem Dreileiter-Drehstromnetz muss der Widerstand Z0 im Mittelpunktleiter gleich unendlich gesetzt werden (I0 = 0), so dass fr die drei Bestimmungsgleichungen der Leiterstrme gilt:
U 1 (Z 2 + Z 3 ) (U 2 Z 3 + U 3 Z 2 ) (Z 1 Z 2 + Z 2 Z 3 + Z 3 Z 1 ) U (Z + Z 1 ) (U 3 Z 1 + U 1 Z 3 ) I2 = 2 3 (Z 1 Z 2 + Z 2 Z 3 + Z 3 Z 1 ) U (Z + Z 2 ) (U 1 Z 2 + U 2 Z 1 ) I3 = 3 1 (Z 1 Z 2 + Z 2 Z 3 + Z 3 Z 1 ) I1 =
L1U12 L2 U23
L1U1 U2
I1 I2 I3
Z1 Z2 Z3
L2 L3
U3
Ein Beispiel ist die Symmetrierschaltung im Induktionsofenbau (Steinmetz-Schaltung):
L1 L2 L3
I1 U12 U31 I2 U23
Z1=R Z2=R
L1 L2 L3
I1 U12 U31 I2 U23 I3
Z1=3R Z2=jX Z3=-jX
I1 U31 I3 I2
X= 3 R Z12=jX Z31=-jX
I3 Z3=R
Z23=R
L3Fr die Leiterstrme gilt: I1 = I 2 = I 3 =
U Ph U wenn X = 3 R ist. = R 3 R
Die Strme sind in Phase mit den zugehrigen Phasenspannungen, d.h. die Schaltung wirkt wie eine rein ohmsche Last mit dem Widerstand R. Der Strom I1 ist unabhngig von der Gre des Widerstandes Z1 = R, da Z2 = - Z3 ist! Da die Induktionsspule zur Erzeugung des Wechselfeldes im Schmelzmaterial ein ohmsch-induktiver Widerstand ist, muss dieser durch eine gesteuerte Parallelkompensation auf cos = 1 kompensiert werden.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
36 6.4 Belastung des Transformators mit maximalem Wirkungsgrad
Pv = P0 + 3 I 2 Rk ,
I=
S U 3
=
P U 3 cos
,
=
P P = P + Pv P + P0 + 3 I 2 Rk
Fr den Wirkungsgrad gilt:
=
P P P + P0 + 3 Rk U 3 cos 2
=
P U 2 cos 2 = f (P ) (P + P0 ) U 2 cos 2 + Rk P 2
Um das Maximum zu finden wird die Funktion f(P) nach P differenziert und gleich Null gesetzt:
d U 2 cos 2 (P + P0 ) U 2 cos 2 + Rk P 2 U 2 cos 2 + 2 P Rk P U 2 cos 2 = 2 dP (P + P0 ) U 2 cos 2 + Rk P 2
[
[
] [(
]
)
]
d =0 dP
= max
U 2 cos 2 (P + P0 ) U 2 cos 2 + R Pk = U 2 cos 2 + 2 P Rk P U 2 cos 2
[(P + P ) U0
[
2
cos 2 + Rk P 2
] [ ] = [U
2
cos 2 + 2 P Rk
] ] P
P0 U 2 cos 2 + Rk P 2 = 2 P 2 Rk P0 U 2 cos 2 = P 2 Rk P2 =2
P0 U 2 cos 2 , Rk
Rk =
Pk 2 3 In
2 2 P0 U 2 cos 2 3 I n P0 Sn cos 2 P = = = S 2 cos 2 Pk Pk
S=
P0 Sn Pk
Anwendungsbeispiel: Ortsnetztransformator mit Sn = 630 kVA Nennleistung, Un =400V, cos=0,9 weist im Prfprotokoll folgende Daten aus: P0=1.350 W, Pk=7.000 W
S=
P0 1.350 Sn = Sn = 0,44 Sn = 44% Sn Pk 7.000 P P S cos S cos = = = 2 2 P + Pv P + P0 + 3 I Rk S cos + P0 + 3 (a I n ) Rk S cos + P0 + a 2 Pk
=
Allgemein gilt fr den Lastfaktor a = S/Sn = (P/cos)/Sn:
= max =0,44 Sn cos
a Sn cos a Sn cos + P0 + a 2 Pk2
0,44 Sn cos + P0 + 3 (0,44 I n ) Rk
=
0,44 Sn 0,9 = 98,93 % 0,44 Sn 0,9 + P0 + o,44 2 Pk
max = 98,93 % bei cos = 0,9 , max = 99,03 % bei cos = 1
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
37
7. Leitungsnetzberechnung7.1 Allgemeine Leitungsgleichungen Herleitung der Leitungsgleichungen
i1 = i(x,t) u1 = u(x,t) x = x1
R'dx
L'dx C'dx G'dx
i2 = i[(x+dx),t] = i1 + di u2 = u[(x+dx),t] = u1 + du
xu 2 t
i 1 = i 2 + G dx u 2 + C dx u1 = i 1 R dx + L dx
i1 + u2 t
x = x2 = x+dx i u = G u + C t x u i = R i + L t x
i i 2u 2u u u L G = R + L + C 2 = R G u + C x t x t t t x 2
Dies fhrt zur Leitungs-Wellengleichung oder Telegraphengleichung:
u 2u 2u C 2 + (R C + G L ) + R G u , u = f (x, t ) = Re 2 U e jt , u = 2 U =L 2 t t x Fr die sinusfmigen Spannungen u(t ) und die Strme i (t ) gilt in der komplexen Ebene mit denZeigergren: U = U ej u
{
}
, I = I e
j i
(U und I sind die Effektivwerte der entsprechenden Gren):
u (t ) = 2 U e jt ,
u = j 2 U e jt , t
i (t ) = 2 I e jt ,
i = j 2 I e jt , t
2u 2u 2 jt = 2 U e , = L C 2 + j (R C + G L ) + R G 2 U e jt 2 2 t x
[
]
d2 U = (R + j L ) (G + j C ) U dx 2Diese Leitungsgleichung ist eine Differentialgleichung zweiter Ordnung mit konstanten Koeffizienten, fr die der Lsungsansatz gilt:
U = U0 e U0 e2
x
,
d2 U 2 = U 0 e x 2 dx
Aus diesem Ansatz folgt fr die komplexe Konstante : x
2
x
= (R + j L ) (G + j C ) U 0 e
= (R + j L ) (G + j C ) , 1,2 = (R + j L ) (G + j C ) =
= + j
nennt man die Fortpflanzungskonstante, ZW ist der Wellenwiderstand der Leitung. ist der Dmpfungsbelag (Dmpfungskonstante), ist der Phasenbelag (Phasenkonstante) der Leitung. Allgemeine Lsung der Leitungsgleichung:
U (x ) = U v e
x
+ Ur e
+ x
Dies ist die Summe aus einer vorlaufenden und einer rcklaufenden Spannungswelle. Wegen:
u i U = R i + L oder = (R + jL ) I folgt fr den Strom I : t x x
I (x ) =
G + jC x + x Uv e Ur e R + jL
(
)
mit Z W =
R + jL als Wellenwiderstand. G + jC
Somit folgt fr den Strom:
I (x ) =
Uv U x + x e r e ZW ZW
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
38 Herleitung der hyperbolischen Form der Leitungsgleichungen Am Leitungsende gilt fr x = l:
U2 = Uv e ZW I 2 = U v e
l l
+Ur e Ur e
+ l + l
U 2 + Z W I 2 = 2U v e U 2 Z W I 2 = 2U r e Uv =
l + l
Daraus folgt fr die Spannung der vorlaufenden Welle:
U 2 + Z W I 2 + l e 2 U Z W I 2 l Entsprechend fr die Spannung der rcklaufenden Welle: U r = 2 e 2Am Leitungsanfang gilt fr x = 0:
U1 = Uv + U r ,
I1 =
Uv Ur ZW ZW
Somit fr die Spannung am Leitungsanfang:+ l
U + Z W I 2 + l U 2 Z W I 2 l e U1 = Uv + U r = 2 e + e = U2 2 2
+e 2
l
+ ZW I 2
e
+ l
e 2
l
U 1 = U 2 cosh l + Z W I 2 sinh l ,
U (x ) = U 2 cosh ( l x ) + I 2 Z W sinh (l x )I (x ) = I 2 cosh (l x ) + U2 sinh (l x ) ZW
I 1 = I 2 cosh l +Sonderflle:
U2 sinh l , ZW
a) nur Lngswiderstnde:
= (R + j L ) (G + j C ) = 0 , Z W = R + jL = G + jC
I1 U1 x=0
R=R'l
L=L'l
I2 = I1 U2
Die Unbestimmtheit des Produktes im zweiten Term der Spannungsgleichung ergibt sich aus der2 3 Reihenentwicklung: sinh x = x + x + ... cosh x = 1 + x + ...
zu: sinh l = R + jL , so da gilt:
3!
2!
x
x=l
U 1 = U 2 + (R + j L ) I 2 , I 1 = I 2
b) verlustlose Leitung, fr R = 0 und G = 0 ergibt sich: =
I1
L=L'l
I2 U2 x=l
= ( 2 L C ) = j = j L C ,Z W = ZW =
(R + j L) (G + j C ) = + j ,
=0U1 x=0Mit c =
C=C'l x1
1 c L L = , v = L C = C C r r v ist die Wellen, c ist die Lichtgeschwindigkeit e jx + e jx e jx e jx = cos x sinh jx = = j sin x cosh jx = 2 2Spannung und Strom bei Leerlaufbetrieb:Spannung U am Leitungsende und Strom am Leitungsanfang in Abhngigkeit von der Leitungslnge bei U1 = 400 kV, f = 50HzSpannung U2 2.000 U2 1.000 0 -1.000 -2.000 0 1500 3000 Lnge in km 4500 Strom I1 2.000 I1 1.000 0 -1.000 -2.000 6000
und c = f folgt: 0 0 1 c 1 1 = 2 = 2 r r 2 , v
Damit ergibt sich fr die Spannung und den Strom am Leitungsanfang der verlustlosen Leitung:
U 1 = U 2 cos 2
l
l C l I 1 = I 2 cos 2 + j U 2 sin 2 L
+ j
l L I 2 sin 2 C
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
397.2 Spannungsfallberechnung auf Leitungen Einphasiger Ersatzschaltplan:
Fr Hchstspannungsleitungen:
Fr Hoch- Mittel- und Niederspannungsleitungen:
I1 U1 G/2
R C/2
L C/2
I2 G/2 U2
R U1
X X=L
I U2
Zeigerdiagramm:
Drehstromleistung;
Re Uq U1 I jX IR U2=U2 j I Ul
P = P2 = 3 U 2 I cos = 3 U n I cos Spannungen:
U l = I R cos + I X sin U q = I X cos I R sin 2 U = U l2 + U q U l
U l = I cos (R + X tan ) = I cos (R `+ X ` tan ) l P U l = I cos l = l , = R `+ X ` tan 3 UnMit dem relativen Spannungsfall: u l =
3 Ul folgt: Un
u u l =
1 100% P l = P l 2 2 Un Un
Fr eine Leitung mit gleich bleibenden Leitungsdaten und mehreren Lastentnahmen gilt:
ln
~
I1
l2 P1
lk
u =P2 Pk Pn
n 100% Pk l k 2 Un k =1
Fr eine Leitung mit gleichmig verteilter Last gilt: Gleichmig verteilte Last p in kW/m
~I1 0 I(x) x
P1 = p l ,
I1 =
P1
3 U n cos
l
x x I (x ) = I 1 1 , P (x ) = P1 1 l l l
u =
P 100% l 1 2 2 Un
mit zustzlicher Punktlast P2 am Leitungsende gilt:
u =
P + P2 100% l 1 2 2 Un
mit
P1 = p l + P2
(Hier ist P1 die Summe aus verteilter Last plus P2) Bei der Leitung mit gleichmig verteilter Last ist der Spannungsfall halb so hoch, als wenn die Gesamtlast am Leitungsende wirksam ist. Dann wre hier: P1 = P2.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
40 7.3 Lastflussberechnung 7.3.1 Herleitung des Knotenpunkt-Potenzialverfahrens Einige Voraussetzungen fr die Geltung und Anwendung des Verfahrens: 1. Symmetrische Belastung im Drehstromnetz 2. Annhernd gleiche Phasenwinkel der Spannungen (sonst Berechnung mit komplexen Gren) 3. Annhernd gleiche Leistungsfaktoren der Lasten Bezeichnungen: Unbekannte Netzknotenpunktspannungen U1, U2,UkUn Speisepunkte mit vorgegebene Spannungen: UI, UII,Us,Um Vorzeichenregel: zuflieende Leistungen positiv, abflieende Leistungen negativ
k 2 i 1 Pi Pi,k Us
Fr den Lngsspannungsfall der Phasenspannungen gilt: U Ph = U i ,ph U k ,ph = I i ,k cos l i ,k , = R `+ X ` tan
~ ~
Fr den verketten Wert der Spannungen im Drehstromsystem gilt: U = (U i U k ) = 3 I i ,k cos l i ,k , mit =
UI
1 gilt: l Pi ,k Un Pi ,k Un
mit: Pi ,k = 3 U n I i ,k cos gilt:
U i ,k = 3 I i ,k cos =
U i ,k = (U i U k ) i ,k = 3 I i ,k cos =
k =1, k i
(Un
n
i
U k ) i ,k =
Ui
k =1, k i
i ,k
n P 1 n Pi ,k = i mit: Pi = Pi ,k Un U n k =1 k =1 n P U k i ,k = i Un k =1,k i
Nun werden alle Punkte k, die Speisespannungen sind, herausgenommen und auf die rechte Seite der Gleichung gebracht undk =1, k i
n
i ,k = i ,i gesetzt:
U i i ,i 11 21 31Mit i ,k =
k =1,k i ,k s
U k i ,k =
n
k = s =I
U
m
s
i ,k
Pi Un P1 P2 P 3
explizit ergibt dies fr k=3 und s=2 folgende Matrizengleichung:
12
22 32
13 U 1 1,I 23 U 2 = 2,I 33 U 3 3,I
1,II U 1 2;II I U II U n 3,II
Wenn man beide Seiten der Gleichung mit dem Widerstandsbelag der Leitung multipliziert, kann man an Stelle der Leitwerte auch die Kehrwerte der Lngen mit l-1 einsetzen: l 111 1 l 21 1 l 31 l 121
1 1 = l i ,k l i ,k (R `+ X ` tan )
l l
1 22 1 32
l 131 U 1 l 1I1 , 1 l 23 U 2 = l 2,1 I 1 l 1 l 33 U 3 3,I
1 l 1II , U l 2,1 I II U U n l 3,1 II II
P1 P2 P 3
Der Lastfluss zwischen den Punkten x und y ergibt sich zu:
Px ,y = (U x U y ) U n x ,y = (U x U y ) D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
Un l x ,y
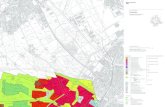
41 7.3.2 Anwendung der Lastflussberechnung nach dem Knotenpunkt-Potenzialverfahren Fr das angegebene Niederspannungsnetz mit der Impedanz, = R `+ X ` tan = 0,22 , Un =400 V km sollen der Lastfluss und die Knotenspannungen berechnet werden. 1 1 Fr die Leitwerte gilt: = 1 = 100 kW 1 = 4,55 Skm xy l xy l xyl xy 0,22 km
Allgemeine Form der Matrizengleichung beim Knotenpunkt-Potenzialverfahren: UI = Un = 400 V
UI
205 m 300 m 225 m 2
205 m 3 200 kW 100 m
11 21 31 1I + 13 21 31
12
22 32
13 U1 1I 1 23 U 2 = 2I U I Un 33 U 3 3I 13
P1 P2 P 3 P1 P2 P 3
12
2I + 23 32
U1 1I 1 23 U 2 = 2I U I Un 31 + 3I + 32 U 3 3I
100 kW
An Stelle der Lambda-Werte kann man auch die Kehrwerte der Leitungslngen in km in die Gleichung einsetzen, wenn man die Lngen-Matrizen mit -1 multipliziert.
1 1 1 1 + 0 l 13 l 1l l 13 U 1 l 1l P1 1 1 1 1 1 1 1 + P2 0 U 2 = U I l 2 l l 23 l 23 Un U l 2l 3 1 P3 1 1 1 1 1 + + l l 21 l 32 l 31 l 3I l 32 3l 1 1 1 1 + 0 205 U 1 205 205 205 1 1 1 1 U = 1 1 U + 0 m 2 225 m I U n 225 100 100 U 1 1 1 1 1 1 3 + + 205 100 205 300 100 300 0,00488 0 0,00976 U 0,00488 1 1 1 0,22 0,01 U 2 = 0,00444 400 V 0 0,01444 m 1km 400 V 0,00488 0,01 m 0,01821 U 3 0,0033
P1 P2 P 3 100 100 kW 200
0,00488 0 , 0,00976 U 1952 0,055 1,897 1 1 V V V 0,01 U 2 = 1,776 0,055 = 1,721 0 0,01444 m 0,00488 0,01 m 0,110 m 1,222 m 0,01821 , U 3 1332 Hieraus ergibt sich der Lsungsvektor fr die Knotenpunktspannungen und den Spannungsfall in %:
U 1 384,44 U 2 = 382,44 V U 380,15 3 Fr den Lastfluss gilt:
u1 3,89 U U n oder mit u = 100% fr u in %: u 2 = 4,39 % Un u 4,96 3 Un 400 = (400 384,44 ) = 138 kW 205 0,22 l I ,1
PI ,1 = Px ,y = (U x U y ) U n x ,y = (U I U1 )
(Anmerkung: vom Punkt x aus abflieende Last wird negativ gezhlt, d.h. Ux > Uy)D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
42 7.3.3 Anwendung der Lastflussberechnung nach dem Praktiker-Verfahren100 kW 1 205 m 3 200 kW 2 100 m
UI
205 m 300 m 225 m
100 kW
Im ersten Schritt werden alle Zweiglasten in die benachbarten Knotenpunkte verlagert50 kW UI 205 m 300 m 1 205 m 50 kW 3 200 kW 30,77 kW 2 69,23 kW 100 m
Im zweiten Schritt werden alle Zweiglasten in den Knotenpunkten zusammengefasst1 UI 205 m 300 m 205 m 3 319,23 kW 30,77 kW 225 m 2 100 m
225 m
Im dritten Schritt werden alle parallelen Leitungen zu einer Ersatzleitung zusammengefasst173,24 m UI 3 319,23 kW 30,77 kW 325 m
Im vierten Schritt werden die Teilleistungen der beiden parallelen Zweige nach der Stromteilerregel berechnet und eingetra325 gen. P = P = 208,23kW1
325 + 173,24
173,24 m UI 208,23 kW 111,00 kW 30,77 kW 325 m 319,23 kW 3
Im fnften Schritt werden alle Leistungen zurck verlagert. z.B. P 205 = 208,23 173,24 = 87,98kW410
Im sechsten Schritt werden alle vorher verlagerten Leistungen addiert und eingetragen100 kW 1 137,98 kW 37,98 kW 3 200 kW 41,77 kW 100 m
1 87,98 kW UI 205 m 300 m 120,25 kW 111,00 kW 225 m 2 205 m 3 319,23 kW 141,77 kW 100 m 225 m UI 205 m 300 m
205 m
120,25 kW 2
30,77 kW
Damit ist der Lastfluss vollstndig bestimmt. Die Knotenspannungen knnen nun mit der Gleichung: Px ,y = (U x U y )U n x,y (U y U x ) =D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
100 kW
Px ,y U n x ,y
berechnet werden.
43
Lastfluss und Spannungen in einem Modellnetz mit 3 Lastpunkten und einer SpeisespannungDas negative Vorzeichen bei den Lastflssen bedeutet: vom Bezugspunkt aus abflieende Leistung. Die Leitungslngen knnen hier direkt in km eingegeben werden (Diese werden nach Tabelle 1 bertragen). U1= 384,44 kV 100 kVA
S1 1
-138,0
-38,0205 m
UI-400,0 UI= 400,0 V
205 m
3-120,2300 m
S3U3= 380,16 V 200 kVA
-141,8225 m
-41,8100 m
2Uebung zur Vorlesung EV/EW Prof. Dr.-Ing. Helmut Alt, FH Aachen
U2= 382,46 V 100 kVA
S2
Lastflussrechnungen werden in der Praxis mit umfangreichen Computerprogrammen unter Verwendung optimierter mathematischer Lsungsalgorithmen z.B. nach dem Newton-RaphsonVerfahren mit komplexen Datenstze durchgefhrt.
Lastfluss und Spannungen in einem Modellnetz mit 3 Lastpunkten und 2 SpeisespannungenDas negative Vorzeichen bei den Lastflssen bedeutet: vom Bezugspunkt aus abflieende Leistung. Die Leitungslngen knnen hier direkt in km eingegeben werden (Diese werden nach Tabelle 1 bertragen). U1= 19,363 kV 5,00 MVA
1
S1
-4,06
-3,136 km
-4,0610 km
UI-9,01 UI= 20,0 kV
10 km
U II-13,99
-3,9615 km
U II =
20,0
kV
-4,9512 km
-0,045 km
-5,9610 km
2Uebung zur Vorlesung EV/EW Prof. Dr.-Ing. Helmut Alt, FH Aachen
U2= 19,069 kV 12,00 MVA
3U3= 19,065 kV 6,00 MVA
S2 S3
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
44 Bei Einspeisungen der Leistung aus Photvoltaikanlagen im Niederspannungsnetz wird das Spannungsniveau im Netz wesentlich durch die Sonneneinstrahlung beeinflut. Bei wolkenlosem Himmel wird die Peakleistung eingespeist, bei trber Wetterlage wird keine Leistung eingespeist, obschon der Leistungsbedarf aller Verbraucher dann sogar stark ansteigt. Dadurch variiert die Spannung in der Nhe der Einspeisestelle realtiv stark.
Lastfluss und Spannungen in einem Modellnetz mit 3 Lastpunkten und PhotovoltaikeinspeisungDas negative Vorzeichen bei den Lastflssen bedeutet: vom Bezugspunkt aus abflieende Leistung. Die Leitungslngen knnen hier direkt in m eingegeben werden (Diese werden nach Tabelle 1 bertragen). U1= 383,75 V 100 kVASolare-Einspeisespannung
1
S1
3Netz-Einspeisung-147,8 kVA 205 m -47,8 kVA 205 m
U II =bedeckt
400,00 VSonne
UI-466,4 kVA UI= 400,00 V
-133,6 kVA 300 m
~ ~U II
S3-133,6 kVA 300 m 15,1 kVA 100 m -184,9 kVA 225 m U3=
378,49 V 300 kVA
2U2= 377,68 V 200 kVA
Uebung zur Vorlesung EV/EW Prof. Dr.-Ing. Helmut Alt, FH Aachen
S2
Im obigem Beispiel liefert die Photovoltaikanlage rund 120 kW Wirkleistung mit dem Leistungsfaktor cos =0,9 auch induktive Blindleistung, also eine Scheinleistung von 133,6 kVA. Dadurch wird die Spannung am Einspeisepunkt gegenber dem Netzpunkt 3 von 378,5 V auf 400 V angehoben. Ziehen Regenwolken auf, so dass die Einspeisung verschwindet und durch 10,8 kVA Bezugsleisung ersetzt wird, sinkt die Spannung am Netzpunkt 3 auf 370 V und am Einspeisepunkt unvermeidbar auf 368 V ab. Bei Schwachlast mit 10 % der Nennlast und voller Sonne kehrt sich der Lastfluss am Speisetrafo um, es werden 61,7 kVA U1= 379,37 V zurck gespeist und die Spannung 100 kVA U II steigt auf 424 V an (mit 56 V 1 S1 Spannungshub). Solare-Einspeisespannung3Netz-Einspeisung-187,6 kVA 205 m -87,6 kVA 205 m U II =bedeckt
368,00 VSonne
UI-610,8 kVA UI= 400,00 V
10,8 kVA 300 m
~ ~U II
S3-188,1 kVA 300 m -35,1 kVA 100 m -235,1 kVA 225 m U3=
369,73 V 300 kVA
2U2= 371,62 V 200 kVA
Uebung zur Vorlesung EV/EW Prof. Dr.-Ing. Helmut Alt, FH Aachen
S2
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
45 7.4 Spannungs-Leistungsdiagramme 7.4.1 Spannungs- und Leistungsverhltnisse bei Gleichstrom 2 U0 I , P = U , P = U U0 P = U I , I = R Ri + R Ri + RSpannung in V
Spannungs- und Leistungsdiagramm einer Spannungsquelle mit Innenwiderstand Ri100 80 60 40 20 0 0 2 4unendlich
250 200 150
=U 1,2
U0
P U
R
R=90 Ohm R=Ri=10 Ohm Spannung U6 Strom I in in A 10 8
U 2 U U 0 + P Ri = 0
100 50 0
U = f (P )
U U = 0 0 P Ri 2 2
2
40
15 Lastwiderstand R in Ohm 0
mit Normierung der Spannung U auf die Nennspannung U0n :u1,2 =
folgt mit: p = P , Pku0 =
Pk =
2 U 0,n
Ri
1 u0 1 u 0 p und fr u0 = 1: u1,2 = p 2 2 2 2 Spannungs- Leistungsdiagramm einer Spannungsquelle mit Innenwiderstandu0=1,0 u0=1,1 Maximalleistung
2
2
U0 , pmax = 1 Pmax = 1 Pk bei u0 = 1 4 4 U 0n1,2
Spannung / Nennspannung u
Der zulssige Betriebsbereich ist in dem Diagramm fr 10 % Spannungsabweichung vom Nennwert der Spannung gekennzeichnet. Der Maximalwert der Leistungsabgabe betrgt bei Nennspannung 1/4 der Kurzschlussleistung Pk. Bei hherer Leerlaufspannung verschiebt sich der Punkt fr die maximale Leistungsabgabe zu hheren Werten der Leistung und Spannung. Der Wirkungsgrad der bertragung mit maximaler Leistung ist nur 50%, da Ri=R ist.7.4.2 Spannungs- und Leistungsverhltnisse bei Wechselstrom/Drehstrom Energiefortleitung im bertragungsnetz
1,0 0,8 0,6
zulssiger Betriebsbereich Leerlauf u0 = 1,0 Maximalleistung bei R=Ri
0,4 0,2 0,0 0,0 0,1 0,2 0,3 0,4
Kurzschluss
u0 = 1,1
Leistungsabgabe / Kurzschlussleistung p
Netz A UA, A
Z = R+jX U
I
U A = U B + U ,
U = jX I
Netz B UB, B
Nherungsweise gilt in Hochspannungsnetzen:
Z jX , U jX Ib
Fr die Verlustleistung gilt: Pv = 3 I 2 R
Pv gilt mit Pv = 3 I 2 R und U als Leiterspannung sowie der S bertragungsleistung S = 3 U I :Fr die spez. Verlustleistung pv =
S R l 3 2 3 I R `l S 3 U = = 2 R l pv = S S U Setzt man in diese Gleichung die bertragungsleistung S in MVA, Die Leiterspannung U in kV, den lngenbezogenen Leitungswiderstand R in /km und die Leitungslnge l` in vielfache von 100 km ein, so ergibt sich die zugeschnittene Zahlenwertgleichung:
2
pv =
S R / l `10 4 %/100km 2 U
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
Leistung in W
Ri
U U0 = P Ri + P R = P Ri + U 2
P=Pmax=250W
46 Die charakteristischen Gleichungen fr die Wirk- und Blindleistungsbertragung ergeben sich bei vernachlssigtem ohmschen Anteil der Leitung aus dem Zeigerdiagramm fr Z = X zu:
X I cos = UA sin = X Iw UA X I sin = UA cos - UB = X Ib UB Iw I
PB = 3 U B I cos = 3 U B Iw = 3 U B PB = 3
U A UB (UA und UB sind Phasenwerte sin der Spannungen) X
UA sin X
Ib
d.h. Die Wirkleistungsbertragung von Punkt A nach Punkt B ist berwiegend vom Leitungswinkel der Spannungen = A-B abhngig. Fr die Leiterspannungswerte von UA Und UB gilt entsprechend:
PB =
U A UB sin X
Die Einspeiseleistung am jeweiligen Netzpunkt ist dem Leistungskoeffizienten k des Verbundnetzes und der bewirkten Freqenznderung proportional:
P = k f
k UCTE-Netz =16.000 bis 20.000 MW/Hz
Die Blindleistungsbertragung ist dagegen berwiegend von der Spannungsdifferenz zwischen der Spannung am Leitungsanfang UA und der Spannung am Leitungsende UE abhngig.
QB = 3 U B I sin = 3 U B I b = 3 U B QB = 3 2 U A U B cos U B X
(
)(
U A cos U B X
Falls UA, UB Leiterspannungen (verkettete Spannungswerte) sind, entfllt der Faktor 3.
Fr UA und UB als Leiterspannungen gilt: QB =
1 2 U A U B cos U B X
)
Die Lastflsse bei Parallelleitungen verteilen sich umgekehrt proportional zu den Zweigimpedanzen. Eine Beeinflussung der Lastaufteilung ist durch Einbringung einer Zusatzspannung in einem Parallelzweig in Form eines Transformators mit Lngs- Quer- oder Schrgregelung mglich. Bei Querregelung wird vornehmlich der Wirkleistungsfluss, bei Lngsregelung der Blindleistungsfluss beeinflusst:I1 Z1 Uz I I2 Z2
I1 = I
Uz Z2 Z 1 +Z 2 Z 1 + Z 2
I2 = I
Uz Z1 + Z 1 +Z 2 Z 1 + Z 2
Bei der Parallelschaltung eines Kabels zu einer Freileitung ergibt sich das Problem ungnstiger Lastverteilung, da die Impedanzen sehr unterschiedlich sind.
z.B. Es wird zu einer 110 kV Freileitung 95/15 Al/St mit 350 A Nennbelastbarkeit ein 110 kV-Kabel NA2XS2Y 3x1x150 mit 319 A Nennbelastbarkeit parallel geschaltet. Die Impedanzen sind: Freileitung: ZFreileitung = (0,30 + j0,395) /km, Kabel: ZKabel = (0,206 + j0,126) /km. Die Zusatzspannung sei gleich Null Uz = 0, dann ergeben sich folgende Teilstrme:
I Freileitung = I 0,33 e j 14,38
I Kabel = I 0,68 e j 6,95
Die stromtragfhigere Freileitung bernimmt nur noch 33 % der Last, das Kabel 68 %. Das Kabel saugt infolge der niedrigeren Impedanz der Freileitung den Strom weg! Die Einfgung einer Zusatzspannung scheidet aus technisch-wirtschaftlichen Grnden aus.
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
47 Bezieht man die Wirk- und Blindleistungen mit den Spannungen als Leiterspannungen auf die Kurzschluleistung Sk =
pB = u A u B sin
sin =
1 pB , u A uB
U An U Bn , so ergeben sich folgende normierte Gleichungen: X U U 2 und q B = u A uB cos uB mit: u A = A , u B = B Un Un 1 1 2 2 2 cos = qB + uB daraus folgt: 1 = 2 2 pB + q B + u B u A u B u A uB
(
)
[
(
)]2
2 2 2 2 2 4 u A u B = p B +q B + 2q B u B + u B
4 2 2 2 2 u B + u B 2q B u A + p B + q B = 0 2 2 2 x 2 + x 2q B u A + pB + q B = 0
( (
) )
x1,2x1,2
u2 u2 2 2 = A q B A q B q B pB mit 2 2 u2 = A pB tan 22 uA 2 2
2
tan =
qB pB
folgt fr: q B = pB tan
2 pB u A tan + pB ,
(
)
2 uA uB = pB tan 2
2 uA 2
2 pB u A tan + pB
2
(
)2 u2 uA 2 A pB 2 2 2
Fr pB = 0 gilt: u B =
2 u2 uA A = u A , Fr tan = 0 gilt: u B = 2 2
2
Spannungs- Leistungsdiagramm einer bertragungsleitungtan phi =0 tan phi =1 tan phi = -1 pB max
Bei rein ohmscher Last ist der Spannungsfall am geringsten. Bei induktiver Last ist der Spannungsfall gro.
1,4
Spannung / Nennspannung uB
Leerlauf 1,2 1,0 0,8 zulssiger Betriebsbereich kapazitive Last phi = -45
Bei kapazitiver Last steigt die Spannung am Lastpunkt an, es besteht die Gefahr der berspannung.
Der zulssige Betriebsbereich ist 0,6 wesentlich kleiner rein ohmsche Last phi = 0 als der mgliche Lastbereich zwi0,4 schen Leerlauf und induktive Last phi = 45 Kurzschluss bzw. 0,2 bis zum Punkt maximaler LastentKurzschluss nahme (Radikant 0,0 der inneren Wurzel 0,0 0,2 0,4 0,6 0,8 1,0 1,2 1,4 grer Null, vergleiWirkleistung / Kurzschlussleistung pB che Ra = Ri bei Gleichstrom). Auch hier ergibt sich ein Punkt maximaler Leistungsabgabe, der aber in der Energietechnik aus Grnden minimaler Leitungsverluste und vertretbarem Spannungsfall bei weitem nicht erreicht wird.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
48
8. Kurzschlussstromberechnung8.1 Ableitung der Allgemeinen Gleichung fr den Kurzschlussstrom
i(t) R X ik(t)
40
u(t)0 -40 0 5 10 15 20 ms
~
u(t)
t
u(t ) = u cos (t ) ,Dgl. 1.Ordnung Homogene Gleichung:
di u (t ) di L L X = i +T mit: T = = = dt R dt R R R L di u i +T = cos(t ) , T = ist die Zeitkonstante des Systems dt R R u (t ) = i R + L di ih + T h = 0 dt
mit dem Lsungsansatz: i h = k e
t T
Partikulre Lsung durch Ansatz in Form des Strgliedes:
i p = A sin t + B cos t
di p dt
= A cos t B sin t mit L multipliziert und eingesetzt in die
Ausgangsdifferenzialgleichung 1. Ordnung ergibt mit T =
L
R di u i +T = (A B T ) sin t + (B + A T ) cos t = (cos t cos + sin t sin ) dt R u sin , R B T + A = u cos Roder A + B T =
=
X : R
Der Koeffizientenvergleich ergibt zwei Gleichungen zur Bestimmung der beiden unbekannten Gren A und B: A B T =
u cos R
Diese ergeben sich aus den Matrizengleichungen: u sin T R u u u cos 1 sin + T cos u sin + T cos R R A= = R = 2 2 R 1 T 1 + (T ) 1 + (T ) T 1
A=
u sin + T cos R R sin + X cos R X =u = u 2 sin + 2 cos 2 2 2 R R R +X Z Z 1 + (T ) u R X A = sin + cos = i (cos sin + sin cos ) = i sin( + ) Z Z Z
entsprechend folgt fr B:
u R X cos + sin = i (cos cos + sin sin ) = i cos( + ) Z Z Z Gesamte Lsung: i (t ) = i h (t ) + i p (t ) mit der Anfangsbedingung: i (t = 0 ) = 0 folgt: B=i (t ) = k e t T
+ i[sin ( + ) sin t + cos ( + ) cos t ] = k e
t T
+ i cos [ t ( + )]
Aus: 0 = k + i[sin( + ) 0 + cos( + ) 1] = k + i cos[( + )] folgt: k = i cos( + ) folgt die
Gesamte Lsung:
T cos[t ( + )] e t cos( + ) i (t ) = i
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
49 8.2 Stosskurzschlussstrom und zeitlicher Verlauf des Kurzschlussstromes Der sich aus der allgemeinen Gleichung fr den Kurzschlussstrom ergebende Maximalwert des Kurzschlussstromes nennt man Stosskurzschlussstrom Is. Diesen findet man, wenn die differnzierte Allgemeine Gleichung fr den Kurzschlusstrom gleich Null gesetzt wird:Allgemeine Gleichung:T i (t ) = i cos[t ( + )] e t cos( + ) Die einhllende Grenzlinie
erhlt man, wenn man den cos-Funktionswert der eckigen Klammer gleich +/- 1 setzt.t 1 T di = i sin[t + ( + )] e cos( + ) =0, dt T 1 sin[t ( + )] = e T cos( + ) Tt
sin[t ( + )] =Fr R 0 gilt: sin[t ( + )] = 0
R T e cos( + ) X [t ( + )] = k mit k = 0, 1, 2, 3,L
t
t 1 = + , fr R = 0 ist = 90 (induktiv) , t 1 = 90t t cos[ 90 + ( 90)] e T cos( 90) = i1 e T sin i (t 1 ) = i
Das Maximun wir fr = 90 oder fr = 270 jeweils am Nulldurchgang der Spannung! Fr den Maximalwert des Stromes gilt somit:t 1 + e T i (t 1 ) = i
1,8 U Zk U 2 Zk I S,max = 1,8 U 2 Zk
Fr den Stosskurzschlussstrom I S gilt: I S = In der Praxis ist X k 10 R k . Somit gilt fr die Zeitkonstante T: T =
Xk L = = R Rk
10 R 1 s 30 ms 1 10 2 50 R s
Der Kurzschlusswechselstrom I k ist der sich zu Beginn des Kurzschlusses ergebende Wechselstromwert: Ik =
c Un mit c = 1,1 ZkKurzschlussstrom
kA50 25 0
Kurzschlussstrom i(t)i(t) o.G.
i(t)
i(t) u.G.
u(t)
kV40 30 20 10 0 -10 -20 -30 -40 100
Beispiel: Un = 20 kV Sn = 60 MVA uk = 10%
= 270
Xk = 0,66 , k = 84 Rk = 0,07 T = 30,3 ms Ik`` = 17,3 kA (fr c = 1) Is = 42,3 kA
-25 -50 0 20 40 60 Zeit in ms 80
In dem Diagramm ist die Generatorspannung fr = 270 und der Kurzschlussstrom dargestellt.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
50 8.3 Kurzschlusswechselstrom und Kurzschlussleistung Aus der Allgemeine Gleichung fr den Kurzschlussstrom:T cos[t ( + )] e t cos( + ) i (t ) = i
ergeben sich folgende fr die Berechnung der dynamischen und thermischen Kurzschlussbeanspruchung der Betriebsmittel gem den VDE Bestimmungen (VDE 0102, 0103) relevanten Effektivwerte: Anfangskurzschlusswechselstrom I K : IK =
2,002 k
Kappa = f(R/X)
c Un 3 Zk
,
Zk =
( R ) + ( X )2 k 2 11 U n ,
,Kappa
1,80 1,60 1,40 1,20 0,0 0,1 0,2 0,3
Fr die Einspeisequelle gilt: Z Q =
S
k ,Q
Mit X Q = 0,995 Z Q , RQ = 0,1 X Q , Sk,Q = 35 GVA Der Kurzschlusswechselstrom I k ist der sich zu Beginn des Kurzschlusses ergebende Wechselstromwert:
c Un mit c = 1,1 I = Zk k
R/X 0,4
0,5
Der Stosskurzschlussstrom betrgt: I S = 2 I k
, Fr die Stossziffer gilt: = 1022 + 0,96899 e Die Kurzschlussleistung ergibt sich zu: S k =
3,0301
R X
Fr Transformatoren gilt: uk U2 X T = 0,995 n , RT = 0,1 X T 100% S n,T Bei Leitungen gilt fr die Umrechnung auf das Spannungsniveau Un: 2 2 U U X L,N = X L N , R L,N = R L N U U
3 Ik Un
Der thermisch wirksame Mittelwert des Kurzschlussstromes ber die Zeit Tk ergibt sich zu:
I th
1 k 2 = i k (t ) dt , I th = I k m + n , Tk 0
T
m - Faktor fr GleichstromgliedKappa = 1,90 2,00 1,50 1,70 1,40 1,10
Der Faktor m kennzeichnet das abklingende Gleichstromglied, n das abklingende Wechselstromglied. Fr generatorferne Kurzschlusspunkte ist der Faktor n = 1. Fr m gilt die Nherung:
m=
2
2
e
x2 0, 6
, x = 2 + lg
Tk 1sUn in kV 110
m1,00 0,50 0,00 10 100
Tk in ms
1000
Beispiel:
Kurzschlussdaten auf der Unterspannungsseite einer 380/110 kV Transformator - Einspeisung mit 350 MVA Nennleistung, uk = 17%, aus einem 380 kV bertragungsnetz mit 35 GVA Kurzschlussleistung:Quellenhinweis Alt, H.: Kurzschlussstromberechnung mit dem programmierbaren Taschenrechner. Elektrizittswirtschaft, Jg. 79(1980), Heft 10, S. 379-382.
Sn in MVA 350
uk in % 17
Tk in s 0,1
SQ in GVA 35
Kappa = m=
1,74 0,63
Xk = Rk = Zk = Ik IS = Sk = Ith =
6,226 0,623 6,257 11,16 27,44 2.127 14,24
Ohm Ohm Ohm kA kA MVA kA
Kurzschlussimpedanz: Kurzschlusswechselstrom: Stosskurzschlussstrom: Kurzschlussleistung: Thermisch wirksamer K.-S.:
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
51 Die Kurzschlussberechnung lt sich vorteilhaft auf einer Excel-Vorlage auf Basis eines Modellnetzes vornehmen. Die gelb und orange gekennzeichneten Eingabedaten sind festen Zellen zugeordnet und hierzu die entsprechenden Gleichungen hinterlegt. Die Ergebnisse erscheinen dann in den gn markierten Zellen. Durch Variation der Leitungsdaten lassen sich vielfltige Anwendungen mit dieser Excel-Vorlage realieren. Die Excel - Tabellenrechnung ist zu einem komfortablen Ersatz des programmierbaren Taschenrechners fr ingenieurtechnische Anwendungen geworden. Die Kurzschluleistung nimmt mit wachsender Impedanz ab, die Kurzschlussstrme steigen mit niedrigerer Spannung an.
Interaktive Kurzschlussdatenberechnung im ModellnetzSk= Tk = 380 kV 35 0,1 GVA s IS = Ik = Sk = Ith = 350 17 110 MVA % IS = kV Ik = Sk = Ith =X in = R in = ZQ
131 53 35 68
kA kA GVA kA
XQ = RQ = = m=
4,5156 0,4516 1,7377
4,5383
0,63
Zk
27 11 2.127 14
kA kA MVA kA
Xk = Rk = = m=
6,2261 0,6226 1,7377
6,2572
0,63
2,72 0,51
2,72 0,51
2,47 0,47
2,92 0,88
R 1,2P X 1,2P 0,255 1,36 30,634
R P,3P X P,3P 0,2396 1,1859 120,003425 7,462024404
Zk
3,77 1,45 IS = Ik = Sk = Ith = 30 12 MVA % IS = 20 kV Ik = Sk = Ith = 0,15 0,07 IS = Ik = Sk = Ith = 15 6 220 8 kA kA MVA kAXk = Rk = = m= 1,987 0,2577 1,6761
Zk
Xk = Rk = = m=
0,01090275 0,00111388 1,7330091 0,62
0,0109595
23 9 1.784 12
kA kA MVA kA
Xk = Rk = = m=
7,412 0,8622 1,7031
7,462
0,59
Zk
IS = Ik = Sk = Ith =
52 21 15 21 400 630 4
kA kA MVA kA V kVA %
17 7 238 9
kA kA MVA kA
Xk = Rk = = m=
1,837 0,1877 1,733
1,8466
0,62
Zk 2,0037
0,55
Quellenhinweis Alt, H.: Kurzschlussstromberechnung mit dem programmierbaren Taschenrechner. Elektrizittswirtschaft, Jg. 79(1980), Heft 10, S. 379-382. D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
52
9. Energiewirtschaft9.1 Strompreisbildung an der Strombrse Die an der Strombrse zugelassenen Makler sammeln die Stromeinkauforder und die Stromangebotsorder in einem Auftragsbuch. Fr diese Order wird in einem Clearingverfahren diejenige Kombination ermittelt, bei der der grte Brsenumsatz bei minimalem berhang nicht bedienter Order entsteht. Das Verfahren mge anhand dem folgenden Beispiel erkennbar werden:
An der Strombrse werden von einem Brsenmakler fnf Lose elektrischer Energie aus verschiedenen Kraftwerken ber je 250 GWh zu Preisen zwischen 50 und 90 /MWh angeboten. Auf der Kuferseite besteht Kaufinteresse in ebenfalls fnf Quoten von 1.250 GWh, wenn der Preis bei 50 /MWh liegt und abnehmend auf 250 GWh wenn der hohe Preis von 90 /MWh zum Zuge kommt.
Stromhandel AuftragsbuchKauf - AngeboteMenge GWh 250 250 250 250 250 Summe GWh 250 500 750 1000 1250 Preis /MWh 90 80 70 60 50 Preis /MWh 50 60 70 80 90
Verkauf - AngeboteMenge GWh 250 250 250 250 250 Summe GWh 250 500 750 1000 1250
Der Brsenmakler ordnet die Angebote nach aufsteigenden Preisen und ermittelt zu jedem Preis die ausfhrbare Menge und den sich ergebenden berhang nicht bedienter Optionen. Der Auktionspreis ist derjenige, bei dem die grte Auftragsmenge ausgefhrt werden kann und der geringste berhang verbleibt. Dies ist im vorliegenden Beispiel bei dem Preis von 70 /MWh fr 750 GWh bei 0 GWh berhang der Fall. Der Umsatz betrgt dann:
Umsatz = 750 GWh 70 /MWh = 52,5 Mio.
Clearing- Verfahren zur PreisbildungAuktionspreis = Preis bei dem die grte Auftragsmenge ausgefhrt wird und der geringste berhang verbleibtPreis Menge Kauf Menge Verkauf Ausfhrbare Menge berhang Umsatz
Mio. /MWh GWh GWh GWh GWh 12,5 50 1250 250 250 1000 30 60 1000 500 500 500 52,5 70 750 750 750 0 40 80 500 1000 500 500 22,5 90 250 1250 250 1000 Sinkt das Kaufinteresse auf 250 GWh ab, weil z.B. viel EEG-Windstrom vorrangig im Netz aufgenommen werden muss, so verringert sich der Strombezugspreis von 70 auf 50 /MWh. Dies wirkt sich jedoch Menge Menge Ausfhrbare wegen der fesPreis berhang Umsatz Kauf Verkauf Menge ten EEGVergtung Mio. /MWh GWh GWh GWh GWh durch den 12,5 50 250 250 250 0 Netzbetreiber 15 60 250 500 250 250 von 90 /MWh insgesamt 17,5 70 250 750 250 500 nicht kosten20 80 250 1000 250 750 entlastend aus. 22,5 90 250 1250 250 1000 D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
53 Bei den Kauf-Angeboten wird das Angebot mit dem hchsten Preis die grte Wahrscheinlichkeit haben bedient zu werden. Ebenso wird bei den Verkaufsangeboten das Angebot mit den niedrigsten Preisen die hchste Wahrscheinlichkeit haben, bedient zu werden. In dem folgenden Beispiel liegen Kaufangebote von 50 GWh zu 100 /MWh vor, bis hin zu 400 GWh, wenn der Preis nur 30 /MWh betragen sollte. Derjenige, der 100 /MWh zu zahlen bereit ist, nimmt den Strom selbstverstndlich auch gerne zu nur 30 /MWh an, so dass bei diesem Preis der Umsatz 1.800 GWh wre. Bei den Verkaufs-Angeboten ist die Tendenz umgekehrt, dort wrde die gesamte Menge von Stromhandel Auftragsbuch 2.600 GWh Kauf - Angebote Verkauf - Angebote angeboten, wenn der Preis Menge Summe Preis Preis Menge Summe 100 /MWh GWh GWh /MWh /MWh GWh GWh wre, bei 50 50 100 30 500 500 30 /MWh sind nur 500 GWh 100 150 90 40 450 950 verfgbar, da 150 300 80 50 400 1.350 die teurer pro200 500 70 60 350 1.700 duzierenden 250 750 60 70 300 2.000 Kraftwerke 300 1.050 50 80 250 2.250 nicht eingesetzt werden. 350 1.400 40 90 200 2.450 400 1.800 30 100 150 2.600 Der Brsenmakler ordClearing- Verfahren zur Preisbildung net die Angebote nach aufsteigenden Preisen Auktionspreis = Preis bei dem die grte Auftragsmenge und ermittelt die zu jeausgefhrt wird und der geringste berhang verbleibt dem Preis ausfhrbare Menge Menge Ausfhrbare Menge und den sich Preis berhang Kauf Verkauf Menge ergebenden berhang nicht bedienter Optio/MWh GWh GWh GWh GWh nen. Der Auktionspreis 30 1.800 500 500 1.300 ist derjenige, bei dem 40 1.400 950 950 450 die grte Auftrags50 1.050 1.350 1.050 300 menge ausgefhrt werden kann und der ge60 750 1.700 750 950 ringste berhang ver70 500 2.000 500 1.500 bleibt. Dies ist im vorlie80 300 2.250 300 1.950 genden Beispiel bei 90 150 2.450 150 2.300 dem Preis von 50 100 50 2.600 50 2.550 /MWh fr 1.050 GWh bei 300 GWh berhang der Fall. Der Umsatz betrgt dann: Umsatz = 1.050 GWh 50 /MWh = 52,5 Mio. Bisherige Spotmarktpreise liegen zwischen dem negativen Wert von -102 /MWh am 22.12.2008 in den frhen Morgenstunden und 1.720 /MWh am 7. Januar 2003 am Abend von 19 bis 20 Uhr. Am 22.12.2008 ergab sich am Spotmarkt der EEX Leipzig ein neuer Rekord bei den negativen Handelspreisen. In der Zeit von 0 Uhr bis 6 Uhr bekam man fr die folgenden Handelsmengen noch Geld dazu: Windleistungseinspeisung vom 17.12. bis 30.12.2008 20.000 Zeit Preis Handelsmenge Installierte Leistung: 23.312 MW, zeitgleiche h /MWh MWh Summenleistung aller 19.868 Anlagen 15.000 Whrend dieser Zeitspanne am 0-1: -9,98 14.912 22.12.08 von 0 bis 6 Uhr wurde der 1-2: -29,59 15.714 Strom verschenkt und noch Geld in Hhe von 5,53 Mio. dazu. 10.000 2-3: -101,52 15.645 3-4: -101,52 15.575 5.000 4-5: -100,50 15.664 5-6: -9,98 15.755 Die Vergtung dafr 0 Summe: 93.265 betrug rd.90 /MWh 17.12 19.12 21.12 23.12 25.12 27.12 29.12 Tage im Dezember 2008 (Stunden-Mittelwerte) Umsatz: -5,53 Mio. 8,4 Mrd. D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.docLeistung in MW
54Dauerlinie und Ganglinie der Day - ahead Strompreise an der Leipziger Strombrse vom EUR/MWh 1.1. bis 8.1.2003 400 Bis zu 1.719,72 EUR/MWh 300
EEX Leipzig European Energy Exchange am Montag 22.12.2008MWh 25.000 Handelsmenge Preis /MWh 80 40 0 -40 -80 -120 1 6 11 Zeit 16 21 Preis
Strompreis
Handelsvolumen: +17,24 Mio. 20.000 - 5,53 Mio. 15.000 Handelsmenge 10.000 5.000 0
200 100 0 1 25 49
Stundenkontrakte
73
97
121
145
169
Durchschnittspreis: p,EEX = 22,70 EUR/MWh
Im Sinne der gesetzlich vorgeschriebenen Transparenz der Brsenhandelsgeschfte wurde eine zentrale neutrale Plattform fr Energiemarktdaten Transparency in Energy Markets eingerichtet, durch die gesetzliche Verffentlichungspflichten erfllt sowie freiwillige Selbstverpflichtungen der Marktteilnehmer umgesetzt werden. Diese Transparenzplattform fr Erzeugungs- und Verbrauchsdaten (www.transparency.eex.com ) wurde durch die EEX zusammen mit den vier deutschen bertragungsnetzbetreibern: 50Hertz Transmission GmbH, Amprion GmbH, EnBW Transportnetze AG und TenneT TSO GmbH in intensiver Zusammenarbeit mit den Verbnden BDEW, VKU, VIK und der Bundesnetzagentur sowie dem Bundesministerium fr Wirtschaft und Technologie ins Leben gerufen. Die EEX ist verantwortlich fr den Betrieb, welcher neben der Betreuung von Meldern und Nutzern die Plausibilisierung, Anonymisierung, Aggregierung sowie Verffentlichung der gemeldeten Daten umfasst.Nachfragekennlinie
Preis in /MWh
Meritorder-Preis den alle Anbieter erhalten A8Preis bei verminderter Nachfrage oder bei unkalkuliert hherer Windeinspeisung
Angebotsmenge prinzipiell aus Kraftwerksart:A1: Laufwasser und Teilmengen thermische (must run) A2: Wasser, Wind und Sonne A3: Wasserkraftwerke A4: Kernkraftwerke A5: Braunkohlekraftwerke, neue A6: Braunkohlekraftwerke, ltere A7 Steinkohlekraftwerke A8: Erdgaskraftwerke
A7 A6
A5 A1 A2 A3 A4
0
A 1 = Menge aus thermischen Kraftwerken deren kurzfristiges runterfahren hohe Zusatzkosten verursacht!
Angebotsmenge
Am Spotmarkt sinkt der Preis des fteren auf Null ab, am 5. 10. und 22.12. 2008 war er in den Morgenstunden aufgrund hoher nicht zeitgerecht kalkulierter Windstromeinspeisung sogar negativ. Wenn EEG-Strom aus Sonnen- Wind- oder Kleinwasserkraftanlagen ins Netz eingespeist wird, muss dieser vorrangig verbraucht werden. Dadurch verringert sich die Nachfrage und es ergibt sich ein neuer, geringerer Strompreis an der Brse. Dieser Effekt fhrt natrlich nicht zu nachhaltig niedrigeren Stromerzeugungskosten. Da diese Stromeinspeisungen ja entsprechend der EEGVergtung unabhngig von der Bedarfslage bereits vergtet wurden und inzwischen eine von den Strombeziehern zu erbringende Subventionshhe von jhrlich rd. 14 Mrd. vorweg verursachen. Der preisreduzierende Merit-Ordereffekt verringert nicht die Stromerzeugungskosten insgesamt aufgrund von Windstromeinspeisungen, sondern optimiert ein wenig die Brennstoffkosten.
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
55 9.2 Versorgungsqualitt und Kenngren zur Versorgungszuverlssigkeit
SAIFI (System Average Interruption Frequency Index)Dieser Index gibt die mittlere Hufigkeit von Versorgungsunterbrechungen pro angeschlossenen Kunden im Betrachtungszeitraum an:
SAIFI =
Summe aller Kundenunte rbrechunge n Summe aller versorgten Kunden
Als Ergebnis erhlt man die Hufigkeit, wie oft ein Kunde z.B. innerhalb eines Jahres unterbrochen wurde.
SAIDI (System Average Interruption Duration Index)Dieser Index gibt die mittlere Dauer von Versorgungsunterbrechungen pro angeschlossenen Kunden im Betrachtungszeitraum an:
SAIDI =
Kumulierte Dauer aller Kundenunte rbrechunge n Summe aller versorgten Kunden
Als Ergebnis erhlt man die durchschnittliche Unterbrechungsdauer eines Kunden z.B. innerhalb eines Jahres im Gebiet des Netzbetreibers.
CAIDI (Cutomer Average Interruption Duration Index)Mit diesem Index wird die mittlere Unterbrechungsdauer eines unterbrochenen Kunden gemessen. CAIDI berechnet sich durch die Division von SAIDI und SAIFI:
CAIDI =
Kumulierte Dauer aller Kundenunterbrechungen SAIDI = Summe aller Kundenunterbrechungen SAIFI
Als Ergebnis erhlt man die durchschnittliche Unterbrechungsdauer aller von der Strung betroffenen Kunden im Netzgebiet des Netzbetreibers. Die Spannungsqualitt ist in der Europanorm EN 50160 geregelt. Quelle: VDNBeispiel zur Messung der Versorgungszuverlssigkeit: Im ungestrten Betriebszustand versorgt ein Netzbetreiber insgesamt 100.000 Kunden. Innerhalb eines Jahres ereignen sich zwei Strungen mit gebietsweisen Unterbrechungen: 1. Strung mit 65 Minuten Spannungsausfall fr 1.000 Kunden 2. Strung mit 45 Minuten Spannungsausfall fr 3.000 Kunden SAIFI (System Average Interruption Frequency Index)
SAIFI =
1.000 + 3.000 1 1 = 0,04 a a 100.000
Im Mittel ist ein Kunde 0,04 mal pro Jahr spannungslos, d.h. einmal in 25 Jahren.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
56 SAIDI (System Average Interruption Duration Index)
SAIDI =
1.000 65 + 3.000 45 min min = 2,0 100.000 a a
Ein beliebiger Kunde ist im Mittel 2 Minuten pro Jahr spannungslos.CAIDI (Customer Average Interruption Duration Index)
CAIDI =
1.000 65 + 3.000 45 min = 50,0 min 4.000
Erfhrt ein Kunde eine Strung, so dauert diese im Mittel 50 Minuten. Nichtverfgbarkeit 1999 bis 2004 durch stochastische Versorgungsunterbrechungen:
Mittlere kundenbezogene Unterbrechungshufigkeit durch stochastische Versorgungsunterbrechungen
D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc
57 Bundeskanzlerin Frau Dr. Merkel bei ihrer Lernreise 2010 im Kernkraftwerk (KKW) Lingen:KKW Lingen Berliner Zeitung vom 27.8.2010
Aha, hier gibts Strom, auch wenn die Sonne nicht scheint und der Wind nicht weht, und noch 2,3 Mrd. extra! und sichere, gut bezahlte Arbeit ohne Verlagerungsgefahr nach ChinaSteinkohle 109,0 TWh (18,3 %)
Brutto - Stromerzeugungsmix 2009Erdgas 77,0 TWh (12,9 %) Minerallprodukte 12,5 TWh (2,1 %) Wasser 19,0 TWh (3,2 %)
Braunkohle 146,5 TWh (24,5 %)
Bruttostromerzeugung 596,8 TWh
Die jungen Leute knnen das, unser Umweltminister Norbert Rttgen muss es noch lernen.
regenerative Stromerzeugung 93,0 TWh (15,6 %) 16 % vom BruttoStromverbrauch 583 TWh
Wind 37,8 TWh (6,3 %)
Biomasse 25,0 TWh (4,2 %) Mll regenerativ 5,0 TWh (0,8 %) Photovoltaik 6,2 TWh (1,0 %)
Kernenergie 134,9 TWh (22,6 %)
sonstige 23,9 TWh (4,0 %)
Jahresganglinie der Stromerzeugung des Kernkraftwerkes Isar 2:
Brenn-elementewechsel mit 21. Revision Netzeinspeisung KKW ISAR 2 KKI 2009 (Platz 2 der Top Ten Internationale Liste)
Monatsganglinie der Stromerzeugung des offshore Windparks Alpha Ventus im Monat Dezember 2010:
80
Offshore-Windleistung im vorvormals E.on, nun Tennet - Netz im Monat Dezember vom 1.- 31.12. 2010
Leistung in MW
60
40
20
0 1 5Zeit (Tage der 1/4 h - Leistungswerte)
9
13
17
21
25
29
Da das zeitliche Windleistungsangebot an verschiedenen Standorten im deutschen Nordseegebiet naturgem zeitlich kaum unterschiedlich sein kann, wird die Verfgbarkeit der Leistung auch bei beliebiger Steigerung der Anzahl Windrder nicht besser, nur der Ordnatenmastab ndert sich dann zu hherer Leistung.D:\FH AKE\Vorlesungsmanuskript ET-EW 2011.doc