198

Anhang 1: Summen über Fakultäten

Beim Koppeln und Umkoppeln von DrehimpulszuBtänden stößt man auf Summen über rationale Ausdrücke mit Fakultäten (von ganzen Zahlen). Dabei steht im Nenner jedes Sum­manden mindestens ein Paar (a + n)!(b - n)!. Es legt die Summationsgrenzen fest: Die Fakultät einer negativen Zahl ist unendlich, und daher führt das genannte Paar auf die Gren­zen -a 5: n 5: b. Die Summationsgrenzen werden im folgenden nicht einzeln angegeben - es wird als selbstverständlich vorausgesetzt, daß keine Fakultäten negativer Zahlen auftreten.

Wenn mehr Glieder (ai+n)! auftreten als (bi-n)!, kann man durch geeignetes Umbenennen (n --+ -n) das Gegenteil erreichen, weshalb wir hier nur den einen Fall aufzählen.

Als erste Summe haben wir Hn

"" ( = oaO , L..., n! a- n)! n

denn sie ist nach dem binomischen Lehrsatz gleich

!.. "" Hn (a) = !.. (1 - l)a = oaO' a! L..., n a!

n

Die Binomialkoeffizienten sind nämlich für beliebiges p gegeben durch

( p) == p(p - 1) ... (p - n + 1) = _ n (n -p - 1) , n n! () n ( a) a! insbesondere ist = I( _ )1'

n n. an.

Aus dem binomischen Lehrsatz folgt das Additionstheorem der Binomialkoeffizienten:

Deshalb gilt auch die Gleichung (zweite Summenformel)

"" 1 (a+b+c+d)! L: (a+n)!(b+n)!(c-n)!(d-n)! = (a+c)!(a+d)!(b+c)!(b+d)!'

Drittens haben wir noch

L (a+n)!(b-n)! _ (a-c)!(b-d)!(a+b+l)! n (c+n)!(d-n)! - (c+d)!(a+b-c-d+l)!'

denn die linke Seite ist (mit k = c + n) gleich

(a-c)!(b-d)! L (a-~+k)e:~=~) k

= HC+d(a- c)!(b- d)! L (c- ~-1) (:~!=~) = (a- c)!(b- d)! (a:!: 1) , k

und das steht auch rechts. Umgekehrt gilt nach diesen beiden Ergebnissen:

(a ± k)! (a - b)!(a - cl! (b±k)!(c±k)! = L n!(-a+b+c±k+n)!(a-b-n)!(a-c-n)!'

n

(a±k)! "" (c-a+n)!(a+b-n)! (b"Fk)!(c+l±k)! = L..., (c-a)!{b+c+l)!n!(b"Fk-n)!'

n

I!lQ

Hier hängt rechts jeweils nur eine Fakultät vom Lauftndex k ab, was wir für weitere Glei­chungen ausnutzen werden. So folgt mit c ~ d:

"n (a-n)! b (a-c)!(a-d)! L, (-) (Hn)!(c-n)!(d-n)! = (-) (b+c)!(b+d)!(a-b-c-d)! "

für a > d,

c (a-c)!(b+c+d-a-l)! =(-) (b+c)!(Hd)!(d-a-l)! tür a < d.

Deshalb haben wir für Umformungen auch noch die Beziehungen

1 1" .. ±k (a+ b+ c- n)! (a±k)!(b'Fk)!(C'Fk)! = (a+b)!((a+e)! L;- (-) (n'Fk)!(b-n)!(c-n)!'

(a - k)! (a - c)!" Hn (a - n)! (Hk)!(e-k)! = (He)! L, (-) (b+n)!(k-n)!(a-b-c-n)!'

n

Während wir also Summen rationaler Ausdrücke mit vier Fakultäten häufig berechnen können, lassen sich solche mit sechs Fakultäten nach dem genannten Verfahren oft umformen. So ist z.B.

"n (a+n)!(b-n)! ~ (-) (e+n)!(d+n)!(e-n)!(f-n)!

" " (a-c)!(a-d)!(b-e)!(b-!)! = L, (-) (b-e-j+n)!(c+n)!(d+n)!(e-n)!(f-n)!(a-c-d-n)!'

n

"n (a-n)!(b-n)! ~ (-) (c+n)!(d-n)!(e-n)!(f-n)!

" c (a - d)!(a - e)!(b - J)!(b - n)! = ~ H (c+J)!(a-d-e+n)!(c+n)!(d-n)!(e-n)!(b--c-j-n)!'

Die erste Gleichung benutzen wir bei der Kopplung von Drehimpulsen in Abschn. 3.6. Bei der Umkopplung brauchen wir

I: (a + n)!(b + n)!(c - n)! " (d+n)!(e+n)!(J-n)!

_" (a-d)!(a-e)!(b+c+l)!(c-!)!(b+n)! - L, (b+ c- j + 1 + n)!(d+ n)!(e+ n)!(j - n)!(a- d- e- n)! .

n

Damit läßt sich nämlich die Gleichung

"n (a + n)!(b - n)!(c - n)! L, (-) (d+ n)!(e+ n)!(J -n)!(g- n)!(h+ 1- n)!

n

_ (a- d)!(a- e)!(b- j)!(b- g)!(c- !)!(c- g)! - (d+h+l)!(e+h+l)!

" n (d + e + h + 1 + n)! x ~ (-) (b-j-g+n)!(c-j-g+n)!(d+n)!(e+n)!(f-n)!(g-n)!(a-d-e-n)!

200

beweisen, falls h = a+b+c-d-e-I-g ist: Schreiben wir nämlich (c-n)!/(e+n)!(h+l-n)! als Summe, so können wir die Summe über n umformen und erhalten

(a - d)!(6 -/)!(6 - g)! (h - e)!(e + h + I)! " )" (h-e+m)!(e+e-m)!(a-e+m)!

X ~ (- m!(b-I-g+n)!(d+n)!(e-m+n)!(f-n)!(g-n)!(a-d-e+m-n)!'

Beim Umwandeln dieser Summe über m kürzen sich zwei Glieder (d + n)! weg:

" ,,(a - d)!(a - e)!(b - n!(b - g)!(c - n)! L..J H (h - c)!(b -1- g + n)!(f - n)!(g - n)! "

" (h-c+m)! x L..J (h + 1- n+ m)!m!(a- d- e+ m- n)!(e- m + n)!(d- m + n)!

m

Ersetzen wir nun m durch k = m - n, so vereinfacht sich die entstehende Summe über n beim Umwandeln wegen der geforderten Bedeutung von h. Wir erhalten nämlich

" H" (a - d)!(a - e)!(b -I)!(b - g)!(c - n!(c - g)! L..J (c-I-g + n)!(b-I- g + n)!(f - n)!(g- n)!(a- d- e- n)! "

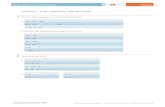
x~ (k+n)!(h+I+~)!(e-k)!(d-k)!' Wird nun über k summiert, so folgt die Behauptung. Umgekehrt gilt also auch

,,( )" (i+1+n)! L: - (a+n)!(b+n)!(c+n)!(d+n)!(e-n)!(f-n)!(g-n)!

(i-c+I)!(i-d+l)! (a + e)!(a + I)!(b + e)!(b + n!(e + g)!(d + g)!

" .. (c+ d+ g+ n)!(a+ e+l- n)!(b+ e+ I-n)! xL..J (-) (c+n)!(d+n)!(e-n)!(f-n)!(i-c-d+l-n)!'

n

falls i = a + b + c + d + e + 1 + g ist.

Anhang 2: Legendre-Polynome

Erzeugende Funktion:

1 00

/:,==;;;=====;;===;;0 = L P,,(cosO) zn ../1 - 2 z cos 0 + Z2 ,,=0

Daraus folgen die Rekursionsformeln:

für Izl < I .

(n + I)P"+l(cosO) - (2n + I) cosO Pn(cosO) + nP"_l(coS 0) = 0

201

und - mit P~ = dPn/dcosO - :

cas () P~(cos 0) - P~_dcos 0) = nPn{cos 0) ,

P~(cos 0) - eas 0 P~-1 (eos 0) = nPn_dcos 0) ,

P~+I (eos 0) - P~,-1 (eos 0) = (2n + 1) Pn(cos 0) ,

- sin2 0 P~(cos 0) = n {cos 0 Pn(cosO) - Pn_l(cos O)}

= (n + 1){Pn+1(cos 0) - cosO Pn(COS On n(n+l) = --- {Pn+dcosO) - Pn_1(cosO)} , 2n + 1

sowie die Differentialgleichung

sin2 0 P;:(cosO) - 2 cosO P~(cosO) + n(n + 1) Pn(cosO) = 0,

Symmetrie: Pn(-cosO) = (-t Pn(cosO) ,

Formel von Rodrigues:

( ) (_)n dn sin2n O 1 '" ()k (2n-2k)! cosn-2kO, Pn cosO = 2" n! deos n () = 2n ~ - kiln - k)!(n - 2k)!

Besondere Werte:

Po (cos 0) = 1,

Pdcos 0) = eos 0,

P2 (cosO) = ! (3cos2 0 -1) = t (1 + 3cos20),

Pz(cosO) = ! (5cos3 0 - 3cos 0) = t (3cosO + 5cos30) ,

P.(cosO) = t(35cos· 0 - 30cas2 0+ 3) = h(9 + 20cos20 + 35 cos 40) ,

für gerades n, sonst null.

Die Legendre-Polynome bilden ein vollständiges Orthogonalsystem in cos 0 für den Bereich O~O~lI':

1 ~

/ Pn(cosO) P",(cosO) dcosO = / Pn(cosO) Pn,(cosO) sin 0 d(I = _2_ {inn' , 2n+ 1

-1 0

~ 2n+l Ö(O-O') L. -- Pn(cosO) Pn(C060') = ö(cosO - cosO') = -'-0-'

O 2 un n=

202

Quellenver zelehnls

ABRAMOWITZ, M. & STEGUN, I.A.: Handbook of mathematical functions (Dover, New York 1 \)70)

ALDER, K. & WINTHER, A.: Nuc!.Phys. AI32(1969)1 ALDER, K. & WINTBER, A.: Phys.Lett. B34(1971)357 APPEL, H.: Numerical tables of 3j-, 6j-, 9j-symbols, F- and r-coefficients (Landolt-Börnstein

1,3; Springer, Berlin 1968) ARIMA, A., BORIE, H. & TANABE, Y.: Progr.Theor.Phys. 11(1954)143 BALIAN, R. & BREZIN, E.: Nuovo Cim. B61(1969)403 BARSCHALL, H.H. & HAEBERLI, W. (Brsg.): Polarization phenomena in nuclear reactions,

Proc.third int.symp.Madison 1970 (Univ.Wisconsin, 1971) BARSHAY, S. & TEMMER, G.M.: Phys.Rev.L<ett. 12(1964)728 BAYMAN, B.F.: Amer.J.Phys. 34(1966)216 BEHKAMI, A.N.: Nuc!. Data Tables AI0(1971)1 BIEDENHARN, L.C.: in Nuclear spectroscopy B (Hrsg. F.Ajzenberg-Selove;Academic Press,

New York 1960) BIEDENHARN, L.C., BLATT, J.M. & ROSE, M.E.: Revs.Mod.Phys. 24(1952)249 BIEDENHARN, L.C. & v.DAM, H.: Quantum theory of angular momentum (Academic Press,

New York 1965) BIEDENHARN, L.C. & LOUCK, J.D.: Angular momentum in quantum physics (Encydopedia

of mathematics and its applications 8, Addison-Wesley, Reading 1981) BIEDENHARN, L.C. & LOUCK, J.D.: The Racah-Wigner-algebra in quantum theory (En-

cyclopedia of mathematics and its applications 9, Addison-Wesley, Reading 1981) BIEDENBARN, L.C. & ROSE, M.E.: Revs.Mod.Phys. 25(1953)729 BLATT, J.M. & BIEDENHARN, L.C.: Revs.Mod.Phys. 24(1952)258 BOHR, A.: Nuc!.Phys. 10(1969)486 BOHR, A. & MOTTELSON, B.R.: Nuclear structure I (Benjamin, New York 1969) BRINK, D.M. & SATCHLER, G.R.: Angular momentum (Oxford Univ. 1968) BROWN, G.E.: Unified theory of nuclear models (North-Holland, Amsterdam 1964) CAOLA, M.J.: J.Phys. All(1978)L23 CARR, R.W. & BAGLIN, J.E.E.: Nuc!. Data Tables 10(1971)143 COESTER, F. & JAUCH, J.M.: Belv.Phys.Acta 26(1953)3 CONDON, E.U. & SHORTLEY, G.H.: The theory of atomic spectra (Carnbridge Univ.,

London 1935) CRAMER, J.G. & BRAITHWAITE, W.J.: Nuc!.Data Tables AI0(1972)469 DAVIDSON, J.P.: Revs.Mod.Phys. 37(1965)105 DEVONS, S. & GOLDFARB, L.J.B.: in Handbuch der Physik 42 (Hrsg. S.Flügge; Springer,

Berlin 1953) DOHRENDORF, M. & LINDNER, A.: in Jahresbericht 1976/77 l.Inst.Exp.Phys.Univ.Ham-

burg (Hrsg. M.Niecke & C.Pegel, Univ.Hamburg) EARP, C.: J.Math.Phys. 22(1981)2357 ECKART, C.: Revs.Mod.Phys. 2(1930)305 EDMONDS, A.R.: Drehimpulse in der Quantenmechanik (Bibl.lnst., Mannheim 1964) FANO, U.: Revs.Mod.Phys. 29(1\)57)74

203

FANO, U. & RACAH, G.: Irreducible tensorial sets (Academic Press, New York 1959) FERGUSON, A.J: Angular correlation methods in gamma-ray spectroscopy (North-HoJland,

Amsterdam 1965) FEYNMAN, R.P.: Quantum electrodynamics (Benjamin, New York 1962) FICK, D.: Einführung in die Kernphysik mit polarisierten Teilchen (BibJ.lnst., Mannheim

1971) M.GELL-MANN & GOLDBERGER, M.L.: Phys.Rev. 91(1953)398 GRODZINS, L.: Progr.NucI.Phys. 7(1959)165 lffiLMERS, K.: Nucl.Phys. 23(11161)594 HOPE, J. & LONGDON, L.W.: Phys.Rev. 101(1956)710 HORIE, H. & SASAKI, K.: Progr.Theor.Phys. 25(1961)475 HUBY, R.: Proc.Phys.Soc. A67(1954)1103 HULL, M.H. & BREIT, G.: in Handbuch der Physik 41/1 (Hrsg. S.Flügge; Springer, Berlin

1959) INNES, F.R. & UFFORD, C.W.: Phys.Rev. 111(1958)194 JAHN, H.A.: Proc.Roy.Soc. A205(1951)192 JAHN, H.A. & HOPE, J.: Phys.Rev. 93(1954)318 JANG, S.: J.Math.Phys. 9(1968)397 JAUCH, J.M. & ROHRLICH, F.: The theory of photons and electrons (Springer, Berlin 1976) van der JEUGT, J., "an den BERGHE, G. & deMEYER, H.: J.Physics AI6(1983)1377 JONKER, J.E. & deVRIES, E.: Nucl.Phys. A105(1967)621 KLEIN, 0.: Z.Phys. 58(1929)730 KRAMERS, H.A.: Proc.Kon.Ned.Akad.Wetenschap 33(1930)959 LAKIN, W.: Phys.Rev. 98(1955)139 LANE, A.M. & THOMAS, R.G.: Revs.Mod.Phys. 30(1958)257 LAWSON, R.D.: Theory of the nucJear sheJl model (Clarendon, Oxford 1980) LII\"DNER, A.: Z.Phys. 171(1963)401 LII\-DNER, A.: Nucl.Phys. A261(1976)253 LlI\"DNER, A.: Nucl.Phys. A268(1976)369 LOUCK, J.D.: Phys.Rev. 110(1958)815 MAYER, M.G. & JENSEN, J.H.D.: Elementary theory of nucJear shell structure (Wiley, New

York 1\)55) MESSIAH, A.: Quantum mechanics I, 11 (North-HoJland, Amsterdam 1961, 1962) MONAHAN, J.E., HOLT, R.J. & LASZEWSKI, R.M.: Atom. Data and Nucl. Data Tables

23(1979)97 MORETTE-deWITT, C. & JENSEN, J.H.D.: Z.Naturf. 8a(1953)267 MOSES, H.E.: Ann.of Phys. 60(1970)275 MOTT, N.F. & MASSAY, H.S.W.: The theory of atomic collisions (Clarendon, Oxford 1965) NE\1ETS, O.F. & YASNOGORODSKII, A.M.: Sov.J.Part.Nucl. 12(1981)170 NEWTON, R.G.: Scattering theory of waves and particJes (McGraw-Hill, New York 1966) NORMAND, J.: A Lie group: rotations in quantum mechanics (North-Holland, Amsterdam

1980) RACAH, G.: Phys.Rev. 62(1942)438 RA:\1ACHANDRAN, G.N. & RAMASESHAN, S.: in Handbuch der Physik 25/1 (Hrsg.

S.Flügge; Springer, Berlin 1961) RASlllD, M.A.: J.of Phys. AI3(1980)2631 RAY, B.S.: Z.Phys. 78(1932)74 REGGE, T.: Nuovo Cim. 10(1958)544 REGGE, T.: Nuovo Cim. 1l(1959)1l6

204

HOSE, M.E.: Multipole fields (Wiley, New York 11l5S) ROSE, M.E.: Elementary theory of angular Illolllentum (Wiley, New York 11l57) ROSE, M.E.: Tripie Correlatiolls (ORNL-251B(1958)) SCHULTEN, K. & GORDON, R.G.: J.Math.Phys. 16(1975)1961 SCHULTEN, K. & GORDON, R.G.: J.Math.Phys. 16(1975)1971 SCHWINGER, J.: On angular momentum (1952), abgedruckt in BIEDENHARN & vanDAM SEYLER, R.G. & WELLER, H.R.: Atom. Data and Nucl. Data Tables 23(11)79)99 de SHALIT, A. & TALMI, 1.: Nuclear shell theory (Academic Press, New York 11)63) SHELEI'IN, L.A.: Sov.Phys.JETP 19(1964)702 SIMONIUS, M.: in BARSCHALL & HAEBEHLI (SAOl) und Phys.Rev.Lett. 11l(IIlB7)279 SIMONIUS, M.: Phys.Lett. 37B(11l71)44B STIEFEL, E. & FÄSSLER, A.: Gruppentheoretische Methoden und ihre Anwendung (Teub­

ner, Stuttgart 1979) STHEATER, R.F. & WIGHTMAN, A.S.: peT. spin and statistics, and all that (Benjamin,

New York 1964) TREIS, W.R.: Grundzüge der Quantentheorie (Teubner, Stuttgart 1984) WAY, K. & HURLEY, F.W.: Directory to tables and reviews of angular-momentulll and

angular-correlation coefficients, l\'ucl.Data Al(11l66)473 WIGNER, E.: Gruppentheorie und ihre Anwendungen auf die Quantenmechanik der Atom­

spektren (Vieweg, Braunschweig 1931) van WINTER, C.: Physica 20(1954)274 WONG, C.W. & CLEMENT, D.M.: Nucl.Phys. A183(1972)210

StlchwortverlllelchnlB.

Abgeschlossene Schale 13.1 AbstammungskoeffIzient 13.3 Absteigeoperator 2.3 Additionstheorem

für Binomialkoeffizienten Al für Kugelfunktionen 1.6 verallgemeinertes 9.7

Analysierstärke 12.6 Asymmetrie der Winkelverteilung 12.5 Aufsteigeoperator 2.3 Austauschsymmetrie 3.15,13.1 Auswahlregel 5.2 Bahndrehimpuls 1.3,7.1 Barshay-Temmer-Theorem 12.13 Berechnung

der Kopplungskoeffizienten 3.11 der Umkopplungskoeff. 4.13,4.11

Besselfunktion 9.3 modifizierte 9.6

Biedenharn-Elliott-Beziehung 4.10 Binomialkoeffizient Al Blatt-Biedenharn-Koeffizient 12.3 Bohrsches Theorem 12.10, 12.14 Bose-System 2.7 Boson 1.5 Clebsch-Gordan-Koeffizient 3.4

Phasenkonventiou 3.3 Rekursionsformel 3.4, 3.7 Sonderfälle 3.8 Symmetrien 3.7 Zusammenhang mit 3j-SymlJol 3.9

Coulomb -kraft 9.6 -streuung 12.11 -welleufunktiou 9.3

Darstellung von Operatoren 5.2 Deltakraft 9.6 Dichteoperator 11.1

für Streuproblem 12.1 für Vielteilchensystem 13.2

Dipolmoment 10.6 DoppelstrelIune; 12.8 Drall 1.4

205

Drehimpuls -darstellung 2.1 -eigenwerte 2.3 -erhaltung 12.1 -komponent 1.6,2.1 -kopplung 3.1 -umkopplung 4.1 -operator 1.4 -quadrat 2.1 -summe 3.1 -unschärfe 2.4 -vertausch gesetz 1.6, 2.1, 6.7

Drehinvarianz 1.6,12.1 Drehmatrix 6.4 Drehoperator 1.3, 6.3 Drehparameter 1.5, 6.1 Drehung 1.1 Drehvektor 1.1, 1.2 Dreiecks

-koeffizient 4.13 -summenregel 4.13 -ungleichung 3.5

Dreierkorrelationsfunktion 8.2 Dreiteilchenstreuung 12.14 Ebene Welle 9.3 Eigen

-drehimpuls 1.4 -parität 12.10 -wertspektrum 2.3,2.7

Einheitsvektor 7.8 sphärischer 5.4

Einteilchen -dichte 13.5,13.12 -operator 13.2

Einzcldrehimpuls 3.1 Elektromagn. Strahlung 10.5, 10.6, 11.8 Eulerwinkel tU

Fermion 1.5 Fermionenoperator 5.4. 13.1 Fouriertransformation 9.8 Gaußkraft 9.6 Gekoppelte Darstellung 3.2 Gemisch 11.1

Gesamtdrehimpuls 1.4, 3.1 Gestreckte Kopplung 3.14 g-Faktor 5.7 Gradientenformel 10.2 Greenfunktion 9.3, 9.6 GruppeneigenschaIt 6.3 Halbzahliger Drehimpuls 1.5 Hankelfunktion 9.3 Helizität 1.6, 10.8 Hundsche Regel 3.15 Impuls

-darstellung 7.5 -operator 9.5

Inkohärente Überlagerung 11.1 Inverses Streu problem 12.12 Irreduzibler Tensoroperator 5.1 Isospin 2.2 Isotropie 11.3 j-Darstellung 12.2 jj-Kopplung 9.6 Kanalspin 12.2 Kirchhoffsche Differentialgleichung 9.3 Koordinaten

gedrehte 6.6 körperfeste 6.2 laborfeste 6.2 Relativ- 8.7

Ko- und Kontravarianz 5.3 Korrelationsfunktion 8.1

koplanare 8.3, 8.7 Kramers-Theorem 2.6 Kreiselfunktion 6.4

Eigenfunktion 6.7, 6.11 Eigenschaften 6.5, 6.11 Orthogonalität 6.10 red uzierte 6.8 Sonderfälle 6.9 Sphärischer Tensor 6.7 Vollständigkeit 6.10

Kugelfunktion 7.2 Additionstheorem 7.6 Drehverhalten 7.6 Reduziertes Matrixelement 7.3 renormierte 7.7 Parität 7.5 Produkt 7.3 Kreiselfunktion 7.3

206

LandEl-Fomlel 5.7 Legendre

-Funktion 7.4 -Polynom A2

Leiteroperator 2.3,2.7 Loch

-operator 13.9 -zustand 13.8

LS-Kopplung 9.6 Madisonkonvention 12.6 Magnetischer Dipol 5.1,10.6 Mehrfachstreuung 12.8 M -Matrix 12.16 Modifizierte Besselfunktion 9.6 Mottquerschnitt 12.13 Multipol

-moment 10.6 -strahlung 10.5 -zerlegung 9.6

Neumannfunktion 9.3 Ortsdarstellung 7.2 Parität 7.5 Paritätserhaltung 12.5, 12.14 Pauli-Operator 2.5 Phasen

-analyse 12.12 -faktor 2.5

Phasenkonvention bei gekoppelten Zuständen 3.3 bei Zeitumkehr 2.6, 3.3 von Condon & Shortley 2.5, 3.3 von Vielteilchenzuständen 13.1 von VVigner 3.3

Photoemission 12.15 Polarisation 11.4, 11.6

längs einer Achse 12.10 von Licht 11.7

Polarisations -stärke 11.5 -transfer 12.7

Polarisierreaktion 12.7 Quadrat des Drehimpulses 1.6,2.1 Quadrupolmoment 10.6 Quantenzahl 2.3

j 2.4,2.7 j ± m 2.7

Quantisierllngsa.chse 2.1

Quasispin 2.2 Racah-Koeffizient 4.3 Racah's Dreieckskoeffizient 4.13 Radialfunktion 9.1-3 Reduzierte Kreiselfunktion 6.8 Reduziertes Matrixelement 5.2

Symmetrie bei herrn. Op. 5.3 eines Einteilchenoperators 9.5 einer spinabhängigen Wechselw. 9.7 eines Tensorproduktes 5.6 einer Wignerkraft 9.6

Regge-Symbol (3j-Symbol) 3.10 Regge-Symmetrie

der Clebseh-Gordan-Koelf. 3.7 der 3j-Symbole 3.10 der 6j-Symbole 4.6 der 9j-Symbole 4.7

Renormierte Kugelfunktion 7.7 Richtungskomponente 7.9 Richtungskorrelation 8.1

koplanare 8.3, 8.7 Richtungsquantenzahl 2,4 Schelepin-Symbol (6j-Symbol) 4.6 Schrödingergleichung 9.1 Seniorität 13,4 Singulettzustand 3.14 Skalar 5.4

-produkt 5.5 Slater-Integral 9.6 Sommerfeldparameter 9.3 Sphärischer Tensor 6.6 Sphärischer Einheitsvektor 5,4 Spin 1.4

-austauschoperator 3.15 -Bahn-Kopplung 3.14,5.6,9.7 -korrelation 12,4 -Spin-Kopplung 3.14 -Tensor 5.5, 5.6, 11,4

Stokesparameter 11.7 Strahlparameter 11.2 Strahlungseinfang 12.15 Streuoperator 12.1 Streuung

geladener Teilchen 12.11 identischer Teilchen 12.13 polarisierter Teilchen 12.4 von Licht 12.15

207

Stufenzerfall 12.14, 12.15 Summen

über Fakultäten Al über 3j-Symbole 4.9 über 6j-Symbole 4.10 über 9j-Symbole 4.11 über 3j-, 6j- und 9j-Symbole 4.12

Teilchen-Loch -Paar 13.11-13 -Parität 5.3 -Symmetrie 13.10

Tensor 5.1 irreduzibler 5.1 -iteration 5.5 -kraft 5.6, 9.7 -operator 5.1 Orthogonalität 5.2 -produkt 5.5 sphärischer 6.6

Tripelkorrelationsfunktion 8.2, 8.3 Triplettzustand 3.14 Übergangs

-operator 12.1 -wahrscheinlichkeit 5.2

Umkopplung 3.1,4.1 Phasenkonvention 3.2 Richtungsquantenzahl 4.2 von Fermionen 13,4 von drei Drehimpulsen 4.3 von vier Drehimpulsen 4,4

Unschärfe 2.4 -beziehung 1.6

Vektor -additionskoeffizient 3.4 -feld 10,4 -kraft 9.7 -kugelfunktion 9,4, 10.1

Vektoroperator 1.6, 5.4 Wirkung auf Kugelfunktion 10.2 - auf Vektorkugelfunktion 10.3

Vektorprodukt 5.5, 7.8 Vert aus eh gesetz 1.6, 5.1, 5.4 Vielteilchenzustand

Gekoppelte Darstellung 13.4 Ungekoppelte Darstellung 13.1

Viererkorrelationsfunktion 8,4-7 W -Koeffizient 4.3

Wigner -Eckart-Theorem 5.2 -koeffizient (Clebsch-G.-K.) 3.4 -kraft 9.6

Wirkungsquerschnitt 12.3 Asymmetrie 12.5 für Dreiteilchenreaktion 12.14 für polarisierte Partner 12.4 für Photonen 12.15

Yukawakraft 9.6 Z-Koeffizient 4.14 Zeemann-Elfekt 5.1 Zeitumkehr 2.6

-invarianz 2.6, 12.9 -operator 2.6 -verhalten 5.3

Zentralkraft 9.1, 9.1 Zerfallsamplitude 12.14 Zirkularpolarisation 10.8 Zweierkorrelationsfunktion 8.1 Zweipotentialformel 12.11 Zweiteilchen

-dichte 13.6, 13.13 -operator 13.2

3j-Symbol 3.9 Berechnung 3.11 Rekursionsformeln 3.12 Sonderfälle 3.13 Symmetrien 3.10

6j-Symbol 4.3 Beredlllllllrr 4.13 Rekllrsionsformeln 4.15 Sonderfälle 4.14 Symmetrien 4.6 Zusammenhang mit 3j-Symbol 4.5

9j-Symbol 4.4 Berechnung 4.17 Sonderfälle 4.16 Symmetrien 4.7 Zusammenhang mit 3j-Symbol 4.5 Zusammenhan!! mit 6.i-Svmbol 4.10

21J8

Teubner Studienbücher Mechanik

Becker: Technische Strömungslehre Eine Einführung in die Grundlagen und technischen Anwendungen der Strömungsmechanik. 5. Aufl. 160 Seiten. DM 21,80

Becker!Bürger: Kontinuumsmechanik Eine Einführung in die Grundlagen und einfache Anwendungen 228 Seiten. DM 34,- (LAMM)

Becker!Piltz: Obungen zur Technischen Strömungslehr. 3. Aufl. 136 Seiten. DM 18,80

Böhme: Strömungsmechanik nlcht-newtonscher Fluide 280 Seiten. DM 34,- (LAMM)

Hahn: Bruchmechanik Einführung in die theoretischen Grundlagen. 221 Seiten. DM 34,- (LAMM)

Magnus:' Schwingungen Eine Einführung in die theoretische Behandlung von Schwingungs­problemen. 3. Aufl. 251 Seiten. DM 28,80 (LAMM)

Magnus!Müller: Grundlagen der Technischen Mechanik 4. Aufl. 300 Seiten. DM 29.80 (LAMM)

MÜller!Magnus: Obungen zur Technischen Mechanik' 2. Aufl. 292 Seiten. DM 29.80 (LAMM)

Wieghardt: Theoretische Strömungslehre Eine Einführung. 2. Aufl. 237 Seiten. DM 28,80 (LAMM)

Preisänderungen vorbehalten