Nichtlineare Optimierung || Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Transcript of Nichtlineare Optimierung || Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen

4 Lösungsverfahren fürOptimierungsprobleme mitNebenbedingungen
Übersicht
4.1 Sattelpunkte, Dualität und Sensitivität . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 298
4.2 Straffunktionen und Strafverfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 306
4.3 Multiplikatorverfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319
4.4 Verfahren für quadratische Optimierungsprobleme . . . . . . . . . . . . . . . . . . . . . . . 328
4.5 SQP-Verfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 337
4.6 Barrierefunktionen und Innere-Punkt-Verfahren . . . . . . . . . . . . . . . . . . . . . . . . . 345
4.7 Numerische Experimente zu Verfahren der restringierten Optimierung . . . . . 349
4.8 Übungsaufgaben zu Kapitel 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 368
In diesem Abschnitt werden wichtige Lösungsverfahren für Optimierungsprobleme mit
Nebenbedingungen motiviert und darauf aufbauend Algorithmen mit zugehörigen Kon-
vergenzaussagen angegeben. Abschließend werden die Algorithmen anhand der Imple-
mentationen unter EdOptLab getestet, wobei an ausgewählten Beispielen auf numeri-
sche Effekte eingegangen wird. Ein Vergleich mit den Lösungsalgorithmen der Optimi-
zation Toolbox von Matlab beschließt die numerischen Experimente. Eine ausführliche
Darlegung der Theorie und der Konvergenzeigenschaften der Verfahren analog dem Kapi-
tel 3 würde den Rahmen dieses Buches sprengen. Bezüglich tiefergehender Darstellungen
verweisen wir auf Bertsekas (1999), Geiger und Kanzow (2002), Jarre und Stoer (2004)
sowie Spellucci (1993).
R. Reinhardt et al., Nichtlineare Optimierung, DOI 10.1007/978-3-8274-2949-0_4,
© Springer-Verlag Berlin Heidelberg 2013

298 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
4.1 Sattelpunkte, Dualität und Sensitivität
Um die betrachteten numerischen Verfahren für Probleme mit Nebenbedingungen besser
motivieren zu können, ergänzen wir die Theorie aus Abschnitt 2.2 um einige Aussagen
zu Sattelpunkten, Dualität und Sensitivität für restringierte Probleme.
Lemma 4.1
Es seien F : X × Y × Z → R mit X ⊂ Rn, Y ⊂ Rm und Z ⊂ Rp. Dann gilt
supy∈Y, z∈Z
infx∈XF (x,y, z) ≤ inf
x∈Xsup
y∈Y, z∈ZF (x,y, z) .
Beweis: Offensichtlich gilt
infx∈XF (x, y, z) ≤ F (x, y, z) ≤ sup
y∈Y, z∈ZF (x,y, z)
für alle (x, y, z) ∈ X × Y × Z und somit auch
supy∈Y, z∈Z
infx∈XF (x,y, z) ≤ inf
x∈Xsup
y∈Y, z∈ZF (x,y, z) ,
womit die Aussage des Lemmas bewiesen ist. �
Definition 4.2Es seien F : X × Y × Z → R mit X ⊂ Rn, Y ⊂ Rm und Z ⊂ Rp. Ein Vektor (x, y, z) ∈X × Y × Z heißt Sattelpunkt von F bezüglich X × Y × Z, wenn
F (x,y, z) ≤ F (x, y, z) ≤ F (x, y, z)
für alle (x,y,z) ∈ X × Y × Z gilt.
Ist (x, y, z) ein Sattelpunkt von F bezüglich X × Y × Z, so ist x ein globales Minimumder Funktion Fy,z : X → R mit Fy,z(x) := F (x, y, z) bzw. (y, z) ein globales Maximum
der Funktion Fx : Y × Z → R mit Fx(y,z) := F (x,y,z). Die Aussage des folgenden
Lemmas folgt nun unmittelbar aus Lemma 4.1 und der Definition eines Sattelpunktes.
Lemma 4.3
Es seien F : X × Y ×Z → R mit X ⊂ Rn, Y ⊂ Rm und Z ⊂ Rp. Das Tripel (x, y, z) istgenau dann ein Sattelpunkt von F bezüglich X × Y × Z, wenn
F (x, y, z) = maxy∈Y, z∈Z
minx∈XF (x,y, z) = min
x∈Xmax
y∈Y, z∈ZF (x,y, z)
gilt.

4.1 Sattelpunkte, Dualität und Sensitivität 299
Der folgende Satz zeigt, dass jeder Sattelpunkt der Lagrange-Funktion eines Optimie-
rungsproblems der Form(P≤=
)mit differenzierbaren Problemfunktionen gleichzeitig ein
KKT-Punkt dieses Problems ist.
Satz 4.4
Es seien f ∈ C1(Rn,R), G ∈ C1(Rn,Rm) und H ∈ C1(Rn,Rp). Ist (x, u, v) ein Sat-telpunkt der Lagrange-Funktion des Optimierungsproblems
(P≤=
)bzgl. Rn × Rm+ × Rp,
dann ist (x, u, v) ein KKT-Punkt und x eine globale Lösung von(P≤=
).
Beweis: Ist (x, u, v) ein Sattelpunkt der Lagrange-Funktion eines Optimierungsproblemsder Form
(P≤=
)bzgl. Rn ×Rm+ ×Rp, so ist x ein globales Minimum der Funktion Lu,v :
Rn → R mit Lu,v(x) := f(x) + uTG(x) + vTH(x) und Lu,v ∈ C1(Rn,R). Mit Satz 2.2
folgt
∇Lu,v(x) = ∇xL(x, u, v) = 0 .
Aufgrund der Sattelpunkteigenschaft des Punktes (x, u, v) gilt weiterhin
L(x,u, v) ≤ L(x, u, v) bzw. (u− u)TG(x) + (v − v)TH(x) ≤ 0
für alle (u,v) ∈ Rm+ ×Rp und somit
∇uL(x, u, v) = G(x) ≤ 0 und ∇vL(x, u, v) = H(x) = 0 .
Weiterhin folgt für die spezielle Wahl u = 0 sowie v = v
uTG(x) ≥ 0
und wegen u ∈ Rm+uT∇uL(x, u, v) = uTG(x) = 0 .
Wiederum wegen der Sattelpunkteigenschaft des Punktes (x, u, v) gilt
L(x, u, v) ≤ L(x, u, v) ,
und es folgt
f(x) = f(x) + uTG(x) + vTH(x) ≤ f(x) + uTG(x) + vTH(x) ≤ f(x)
für alle x ∈ M = {x ∈ Rn| G(x) ≤ 0, H(x) = 0}, womit die Aussage des Satzesbewiesen ist. �
Die Umkehrung von Satz 4.4 gilt i. Allg. nicht (siehe Aufgabe 4.2). Für konvexe Op-
timierungsprobleme mit differenzierbaren Problemfunktionen gilt jedoch:

300 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Satz 4.5
Es seien f ∈ C1(Rn,R), G = (g1, · · · , gm)T ∈ C1(Rn,Rm), H = (h1, · · · , hp)T , f konvexüber Rn, gi : Rn → R konvex über Rn für alle i ∈ {1, · · · ,m} und hj : Rn → R affin-linear
für alle j ∈ {1, · · · , p}. Ein Punkt (x, u, v) ist genau dann ein Sattelpunkt der Lagrange-Funktion des konvexen Optimierungsproblems
(P f,≤ konv.= aff.−l.
)bzgl. Rn ×Rm+ ×Rp, wenn
(x, u, v) ein KKT-Punkt von(P f,≤ konv.= aff.−l.
)ist.
Beweis: Mit Satz 4.4 genügt es zu zeigen, dass jeder KKT-Punkt (x, u, v) des kon-
vexen Problems(P f,≤ konv.= aff.−l.
)ein Sattelpunkt der zugehörigen Lagrange-Funktion ist.
Wir betrachten hierfür wiederum die im Beweis von Satz 4.4 definierte Funktion Lu,v.
Aufgrund der Konvexität der Funktionen f und g1, · · · , gm sowie der affinen Lineari-
tät der Funktionen h1, · · · , hp ist die Funktion Lu,v eine konvexe Funktion über Rn. Istnun (x, u, v) ein KKT-Punkt des konvexen Optimierungsproblems, so gilt aufgrund der
KKT-Bedingungen
∇xL(x, u, v) = ∇Lu,v(x) = 0 ,
und mit Satz 2.3 folgt
Lu,v(x) ≤ Lu,v(x) bzw. L(x, u, v) ≤ L(x, u, v)
für alle x ∈ Rn. Weiterhin gilt aufgrund der KKT-Bedingungen
∇uL(x, u, v) = G(x) ≤ 0, u ≥ 0, uT∇uL(x, u, v) = uTG(x) = 0 sowie
∇vL(x, u, v) = H(x) = 0 .
Es ergibt sich für alle (u,v) ∈ Rm+ ×Rp
L(x, u, v) = f(x) + uTG(x) + vTH(x)
= f(x)
≥ f(x) + uTG(x) + vTH(x)
= L(x,u,v)
und zusammengefasst
L(x,u, v) ≤ L(x, u, v) ≤ L(x, u, v)
für alle (x,u, v) ∈ Rn ×Rm+ ×Rp. �
Für die Lagrange-Funktion L eines Optimierungsproblems der Form(P≤=
)mit steti-
gen Problemfunktionen f , G und H sowie zulässigem Bereich M gilt
supu∈Rm+ , v∈Rp
L(x,u, v) = supu∈Rm+ , v∈Rp
(f(x) +G(x)Tu+H(x)Tv
)=
{f(x) , falls x ∈M∞ , sonst

4.1 Sattelpunkte, Dualität und Sensitivität 301
und somit
infx∈Rn
supu∈Rm+ , v∈Rp
L(x,u,v) = infx∈Mf(x) .
Vereinbaren wir weiterhin
dom q :=
{(u, v) ∈ Rm+ ×Rp
∣∣∣∣ infx∈RnL(x,u, v) > −∞
},
dann gilt für die Funktion
q : dom q ⊂ Rm+ ×Rp → R mit q(u, v) := infx∈RnL(x,u, v)
offensichtlich
supu∈Rm+ , v∈Rp
infx∈RnL(x,u, v) = sup
(u,v)∈dom q
q(u, v) .
Die Problemstellungen
(P ) MIN {f(x) | x ∈M } ,(D) MAX {q(u, v) | (u,v) ∈ dom q }
werden zueinander duale Problemstellungen genannt. Dabei wird (P ) als primales Pro-
blem und (D) als duales Problem bezeichnet. Die zugehörigen Zielfunktionen f bzw. q
heißen primale Zielfunktion bzw. duale Zielfunktion. Weiterhin ist dom q eine konvexe
Menge, die duale Zielfunktion q konkav über dom q und somit jede lokale Lösung des
dualen Problems auch eine globale Lösung (siehe Aufgabe 4.3).
Beispiel 4.6
Wir betrachten das primale (lineare) Optimierungsproblem
(P ) MIN{cTx
∣∣ Ax = b, x ≥ 0}
mit A ∈ R(p,n), c,x ∈ Rn sowie b ∈ Rp und zugehöriger Lagrange-Funktion L : Rn ×Rn+ ×Rp → R mit
L(x,u, v) := cTx+ (−x)Tu+ (b−Ax)Tv = bTv +(c− u−ATv
)Tx .
Offensichtlich gilt für die duale Zielfunktion q : Rn+ ×Rp → R mit
q(u,v) := infx∈RnL(x,u,v) =
{−∞ , falls c−ATv �= u ≥ 0
bTv , falls c−ATv = u ≥ 0,
und das duale Problem zu (P ) lautet
(D) MAX{bTv
∣∣ ATv ≤ c} .�

302 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Mit Lemma 4.1 folgt unmittelbar:
Satz 4.7 (Schwache Dualität)
Es seien (P ) ein primales Problem mit Zielfunktion f und zulässigem Bereich M sowie
(D) das zugehörige duale Problem mit dualer Zielfunktion q und dual zulässigem Bereich
dom q. Dann gilt
sup(u,v)∈dom q
q(u,v) ≤ infx∈Mf(x) .
Mit anderen Worten besagt Satz 4.7, dass der duale Zielfunktionswert eines jeden dual
zulässigen Punktes eine untere Schranke für den optimalen Zielfunktionswert des pri-
malen Problems ist. Umgekehrt liefert auch der primale Zielfunktionswert eines jeden
primal zulässigen Punktes eine obere Schranke für den optimalen Zielfunktionswert des
dualen Problems.
Beispiel 4.8
Wir betrachten das primale Optimierungsproblem
(P ) MIN{f(x) = x2
1 + x22
∣∣ g(x1, x2) = 2− x1 ≤ 0}
mit der globalen Lösung x = (2, 0)T und optimalem primalen Zielfunktionswert f(2, 0) =
4. Für die zugehörige Lagrange-Funktion L gilt
infx∈R2L(x, u) = inf
x∈R2
(x2
1 + x22 + u (2− x1)
)= − 1
4u2 + 2u ,
und das duale Problem zu (P ) lautet
(D) MAX
{q(u) = −1
4u2 + 2u
∣∣∣∣ u ∈ R+
}.
Weiterhin ist offensichtlich u = 4 die globale Lösung des dualen Problems mit optimalem
dualen Zielfunktionswert q(4) = 4. �
Im Gegensatz zu linearen Optimierungsproblemen (siehe z. B. Beispiel 4.8) gilt für ein
Paar dualer Probleme i. Allg. jedoch nicht
sup(u,v)∈dom q
q(u,v) = infx∈Mf(x) ,
sondern es können durchaus sogenannte Dualitätslücken mit
sup(u,v)∈dom q
q(u, v) < infx∈Mf(x)
auftreten, womit in diesem Fall auch der Optimalwert des dualen Problems keine scharfe
untere Schranke für den optimalen Zielfunktionswert des primalen Problems darstellt.

4.1 Sattelpunkte, Dualität und Sensitivität 303
Beispiel 4.9
Das primale Optimierungsproblem
(P ) MIN {f(x) | g(x) = −x ≤ 0}
mit
f(x) =
⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩2x+ 4 , falls x < −2−x2 − 2x , falls − 2 ≤ x < 0x2 − 2x , falls 0 ≤ x < 22x− 4 , falls 2 ≤ x
besitzt die globale Lösung x = 1. Für die zugehörige Lagrange-Funktion L gilt
L(x, u) =
⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩(2− u)x+ 4 , falls x < −2−x2 − (2 + u)x , falls − 2 ≤ x < 0x2 − (2 + u)x , falls 0 ≤ x < 2(2− u)x− 4 , falls 2 ≤ x
und
infx∈R
L(x, u)
{−∞ , falls u �= 2
−4 , falls u = 2,
womit zwischen dem optimalen dualen Zielfunktionswert q(2) = −4 und dem optimalen
primalen Zielfunktionswert f(1) = −1 eine (endliche) Dualitätslücke besteht. �
Existieren jedoch ein x ∈ M und ein (u, v) ∈ dom q mit q(u, v) = f(x), so ist offen-
sichtlich x eine globale Lösung des primalen Problems und (u, v) eine globale Lösung
des dualen Problems. Mit Lemma 4.3 folgt weiterhin unmittelbar:
Satz 4.10 (Starke Dualität)
Es seien (P ) ein primales Problem der Form(P≤=
)mit Zielfunktion f und zulässigem
BereichM sowie (D) das duale Problem zu (P ) mit dualer Zielfunktion q und dual zuläs-
sigem Bereich dom q. Das Tripel (x, u, v) ist genau dann ein Sattelpunkt der zugehörigen
Lagrange-Funktion L bezüglich Rn ×Rm+ ×Rp, wenn
L(x, u, v) = max(u,v)∈dom q
q(u, v) = minx∈Mf(x)
gilt.
Für konvexe Optimierungsprobleme mit differenzierbaren Problemfunktionen folgt aus
Satz 4.5 und Satz 4.10:

304 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Satz 4.11 (Starke Dualität bei konvexen Optimierungsproblemen)
Es seien f ∈ C1(Rn,R), G = (g1, · · · , gm)T ∈ C1(Rn,Rm), H = (h1, · · · , hp)T , f konvexüber Rn, gi : Rn → R konvex über Rn für alle i ∈ {1, · · · ,m} und hj : Rn → R affin-
linear für alle j ∈ {1, · · · , p}. Für das konvexe Optimierungsproblem(P f,≤ konv.= aff.−l.
)mit
zulässigem Bereich M sind die folgenden Aussagen äquivalent:
(a) (x, u, v) ist ein KKT-Punkt von(P f,≤ konv.= aff.−l.
).
(b) (x, u, v) ist ein Sattelpunkt der Lagrange-Funktion L von(P f,≤ konv.= aff.−l.
)bzgl. Rn×
Rm+ ×Rp.
(c) Für die Lagrange-Funktion L von(P f,≤ konv.= aff.−l.
)gilt
L(x, u, v) = max(u,v)∈dom q
q(u, v) = minx∈Mf(x) .
Zum Abschluss dieses Abschnittes wollen wir noch einen zweiten Zugang zu den Duali-
tätsaussagen anführen, welcher für numerische Zwecke zwar kaum Bedeutung hat, aber
bei der Entwicklung von Lösungsverfahren für Probleme mit Nebenbedingungen ein wich-
tiges Denkmodell liefert. Wir werden später diesen Zugang in abgewandelter Form im-
mer wieder aufgreifen. Dafür wollen wir für Optimierungsprobleme der Form(P≤
)mit
stetigen Problemfunktionen f und G sowie zulässigem Bereich M �= ∅ die „Empfindlich-keit“ der ggf. existierenden optimalen Lösungen gegenüber Änderungen der Nebenbedin-
gungen betrachten. Die Funktion λ : Λ ⊂ Rm → R mit
λ(b) := infx{f(x) | G(x) ≤ b} und Λ := {b ∈ Rm | ∃x ∈ Rn mit G(x) ≤ b}
heißt Sensitivitätsfunktion des Optimierungsproblems(P≤
). Oft definiert man zusätzlich
λ(b) :=∞ für alle b /∈ Λ, und setzt somit die Sensitivitätsfunktion auf dem gesamten Rm
fort. Die so definierte Sensitivitätsfunktion λ ist monoton fallend, d. h. für alle b1, b2 ∈ Λmit b1 ≤ b2 gilt λ(b1) ≥ λ(b2), jedoch i. Allg. nicht differenzierbar (auch im Falle
differenzierbarer Problemfunktionen). Sind ferner alle Koordinatenfunktionen gi konvex
über Rn, so ist Λ eine konvexe Menge (siehe Aufgabe 4.4) und λ konvex über Λ (siehe
beispielsweise Elster et al. (1977)). Für jedes festes u ∈ Rm+ definieren wir nun
ρ(u) := sup{ρ ∈ R
∣∣ ρ− uTb ≤ λ(b) ∀ b ∈ Λ}und darauf aufbauend für den Fall ρ(u) > −∞ eine affin-lineare Funktion
l : Rm → R mit l(b) := ρ(u)− bTu ,
welche den Graphen der Sensitivitätsfunktion λ „stützt“. Mit

4.1 Sattelpunkte, Dualität und Sensitivität 305
s(x, b) :=
{0 , falls G(x) ≤ b∞ , sonst
und der Definition der dualen Zielfunktion für Problemstellungen der Form(P≤
)folgt
ρ(u) = infb∈Λ
(infx∈Rn
{f(x)| G(x) ≤ b}+ uTb)= infb∈Λ
infx∈Rn
(f(x) + uTb+ s(x, b)
)= inf
x∈Rninfb∈Λ
(f(x) + uTb+ s(x, b)
)= infx∈Rn
(f(x) + inf
b∈Λ
{uT b | G(x) ≤ b
})= inf
x∈Rn
(f(x) +G(x)Tu
)= infx∈RnL(x,u)
und somit infx∈Mf(x) = λ(0) ≥ sup
u∈Rm+
ρ(u) = supu∈Rm+
infx∈RnL(x,u) = sup
u∈dom qq(u), was einen
Zusammenhang zwischen λ und dem schwachen Dualitätssatz herstellt.
Beispiel 4.12
Wir betrachten erneut das primale Problem (P ) aus Beispiel 4.9 mit zulässigem Bereich
M = {x ∈ R | g(x) = −x ≤ 0}. Für die Sensitivitätsfunktion λ : R → R von (P ) gilt
λ(b) :=
⎧⎪⎪⎪⎪⎨⎪⎪⎪⎪⎩−2b− 4 , falls b < −2b2 + 2b , falls − 2 ≤ b < −1
−1 , falls − 1 ≤ b < 52
−2b+ 4 , falls 52 ≤ b
, ρ(u) =
{−∞ , falls u �= 2
−4 , falls u = 2
und infx∈Mf(x) = λ(0) = −1 > −4 = sup
u∈dom qq(u). �
−8 −6 −4 −2 0 2 4 6 8−8
−6
−4
−2
0
2
4
b
λ
max D = ρ(2)
inf P = λ(0)
Dualitätslücke
Stützpunkt
l
Abb. 4.1 Sensitivitätsfunktion λ und stützende affin-lineare Funktion l für Beispiel 4.12

306 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
4.2 Straffunktionen und Strafverfahren
Die in diesem Abschnitt betrachteten sogenannten Strafverfahren zählen historisch ge-
sehen mit zu den ersten Verfahrensansätzen zur Lösung von restringierten nichtlinearen
Optimierungsproblemen. Hierbei wird im Idealfall das ursprüngliche restringierte Pro-
blem durch die Lösung einer Folge von unrestringierten Problemen ersetzt, wobei die
Zielfunktionen dieser Folge von unrestringierten Problemen eine Verletzung der Neben-
bedingungen bzgl. des zugrundeliegenden restringierten Optimierungsproblems mit ei-
nem wachsenden Folgenparameter immer stärker „bestrafen“. Von zentraler Bedeutung
für die Beschreibung der Strafverfahren ist deshalb der Begriff der Straffunktion, den wir
im Folgenden einführen wollen. Wir betrachten dafür ein Optimierungsproblem der Form(P≤=
)mit zumindest stetigen Problemfunktionen f , G und H sowie zulässigem Bereich
M . Ferner sei Ψ : Rn → R+ eine stetige Funktion mit
Ψ(x) = 0⇔ x ∈M sowie Ψ(x) > 0⇔ x /∈M .
Die (stetige) Funktion S : Rn ×R++ → R mit
S(x, r) := f(x) + rΨ(x) (4.1)
wird als Straffunktion, der Parameter r > 0 als Strafparameter und die Funktion Ψ als
Strafterm für die Problemstellung(P≤=
)bezeichnet. Für nicht zulässige Punkte x wird
zu dem entsprechenden Wert der Zielfunktion also ein positives Vielfaches des Straf-
terms addiert. Wir werden uns bei unseren weiteren Betrachtungen in diesem Abschnitt
zunächst auf eine spezielle Klasse von Straffunktionen, die sogenannten quadratischen
Straffunktionen, beschränken.
Für einen Vektor a ∈ Rm sei der Vektor [a]+ ∈ Rm koordinatenweise definiert durch
[a]+i := max{0, ai} mit i ∈ {1, · · · ,m} .
Die Funktion S : Rn ×R++ → R mit
S(x, r) := f(x) + r(‖ [G(x)]+ ‖2 + ‖H(x)‖2
)wird als quadratische Straffunktion für die Problemstellung
(P≤=
)bezeichnet, und für
jedes (feste) r > 0 lässt sich der ursprünglichen Problemstellung(P≤=
)nun ein unrestrin-
giertes Optimierungsproblem gemäß(SP≤=
)r
MIN{Sr(x) := f(x) + r
(‖ [G(x)]+ ‖2 + ‖H(x)‖2
)∣∣∣ x ∈ Rn}
zuordnen.

4.2 Straffunktionen und Strafverfahren 307
Die den Strafverfahren (mit quadratischer Straffunktion) zugrundeliegende Idee besteht
nun darin, für eine streng monoton wachsende Folge von Strafparametern {rk}k∈Nglobale
(oder auch lokale) Lösungen xk der zugehörigen unrestringierten Optimierungsprobleme(SP≤=
)rkzu bestimmen, natürlich in der Hoffnung, sich damit einer globalen (oder auch
lokalen) Lösung des ursprünglichen restringierten Optimierungsproblems(P≤=
)anzunä-
hern. Ein entsprechender Prinzipalgorithmus kann wie folgt formuliert werden:
Algorithmus 21 (Prinzipalgorithmus Strafverfahren)
S0 Wähle r0 > 0, und setze k := 0.
S1 Bestimme xk ∈ arg minx∈RnS(x, rk) .
S2 Gilt G(xk) ≤ 0 und H(xk) = 0, dann STOPP.
S3 Wähle rk+1 > rk, setze k := k + 1, und gehe zu S1.
Wir setzen also bei der Formulierung von S1 die Existenz globaler Lösungen voraus
und möchten zunächst die (theoretische) Abbruchbedingung in S2 motivieren. Aus der
Definition der Straffunktion S folgt für alle Iterierten xk
f(xk) ≤ S(xk, rk) ≤ infx∈MS(x, rk) = inf
x∈Mf(x) . (4.2)
Gilt nun G(xk) ≤ 0 und H(xk) = 0, so folgt f(xk) ≥ infx∈Mf(x) wegen xk ∈ M bzw.
f(xk) = minx∈Mf(x) wegen (4.2), womit xk eine globale Lösung des ursprünglichen Pro-
blems(P≤=
)ist. Bei den folgenden Betrachtungen beschränken wir uns zunächst auf
Problemstellungen der Form (P=).
Satz 4.13
Es seien f ∈ C0(Rn,R), H ∈ C0(Rn,Rp), M := {x ∈ Rn | H(x) = 0} �= ∅ und
{rk}k∈N⊂ R++ eine streng monoton wachsende Folge mit lim
k→∞rk = ∞. Dann gilt
für jede durch den Prinzipalgorithmus 21 für das Optimierungsproblem (P=) erzeugte
Folge{xk
}k∈N
:
(a) Die Folge{S(xk, rk)
}k∈N
ist monoton wachsend.
(b) Die Folge{‖H(xk)‖
}k∈N
ist monoton fallend.
(c) Die Folge{f(xk)
}k∈N
ist monoton wachsend.
(d) Es gilt limk→∞H(xk) = 0.
(e) Jeder Häufungspunkt der Folge{xk
}k∈N
ist (globale) Lösung von (P=).

308 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Beweis:
Zu (a): Offensichtlich gilt wegen xk ∈ arg minx∈RnS(x, rk) und rk+1 > rk > 0
S(xk, rk) ≤ S(xk+1, rk) ≤ S(xk+1, rk+1)
für alle k ∈ N.Zu (b) und (c): Wiederum wegen xk ∈ arg min
x∈RnS(x, rk) gilt
S(xk, rk) + S(xk+1, rk+1) ≤ S(xk+1, rk) + S(x
k, rk+1)
für alle k ∈ N. Mit der Definition der Funktion S folgt
(rk − rk+1)(‖H(xk)‖2 − ‖H(xk+1)‖2
)≤ 0
und somit wegen rk+1 > rk
‖H(xk)‖2 − ‖H(xk+1)‖2 ≥ 0
für alle k ∈ N. Dies impliziert jedoch unmittelbar
‖H(xk)‖ ≥ ‖H(xk+1)‖
und damit wegen S(xk, rk) ≤ S(xk+1, rk) sowie rk > 0 auch
f(xk+1)− f(xk) ≥ rk(‖H(xk)‖2 − ‖H(xk+1)‖2
)≥ 0
für alle k ∈ N.Zu (d): Wegen M �= ∅ gilt inf
x∈Mf(x) <∞. Mit (c) sowie (4.2) folgt
f(x0) + rk‖H(xk)‖2 ≤ S(xk, rk) <∞
für alle k ∈ N und somit wegen limk→∞rk =∞ unmittelbar lim
k→∞H(xk) = 0.
Zu (e): Es seien x ein Häufungspunkt der Folge{xk
}k∈N
und {xk(l)}l∈N eine gegen x
konvergente Teilfolge. Mit (d) folgt H(x) = 0 und somit x ∈ M . Weiterhin gilt wegen(4.2)
infx∈Mf(x) ≤ f(x) = lim
l→∞f(xk(l)) ≤ lim
l→∞S(xk(l), rk(l)) ≤ inf
x∈Mf(x)
und damit f(x) = minx∈Mf(x). �
Sind für Problemstellungen der Form (P=) die Problemfunktionen f und H stetig dif-
ferenzierbar, dann sind auch die Funktionen Sr für alle r stetig differenzierbar, und es
gilt
∇Sr(x) = ∇f(x) + 2r∇H(x)H(x) .

4.2 Straffunktionen und Strafverfahren 309
Nach Satz 2.2 gilt also für die Iterierten xk des Prinzipalgorithmus 21
0 = ∇f(xk) + 2rk∇H(xk)H(xk) . (4.3)
Ein Vergleich von (4.3) mit den KKT-Bedingungen des ursprünglichen Problems (P=)
zeigt, dass die Werte
vk := 2rkH(xk) (4.4)
als Näherung der Lagrange-Multiplikatoren betrachtet werden können, was wiederum die
Verletzung der KKT-Bedingungen in (xk,vk) und der Zulässigkeit beispielsweise gemäß
‖∇f(x) + 2r∇H(x)H(x)‖∞ < ε und ‖H(x)‖∞ < ε
für ein vorgegebenes ε > 0 als praktisches Abbruchkriterium in S2 des Prinzipalgorith-
mus 21 nahelegt. Zur weiteren Motivation dieser Vorgehensweise dient der folgende Satz:
Satz 4.14
Es seien f ∈ C1(Rn,R), H = (h1, · · · , hp)T ∈ C1(Rn,Rp), {rk}k∈N⊂ R++ eine
streng monoton wachsende Folge mit limk→∞rk = ∞,
{xk
}k∈N
eine durch den Prin-
zipalgorithmus 21 für das zugehörige Optimierungsproblem (P=) erzeugte Folge mit
limk→∞xk = x und die Folge
{vk
}k∈N
⊂ Rp definiert gemäß (4.4). Sind ferner die Gradi-
enten ∇h1(x), · · · ,∇hp(x) linear unabhängig, dann gilt:
(a) Es existiert ein v ∈ Rp mit limk→∞vk = v.
(b) x ist eine (globale) Lösung, und das Paar (x, v) ist ein KKT-Punkt von (P=).
Beweis:
Zu (a): Wegen der linearen Unabhängigkeit der Gradienten ∇h1(x), · · · ,∇hp(x) gilt
rang∇H(x) = rang∇H(x)T = p
und somit wegen limk→∞xk = x und der stetigen Differenzierbarkeit von H
rang∇H(xk) = rang∇H(xk)T = p
für alle hinreichend großen k. Damit sind aber sowohl die Matrix ∇H(x)T∇H(x) alsauch die Matrix ∇H(xk)T∇H(xk) für alle hinreichend großen k invertierbar. Wegen
(4.3) und (4.4) folgt
0 = ∇H(xk)T∇f(xk) +∇H(xk)T∇H(xk)vk

310 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
und daher wegen limk→∞xk = x
limk→∞vk = − lim
k→∞(∇H(xk)T∇H(xk)
)−1∇H(xk)T∇f(xk)
= −(∇H(x)T∇H(x)
)−1∇H(x)T∇f(x)=: v ,
womit die Aussage (a) bewiesen ist.
Zu (b): Wegen H ∈ C1(Rn,Rp), limk→∞rk =∞, lim
k→∞xk = x, (4.4) sowie (a) folgt
H(x) = limk→∞H(xk) = lim
k→∞vk
2rk= 0 ,
weshalb x nach Satz 4.13 (e) eine (globale) Lösung des Optimierungsproblems (P=) ist.
Da weiterhin in x die Regularitätsbedingung (LICQ) erfüllt ist, existiert nach Satz 2.22,
Satz 2.26, Satz 2.28 und Aufgabe 2.12 ein eindeutig bestimmter Lagrange-Multiplikator
v ∈ Rm mit 0 = ∇f(x) +∇H(x)v bzw. 0 = ∇H(x)T∇f(x) +∇H(x)T∇H(x)v. UnterVerwendung der Ausführungen und der Definition von v im Beweis von (a) folgt nun
v = v und somit 0 = ∇f(x) +∇H(x)v, wodurch auch die Aussage (b) gezeigt ist. �
Wir bemerken nochmals, dass wir bei der Formulierung von Satz 4.13 und Satz 4.14
implizit vorausgesetzt haben, dass für alle Strafparameter rk die in Schritt S1 des Prin-
zipalgorithmus 21 betrachteten Funktionen globale Minimalstellen über Rn besitzen (wasi. Allg. nicht der Fall ist) und diese globalen Minimalstellen sogar jeweils exakt bestimmt
werden können. Sind für Problemstellungen der Form(P≤
)die Problemfunktionen f
und G stetig differenzierbar, dann sind die Funktion Sr für alle r ebenfalls stetig diffe-
renzierbar, und es gilt
∇Sr(x) = ∇f(x) + 2r∇G(x) [G(x)]+ . (4.5)
Da weiterhin G(x) ≤ 0 äquivalent zu [G(x)]+ = 0 ist, lassen sich die Aussagen der Sätze
4.13 und 4.14 auf Problemstellungen der Form(P≤
)und damit auch auf die allgemeine
Problemstellung(P≤=
)übertragen, worauf wir jedoch nicht weiter eingehen wollen.
Beispiel 4.15
Wir betrachten das Optimierungsproblem (Problem Nr. 101)
MIN{f(x) = −x2
1 + x22 | 0 ≤ x1 ≤ 1, −1 ≤ x2 ≤ 1
}mit (globaler) Lösung x = (1, 0)T und optimalen Zielfunktionswert f(x) = −1 (sieheAufgabe 2.15) sowie zugehöriger quadratischer Straffunktion
Sr(x) = −x21 + x
22 + r
(([−x1]
+)2+([x1 − 1]+
)2+([−x2 − 1]+
)2+([x2 − 1]+
)2).

4.2 Straffunktionen und Strafverfahren 311
Für alle r > 0 ist zunächst x = (0, 0)T ein Sattelpunkt von Sr. Ist weiterhin für r > 0
der Punkt x(r) eine globale Minimalstelle von Sr über R2, so muss x2(r) = 0 gelten, und
es genügt (für ein festes r > 0) zur Minimierung von Sr die Hilfsfunktion
Sr(x1) := −x21 + r
(([−x1]
+)2+([x1 − 1]+
)2)
=
⎧⎪⎪⎨⎪⎪⎩(r − 1)x2
1 , falls x1 < 0
−x21 , falls 0 ≤ x1 ≤ 1
(r − 1)x21 − 2rx1 + r , falls 1 < x1
zu betrachten. Gilt 0 < r ≤ 1, so besitzt die zugehörige Hilfsfunktion Sr und somit
die entsprechende Straffunktion Sr keine globale Minimalstelle. Für r > 1 ist jedoch
x(r) =(rr−1, 0)T
mit Sr(x(r)) = − rr−1
die globale Minimalstelle der Straffunktion Srüber R2, und es gilt lim
r→∞x(r) = x = (1, 0)T sowie lim
r→∞Sr(x(r)) = f(x) = −1. �
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
(r = 0)
−3
−3
−2.5
−2.5
−2
−2
−2
−1.5
−1.5
−1.5
−1
−1
−1
−1
−0.9
−0.9
−0.9
−0.5
−0.5
−0.5
−0.5
−0.25
−0.25
0
0
0
0
0
0
0
0.250.25
0.250.25
0.5
0.50.5
0.50.5
1
11
1
11
1.51.5
1.51.5
22
220.5
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 0.9
−3
−2.5
−2.5
−2
−2
−2
−1.5
−1.5
−1.5
−1
−1
−1
−1
−0.9
−0.9
−0.9
−0.5
−0.5
−0.5
−0.5
−0.25
−0.25
0
0
0
0
0
0
0.25
0.25
0.250.25
0.5
0.50.5
0.5
0.50.5
1
11
1
11
1.51.5
1.51.5
22
22
0
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 1
−2.5
−2
−2
−1.5
−1.5
−1.5
−1
−1
−1
−1
−0.9
−0.9
−0.9
−0.5
−0.5
−0.5
−0.5
−0.25
−0.25
0
0
0
0
0
0.250.25
0.250.25
0.5
0.50.5
0.5
0.50.5
1
11
1
11
1.51.5
1.51.5
22
22
0
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 5
−1.2
2
−1
−1 −1
−0.9
−0.9
−0.9
−0.5
−0.5
−0.5
−0.5
−0.25
−0.25
0
0
0
0
00
0.25
0.25
0.25
0.25
0.5
0.5
0.5
0.5
0.5
0.50.5
0.5
1
11 1
1
1
11
1
22
2
2
22
2
2
4
4
4
40 1 2
−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 25
−1
−0.9
−0.9
−0.5
−0.5−0
.25
−0.250
0
0
0
0
0.25
0.25
0.25
0.25
0.5
0.5
0.5
0.5
1
11
1
1
1
12
22
2
2
22
2
4
4 44
4
444
4
9
9
9
9
9
16
1616
25
25
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 50
−1−0
.9
−0.5−0
.25
−0.25
0
0
0
00.25
0.25
0.25
0.25
0.5
0.5
0.51
1 1
1
11
1
2
2 2
2
22
24
4
4 4
4
44
49
9
9 9
9
9
99
9
16
16
16
16
16
25
2525
3636
36
49
49
Abb. 4.2 Höhenlinien der Zielfunktion (r = 0) und der zugehörigen quadratischen Straffunktionmit Strafparameter r = 0.9, 1, 5, 25, 50 für Beispiel 4.15

312 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
In Analogie zum vorhergehenden Abschnitt wollen wir für quadratische Straffunktionen
einen zweiten Zugang über die Sensitivitätsfunktion diskutieren. Wir betrachten wieder-
um ein Optimierungsproblem der Form(P≤
)mit zumindest stetigen Problemfunktionen
f und G, zulässigem Bereich M �= ∅ sowie Sensitivitätsfunktion λ. Für jedes feste r > 0definieren wir nun
ρ(r) := sup{ρ ∈ R
∣∣∣ ρ− r ‖b‖2 ≤ λ(b) ∀ b ∈ Λ}
mit der Absicht, den Graphen der Sensitivitätsfunktion λ des Problems(P≤
)durch
quadratische Funktionen
π : Rm → R mit π(b) := ρ(r) − r‖b‖2
zu „stützen“. Analog der Schlussweise im vorhergehenden Abschnitt folgt
ρ(r) = infx∈Rn
(f(x) + r‖ [G(x)]+ ‖2
)= infx∈RnSr(x) .
Vereinbaren wir nun
domΘ :=
{r > 0
∣∣∣∣ infx∈RnSr(x) > −∞
}und
Θ : domΘ→ R mit Θ(r) := infx∈RnSr(x) ,
so können wir durch
MAX {Θ(r) | r ∈ domΘ}
ein anderes „duales“ Problem zu (P ) formulieren, für welches
infx∈Mf(x) = λ(0) ≥ sup
r>0ρ(r) = sup
r>0infx∈RnSr(x) = sup
r∈dom ΘΘ(r) (4.6)
gilt. Offensichtlich ist die Funktion Θ monoton wachsend, und in (4.6) kann Gleichheit
i. Allg. nur für r→∞ erreicht werden.
Beispiel 4.16
Wir betrachten erneut das primale Problem (P ) aus Beispiel 4.8 mit der globalen Lösung
x = (2, 0)T und optimalen primalen Zielfunktionswert f(x) = 4. Für die Sensitivitäts-
funktion λ : R → R von (P ) gilt
λ(b) :=
{(b− 2)2 , falls b < 2
0 , falls b ≥ 2
und somit λ(0) = f(x) = 4. Weiterhin folgt für alle r > 0
ρ(r) = infx∈R2Sr(x) = inf
x∈R2
(x2
1 + x22 + r([2 − x1]
+)2)= S(x(r), r)

4.2 Straffunktionen und Strafverfahren 313
mit
x(r) =
(2r
1 + r, 0
)Tsowie ρ(r) =
4r
1 + r.
Die die Sensitivitätsfunktion λ „stützenden“ quadratischen Funktionen π : R → R haben
daher die Form
π(b) =4r
1 + r− rb2
und berühren („stützen“) den Graphen der Sensitivitätsfunktion λ in den Punkten(2
1 + r,
4r2
(1 + r)2
)T.
Ferner gilt limr→∞x(r) = (2, 0)T sowie sup
r>0ρ(r) = lim
r→∞ρ(r) = 4. �
−2 −1 0 1 2 3 4
−2
0
2
4
6
8
10
b
λπ, r = 100π, r = 10π, r = 5π, r = 1λ(0)ρ(100)ρ(10)ρ(5)ρ(1)
Abb. 4.3 Sensitivitätsfunktion λ und stützende quadratische Funktionen π für Beispiel 4.16
Die bisher betrachteten Strafverfahren (mit quadratischen Straffunktionen) haben (wie
bereits erwähnt) den Nachteil, dass i. Allg. eine (globale) Lösung der unrestringierten
Hilfsprobleme(SP≤=
)rnur für r→∞ auch eine (globale) Lösung des ursprünglichen Pro-
blems(P≤=
)ist und die Hilfsprobleme mit wachsendem Strafparameter r immer schlechter
konditionierte Hesse-Matrizen besitzen. So gilt im Beispiel 4.16
∇2xS≤(x(r), r) =
(2 + 2r 0
0 2
),
d. h. die spektrale Konditionszahl der Hesse-Matrix ∇2xS≤(x(r), r) strebt mit r gegen
unendlich (siehe auch Beispiel 4.15). Es existieren jedoch sogenannte exakte Straffunk-
tionen, die diesen Nachteil für gewisse Problemklassen nicht aufweisen.

314 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Definition 4.17
Es seien x eine lokale Lösung eines Optimierungsproblems der Form(P≤=
)mit stetigen
Problemfunktionen f , G und H sowie S : Rn × R+ → R eine Straffunktion für die
Problemstellung(P≤=
)gemäß (4.1). Die Straffunktion S heißt exakt in x, wenn ein
r > 0 existiert, sodass x für alle r ≥ r auch eine lokale Minimalstelle der Funktion
Sr : Rn → R mit Sr(x) := S(x, r)
über Rn ist.
Beispielsweise ist unter zusätzlichen Voraussetzungen durch die sogenannten lq-
Straffunktionen
Sq : Rn ×R+ → R mit Sq(x, r) := f(x) + r
∥∥∥∥∥([G(x)]+
H(x)
)∥∥∥∥∥q
mit 1 ≤ q ≤ ∞ eine Klasse exakter Straffunktionen gegeben. Der nachfolgende Satz zeigt,
dass wir uns beim Nachweis der Exaktheit der lq-Straffunktionen beispielsweise auf die
l1-Straffunktion
S1 : Rn ×R+ → R mit S1(x, r) := f(x) + r(‖ [G(x)]+ ‖1 + ‖H(x)‖1
)beschränken können.
Satz 4.18
Existiert für ein Optimierungsproblem der Form(P≤=
)mit stetigen Problemfunktionen
f , G und H sowie lokaler Lösung x ein q, sodass die zugehörige lq-Straffunktion S q exakt
in x ist, so sind für alle q mit 1 ≤ q ≤ ∞ die zugehörigen lq-Straffunktionen Sq exakt in
x.
Beweis: Wir vereinbaren zunächst
Ψq(x) :=
∥∥∥∥∥([G(x)]+
H(x)
)∥∥∥∥∥q
und Ψq(x) :=
∥∥∥∥∥([G(x)]+
H(x)
)∥∥∥∥∥q
mit 1 ≤ q, q ≤ ∞. Aufgrund der Normäquivalenz im Rm+p, und da nach Voraussetzung
S q exakt in x ist, existieren ein C ≥ 1, ein r′ > 0 und eine ε-Umgebung Uε(x) mit
Ψq(x) ≤ CΨq(x) und S qr′(x) ≤ Sqr′(x)
für alle x ∈ Uε(x) und alle r′ ≥ r′, woraus unmittelbar
SqCr′(x) = Sqr′(x) = S
qr′(x) ≤ S
qr′(x) = f(x) + r
′Ψq(x) ≤ f(x) + r′CΨq(x) = SqCr′(x)

4.2 Straffunktionen und Strafverfahren 315
für alle x ∈ Uε(x) und alle r′ ≥ r′ folgt. Somit ist x auch eine lokale Minimalstelle vonSqr über Rn für alle r ≥ r := Cr′ und die gewünschte Aussage bewiesen. �
Wir formulieren nun zunächst ein Exaktheitsresultat für die l1-Straffunktion bei kon-
vexen Problemstellungen.
Satz 4.19
Ist (x, u, v) ∈ Rn × Rm × Rp ein KKT-Punkt des konvexen Optimierungsproblems(P f,≤ konv.= aff.−l.
)mit f ∈ C1(Rn,R) und G ∈ C1(Rn,Rm), dann ist x für alle
r > r := max {‖u‖∞, ‖v‖∞}
sowohl eine globale Lösung von(P f,≤ konv.= aff.−l.
)als auch eine strenge globale Minimalstelle
von S1r : Rn → R mit S1
r (x) := f(x) + r(‖ [G(x)]+ ‖1 + ‖H(x)‖1
)über Rn.
Beweis: Ist (x, u, v) ein KKT-Punkt von(P f,≤ konv.= aff.−l.
), so ist x nach Satz 2.24 eine
globale Lösung des konvexen Optimierungsproblems, und es gilt
∇f(x) +∇G(x)u+∇H(x)v = 0, G(x) ≤ 0, u ≥ 0, uTG(x) = 0 sowie H(x) = 0 .
Mit Satz 1.68 (a) und der Definition von r folgt
S1r (x) = f(x) +G(x)T u+H(x)T v
= f(x) +G(x)T u+H(x)T v + (∇f(x) +∇G(x)u+∇H(x)v)T (x− x)= f(x) +∇f(x)T (x− x) +
(G(x) +∇G(x)T (x− x)
)Tu
+(H(x) +∇H(x)T (x− x)
)Tv
≤ f(x) +G(x)T u+H(x)T v
= f(x) +m∑i=1
uigi(x) +p∑j=1
vjhj(x)
≤ f(x) +m∑i=1
ui [gi(x)]+ +
p∑j=1
|vj | |hj(x)|
≤ f(x) +m∑i=1
r [gi(x)]+ +
p∑j=1
r |hj(x)|
= f(x) + r(‖ [G(x)]+ ‖1 + ‖H(x)‖1
)< f(x) + r
(‖ [G(x)]+ ‖1 + ‖H(x)‖1
)= S1
r (x)
für alle x ∈ Rn und alle r > r, womit die Aussage gezeigt ist. �
Für nichtkonvexe Problemstellungen kann die in Satz 4.19 formulierte „globale“ Exakt-
heit der lq-Straffunktionen i. Allg. nicht garantiert werden (siehe Beispiel 4.21). Es gilt
jedoch der folgende Satz, den wir ohne Beweis zitieren.

316 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Satz 4.20 (Bertsekas (1999))
Es sei x eine lokale Lösung des Optimierungsproblems(P≤=
)mit f ∈ C2(Rn,R), G ∈
C2(Rn,Rm), H ∈ C2(Rn,Rp) sowieM := {x ∈ Rn | G(x) ≤ 0, H(x) = 0}. Sind in x dieRegularitätsbedingung (LICQ) und im eindeutig bestimmten zugehörigen KKT-Punkt
(x, u, v) von(P≤=
)das hinreichende Optimalitätskriterium 2. Ordnung nach Satz 2.32
erfüllt, dann ist x für alle
r > r := max {‖u‖∞, ‖v‖∞}
sowohl eine strenge lokale Minimalstelle von f über M als auch eine strenge lokale Mini-
malstelle von S1r : Rn → R mit S1
r (x) := f(x) + r(‖ [G(x)]+ ‖1 + ‖H(x)‖1
).
Beispiel 4.21
Wir betrachten erneut das Optimierungsproblem aus Beispiel 4.15 (Problem Nr. 101)
mit (globaler) Lösung x = (1, 0)T , den eindeutig bestimmten zugehörigen Lagrange-
Multiplikatoren u = (0, 2, 0, 0)T und der l1-Straffunktion
S1(x, r) = −x21 + x
22 + r
([−x1]
+ + [x1 − 1]+ + [−x2 − 1]+ + [x2 − 1]+).
Offensichtlich besitzt für alle r > 0 wegen
limx1→∞
S1r (x1, 0) = lim
x1→∞(−x2
1 + r(x1 − 1))= −∞
die korrespondierende Funktion S1r keine globale Minimalstelle über Rn, und x ist nur
für r > 2 eine lokale Minimalstelle von S1r . �
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 1
−2.5
−2
−2
−1.5
−1.5
−1.5
−1
−1
−1
−1
−0.75
−0.75
−0.5
−0.5
−0.5
−0.5
−0.25
−0.25
−0.25
0
0
0
0
0.25
025
0.25
0.5
0.5
0.5
0.5
0.5
0.5
1
11
1
11
1.51.5
1.51.5
22
22
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 2
−1.75
−1.5
−1.5
−1.25
−1.25
−1
−1
−0.9
−0.9
−0.9
−0.75
−0.75
−0.5
−0.5
−0.5−0.5
−0.25
−0.25
−0.25
00
0
0
00
0.25
0.25
0.25
0.50.5
0.5
0.5
0.5
0.50.5
1
11
1
1
11
1
1.51.5
1.5
1.51.5
1.5
22
2
22
2
33
33
0 1 2−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
r = 3
−0.9
−0.9
−0.75
−0.75
−0.7
5
−0.75
−0.625
−0.625
−0.5−0.5
−0.5 −0.5
−0.25−0.25
−0.2
5
−0.25−0.25
00
0
0
0 0
0.25
0.25
0.250.25
0.50.5
0.5
0.5
0.5
0.5 0.5
111
1
11 1
1.5
1.51.5 1.5
1.5
1.51.5 1.5
2
22 2
2
22 2
33
33
Abb. 4.4 Höhenlinien der l1-Straffunktion mit Strafparameter r = 1, 2, 3 für Beispiel 4.21

4.2 Straffunktionen und Strafverfahren 317
Wir bemerken, dass für eine beliebige lq-Norm mit 1 ≤ q ≤ ∞ die Aussagen der Sätze
4.19 und 4.20 erhalten bleiben, wenn
r :=
∥∥∥∥∥(u
v
)∥∥∥∥∥q′
= max‖(u,v)‖q=1
∣∣uTu+ vTv∣∣ (induzierte Matrixnorm der Matrix (uT , vT ))
mit 1q+ 1q′= 1 für 1 < q, q′ < ∞ bzw. q′ = 1 für q = ∞ gesetzt wird. Weiterhin lassen
sich auf Grund der Normäquivalenz die Aussagen der Sätze 4.18, 4.19 und 4.20 sogar
auf beliebige Normen im Rm+p übertragen. Der nachfolgende Satz offenbart jedoch den
grundlegenden Nachteil von exakten Straffunktionen.
Satz 4.22
Es seien f ∈ C1(Rn,R), G ∈ C1(Rn,Rm) sowie H ∈ C1(Rn,Rp) und x eine lokale
Lösung des zugehörigen Optimierungsproblems(P≤=
)mit ∇f(x) �= 0. Dann gilt: Ist
S : Rn ×R+ → R mit S(x, r) := f(x) + rΨ(x) eine in x exakte Straffunktion, dann istder Strafterm Ψ in x nicht differenzierbar.
Beweis: Ist S : Rn×R+ → R mit S(x, r) := f(x)+rΨ(x) eine in x exakte Straffunktion,dann existiert per Definition ein r > 0, sodass x für alle r ≥ r eine lokale Minimalstelleder Funktion Sr : Rn → R mit Sr(x) := S(x, r) über Rn ist. Angenommen, der StraftermΨ : Rn → R+ sei differenzierbar in x (und damit auch die Straffunktion S), dann giltnach Satz 2.2
0 = ∇xS(x, r) = ∇f(x) + r1∇Ψ(x) = ∇f(x) + r2∇Ψ(x)
für alle r2 > r1 ≥ r, und es folgt sukzessive
0 = (r2 − r1)∇Ψ(x), 0 = ∇Ψ(x) sowie 0 = ∇f(x)
− im Widerspruch zur Voraussetzung ∇f(x) �= 0. �
Da wir uns in diesem Buch überwiegend auf Verfahren für glatte Optimierungsprobleme
beschränken, wollen wir an dieser Stelle nicht weiter auf Strafverfahren mit exakten
Straffunktionen eingehen. Wir werden jedoch im Abschnitt 4.5 im Rahmen unserer Aus-
führungen zu den SQP-Verfahren noch einmal auf die l1-Straffunktion zurückkommen
und wollen abschließend in Analogie zu den quadratischen Straffunktionen auch für
die exakten lq Straffunktionen den Zusammenhang mit der Sensitivitätsfunktion disku-
tieren. Wir betrachten auch hier wiederum ein Optimierungsproblem der Form(P≤
)mit zumindest stetigen Problemfunktionen f und G, zulässigem Bereich M �= ∅ sowieSensitivitätsfunktion λ. Für eine festgewählte lq-Norm und jedes r > 0 definieren wir
nun
ρ(r) := sup{ρ ∈ R
∣∣ ρ− r ‖b‖q ≤ λ(b)∀b ∈ Λ}

318 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
mit der Absicht, den Graphen der Sensitivitätsfunktion λ durch Funktionen der Form
κ : Rm → R mit κ(b) := ρ(r) − r‖b‖q
(also durch nach unten geöffnete Hyperkegel) zu „stützen“. Wiederum analog der vorher-
gehenden Schlussweisen folgt
ρ(r) = infx∈Rn
(f(x) + r‖ [G(x)]+ ‖
)= infx∈RnSqr (x)
mit Sqr : Rn → R und Sqr (x) := Sq(x, r) = f(x) + r
∥∥[G(x)]+∥∥q.
Vereinbaren wir nun
domΞ :=
{r > 0
∣∣∣∣ infx∈RnSqr (x) > −∞
}und
Ξ : domΞ→ R mit Ξ(r) := infx∈RnSqr (x) ,
so können wir durch
MAX {Ξ(r) | r ∈ domΞ}
ein weiteres „duales“ Problem zu (P ) formulieren, für welches
infx∈Mf(x) = λ(0) ≥ sup
r>0ρ(r) = sup
r>0infx∈RnSqr (x) = sup
r∈dom ΞΞ(r)
gilt. Offensichtlich ist auch die Funktion Ξ monoton wachsend. Im Gegensatz zur qua-
dratischen Straffunktion kann aber hier λ(0) = supr>0ρ(r) nach Satz 4.18 und Satz 4.19
bei konvexen Optimierungsproblemen bereits für endliches r erreicht werden, sofern der
Anstieg der Empfindlichkeitsfunktion λ in b = 0 längs aller Richtungen nach unten
beschränkt ist. Bei nichtkonvexen Problemen darf hierfür die Empfindlichkeitsfunktion
zusätzlich nicht stärker als linear fallen.
Beispiel 4.23
Wir betrachten erneut das primale Problem (P ) aus Beispiel 4.8 mit der globalen Lösung
x = (2, 0)T und λ(0) = 4. Für die Funktionen
κ : R → R mit κ(b) := ρ(r) − r|b|
gilt hier
ρ(r) =
{2r − r2
4 , falls 0 < r < 4
4 , falls 4 ≤ r.
�
Für tiefergehende Untersuchungen bzgl. Straffunktionen und Strafverfahren verweisen wir
auf Bertsekas (1982), Bertsekas (1999), Fiacco und McCormick (1968), Fletcher (1987),
Geiger und Kanzow (2002) sowie Großmann und Kleinmichel (1976).

4.3 Multiplikatorverfahren 319
−2 −1 0 1 2 3 4
−2
0
2
4
6
8
10
b
λκ, r = 10κ, r = 4κ, r = 2κ, r = 1λ(0)ρ(10)ρ(4)ρ(2)ρ(1)
Abb. 4.5 Sensitivitätsfunktion λ und stützende Funktionen κ für Beispiel 4.23
4.3 Multiplikatorverfahren
Die sogenannten Multiplikatorverfahren ähneln den im vorhergehenden Abschnitt be-
trachteten Strafverfahren. Sie sind jedoch bzgl. ihrer numerischen Eigenschaften vorteil-
hafter. Wir betrachten wiederum zunächst Problemstellungen der Form (P=) mit zwei-
mal stetig differenzierbaren Problemfunktionen f und H sowie zugehöriger Lagrange-
Funktion L : Rn ×Rp → R gemäß
L(x,v) := f(x) +H(x)Tv .
Für ein fest vorgegebenes r > 0 heißt die ebenfalls zweimal stetig differenzierbare Funk-
tion Lr : Rn ×Rp → R mit
Lr(x,v) := f(x) +H(x)Tv + r‖H(x)‖2
verallgemeinerte Lagrange-Funktion des Optimierungsproblems (P=). Offensichtlich
stimmt die verallgemeinerte Lagrange-Funktion mit der Lagrange-Funktion des Opti-
mierungsproblems
(P=)r MIN{Sr(x) := f(x) + r‖H(x)‖2
∣∣ H(x) = 0}
(4.7)
überein.
Ist nun (x, v) ∈ Rn ×Rp ein KKT-Punkt von (P=), dann gilt
∇xL(x, v) = ∇f(x) +∇H(x)v = 0 sowie ∇vL(x, v) = H(x) = 0 ,

320 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
und es folgt für die verallgemeinerte Lagrange-Funktion
∇xLr(x, v) = ∇f(x) +∇H(x)v + 2r∇H(x)H(x) = 0 .
Somit ist x gleichzeitig ein stationärer Punkt der Funktion
Lr,v : Rn → R mit Lr,v(x) := Lr(x, v) .
Ist in (x, v) für das Problem (P=) sogar das hinreichende Optimalitätskriterium 2. Ord-
nung nach Satz 2.32 erfüllt, d. h. gilt
dT∇2xL(x, v)d > 0
für alle d ∈ Rn \ {0} mit ∇H(x)Td = 0, so zeigt Satz 4.25, dass x nicht nur eine lokale
Lösung von (P=) ist, sondern für hinreichend große endliche Strafparameter r (analog
den exakten Straffunktionen) auch eine lokale Minimalstelle der Funktion Lr,v über Rn
ist. Zum Beweis dieser Aussage benötigen wir das folgende Lemma.
Lemma 4.24
Es seien P ∈ R(n,n) symmetrisch, Q ∈ R(n,n) positiv semi-definit und dTPd > 0 für alle
d ∈ Rn \ {0} mit Qd = 0. Dann existiert ein α > 0 mit P + αQ ∈ SPDn für alle α ≥ α.
Beweis: Angenommen, für jedes k ∈ N mit k ≥ 1 existiert ein dk ∈ Rn \ {0} mit
(dk)T (P + kQ)dk = (dk)TPdk + k(dk)TQdk ≤ 0
bzw.
(dk)TQdk ≤ −1k(dk)TPdk . (4.8)
O. B. d. A. gelte ‖dk‖ = 1 für alle k ≥ 1. Dann existiert eine konvergente Teilfolge
{dk(i)}i∈N von {dk}k∈N mit limi→∞dk(i) = d∗ �= 0. Mit (4.8) und aufgrund der positiven
Semidefinitheit der Matrix Q folgt
(d∗)TPd∗ ≤ 0 und (d∗)TQd∗ = 0 .
Weiterhin gilt jedoch auch
0 = (d∗)TQd∗ = (d∗)TQ12Q
12d∗ = ‖Q 1
2d∗‖2
und somit
Q12d∗ = 0 bzw. Qd∗ = 0
− im Widerspruch zur Voraussetzung, dass dTPd > 0 für alle d ∈ Rn \ {0} mit Qd = 0
gilt. �

4.3 Multiplikatorverfahren 321
Satz 4.25
Es seien f ∈ C2(Rn,R), H ∈ C2(Rn,Rp) und (x, v) ∈ Rn × Rp ein KKT-Punkt deszugehörigen Optimierungsproblems (P=). Ist in (x, v) das hinreichende Optimalitätskri-
terium 2. Ordnung nach Satz 2.32 erfüllt, so existiert ein r > 0, sodass x für alle r ≥ reine strikte lokale Minimalstelle der Funktion
Lr,v : Rn → R mit Lr,v(x) := f(x) +H(x)T v + r‖H(x)‖2
über Rn ist.
Beweis: Da (x, v) ∈ Rn×Rp ein KKT-Punkt von (P=) ist, gilt (wie bereits ausgeführt)
∇Lr,v(x) = ∇f(x) +∇H(x)v + 2r∇H(x)H(x) = 0 .
Wegen H(x) = 0 folgt weiterhin
∇2Lr,v(x) = ∇2xL(x, v) + 2r∇H(x)∇H(x)T .
Da in (x, v) das hinreichende Optimalitätskriterium 2. Ordnung nach Satz 2.32 erfüllt
ist, gilt
0 < dT∇2xL(x, v)d
für alle d ∈ Rn \{0} mit ∇H(x)Td = 0 bzw. ∇H(x)∇H(x)Td = 0. Mit P := ∇2xL(x, v)
und Q := ∇H(x)∇H(x)T existiert nach Lemma 4.24 ein r > 0 mit ∇2Lr,v(x) ∈ SPDn
für alle r ≥ r. Die Aussage des Satzes folgt nun unmittelbar mit Satz 2.5. �
Im Allgemeinen ist natürlich weder r > 0 noch der Lagrange-Multiplikator v be-
kannt. Aus diesem Grund muss bei der Implementierung von Multiplikatorverfahren
der optimale Lagrange-Multiplikator geeignet approximiert werden. Sind rk der aktuelle
Strafparameter, vk eine aktuelle Näherung von v und xk+1 ein stationärer Punkt von
Lrk,vk : Rn → R mit Lrk ,vk(x) := f(x) +H(x)Tvk + rk‖H(x)‖2 ,
dann gilt
∇Lrk,vk(xk+1) = ∇f(xk+1) +∇H(xk+1)
(vk + 2rkH(x
k+1))= 0 .
Da andererseits für einen KKT-Punkt (x, v) des Optimierungsproblems (P=)
∇xL(x, v) = ∇f(x) +∇H(x)v = 0
gilt, erscheint es naheliegend als neue Näherung für v
vk+1 := vk + 2rkH(xk+1)
zu wählen.

322 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
In Analogie zur Straffunktion wird durch den Term rk‖H(x)‖2 in Lrk,vk die Verletzung
der Nebenbedingung H(x) = 0 mit dem Ziel „bestraft“, dass sich die Iterierten dem
zulässigen Bereich nähern. Erfolgt in einer Iteration diese Annäherung an den zulässigen
Bereich (beispielsweise bzgl. der l∞-Norm) nicht hinreichend gut, so bietet es sich (in
Analogie zu den Strafverfahren) an, auch den Strafparameter rk+1 im Vergleich zu rk zu
erhöhen. Die bisherigen Betrachtungen motivieren den folgenden Prinzipalgorithmus für
Multiplikatorverfahren bei Problemstellungen der Form (P=).
Algorithmus 22 (Prinzipalgorithmus Multiplikatorverfahren (P=))S0 Wähle x0 ∈ Rn, v0 ∈ Rp, r0 > 0 sowie β ∈ (0, 1), und setze k := 0.
S1 Ist (xk,vk) ein KKT-Punkt von (P=), dann STOPP.
S2 Bestimme xk+1 ∈ arg minx∈RnLrk,vk (x) .
S3 Setze vk+1 := vk + 2rkH(xk+1).
S4 Gilt ‖H(xk+1)‖∞ ≥ β‖H(xk)‖∞, dann wähle rk+1 > rk.
S5 Gilt ‖H(xk+1)‖∞ < β‖H(xk)‖∞, dann setze rk+1 := rk.
S6 Setze k := k + 1, und gehe zu S1.
Offensichtlich besitzen die Probleme (P=) und (P=)r für alle r > 0 die gleichen lokalen
Lösungen. Ist (x, v) ∈ Rn×Rp ein KKT-Punkt von (P=), so ist unter den Voraussetzun-
gen von Satz 4.25 für alle r ≥ r die Hesse-Matrix ∇2Lr,v(x) in einer hinreichend kleinen
Umgebung von x positiv definit. Basierend auf dieser Beobachtung lassen sich mit Hilfe
des Satzes über implizite Funktionen die folgenden Differenzierbarkeitseigenschaften der
zugehörigen Familie von dualen Zielfunktionen beweisen.
Satz 4.26 (Bertsekas (1982))
Es seien f ∈ C2(Rn,R), H ∈ C2(Rn,Rm) und (x, v) ein KKT-Punkt von (P=), in dem
das hinreichende Optimalitätskriterium 2. Ordnung nach Satz 2.32 erfüllt ist. Weiterhin
seien ∇h1(x), · · · ,∇hp(x) linear unabhängig und r hinreichend groß. Dann existieren
ε(r) > 0 und δ(r) > 0, sodass für alle v ∈ Uδ(r)(v) eine lokale Lösung x(v) des Problems
MIN{Lr,v(x) | x ∈ Uε(r)(x)}
existiert und die (lokal definierte) duale Zielfunktion
qr(v) := infx∈Uε(r)(x)
Lr,v(x)
die folgenden Eigenschaften besitzt:

4.3 Multiplikatorverfahren 323
(a) qr ∈ C2(Uδ(r)(v),R),
(b) ∇qr(v) = H(x(v)),
(c) ∇2qr(v) = −∇xH(x(v))T [∇2xLr,v(x(v))]
−1∇xH(x(v)) und
(d) qr(v) = supv∈Uδ(r)(v)
q(v) = infx∈Uε(r)(x)
{Sr(x) | H(x) = 0}.
Wir bemerken, dass S3 im Algorithmus 22 mit Satz 4.26 (b) somit als ein Gradienten-
schritt zur Maximierung der (lokal konkaven) dualen Zielfunktion mit der (Konstant-)
Schrittweite 2r interpretiert werden kann. Der soeben formulierte Satz 4.26 bildet die
wesentliche Grundlage für tiefergehende Untersuchungen bzgl. der Multiplikatorverfah-
ren.
Wir wollen nun unsere bisherigen Überlegungen bzgl. der Multiplikatorverfahren auf
Optimierungsprobleme der Form(P≤
)mit zweimal stetig differenzierbaren Problem-
funktionen f und G übertragen. Für einen Vektor a ∈ Rm sei der Vektor [a]2 ∈ Rm
komponentenweise definiert durch
[a]2i := a2i mit i ∈ {1, · · · ,m} .
Durch die Einführung von zusätzlichen Variablen si ∈ R mit i ∈ {1, · · · ,m} lassen sichdie Ungleichungsnebenbedingungen gi(x) ≤ bi äquivalent als Gleichungsnebenbedingun-gen gi(x) + s2i = bi formulieren. Mit s := (s1, · · · , sm)T ist somit das Problem
(P≤
)äquivalent zu
MIN{f(x)| G(x) + [s]2 = 0} . (4.9)
Für ein fest vorgegebenes r > 0 lautet somit die verallgemeinerte Lagrange-Funktion
Lr : Rn ×Rm ×Rm → R von (4.9)
Lr(x,u, s) := f(x) + (G(x) + [s]2)Tu+ r‖G(x) + [s]2 ‖2 .
Die Minimierung der Funktion Lr bzgl. s liefert (siehe Aufgabe 4.9)
Lr(x,u) := mins∈Rm
Lr(x,u, s) = f(x) +m∑i=1
(ui(gi(x) + z
∗i ) + r (gi(x) + z
∗i )
2)
mit z∗i :=[−(ui2r + gi(x)
)]+. Für ein i ∈ {1, · · · ,m} gilt nun
ui(gi(x) + z∗i ) + r (gi(x) + z∗i )
2 =
{− 1
4ru2i , falls −
(ui2r + gi(x)
)≥ 0
uigi(x) + rg2i (x) , falls −(ui2r + gi(x)
)< 0
= 14r
(([ui + 2rgi(x)]+
)2 − u2i
),

324 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
und es folgt
Lr(x,u) = f(x) +1
4r
m∑i=1
(([ui + 2rgi(x)]+
)2 − u2i
).
Die so definierte und i. Allg. nur einmal stetig differenzierbare Funktion Lr : Rn×Rm →R heißt verallgemeinerte Lagrange-Funktion des Optimierungsproblems
(P≤
).
Definieren wir Lr,u : Rn → R mit Lr,u(x) := Lr(x, u) für festes u ∈ Rm, so können wirunter Beachtung von
∇Lr,u(x) = ∇f(x) +m∑i=1
[ui + 2rgi(x)]+∇gi(x) = ∇f(x) +∇G(x)[u+ 2rG(x)]+
den Prinzipalgorithmus 22 unmittelbar auf Problemstellungen der Form(P≤
)übertra-
gen.
Algorithmus 23 (Prinzipalgorithmus Multiplikatorverfahren(P≤
))
S0 Wähle x0 ∈ Rn, u0 ∈ Rm, r0 > 0 sowie β ∈ (0, 1), und setze k := 0.
S1 Ist (xk,uk) ein KKT-Punkt von(P≤
), dann STOPP.
S2 Bestimme xk+1 ∈ arg minx∈RnLrk,uk (x) .
S3 Setze uk+1 := [uk + 2rG(x)]+.
S4 Gilt ‖[G(xk+1)]+‖∞ ≥ β‖[G(xk)]+‖∞, dann wähle rk+1 > rk.
S5 Gilt ‖[G(xk+1)]+‖∞ < β‖[G(xk)]+‖∞, dann setze rk+1 := rk.
S6 Setze k := k + 1, und gehe zu S1.
Beispiel 4.27
Um die Arbeisweise einer Implementierung des Algorithmus 23 mit numerisch sinnvollen
Abbruchtoleranzen in S1 und S2 zu verdeutlichen, betrachten wir das Optimierungspro-
blem (Problem Nr. 109)
MIN
{f(x) =
10
3x1x2 +
1
6x1
∣∣∣∣ x21 +
5
2x2
2 ≤19
16, −x1 + x2 ≤
3
5
}mit globaler Lösung x =
(34 ,−
12
)Tund lokaler Lösung x ≈ (−0.325, 0.275)T. Im Schritt
S0 wählen wir x0 := (−0.8,−0.8)T , u0 := (0, 0)T , β = 0.25 und r0 := 5. Weiter-
hin verwenden wir zur Minimierung in S2 ein BFGS-Verfahren (innere Iterationen). In
der Abb. 4.6 sind oben links bzw. rechts die Höhenlinien der Zielfunktion f bzw. die
Höhenlinien der Funktion Lr0,u0 dargestellt. In der ersten äußeren Iteration liefert das
BFGS-Verfahren (bei voreingestellter grober Abbruchbedingung) den Punkt x1 als Nä-
herung für die lokale Minimalstelle von Lr0,u0 , und es ergeben sich u1 ≈ (0, 1.63)T sowie

4.3 Multiplikatorverfahren 325
r1 = r0 = 5. Die Höhenlinien der Funktion Lr1,u1 sind unten links dargestellt. Im zweiten
äußeren Iterationsschritt macht das BFGS-Verfahren zu Beginn der inneren Iteration in
S2 einen großen Schritt, umgeht dadurch die lokale Minimalstelle x ≈ (−0.319, 0.269)T
der Funktion Lr1,u1 in der Nähe von x, endet in unmittelbarer Nähe der gesuchten
Lösung x im Punkt x2 und liefert u2 = (1, 0)T . Da in dieser äußeren Iteration die Ver-
letzung der Restriktionen gemäß S4 nicht genug verringert wurde, wird darüberhinaus
r2 := 10r1 = 50 gesetzt. Unten rechts findet der Leser die entsprechende Abbildung für
die dritte äußere Iteration im vergrößerten Maßstab, wobei x3 der Lösung x im Rah-
men der Zeichengenauigkeit entspricht. Bei kleinen Änderungen des Startpunktes (z. B.
x0 = (−1,−1)T , r0 = 5) oder von r0 (z. B. x0 = (−0.8,−0.8)T , r0 = 6) konvergiert das
Verfahren gegen die lokale Lösung x. �
-1 -0.5 0 0.5 1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
x1
x2
Lr( x , u ) = f(x), r u = 0, = [0,0]
-3
-3
-2
-2
-2
-1
-1
-1
-1
-0.5
-0.5
-0.5
-0.5
-0.2
5
-0.25
-0.2
5
-0.250
0 0
0
000.25
0.25
0.250.25
0.50.5
0.50.5
11
11
22
22
2.001
2.001
2.001
2.001
-1 -0.5 0 0.5 1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
x2
Lr( x , u ), r u = 5, = [0,0]
-1
-1
-0.5-0
.5 -0.5
-0.5
-0.25-0
.25
-0.25
-0.25
-0.2
500
00
0 0
00
0.25
0.25
0.25
0.25
0.25 0.25
0.5
0.5
0.5
0.5
0.5
0.5 0.5
1
11
1
1
1
1
1
2
2 2
2
2
22
2
4
4 4
4
4
44
4
4.774.77
4.77
4.77 4.77
4.774.77
4.77
4.77 4.77
x1
x1
x0
-1 -0.5 0 0.5 1
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
x1
x2
Lr( x , u ), r u = 5, = [0,1.63]
-1
-1
-1
-0.5
-0.5
-0.25-0.25
-0.25
-0.250
0
0
0
0 0
0.25
0.250.25
0.25
0.5
0.5
0.5
0.5
0.5
1
11
1
1
11
2
2 2
2
2
22
2
4
4 4
4
4
44
x1
x2
BFGS durchtunnelt lokales Minimum0.7 0.72 0.74 0.76 0.78 0.8
-0.55
-0.54
-0.53
-0.52
-0.51
-0.5
-0.49
-0.48
-0.47
-0.46
-0.45
x1
x2
Lr( x , u ), r u = 50, = [1,0]
-1.12
-1.12
-1.1
2
-1.12
-1.12
-1.1
-1.1
-1.1
-1.1
-1.1
-1.1
-1.1
-1.1
-1.07
-1.07
-1.07
-1.07
-1.07
-1.07
-1.03
-1.03
-1.03
-1.03
-1.03
-1
-1
-1
-1
-1
-1
-0.9
-0.9
-0.9
-0.8
-0.8
-0.7
-0.7
-0.6
-0.6
-0.5-0.4
-0.3
-1.114
-1.114
-1.114
-1.114
-1.114-1.114
-1.114
-1.114
-1.114
-1.114
x3
x2
Abb. 4.6 Höhenlinien von f und Lrk,uk mit k = 0, 1, 2 für Beispiel 4.27

326 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Grundlegende Konvergenzbetrachtungen für Multiplikatorverfahren sind in Bertsekas
(1982) aufgeführt. Wir geben hier stellvertretend einen Konvergenzsatz für glatte konvexe
Probleme an, der auch als starker Dualitätssatz gedeutet werden kann. Dazu formulieren
wir zunächst ein modifiziertes Multiplikatorverfahren mit konstantem Strafparameter r.
Algorithmus 24 (Modifiziertes Multiplikatorverfahren für(P≤
))
S0 Wähle x0 ∈ Rn, u0 ∈ Rm sowie r > 0, und setze k := 0.
S1 Ist (xk,uk) ein KKT-Punkt von(P≤
), dann STOPP.
S2 Bestimme xk+1 ∈ arg minx∈RnLr,uk (x) .
S3 Setze uk+1 := [uk + 2rG(x)]+.
S4 Setze k := k + 1, und gehe zu S1.
Für dieses Verfahren gilt der folgende Konvergenzsatz:
Satz 4.28 (Großmann und Terno (1997))
Es seien f ∈ C1(Rn,R) sowie G ∈ C1(Rn,Rm) konvex über Rn und (x, u) ein Sattel-punkt der zugehörigen Lagrange-Funktion L. Dann ist (x, u) für beliebiges r > 0 auch
ein Sattelpunkt der verallgemeinerten Lagrange-Funktion Lr. Weiterhin ist jeder Häu-
fungspunkt der durch den Algorithmus 24 erzeugten Folge{xk
}k∈N eine Lösung des
zugehörigen Ausgangsproblems(P≤
).
Für nichtkonvexe Probleme benötigt man für einen Konvergenzbeweis des Algorithmus
24 weit schärfere zusätzliche Voraussetzungen, wie z. B. die strikte Komplementarität im
Lösungspunkt und die Erfüllung der linearen Unabhängigkeitsbedingung für die aktiven
Restriktionen. Diese beiden Bedingungen garantieren dann die zweifache stetige Diffe-
renzierbarkeit von Lr nach x, und ein Satz analog zu Satz 4.26 kann formuliert werden.
Im Gegensatz zur Anwendung auf konvexe Problemstellungen sind die Multiplikator-
verfahren trotz vorhandener Konvergenzbeweise bei nichtkonvexen Problemen weniger
erfolgreich (siehe Spellucci (1993)).
In Analogie zu den beiden vorhergehenden Abschnitten wollen wir auch für Multiplikator-
verfahren einen zweiten Zugang über die Sensitivitätsfunktion diskutieren. Wir betrach-
ten wiederum ein Optimierungsproblem der Form(P≤
)mit zweimal stetig differenzier-
baren Problemfunktionen f und G, zulässigem BereichM �= ∅ sowie Sensitivitätsfunktionλ. Für festes u ∈ Rm und festes r > 0 definieren wir zunächst
ρ(u, r) := sup{ρ ∈ R
∣∣∣ ρ− uT b− r ‖b‖2 ≤ λ(b) ∀ b ∈ Λ}

4.3 Multiplikatorverfahren 327
mit der Absicht, den Graphen der Sensitivitätsfunktion λ (falls möglich) nun durch qua-
dratische Funktionen
π : Rm → R mit π(b) := ρ(u, r) − uTb− r ‖b‖2
zu „stützen“. Analog der Schlussweisen in den beiden vorhergehenden Abschnitten und
den entsprechenden Ausführungen in diesem Abschnitt folgt
ρ(u, r) = infx∈Rn
(f(x) + inf
b∈Λ
{uTb+ r‖b‖2 | G(x) ≤ b
})= inf
x∈Rn
(f(x) + inf
s∈Rm
(uT
(G(x) + [s]2
)+ r‖G(x) + [s]2 ‖2
))= inf
x∈Rn
(f(x) + 1
4r
m∑i=1
([ui + 2rgi(x)]
2+ − u2
i
))= inf
x∈RnLr(x,u) .
Vereinbaren wir nun für r > 0
domΩr :=
{u ∈ Rm
∣∣∣∣ infx∈RnLr(x,u) > −∞
}und
Ωr : domΩr → R mit Ωr(u) := infx∈RnLr(x,u) ,
so können wir durch
MAX {Ωr(u) | u ∈ domΩr }
eine von r > 0 abhängige Familie von „dualen“ Problemen formulieren, für welche unter
zusätzlichen Voraussetzungen (beispielsweise Konvexität der Problemstellung mit erfüll-
ter Regularitätsbedingung) sogar für hinreichend große r
minx∈Mf(x) = λ(0) = ρ := max
u∈dom ΩrΩr(u)
gilt.
Beispiel 4.29
Wir betrachten nochmals das primale Problem (P ) aus Beispiel 4.8 mit der globalen
Lösung x = (2, 0)T , zugehörigem Lagrange-Multiplikator u = 4 und λ(0) = 4. Für die
mit u korrespondierenden quadratischen Funktionen
π : R → R mit π(b) := ρ(4, r)− 4b− rb2 ,
gilt offensichtlich ρ(4, r) = λ(0) = 4 für alle r ≥ 0. Es existieren also Parabeln, die den
Graphen von λ im Punkt 0 stützen, und der zugehörige Strafparameter r ist endlich (vgl.
Abb. 4.3). �

328 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
−2 0 2 4
−2
0
2
4
6
8
10
b
λπ, r = 10π, r = 4π, r = 2π, r = 1π, r=0λ(0)
Abb. 4.7 Sensitivitätsfunktion λ und stützende quadratische Funktion π für Beispiel 4.29
Bezüglich weiterer Ausführungen zu Multiplikatorverfahren verweisen wir auf Bertsekas
(1982), Bertsekas (1999), Fletcher (1987), Großmann und Kaplan (1979), Großmann und
Terno (1997) sowie Spellucci (1993).
4.4 Verfahren für quadratischeOptimierungsprobleme
In diesem Abschnitt wollen wir uns mit quadratischen Optimierungsproblemen beschäf-
tigen − der wohl einfachsten Klasse von nichtlinearen Optimierungsproblemen. Unter ei-
nem quadratischen Optimierungsproblem versteht man Problemstellungen mit einer qua-
dratischen Zielfunktion und (affin-)linearen Nebenbedingungen, also Problemstellungen
der Form
(QP≤=
)MIN
{f(x) = 1
2xTQx+ bTx+ c
∣∣∣∣∣ aTi x ≤ βi, i ∈ {1, · · · ,m}aTi x = βi, i ∈ {m+ 1, · · · ,m+ p}
},
(QP≤
)MIN
{f(x) = 1
2xTQx+ bTx+ c
∣∣ aTi x ≤ βi, i ∈ {1, · · · ,m} }bzw.
(QP=) MIN{f(x) = 1
2xTQx+ bTx+ c
∣∣ aTi x = βi, i ∈ {1, · · · , p} }mit symmetrischer Matrix Q ∈ R(n,n), b ∈ Rn, c ∈ R, ai ∈ Rn und βi ∈ R.

4.4 Verfahren für quadratische Optimierungsprobleme 329
Lemma 4.30
Es seien ai ∈ Rn und βi ∈ R für alle i ∈ {1, · · · ,m+ p}, sowie
M :=
{x ∈ Rn
∣∣∣∣∣ aTi x ≤ βi, i ∈ {1, · · · ,m}aTi x = βi, i ∈ {m+ 1, · · · ,m+ p}
},
dann ist für alle x ∈M die Regularitätsbedingung (CQ) erfüllt.
Beweis: Es seien x ∈M , I(x) ={i∣∣ aTi x = βi, i ∈ {1, 2, · · · ,m}} und somit
K(x) =
{y ∈ Rn
∣∣∣∣∣ aTi y ≤ 0, i ∈ I(x)aTi y = 0, i ∈ {m+ 1, · · · ,m+ p}
}.
Mit Lemma 2.15 genügt es zu zeigen, dass K(x) ⊂ T (M,x) gilt. Es seien dafür d ∈ K(x),d �= 0 und {xk}k∈N mit xk := x+ 1
kd. Für die so definierte Folge gilt
limk→∞xk = x und lim
k→∞xk − x‖xk − x‖ =
d
‖d‖ .
Weiterhin gilt für alle k und i ∈ I(x) bzw. i ∈ {m+ 1, · · · ,m+ p}
aTi xk ≤ βi bzw. aTi xk = βi
sowie für alle hinreichend großen k und i ∈ {1, 2, · · · ,m} \ I(x)
aTi xk = aTi x+
1
kaTi d < βi +
1
kaTi d ≤ βi .
Somit ist xk ∈M für alle hinreichend großen k und damit offensichtlich d ∈ T (M,x). �
Mit Satz 2.22 und Lemma 4.30 folgt unmittelbar:
Satz 4.31
Ist x eine lokale Lösung des Optimierungsproblems(QP≤=
), dann existieren Multiplika-
toren u ∈ Rm und v ∈ Rp, sodass (x, u, v) ein KKT-Punkt von(QP≤=
)ist.
Wir betrachten nun zunächst quadratische Optimierungsprobleme der Form (QP=) und
vereinbaren
A :=
⎛⎜⎜⎝aT1...
aTp
⎞⎟⎟⎠ ∈ R(p,n) und β :=
⎛⎜⎜⎝β1
...
βp
⎞⎟⎟⎠ ∈ Rp .

330 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Nach Satz 4.31 existieren zu jeder lokalen Lösung x von (QP=) Lagrange-Multiplikatoren
v ∈ Rp derart, dass (x, v) die zugehörigen KKT-Bedingungen(Q AT
A 0
)(x
v
)=
(−bβ
)(4.10)
erfüllt. Die Bestimmung eines KKT-Punktes für Problemstellungen der Form (QP=)
reduziert sich somit auf das Lösen eines linearen Gleichungssystems.
Satz 4.32
Für ein Optimierungsproblem der Form (QP=) sei dTQd > 0 für alle d ∈ Rn \ {0} mit
Ad = 0. Dann gilt:
(a) Ist (x, v) ∈ Rn × Rp ein KKT-Punkt des Optimierungsproblems (QP=), dann ist
x die eindeutig bestimmte globale Lösung von (QP=).
(b) Sind die Vektoren a1, · · · ,ap linear unabhängig, dann besitzt das Gleichungssystem(4.10) eine eindeutige Lösung (x, v)T und das Optimierungsproblem (QP=) somit
den eindeutig bestimmten KKT-Punkt (x, v) ∈ Rn ×Rp.
Beweis:
Zu (a): Für einen beliebigen zulässigen Punkt x von (QP=) mit x �= x gilt A(x− x) = 0
und somit wegen (4.10)
f(x) = f(x) + 12xTQx+ bTx− 1
2 xTQx− bT x
= f(x) + 12 (x− x)
TQ (x− x) + (Qx+ b)T (x− x)
> f(x) + (Qx+ b)T (x− x)= f(x)− vTA (x− x)= f(x) .
Zu (b): Offensichtlich genügt es wegen (a) zu zeigen, dass das zu (4.10) korrespondierende
homogene lineare Gleichungssystem(Q AT
A 0
)(x
v
)=
(0
0
)
nur die triviale Lösung x = 0 und v = 0 besitzt. Angenommen es gilt dTQd > 0 für alle
d ∈ Rn \ {0} mit Ad = 0, Qx+ATv = 0 und Ax = 0, dann folgt
xTQx+ xTATv = xTQx+ vTAx = xTQx = 0

4.4 Verfahren für quadratische Optimierungsprobleme 331
und somit sowohl x = 0 als auch ATv = 0. Da nach Voraussetzung die Vektoren
a1, · · · ,ap linear unabhängig sind, folgt weiterhin rangA = rangAT = p und somit
ebenfalls v = 0. �
Setzen wir x = xk + d mit Axk = β, so erhalten wir als äquivalente Formulierung
zu (4.10) (Q AT
A 0
)(d
v
)=
(−b−Qxk
β −Axk
)bzw. (
Q AT
A 0
)(d
v
)=
(−∇f(xk)
0
). (4.11)
Diese Darstellung wird sich für unser weiteres Vorgehen, speziell bei der Herleitung und
Formulierung eines iterativen Verfahrens zur Lösung von quadratischen Problemstellun-
gen der allgemeinen Form(QP≤=
), als nützlich erweisen.
Wir betrachten nun Problemstellungen der Form(QP≤=
)und vereinbaren
A(1) :=
⎛⎜⎜⎝aT1...
aTm
⎞⎟⎟⎠ ∈ R(m,n) und β(1) :=
⎛⎜⎜⎝β1
...
βm
⎞⎟⎟⎠ ∈ Rm
bzw.
A(2) :=
⎛⎜⎜⎝aTm+1
...
aTm+p
⎞⎟⎟⎠ ∈ R(p,n) und β(2) :=
⎛⎜⎜⎝βm+1
...
βm+p
⎞⎟⎟⎠ ∈ Rp.
Wiederum nach Satz 4.31 existieren nun zu jeder lokalen Lösung x von(QP≤=
)Lagrange-
Multiplikatoren u ∈ Rmund v ∈ Rp derart, dass der Vektor (x, u, v) die zugehörigenKKT-Bedingungen
(Q (A(1))T (A(2))T
A(2) 0 0
)⎛⎜⎜⎝x
u
v
⎞⎟⎟⎠ =
(−bβ(2)
), A(1)x ≤ β(1), u ≥ 0 und uTA(1)x = 0
erfüllt. Die Lösung dieses Systems von linearen Gleichungen und linearen Ungleichungen
zur Bestimmung eines KKT-Punktes (x, u, v) ist im Vergleich zur Lösung des linearen
Gleichungssystems (4.10) erheblich schwieriger. Dies liegt darin begründet, dass für eine
unbekannte Lösung x natürlich auch die Indexmenge der aktiven Ungleichungsneben-
bedingungen unbekannt ist. Die wesentliche Idee zur Bestimmung eines KKT-Punktes
(x, u, v) eines Optimierungsproblems der Form(QP≤=
)mittels der sogenannten Strate-
gie der aktiven Indizes besteht nun darin, iterativ gleichungsrestringierte quadratische

332 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Hilfsprobleme zu lösen, die sich dadurch ergeben, dass in einem aktuellen und zulässigen
Iterationspunkt xk von den m Ungleichungsnebenbedingungen lediglich eine Teilmenge
der in xk aktiven Ungleichungsnebenbedingungen berücksichtigt werden. Mit
I(xk) ⊂ I(xk) :={i∣∣ aTi xk = βi, i ∈ {1, 2, · · · ,m}}
lautet also das im Iterationspunkt xk betrachtete Hilfsproblem
(QP=)k MIN
{f(x) =
1
2xTQx+ bTx+ c
∣∣∣∣ A(1)k x = β
(1)k , A
(2)x = β(2)
},
wobei die Matrix A(1)k aus A(1) bzw. der Vektor β(1)
k aus β(1) durch Streichen aller Zeilen
aTi bzw. aller Komponenten βi mit i ∈ {1, · · · ,m}\ I(xk) unter Beibehaltung der Zeilen-bzw. Koordinatenindizes i ∈ I(xk) entstehen. Analog der vorhergehenden Ausführungenerfüllt jeder KKT-Punkt (xk+1, uk+1,vk+1) ∈ Rn × R|I(x
k)| × Rp dieses Hilfsproblemsdas Gleichungssystem⎛⎜⎜⎝
Q (A(1)k )T (A(2))T
A(1)k 0 0
A(2) 0 0
⎞⎟⎟⎠⎛⎜⎜⎝x
u
v
⎞⎟⎟⎠ =
⎛⎜⎜⎝−bβ
(1)k
β(2)
⎞⎟⎟⎠ ,welches mit x = xk + d analog (4.11) äquivalent zu⎛⎜⎜⎝
Q (A(1)k )T (A(2))T
A(1)k 0 0
A(2) 0 0
⎞⎟⎟⎠⎛⎜⎜⎝d
u
v
⎞⎟⎟⎠ =
⎛⎜⎜⎝−∇f(xk)
0
0
⎞⎟⎟⎠ (4.12)
ist. Es seien nun (dk, uk+1,vk+1) ∈ Rn × R|I(xk)| × Rp eine Lösung von (4.12) (wobei
die Koordinatenindizes von uk+1 entsprechend den Zeilen- bzw. Koordinatenindizes von
A(1)k bzw. β(1)
k gewählt werden) sowie (dk,uk+1,vk+1) ∈ Rn×Rm×Rp mit uk+1i := uk+1
i
für alle i ∈ I(xk) und uk+1i := 0 für alle i ∈ {1, · · · ,m} \ I(xk). Weiterhin setzen wir im
Folgenden dTQd > 0 für alle d ∈ Rn \ {0} mit A(2)d = 0 voraus, womit xk + dk nach
Satz 4.32 (a) die eindeutig bestimmte globale Lösung von (QP=)k ist.
Zur Herleitung eines iterativen Verfahrens (siehe auch Fletcher (1971)) zur Bestimmung
eines KKT-Punktes des ursprünglichen Problems(QP≤=
)mittels der Strategie der akti-
ven Indizes analysieren wir die hierbei auftretenden Fälle:
Gilt dk = 0 und uk+1 ≥ 0, so ist (xk,uk+1, vk+1) auch ein KKT Punkt von(QP≤=
).
Ist dk = 0 und uk+1i < 0 für mindestens einen Index i ∈ I(xk), so erfüllt (xk,uk+1,vk+1)
nicht die KKT-Bedingungen von(QP≤=
). Da jedoch in diesem Fall xk die eindeutig be-
stimmte globale Lösung von (QP=)k ist, bietet es sich an, für das im nächsten Iterations-
schritt zu betrachtende Hilfsproblem den zulässigen Bereich zu vergrößern, d. h. einen
Index aus der Menge I(xk) zu entfernen. Als Wahl für diesen zu entfernenden Index

4.4 Verfahren für quadratische Optimierungsprobleme 333
bietet sich ein Index j ∈ I(xk) mit minimalen Lagrange-Multiplikator uk+1j an.
Gilt dk �= 0 und ist xk +dk zulässig für das ursprüngliche Problem(QP≤=
), so erscheint
es wegen
f(xk + dk) = f(xk) +∇f(xk)Tdk + 12
(dk
)T ∇2f(xk)dk
= f(xk)−(uk+1
)TA
(1)k d
k −(vk+1
)TA(2)dk − 1
2
(dk
)TQdk
= f(xk)− 12
(dk
)TQdk
< f(xk)
naheliegend, (xk+1,uk+1, vk+1) mit xk+1 := xk + dk zu setzen und für das (evtl.) im
nächsten Iterationsschritt zu betrachtende Hilfsproblem die Indexmenge I(xk) nicht zu
verändern.
Ist schließlich dk �= 0 und xk + dk nicht zulässig für das ursprüngliche Problem(QP≤=
),
dann existiert wegen der Zulässigkeit von xk, der Wahl von I(xk) und (4.12) mindestens
ein Index i ∈ {1, · · · ,m} \ I(xk) mit aTi dk > 0. Setzen wir nun (xk+1,uk+1, vk+1) mit
xk+1 := xk + tkdk und
tk = min
{βi − aTi xk
aTi dk
∣∣∣∣ i ∈ {1, · · · ,m} \ I(xk), aTi dk > 0} ∈ [0, 1) ,so gilt f(xk+1) = f(xk) +
(12t2k − tk
) (dk
)TQdk < f(xk) falls tk ∈ (0, 1), aTi xk+1 ≤ βi
für alle i ∈ {1, · · · ,m} \ I(xk), aTi xk+1 = βi für alle i ∈ I(xk), aTi xk+1 = βi für alle
i ∈ {m+1, · · · ,m+p} und somit die Zulässigkeit von xk+1 für das ursprüngliche Problem(QP≤=
). Ferner gilt aTj x
k+1 = βj für jedes j ∈ {1, · · · ,m} \ I(xk) mit aTj dk > 0 und
tk =βj − aTj xk
aTj dk.
In diesem Fall erscheint es nun naheliegend für das (evtl.) im nächsten Iterationsschritt
zu betrachtende Hilfsproblem, die Indexmenge I(xk) um einen solchen Index j zu er-
weitern. Diese vollständige Fallunterscheidung motiviert den folgenden Algorithmus für
quadratische Problemstellungen der Form(QP≤=
)mit nichtleerem zulässigen Bereich:
Algorithmus 25 (Strategie der aktiven Indizes für(QP≤=
))
S0 Bestimme ein für(QP≤=
)zulässiges x0 ∈ Rn und zugehörige Lagrange-Multiplika-
toren u0 ∈ Rm und v0 ∈ Rp, setze
k := 0 sowie I(x0) :={i∣∣ aTi x0 = βi, i ∈ {1, 2, · · · ,m}
}.
S1 Ist (xk,uk, vk) ein KKT-Punkt von(QP≤=
), dann STOPP.
S2 Bestimme eine Lösung (dk, uk+1,vk+1) von (4.12), und setze
uk+1i := uk+1
i für alle i ∈ I(xk) sowie uk+1i := 0 für alle i ∈ {1, · · · ,m} \ I(xk) .

334 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
S3 Ist dk = 0 und uk+1 ≥ 0, dann setze
xk+1 := xk, I(xk+1) := I(xk) ,
und gehe zu S7.
S4 Ist dk = 0 und uk+1i < 0 für mindestens ein i ∈ I(xk), dann bestimme einen Index
j ∈ I(xk) mituk+1j = min
{uk+1i
∣∣ i ∈ I(xk)} ,setze
xk+1 := xk, I(xk+1) := I(xk) \ {j} ,
und gehe zu S7.
S5 Ist dk �= 0 und xk + dk zulässig für(QP≤=
), dann setze
xk+1 := xk + dk, I(xk+1) := I(xk) ,
und gehe zu S7.
S6 Ist dk �= 0 und xk + dk nicht zulässig für(QP≤=
), dann bestimme einen Index
j ∈ {1, · · · ,m} \ I(xk) mit
βj − aTj xk
aTj dk
= min
{βi − aTi xk
aTi dk
∣∣∣∣ i ∈ {1, · · · ,m} \ I(xk), aTi dk > 0} ,setze
tk :=βj − aTj xk
aTj dk, xk+1 := xk + tkd
k, I(xk+1) := I(xk) ∪ {j} ,
und gehe zu S7.
S7 Setze k := k + 1, und gehe zu S1.
Beispiel 4.33
Wir betrachten das Optimierungsproblem (Problem Nr. 122)
MIN
⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎩f(x) =
1
2(x2
1 + x22) + 2x1 + x2
∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣∣
g1(x) = −x1 − x2 ≤ 0
g2(x) = x2 − 2 ≤ 0
g3(x) = x1 + x2 − 5 ≤ 0
g4(x) = −x1 + x2 − 2 ≤ 0
g5(x) = x1 − 5 ≤ 0
g6(x) = x2 − 1 ≤ 0
⎫⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭.

4.4 Verfahren für quadratische Optimierungsprobleme 335
Die Tab. 4.1 und die Abb. 4.8 veranschaulichen die Arbeitsweise des Algorithmus 25. �
xk I(xk) dk+1 u1 u2 u3 u4 u5 u6 Bemerkung
x0 {3, 5} = 0 0 0 < 0 0 < 0 0 x1 = x0
x1 {3} �= 0 x1 + dk /∈Mx2 {2, 3} = 0 0 > 0 < 0 0 0 0 t1 < 1, x3 = x2
x3 {2} �= 0 x3 + d4 /∈Mx4 {2, 4} = 0 0 < 0 0 > 0 0 0 t4 < 1, x5 = x4
x5 {4} �= 0 x5 + d6 /∈Mx6 {1, 4} = 0 > 0 0 0 < 0 0 0 t6 < 1, x7 = x6
x7 {1} �= 0 x7 + d8 ∈Mx8 {1} = 0 > 0 0 0 0 0 0 Lösung
Tab. 4.1 Aktive Mengenstrategie für Beispiel 4.33
−3 −2 −1 0 1 2 3 4 5 6−3
−2
−1
0
1
2
3
4
5
6
x1
x2
−2.374
−2.25
−2
−2 −1.5
−1.5
−0.5
−0.5
−0.5
1.5
1.5
5.5
5.5
5.5
13.5
13.5
13.5
13.529.5
29.5
29.5
x0=x1
d1= 0
x1+d2
x3=x2= x1+t1d2
d3= 0
x3+d4 x5=x4=x3+t4d4
d5= 0
x5+d6
x7=x6=x5+t6d6d7= 0
x8=x7+d8
d9= 0, x8 opt. Lösung
g5
≤0
g2 ≤ 0
g4≤
0
g6 ≤ 0
g3 ≤
0
g1 ≤
0
Abb. 4.8 Iterationsverlauf des Algorithmus 25 für Beispiel 4.33

336 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Wir bemerken zunächst, dass die Bestimmung eines zulässigen Punktes oder die Fest-
stellung, dass der zulässige Bereich leer ist, analog der Vorgehensweise beim Simplex-
Algorithmus zur Lösung linearer Optimierungsprobleme erfolgen kann (siehe beispiels-
weise Padberg (1999)), worauf wir nicht weiter eingehen. Stattdessen wollen wir nun in
Analogie zu unserer Vorgehensweise bei Problemstellungen der Form (QP=) hinreichende
Bedingungen für die eindeutige Lösbarkeit des linearen Gleichungssystems (4.12) in S2
des Algorithmus 25 formulieren, wobei wir jeweils annehmen, dass (x0,u0, v0) kein KKT-
Punkt von(QP≤=
)sein möge. Als unmittelbare Folgerung aus Satz 4.32 (b) erhalten wir:
Satz 4.34
Für ein Optimierungsproblem der Form(QP≤=
)sei dTQd > 0 für alle d ∈ Rn \ {0} mit
A(2)d = 0. Sind für(QP≤=
)im k-ten Iterationsschritt von Algorithmus 25 die Vektoren
ai mit i ∈ I(xk) ∪ {m + 1, · · · ,m + p} linear unabhängig, dann besitzt das zugehörigeGleichungssystem (4.12) eine eindeutige Lösung.
Weiterhin gilt:
Satz 4.35
Sind für ein Optimierungsproblem der Form(QP≤=
)im k-ten Iterationsschritt von Algo-
rithmus 25 die Vektoren ai mit i ∈ I(xk)∪ {m+1, · · · ,m+ p} linear unabhängig, dannsind auch die Vektoren ai mit i ∈ I(xk+1) ∪ {m+ 1, · · · ,m+ p} linear unabhängig.
Beweis: Wird I(xk+1) in S3, S4 oder S5 von Algorithmus 25 gesetzt, so gilt I(xk+1) ⊂I(xk) und die gewünschte Aussage folgt unmittelbar. Wird jedoch I(xk+1) in S6 gesetzt,
so gilt I(xk+1) = I(xk)∪{j} mit j ∈ {1, · · · ,m} \ I(xk) sowie aTj dk > 0. Angenommen,die Vektoren ai mit i ∈ I := I(xk+1) ∪ {m + 1, · · · ,m + p} sind linear abhängig, dannexistieren γi ∈ R mit
aj =∑i∈I\{j}
γiai ,
und es folgt mit (4.12)
aTj dk =
∑i∈I\{j}
γiaTi dk = 0
− im Widerspruch zu aTj dk > 0. �
Nach Satz 4.34 und Satz 4.35 ist S2 im Algorithmus 25 für ein Optimierungsproblem der
Form(QP≤=
)mit dTQd > 0 für alle d ∈ Rn \ {0} und A(2)d = 0 somit wohldefiniert,
sofern die Vektoren ai mit i ∈ I(x0) ∪ {m+ 1, · · · ,m+ p} linear unabhängig sind.Die in den beiden vorausgehenden Sätzen formulierte Voraussetzung dTQd > 0 für alle
d ∈ Rn \ {0} mit A(2)d = 0 ist natürlich trivialerweise erfüllt, wenn Q ∈ SPDn gilt.

4.5 SQP-Verfahren 337
In diesem Fall kann gezeigt werden, dass der Algorithmus 25 nach endlich vielen Ite-
rationen eine Lösung von(QP≤=
)liefert, und alle unseren bisherigen Ausführungen für
Problemstellungen der Form(QP≤=
)lassen sich unmittelbar auf Problemstellungen der
Form(QP≤
)übertragen.
Bezüglich effizienter Lösungsverfahren für lineare Gleichungssysteme verweisen wir auf
Hoffmann et al. (2005, 2006) und Kanzow (2005). Wir bemerken, dass es neben der hier
beschriebenen Strategie der aktiven Indizes eine Vielzahl weiterer Verfahren zur Lösung
von quadratischen Optimierungsproblemen bzw. von nichtlinearen Optimierungsproble-
men mit linearen Nebenbedingungen gibt. Für weitergehende diesbezügliche Ausführun-
gen verweisen wir beispielsweise auf Alt (2002), Fletcher (1987), Geiger und Kanzow
(2002), Gill und Murray (1978), Gill et al. (1981), Goldfarb (1972), Goldfarb und Idnani
(1981), Goldfarb und Idnani (1983), Großmann und Terno (1997) sowie Spellucci (1993).
4.5 SQP-Verfahren
Eine der wichtigsten Verfahrensklassen zur Lösung von nichtlinearen Optimierungspro-
blemen mit Nebenbedingungen sind die sogenannten SQP-Verfahren (engl. sequential
quadratic programming). Die grundlegende Idee dieser Verfahrensklasse besteht darin,
anstelle des Ausgangsproblems eine Folge von quadratischen Optimierungsproblemen zu
lösen (siehe Wilson (1963)).
Ausgangspunkt für die SQP-Verfahren ist das sogenannte Newton-Lagrange-Verfahren.
Zur Herleitung der Idee dieses Verfahrens betrachten wir ein Optimierungsproblem der
Form (P=) mit f ∈ C2(Rn,R) und H ∈ C2(Rn,Rp). Mit der zugehörigen Lagrange-
Funktion
L : Rn ×Rp → R und L(x, v) := f(x) +H(x)Tv
sind die KKT-Bedingungen durch das i. Allg. nichtlineare Gleichungssystem(∇xL(x, v)∇vL(x, v)
)=
(∇f(x) +∇H(x)v
H(x)
)= 0 (4.13)
gegeben. Wenden wir nun das (ungedämpfte) Newton-Verfahren auf (4.13) an, so erhalten
wir im Iterationspunkt (xk,vk) ∈ Rn ×Rp als zugehörige Newton-Gleichung(∇2xL(x
k, vk) ∇H(xk)∇H(xk)T 0
)(d
q
)= −
(∇f(xk) +∇H(xk)vk
H(xk)
)(4.14)
und somit den folgenden Prinzipalgorithmus zur Bestimmung eines KKT-Punktes des
ursprünglichen Problems (P=).

338 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Algorithmus 26 (Newton-Lagrange-Verfahren für (P=))
S0 Wähle (x0,v0) ∈ Rn ×Rp, und setze k := 0.
S1 Ist (xk,vk) ein KKT-Punkt von (P=), dann STOPP.
S2 Bestimme eine Lösung (dk, qk) ∈ Rn ×Rp des linearen Gleichungssystems (4.14).
S3 Setze (xk+1, vk+1) := (xk + dk,vk + qk), k := k + 1, und gehe zu S1.
Durch unmittelbare Übertragung der Konvergenzaussagen aus Satz 3.7 für das Newton-
Verfahren auf den Algorithmus 26 erhalten wir:
Satz 4.36
Es seien f ∈ C2(Rn,R), H ∈ C2(Rn,Rp), (x, v) ∈ Rn ×Rp ein KKT-Punkt des zugehö-rigen Optimierungsproblems (P=) und die Matrix
Φ(x, v) :=
(∇2xL(x, v) ∇H(x)∇H(x)T 0
)
invertierbar. Dann existiert eine ε-Umgebung Uε(x, v), sodass für jeden Startpunkt
(x0,v0) ∈ Uε(x, v) das SQP-Verfahren durchführbar ist und die durch den Algorith-
mus 26 erzeugte Folge{(xk, vk)
}k∈N
Q-superlinear gegen (x, v) konvergiert. Gilt dar-
über hinaus, dass ∇2f(x∗) und ∇2hj für alle j ∈ {1, · · · , p} in einer Umgebung von
x Lipschitz-stetig sind, dann konvergiert die durch den Algorithmus 26 erzeugte Folge{(xk,vk)
}k∈N
Q-quadratisch gegen (x, v).
Eine hinreichende Bedingung für die die Invertierbarkeit der Matrix Φ(x, v) liefert das
folgende Lemma:
Lemma 4.37
Es seien f ∈ C2(Rn,R), H ∈ C2(Rn,Rp) und (x, v) ∈ Rn ×Rp ein KKT-Punkt des zu-gehörigen Optimierungsproblems (P=). Sind die Gradienten ∇h1(x), · · · ,∇hp(x) linearunabhängig und gilt yT∇2
xL(x, v)y > 0 für alle y ∈ Rn \ {0} mit ∇H(x)Ty = 0, so ist
die zugehörige Matrix Φ(x, v) aus Satz 4.36 invertierbar.
Der Beweis von Lemma 4.37 erfolgt analog dem Beweis von Satz 4.32 (b) und sei dem
Leser als Aufgabe 4.10 überlassen.
Setzen wir λ := vk + q, so ergibt sich als äquivalente Formulierung zu (4.14)(∇2xL(x
k,vk) ∇H(xk)∇H(xk)T 0
)(d
λ
)= −
(∇f(xk)H(xk)
). (4.15)

4.5 SQP-Verfahren 339
Dieses lineare Gleichungssystem entspricht jedoch den KKT-Bedingungen des quadrati-
schen Optimierungsproblems
(SQP=)k MIN
{1
2dT∇2
xL(xk,vk)d+∇f(xk)Td
∣∣∣∣ ∇H(xk)Td = −H(xk)} ,womit der Algorithmus 26 auch wie folgt formuliert werden kann:
Algorithmus 27 (SQP-Verfahren für (P=))
S0 Wähle (x0,v0) ∈ Rn ×Rp, und setze k := 0.
S1 Ist (xk,vk) ein KKT-Punkt von (P=), dann STOPP.
S2 Bestimme einen KKT-Punkt (dk,λk) ∈ Rn ×Rp des quadratischen Optimierungs-problems (SQP=)k.
S3 Setze (xk+1, vk+1) := (xk + dk,λk), k := k + 1, und gehe zu S1.
Während sich das Newton-Lagrange-Verfahren (Alg. 26) nicht ohne weiteres auf Problem-
stellungen der Form(P≤=
)übertragen lässt, liegt die Übertragung des Algorithmus 27
für diese allgemeinen Problemstellungen auf der Hand. Setzen wir die Problemfunktionen
f , G und H als zweimal stetig differenzierbar voraus und linearisieren in jedem Itera-
tionspunkt auch die Ungleichungsnebenbedingungen, so führt dies auf das quadratische
Hilfsproblem
(SQP≤=
)k
MIN
{1
2dT∇2
xL(xk,uk, vk)d+∇f(xk)Td
∣∣∣∣ ∇G(xk)Td ≤ −G(xk)∇H(xk)Td = −H(xk)
}
und wir erhalten in Analogie zu Algorithmus 27 den folgenden Prinzipalgorithmus:
Algorithmus 28 (SQP-Verfahren für(P≤=
))
S0 Wähle (x0,u0,v0) ∈ Rn ×Rm ×Rp, und setze k := 0.
S1 Ist (xk,uk, vk) ein KKT-Punkt von(P≤=
), dann STOPP.
S2 Bestimme einen KKT-Punkt (dk,λk,μk) ∈ Rn×Rm×Rp des quadratischen Opti-mierungsproblems
(SQP≤=
)k.
S3 Setze (xk+1,uk+1,vk+1) := (xk + dk,λk,μk), k := k + 1, und gehe zu S1.
Für den Algorithmus 28 gilt die folgende lokale Konvergenzaussage:

340 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Satz 4.38
Es seien f ∈ C2(Rn,R), G ∈ C2(Rn,Rm), H ∈ C2(Rn,Rp), (x, u, v) ∈ Rn ×Rm × Rp ein KKT-Punkt des zugehörigen Optimierungsproblems
(P≤=
)und I(x) :=
{i | gi(x) = 0, i ∈ {1, 2, · · · ,m}}. Gilt ui > 0 für alle i ∈ I(x), sind die Gradi-
enten ∇gi(x) mit i ∈ I(x) sowie ∇h1(x), · · · ,∇hp(x) linear unabhängig und gilt
yT∇2xL(x, u, v)y > 0 für alle y ∈ Rn \ {0} mit ∇gi(x)Ty = 0 für alle i ∈ I(x) und
∇H(x)Ty = 0, dann existiert eine ε-Umgebung Uε(x, u, v), sodass für jeden Start-
punkt (x0,u0,v0) ∈ Uε(x, u, v) das SQP-Verfahren durchführbar ist und die durch denAlgorithmus 28 erzeugte Folge
{(xk,uk, vk)
}k∈N
Q-superlinear gegen (x, u, v) konver-
giert. Gilt darüber hinaus, dass ∇2f(x∗), ∇2gi für alle i ∈ {1, · · · ,m} und ∇2hj für alle
j ∈ {1, · · · , p} in einer Umgebung von x Lipschitz-stetig sind, dann konvergiert die durchden Algorithmus 28 erzeugte Folge
{(xk,uk, vk)
}k∈N
Q-quadratisch gegen (x, u, v).
Bezüglich des Beweises von Satz 4.38 verweisen wir auf Geiger und Kanzow (2002).
Im Allgemeinen müssen für die quadratischen Hilfsprobleme(SQP≤=
)kkeine zulässigen
Punkte existieren. Dies ist offensichtlich der Fall, wenn G(xk) > 0 und ∇G(xk) = 0
oder H(xk) �= 0 und ∇H(xk) = 0 gilt. Sind jedoch alle Koordinatenfunktionen gi von G
konvex über Rn sowie alle Koordinatenfunktionen hj von H affin-linear und besitzt das
ursprüngliche Optimierungsproblem(P≤=
)einen nichtleeren zulässigen Bereich, so kann
gezeigt werden, dass für alle (xk,uk,vk) auch das quadratische Optimierungsproblem(SQP≤=
)keinen nichtleeren zulässigen Bereich besitzt(siehe Aufgabe 4.11). Es existieren
jedoch modifizierte SQP-Verfahren, bei denen garantiert werden kann, dass deren zuläs-
sige Bereiche auch im nichtkonvexen Fall stets nichtleer sind, sofern nur das ursprüngliche
Optimierungsproblem(P≤=
)einen nichtleeren zulässigen Bereich besitzt (siehe beispiels-
weise Bonnans et al. (2003), Geiger und Kanzow (2002), Jarre und Stoer (2004), Powell
(1978) sowie Spellucci (1993)).
Die Verwendung der exakten Hesse-Matrizen ∇2xL(x
k,uk, vk) in den bisher formulierten
SQP-Verfahren ist natürlich sehr aufwendig. Aufgrund der hohen Kosten zur Berechnung
dieser Hesse-Matrizen, und da i. Allg. diese Matrizen nicht positiv definit sind, bietet
sich in der Praxis der Einsatz von Quasi-Newton-Aufdatierungen bzw. von modifizierten
Quasi-Newton-Aufdatierungen an (siehe Abschnitt 3.5). Der folgende Algorithmus ist
Powell (1978) entnommen.
Algorithmus 29 (SQP-Verfahren mit modifiziertem BFGS-Update)
S0 Wähle (x0,u0,v0) ∈ Rn ×Rm ×Rp, Q0 ∈ SPDn, und setze k := 0.
S1 Ist (xk,uk, vk) ein KKT-Punkt von(P≤=
), dann STOPP.

4.5 SQP-Verfahren 341
S2 Bestimme einen KKT-Punkt (dk,λk,μk) ∈ Rn×Rm×Rp des quadratischen Opti-mierungsproblems
(SQP≤=
)Qk
MIN
{1
2dTQkd+∇f(xk)Td
∣∣∣∣ ∇G(xk)Td ≤ −G(xk)∇H(xk)Td = −H(xk)
}.
S3 Setze
(xk+1,uk+1,vk+1) := (xk + dk,λk,μk) ,
zk := ∇Lx(xk+1,uk, vk)−∇Lx(xk,uk,vk) ,
τk :=
⎧⎪⎨⎪⎩1 , falls (dk)Tzk ≥ 0.2(dk)TQkd
k
0.8(dk)TQkd
k
(dk)TQkdk − (dk)Tzk
, falls (dk)Tzk < 0.2(dk)TQkdk,
qk := τkzk + [1− τk]Qkdk ,
Qk+1 := Qk −Qkd
k(dk)TQk(dk)TQkd
k+qk(qk)T
(qk)Tdk,
k := k + 1 ,
und gehe zu S1.
Wir verzichten auf eine Konvergenzanalyse des Algorithmus 29 und verweisen diesbezüg-
lich ebenfalls auf Powell (1978). Stattdessen wollen wir auf eine Eigenschaft des quadra-
tischen Hilfsproblems(SQP≤=
)Qk
eingehen, die sich für unsere weiteren Ausführungen
als nützlich erweisen wird. Ist (dk,λk,μk) ein KKT-Punkt von(SQP≤=
)Qk, so gilt
Qkdk +∇f(xk) +∇G(xk)λk +∇H(xk)μk = 0 ,
G(xk) +∇G(xk)Tdk ≤ 0 ,λk ≥ 0,(λk
)T (G(xk) +∇G(xk)Tdk
)= 0 und
H(xk) +∇H(xk)Tdk = 0 .
Für dk = 0 ergibt sich
∇f(xk) +∇G(xk)λk +∇H(xk)μk = 0 ,
G(xk) ≤ 0 ,λk ≥ 0,(λk
)TG(xk) = 0 sowie
H(xk) = 0 ,
und somit ist (xk,λk,μk) ein KKT-Punkt des ursprünglichen Problems von(P≤=
).
In Analogie zum Newton-Verfahren lassen sich die bisher formulierten (ungedämpften)
SQP-Verfahren durch die Einführung von Schrittweiten gemäß
(xk+1,uk+1, vk+1) := (xk + tkdk,λk,μk)

342 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
mit tk > 0 globalisieren, sodass sie unter gewissen zusätzlichen Voraussetzungen für
beliebige Startpunkte gegen eine lokale Lösung konvergieren. Da die Iterierten xk für
das ursprüngliche Problem i. Allg. nicht zulässig sind, ist jedoch für die Bestimmung
einer geeigneten Schrittweite tk bzw. für die Bewertung einer neuen Näherung xk+1
nicht nur die Verkleinerung des Zielfunktionwertes f(xk+1) im Vergleich zu f(xk) zu
betrachten, sondern es muss auch die Verletzung der Zulässigkeit berücksichtigt bzw.
„bestraft“ werden. Dies legt unmittelbar die Verwendung von exakten Straffunktionen
zur Schrittweitensteuerung nahe, wobei wir unsere diesbezüglichen Betrachtungen auf
die bereits eingeführte l1-Straffunktion
S1 : Rn ×R+ → R mit S1(x, r) := f(x) + r(‖ [G(x)]+ ‖1 + ‖H(x)‖1
)beschränken. Zwar ist für festes r > 0 nach Satz 4.22 die Funktion
S1r : Rn → R mit S1
r (x) := f(x) + r(‖ [G(x)]+ ‖1 + ‖H(x)‖1
)nicht differenzierbar, es existieren jedoch für alle x,d ∈ Rn die einseitigen Richtungs-ableitungen
S1′
r (x;d) = limt↓+0
S1r (x+ td)− S1
r (x)
t.
Es gilt (siehe beispielsweise Geiger und Kanzow (2002))
S1′
r (x;d) = ∇f(x)Td−r
∑j∈J−(x)
∇hj(x)Td
+r∑i∈I(x)
max{0,∇gi(x)Td
}+ r
∑j∈J(x)
∣∣∇hj(x)Td∣∣+r
∑i∈I+(x)
∇gi(x)Td+ r∑
j∈J+(x)
∇hj(x)Td
(4.16)
mit
I−(x) := {i | gi(x) < 0, i ∈ {1, · · · ,m}}, J−(x) := {j | hj(x) < 0, j ∈ {1, · · · , p}},I(x) := {i | gi(x) = 0, i ∈ {1, · · · ,m}}, J(x) := {j | hj(x) = 0, j ∈ {1, · · · , p}},I+(x) := {i | gi(x) > 0, i ∈ {1, · · · ,m}} und J+(x) := {j | hj(x) > 0, j ∈ {1, · · · , p}}.
Satz 4.39
Es seien f ∈ C1(Rn,R), G ∈ C1(Rn,Rm), H ∈ C1(Rn,Rp), x∗ ∈ Rn, Q ∈ SPDn,(d, λ, μ) ∈ Rn ×Rm ×Rp ein KKT-Punkt des quadratischen Optimierungsproblems
(SQP≤=
)Q
MIN
{1
2dTQd+∇f(x∗)Td
∣∣∣∣ ∇G(x∗)Td ≤ −G(x∗)∇H(x∗)Td = −H(x∗)
}
mit d �= 0, r ≥ max{‖λ‖∞, ‖μ‖∞
}und
S1 : Rn ×R+ → R mit S1(x, r) := f(x) + r(‖ [G(x)]+ ‖1 + ‖H(x)‖1
)

4.5 SQP-Verfahren 343
eine l1-Straffunktion für das zugehörige Optimierungsproblem(P≤=
). Dann gilt
S1′
r (x∗; d) < 0 ,
d. h. d ist eine Abstiegsrichtung von S1r in x
∗.
Beweis: Da (d, λ, μ) ∈ Rn×Rm ×Rp nach Voraussetzung ein KKT-Punkt des quadra-tischen Optimierungsproblems
(SQP≤=
)Q
MIN
{1
2dTQd+∇f(x∗)Td
∣∣∣∣ ∇G(x∗)Td ≤ −G(x∗)∇H(x∗)Td = −H(x∗)
}
ist, gilt
Qd+∇f(x∗) +∇G(x∗)λ+∇H(x∗)μ = 0 ,
G(x∗) +∇G(x∗)T d ≤ 0 , λT(G(x∗) +∇G(x∗)T d
)= 0 sowie
H(x∗) +∇H(x∗)T d = 0 .
Es folgt
∇f(x∗) = −Qd−m∑i=1
λi∇gi(x∗)−p∑j=1
μj∇hj(x∗) ,
∇gi(x∗)T d ≤ −gi(x∗) für alle i ∈ {1, 2, · · · ,m} ,max
{0,∇gi(x∗)T d
}= 0 für alle i ∈ I(x∗) ,
λi∇gi(x∗)T d ≤ −λigi(x∗) für alle i ∈ {1, 2, · · · ,m} ,∇hj(x∗)T d = −hj(x∗) für alle j ∈ {1, 2, · · · , p} ,
∇hj(x∗)T d = 0 für alle j ∈ J(x∗)
und mit (4.16)
S1′
r (x∗; d) ≤ −dTQd+
∑i∈I−(x∗)
λigi(x∗) +∑
i∈I+(x∗)
(λi − r
)gi(x∗)
+∑
j∈J−(x∗)
(μj + r) hj(x∗) +∑
j∈J+(x∗)
(μj − r) hj(x∗) .
Schließlich ergibt sich mit λ ≥ 0, r ≥ max{‖λ‖∞, ‖μ‖∞
}, Q ∈ SPDn sowie d �= 0
S1′
r (x∗; d) ≤ −dTQd < 0 . (4.17)
�
Aufgrund des letzten Satzes und unserer bisherigen Überlegungen können wir nun
ein SQP-Verfahren mit Schrittweitensteuerung formulieren, wobei wir eine Armijo-
Schrittweitenstrategie verwenden.

344 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Algorithmus 30 (Gedämpftes SQP-Verfahren)
S0 Wähle (x0,u0, v0) ∈ Rn×Rm×Rp, Q0 ∈ SPDn, r0 > 0, ε > 0, α ∈ (0, 1), q ∈ (0, 1),und setze k := 0.
S1 Ist (xk,uk, vk) ein KKT-Punkt von(P≤=
), dann STOPP.
S2 Bestimme einen KKT-Punkt (dk,λk,μk) ∈ Rn×Rm×Rp des quadratischen Opti-mierungsproblems
(SQP≤=
)Qk
MIN
{1
2dTQkd+∇f(xk)Td
∣∣∣∣ ∇G(xk)Td ≤ −G(xk)∇H(xk)Td = −H(xk)
}.
S3 Gilt dk = 0, dann setze (xk+1,uk+1, vk+1) := (xk,λk,μk), k := k+1, und gehe zu
S1.
S4 Setze tk := 1.
S5 Gilt S1rk(xk + tkd
k) ≤ S1rk(xk) + αtkS1′
rk(xk;dk), dann gehe zu S7.
S6 Setze tk := qtk, und gehe zu S5.
S7 Setze
(xk+1,uk+1, vk+1) := (xk + tkdk,λk,μk) ,
zk := ∇Lx(xk+1,uk,vk)−∇Lx(xk,uk,vk) ,
τk :=
⎧⎪⎨⎪⎩1 , falls (dk)Tzk ≥ 0.2(dk)TQkd
k
0.8(dk)TQkd
k
(dk)TQkdk − (dk)Tzk
, falls (dk)Tzk < 0.2(dk)TQkdk,
qk := τkzk + [1 − τk]Qkdk ,
Qk+1 := Qk −Qkd
k(dk)TQk(dk)TQkd
k+qk(qk)T
(qk)Tdk,
rk+1 := max{rk, max
{‖uk+1‖∞, ‖vk+1‖∞
}+ ε
},
k := k + 1 ,
und gehe zu S1.
In Schritt S5 kann man mit (4.17) die Richtungsableitung auf der rechten Seite durch
die leichter berechenbare obere Abschätzung
S1rk(x
k + tkdk) ≤ S1
rk(xk)− αtk(dk)TQkdk. (4.18)
ersetzen, wobei die Konvergenzaussagen erhalten bleiben (siehe Geiger und Kanzow
(2002)). Wünschenswert wäre, dass das gedämpfte SQP-Verfahren nach endlich vielen

4.6 Barrierefunktionen und Innere-Punkt-Verfahren 345
Schritten in das ungedämpfte SQP-Verfahren übergeht, d. h. die Schrittweite tk = 1 die
Armijo-Bedingung erfüllt und der Algorithmus 30 mindestens superlinear konvergiert.
Für diesbezügliche Konvergenzaussagen verweisen wir auf Han (1977). Es existieren je-
doch Beispiele, bei denen in jeder noch so kleinen Umgebung der Lösung des Ausgangs-
problems (P≤= ) Punkte existieren, sodass für diese die Schrittweite 1 in Richtung d ge-mäß S2 des Algorithmus 30 nicht akzeptiert wird. Dieser Effekt wird als Maratos-Effekt
bezeichnet (siehe Maratos (1978)). Strategien zur Vermeidung des Maratos-Effektes wer-
den beispielsweise in Geiger und Kanzow (2002), Wächter und Biegler (2005), Jarre und
Stoer (2004) sowie Spellucci (1993) diskutiert, indem man nichtmonotone Line Search-
Strategien betrachtet oder den Line Search durch eine Schrittweitensuche längs einer
geeigneten Parabel ersetzt oder auch Trust-Region-Strategien mit sogenannten Filtern
zur Globalisierung einsetzt. Eine weitere Möglichkeit zur Schrittweitensteuerung ist die
Verwendung von (modifizierten) glatten exakten Straffunktionen wie der verallgemeiner-
ten Lagrange-Funktion (siehe beispielsweise Bertsekas (1982) sowie Schittkowski (1983)).
Zum Abschluss dieses Abschnittes bemerken wir, dass eine Vielzahl von Variationen der
SQP-Verfahren existieren und verweisen für weitergehende diesbezügliche Ausführungen
beispielsweise auf Fletcher und Leyffer (2002), Fletcher et al. (2002), Gill et al. (1981),
Jäger und Sachs (1997), Nocedal und Wright (2006), Powell (1978) und Schittkowski
(1983).
4.6 Barrierefunktionen und Innere-Punkt-Verfahren
Wir betrachten Problemstellungen der Form(P≤
)MIN{f(x)| x ∈M} mit M := {x ∈ Rn| G(x) ≤ 0}
mit stetigen Problemfunktionen f und G = (g1, · · · , gm)T . Die im Folgenden betrach-
teten Barrierefunktionen stehen in einem engen Zusammenhang mit den in Abschnitt
4.2 betrachteten Straffunktionen. Während bei den Straffunktionen die Verletzung der
Nebenbedingungen durch die Addition eines Straftermes bestraft wurde, wird bei Bar-
rierefunktionen durch die Addition eines Barriereterms versucht, die Verletzung der Un-
gleichungsnebenbedingungen des Problems(P≤
)zu verhindern. Für die Problemstellung(
P≤)definieren wir zunächst
M0 := {x ∈ Rn| G(x) < 0} .
Die Menge M 0 wird als strikt zulässige Menge, strikt zulässiger Bereich oder auch als
striktes Inneres von M bezeichnet, wobei wir darauf hinweisen, dass i. Allg. natürlich
nicht M0 = intM gilt (siehe Aufgabe 4.12). Ist weiterhin ψ : M0 → R eine stetige
Funktion und gilt
limk→∞ψ(xk) =∞

346 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
für jede Folge {xk}k∈N ⊂M0 mit limk→∞xk ∈M \M0, so wird die Funktion
B :M0 ×R++ → R mit B(x, r) := f(x) + r ψ(x)
als Barrierefunktion und der Parameter r > 0 als Barriereparameter für die Problemstel-
lung(P≤
)bezeichnet. Wir werden uns bei unseren weiteren Betrachtungen in diesem
Abschnitt auf eine spezielle Barrierefunktion, die sogenannte logarithmische Barriere-
funktion (siehe Frisch (1955)) mit dem Barriereterm
ψ(x) := −m∑i=1
ln(−gi(x))
beschränken und verweisen bzgl. weiterer Barrierefunktionen beispielsweise auf Jensen
und Polyak (1994), Polyak (1992), Polyak und Teboulle (1997) sowie Powell (1995).
Für jedes (feste) r > 0 lassen sich der ursprünglichen Problemstellung(P≤
)logarithmi-
sche Barriereprobleme gemäß
(BP≤
)r
MIN
{Br(x) := f(x)− r
m∑i=1
ln(−gi(x))
∣∣∣∣∣ x ∈M0
}
zuordnen, hier nun in der Hoffnung, dass sich für eine streng monoton fallende Nullfolge
von Barriereparametern {rk}k∈N⊂ R++ die (lokalen bzw. globalen) Lösungen der zuge-
hörigen Barriereprobleme(BP≤
)rkeiner (lokalen bzw. globalen) Lösung des ursprüngli-
chen Optimierungsproblems(P≤
)annähern. Diese klassischen Barriereverfahren findet
man einschließlich einer Konvergenztheorie z. B. in Fiacco und McCormick (1968) sowie
Großmann und Kleinmichel (1976). Sind die Problemfunktionen f sowie gi konvex, so
ist offensichtlich auch die Funktion Br konvex. Für die Konvergenz der Barriereverfah-
ren ist vorauszusetzen, dass jeder zulässige Punkt durch Punkte aus M0 beliebig genau
approximiert werden kann, d. h. man setzt voraus, dass M0 �= ∅ und clM0 = M gilt
(siehe auch Aufgabe 4.13).
Beispiel 4.40Wir betrachten das konvexe Optimierungsproblem (Problem Nr. 172)
MIN{f(x) = x1 + x
22
∣∣− x1 ≤ 0, −x2 ≤ 0}
mit der globalen Lösung x = (0, 0)T . Für r > 0 lauten die zugehörigen (logarithmischen)
Barriereprobleme
MIN{Br(x) := x1 + x
22 − r (ln(x1) + ln(x2))
∣∣− x1 < 0, −x2 < 0}.
Wegen
∇Br(x) =(
1− rx1
2x2 − rx2
)

4.6 Barrierefunktionen und Innere-Punkt-Verfahren 347
ergibt sich für die eindeutigen globalen Lösungen der Barriereprobleme x(r) =(r,√r2
)T,
und es gilt limr↓0x(r) = x. In Abb. 4.9 sind für r = 10, 5, 1, 0.5, 0.1, 0.01 jeweils die Höhen-
linien der entsprechenden Barrierefunktionen Br und die Lösungskurve r �→ x(r) ge-zeichnet. �
0 5 10 150
5
10
15
x1
x2
r = 10
222
-16-15 -10-10
-5-5-500
55 1010202020
404040
808080
160160160
0 2 4 6 8 100
2
4
6
8
10
x1
x2
r = 5
222
-2.7-2
-1
-1-1
000 222444
888151515
303030
454545606060
757575
0 0.5 1 1.5 20
0.5
1
1.5
2
x1
x2
r = 1
22
2 21.85
1.9
1.9
22
2 2
2.52.5
2.5
2.52.5 2.5
33
3
3
3 3
3.53.5
3.5
3.5 3.5 3.5
444
4 4 4
0 0.2 0.4 0.6 0.8 1
0
0.2
0.4
0.6
0.8
1
x1
x2
r = 0.5
2
2
2 2
1.45
1.5
1.5
1.5
1.751.75
1.75
1.75
1.75 1.75
2
2
2 2
2.25
2.25
2.25 2.25
2.5
2.5
2.5 2.5 2.5
0 0.1 0.2 0.3 0.4 0.50
0.1
0.2
0.3
0.4
0.5
x1
x2
r = 0.1
0.54
0.54
0.55
0.55
0.575
0.575
0.6
0.6
0.6
0.6
0.65
0.65
0.65
0.7
0.7
0.7
0.7
0.80.8
0.8
0 0.1 0.2 0.30
0.1
0.2
x1
x2
r = 0.01
0.09 0.1
0.15
0.15
0.20.2
0.2
0.250.25
0.25
0.3
0.3
0.3 0.350.35
Abb. 4.9 Höhenlinien der Barrierefunktion Br mit r = 10, 5, 1, 0.5, 0.1, 0.01 für Beispiel 4.40
Im Gegensatz zu den Straffunktionen stimmen die Höhenlinien der Barrierefunktion für
jedes r > 0 auf dem zulässigen Bereich nicht mit den Höhenlinien der Zielfunktion f
überein, und die Barrierefunktion ist außerhalb des zulässigen Bereiches nicht definiert.
In Analogie zu den quadratischen Strafverfahren sind jedoch auch die Hesse-Matrizen
der Barriereprobleme für r ↓ 0 immer schlechter konditioniert (siehe Beispiel 4.40). Ausdiesem Grund haben sowohl die Barriereverfahren als auch die Strafverfahren für die
Lösung von Optimierungsproblemen mit Nebenbedingungen heute nicht mehr die Be-
deutung wie in den siebziger Jahren des vorigen Jahrhunderts.
Durch andere Ansätze wurde die Barrierefunktion bei der Lösung von insbesondere groß-
dimensionalen Optimierungsproblemen wieder interessant. Vornehmlich im letzten Jahr-
zehnt wurden die sogenannten Innere-Punkt-Verfahren (engl. interior-point methods)
untersucht, die eng mit den Barriereverfahren verknüpft sind. Ursprünglich wurden diese
Innere-Punkt-Verfahren für die Lösung großdimensionaler linearer Optimierungsproble-

348 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
me entwickelt, bei denen die Rechenzeit der Simplexverfahren mit der Problemgröße ex-
ponentiell wachsen kann. In Padberg (1999), Geiger und Kanzow (2002) sowie Jarre und
Stoer (2004) findet man Darstellungen dieser Verfahren für lineare Optimierungsprobleme
einschließlich der zugehörigen Konvergenztheorie. Wir erläutern hier nur das Grundprin-
zip dieser Verfahrensklasse an einem Optimierungsproblem mit Ungleichungsnebenbedin-
gungen, um die Zusammenhänge und Unterschiede zur Vorgehensweise bei Barrierever-
fahren zu demonstrieren und überführen die Ungleichungsnebenbedingungen G(x) ≤ 0
durch die Einführung von Schlupfvariablen y ∈ Rm+ in das System G(x)+y = 0, y ≥ 0.
Dem zu(P≤=
)äquivalenten Optimierungsproblem
MIN{f(x)| G(x) + y = 0, x ∈ Rn, y ∈ Rm+}
wird gemäß
(BP≤=
)r
MIN
{f(x)− r
m∑i=1
ln(yi)
∣∣∣∣ G(x) + y = 0, x ∈ Rn, y ∈ Rm}
eine Familie von Barriereproblemen mit Gleichungsnebenbedingungen zugeordnet, wobei
zu beachten ist, dass die Zielfunktion nur auf der offenen Menge G = Rm×Rm++ definiert
ist. Nach kurzer Rechnung ergeben sich für jedes r > 0 die folgenden KKT-Bedingungen
gemäß
(KKT )r
∇f(x) +∇G(x)u = 0
G(x) + y = 0
uiyi = r, i = 1, 2, . . . ,m
y > 0, u > 0.
Unter Beachtung von y > 0 und u > 0 dient nun das nichtlineare Gleichungssys-
tem in den (KKT )r-Bedingungen als Ausgangspunkt für eine Klasse von Innere-Punkt-
Verfahren. Man führt dabei für gewähltes rk > 0 nur jeweils eine Iteration zur Lösung
des von rk abhängigen Gleichungssystems aus und bestimmt damit eine Näherungslösung
(xk,yk,uk) ∈ Rn×Rm×Rm von (KKT )rk . Anschließend wird der Parameter rk wie bei
den Barriereverfahren verkleinert. Ausgehend von der zuvor berechneten Näherungslö-
sung wird mit dem neuen Parameter rk+1 wieder mit einem Schritt eine Näherungslösung
(xk+1,yk+1,uk+1) von (KKT )rk+1bestimmt.
Für M0 �= ∅ und clM0 = M gelingt es, unter den üblichen Differenzierbarkeitsvor-
aussetzungen, bei strenger Komplementarität im Lösungspunkt und bei Gültigkeit der
hinreichenden Optimalitätsbedingungen 2. Ordnung zu zeigen, dass für r ↓ 0 die exaktenLösungen der Familie von (KKT )r-Bedingungen innere Punkte des zulässigen Berei-
ches von(P≤
)sind (daher der Name Innere-Punkt-Verfahren) und gegen eine lokale
Lösung von(P≤
)konvergieren. Die von r abhängige Trajektorie der exakten Lösungen
(x(r),y(r),u(r)) wird häufig zentraler Pfad genannt.
Bei geeigneter Steuerung von rk > 0 mit limk→∞rk = 0 konvergieren auch die obigen

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 349
Einschritt-Näherungslösungen xk gegen eine lokale Lösung von(P≤
)mit mindestens
linearer Konvergenzgeschwindigkeit. Manche Innere-Punkt-Verfahren sind sogar superli-
near konvergent. Wegen der approximativen Lösung der Gleichungen in den (KKT )r-
Bedingungen ist in der Anfangsphase der Inneren-Punkt-Methoden die Zulässigkeit bzgl.
der Originalnebenbedingungen nicht garantiert, obwohl die Variablen y und u stets posi-
tiv sind. Erst in einer hinreichend kleinen Umgebung einer lokalen Lösung von(P≤
)wird
diese Zulässigkeit garantiert. Sowohl die entsprechenden Konvergenzbeweise, die in der
Regel die Strategie für die Verkleinerung von r liefern, als auch die Implementierung der
zugehörigen Algorithmen sind sehr umfangreich und aufwändig. Für die Bestimmung der
Näherungslösungen der (KKT )r-Bedingungen werden globalisierte Schritte von inexak-
ten Newton-Verfahren, Quasi-Newton-Verfahren oder SQP-Verfahren mit Gleichungsne-
benbedingungen unter Beachtung der Positivität von y und u ausgeführt.
Es muss beachtet werden, dass die Forderung nach zulässigen Iterierten (hier zumin-
dest in der lokalen Phase) i. Allg. einen höheren Rechenaufwand gegenüber Verfah-
ren erfordern, bei denen die Lösungen durch Iterierte approximiert werden, die erst im
Grenzpunkt zulässig sind. Die meisten Innere-Punkt-Verfahren, beispielsweise das in der
OTB implementierte Innere-Punkt-Verfahren, gestatten nicht zulässige Startpunkte. Das
Verfahren aus der OTB benutzt als Gleichungssystemlöser ein SQPmax-Verfahren auf
Richtungssuch- und Trust-Region-Basis. Der TR-Schritt führt im Falle der Nichtkon-
vexität mit der inexakten Lanczos-Methode einen Abstieg in Richtungen mit negativer
Krümmung von f aus. Damit verhindert man, dass das Verfahren in Punkten stagniert,
in denen die notwendigen Bedingungen 2. Ordnung nicht erfüllt sind. Die genaue Be-
schreibung des in der OTB verwendeten Verfahrens findet der Leser in Waltz et. al.
(2006).
Für weitergehende Ausführungen zu Innere-Punkt-Verfahren für nichtlineare Optimie-
rungsprobleme mit Nebenbedingungen verweisen wir auf Byrd et al. (1999), Jarre und
Stoer (2004), Waltz et. al. (2006), Wächter und Biegler (2006) [freie Software IPOPT]
und Wright (1997) sowie dort zitierte weitere Literatur zu Inneren-Punkt-Verfahren.
4.7 Numerische Experimente zu Verfahren derrestringierten Optimierung
Anhand der angegebenen Algorithmen wird deutlich, dass die Anzahl der zu wählenden
Startparameter gegenüber Algorithmen für nichtrestringierte Probleme z. T. erheblich
größer ist. Dies impliziert auch einen größeren Umfang der möglichen numerischen Expe-
rimente. Wir haben in diesem Abschnitt Testbeispiele und Startparameter ausgewählt,
die besondere Effekte bei der Lösung der Probleme aufzeigen.

350 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Wir vereinbaren, dass ein Verfahren regulär abbbricht, wenn für vorgegebenen Abbruch-
parameter ε > 0 folgende drei Bedingungen gleichzeitig erfüllt sind:
‖∇f(xk) +m∑j=1
uj∇gj(xk) +p∑i=1
vi∇hi(xk)‖∞ < ε, (4.19)
‖(u1g1(xk), ..., umgm(x
k))T ‖2 < ε, (4.20)
‖[G(xk)]+‖1 + ‖[H(xk)]+‖1 < ε. (4.21)
Die Bedingungen (4.19) und (4.20) representieren die KKT-Bedingungen ohne Berück-
sichtigung der Zulässigkeit. Das Maximum dieser Abbruchbedingungen („KKT“) wird
in den Abbildungen und in den Tabellen dargestellt. Bedingung (4.21) beschreibt die
Summe der absoluten Zulässigkeitsverletzungen („err(g,h)“). Diese wird ebenfalls in
den Abbildungen und in den Tabellen ausgewiesen. Die Nichtnegativität der Lagrange-
Multiplikatoren für die Ungleichungsrestriktionen wird durch die jeweiligen Algorithmen
gesichert. Wenn nichts anderes vermerkt ist, wird ε = 10−6 gesetzt. Bei jedem der fol-
genden zwei Bedingungen wird das Verfahren ebenfalls abgebrochen:
(1) Die maximal vorgebene Anzahl von äußeren Iterationen („maxit“) ist überschrit-
ten.
(2) Zusätzlich zu (4.21) gilt für den Abstand zweier aufeinanderfolgender äußerer Ite-
rierter
‖xk − xk−1‖2 < 0.01 ε.
Die Multiplikatoren u für Ungleichungen und v für Gleichungen werden in einem Vektor
y zusammengefasst. Bei der Analyse der Anzahlen der Funktionswert-, Gradienten- und
Hesse-Matrizenaufrufe unserer „Kostenanalyse“ ist zu beachten, dass z. B. unter nf =
4 bzw. ng = 6 bzw. nh = 13 zu verstehen ist, dass die Zielfunktion und alle Restrikti-
onsfunktionen 4-mal, die Gradienten der Zielfunktion und aller Restriktionsfunktionen
6-mal sowie die Hesse-Matrizen der Zielfunktion und aller Restriktionsfunktionen 13-
mal berechnet worden sind. Die Größe der Problemstellung bezogen auf die Anzahl der
Restriktionen wurde nicht berücksichtigt.
4.7.1 Experimente zu Straf- und Multiplikatorverfahren
Zunächst ein paar Bemerkungen zur Realisierung der Algorithmen. Die Steuerung des
Strafparameters r ist bei diesen Verfahren nicht einheitlich. Beim Multiplikatorverfah-
ren wird r nur dann erhöht (in EdOptLaB mit dem Faktor 10 multipliziert), wenn die
Annäherung an die zulässige Menge zu langsam erfolgt, d. h. wenn die maximale Ver-
letzung der Restriktionen im Vergleich zur vorhergehenden Iteration nicht unter 25 %
liegt. Beim Strafverfahren wird der Strafparameter ständig erhöht. Ist hier die Annähe-
rung an den zulässigen Bereich zu langsam, so multiplizieren wir r mit max{5, ‖y‖∞}

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 351
und andernfalls mit zwei. Der aktuelle Multiplikator wird für die Gleichungen mit (4.4)
und für die Ungleichungen gemäß (4.5) geschätzt. Die Lösung der entsprechenden unre-
stringierten Hilfsprobleme bestimmen wir unter EdOptLab mit einem BFGS-Verfahren.
Die Abbruchtoleranz für dieses BFGS-Verfahren wird an die Abbruchtoleranz im Straf-
und Multiplikatorverfahren (äußeres Verfahren) angepasst. Zu Beginn des äußeren Ver-
fahrens ist die Toleranz für das (innere) BFGS-Verfahren relativ groß und wird nach
einem Vorschlag von Spellucci (1993) pro Iteration im äußeren Verfahren solange um
2 Zehnerpotenzen verkleinert, bis die Abbruchtoleranz des äußeren Verfahrens erreicht
ist. Das BFGS-Verfahren bricht auch ab (Safeguard), wenn 100 BFGS-Schritte (inne-
re Iterationen) erreicht sind und übergibt den letzten (inneren) Iterationspunkt an das
äußere Verfahren zur weiteren Verarbeitung. Wenn das Multiplikatorverfahren die regu-
lären Abbruchbedingungen näherungsweise erfüllt und der sogenannte Fletcher-Vektor
yT = (uT , vT ), der sich als Lösung der least-square-Aufgabe
MIN{‖∇f(xk) +∇G(xk)u+∇H(xk)v‖2 | u ∈ Rm+ , v ∈ Rp}
ergibt, einen kleineren Wert in (4.19) liefert als der Vektor y nach Schritt S3, dann wird
zur Aufdatierung des Multiplikators der Fletcher-Vektor benutzt. In den Tabellen wird
dies durch „Info = 0.1“ gekennzeichnet.
Experiment 4.7.1 (Strafverfahren (SV) vs. Multiplikatorverfahren (MV))
MMV01.m: Wir betrachten das Problem Nr. 116 (Spellucci (1993), S. 397) mit der
streng konkaven Zielfunktion
f(x) =100
(x1 + x2 − 3.5)2 + 4(x2 − x1 + 0.5)2
sowie den beiden konvexen Restriktionen g1(x) = x21+x2−1 ≤ 0 und g2(x) = x2
1−x2−1 ≤0. Wegen der strengen Konkavität der Zielfunktion sind lokale Minima immer Randpunk-
te der zulässigen Menge. Wir starten im Punkt x0 = (−1,−1.5)T das SV sowie das MV
und vergleichen zunächst die Kosten und die Anzahl der Iterationen. In den Tabellen
4.2 und 4.3 erkennt man die Überlegenheit des MV in allen Bewertungen: Iterationsan-
zahl (SV:10/MV:6), Kosten (564/209), CPU-Zeit (0.516/0.203 Sek.), Genauigkeit nach
gleicher Iterationsanzahl (Iteration 6: 10−4/10−7). Obwohl beide Verfahren nach 2-3 Ite-
rationen (siehe Abb. 4.10) in eine relativ kleine Umgebung der Optimalstelle gelangen,
braucht doch das SV wesentlich länger und wesentlich mehr Aufwand, um die Genauigkeit
des Ergebnisses weiter zu verbessern.

352 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
0 2 4 6 8 1010−7
10−6
10−5
10−4
10−3
10−2
10−1
100
101
Iterationsindex
max
(KK
T,V
erl.
d. R
estr.
)
0 200 400 60010−7
10−6
10−5
10−4
10−3
10−2
10−1
100
101
Kosten
SV (0.516")MV (0.203")
Abb. 4.10 Iterations- und Kostenanalyse für SV und MV im Exp. 4.7.1
--------------------------------------------------------------------
it nf ng fiter in_it r err (g,h) KKT
--------------------------------------------------------------------
0 2 2 2.77777 e +000 0 1.17e +000 1.50 e+000 2.64 e+000
1 21 12 2.33247 e +000 10 1.17e +000 1.15 e+000 1.55 e+000
2 78 38 3.36133 e +000 21 1.35e +001 8.74e -002 4.60e -002
3 92 43 3.38936 e +000 5 2.70e +001 4.46e -002 2.36e -002
4 145 66 3.41578 e +000 14 2.70e +002 4.54e -003 2.41e -003
5 162 71 3.41729 e +000 5 5.39e +002 2.27e -003 1.21e -003
6 199 83 3.41865 e +000 9 5.39e +003 2.28e -004 1.21e -004
7 220 88 3.41872 e +000 5 1.08e +004 1.14e -004 6.04e -005
8 258 100 3.41879 e +000 9 1.08e +005 1.14e -005 6.04e -006
9 280 104 3.41879 e +000 4 2.16e +005 5.69e -006 3.02e -006
10 328 118 3.41880 e +000 8 2.16e +006 5.69e -007 3.02e -007
--------------------------------------------------------------------
Tab. 4.2 Iterationsverlauf des SV für Problem Nr. 116 im Exp. 4.7.1
---------------------------------------------------------------------
it nf ng fiter in_it Info r err (g,h) KKT
---------------------------------------------------------------------
0 2 2 2.777778 e+000 0 0.0 1.17 e+000 1.50 e+000 9.26e -001
1 21 12 2.332477 e+000 10 0.0 1.17 e+000 1.15 e+000 1.55 e +000
2 64 31 3.394840 e+000 13 0.0 1.17 e+001 7.13e -002 6.78e -002
3 80 38 3.420619 e+000 7 0.0 1.17 e+001 3.18e -003 3.50e -003
4 93 43 3.418748 e+000 5 0.0 1.17 e+001 1.74e -004 1.60e -004
5 102 46 3.418808 e+000 3 0.0 1.17 e+001 7.78e -006 8.54e -006
6 111 49 3.418803 e+000 3 1.0 1.17 e+001 4.24e -007 3.90e -007
---------------------------------------------------------------------
Tab. 4.3 Iterationsverlauf des MV für Problem Nr. 116 im Exp. 4.7.1

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 353
Besonders auffallend ist der große Unterschied in den Strafparameterwerten zwischen
beiden Verfahren. Die großen Strafparameter bis zu r = 107 bei den SV erhöhen einer-
seits die Anzahl der inneren BFGS-Iterationen und andererseits die CPU-Zeit bei der
Schrittweitenbestimmung. Bei zusätzlich schlecht konditionierten Problemen kann dies
dazu führen, dass die inneren BFGS-Schritte nicht mehr korrekt ausführbar sind. Demge-
genüber arbeitet das BFGS-Verfahren bei den MV wegen der viel kleineren Strafparame-
terwerte wesentlich effektiver. Insbesondere kurz vor Abbruch der Verfahren benötigen
die MV deutlich weniger innere BFGS-Schritte. Eine Verwendung des Fletcher-Vektors
brachte bei diesem Beispiel im MV keine Vorteile (Info = 0). Sehr häufig wird bei MV
mit dem Lagrange-Multiplkator y = 0 begonnen. Dadurch stimmt die erste Iteration bei
SV und MV überein. �
Experiment 4.7.2 (MV vs. SV bei Verletzung der (LICQ))
straf04.m: Es gibt Problemstellungen, bei denen MV gegenüber SV nicht im Vorteil
sind. Für die Konvergenztheorie der MV ist im Gegensatz zum SV die Gültigkeit der
Regularitätsbedingung (LICQ) im Optimalpunkt von entscheidender Bedeutung (siehe
beispielsweise Bertsekas (1982), S. 161). Ist diese verletzt, dann verliert das MV seine
guten Konvergenzeigenschaften.Wir zeigen dies am Problem Nr. 110 (siehe Beispiel 2.17).
Das SV und das MV brechen nach 17 Iterationen wegen zu großem Strafparameter ab,
da höhere Strafparameter vom inneren BFGS-Verfahren zur freien Minimierung nicht
mehr verarbeitet werden können. Beide Verfahren nähern sich dem Lösungspunkt sehr
langsam. Die Vorzüge des MV kommen nicht mehr zur Geltung. Das MV erfordert sogar
einen viel höheren Aufwand, da der Summand mit dem Multiplikator in der Lagrange-
Funktion, welcher lt. Theorie gegen unendlich geht, die Kondition der Hesse-Matrix der
Lagrange-Funktion zusätzlich verschlechtert, sodass das innere BFGS-Verfahren häufiger
als beim Strafverfahren mit Überschreiten der maximalen Iterationsanzahl beendet wird.
Ein Vergleich liefert: Iterationsanzahl (SV:17/MV:17), Kosten (1762/7223), CPU-Zeit
(0.922/2.859 Sek.), Summe der inneren BFGS-Iterationen (298/813). Wir verzichten hier
auf die zugehörigen Tabellen und grafischen Darstellungen, die bei Durchführung des
Experimentes erzeugt werden. �
Experiment 4.7.3 (Untersuchungen zur superlinearen Konvergenz von MV)
straf05.m: Wir betrachten das Problem Nr. 106
MIN{e3x1+4x2 | x21 + x
22 = 1, x1, x2 ∈ R}
mit konvexer Zielfunktion und einer Gleichungsrestriktion. Anhand dieses Beispiels dis-
kutieren wir auch die Bedeutung der Wahl des Strafparameters zu Beginn der Verfahren.
Falls r0 nicht explizit vorgegeben ist, wird unter EdOptLab der Startwert für den Straf-
parameter gemäß
r0 :=m∑i∈I
‖∇f(x0)‖2
‖∇gi(x0)‖2+p∑j∈J
‖∇f(x0)‖2
‖∇hj(x0)‖2(4.22)

354 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
mit I = {i ∈ {1, 2, ...,m} | ‖∇gi(x0)‖ ≥ γ > 0} und J = {j ∈ {1, 2, ..., p} | ‖∇hi(x0)‖ ≥γ > 0} und γ = 10−5 gewählt. Ist diese oft benutzte Näherung für einen Startwert r0 zu
klein, dann kann sich die Anzahl der äußeren Iterationen sehr stark erhöhen. Bei SV wird
dies durch die ständige Vergrößerung des Strafparameters r ausgeglichen. Im Gegensatz
hierzu kann bei MV mit einem kleinen Startparameter r0 die Abfrage der Restriktions-
verletzung in S5 von Algorithmus 22 bzw. 23 stets erfüllt sein, sodass der Strafparameter
im Verlauf des Verfahrens nicht erhöht wird. In dem hier betrachteten Beispiel tritt ge-
nau dieser Sachverhalt ein und sowohl das SV als auch das MV benötigen elf Iterationen.
Erhöht man den Startwert r0 auf 2 oder mehr, so benötigt das MV im Vergleich zum SV
nur noch ungefähr die Hälfte der Iterationen. In diesem Beispiel sind die durchschnitt-
lichen BFGS-Schritte ab der 2. Iteration im SV und MV etwa gleich. Damit verringern
sich die Kosten beim MV gegenüber dem SV erheblich, wenn der Startparameter nicht
zu groß ist. Es ist auch erkennbar, dass die Wahl eines zu hohen r0 eine im Vergleich
zu den folgenden Iterationsschritten unverhaltnismäßig hohe Anzahl von inneren BFGS-
Iterationen nach sich zieht. Aus diesem Grunde ist die Wahl des ersten Strafparameters
entscheidend für die Effektivität der Verfahren. Ein zu hoher Anfangsparameter r kann
sogar zur Divergenz beider Verfahren führen (siehe Experiment 4.7.4). In Tab. 4.4 werden
für verschiedene Startwerte von r die Anzahl der benötigten Iterationen, die Kosten, die
Anzahl der inneren BFGS-Iterationen für den ersten und zweiten Iterationsschritt und
die durchschnittliche Anzahl der inneren BFGS-Iterationen pro Iteration ab der zwei-
ten Iteration zusammengestellt. Der Wert für den Strafparameter r0 in der ersten Zeile
entspricht dem Schätzwert gemäß (4.22).
r0 Iter . Kosten BFGS BFGS BFGS /it
1. It 2. It. ab 2. It
SV MV SV MV SV MV SV MV SV MV
----------------------------------------------------
0.00161 11 11 249 231 8 8 11 10 4 5
1 9 5 209 113 14 14 4 4 4 3
2 8 4 174 121 14 14 9 9 3 5
10 7 3 195 132 25 25 2 2 3 2
100 5 2 261 219 36 36 2 2 3 2
1000 3 2 436 424 81 81 2 2 2 2
----------------------------------------------------
Tab. 4.4 Vergleich zwischen SV und MV für Problem Nr. 106 bei verschiedenen Startwerten r0im Exp. 4.7.3
straf06.m: In Bertsekas (1982) wird gezeigt, dass die MV unter entsprechenden Voraus-
setzungen superlinear konvergent sind, wenn wie bei den SV der Strafparameter r nach
unendlich geht. Wenn die Lösung auf dem Rand des zulässigen Bereiches liegt, dann ist
die superlineare Tendenz nur noch bzgl. der Abnahme der Verletzung der Zulässigkeit
erkennbar, da die Genauigkeit bei der Erfüllung der Kuhn-Tucker-Bedingungen durch die

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 355
intern vorgegebenen Abbruchbedingungen des BFGS-Verfahrens bestimmt wird . Das fol-
gende Experiment zeigt bei Problem Nr. 106 deutlich eine superlineare Annäherung an
den Restriktionsrand (siehe Abb. 4.11). Das innere BFGS-Verfahren erfüllt nach zwei äu-
ßeren Iterationen die geforderte Abbruchtoleranz von 10−6, d. h. die KKT-Bedingungen
sind ab dieser Iteration beim Multiplikatorverfahren mit dieser Toleranz erfüllt. Eine wei-
tere Verkleinerung der Toleranz beim inneren BFGS-Verfahren ist nicht mehr sinnvoll.
Dies würde nur die CPU-Zeit erhöhen. Es gibt deutliche Einsparungen bei MV mit stän-
diger Erhöhung des Strafparameters (MVm) gemäß rk+1 = 10rk im Vergleich zu MV
ohne ständige Erhöhung des Strafparameters (MVo) in den Iterationen (MVo: 6/MVm:
11), Kosten (162/231) und der Summe der BFGS-Iterationen (33/53). Dies liegt darin be-
gründet, dass bis zum regulären Abbruch des MV der Strafparameter mit r6 = 161 noch
hinreichend klein ist. Die ständige Erhöhung des Strafparameters bewirkt bei MV also
einerseits eine Vergrößerung der Anzahl an inneren BFGS-Iterationen und andererseits
eine Verringerung der Anzahl der äußeren Iterationen. Aufgrund dieser beiden gegenläu-
figen Tendenzen und möglicher numerischer Probleme bei den inneren BFGS-Iterationen
ist es oft nicht vorteilhaft, bei MV den Strafparameter ständig zu erhöhen.
0 1 2 3 4 5 6 7 8 9 10 11 12
10-6
10-3
100
Ver
l. d.
Opt
. Bed
.
Iterationsindex
Max. Verletzung der Restrikt.Verletzung der KKT-Bed.
VMolineareTendenz
Toleranz
innere Genauigkeitssteuerungbeim BFGS
0 1 2 3 4 5 6
10-6
10-3
100
Iterationsindex
innere Genauigkeitssteuerungbeim BFGS
Toleranz
superlineareTendenz
MVm
Abb. 4.11 Superlineare Konvergenz von MVm und lineare Konvergenz von MVo für ProblemNr. 106 im Exp. 4.7.3
straf07.m:Wir vergleichen die Iterationsanzahl, die Kosten und die Summe der BFGS-
Iterationen bei allen implementierten Problemen für das MVo und MVm unter Benutzung
des Startwertes r0 gemäß der Schätzung (4.22), wobei wir hier nur einige Beispiele zu-
sammenstellen, bei denen es im Iterationsverlauf größere Unterschiede und bei ständig
wachsendem r eine superlineare Tendenz gibt. Beim Experiment werden die je Problem
und Verfahren entstehenden Tabellen und grafischen Darstellungen sowie die Tabelle 4.5
auf einem temporären Verzeichnis gespeichert und können von diesem abgerufen wer-
den. �

356 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Problem it Kosten BFGS /it
ab 2. it
MVo MVm MVo MVm MVo MVm
----------------------------------------
106 11 6 231 162 5 5
116 4 3 157 193 5 8
115 9 5 275 204 6 8
117 8 4 204 157 5 8
118 10 4 213 117 5 5
120 6 4 133 102 3 4
121 7 4 213 166 5 7
123 5 3 121 105 3 3
136 10 5 380 205 6 6
156 6 3 500 326 8 8
157 4 3 486 450 3 3
Tab. 4.5 Vergleich von MVm und MVo für verschieden Probleme im Exp. 4.7.3
Experiment 4.7.4 (SV konvergiert nicht gegen KKT-Punkt)
straf08.m: Wenn man den Strafparameter zu Beginn eines SV zu hoch wählt, hat die
Zulässigkeit der Iterierten zu hohe Priorität und das SV stagniert auf dem Rand des zu-
lässigen Bereiches. Wir demonstrieren dies anhand des Problems Nr. 106 für r0 = 1010.
In diesem Fall wird das Verfahren mit zu kleiner Schrittweite beendet (siehe Abb. 4.12,
links). Wählen wir jedoch r0 gemäß der Schätzung (4.22), so wird die Lösung durch das
SV gut approximiert (siehe Abb. 4.12, rechts). Im ersten Fall erkennt man an der (hier
nicht aufgeführten) Iterationstabelle, dass das BFGS-Verfahren in allen äußeren Itera-
tionen die Minimierung gemäß Schritt S2 nicht mehr ordnungsgemäß ausführt, sondern
nach 100 inneren Iteration ein Abbruch des BFGS-Verfahrens erfolgt. �
−1 −0.5 0 0.5 1
−1
−0.5
0
0.5
1
x1
x2
0.001
0.01
0.01
0.1
0.1
0.1
1
1
1
1
10
10
10
100
100
0.00929
0.00929
0.00929
0.00929
−1 −0.5 0 0.5 1
−1
−0.5
0
0.5
1
x1
x2
0.001
0.01
0.01
0.1
0.1
0.1
1
1
1
1
10
10
10
100
100
0.00674
0.00674
0.00674
0.00674
Abb. 4.12 SV konvergiert nicht gegen KKT-Punkt für Problem Nr. 106 im Exp. 4.7.4 bei zugroßem r0

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 357
Experiment 4.7.5 (Höhenlinien der Straf- und verallgemeinerten Lagrange-
Funktion)
straf09.m: Wir betrachten das Problem Nr. 108
MIN{−x1 − x2 | x21 + x
22 − 1 ≤ 0} .
Nach Berechnung der optimalen Lösung mit SV erzeugen wir zusätzlich zur Abbildung
des Iterationsverlaufes (siehe Abb. 4.13, links) die Höhenlinien der quadratischen Straf-
funktion für den Strafparameter r = 7.61 × 105 im letzten Iterationsschritt (siehe Abb.
4.13, rechts). Die schlechte Kondition des Problems ist deutlich erkennbar (vgl. die hohen
Werte der Höhenlinien für die quadratische Straffunktion mit denen der Zielfunktion).
In Analogie hierzu erzeugen wir für das MV ebenfalls zusätzlich zur Abbildung des
Iterationsverlaufes (siehe Abb. 4.14, links oben) die Höhenlinien der verallgemeinerten
Lagrange-Funktion (siehe Abb. 4.14, rechts oben), der quadratischen Straffunktion (siehe
Abb. 4.14, links unten) und der Lagrange-Funktion (siehe Abb. 4.14, rechts unten) für
den Strafparameter r = 3.92 im letzten Iterationsschritt und den (optimalen) Lagrange-
Multiplikator u = 1√2. Die Höhenlinien der verallgemeinerten Lagrangefunktion sind
gegenüber den Höhenlinien der Zielfunktion im zulässigen Bereich leicht verschoben. Am
Rand und außerhalb des zulässigen Bereiches sind die Höhenlinienwerte nur im zwei-
stelligen Bereich. Zum Vergleich befindet sich das Minimum der Straffunktion bei diesem
Strafparameter noch deutlich außerhalb des zulässigen Bereiches. Ausnahmsweise hat die
Lagrange-Funktion mit optimalem Lagrange-Multiplikator sogar ein lokales Minimum im
Lösungspunkt. �
−1.5 −1 −0.5 0 0.5 1 1.5−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
−2
−2
−1
−1
−1
−0.5
−0.5
−0.5
−0.5
0
0
0
0
0.5
0.5
0.5
0.5
1
1
1
2
2
−1.414
−1.414
−1.414
−1.414
SV
Zielfunktion
−1.5 −1 −0.5 0 0.5 1 1.5−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
2547954
1276
361
1276361
1276361
1276361
481649
481649
481649
481649
4816
49
481649
481649
481649
4816
49
80474
80474 80474
8047
4
80474
80474
80474
−1
−1
−1
−0.5
−0.5
−0.5
−0.5
0
0
0
0
0
0.5
0.5
0.5
0.5
0.5
0.5
1
1
1
1
1
12
22
2
22
2
L2−Straffunktion
Abb. 4.13 Höhenlinien bei SV für Problem Nr. 108 im Exp. 4.7.5

358 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
−1.5 −1 −0.5 0 0.5 1 1.5−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
−2
−2
−1
−1
−1
−0.5
−0.5
−0.5
−0.5
0
0
0
0
0.5
0.5
0.5
0.5
1
1
1
2
2
−1.414
−1.414
−1.414
−1.414
MV
Zielfunktion
−1.5 −1 −0.5 0 0.5 1 1.5−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
12.869
12.86912.869
12.8695.149
5.14
9
5.149
5.1495.149
5.149
5.149
−1.276
−1.276
−1
−1
−1
−0.5
−0.5
−0.5
−0.5
−0.5
0
0
0
0
0
0
0.5
0.50.5
0.5
0.5
0.5
0.5
1
11
1
1
1
1
1
2
2
2
2
2
2
2
2
Verallgemeinerte Lagrangefunktion
−1.5 −1 −0.5 0 0.5 1 1.5−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
−1.414
10.395
10.39510.395
10.3954.336
4.33
6
4.336
4.3364.336
4.336
4.336
−1.438
−1
−1
−1
−1
−0.5
−0.5
−0.5
−0.5
−0.5
0
0
0
0
0
0
0.5
0.50.5
0.50.5
0.5
0.5
1
1
1
1
1
1
1
1
2
2
2
2 2
2
2
2
L2−Straffunktion
−1.5 −1 −0.5 0 0.5 1 1.5−1.5
−1
−0.5
0
0.5
1
1.5
x1
x2
3.527
−1.223
−1.2
23
−1.223
−1.357
−1.357
−1
−1
−1
−1
−1
−0.5
−0.5
−0.5
−0.5
0
0
0 0
0.5
0.5
0.50.5
1
1
1
11
2
2
2
22
Lagrangefunktion
Abb. 4.14 Höhenlinien bei MV für Problem Nr. 108 im Exp. 4.7.5
4.7.2 Experimente zu SQP- und Innere-Punkt-Verfahren
Für die SQP-Verfahren in der Implementation gemäß Algorithmus 30 wollen wir demons-
trieren, dass quadratische Konvergenz möglich ist, dass die quadratischen Teilprobleme
schon bei einfachen Beispielen nicht lösbar sein können (wenn man dagegen keine Vor-
kehrungen trifft), und dass das Erzwingen der Zulässigkeit bei Gleichungsrestriktionen
die Schrittweite erheblich verringern kann (Maratos-Effekt). Trotzdem sind die SQP-
Verfahren oft wesentlich schneller als die Multiplikatorverfahren, die wir immer als Ver-
gleich mit zu Rate ziehen werden. Bei Auftreten des Maratos-Effektes kann das lokale

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 359
Verfahren durchaus quadratisch konvergent sein, denn das globalisierte Verfahren erkennt
aufgrund der benutzten Globalisierungsstragie nicht, dass die Schrittweite 1 benutzt wer-
den kann und mit dieser Schrittweite die Konvergenz gesichert ist. Unter EdOptLab
stellen wir sechs SQP-Verfahren für die Probleme (P≤= ) zur Verfügung. Die Dämpfungder Schrittweite erfolgt immer mit der modifizierten Armijo-Regel gemäß (4.18). Die Op-
timization Toolbox von Matlab (OTB) stellt je Version von Matlab noch 1-2 weitere
SQP-Verfahren zur Verfügung (siehe (7) und (8)), die wir zum Vergleich anführen und
testen.
(1) SQP lokal: Lokales Newton-Langrange-Verfahren,
(2) SQPmax-V1: Gedämpftes SQP-Verfahren mit μk := max{1, ‖∇f(xk)‖
}, Qk :=
μkEn und l∞-Straffunktion,
(3) SQPmax-V2: Gedämpftes SQP-Verfahren mit 0.8-BFGS-Aufdatierung für Qknach Fletcher und l∞-Straffunktion,
(4) SQPmax-V3: Gedämpftes SQP-Verfahren mit (ggf. regularisierter) Hesse-Matrix
von L für Qk und l∞-Straffunktion,
(5) SQPL1: Gedämpftes SQP-Verfahren mit 0.8-BFGS-Aufdatierung nach Fletcher
für Qk und l1-Straffunktion bei r ≥ ‖y‖∞,
(6) SQPL1g: Gedämpftes SQP-Verfahren mit 0.8-BFGS-Aufdatierung nach Fletcher
für Qk und l1-Straffunktion mit individueller Bestrafung der Verletzung der Zu-
lässigkeit bei jeder Restriktion mit ggf. unterschiedlichem Strafparameter gemäß
ri ≥ |yi|,
(7) OTB-ASmax: SQP-Verfahren mit aktiver Mengenstrategie und BFGS-Aufdatie-
rung sowie l∞-Straffunktion (Quellcode in OTB publiziert),
(8) OTB-sqp: SQP-Verfahren nach Nocedal und Wright mit BFGS-Aufdatierung bei
ständiger Zulässigkeit bzgl. Box-Beschränkungen (Quellcode in OTB nicht publi-
ziert).
Für die Verfahren (1)-(6) gibt es je zwei Varianten. Bei der ersten führt ein nichtlös-
bares quadratisches Teilproblem sofort zum Abbruch des Verfahrens. Bei der zweiten
Variante wurde die Erweiterung von Geiger und Kanzow (2002) (siehe Algorithmus 5.47)
hinzugefügt, die im Falle der Nichtlösbarkeit eines quadratischen Teilproblems ein zuge-
höriges erweitertes quadratisches Teilproblem löst. Bei der Erweiterung wird anstelle des
Problems
MIN
{12dTQd+ cTd
∣∣∣∣A1d = b1, A2d ≤ b2
}

360 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
das quadratische Problem
MIN
⎧⎪⎪⎨⎪⎪⎩1
2dTQd+ cTd+ rS(η+,η−, ξ)
∣∣∣∣∣∣∣∣A1d− η+ + η− = b1
A2d− ξ ≤ b2
η+,η−, ξ ≥ 0
⎫⎪⎪⎬⎪⎪⎭gelöst, wobei S(η+,η−, ξ) die Summe aller Zusatzvariablen η+
i ,η−
i , ξj ist und damit
wegen der Nichtnegativität dieser Variablen als Strafterm wirkt. Ist der Strafparameter
groß genug, dann werden bei der Lösung des erweiterten Problems diese Zusatzvariablen
Null, wenn das Originalproblem lösbar ist. Mit dieser Erweiterung ergeben sich analoge
Konvergenzsätze. Wenn anstelle der obigen Erweiterung des Hilfsproblems least-square-
Lösungen des quadratischen Hilfsproblems berechnet werden, spricht man häufig von
LSSQP-Verfahren.
Experiment 4.7.6 (Kostenanalyse von MV im Vergleich zu SQP-Verfahren)
SQP02.m:Wir vergleichen das MV mit den SQP-Verfahren (1)-(6) hinsichtlich der Ite-
rationsanzahl und der kumulierten Kosten für das Problem Nr. 106. In der Abbildung
4.15 erkennen wir deutlich die Vorteile der SQP-Verfahren mit der BFGS-Aufdatierung
(SQPmax-V2, SQPL1, SQPL1g). Die Variante SQPmax-V3 mit regularisierten Hesse-
Matrizen zeigt ein ähnliches Verhalten wie die Newton-Verfahren mit regularisierter
Hesse-Matrix. Es sind zu viele Iterationen erforderlich, bis der lokale Konvergenzbereich
erreicht wird. Die Schrittweite 1 ist bei Regularisierung nicht immer die beste Wahl.
Außerdem sind bereits die Kosten für die Berechnung der Hesse-Matrizen hoch. Wie
erwartet schneidet die steilste Abstiegsvariante SQPmax-V1 schlecht ab. Im Falle der
Nichtregularität der Matrix Q des quadratischen Hilfsproblems im Optimalpunkt wie z.
B. bei Problem Nr. 110 zeigen sich bei den SQP-Verfahren in unserer Implementation
Effektivitätsverluste ähnlich zur Anwendung der MV. �
0 10 20 30 40 5010−10
10−5
100
105
Iterationen
max
(KK
T, e
rr(g
,h))
0 100 200 300Kosten
MV (0.359")SQPlok (0.109")SQPmax−V1 (0.609")SQPmax−V2 (0.047")SQPmax−V3 (0.234")SQPL1 (0.063")SQPL1g (0.063")
Abb. 4.15 Iterations- und Kostenanalyse für MV und SQP-Verfahren im Exp. 4.7.6

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 361
Experiment 4.7.7 (Maratos-Effekt)
SQP03.m: Wir betrachten das Problem Nr. 107 (siehe Powell (1986))
MIN{2(x21 + x
22 − 1)− x1 | x2
1 + x22 = 1, x1, x2 ∈ R}
und starten SQPL1 im Punkt x0 = (0.1322,−0.9713)T mit der Abbruchtoleranz 10−10.
Ab der siebten Iteration verhält sich das Verfahren wie ein lokales SQP-Verfahren, d.
h. bis zum Abbruch ist die Schrittweite ständig 1 (siehe Tab. 4.6). Wir bemerken, dass
unabhängig davon, wie nahe der Startpunkt x0 bei der Lösung x∗ = (1, 0)T auf der
Kreislinie gewählt wird, die ersten Schrittweiten stets kleiner als 1 sind. �
-------------------------------------------------------------------
it nf ng nh fiter t r err (g,h) KKT
-------------------------------------------------------------------
0 1 1 0 -2.1040e -001 0.00 3.99e +000 3.91e -002 3.89e +000
1 5 2 0 -3.1420e -001 0.25 1.94e +000 3.21e -002 9.56e -001
2 11 3 0 -4.2544e -001 0.06 1.45e +000 8.13e -002 9.48e -001
3 15 4 0 -5.4484e -001 0.25 1.74e +000 9.70e -002 6.13e -001
4 20 5 0 -6.2754e -001 0.13 1.62e +000 1.13e -001 4.67e -001
5 24 6 0 -7.1142e -001 0.25 1.60e +000 1.23e -001 3.68e -001
6 27 7 0 -7.7948e -001 0.50 1.55e +000 1.33e -001 1.81e -001
7 29 8 0 -9.2463e -001 1.00 1.52e +000 4.99e -002 1.93e -002
............... stets Schrittweite 1 ...........................
11 37 12 0 -1.0000e+000 1.00 1.50e +000 4.80e -014 6.33e -011
-------------------------------------------------------------------
Tab. 4.6 Iterationsverlauf von SQPL1 für Problem Nr. 107 im Exp. 4.7.7, Maratos-Effekt
Experiment 4.7.8 (Nichtlösbarkeit der quadratischen Hilfsprobleme)SQP04.m: Wir betrachten das nichtkonvexe Problem Nr. 115 (Hook und Schittkowski
(1981), Nr.15)
MIN{(x2 − x2
1)2 + (1− x1)
2∣∣ 1− x1x2 ≤ 0, −x1 − x2x2 ≤ 0, x1 ≤ 0.5
}und starten SQPL1 im Punkt x0 = (−1.0747, 1.9828). Nach einer Iteration stoppt dasVerfahren wegen Unlösbarkeit des quadratischen Hilfsproblems in einem nicht statio-
närem Punkt (siehe Abb. 4.16, 1. Trajektorie und siehe Tab. 4.7 oberer Teil). Wird in
x1 nun das erweiterte quadratische Hilfsproblem gelöst (SQPL1ex), dann konvergiert
das Verfahren gegen eine lokale Lösung, wobei diese Erweiterung nur einmal erforder-
lich ist (siehe Tab. 4.7, Info=0.1 bei it=2). Für gewisse Startpunkte in unmittelbarer
Nähe von x0 sind alle quadratischen Hilfsprobleme lösbar und das Verfahren SQPL1
konvergiert (siehe Abb. 4.16, 2. Trajektorie). Dieses Experiment zeigt, wie wichtig es ist,
bei Nichtlösbarkeit der quadratischen Hilfsprobleme durch geeignete Erweiterung dieser
Hilfsprobleme trotzdem Abstiegsrichtungen bestimmen zu können. �

362 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
-3 -2 -1 0 1 2 3-2
-1
0
1
2
3
4
x1
x2 0.
251
0.25
10.
5
0.5
0.5
1
1
1
1
1
2
2
2
2
2
4
4
44
4
4
8
8
8
8
88
8
8
16
16
16
16
16
16
16
32
32
32
32
32
32
64
64
64
64
SQPL1
SQPL1
SQPL1ex
Abb. 4.16 Iterationsverlauf von SQPL1 und SQPL1ex für Problem Nr. 115 im Exp. 4.7.8,Nichtlösbarkeit eines quadratischen Hilfsproblems für SQPL1
-------------------------------------------------------------------
it nf ng nh fiter Info t r err (g,h) kkt
-------------------------------------------------------------------
0 1 1 0 4.9897 e +000 0.0 0.00 3.09 e+000 3.13e +000 1.66 e+000
1 3 2 0 2.0547 e +000 0.0 1.00 2.04e -001 1.03e +000 2.27 e+000
---- QP in x1 nicht lösbar , erweitertes QP lösbar , es folgt x2 ----
2 8 3 0 1.7680 e +000 0.1 0.13 2.04e -001 1.06e +000 6.21 e+000
------------- ab x2 wieder alle QP lösbar -------------------------
3 10 4 0 1.1147 e +000 0.0 1.00 6.05e -001 7.66e -001 2.81 e+000
4 12 5 0 7.4548 e +000 0.0 1.00 2.46 e+001 0.00e +000 4.28 e+001
5 14 6 0 3.3125 e +000 0.0 1.00 3.41 e+001 0.00e +000 1.01 e+001
6 16 7 0 3.3125 e +000 1.0 1.00 1.85 e+001 0.00e +000 3.55e -015
-------------------------------------------------------------------
Tab. 4.7 Iterationsverlauf von SQPL1ex für Problem Nr. 115 im Exp. 4.7.8

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 363
Experiment 4.7.9 (Lokales Newton-Lagrange-Verfahren divergent)
SQP05.m: Wir betrachten das Problem Nr. 151
MIN
⎧⎪⎪⎨⎪⎪⎩(x1 − 1)2 +4∑k=1
(xk − xk+1)2
∣∣∣∣∣∣∣∣−3√2 + x1 + x2
2 + x33 = 2
−2√2 + x2 − x2
3 + x4 = −2x1x5 = 2
⎫⎪⎪⎬⎪⎪⎭und vergleichen das Lösungsverhalten von
1. SQP lokal (Newton-Lagrange-Verfahren),
2. SQP lokal (SQP-Umformulierung mit regularisierter Hesse-Matrix) und
3. gedämpftem SQP-Verfahren SQPL1,
wobei jeweils der Startpunkt x0 = (−1, 2, 1,−2,−2)T gewählt wird. Das Newton-
Lagrange-Verfahren ist divergent (siehe Abb. 4.17, links)). Das lokale SQP-Verfahren
mit regularisierter Hesse-Matrix erreicht ein lokales Minimum (fmin ≈ 27.87), ist aber
wegen der fortlaufenden Regularisierung nur linear konvergent (ohne Abbildung). Da-
gegen konvergiert SQPL1 in der Tendenz superlinear gegen das gleiche lokale Minimum
und hat nach 12 Iterationen die voreingestellte Abbruchtoleranz erreicht (siehe Abb. 4.17,
rechts)). Die anderen implementierten SQP-Verfahren mit Ausnahme von SQPmax-V1
verhalten sich ähnlich wie SQPL1. �
0 20 40 60 80 100100
105
1010
Ver
l. de
r Opt
. Bed
.
Iterationsindex
SQP lokal
0 2 4 6 8 10 1210−15
10−10
10−5
100
Ver
l. de
r Opt
. Bed
.
Iterationsindex
Max. Verletzung der Restrikt.Verletzung der KKT−Bed.
SQPL1
Abb. 4.17 Divergenz des Newton-Lagrange-Verfahrens und Konvergenz von SQPL1 für Problem151 im Exp. 4.7.9
Wir vergleichen abschließend Varianten des Innere-Punkt-Verfahrens aus der OTB von
Matlab mit den SQP-Verfahren. Das Innere-Punkt-Verfahren erlaubt mehrere Aus-
wahlmöglichkeiten bei den intern benutzten Trust-Region-Verfahren zur approximati-
ven Lösung des nichtlinearen (KKT )r-Gleichungssystems. Man kann dabei die exakten
Hesse-Matrizen (OTB-IP-TR-Newt), BFGS-Aufdatierungen (OTB-IP-TR-BFGS)
oder Limited Memory BFGS-Aufdatierungen (OTB-IP-TR-LM-BFGS) benutzen.

364 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Experiment 4.7.10 (Lineare Konvergenz bei Verletzung der (LICQ))
IP03.m: Wir betrachten das Problem Nr. 103
MIN
{1
4(x2
1)− x2
∣∣∣∣ − x21 − (x2 − 1)2 ≤ −1, (x1 + 1)2 + x2
2 ≤ 1, −x1 ≤ 1
},
bei dem im Lösungspunkt x∗ = (−1, 1)T zwar die (MFCQ) (und damit notwendiger-
weise die KKT-Bedingungen) aber nicht die (LICQ) erfüllt ist.
Zunächst verwenden wir das Verfahren OTB-IP-TR-Newt, welches ab der dritten Iterati-
on zulässige Punkte erzeugt, jedoch nur linear gegen die globale Minimalstelle konvergiert
und nach 40 Iterationen durch Unterschreiten der Schritttoleranz abbricht (siehe Abb.
4.18). Dabei gehen die Multiplikatoren der sich im Lösungspunkt berührenden Restriktio-
nen im Verlauf des Verfahrens gegen unendlich (y40 = (6.25×104, 0.1, 1.25×105)T ), was
die numerischen Probleme des Verfahrens erklärt. Auch die Verwendung von OTB-IP-
TR-BFGS und OTB-IP-TR-LM-BFGS ändert nichts an diesem prinzipiellen Verhalten.
Demgegenüber benötigen alle SQP-Verfahren (1) bis (8) für den Standardstartpunkt bis
zum Abbruch lediglich sieben Iterationen, konvergieren jedoch auf gleicher Trajektorie
nicht gegen den Lösungspunkt, sondern gegen den KKT-Punkt x = (0, 0)T , in dem
das notwendige Kriterium 2. Ordnung nicht erfüllt ist (siehe Abb. 4.19, links oben). In
Abhängigkeit von der Wahl anderer Startpunkte konvergieren die SQP-Verfahren auch
gegen die Lösung x∗ mit ähnlichen Problemen wie die Inneren-Punkt-Verfahren (siehe
Abb. 4.19, rechts oben). Die Konvergenz gegen x∗ ist nach unseren Tests für alle Varian-ten der Innere-Punkt-Verfahren aus der OTB unabhängig von der Wahl des Startpunktes
gewährleistet (siehe Abb. 4.19, unten). �
-2
0
2xi x1 x2
0 10 20 30 40
10-6
10-3
100
Ver
l. d.
Opt
. Bed
.
Iterationsindex
Max. Verletzung der Restrikt.Verletzung der KKT-Bed.
Ab Iteration 3 zul ssigToleranz
nur R-lineareKonvergenz Abbruch:
Schritt-Toleranz
-1.5 -1 -0.5 0 0.5 1
-1
-0.5
0
0.5
1
x1
x2
1
11
1
0.5
0.50.5
0.5
0
00
0
-0.5
-0.5-0.5
-0.5
-1
-1
-1
-0.749
-0.749-0.749
-0.749
-0.749-0.749
OTB-IP-TR-Newt
globales MinimumLICQ verletzt
KKT-Punktkein Minimum
Abb. 4.18 Lineare Konvergenz von OTB-IP-TR-Newt für Problem Nr. 103 im Exp. 4.7.10,(LICQ) im Optimalpunkt nicht erfüllt

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 365
-1.5 -1 -0.5 0 0.5 1
-1
-0.5
0
0.5
1
x1
x2
1
11
1
0.5
0.50.5
0.5
0
00
0
-0.5
-0.5-0.5
-0.5
-1
-1
-1
SQPmax-V1SQPmax-V2SQPmax-V3SQPL1SQPL1gOTB-ASmaxOTB-sqp
-1.5 -1 -0.5 0 0.5 1
-1
-0.5
0
0.5
1
x1
x2
1
11
1
0.5
0.50.5
0.5
0
00
0
-0.5
-0.5-0.5
-0.5
-1
-1
-1
S1S2
S3
S4
S5
S6S7
Multistart aller SQP-Verfahren
-1.5 -1 -0.5 0 0.5 1
-1
-0.5
0
0.5
1
x1
x2
1
11
1
0.5
0.50.5
0.5
0
00
0
-0.5
-0.5-0.5
-0.5
-1
-1
-1
Multistart von OTB-IP-TR-LM-BFGS
S1
S2
-1.5 -1 -0.5 0 0.5 1
-1
-0.5
0
0.5
1
x1
x2
1
1 1
1
0.5
0.50.5
0.5
0
0 0
0
-0.5
-0.5-0.5
-1
-1
-1
-0.748-0.748
-0.748
-0.748-0.748
-0.748
OTB-IP-TR-LM-BFGS
KKT ohne Bed. 2. Ord.als Startpunkt
Abb. 4.19 Iterationsverlauf von SQP- und Inneren-Punkt-Verfahren für Problem Nr. 103 imExp. 4.7.10, z. T. Konvergenz zum nichtoptimalen KKT-Punkt
Experiment 4.7.11 (Superlineare Konvergenz bei erfüllter (LICQ))
IP05.m: Wir betrachten wieder das nichtkonvexe Problem Nr. 115 (siehe Exp. 4.7.8).
Bei diesem Problem ist in beiden lokalen Lösungspunkten x∗1 = (0.5, 2)T ,x∗2 = (−1,−1)Tdie (LICQ) erfüllt.
Alle Varianten des Innere-Punkt-Verfahrens haben nach wenigen Iterationen zulässige
Iterationspunkte, aber die Verletzung der KKT-Bedingungen geht nur linear gegen Null
mit einem kleinen Konvergenzfaktor von z. B. C ≈ 0.05 beim OTB-IP-TR-Newt. (siehe
Abb. 4.20) bzw. OTB-IP-TR-LM-BFGS (siehe Tab. 4.8). Eine bessere Konvergenz kann
nicht erzielt werden, da der Parameter r, der die Verletzung der Schlupfbedingungen
darstellt, einerseits laut Algorithmus nur linear verkleinert wird und andererseits unter
EdOptLab in der KKT-Abbruchbedingung direkt ausgewertet wird.
Die SQP-Verfahren konvergieren dagegen superlinear bis quadratisch in Bezug auf die

366 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Verletzung der Nebenbedingungen sowie der KKT-Bedingungen (s. Tab. 4.9 bis Tab.
4.12) und sind damit wesentlich schneller als Innere-Punkt-Verfahren. Sie haben dafür
aber nur im Ausnahmefall zulässige Iterierte. �
0 1 2 3 4 5 6 7 8 9 10 11 12
10-9
10-6
10-3
100
10-1
103
lineare Konvergenz, C = 0.05
Max. Verletzung der Restrikt.Verletzung der Schlupf-Bed.
g(xk) < 0
Abb. 4.20 Iterationsanalyse von OTB-IP-TR-Newt für Problem Nr. 115 im Exp. 4.7.11
--------------------------------------------------------------
it nf ng nh fiter +r- r-TR err (g,h) KKT
--------------------------------------------------------------
0 1 1 0 1.000 e+000 0 1.41 e+000 1.00 e+000 1.92e +000
1 3 3 0 9.706 e -001 -1 1.02 e+000 1.00 e+000 1.89e +000
2 5 5 0 9.459 e -001 -1 1.01 e+000 1.00 e+000 1.87e +000
3 7 7 0 8.681 e -001 1 1.25 e+000 9.95e -001 1.80e +000
4 8 8 0 3.823 e -001 1 6.58 e+000 6.97e -001 1.65e +000
5 10 10 0 3.915 e -001 -1 9.97e -001 6.89e -001 1.67e +000
------------ ab hier zulässig --------------------------------
6 11 11 0 3.361 e+000 1 5.00 e+000 0.00 e+000 4.45e +000
7 12 12 0 3.390 e+000 -1 2.92 e+000 0.00 e+000 6.44e -001
8 13 13 0 3.512 e+000 1 5.78 e+000 0.00 e+000 2.13e -002
9 14 14 0 3.316 e+000 -1 2.75 e+000 0.00 e+000 2.24e -002
-- lok . Minimum fast erreicht , Verbesserung dauert zu lange --
10 15 15 0 3.313 e+000 -1 2.60 e+000 0.00 e+000 2.42e -003
11 16 16 0 3.313 e+000 -1 3.80e -002 0.00 e+000 4.44e -005
12 17 17 0 3.313 e+000 1 2.81 e+000 0.00 e+000 8.64e -004
13 18 18 0 3.313 e+000 -1 1.70 e+000 0.00 e+000 8.89e -008
14 19 19 0 3.313 e+000 0 2.80 e+000 0.00 e+000 2.15e -009
--------------------------------------------------------------
Tab. 4.8 Iterationsverlauf von OTB-IP-TR-LM-BFGS für Problem Nr. 115 im Exp. 4.7.11

4.7 Numerische Experimente zu Verfahren der restringierten Optimierung 367
-------------------------------------------------------------------
it nf ng nh fiter t err (g,h) KKT
-------------------------------------------------------------------
0 1 1 0 5.0336000 e +000 1.00 e +000 2.20 e +000 7.51e +000
1 3 2 0 3.6110556 e -001 1.00 e +000 7.08e -001 3.60e +000
2 6 3 0 2.0056184 e +000 7.00e -001 2.13e -001 2.11e +000
-------------- zulässig bis auf MACHEPS ---------------------------
3 8 4 0 3.3125000 e +000 1.00 e +000 1.11e -016 1.64e +000
------ Genauigkeitssprung um 16 Stellen ---------------------------
4 9 4 0 3.3125000 e +000 7.00e -001 1.11e -016 1.11e -016
-------------------------------------------------------------------
Tab. 4.9 Iterationsverlauf von OTB-sqp für Problem Nr. 115 im Exp. 4.7.11
-------------------------------------------------------------------
it nf ng nh fiter step r err (g,h) KKT
-------------------------------------------------------------------
0 1 1 0 5.0336 e+000 0.00 6.57e +000 2.20 e +000 6.51e +000
1 3 2 0 3.6111 e -001 1.00 6.97e +000 7.08e -001 3.60e +000
--------- ab hier zulässig ----------------------------------------
2 5 3 0 3.3125 e+000 1.00 7.96e +000 0.00 e +000 8.63e +000
3 7 4 0 3.3125 e+000 1.00 2.55e +001 0.00 e +000 3.55e -015
-------------------------------------------------------------------
Tab. 4.10 Iterationsverlauf von SQPmax-V2 für Problem Nr. 115 im Exp. 4.7.11
-------------------------------------------------------------------
it nf ng nh fiter step r err (g,h) KKT
-------------------------------------------------------------------
0 1 1 0 5.0336 e+000 0.00 6.57e +000 2.20 e +000 6.51e +000
1 3 2 0 3.6111 e -001 1.00 6.97e +000 7.08e -001 3.60e +000
--------- ab hier zulässig ----------------------------------------
2 5 3 0 3.3125 e+000 1.00 7.96e +000 0.00 e +000 8.63e +000
3 7 4 0 3.3125 e+000 1.00 2.55e +001 0.00 e +000 3.55e -015
-------------------------------------------------------------------
Tab. 4.11 Iterationsverlauf von SQPmax-V2 für Problem Nr. 115 im Exp. 4.7.11
-------------------------------------------------------------------
it nf ng nh fiter Info step r err (g,h) KKT
-------------------------------------------------------------------
0 1 1 0 1.0000 e+000 0.0 0.00 6.32e +001 1.00 e +000 2.00e +000
1 3 2 0 3.1250 e -001 0.1 1.00 6.32e +001 1.00 e +000 6.32e +001
------------------ ab hier zulässig ------------------------------
2 5 3 0 3.3125 e+000 0.0 1.00 5.51e +003 0.00 e +000 1.09e +004
---------- Genauigkeitssprung um 19 Stellen !!!-------------------
3 7 4 0 3.3125 e+000 1.0 1.00 2.76e +003 0.00 e +000 3.55e -015
-------------------------------------------------------------------
Tab. 4.12 Iterationsverlauf von SQPL1ex für Problem Nr. 115 im Exp. 4.7.11

368 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
4.8 Übungsaufgaben zu Kapitel 4
Aufgabe 4.1
Beweisen Sie Lemma 4.3.
Aufgabe 4.2
Zeigen Sie, dass der zur globalen Lösung zugehörige KKT-Punkt des Optimierungspro-
blems
MIN{f(x) = −e−x
2∣∣∣ g(x) = 1− x ≤ 0
}kein Sattelpunkt der entsprechenden Lagrange-Funktion ist.
Aufgabe 4.3
Zeigen Sie:
Für ein Optimierungsproblem der Form(P≤=
)mit zugehöriger Lagrange-Funktion
L : Rn ×Rm ×Rp → R ist
dom q :=
{(u, v) ∈ Rm+ ×Rp
∣∣∣∣ infx∈RnL(x,u, v) > −∞
}eine konvexe Menge und die duale Zielfunktion
q : dom q ⊂ Rm+ ×Rp → R mit q(u, v) := infx∈RnL(x,u, v)
eine konkave Funktion über dom q.
Aufgabe 4.4
Zeigen Sie:
Sind alle Koordinatenfunktionen gi der Funktion G : Rn → Rm konvex über Rn, so istdie Menge Λ := {b ∈ Rm | ∃x ∈ Rn mit G(x) ≤ b} eine konvexe Menge.
Aufgabe 4.5
Gegeben sei das primale Problem
(P ) MIN {f(x) | g(x) = −x+ 2 ≤ 0} mit f(x) ={x , falls x < 0
x2 − 4x , falls 0 ≤ x.
Bestimmen Sie die globale Lösung x von (P ), den zugehörigen optimalen (primalen) Ziel-
funktionswert f(x), die Sensitivitätsfunktion λ von (P ), das duale Problem (D) zu (P ),
die globale Lösung von (D) sowie den zugehörigen optimalen dualen Zielfunktionswert.
Aufgabe 4.6
Gegeben sei das Optimierungsproblem
(P ) MIN{f(x) := x2 + 1
∣∣h(x) = x− 2 = 0}
mit der globalen Minimalstelle x = 2.

4.8 Übungsaufgaben zu Kapitel 4 369
(a) Bestimmen Sie für alle r > 0 die (eindeutig bestimmte) globale Minimalstelle x∗
der Funktion
Sr : R → R mit Sr(x) := f(x) + r(h(x))2 = x2 + 1 + r(x− 2)2 .
über R.
(b) Bestimmen Sie das minimale r > 0, sodass x für alle r ≥ r auch die (eindeutigbestimmte) globale Minimalstelle der Funktion
S1r : R → R mit S1
r (x) := f(x) + r‖h(x)‖1 = x2 + 1 + r|x− 2|
über R ist.
Aufgabe 4.7
Gegeben sei das Optimierungsproblems aus Beispiel 2.16
MIN
{f(x) =
1
2(x1 + 1)2 +
1
2x2
2
∣∣∣∣∣ g1(x1, x2) = −x1 + (x2 + 1)2 − 1 ≤ 0
g2(x1, x2) = −x1 + (x2 − 1)2 − 1 ≤ 0
}
mit der globalen Lösung x = (0, 0)T und den eindeutig bestimmten zugehörigen
Lagrange-Multiplikatoren u =(
12 ,
12
)T. Zeigen Sie, dass x für alle r mit
0 < r < r := max {‖u‖∞} =12
keine globale Minimalstelle der Funktion
S1r : R2 → R mit S1
r (x) := f(x) + r(∥∥∥[(g1(x1, x2), g2(x1, x2))
T]+
∥∥∥1
)über R2 ist.
Aufgabe 4.8
Es sei G = (g1, · · · , gm)T : Rn → Rm mit gi : Rn → R konvex über Rn für alle
i ∈ {1, · · · ,m}. Zeigen Sie, dass die Funktion Ψq : Rn → R mit Ψq(x) =∥∥[G(x)]+∥∥
q
und 1 ≤ q ≤ ∞ ebenfalls konvex über Rn ist.
Aufgabe 4.9
Es seien G ∈ C2(Rn,Rm) und r > 0. Zeigen Sie, dass für die Funktion
Γr : Rn ×Rm ×Rm → R mit Γr(x,u, s) := (G(x) + [s]2)Tu+ r‖G(x) + [s]2 ‖2
gilt:
mins∈Rm
Γr(x,u, s) =m∑i=1
(ui(gi(x) + z
∗i ) + r (gi(x) + z
∗i )
2)
mit z∗i :=[−(ui2r + gi(x)
)]+.

370 4 Lösungsverfahren für Optimierungsprobleme mit Nebenbedingungen
Aufgabe 4.10
Beweisen Sie Lemma 4.37.
Aufgabe 4.11
Es seien f ∈ C2(Rn,R), G = (g1, · · · , gm)T ∈ C2(Rn,Rm), gi konvex über Rn für allei ∈ {1, · · · ,m} sowie H = (h1, · · · , hp)T mit hj : Rn → R und hj affin-linear für alle
j ∈ {1, · · · , p}. Zeigen Sie:Besitzt das zugehörige Optimierungsproblems
(P≤=
)einen nichtleeren zulässigen Be-
reich, dann besitzt für alle (xk,uk, vk) ∈ Rn ×Rm ×Rp auch das Optimierungsproblem(SQP≤=
)keinen nichtleeren zulässigen Bereich.
Aufgabe 4.12
Es seien G ∈ C0(Rn,Rm), M := {x ∈ Rn| G(x) ≤ 0} und M0 := {x ∈ Rn| G(x) < 0}.Zeigen Sie:
Sind alle Koordinatenfunktionen gi mit i ∈ {1, · · · ,m} konvex über M und ist M0 �= ∅,dann gilt M0 = intM .
Aufgabe 4.13
Gegeben seien die Funktion g : R → R mit
g(x) =
⎧⎪⎪⎨⎪⎪⎩x2 − 1 , falls x ≤ 1 ,
0 , falls 1 < x ≤ 2 .
x− 2 , falls 2 < x .
sowie die Mengen M := {x ∈ R| g(x) ≤ 0} und M0 := {x ∈ R| g(x) < 0}. Zeigen SieclM0 �M und M0 � intM .
Aufgabe 4.14
Gegeben sei das Optimierungsproblem
(P≤
)MIN
{f(x) = x1 + x2
∣∣∣∣∣ g1(x1, x2) = (x1 − 1)2 − x2 ≤ 0
g2(x1, x2) = −x1 ≤ 0
}.
(a) Bestimmen Sie die Lösung x des Optimierungsproblems.
(b) Zeigen Sie, dass limr↓0x(r) = x für die Lösungen x(r) der zugehörigen (logarithmi-
schen) Barriereprobleme gilt.















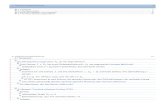

![t q]= dt L q,q ,t - physik.tu-freiberg.de · Bewegungsgleichung 4./5. Lösung durch Integration ... ungedämpfter harmonischer Oszillator (Federkraftschwinger) Nebenbedingungen y](https://static.fdokument.com/doc/165x107/5b9f33a609d3f204248cdc8e/t-q-dt-l-qq-t-bewegungsgleichung-45-loesung-durch-integration-ungedaempfter.jpg)
